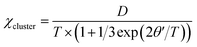Open Access Article
Open Access ArticleMolecule-like cluster magnetism and cationic order in the new hexagonal perovskite Ba4Sn1.1Mn2.9O12†
Junkun Wua,
Xiaohui Yana,
Wenbin Guoa,
Xiaoming Wangb,
Congling Yin *a and
Xiaojun Kuang
*a and
Xiaojun Kuang *ac
*ac
aMOE Key Laboratory of New Processing Technology for Nonferrous Metal and Materials, Guangxi Key Laboratory of Optic and Electronic Materials and Devices, College of Materials Science and Engineering, Guilin University of Technology, Guilin 541004, P. R. China. E-mail: congling.yin@glut.edu.cn
bKey Lab Macromolecular Science of Shaanxi Province, College of Chemistry and Chemical Engineering, Shaanxi Normal University, Xian 710062, P. R. China
cCollege of Chemistry and Bioengineering, Guilin University of Technology, Guilin 541004, P. R. China
First published on 17th December 2021
Abstract
The new hexagonal perovskite phase of composition Ba4Sn1.1Mn2.9O12 has been synthesized by solid-state reactions at 1673 K. The crystal structure has been investigated using X-ray and neutron diffraction. The hexagonal perovskite structure has an ordered arrangement of Sn and Mn ions on the corner-sharing octahedral centers and the face-sharing octahedral centers respectively. Short Mn–Mn distances have been evidenced in the face-sharing trimer of MnO6 octahedra. The magnetic susceptibility shows magnetic cluster behavior, with cluster formation temperature ∼220 K. Antiferromagnetic order has been observed at TN ∼ 6 K. Ba4Sn1.1Mn2.9O12 is a semiconductor with a transport activation energy of 0.61 eV.
1 Introduction
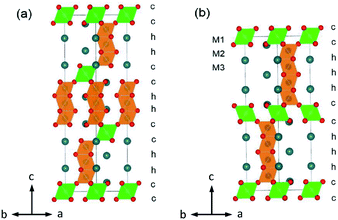
Manganese oxides have attracted enormous attention during the last decades mainly due to their technological applications as heterogeneous catalysts,1 Li batteries,2,3 SOFC electrode materials,4 and magnetic5 and also CMR materials.6 This has motivated the investigation of the hexagonal perovskite BaMnO3−δ system, which shows a diversity of crystal structures and magnetic properties.7–11 A series of BaMnO3−δ polytypes have been found, for example, 2H → 15R → 8H → 6H → 10H → 4H, as the oxygen vacancy δ increases.7,10 Additional polymorphs (i.e. 9R-Ba0.875Sr0.125MnO3) are generated upon Sr substitution on the Ba site.10 Further perovskite polytypes may be produced when Mn is replaced by other cations.Many Mn-substituted BaMxMn1−xO3 systems have been investigated, for instance, with M = Ca,12,13 Ti,14,15 In,16,17 Sn,18 Sb,19 Fe,20 Ru,21,22 Ir,23 and rare earth Ln.24,25 This led to the uncovering of a range of M-cation (partially) ordered 12R perovskites Ba4Ti2Mn2O12,14 Ba4InMn3O11.5,16 Ba4REMn3O12 (RE = Ce and Pr),24 Ba4YMn3O11.5,26 and Ba4NbMn3O12.27 The Ba4MMn3O12 12R perovskite consists of close-packed BaO3 layers in a (cchh)3 sequence. The larger-sized substituted M ions are hosted in the corner-sharing octahedral center M1, and the Mn ions occupy the face-sharing octahedral centers M2 and M3, as shown in Fig. 1a. Partial disorder of M and Mn elements occurs on the M2 site when the M ion has a similar size with 6-coordinated Mn4+ (0.53 Å), i.e. Ti4+ (0.605 Å, CN = 6).28
The BaMnO3−δ polymorphs show the long-range antiferromagnetic (AFM) order of all the Mn spins, with TN = 220–270 K.9,10 However, the magnetic order is suppressed in the 12R perovskites with trimers of face-sharing MnO6 octahedra on low-content nonmagnetic doping. No magnetic order is observed for Ba4InMn3O11.5 (ref. 16) and Ba4Ti2Mn2O12,14 whilst Ba4YMn3O11.5 (ref. 26) and Ba4CeMn3O12 (ref. 29) undergoes an AFM transition at TN = 4–6 K. The Ba4NbMn3O12 sample experiences a ferrimagnetic transition at 42 K and an additional magnetic abnormality at ∼6 K.27 The latter one should be AFM transition, as suggested by first-principle calculations.30 Furthermore, Ba4NbMn3O12 and Ba4Ti2Mn2O12 show cluster magnetism, with linear Mn3 (and Mn2) magnetic clusters arranged in triangular plains, leading to magnetic frustrations.30,31 Therefore, the 12R perovskite materials are potential quantum materials, such as quantum spin liquid.32,33 The exploration of new 12R perovskite BaMxMn1−xO3 is of great interest.
The BaSn1−xMnxO3 system contains one cation-ordered perovskite 10H Ba5Sn1.1Mn3.9O15.18 The Ba5MMn4O15 10H polytype has close-packed BaO3 layers in (cchhh)2 sequences, and features tetramers of face-sharing MnO6 octahedra, alternating with MO6 octahedra (Fig. 1b). Considering the close relationship between the 10H and 12R perovskites, we wonder whether the 12R polymorph BaSn1−xMnxO3 can exit. If the 12R BaSn1−xMnxO3 is stabilized, it would be a good material with magnetic clusters and frustration. Motived by such ideas, we investigate a series of BaSn1−xMnxO3. Herein we report the synthesis, crystal structure, and physical properties of 12R Ba4Sn1.1Mn2.9O12 perovskite.
2 Experimental
2.1 Synthesis
The polycrystalline Ba4Sn1+xMn3−xO12 (−0.1 < x < 0.2) were prepared via high-temperature solid-state reaction, using BaCO3 (99.5%, Alfa Aesar), SnO2 (99%, Alfa Aesar), and MnO2 (99.5%, Alfa Aesar) reagents as raw materials. These starting materials were carefully weighed according to the correct stoichiometries, and mixed thoroughly with alcohol in an agate mortar and pestle, and heated in an alumina crucible at 1273 K for 10 h to decompose the carbonate. Then the material was reground, pressed into pellets (20 tons per cm2), and placed on the platinum foil, and sintered at 1673 K for a total of 24 h with heating and cooling rates of 5 K min−1, leading to dense pellet ceramic samples. At several intervening steps, the material was re-ground and re-pressed, and powder X-ray diffraction (XRD) was performed at each step to track the reaction to completion. The densities of the final ceramic pellets were calculated using their geometric sizes (diameters and thicknesses) and the masses.2.2 Characterization
The phase purity of the samples was characterized by XRD using a Panalytical X'pert Powder diffractometer with Cu Kα radiation operated at 40 kV and 40 mA. Data were collected over the 2θ range 5–120° for Rietveld analysis carried out using the Topas Academic software.34 Bond valence sums (BVS) were calculated by Brown and Altermatt's method.35Time-of-flight (TOF) neutron diffraction data were collected from ∼5 g fine powder samples of Ba4Sn1.1Mn2.9O12 using the general-purpose powder diffractometer (GPPD) at the China Spallation Neutron Source (CSNS). Selected area electron diffraction (SAED) patterns were recorded using a JEOL JEM-2100F transmission electron microscopy (TEM) with a point resolution of 1.9 Å and operated at 200 kV.
Magnetic susceptibility data were acquired using a Quantum Design MPMS-3 superconducting quantum interference device (SQUID) magnetometer. DC magnetic susceptibilities were recorded in a 1000 Oe applied field while warming the sample from 2 to 300 K, following both zero-field cooling (ZFC) and field cooling (FC). AC magnetic susceptibilities from 2 K to 10 K were also measured at step mode at different frequencies of 100 Hz, 250 Hz, 500 Hz, and 1000 Hz.
AC impedance spectroscopy (IS) measurements were carried out from room temperature (RT) to 773 K using a Solartron 1260 frequency response analyzer over the 10−1–107 Hz frequency range. Before the IS measurements, the silver paste was coated on the opposite faces of the pellets and fired at 823 K for 30 min to remove the organic component and form electrodes. The impedance data analysis and equivalent circuit fitting were carried out with Zview software.
Inductively coupled plasma optical emission spectroscopy (ICP-OES) was performed on the Ba4Sn1.1Mn2.9O12 sample to determine the cationic contents using a PerkinElmer Optima 8000 inductively coupled plasma optical emission spectrometer. The scanning electron microscopy (SEM) imaging and X-ray energy dispersive spectroscopy (EDS) elemental analysis were performed using a GeminiSEM 300 (ZEISS, Germany) scanning electron microscope equipped with an Ultim Max (Oxford, U.K.) EDS spectrometer.
3 Results and discussions
3.1 Phase formation
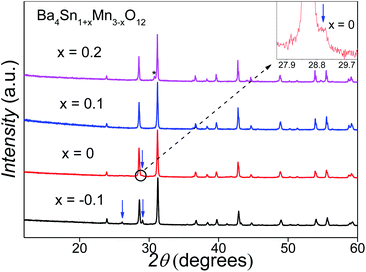
The initial Ba4SnMn3O12 samples consisted of mixed 12R and 10H perovskite phases (Fig. 2). The Sn doping amount was varied to eliminate the 10H phase, and the XRD patterns of the Ba4Sn1+xMn3−xO12 are shown in Fig. 2. The amount of the 10H phase is reduced at an increase of x from −0.1 to 0.1 and a single-phase 12R product is obtained at the composition of Ba4Sn1.1Mn2.9O12. Further increasing the Sn substitution rate leads to a secondary Sn-rich cubic perovskite phase, i.e. BaSnO3, as marked with an asterisk. The ICP analysis on the Ba4Sn1.1Mn2.9O12 sample shows the Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn
Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratio of 4.03
Mn ratio of 4.03![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.07
1.07![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.84, which is essentially identical to the initial cationic ratio. This observation confirms the chemical composition of Ba4Sn1.1Mn2.9O12 for the 12R perovskite phase.
2.84, which is essentially identical to the initial cationic ratio. This observation confirms the chemical composition of Ba4Sn1.1Mn2.9O12 for the 12R perovskite phase.
The XRD pattern of Ba4Sn1.1Mn2.9O12 is similar to that of Ba4NbMn3O12 (ref. 27) and can be indexed using a rhombohedral hexagonal unit cell with lattice parameters a = 5.7289(4) Å, and c = 28.163(3) Å. The selected area electron diffraction (SAED) pattern along [100] zone axis is shown in Fig. 3. No superstructure reflections are seen, and all the observed reflections agree with the indexing results. The systematic absence of the reflections h![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) 0l: h – l ≠ 3n and 000l: l ≠ 3n is consistent with the space group R
0l: h – l ≠ 3n and 000l: l ≠ 3n is consistent with the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.
m.
 | ||
| Fig. 3 The SAED patterns collected along [100] direction for Ba4Sn1.1Mn2.9O12. The indexations were performed using the hexagonal cell (a ∼ 5.72 Å and c ∼ 28.2 Å). | ||
3.2 Crystal structure
Due to their weak X-ray scattering ability, the light oxygen atoms are not well located with X-ray diffraction in the presence of heavy elements such as barium. Neutron diffraction (ND) is more sensitive to oxygen because the neutron scattering length of oxygen (5.083 fm) is comparable to that of Ba (5.07 fm).36 Therefore, to find the oxygen position and possible vacancies, neutron diffraction data were collected on the Ba4Sn1.1Mn2.9O12 sample. The Rietveld refinements against the XRD and ND data simultaneously were performed, using the 12R Ba4NbMn3O12 structural model (Fig. 1a). In the first step, the occupancies of Sn and Mn at M1, M2, and M3 sites were refined with the total occupancies on each site subject to unity. A negative value of Sn on the M3 site was found, excluding the presence of Sn at the M3 site. In the following refinement, the occupancies of Sn and Mn were refined only at M1 and M2 sites, with the ratio of Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
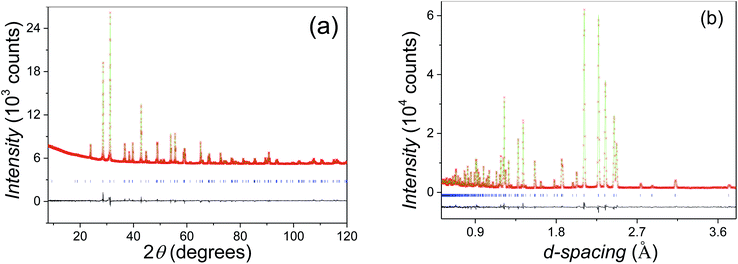
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn constrained by the initial stoichiometry. In the second step, the oxygen occupancies were refined, and no vacancies were found at both O1 and O2 sites within the refinement error. Therefore, the oxygen occupancies at both sites were set as unity. The final refinement gave a good fit (Fig. 4a and b), with overall Rwp and χ2 parameters of 4.99% and 1.20 respectively. The refined structural parameters and selected bond distances and angles are listed in Tables 1 and 2, respectively. The Beq parameters for atoms of the same type on the different sites show a small difference within 20%. The large discrepancy of Beqs between the M1 and M2 sites keeps with their different dominated elements, i.e. Sn and Mn respectively.
Mn constrained by the initial stoichiometry. In the second step, the oxygen occupancies were refined, and no vacancies were found at both O1 and O2 sites within the refinement error. Therefore, the oxygen occupancies at both sites were set as unity. The final refinement gave a good fit (Fig. 4a and b), with overall Rwp and χ2 parameters of 4.99% and 1.20 respectively. The refined structural parameters and selected bond distances and angles are listed in Tables 1 and 2, respectively. The Beq parameters for atoms of the same type on the different sites show a small difference within 20%. The large discrepancy of Beqs between the M1 and M2 sites keeps with their different dominated elements, i.e. Sn and Mn respectively.
| Atom | Site | x, y, z | Occupancy | Beq | BVS |
|---|---|---|---|---|---|
a a = 5.72904(3) Å, and c = 28.1637(3) Å space group: R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. m. |
|||||
| Ba1 | 6c | 2/3, 1/3, 0.04672(5) | 1 | 0.94(7) | 2.37 |
| Ba2 | 6c | 0, 0, 0.12840(4) | 1 | 0.88(7) | 2.23 |
| (Sn/Mn)M1 | 3a | 0, 0, 0 | 0.881(3)/0.119(3) | 0.83(3) | 4.24/2.81 |
| (Mn/Sn)M2 | 6c | 1/3, 2/3, 0.07695(8) | 0.891(1)/0.109(1) | 1.46(5) | 3.84/5.43 |
| MnM3 | 3b | 1/3, 2/3, 1/6 | 1 | 1.19(6) | 4.10 |
| O1 | 18h | 0.48062(9), 0.51938(9), 0.12380(4) | 1 | 1.07(6) | |
| O2 | 18h | 0.49856(11), 0.50144(11), 0.29189(4) | 1 | 1.20(6) | |
| Bond length (Å) | Bond length (Å) | Bond angle (degree) |
|---|---|---|
| (Sn/Mn)M1–O2 (×6) 2.0334 (10) | MnM3–O1 (×6) 1.8933 (9) | (Sn/Mn)M1–O2–MnM2 176.400 (2) |
| (Mn/Sn)M2–O1 (×3) 1.966 (3) | MnM2–MnM3 2.523 (5) | MnM2–O1–MnM3 81.626(3) |
| (Mn/Sn)M2–O2 (×3) 1.918 (3) |
In the crystal structure of 12R Ba4Sn1.1Mn2.9O12, the M1 site is dominated by the Sn atom (occupancy ∼ 88.1%), and the M2 site is dominated by the Mn atom (occupancy ∼ 89.1%). The BVS values of Mn atom at M1 and M2 sites (2.81 and 3.84 respectively) are smaller than 4, whilst that of Sn atom shows larger values than 4 (4.24 at M1 site and 5.43 at M2 site). This discrepancy arises from the mixed Sn and Mn occupancy because the average bond lengths are used in BVS calculations. But both Mn and Sn atoms most likely show the oxidation states of +4 on local M1 and M2 sites, although trace amounts of Mn3+ at M1 site and compensating oxygen vacancies (within the refinement errors) cannot be excluded. Similar phenomena have been observed in the 10H Ba5Sn1.1Mn3.9O15 polymorphs.18
It should be noted about the distortion of outer MnO6 octahedra in the trimers. The Mn at the M2 site shifts toward the c-BaO3 layers, forming three shorter MnM2–O2 bonds (∼1.91 Å) and three longer MnM2–O1 bonds (∼1.96 Å). The inner MnM3O6 octahedron is undistorted and constrained by its local symmetry of D3d on the M3 site. Due to the distortion, the Mn–Mn distance inside the trimers (∼2.52 Å) is larger than that (2.407 Å) between undistorted MnO6 octahedrons in 2H BaMnO3.37 This suggests that octahedron distortion may help to stabilize the formation of MnO6 octahedral trimers. This short Mn–Mn distance is comparable with that in elemental α-Mn38 and may suggest a degree of d-orbital overlap between neighboring Mn ions within each trimer forming Mn3 (and minor Mn2) magnetic clusters.
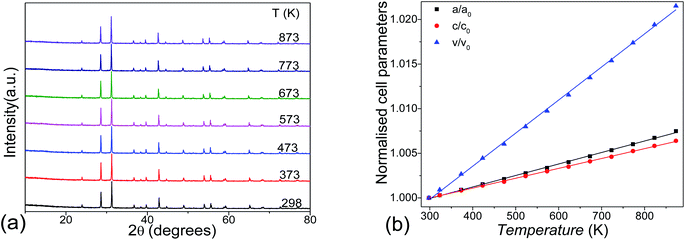
Thermal stability was investigated by the temperature varied XRD, as shown in Fig. 5a. No phase transition exists in the title compound until 873 K. The lattice parameters increase linearly as the temperature increases, showing anisotropic thermal expansions of αa = 12.5 × 10−6 K−1 and αc = 10.6 × 10−6 K−1. This leads to an overall linear volume expansion of αV = 35.9 × 10−6 K−1 at 300–873 K temperature range (Fig. 5b).
3.3 Magnetic properties
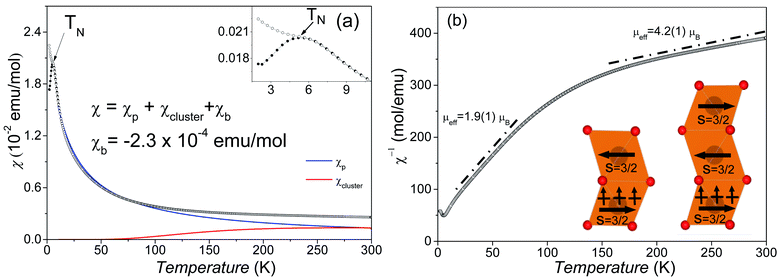
The temperature-dependent DC magnetic susceptibilities per Mn ions are shown in Fig. 6a. The susceptibilities change little at 150–300 K and start to increase steeply as the temperature goes down. The maximum value of ZFC susceptibility is observed at about 6.0 K, below which ZFC and FC data are divergent. It suggests an antiferromagnetic (AFM) phase transition around TN = 6 K.Surprisingly, the magnetic susceptibilities above 6 K do not obey the Curie–Weiss law, as shown in Fig. 6b. The attempt fit on 150–300 K yields an μeff = 4.2(1) μB per Mn4+, reasonably close to the spin-only value of Mn4+ 3.9 μB, but an enormously large θCW = −565 K compared with TN. The Curie–Weiss fit on 25–80 K yields a much smaller μeff = 1.9(1) μB per Mn4+ and a small θCW = −22 K. This reduced magnetic moment at intermediate temperatures indicates the formation of AFM magnetic clusters. Considering the crystal structure, the magnetic clusters are predominantly the Mn3 (Fig. 6b inset) inside the trimers of face-sharing MnO6 octahedra. The minor Mn2 clusters (Fig. 6b inset) are also present due to diamagnetic Sn4+ replacing ∼10.9% Mn4+ on the M2 site. The Mn3 (and Mn2) magnetic linear clusters are observed in the 12R Ba4NbMn3O12 (ref. 27 and 30) and Ba4Ti2Mn2O12 (ref. 31) perovskite. The susceptibility of these magnetic clusters, χcluster, can be estimated using an analog expression of a spin S = ½ dimmer.39
Good fits were obtained (Fig. 6a), leading to C = 0.42(1) K emu Oe−1, θ = −17.1(1) K, D = 0.99(1) K emu Oe−1, and θ′ = 218.7(1) K. The negative Weiss constant indicates antiferromagnetic interactions between the Mn spins. The θ = −17.1(1) K is comparable with the TN as expected. The cluster formation temperature θ′ depends on the magnetic exchange interaction inside the MnO6 trimers and is reasonably close to the exchange constant (Ja/kB = 200 K) in the dimer and trimer of MnO6 octahedra.30 The overall magnetic moment 3.05(1) μB mol−1 Mn4+, as calculated using μeff = (8C + 6D)1/2, is lower than its spin-only value (3.87 μB). This small difference can be acceptable given the presence of both Mn2 and Mn3 clusters and the roughness of the cluster model. If we ignore the contribution of minor Mn2 clusters, then the effective magnetic moments μeff per Mn3 linear cluster 3.17(1) μB, as calculated from (24C)1/2, is essentially identical with the calculated value of 3.05 μB mol−1 Mn4+. This observation seems coincidental and comes from the AFM nature of the Mn3 linear clusters. Similarly, the Ba4NbMn3O12 has one Mn3+ ion and two Mn4+ ions in each trimer of MnO6 octahedra, thus the μeff per Mn3 cluster is equal to the μeff of Mn3+.27,30 The minor Mn2 clusters are expected to have a ground state of μeff = 0 μB. The residual Mn spins of dominant Mn3 clusters order at temperatures below TN = 6 K via antiferromagnetic Mn4+–O–(Sn4+/Mn4+)M1–O–Mn4+ exchange interactions. Similar AFM order below 10 K has been observed for the 12R Ba4MMn3O12−δ (M = Y, Nb, and Ce) with Mn3 linear clusters.25–27
In addition, the AC magnetic susceptibility χ′ shows a frequency-independent maximum at about 6 K, as shown in Fig. 7a. This observation rules out a spin glass transition at TN = 6 K and suggests the long-range AFM transition instead. The AFM order is most likely canted, which leads to a weak ferromagnetic component below TN, although further neutron diffraction study would be useful to characterize this ground state more fully. This is evidenced by small magnetic hysteresis and saturation in the 2 K M–H curve (Fig. 7b), showing magnetic anisotropy with coercive fields of 50 mT and a saturated moment Ms = 0.09(1) μB. These ferromagnetic components disappear above TN, as indicated by the linear M–H curve at 20 K and 100 K. The weak ferromagnetism below TN may come from trace amounts of Mn3+ at M1 site. The hexagonal average lattice symmetry does not allow long-range orbital order, but when Mn3+ ions are present at the M1 sites, local orbital order with respect to the Mn4+ ions at the six neighboring M2 sites is likely in such a highly connected manganite network. This gives rise to ferromagnetic MnM1–O–MnM2 interactions, as found in long-range orbitally ordered La0.5Ca0.5MnO3.41
3.4 Conductivity and morphology
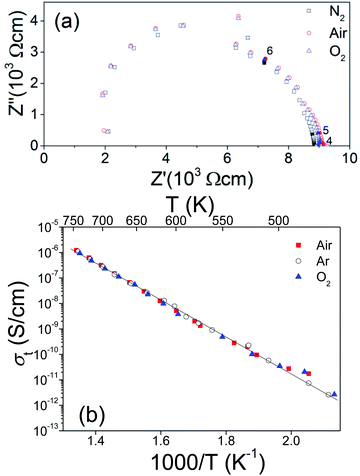
To explore the transport properties of Ba4Sn1.1Mn2.9O12, AC impedance data was collected on the dense pellet, which has 93% of the theoretical density. Fig. 8a shows typical complex impedance plots at 573 K measured at different atmospheres, which are essentially identical and consist of one asymmetric semicircle arc. The capacitances for this arc vary within 10−12 to 10−11 F cm−1, which could be ascribed to mixed bulk and grain boundary responses. No apparent electrode responses were observed in the impedance data. Fig. 8b shows the total conductivities of the Ba4Sn1.1Mn2.9O12 pellets, which are almost independent of atmospheres. This keeps with very low content of oxygen vacancies in Ba4Sn1.1Mn2.9O12. The conductivities vary from 10−11 to 10−6 S cm−1 in the temperature range 473–750 K. The Arrhenius plots show constant activation energy (Ea) of 0.61(1) eV for the Ba4Sn1.1Mn2.9O12.The SEM images in backscattering mode (Fig. 9) show the cross-section morphology of Ba4Sn1.1Mn2.9O12 ceramic, which has homogeneous elements distribution and well-defined grain boundaries. The grain sizes are mainly distributed in the range of 2–10 μm range (Fig. 9a), without significantly anisotropic grain growth, keeping with its good density. The Ba, Sn, Mn elements are uniformly distributed in the cross-section of the pellet, and the Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn
Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratio of 3.8
Mn ratio of 3.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.1
1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 keeps with their stoichiometric ratio (Fig. 9b–d).
2.5 keeps with their stoichiometric ratio (Fig. 9b–d).
4 Conclusions
The new 12R perovskite Ba4Sn1.1Mn2.9O12 has been synthesized by high-temperature solid-state reactions. The material has an ordered arrangement of Sn and Mn cations, and trimers of face-sharing MnO6 octahedra arranged in triangular plains. Within trimers of MnO6 octahedra, the outer MnM2O6 octahedra are distorted but the inner MnM3O6 octahedra are undistorted. The magnetism of Ba4Sn1.1Mn2.9O12 perovskite can be described in the picture of molecular-like Mn3 and minor Mn2 linear clusters. These magnetic cluster forms at ∼220 K due to the strong AFM interaction inside the clusters, and has the effective moment of one Mn4+ spin per Mn3 cluster and zero spin per Mn2 cluster. Weaker inter-cluster magnetic interaction ordered these magnetic clusters antiferromagnetically at lower temperature TN ∼ 6 K. The Ba4Sn1.1Mn2.9O12 sample has a semiconducting behavior with a transport activation energy of 0.61 eV. Ba4Sn1.1Mn2.9O12 is another rare example of a periodical lattice that shows molecular-like cluster magnetism due to the cationic order beyond orbital molecules.42Conflicts of interest
There are no conflicts to declare.Acknowledgements
The National Natural Science Foundation of China (No. 51662013, 22161014, 21850410458), Guangxi Natural Science Foundation (No. 2020GXNSFAA297220, 2019GXNSFGA245006, AD19245097), and the Foundation of Guilin University of Technology (No. GUTQDJJ2018115) are acknowledged for their financial support. We acknowledge Prof. He Lunhua at China Spallat Neutron Source for the support in neutron data collection in this work.Notes and references
- Q. Feng, H. Kanoh and K. Ooi, J. Mater. Chem., 1999, 9, 319–333 RSC.
- P. Strobel and C. Mouget, Mater. Res. Bull., 1993, 28, 93–100 CrossRef CAS.
- A. R. Armstrong and P. G. Bruce, Nature, 1996, 381, 499–500 CrossRef CAS.
- M. Mogensen, K. V. Jensen, M. J. Jørgensen and S. Primdahl, Solid State Ionics, 2002, 150, 123–129 CrossRef CAS.
- G. H. Jonker and J. H. Van Santen, Physica, 1950, 16, 337–349 CrossRef CAS.
- J. M. Longo and J. A. Kafalas, J. Solid State Chem., 1969, 1, 103–108 CrossRef CAS.
- T. Negas and R. S. Roth, J. Solid State Chem., 1971, 3, 323–339 CrossRef CAS.
- J. M. Gonzalez-Calbet, M. Parras, J. M. Alonso and M. Valletregi, J. Solid State Chem., 1993, 106, 99–110 CrossRef CAS.
- J. J. Adkin and M. A. Hayward, J. Solid State Chem., 2006, 179, 70–76 CrossRef CAS.
- J. J. Adkin and M. A. Hayward, Chem. Mater., 2007, 19, 755–762 CrossRef CAS.
- J. Varignon and P. Ghosez, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 140403 CrossRef.
- N. Floros, C. Michel, M. Hervieu and B. Raveau, Chem. Mater., 2000, 12, 3197–3201 CrossRef CAS.
- N. Floros, C. Michel, M. Hervieu and B. Raveau, J. Solid State Chem., 2002, 168, 11–17 CrossRef CAS.
- G. M. Keith, C. A. Kirk, K. Sarma, N. M. Alford, E. J. Cussen, M. J. Rosseinsky and D. C. Sinclair, Chem. Mater., 2004, 16, 2007–2015 CrossRef CAS.
- L. Miranda, A. Feteira, D. Sinclair, K. Boulahya, M. Hernando, J. Ramirez, A. Varela, J. M. Gonzalez-Calbet and M. Parras, Chem. Mater., 2009, 21, 1731–1742 CrossRef CAS.
- N. Créon, C. Michel, M. Hervieu, A. Maignan and B. Raveau, Solid State Sci., 2003, 5, 243–248 CrossRef.
- C. L. Yin, G. B. Li, T. N. Jin, L. P. You, J. L. Tao, J. W. Richardson, C. Loong, J. L. Sun, F. H. Liao and J. H. Lin, Chem. Mater., 2008, 20, 2110–2116 CrossRef CAS.
- C. L. Yin, G. B. Li, T. N. Jin, J. L. Tao, J. W. Richardson, C. Loong, F. H. Liao and J. H. Lin, J. Alloys Compd., 2010, 489, 152–156 CrossRef CAS.
- C. L. Yin, G. B. Li, W. A. Kockelmann, F. H. Liao, J. P. Attfield and J. H. Lin, Chem. Mater., 2010, 22, 3269–3276 CrossRef CAS.
- L. Miranda, D. C. Sinclair, M. Hernando, A. Varela, A. Wattiaux, K. Boulahya, J. M. Gonzalez-Calbet and M. Parras, Chem. Mater., 2009, 21, 5272–5283 CrossRef CAS.
- J. G. Zhao, L. X. Yang, Y. Yu, F. Y. Li, R. C. Yu and C. Q. Jin, J. Solid State Chem., 2008, 181, 1767–1775 CrossRef CAS.
- C. L. Yin, G. B. Li, W. A. Kockelmann, J. H. Lin and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 094420 CrossRef.
- N. A. Jordan and P. D Battle, J. Mater. Chem., 2003, 13, 2220–2226 RSC.
- A. F. Fuentes, K. Boulahya and U. Amador, J. Solid State Chem., 2004, 177, 714–720 CrossRef CAS.
- M. A. Macías, O. Mentre, S. Colis, G. J. Cuello and G. H. Gauthier, J. Solid State Chem., 2013, 198, 186–191 CrossRef.
- X. J. Kuang, C. Bridges, M. Allix, J. B. Claridge, H. Hughes and M. J. Rosseinsky, Chem. Mater., 2006, 18, 5130–5136 CrossRef CAS.
- L. T. Nguyen, T. Kong and R. J. Cava, Mater. Res. Express, 2019, 6, 056108 CrossRef CAS.
- R. D. Shannon, Acta Crystallographica Section A, 1976, 32, 751–767 CrossRef.
- M. A. Macías, O. Mentré, C. Pirovano, P. Roussel, S. Colis and G. H. Gauthier, New J. Chem., 2015, 39, 829–835 RSC.
- S. V. Streltsov and D. I. Khomskii, JETP Lett., 2018, 108, 686–690 CrossRef CAS.
- F. A. Garcia, U. F. Kaneko, E. Granado, J. Sichelschmidt, M. Hölzel, J. G. S. Duque, C. A. J. Nunes, R. P. Amaral, P. Marques-Ferreira and R. Lora-Serrano, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 224416 CrossRef.
- A. J. Browne, A. Krajewska and A. S. Gibbs, J. Mater. Chem. C, 2021, 9, 11640–11654 RSC.
- L. T. Nguyen and R. J. Cava, Chem. Rev., 2021, 121, 2935–2965 CrossRef CAS PubMed.
- A. Coelho, Topas Academic Version 5, Coelho Software, Brisbane, Australia, 2012 Search PubMed.
- I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247 CrossRef.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef.
- E. J. Cussen and P. D. Battle, Chem. Mater., 2000, 12, 831–838 CrossRef CAS.
- J. A. Oberteuffer and J. A. Ibers, Acta Crystallogr., Sect. B: Struct. Sci., 1970, 26, 1499–1504 CrossRef CAS.
- F. E. Mabbs and D. J. Machin, Magnetism and Transition Metal Complexes, Dover Publication, Inc., Mineola, New York, 2007 Search PubMed.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536 CrossRef CAS.
- E. Dagotto, T. Hotta and A. Moreo, Phys. Rep., 2001, 344, 1–153 CrossRef CAS.
- J. P. Attfield, APL Mater., 2015, 3, 041510 CrossRef.
Footnote |
| † CCDC 2117124. For crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ra07841k |
| This journal is © The Royal Society of Chemistry 2021 |