 Open Access Article
Open Access ArticleEffects of low-molecular-weight organic acids on the dissolution of hydroxyapatite nanoparticles†
Dengjun
Wang
a,
Yunsong
Xie
b,
Deb P.
Jaisi
*a and
Yan
Jin
*a
aDepartment of Plant and Soil Sciences, University of Delaware, Newark, DE 19716, USA. E-mail: jaisi@udel.edu; yjin@udel.edu; Fax: +1 302 831 0605; Tel: +1 302 831 1376 Tel: +1 302 831 6962
bDepartment of Physics and Astronomy, University of Delaware, Newark, DE 19716, USA
First published on 16th May 2016
Abstract
Hydroxyapatite nanoparticles (HANPs) have recently been advocated as a highly efficient and environmentally benign ‘green’ phosphorus (P) nanofertilizer in modern agriculture. However, knowledge of how low-molecular-weight organic acids (LMWOAs) secreted by plants in agricultural soils mediate the dissolution of HANPs and release of dissolved phosphate is nonexistent. Here, three of the most commonly occurring LMWOAs (acetic, oxalic, and citric acids) were evaluated for their roles in HANPs dissolution in both batch and column systems. Particularly, O-isotopic ratios of dissolved phosphate during HANPs dissolution were measured to disentangle mechanisms controlling isotope fractionation. Our results reveal that in a batch system HANPs dissolution was very fast but the overall dissolution efficiency was low (≤30%), unlike in a column system where ∼100% dissolution was achieved. The low dissolution efficiency of HANPs in the batch system was due predominantly to rapid consumption of protons, whereas in the column system the HANPs were progressively dissolved by low pH LMWOAs and reaction products were eluted out. Regardless of LMWOA type and experimental system, the isotopically lighter phosphate (P16O4) was preferentially released during the initial phases of dissolution and dissolved phosphate became gradually P18O4-enriched with time. This fractionation was less in batch (−0.3‰ to +1.1‰) than in column (−1.3‰ to +1.1‰) systems due primarily to lower dissolution efficiency and higher P16O4 and P18O4 exchange between HANPs and dissolved phosphates. The Rayleigh model well described O-isotopic fractionation of dissolved phosphate under different LMWOAs. Overall, our findings provide important insights into the dissolution kinetics and O-isotopic evolution of phosphate-based NPs that are relevant to plant–soil systems particularly at the rhizosphere.
Nano impactThe roles of naturally occurring low-molecular-weight organic acids (LMWOAs) in the dissolution of hydroxyapatite nanoparticles (HANPs) were explored. Our results indicate that phosphate release during HANPs dissolution is highly dependent on the type of LMWOA, which has important implications when HANPs are used as a promising phosphorus (P) nanofertilizer in agricultural soils particularly at the rhizosphere. Furthermore, a stable oxygen isotope technique was employed for the first time to accurately trace O-isotopic fractionation and evolution of phosphate during HANPs dissolution in abiotic systems. Given that the HANPs pool has distinct phosphate oxygen isotope signatures compared to soil P pools, the isotope technique could be used to identify whether plant uptake of P comes from HANPs or from soils and thus to evaluate the use efficiency of HANPs by plants in agricultural soils. |
1. Introduction
Nanotechnology has been increasingly used as a powerful tool to augment plant nutrient uptake, maximize crop productivity, and improve food quality and thus the sustainability of modern agriculture.1,2 Apatite is the primary phosphate mineral reserve on earth and has long been used for manufacturing phosphorus (P) fertilizers, but this reserve is diminishing rapidly.3 Structurally, apatite has a hexagonal atomic framework, in which there is a dominant element (primarily Ca) on two of the cation sites and P on the third cation site (e.g., calcium phosphate apatite). Another structural site of the calcium phosphate apatite can accommodate F, Cl, and OH, forming fluorapatite, chlorapatite, and hydroxyapatite, respectively.4 Recent studies suggest that synthesized hydroxyapatite nanoparticles (HANPs; Ca5(PO4)3OH) may be used as an efficient and environmentally friendly ‘green’ P nanofertilizer for crop production with reduced negative impacts, compared to commonly used commercial fertilizers, on water quality due to their nanoscale dimensions, large reactive surface area, and low leaching potential.5,6 For example, Liu and Lal5 showed that HANPs increased the growth rate and seed yield of soybeans cultivated in a greenhouse by 33% and 20%, respectively, compared to soybeans that received a regular P fertilizer (Ca(H2PO4)2). Montalvo et al.,6 however, reported that HANPs were more efficient than bulk-sized hydroxyapatite, but not as efficient as commercial fertilizers in wheat uptake of P in Andisols and Oxisols rich in iron and aluminum oxides. Clearly, research on the evaluation of HANPs as a promising P nanofertilizer is in the very early stages of development, and systematic studies are needed on P release kinetics of HANPs to address questions of whether and how HANPs could surpass commercial fertilizers for steady supply of P to plants, and/or offer other environmental advantages such as limited P leaching and loss or conditioning soil pH.Biogeochemical cycling including plant uptake of P in soils is initiated after dissolution of apatite,7 such as HANPs when they are used as a promising P nanofertilizer. Dissolution of apatite in soils particularly in the rhizosphere is predominantly controlled by protons and low-molecular-weight organic acids (LMWOAs) that are released as organic matter decomposition products, microbial metabolites, or root exudates at concentrations ranging from micro- to millimolar.8–10 The most frequently occurring mono-, di-, and tri-carboxylic LMWOAs in the rhizosphere are acetic, oxalic, and citric acid, respectively.8–10 The proposed mechanisms of apatite dissolution by LMWOAs include (1) proton-promoted dissolution (LMWOA elevates proton concentration); (2) ligand-controlled dissolution (LMWOA complexes with apatite and then breaks the metal–oxygen bond); and (3) formation of aqueous metal–ligand complexes that decrease the extent of relative saturation of metal (e.g., Ca2+) in solution.11–13 Understanding the kinetics and mechanisms of HANPs dissolution by LMWOAs will provide necessary information for identifying effective approaches for improving HANPs' use efficiency and crop productivity simultaneously in agricultural soils.
Oxygen isotope ratios of phosphate in apatite mineral and dissolved phosphate (δ18OP) have been increasingly applied as a powerful environmental geochemical indicator to gain better knowledge of environmental/temperature conditions under which apatite minerals (e.g., tooth enamel, bones, and fish remains) are formed14–16 and for tracing sources and understanding the biogeochemical cycling of P in natural environments.17–20 This is because phosphate is primarily cycled in biological systems where rapid O-isotope exchange occurs between phosphate and ambient water via enzyme-catalyzed reactions, which may lead to complete isotope exchange.17,21 In contrast, in abiotic systems, O-isotope exchange between phosphate and water is negligible at low temperature (<80 °C) and near-neutral pH conditions.22,23 To expand the application of δ18OP values as an indicator of mineral dissolution and P uptake by plants, additional understanding of the physicochemical and biological processes and reactions leading to potential isotope fractionation is required.24 To date, although several aspects of O-isotopic systematics involving microbial metabolism in biological systems17,18 and abiotic interactions such as phosphate sorption,25 desorption,25 transport,26,27 and mineral precipitation28 and transformation25,29 have been characterized in limited systems and environments, research dedicated to isotope effects associated with apatite dissolution is rare.28 Particularly, O-isotopic fractionation during apatite dissolution by LMWOAs in plant–soil systems has not been explored.30
Our objectives were to (1) unravel the roles of LMWOAs (acetic, oxalic, and citric acids) in the dissolution of HANPs in both batch and column systems and (2) decipher the mechanisms of O-isotopic fractionation and isotope evolution during HANPs dissolution by LMWOAs in abiotic systems. Our results provide insights into the dissolution kinetics of phosphate-based NPs and expand the phosphate oxygen isotope systematics to differentiate reactions during apatite dissolution and isotope exchange when the dissolution is initiated.
2. Materials and methods
2.1. HANPs and LMWOAs
HANPs were purchased from Nanjing Emperor Nanomaterial Co. Ltd., China. The physicochemical properties of HANPs have been well characterized previously.31,32 Briefly, HANPs are single-phase pure hydroxyapatite minerals and display a rod morphology with dimensions of 20 nm (width) by 100 nm (length). The Ca/P molar ratio of the HANPs is 1.65 and the specific surface area (SSA) is 154 m2 g−1 (N2-BET method). The three most commonly occurring LMWOAs, i.e., acetic, oxalic, and citric acids, were chosen as model organic compounds, and an environmentally relevant concentration of 1 mM (ref. 8 and 9) was used.2.2. Batch and column experiments
Laboratory-scale batch and column experimental systems under oxic condition and light were used to elucidate HANPs dissolution kinetics under different LMWOAs. Prior to use, batch and column experimental apparatuses (polypropylene tube and glass chromatography column) were soaked in 1 N HNO3 overnight and then thoroughly cleaned with DI water. Batch experiments were performed in polypropylene tubes, where phosphate released during dissolution was monitored as a function of time. Briefly, 8 or 40 mg of HANPs powder was weighed into tubes containing 40 mL of DI water (control experiment) or 1 mM LMWOAs (acetic, oxalic, and citric acids), yielding 0.2 or 1 g L−1 HANPs. The high concentration (1 g L−1) was included because it has been commonly used in mineral dissolution studies.33 All batch experiments were conducted in triplicate and the tubes were shaken at 100 rpm for 120 h at 25 °C. The shaking speed was sufficient to keep the suspension well mixed but without causing turbulence that might cause abrasion of the HANPs.33 At each sampling interval, a 2.5 mL aliquot was extracted from each tube and immediately ultrafiltrated using a stirred ultrafiltration cell (Amicon Model 8010, Millipore Corp., Bedford, MA) with a 10 kDa cellulose membrane (PLGC02510) equivalent to nominal particle sizes of 5–6 nm (ref. 34) to separate dissolved phosphate. P species in the ultrafiltrate are assumed to be dissolved PO43− ions because undissolved (or partially dissolved) HANPs cannot pass through the 10 kDa membrane.32 The clear ultrafiltrate exhibited no detectable plasmon resonance optical absorption peak,35 confirming the ability of ultrafiltration to remove undissolved HANPs.Complementary to mechanistic examination of HANPs dissolution by LMWOAs in the batch system, additional sample characterizations were performed. The average hydrodynamic diameters (DH) of HANPs under different LMWOAs versus time were analyzed using a dynamic light scattering method (DLS; Möbiuζ, Wyatt Technology Corp., Santa Barbara, CA). Furthermore, after completion of the batch experiments, some undissolved (or partially dissolved) HANPs were freeze-dried and analyzed using a transmission electron microscope (JEM 2010F TEM, JEOL, Japan) to investigate the morphological changes of HANPs after interacting with LMWOAs.
Particularly, column experiments were conducted to aid in better interpretation of kinetic data as in such experiments reaction products are continuously removed and therefore back reaction and reaction inhibition can be avoided.33 Column experiments were conducted in duplicate using a sequential deposition–dissolution procedure. Briefly, a glass chromatography column (1.6 cm inner diameter × 9 cm long) was dry-packed with 31.5 g of quartz sand (688 μm in diameter) that was thoroughly cleaned previously (1 N HNO3 and 1 N NaOH, respectively) to remove any adsorbed clays and/or metal oxide impurities,32 yielding a bulk density of 1.74 g cm−3 and pore volume (PV) of 7.4 mL. Twenty PVs of DI water (pH 6.5) were subsequently injected in an upflow mode at an environmentally relevant flow rate (q) of 0.044 cm min−1 (ref. 36) to slowly saturate the column (retention time for tracer is 74 min). The gravimetrically measured porosity of the packed column was approximately 0.32. Following the saturation step, a deposition experiment was initiated by injecting 5 PVs of 0.2 g L−1 HANPs suspension (pH 6.5) into the column, followed by elution with 5 PVs of DI water (pH 6.5) at q = 0.044 cm min−1. The 0.2 g L−1 HANPs concentration used in both batch and column deposition experiments was consistent with that in a HANPs transport study.32 The deposition experiments mimic nanomaterials' accidental release and subsequent transport along the soil profile,37 or intentional application of NPs (e.g., NZVI) for environmental remediation.38 After completion of the deposition experiment, the HANPs dissolution experiment was initiated by continuously injecting 20 PVs of 1 mM LMWOA (acetic, oxalic, or citric acid) at q = 0.044 cm min−1. Our preliminary experiments revealed that 20 PVs of LMWOA were adequate to dissolve the HANPs retained in the column.
Column effluents were collected continuously using a fraction collector (Foxy Jr., Teledyne Isco, Lincoln, NE). The concentrations of dissolved phosphate in samples from batch and column experiments were measured on a spectrophotometer (Beckman DU 640, Beckman Instruments Inc., Fullerton, CA) using the phosphomolybdate blue colorimetric method,39 whereas the concentrations of HANPs in column deposition experiments were determined spectrophotometrically at the wavelength of 300 nm.40 The pH of HANPs suspensions and effluents in batch and column experiments was monitored using a pH meter (Accumet Excel XL50, Fisher Scientific). To fully understand the mechanisms of HANPs dissolution by LMWOAs, the chemical speciation of LMWOAs versus pH was calculated using the Visual MINTEQ 3.0 software.
2.3. Phosphate oxygen isotope ratio measurements
Ultrafiltrate and effluent samples from batch and column experiments (i.e., dissolved phosphate) and selected solid-phase samples that were intercepted by the 10 kDa membrane (undissolved and/or partially dissolved HANPs) in batch experiments were individually processed for O-isotopic analyses. All samples were purified using sequential precipitation and recrystallization methods.24 Briefly, each sample was first treated with Supelite DAX-8 resin (Supelco, Bellefonte, PA) to remove dissolved organic matter (e.g., LMWOAs),41 precipitated as ammonium phosphomolybdate (APM), and then recrystallized as magnesium ammonium phosphate (MAP), as described by Jaisi and Blake.24 MAP was dissolved and the resulting solution was treated using AG X-8 cation resin (Bio-Rad) to remove Ca2+ and other cations. The purified phosphate solution was finally precipitated as silver phosphate (Ag3PO4).The δ18OP values were measured by online high-temperature thermal decomposition of Ag3PO4 to CO gas at 1460 °C using a Thermo-Chemolysis Elemental Analyzer (TC/EA) coupled to a Delta V continuous flow isotope ratio monitoring mass spectrometer (IRMS; Thermo, Bremen, Germany) with an analytical precision of ≤0.3‰ at the Stable Isotope Facility at the University of Delaware. The δ18OP values were calibrated against two Ag3PO4 standards, YR-1aR-02 (−5.49‰) and YR-3.2 (+33.63‰). For each run, the oxygen yield from Ag3PO4 was calculated and those within ±10% of that of an internal laboratory Ag3PO4 standard (Fisher Scientific) were accepted for isotope analyses. All O-isotopic data are reported relative to the Vienna Standard Mean Ocean Water (VSMOW) standard in units of permil (‰).
2.4. Data analyses
The dissolution efficiency (%) of HANPs in the batch experiments was calculated based upon the concentration ratio between dissolved phosphate and total phosphate in the suspension.The dissolution rate (R; mol m−2 s−1)33,42,43 of HANPs in batch and column experiments was determined as follows:
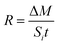 | (1) |
The two-site dissolution model45–47 was applied to describe HANPs dissolution kinetics under different LMWOAs in the batch experiments. Site 1 predominates when dissolution occurs under unsaturated solutions, e.g., during the initial phases of dissolution, whereas site 2 becomes active during later stages particularly when dissolution approaches equilibrium, e.g., (partial) saturation solutions.
 | (2) |
| C[PO43−]t = C[PO43−]max1 × (1 − e-k1t) + C[PO43−]max2 × (1 − e-k2t) | (3) |
The Rayleigh model has been widely used to describe trends on isotope fractionation48 and was used to quantify 18O enrichment factor (ε0; ‰) in dissolved phosphates:
 | (4) |
One-way ANOVA analysis was conducted to identify statistically significant differences among measured δ18OP values using Tukey's Honestly Significant Difference (HSD) test. The statistical analyses were performed using SPSS 16.0 software, and the differences of means were considered significant at p < 0.05.
3. Results and discussion
3.1. Dissolution of HANPs in batch experiments
Dissolution of HANPs in terms of efficiency and rate at initial HANPs concentrations (C0) of 0.2 and 1 g L−1 under three LMWOAs (1 mM acetic, oxalic, and citric acid) in the batch system is shown in Fig. 1. A very rapid release of dissolved phosphate occurred initially (∼0.2 h; Fig. 1a and c), and the release of dissolved phosphate then either remained constant or, in some cases, decreased slightly with time (C0 = 1 g L−1) until a steady state was reached. The dissolution efficiency followed the order acetic < oxalic < citric acid and was much higher at lower C0 (0.2 g L−1). These results were supported by the fact that the R value varied in the same order, acetic < oxalic < citric acid, and was larger at lower C0 (Fig. 1b and d). Similar findings were observed on the dissolution of apatite minerals by inorganic33,42 and organic acids (e.g., LMWOAs).33,49 This is due primarily to proton-promoted (mechanism 1) and ligand-controlled dissolution (mechanism 2; as shown in the ESI,† Fig. S1) and approaching solution saturation with respect to the dissolving species and/or possible secondary mineral phases in the batch system, which are discussed below in detail.In a batch system, solution saturation impacts mineral dissolution rate.33,42 For undersaturated conditions, the activity of a chemical species between solid and solution decreases when its concentration in solution elevates, resulting in a reduction in dissolution rate as the solution approaches saturation (e.g., PO43− ion; Fig. 1). On the other hand, removal of ions due to precipitation has an opposite effect. For example, oxalic acid can precipitate as Ca-oxalate, which promotes HANPs dissolution by lowering Ca2+ concentration in the solution.33,53
We additionally analyzed the relationships between average dissolution rate (Rave) and the number of carboxyl groups (N) and Rave and consumed amount of protons when the dissolution reaction reaches equilibrium, respectively at C0 = 0.2 and 1 g L−1 in the batch experiments (ESI,† Fig. S5). The value of Rave increased linearly with N (Fig. S5a†), confirming that the carboxyl group affects the dissolution rate of HANPs. The Rave values were much smaller at C0 = 1 g L−1 than at C0 = 0.2 g L−1 due primarily to more rapid depletion of protons. In addition, the Rave value was observed to increase linearly with consumed amount of protons and the slope was higher at lower C0 (Fig. S5b†), consistent with the correlation between R and ΔpH (Fig. 2c and d). These results clearly verify that the amount of protons controls HANPs dissolution and the effect is more pronounced at lower C0 in the batch experiments. The Rave values obtained in our study, i.e., (2.3 ± 0.005) × 10−10 to (3.1 ± 0.1) × 10−9 mol m−2 s−1, are consistent with those in published literature on apatite minerals,33,42,50 because R is normalized by the initial surface area of apatite. For example, within pH 2.2–6.7, Valsami-Jones et al.50 found that R ranged from 1.8 × 10−9 to 3.0 × 10−9 mol m−2 s−1 for natural apatite and from 4.5 × 10−11 to 2.3 × 10−9 mol m−2 s−1 for synthetic apatite. Welch et al.33 observed that R increased from 2 × 10−10 to 2 × 10−9 mol m−2 s−1 for natural apatite when pH was decreased from 5.5 to 4.0. The small discrepancy in R between our and past studies could be due to a number of factors including differences in experimental procedures (solution type, volume, and saturation state, and shaking rate) and properties of apatite mineral (size, surface roughness, and surface area), which altogether influence apatite solubility and reactivity.
To better discern the contribution of proton and ligand to HANPs dissolution in the batch experiments, the linear slopes of R vs. ΔpH and R vs. N are compared (Fig. 2 and S5a†). Our results show that the linear slope of R vs. N was steeper at lower C0 (Fig. S5a†), indicative of greater contribution of ligand at lower C0, recalling that protons also play more pronounced roles at lower C0, both of which contribute to the greater dissolution of HANPs at lower C0 (Fig. 1). Most notably, the linear slope (absolute value) of R vs. ΔpH was 1–2 orders of magnitude greater than that of R vs. N (note that the slope of R vs. consumed amount of protons is a different story because the values of consumed proton amount are not on the same magnitude as those of ΔpH and N, as shown in Fig. 2 and S5†), demonstrating the dominant role of protons in HANPs dissolution in batch experiments, which is in agreement with the results obtained from the two-decay-coefficient model (Fig. S3 and Table S1†). These findings are expected because >90% HANPs dissolution was completed during early stages (e.g., 0.2 h; Fig. 1) where proton concentration is high.
Previous studies demonstrate a linear dependence between dissolution rate and rate constant on HANPs dissolution under acidic pH conditions.42,43 A similar linear relationship was obtained between Rave and k1 (reflects the contribution of proton) under different C0 and LMWOAs in the batch experiments (ESI† Fig. S6). These findings again substantiate the predominance of protons in HANPs dissolution in the batch experiments. Please note that although citric acid has an additional OH− group, which would affect the dissolution of HANPs, the contribution of the OH− group to HANPs dissolution is expected to be negligible because (1) protons control the overall dissolution of HANPs (described above), and (2) the OH− group plays a less important role in HANPs dissolution compared to that of the COOH− group.
Monitoring the changes in size and morphology of HANPs during dissolution by LMWOAs shows that the DH value of HANPs decreased drastically during early phases of dissolution (0–10 min) and then remained constant throughout steady-state conditions (ESI† Fig. S7), consistent with the trends of HANPs dissolution kinetics (Fig. 1). The DH value of HANPs was in the order acetic > oxalic > citric acid, again confirming the greater role of citric acid in accelerating HANPs dissolution than that of oxalic and acetic acids. The TEM images show that the pristine HANPs are rod-shaped, measuring 20 nm wide and 100 nm long (ESI† Fig. S8a). In LMWOA solution, etching of HANPs led to the formation of different shaped HANPs (spherical, ellipsoidal, diamond, and triangular; Fig. S8b–d†) because etching is not likely to be controlled by crystal defect-induced dissolution on HANPs surfaces due to large SSA and high surface free energy. This information could be helpful for synthesizing apatite-type nanofertilizers having different shapes because the efficiency of a nanofertilizer in soils (porous medium) is dependent on its mobility, which is related to particle shape.59,60 It should be mentioned that in this study, R (and Rave) is normalized to the initial surface area of HANPs (eqn (1)), which is a fixed value at a given C0. Nonetheless, the size and shape of HANPs were observed to be altered during dissolution (Fig. S7 and S8†), which would affect R. Because the dissolution efficiency of HANPs varied in the order of acetic < oxalic < citric acid and was lower at higher C0 (Fig. 1a and b), the actual surface area of HANPs during dissolution is expected to follow the trend of acetic > oxalic > citric acid and is greater at higher C0. Consequently, the actual value of R (and Rave) would follow the same trend of acetic < oxalic < citric acid (i.e., the same as that obtained by normalizing the initial surface area of HANPs) and be much larger for citric than oxalic and acetic acids particularly at lower C0.
3.2. Dissolution of HANPs in column experiments
The breakthrough curve and retention profile of HANPs at C0 = 0.2 g L−1 in the column deposition experiment are presented in the ESI† Fig. S9, which show that the mobility of HANPs was rather limited (∼5% broke through) and most of the HANPs were retained (∼7.03 mg of HANPs) particularly near the column inlet (0–3 cm), consistent with our previous results.31,32 These phenomena are largely due to aggregation and straining of HANPs in a porous medium. No wall effect and preferential flow occurred in the transport experiments because of the symmetrical breakthrough curve of the tracer (ESI† Fig. S10).The effect of LMWOA type on the dissolution of HANPs (C0 = 0.2 g L−1) in the column system is shown in Fig. 3. An initial peak of dissolved phosphate occurred after the onset of HANPs dissolution, which was the lowest for acetic and the highest for citric acid. The higher peak of dissolved phosphate in citric than oxalic and acetic acids is consistent with the greater capability of citric acid, allowing faster dissolution of HANPs (as observed in the batch system). In contrast, the duration of the phosphate peak varied in the order of acetic > oxalic > citric acid (Fig. 3a), i.e., the peak plateau maintained ∼6, 3, and 1 PV, respectively, in acetic, oxalic, and citric acid. To demonstrate more explicitly that the plateau of phosphate release is a general phenomenon in column dissolution experiments, a 5-fold higher loading of HANPs (5 PVs of 1 g L−1 HANPs suspensions) was used in the column deposition experiment. A much longer duration (∼35 PVs) and lower peak value (Ci/C0 = 0.007) of dissolved phosphate were obtained (ESI† Fig. S11a) compared to those at a lower HANPs loading (Fig. 3a). These observations are anticipated because HANPs dissolution in a dynamic column system removes dissolved phosphate and maintains undersaturated conditions,44 yielding a ∼100% dissolution (96.3–105%; Fig. 3a) of HANPs, and the lower peak value observed at a higher HANPs loading in the column system reflects a slower dissolution rate, with the order consistent with that of the batch system. The trend of pH change upon the injection of LMWOAs (Fig. 3b and S11b†) is in excellent agreement with that of HANPs dissolution kinetics (Fig. 3a and S11a†), indicative of the predominance of proton in HANPs dissolution in the column system. Release of phosphate decreased progressively and tended to approach zero. Such a gradual decrease in phosphate release is frequently encountered in flow-through column experiments44 and has been attributed to the reduced HANPs that are available for dissolution. At the end of the column dissolution experiments, effluent pH became close to the initial pH of 1 mM LMWOAs (Fig. 3b). Interestingly, at the end of the column experiments, pH in the effluent was 1.7–2.4 pH units lower than the equilibrium pH of HANP–LMWOA suspension in batch experiments (Fig. 2b), again substantiating that pH is the key factor controlling the rate and extent of HANPs dissolution.
3.3. Phosphate oxygen isotope fractionation during HANPs dissolution
To decipher the mechanisms controlling phosphate oxygen isotope fractionation and isotope evolution over time during HANPs dissolution by LMWOAs, δ18OP values of dissolved phosphate and undissolved HANPs were measured. The Δ18OP values (i.e., difference in isotope values between dissolved phosphate and bulk (starting) HANPs) under three LMWOAs in both batch and column experiments are presented in Fig. 4, which shows that the Δ18OP was negative at first and then increased unidirectionally towards a positive value over the course of dissolution. Conversely, the Δ18OP values between undissolved and bulk HANPs in 1 mM oxalic acid in batch experiments (ESI† Fig. S12) show that its Δ18OP was positive initially and decreased gradually with phosphate release. These observations suggest that the lighter isotopes in the P–O bond (P16O4) are preferentially broken and released to the solution during early stages of dissolution, resulting in products (dissolved phosphate) with lighter isotopes, which is a common feature for oxygen isotope fractionation of oxyanions, e.g., nitrate,61 carbonate,62 and sulfate,63 in biogeochemical reactions. This is because lighter isotopes are more reactive due to lower mass and bond energy (mass-dependent fractionation).64 As the dissolution proceeded, efficient ion exchange between aqueous and solid phases yielded a reversal in the direction of the initial fractionation pattern (Δ18OP changed from negative to positive), consistent with past results28,65 on O-isotopic fractionation between apatite mineral and dissolved phosphate. A small fractionation (Δ18OP ≤ 1.3‰) occurred during HANPs dissolution in three LMWOAs (Fig. 4), consistent with those (<3‰) on phosphate oxygen isotope fractionation during abiotic reactions.25–28 These findings substantiate the fact that phosphate oxygen isotope fractionation is insignificant during apatite dissolution in abiotic systems.Our Δ18OP data matched well with HANPs dissolution kinetics in both batch and column experiments: the Δ18OP increased from a negative value to zero at t ≈ 1 h (Fig. 4a) and 2.5 PV (3.1 h) (Fig. 4b), respectively, in batch and column experiments at which time HANPs dissolution just reached equilibrium (Fig. 1 and 3). The increase in Δ18OP with HANPs dissolution in batch experiments is attributed predominately to enhanced exchange between P16O4 and P18O4 isotopes. The similar trend observed in column experiments, however, is due to preferential depletion of light isotopes in the reactant pool and the fact that ∼100% HANPs were dissolved (Fig. 3a) based on isotope mass balance. Smaller isotope fractionation in batch (−0.3‰ to +1.1‰) than that in column (−1.3‰ to +1.1‰) experiments is a result of lower dissolution efficiency (≤30% vs. ∼100%; Fig. 1 and 3), faster mass transfer rate (1 h vs. 3.1 h to reach equilibrium; Fig. 1 and 3), and greater ion (P16O4 and P18O4) exchange between HANPs and dissolved phosphates. Faster mass transfer rate results in less isotope fractionation, which is analogous to the mechanism that the more strongly bonded the isotope (corresponds to less mass transfer rate), the larger the fractionation effect.64 For instance, Turner66 reported that the C isotope enrichment factor during calcium carbonate precipitation was 1.4‰ under slow precipitation conditions (i.e., low mass transfer rate), but this fractionation appeared to diminish during rapid precipitation conditions. The above interpretation is supported by the fact that during early states of dissolution, O-isotopic fractionation was significantly (p = 0.017 < 0.05; ANOVA analysis) smaller in batch than in column systems (−0.3‰ vs. −1.3‰; Fig. 4). Irrespective of the experimental system, the Δ18OP followed the order of acetic > oxalic > citric acid, which again can be interpreted by the differences in their mass transfer rate, i.e., Racetate < Roxalate < Rcitrate (described above).
4. Conclusions and environmental implications
Both batch and column experiments were conducted to unravel the dissolution kinetics of HANPs under different types of LMWOAs. Our results indicate that the dissolution of HANPs is dependent on the experimental system, solution pH, ligand type, and/or dissolution stage. Specifically, protons plays a dominant role in HANPs dissolution during early stages particularly for the column system, whereas organic ligands take over the dissolution during later stages in the batch system. The isotopically lighter phosphate (P16O4) was preferentially released during early stages of dissolution and dissolved phosphate became gradually P18O4-enriched with time. The O-isotopic evolution of dissolved phosphate under three LMWOAs can be well described by the Rayleigh fractionation model.Our study provides several insights into dissolution kinetics and bioavailability of HANPs in plant–soil systems where they are being proposed as a P nanofertilizer. It is well-recognized that even though the total amount of P in soils greatly exceeds crop requirement, the plant-available P is insufficient particularly in most acidic soils (pH <5.5) that occupy ∼30% of the world's arable land.67 Our data suggest that direct application of HANPs in these acidic soils is expected to provide bioavailable P (PO43− ion) for crop growth in a timely fashion due to quick proton-promoted dissolution. The dissolution rate constant could be much higher in the rhizosphere where acetic, oxalic, and citric acids are present in large quantities and undergo both proton- and ligand-promoted dissolution of the HANPs. The dissolution of HANPs is greatest for citric followed by oxalic acids, and acetic acid is the least effective at releasing P. However, acetic acid appears to be the most efficient at furnishing P nutrient during the crop growing period attributed to its low HANPs dissolution rate, thereby providing P in an appreciable quantity for a long time (Fig. 3a and S11a†).
Over a wide range of environmentally relevant temperatures (3–37 °C) and δ18OW values (water oxygen isotope ratios, −9‰ to −3‰),19,20,68 the δ18OP equilibrium value of dissolved phosphate ranges from 11.0‰ to 23.0‰ (Fig. 6), which is different from the δ18OHANPs value (10.7‰) of bulk HANPs with Δ18OP = 0.3–12.3‰. Consequently, the dissolved phosphates from HANPs dissolution are expected to cycle and attain equilibrium due to enzymatically catalyzed hydrolysis in agricultural soils. An important distinction to be made here is the original isotope composition vs. the equilibrium isotope composition. If the original isotope composition of HANPs (or corresponding dissolution products) is far from equilibrium (Fig. 6) under environmentally relevant conditions, identification of the source signature will be straightforward. Clearly, significant isotope excursion is needed in the systems at low temperatures (Fig. 6a) and high δ18OW values (Fig. 6b) to achieve isotope equilibrium. During isotope excursion to achieve equilibrium, several reactions may occur: dissolved phosphate could be sorbed or occluded in soils and thus could retain original or partially exchanged isotope signals for a longer time and allow identification of source(s). Even if soil P pools are transformed, the trend of isotope excursion may provide useful information that could help identify the pathway of this transformation.29 Overall, given that the HANPs pool has distinct phosphate oxygen isotope signatures compared to soil P pools,29 the O-isotope technique could be used to identify whether plant uptake of P comes from HANPs or from soils, and thus to evaluate the use efficiency of HANPs by plants in agricultural soils.
 | ||
| Fig. 6 Calculated equilibrium value of dissolved phosphate (δ18OP) under a wide range of environmentally relevant temperatures (a; from 3 to 37 °C) and water oxygen isotopes (δ18OW) (b; water oxygen isotope ratios, from −9‰ to −3‰) using the equation of Chang and Blake.68 The dash line represents the δ18OHANPs value (10.7‰) of the bulk (starting) HANPs. | ||
Acknowledgements
This research was funded by the U.S. Department of Agriculture (NIFA Awards 2013-67019-21373 and 2015-67020-23603). We appreciate Yimin Wang (College of Environment, Hohai University) for assisting the speciation calculation of LMWOAs.References
- B. S. Sekhon, Nanotechnol., Sci. Appl., 2014, 7, 31–53 CrossRef PubMed.
- R. Liu and R. Lal, Sci. Total Environ., 2015, 514, 131–139 CrossRef CAS PubMed.
- D. Cordell, J. O. Drangert and S. White, Glob. Environ. Change, 2009, 19, 292–305 CrossRef.
- J. M. Hughes and J. F. Rakovan, Elements, 2015, 11, 165–170 CrossRef CAS.
- R. Liu and R. Lal, Sci. Rep., 2014, 4, 5686–5691 CAS.
- D. Montalvo, F. Degryse and M. J. McLaughlin, Soil Sci. Soc. Am. J., 2015, 79, 577–584 CrossRef CAS.
- E. Frossard, M. Brossard, M. J. Hedley and A. Metherell, in Phosphorus Cycling in Terrestrial and Aquatic Ecosystems: A Global Perspective, ed. H. Tiessen, SCOPE/John Wiley, 1995, pp. 107–137 Search PubMed.
- T. R. Fox and N. B. Comerford, Soil Sci. Soc. Am. J., 1990, 54, 1139–1144 CrossRef CAS.
- D. L. Jones, Plant Soil, 1998, 205, 25–44 CrossRef CAS.
- P. Hinsinger, Plant Soil, 2001, 237, 173–195 CrossRef CAS.
- G. Furrer and W. Stumm, Geochim. Cosmochim. Acta, 1986, 50, 1847–1860 CrossRef CAS.
- B. Zinder, G. Furrer and W. Stumm, Geochim. Cosmochim. Acta, 1986, 50, 1861–1869 CrossRef CAS.
- J. I. Drever and L. L. Stillings, Colloids Surf., A, 1997, 120, 167–181 CrossRef CAS.
- A. Longinelli and S. Nuti, Earth Planet. Sci. Lett., 1973, 19, 373–376 CrossRef CAS.
- R. E. Barrick and W. J. Showers, Science, 1994, 265, 222–224 CAS.
- R. E. Blake, S. J. Chang and A. Lepland, Nature, 2010, 464, 1029–1032 CrossRef CAS PubMed.
- R. E. Blake, J. R. O'Neil and G. A. Garcia, Geochim. Cosmochim. Acta, 1997, 61, 4411–4422 CrossRef CAS.
- A. Paytan, Y. Kolodny, A. Neori and B. Luz, Global Biogeochem. Cycles, 2002, 16, 13 CrossRef.
- D. C. Gooddy, D. J. Lapworth, S. A. Bennett, T. H. E. Heaton, P. J. Williams and W. J. Surridge, Water Res., 2016, 88, 623–633 CrossRef CAS PubMed.
- D. C. Gooddy, D. J. Lapworth, M. J. Ascott, S. A. Bennett, T. H. E. Heaton and W. J. Surridge, Environ. Sci. Technol., 2015, 49, 9020–9028 CrossRef CAS PubMed.
- R. E. Blake, J. R. O'Neil and A. V. Surkow, Am. J. Sci., 2005, 305, 596–620 CrossRef CAS.
- C. Lecuyer, P. Grandjean and S. M. F. Sheppard, Geochim. Cosmochim. Acta, 1999, 63, 855–862 CrossRef CAS.
- J. R. O'Neil, T. W. Vennemann and W. F. McKenzie, Geochim. Cosmochim. Acta, 2003, 67, 3135–3144 CrossRef.
- D. P. Jaisi and R. E. Blake, Adv. Agron., 2014, 125, 1–53 CrossRef.
- D. P. Jaisi, R. E. Blake and R. K. Kukkadapu, Geochim. Cosmochim. Acta, 2010, 74, 1309–1319 CrossRef CAS.
- D. P. Jaisi, J. Contam. Hydrol., 2013, 154, 10–19 CrossRef CAS PubMed.
- D. Wang, Y. Jin and D. P. Jaisi, J. Contam. Hydrol., 2015, 182, 194–209 CrossRef CAS PubMed.
- Y. Liang and R. E. Blake, Chem. Geol., 2007, 238, 121–133 CrossRef CAS.
- S. R. Joshi, X. Li and D. P. Jaisi, Soil Sci. Soc. Am. J., 2016, 80, 69–78 CrossRef.
- F. Tamburini, V. Pfahler, C. von Sperber, E. Frossard and S. M. Bernasconi, Soil Sci. Soc. Am. J., 2013, 78, 38–46 CrossRef.
- D. Wang, S. A. Bradford, R. W. Harvey, B. Gao, L. Cang and D. M. Zhou, Environ. Sci. Technol., 2012, 46, 2738–2745 CrossRef CAS PubMed.
- D. Wang, Y. Jin and D. P. Jaisi, Environ. Sci. Technol., 2015, 49, 8461–8470 CrossRef CAS PubMed.
- S. A. Welch, A. E. Taunton and J. F. Banfield, Geomicrobiol. J., 2002, 19, 343–367 CrossRef CAS.
- A. I. Schafer, A. G. Fane and T. D. Waite, Desalination, 2000, 131, 215–224 CrossRef CAS.
- J. Liu and R. H. Hurt, Environ. Sci. Technol., 2010, 44, 2169–2175 CrossRef CAS PubMed.
- T. Harter, S. Wagner and E. R. Atwill, Environ. Sci. Technol., 2000, 34, 62–70 CrossRef CAS.
- B. Nowack, J. F. Ranville, S. Diamond, J. A. Gallego-Urrea, C. Metcalfe, J. Rose, N. Horne, A. A. Koelmans and S. J. Klaine, Environ. Toxicol. Chem., 2012, 31, 50–59 CrossRef CAS PubMed.
- W. X. Zhang, J. Nanopart. Res., 2003, 5, 323–332 CrossRef CAS.
- J. Murphy and J. P. Riley, Anal. Chim. Acta, 1962, 27, 31–36 CrossRef CAS.
- D. Wang, L. Chu, M. Paradelo, W. J. G. M. Peijnenburg, Y. Wang and D. Zhou, J. Colloid Interface Sci., 2011, 360, 398–407 CrossRef CAS PubMed.
- F. Tamburini, S. M. Bernasconi, A. Angert, T. Weiner and E. Frossard, Eur. J. Soil Sci., 2010, 61, 1025–1032 CrossRef CAS.
- M. W. Guidry and F. T. Mackenzie, Geochim. Cosmochim. Acta, 2003, 67, 2949–2963 CrossRef CAS.
- C. Chairat, J. Schott, E. H. Oelkers, J. E. Lartigue and N. Harouiya, Geochim. Cosmochim. Acta, 2007, 71, 5901–5912 CrossRef CAS.
- K. W. Ulrich, A. Singh, E. J. Schofield, J. R. Bargar, H. Veeramani, J. O. Sharp, R. Bernier-Latmani and D. E. Giammar, Environ. Sci. Technol., 2008, 42, 5600–5606 CrossRef CAS PubMed.
- S. V. Dorozhkin, Prog. Cryst. Growth Charact. Mater., 2002, 44, 45–61 CrossRef CAS.
- J. L. Fox, W. I. Higuchi, M. B. Fawzi and M. S. Wu, J. Colloid Interface Sci., 1978, 67, 313–320 CrossRef.
- M. B. Fawzi, J. L. Fox, M. G. Dedhiya, W. I. Higuchi and J. J. Hefferren, J. Colloid Interface Sci., 1978, 67, 304–311 CrossRef CAS.
- W. Dansgaard, Tellus, 1964, 16, 436–468 CrossRef.
- K. Kpomblekou and M. A. Tabatabai, Agric., Ecosyst. Environ., 2003, 100, 275–284 CrossRef.
- E. Valsami-Jones, K. V. Ragnarsdottir, A. Putnis, D. Bosbach, A. J. Kemp and G. Cressey, Chem. Geol., 1998, 151, 215–233 CrossRef CAS.
- L. Wu, W. Forsling and P. W. Schindler, J. Colloid Interface Sci., 1991, 147, 178–185 CrossRef CAS.
- W. Stumm, Colloids Surf., A, 1997, 130, 143–166 CrossRef.
- K. W. Goyne, S. L. Brantley and J. Chorover, Chem. Geol., 2006, 234, 28–45 CrossRef CAS.
- J. I. Drever, Geochim. Cosmochim. Acta, 1994, 58, 2325–2332 CrossRef CAS.
- M. R. T. Filgueiras, D. Mkhonto and N. H. de Leeuw, J. Cryst. Growth, 2006, 294, 60–68 CrossRef CAS.
- C. Christophe, T. Marie-Pierre, F. K. Pascale, U. Stephane, P. Marie-Claire, T. Zornitza and K. Antoine, Geochim. Cosmochim. Acta, 2013, 106, 287–306 CrossRef.
- J. Liu, D. A. Sonshine, S. Shervani and R. H. Hurt, ACS Nano, 2010, 4, 6903–6913 CrossRef CAS PubMed.
- T. S. Peretyazhko, Q. Zhang and V. L. Colvin, Environ. Sci. Technol., 2014, 48, 11954–11961 CrossRef CAS PubMed.
- S. Aramrak, M. Flury, J. B. Harsh, R. L. Zollars and H. P. Davis, Langmuir, 2013, 29, 5770–5780 CrossRef CAS PubMed.
- M. B. Seymour, G. Chen, C. Su and Y. Li, Environ. Sci. Technol., 2013, 47, 8391–8398 CAS.
- C. Kendall, in Isotope Tracers in Catchment Hydrology, ed. C. Kendall and J. J. McDonnell, Elsevier Science, Amsterdam, 1998, pp. 519–576 Search PubMed.
- J. R. O'Neil, R. N. Clayton and T. K. Mayeda, J. Chem. Phys., 1969, 51, 5547–5558 CrossRef.
- A. V. Turchyn, B. Volker, T. W. Lyons, G. S. Engel, N. Balci, D. P. Schrag and B. Brunner, Geochim. Cosmochim. Acta, 2010, 74, 2011–2024 CrossRef CAS.
- J. F. Duncan and G. B. Cook, Isotopes in Chemistry, Clarendon Press, Oxford, 1968, p. 273 Search PubMed.
- D. P. Jaisi, R. K. Kukkadapu, L. M. Stout, T. Varga and R. E. Blake, Environ. Sci. Technol., 2011, 45, 6254–6261 CrossRef CAS PubMed.
- J. V. Turner, Geochim. Cosmochim. Acta, 1982, 46, 1183–1191 CrossRef CAS.
- H. R. von Uexkull and E. Mutert, Plant Soil, 1995, 171, 1–15 CrossRef CAS.
- S. J. Chang and R. E. Blake, Geochim. Cosmochim. Acta, 2015, 150, 314–329 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Includes Tables S1 and S2 and Fig. S1–S12. See DOI: 10.1039/c6en00085a |
| This journal is © The Royal Society of Chemistry 2016 |





