Insight into the effects of surface oxidation and carbonization on the electronic properties of silicon quantum dots and silicon slabs: a density functional study

Abstract

In this work, we investigated the effects of surface backbond-oxygen oxidation and surface substitute-carbon carbonization on carrier recombination and transportation of 10-, 12- and 14 Å Si quantum dots (QDs). In general, surface oxidation lowered the density of states (DOS) near the Fermi level and induced the inward shift of the frontier-level isosurface, whereas surface carbonization induced the opposite effects. As indicated by the calculation, surface oxidation suppressed carrier recombination and carrier transportation, while surface carbonization enhanced it. Our further studies revealed that the effects of surface oxidation and carbonization were also applicable to Si slabs with different orientations. In summary, our work suggested that to dope a certain amount of oxygen into surface carbonized Si quantum-dots or Si bulk material might be a pathway to passivate surface defects by means of surface oxidation.

---

1. Introduction

The quantum confinement effect makes silicon quantum dots (Si QDs) interesting if the diameter of the Si QD approaches or is below the exciton Bohr radius (about 5 nm).^1,2 Due to the adjustable energy band gap, Si QDs have great potential to be used in new-generation electronic devices including solar cells.^3,4 Si QD embedded in SiC matrix is considered as one of the promising candidate material for solar cell because of its adjustable band gap and low carrier transport barrier.^3,5,6 However, Si QD embedded in SiC matrix shows poor photoluminescence (PL) performance,⁷ which probably resulted from significant intrinsic defects as well as surface carrier recombination.^5,8,9 It is noted that Si QD embedded in SiO_x matrix exhibits good PL performance.^10–12 This indicates that carrier recombination is much lower in the SiO_x-matrix Si QD, because PL performance should deteriorate if surface carrier recombination is severe.¹³

It is inspired that to dope oxygen into SiC-matrix Si QD might be beneficial to passivate surface defects and to reduce carrier recombination. Unfortunately, to prove this assumption by means of experiment is difficult because of the experimental difficulty in qualitatively determination of the effects of oxygen passivation for Si-QD materials. Also, to study the effects of oxygen doping on electronic structure of Si QDs through experiment seems unfeasible. In this case, employing first-principle calculation tools^14,15 to compare the effects of surface oxidation and carbonization on electronic properties of Si QD is necessary.

In this work, we used DMol3 (local density functional calculations on molecule)^16,17 and CASTEP (Cambridge Serial Total Energy Package)¹⁸ software packages that are based on density functional theory (DFT) to study the effects of surface oxidation and carbonization on Si QDs and Si slabs. We found that surface oxidation could reduce the density of state (DOS) near Fermi level in Si QDs and Si slabs, which suggested that surface oxidation was good to reduce surface recombination of Si QDs and Si slabs. To dope a certain amount of oxygen impurity to realize surface oxidation might be an effective pathway to suppress the surface recombination of SiC-matrix Si QDs.

2. Experimental details

2.1 Model and method

We built the models of Si QDs and Si slabs to study the effects of surface carbonization and oxidation on Si QD and Si crystal.

The model of surface carbonization of Si QD was presented as following. Firstly, we built a 12 Å-diameter Si QD (Si₄₇H₆₀) with surface terminated by H and looked for the preferential doping position of carbon. Population analysis revealed that there were seven different chemical states of Si. Each Si with different chemical state was substituted by C. And then, we optimized all the C-substituted Si QDs, compared their system total energies, identified the most stable structure, and discovered the preferential substitute position of carbon. Finally, we built the surface carbonization Si QDs, optimized the structures, and studied the electronic structures.

Apart from Si QD, we built (100)-, (111)-, and (110)-orientation Si slabs with 8, 8, and 9 layers to investigate the effects of carbonization on Si crystal. The thickness of vacuum is 12 Å to make sure to avoid interaction between the neighboring slabs. We only considered the clean surface which was not terminated by hydrogen and only considered the cases of C covering the top layer of Si slab. The top three layers of each Si slab were fully relaxed to simulate Si surface, while the inner layers were totally fixed to simulate Si bulk. We relaxed the Si slabs, compared their system total energies, and identified the most stable structure. It should be mentioned that surface reconstruction of Si slab was not considered in the work.

As for surface oxidation, we mainly concerned the preferential oxidation state of backbond O, since backbond O is believed as the most possible oxidation state and it prefer to oxidize the outmost surface Si.¹⁹ Then, we used backbond O to oxidize the outmost surface Si atoms with different chemical state, optimized all the structures, compared their system total energy, and found the most stable structure. After that, we built the Si QDs with its outmost Si oxidized by backbond O, optimized the geometry, and studied the electronic structure. Besides, we also studied the effects of surface oxidation on Si slab. The study method was similar to that of carbonization for Si slab. We only considered the case of O covering the top layer.

2.2 Details of calculation

The calculations were performed using the modules of materials studio: DMol3 (ref. 16 and 17) and CASTEP.¹⁸ The optimization of Si QD was carried out using DMol3 in the framework of all-electron DFT. Becke–Lee–Yang–Parr (BLYP) functional at the generalized gradient approximation (GGA) level was adopted as correlation exchange functional. Double numerical basis sets augmented with p-polarization functions (DNP basis sets) were used as the atomic orbital basis functions. Energy, maximum forces, and maximum displacement of convergence tolerance during geometry optimization were set at 1.0 × 10⁻⁵ Ha per atom, 0.002 Ha Å⁻¹ and 0.005 Å, respectively. The self-consistent field (SCF) convergence threshold was 1 × 10⁻⁶.

Si slab models were calculated using CASTEP. During CASTEP calculation, Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) level was adopted as the correlation exchange functional. Ultrasoft pseudopotential, a cutoff of 350 eV for plane wave basis set, and the k-point grid of 5 × 5 × 1 were adopted. Energy, maximum forces, and maximum stresses of convergence tolerance during geometry optimization were set at 5.0 × 10⁻⁶ eV per atom, 0.01 eV Å⁻¹ and 0.02 GPa, respectively. The SCF convergence threshold of 1.0 × 10⁻⁶ eV per atom was adopted.

3. Results and discussion

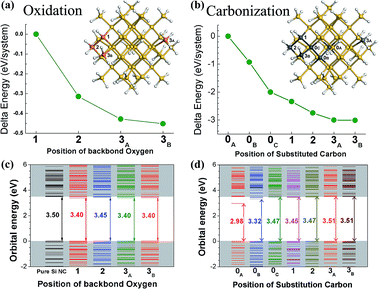
Fig. 1(a) and (b) show the delta system-total energy of the 12 Å Si QD with different oxidized and carbonized states, and the inserts of Fig. 1(a) and (b) are the 12 Å Si QDs whose O-oxidized and C-substituted atoms are marked using orange and gray, respectively. The number of the mark denotes the number of hydrogen surrounding Si, and the subscript letter was used to identify different chemical environment. In this work, we employed Mulliken population analysis^20,21 that provides a means to estimate partial atomic charges by the methods of computational chemistry based on the linear combination of atomic/molecular orbital method. Different surrounding atom coordination leads to different atom charge. There are seven different chemical states of Si in 12 Å Si QD according to the calculation. For the carbonization model, each Si with different chemical states was substituted by C. For the oxidation model, only the surface Si was oxidized by backbond O, since backbond O is considered as the most possible oxidation state that prefers to oxidize the surface Si.¹⁹ After optimizing geometry structures and comparing system-total energies, the most stable oxidized or carbonized Si-QD structure was identified.

Fig. 1 (a and b) show the delta system-total energy of the 12 Å Si QD with different oxidized and carbonized states; the inserts show the 12 Å Si QD whose O-oxidized and C-substituted atoms are marked using orange and gray, respectively; (c and d) show orbital energies of the various O-oxidized and C-substituted 12 Å Si QD.

As shown in Fig. 1(a) and (b), backbond O and substitution C at the “3_A” and “3_B” positions led to the lowest system-total energy. The results indicated that backbond O and substitution C preferred to react with the outmost Si of Si QD. The preferential oxidation and carbonization for the outmost Si was in agreement with the self-purity effect.^22,23

Fig. 1(c) and (d) show the orbital energies of the different O-oxidized and C-substituted Si QDs. The energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the H-passivation 12 Å Si QD is 3.50 eV. surface oxidation and carbonization both altered energy band gap of Si QDs. When the backbond O was inserted into “1”, “2”, and “3” Si, the energy gaps were all reduced. Surface oxidation reduced energy band gap, which was in agreement with the existing calculation results^24–27 and experiment evident.²⁸ However, there were two influences of surface C-substitution on energy gap. When the C substituted “0”,“1” and “2” Si, the energy gaps were reduced; while the C substituted “3” Si, the energy gap was increased. Apparently, energy band gap increased if C substituted for the outmost Si, the “3” Si; otherwise, it reduced if C substituted for the non-outmost Si.

We built three Si-QD structures to compare the effects of surface carbonization and oxidation, as shown in Fig. 2(a). The outmost Si, the “3” Si, were all carbonized or oxidized. The chemical components of the three Si QDs are Si₄₇H₆₀, Si₃₅C₁₂H₆₀, and Si₄₇O₁₂H₆₀ respectively. It was found that the energy gaps of Si₄₇H₆₀, Si₃₅C₁₂H₆₀, and Si₄₇O₁₂H₆₀ were 3.50, 3.72 and 2.64 eV respectively, as shown in Fig. 2(d). Obviously, increment of surface substituted C enlarged the energy gap, whereas increment of backbond O shrunk the energy gap.

Fig. 2 (a–c) show the pure H-passivation (Si₄₇H₆₀), carbonization (Si₃₅C₁₂H₆₀) and oxidization (Si₄₇O₁₂H₆₀) 12 Å Si QDs; (d and e) show the orbital energies and DOSs of the responding Si QD. The insert of (e) is the amplificatory DOSs near Fermi level.

Before the following discussion, it needs to clarify two issues herein. First, Fermi level is the term used to describe the top of the collection of electron energy levels at absolute zero temperature; no electrons will have enough energy to rise above Fermi level at this temperature. In the calculation of CASTEP or DMol3, Fermi level is generally set at the top of valance band because first-principle calculation only considers electronic structure at absolute zero temperature.

Second, the discussion of recombination of carrier is based on Shockley–Read–Hall (SRH) statistics that is developed to describe the transition rate of carrier, as seen in eqn (1). SRH statistics has considered both cases of carrier distribution, i.e., balance and non-balance states. It is supposed that SRH statistics is eligible to describe the carrier distribution at excited state since excited state is one of the non-balance states. According to SRH statistics, energy level near the mid gap of un-doped semiconductor or near Fermi level of doped semiconductor is the so-called deep energy level that is the effective recombination and generation center.²⁹ If energy level locates near Fermi level, it will be the effective recombination center of carrier.

where U is the net transition rate (U = R_e − G_th), R_e the recombination rate, G_th the thermal generation rate, σ_n and σ_p the electron and hole capture cross sections, v_th the thermal velocity, N_t the density of trap, E_t and E_i the trap level and intrinsic Fermi level, p and n the concentration of hole and electron, n_i the intrinsic concentration of carrier, k Boltzmann constant, T the absolute temperature.

Fig. 2(e) shows the DOSs of the three 12 Å Si QD. It was found that the DOS near Fermi level was the highest in the carbonized Si QD whereas it was the lowest in the oxidized one. DOS is the term to describe the number of states per interval of energy at each energy level that is available to be occupied by electrons. Reasonably, higher DOS at Fermi level means higher possibility of recombination of carrier. Lowering DOS near Fermi level is helpful to reduce carrier recombination. According to the calculation, it suggested that surface carbonization might induce recombination defect states into Si-QD materials, which was quite coincident with the existing reports.^5,8,9 In comparison with surface carbonization, surface oxidation reduced DOS near Fermi level by one third, which suggested that surface oxidation was beneficial to suppress carrier recombination of the 12 Å Si QDs.

The isosurface of HOMO and LUMO of the Si₄₇H₆₀, Si₃₅C₁₂H₆₀, and Si₄₇O₁₂H₆₀ Si QDs is presented in Fig. 3. In comparison with the H-passivation Si QD, isosurface of the carbonized one clearly shifted outwards to QD entity with a part of LUMO isosurface locating on the outmost atoms, though outward shift of HOMO isosurface was not as obvious as LUMO one. In contrast, LUMO and HOMO isosurface of the oxidized Si QD generally shifted inwards to QD entity. It is known that HOMO and LUMO orbital are the so-called frontier levels.^30,31 Frontier levels are more fierce than other orbital levels in terms of reactivity, as pointed out by Kenichi Fukui.^30,31 Inward shift of isosurface would lower surface recombination of Si QD.

Fig. 3 (a–c) show LUMO isosurface and (d–f) show the HOMO isosurface of the pure H-passivated (Si₄₇H₆₀), carbonized (Si₃₅C₁₂H₆₀) and oxidized (Si₄₇O₁₂H₆₀) 12 Å Si QDs.

Furthermore, it needs to point out that the inward shift of frontier level would reduce the overlap of electronic levels between neighboring Si QDs and lower the possibility of carrier transport between neighboring Si QDs, as carrier transportation largely depends on overlap of electronic levels.⁴ In other words, surface oxidation resulted in lower carrier transport and lower conductivity, in agreement with the previous study.³²

Apart from the 12 Å Si QD, we also considered the effects of surface back-O oxidation and substitute-C carbonization on electronic structure of 10 Å (Si₃₀H₄₀/Si₂₆O₄H₄₀/Si₂₆C₄H₄₀) and 14 Å (Si₇₁H₈₄/Si₅₉O₁₂H₈₄/Si₅₉C₁₂H₈₄) Si QDs, as shown in Fig. 4. Surface oxidation lead to the shrink of energy band gap in 10- and 14 Å Si QDs, while surface carbonization lead to the broadening of band gap. Besides, surface oxidation reduced DOS at Fermi level in 10- and 14 Å Si QDs, compared with surface carbonization. Till now, we had considered the 10-, 12- and 14 Å Si QDs and found that the effects of surface carbonization and surface oxidation were generally coherent in these Si QDs. However we should not simply extrapolate the effects to Si QDs with other size, because maybe some un-considered factors will influence the electronic structures. Anyway, the consideration of the 10-, 12- and 14 Å Si QDs still provided a good way to estimate the effects of surface carbonization and surface oxidation on Si QDs.

Fig. 4 (a–b) and (c–d) show – orbital energy, DOS and local amplificatory DOS near Fermi level of the pure H-passivation, surface carbonized and surface oxidized 10 Å (Si₃₀H₄₀/Si₂₆O₄H₄₀/Si₂₆C₄H₄₀) and 14 Å Si QDs (Si₇₁H₈₄/Si₅₉O₁₂H₈₄/Si₅₉C₁₂H₈₄), respectively.

Moreover, we also built three Si slabs whose top layers were covered with Si, C and O respectively, as shown in Fig. 5(a). The brown, yellow and green balls represent bulk Si, surface Si and surface covering atoms (Si, C or O) respectively. After geometer relaxation, the DOSs of these relaxed slabs were studied, as shown in Fig. 5(b). It was found that all the Si slabs had DOS across band gap. The DOS near Fermi level of the carbon-covered slab was higher than that of the Si-covered slab in both (100)- and (110)-orientations, but slightly lower in (111)-orientation, which meant that carbon covering generally resulted in more serious carrier recombination. In contrast, oxygen covering reduced DOSs near Fermi level in (100)- (110)- and (111)-orientation Si slabs, which suggested that oxygen covering suppressed the carrier recombination and benefited defects passivation.

Fig. 5 Show the (a) models and (b) DOSs of the surface H-passivated, carbonized and oxidized Si slabs with (100)-, (111)-, (110)- orientations. The curves at the bottom of Fig. 5(b) are the amplificatory DOSs near Fermi level.

4. Conclusion

We studied the effects of surface backbond-O oxidation, and surface substitute-C carbonization on carrier recombination relative electronic properties of the 10-, 12- and 14 Å Si QDs. The backbond O and the substitute C preferred to react with the outmost Si connecting three H atoms. Generally, surface oxidation effectively lowered the DOS near Fermi level and induced inward shift of frontier-level isosurface. It meant that that surface oxidation reduced carrier recombination and also suppressed carrier transportation of Si QD. However, surface carbonization generally brought opposite effects, i.e., it raised carrier recombination and carrier transportation. Apart from Si QDs, surface oxidation was also effective to reduce DOS near Fermi level in Si slabs with (100)-, (111)-, or (110)-orientation. In summary, our study suggested that surface oxidation might be helpful to reduce DOS near Fermi level in both Si QDs and Si slabs in comparison with surface carbonization. However the effects still cannot be simply extrapolated to Si QDs with other size, because maybe some un-considered factors would influence the electronic structures. Anyway, it was inspired that to add oxygen impurity to Si QD and Si crystalline particles may be a beneficial pathway to passivate defects of these materials.

Acknowledgements

The authors would like to thank the financial supports by Natural Science Foundation of China (Grant no. 61106096, 11344012 and 11204146), Natural Science Foundation of Ningbo (Grant no. 2014A610036), and the support from Ningbo Key Laboratory of Silicon and Organic Thin Film Optoelectronic Technologies.

Notes and references

1. C. Bulutay, S. Ossicini and G. Conibeer, Silicon Nanocrystals: Fundamentals, Synthesis and Applications, ed. L. Pavesi and R. Turan, Wiley-VCH, Germany, 2010, vol. 5–41, pp. 555–582.
2. E. G. Barbagiovanni, D. J. Lockwood, P. J. Simpson and L. V. Goncharova, Appl. Phys. Rev., 2014, 1(1), 011302.
3. G. Conibeer, Applications of Si Nanocrystals in Photovoltaic Solar Cells, in Silicon Nanocrystals: Fundamentals, Synthesis and Applications, ed. L. Pavesi and R. Turan, Wiley-VCH, Germany, 2010, pp. 555–582.
4. J.-W. Luo, P. Stradins and A. Zunger, Energy Environ. Sci., 2011, 4(7), 2546–2557.
5. P. Loper, M. Canino, D. Qazzazie, M. Schnabel, M. Allegrezza, C. Summonte, S. W. Glunz, S. Janz and M. Zacharias, Appl. Phys. Lett., 2013, 102, 033507.
6. S. Gutsch, J. Laube, A. Hartel, D. Hiller, N. Zakharov, P. Werner and M. Zacharias, J. Appl. Phys., 2013, 133703.
7. S. K. Ray, S. Maikap, W. Banerjee and S. Das, J. Phys. D: Appl. Phys., 2013, 46, 153001.
8. L. E. Ramos, E. Degoli, G. Cantele, S. Ossicini, D. Ninno, J. Furthmuller and F. Bechstedt, J. Phys.: Condens. Matter, 2007, 19, 466211.
9. Z. Ni, X. Pi and D. Yang, RSC Adv., 2012, 2, 11227–11230.
10. L. Pavesi, L. Dal Negro, C. Mazzoleni, G. Franzo and F. Priolo, Nature, 2000, 408(6811), 440–444.
11. M. Zacharias, J. Heitmann, R. Scholz, U. Kahler, M. Schmidt and J. Blasing, Appl. Phys. Lett., 2002, 80(4), 661–663.
12. B. G. Fernandez, M. Lopez, C. Garcia, A. Perez-Rodriguez, J. R. Morante, C. Bonafos, M. Carrada and A. Claverie, J. Appl. Phys., 2002, 91(2), 798–807.
13. L. Tsakalakos, Mater. Sci. Eng., R, 2008, 62(6), 175–189.
14. D. S. Sholl and J. A. Steckel, Density functional theory – a practical introduction, John Wiley & Sons, Inc., New Jersey, 2009.
15. I. N. Levine, Quantum Chemistry, Pearson Education, New Jersey, 6th edn, 2008.
16. B. Delley, J. Chem. Phys., 1990, 92(1), 508–517.
17. B. Delley, J. Chem. Phys., 2000, 113(18), 7756–7764.
18. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220(5–6), 567–570.
19. X. B. Chen, X. D. Pi and D. R. Yang, J. Phys. Chem. C, 2010, 114(19), 8774–8781.
20. W. J. Hehre, J. Mol. Struct., 1997, 41(1), 163.
21. R. S. Mulliken, J. Chem. Phys., 1955, 23(10), 1833–1840.
22. S. C. Erwin, L. Zu, M. I. Haftel, A. L. Efros, T. A. Kennedy and D. J. Norris, Nature, 2005, 436(7047), 91–94.
23. M. Shim and P. Guyot-Sionnest, Nature, 2000, 407(6807), 981–983.
24. C. Bulutay and S. Ossicini, Electronic and Optical Properties of Silicon Nanocrystals, in Silicon Nanocrystals: Fundamentals, Synthesis and Applications, ed. L. Pavesi and R. Turan, Wiley-VCH, Germany, 2010, pp. 18–22.
25. D. König, J. Rudd, M. A. Green and G. Conibeer, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035339.
26. M. Luppi and S. Ossicini, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035340.
27. K. Seino, F. Bechstedt and P. Kroll, Nanotechnology, 2009, 20, 135702.
28. G. Conibeer, Applications of Si Nanocrystals in Photovoltaic Solar Cells, in Silicon Nanocrystals: Fundamentals, Synthesis and Applications, ed. L. Pavesi and R. Turan, Wiley-VCH, Germany, 2010, pp. 559–562.
29. S. M. Sze and K. K. Ng, Physics of semiconductor devices, Joan Wiley & Song, Inc., New Jersey, 3rd edn, 2007.
30. K. Fukui and H. Fujimoto, Frontier Orbitals and Reaction Paths: Selected Papers of Kenichi Fukui, World Scientific Publishing Co Pte Ltd, 1997.
31. K. Fukui, Science, 1982, 218(4574), 747–754.
32. K. Seino, F. Bechstedt and P. Kroll, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075312.

---