Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A kinetic study of mechanically activated atom exchange: the effect of milling frequency and ball mass†
Maria
Carta‡
a,
Stipe
Lukin‡
b,
Francesco
Delogu
 *a and
Ivan
Halasz
*b
*a and
Ivan
Halasz
*b
aDepartment of Mechanical, Chemical and Materials Engineering, CSGI research unit, University of Cagliari, via Marengo 2, Cagliari, Italy. E-mail: francesco.delogu@unica.it
bDivision of Physical Chemistry, Ruđer Bošković Institute, Bijenička 54, Zagreb, Croatia. E-mail: ivan.halasz@irb.hr
First published on 20th May 2024
Abstract
This study investigates the mechanochemical reaction of hydrogen isotope exchange between solid benzoic acid and liquid heavy water. The systematic change of milling conditions revealed that the reaction rate scales with the milling frequency and the mass of the milling balls. The ball size being always the same, faster reactions stem from the use of higher milling frequencies and heavier balls. The kinetic curves are described by a kinetic model that accounts for the statistical, deformational and chemical factors involved in mechanochemical transformations. The results indicate that the reaction is driven by the generation of a new interface area caused by the deformation of the solid reactants.
1. Introduction
Starting from the end of the 1960s, mechanochemistry has reiteratively gone through periods of expansion.1–3 After first changing the face of metallurgy, and then of materials science, it is presently innovating the synthetic strategies of inorganic and organic chemistry within the framework of green chemistry.1–3 And yet, the proper identification and understanding of the kinetic and mechanistic features of mechanochemical reactions has remained an open issue despite its particular significance for fundamental science and practical exploitation.The challenging nature of kinetic studies in mechanochemistry is well known.4 Mechanochemical transformations have multifaceted character and their inherent complexity emerges regardless of the system investigated and the method of mechanical processing utilized. In any case, the physical and chemical changes occur simultaneously across a broad range of length and time scales. This is especially evident for mechanochemical transformations activated by ball milling (BM).5
The BM of powders is based on the occurrence of impacts between milling tools. During individual impacts, a few cubic millimetres of powder are compressed within a few hundred microseconds at the most.6 The consequent dynamic compaction takes place at high strain rates7 and results in the uneven distribution of local mechanical stresses.8 Intense forces build up at the contact points between powder particles, determining comminution and deformation on the micrometre scale over time intervals of microseconds.8 Local shearing allows the generation of interfaces where dislocation activity can affect the surroundings of individual atoms and molecules at rates of nanometres per nanosecond.9 Eventually, molecules may react with each other as long as local temperatures, which can decrease at rates of about tens of Kelvin degrees per nanosecond,10 ensure the necessary energy and mobility.
Consequently, mechanochemical reactions are a concoction of factors related to mechanical energy deposited during the impacts, mutual exposure of fresh surfaces of reactant phases and intrinsic chemical behaviour of reactant molecules as they come in contact.11,12 Separating each of these contributions to the overall mechanochemical transformation has proved to be demanding. We have recently been able to study in macroscopic13 and microscopic14 detail a purely mechanically activated reaction that does not depend on mixing, but solely on the absorption of mechanical energy during impacts. First, we have demonstrated a linear relationship between the reaction rate and the kinetic energy that the reacting system absorbed from the milling ball.13 Second, we have realised that the overall reaction rate observed on the bulk stems from minute transformations occurring upon each individual impact.14
Here, we study the mechanochemical process in the other extreme, where we expect the reaction to be dominated by interface generation and mixing. For this purpose, we investigate the hydrogen isotope exchange (HIE) between solid benzoic acid and liquid heavy water (D2O) (Scheme 1). We expect the statistical distribution of deuterium atoms to be established resulting with 1/3 benzoic acid molecules with protium and 2/3 deuterated benzoic acid. There will also be 4/9 water molecules as HOD or DOH, 4/9 as DOD and 1/9 as HOH.
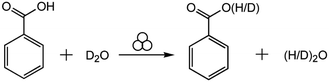 | ||
| Scheme 1 The mechanochemical reaction of hydrogen isotope exchange between solid benzoic acid and liquid heavy water. | ||
The primary objective of the study is to verify the occurrence of the HIE reaction under BM conditions and to examine its kinetics. To this aim, we monitored the reaction in situ by Raman spectroscopy and estimated the relative amounts of the hydrogenated and deuterated species. We systematically changed the milling frequency as well as the mass of the two milling balls used in experiments. We had the foresight to use milling balls made of different materials with the aim of using balls with the same volume. In this way, we avoid undesired kinetic effects related to the different ball volume and, possibly, the different amount of powder effectively compressed during individual impacts. We show that HIE occurs without difficulties according to a sigmoidal kinetics. The reaction rate changes with both the milling frequency and the ball mass.
2. The system
Benzoic acid is a white crystalline solid poorly soluble in water at room temperature, only about 3.5 g of benzoic acid can be dissolved in 1.0 L of water.15 In aqueous solution, it is a weak acid with a dissociation constant approximately equal to 6.4 × 10−5 mol L−1.16 In the presence of D2O, the acidic hydrogen of the carboxylic group exchanges with deuterium forming, on the bulk, a partially deuterated sample of benzoic acid. The poor solubility of benzoic acid does not allow rapid H/D exchange and, in the absence of external factors, no significant progression of the deuteration process can be expected in the solid benzoic acid in short observation times. Indeed, HIE can only affect the small amount of benzoic acid dissolved in D2O and the molecules lying at the liquid–solid interface. Therefore, the area of the liquid–solid interface represents an intrinsic limiting factor of the deuteration process. Under these conditions, mechanical processing by BM can be very effective in speeding up the deuteration through the continuous generation of fresh interface area that can then participate in the HIE reaction.3. Mechanically activated deuteration
BM was performed utilizing an InSolido Technologies IST500 ball mill that makes a cylindrical jar undergo a pendulum-like oscillation in the horizontal plane. Reactions were conducted in PMMA jars with rounded bases using two 7-mm balls made from either stainless steel (SS, mass of each 1.42 g), zirconia (ZrO2, 1.06 g), tungsten carbide (WC, 2.86 g) and one combination that used one SS ball and one WC ball (FeWC, 1.42 g and 2.86 g). The balls of different materials have different mass, but the same size. In each reaction, 2 mmol of benzoic acid was weighed in one half of the jar and 2 mmol of D2O was added using a micropipette in the other half. Then, the two halves were snap-closed together carefully to ensure no contact between the solid and the liquid prior to the initiation of milling.Reactions were conducted in duplicate or triplicate at five different frequencies, namely 25.0, 27.5, 30.0, 32.5, and 35.0 Hz. For any given milling frequency, we changed the ball mass, but not the ball size. In this way, at least to a first approximation, the changes in the rate of HIE cannot be ascribed to a change in the ball size and possible changes in the geometry of ball impacts.
Deuteration was monitored by in situ Raman spectroscopy as described elsewhere in detail.17 As previously shown, benzoic acid remains a pure solid phase without a change of its polymorphic form, and it also remains in the form of a free flowing powder.18 In the course of BM, only the carboxylic H atom becomes partially replaced by D, together with the formation of HOD and H2O from D2O. Exchange with D at benzoic acid is observable in the Raman spectrum of the reaction mixture as an increase of intensity of the band at 765 cm−1 and a corresponding decrease in intensity of the band at 793 cm−1. Reaction profiles were obtained by fitting the changes in the intensity of the Raman band at 765 cm−1 belonging to deuterated benzoic acid, as described before.18 Prior to fitting, the spectral range between 560 cm−1 and 870 cm−1 was baseline-corrected. The spectra were then internally normalized based on the intensity of the Raman peak at 612 cm−1, which remains unaffected upon HIE. Full details on the experimental methods can be found in the ESI.†
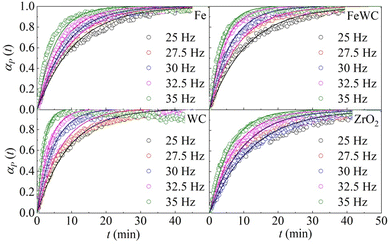
The change of the obtained peak intensities with the BM time constitutes the reaction profile for each reaction. The reaction profiles at different frequencies for the different pairs of milling balls are shown in Fig. 1. It can be seen that the kinetic curves have the same shape. At first glance, the curves seem to have merely an exponential character. However, a closer look at the initial stages of the kinetics suggests that the curves are slightly sigmoidal, with a very short induction period. In all the different cases, the effect of the milling frequency is evident. The rate of deuteration increases as the milling frequency increases. Nevertheless, a change in the milling frequency does not change the shape of the kinetic curve. Therefore, we can say that the transformation is isokinetic with the milling frequency, which involves the different curves being made to overlap with one another if their abscissae are scaled by a suitable factor (see ESI† for details).
 | ||
| Fig. 1 The molar fraction of deuterated benzoic acid, αP(t), as a function of time, t. Data refer to the BM experiments performed using balls made of different materials. | ||
4. Kinetic modelling
The phenomenological relationships so far can find a more formal description within the framework of a kinetic model able to take into account the inherent features of the mechanical processing by BM. The model has been fully described elsewhere,11 but details can be also found in the ESI.† The model takes into account the statistical nature of the mechanical processing by BM and relates the mechanochemical transformation to individual impacts. To this aim, it is assumed that the volume of powder compressed during individual impacts experiences heterogeneous mechanical loading conditions. Accordingly, the mechanochemical transformation occurs only in the set of small sub-volumes v* where the intensity of mechanical loading exceeds a certain threshold, thus enforcing critical loading conditions (CLCs). It is also assumed that the volumes v* are stochastically involved in CLCs and that the total volume affected by CLCs, v, does not change during the mechanical processing. Under these circumstances, the sub-volumes v* are affected by CLCs at a rate k corresponding to the product between the frequency of impacts and the ratio between v and the total volume of powder, V, inside the jar. The volume fraction of powder, χi(t), that has undergone CLCs i times after a time interval t can be expressed as| χi(t) = [(kt)i/i!]exp(−kt). | (1) |
Concerning the chemical changes induced by CLCs in sub-volumes ν*, it is reasonable to associate to volume fractions χi(t) specific values αP,i of the transformation degree in sub-volumes v* after i CLCs. Therefore, the total transformation degree, αP(t), can be written as the weighted average of the transformation degrees αP,i over the volume fractions χi(t)
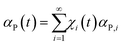 | (2) |
| Si = S0Sfin/[S0 + (Sfin − S0)exp(−ri)] | (3) |
| αP,i = 1−{[S0exp(ri) + (Sfin − S0)]/Sfin}−2ΠSfin/[rSAB(NA,0 + NB,0)], | (4) |
Eqn 2 combines three main factors, namely the statistics of mechanical processing through eqn 1, the mechanical deformation, or rheology, of reactant phases through the increase of the interface area described by eqn 3 and the chemical behaviour of molecular species at the interface based on the reaction probability is taken into account in eqn 4. The statistical, deformational and chemical factors cover, in principle, the main processes involved in the kinetics of mechanochemical reactions. Therefore, eqn 2 can provide a key to interpret the experimental evidence.
In the case of deuteration studied here, we have two reactant phases with very different properties. At room temperature, the benzoic acid is a solid with the melting point at around 120 °C, while D2O is a liquid. Given the relatively low melting point of benzoic acid, the sudden compression of the solid at impacts can be expected to induce significant deformation. Combined with the mobility and permeability of the liquid phase, such deformation can generate relatively large interface areas between the reactants. The fact that the chemical reaction can occur only once the reactants are in contact at the interface makes the kinetic curve intrinsically sigmoidal, in principle. The slope of the sigmoidal curve depends on both the rates of interface area generation and chemical reaction at the interface. In our case, both these rates can be expected to be relatively high, which means that the sigmoidal shape cannot be very pronounced. Indeed, this is what we actually observe.
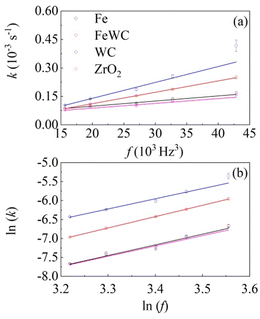
We used eqn 2 to best fit the experimental kinetic curves and the results are shown in Fig. 2. The model curves almost overlap the experimental data. In all the different cases, the model quantities related to the deformational and chemical factors do not differ significantly from case to case. This suggests that individual impacts induce an extensive deformation of the solid phase and that, accordingly, interface area is generated effectively. Under such circumstances, the reaction rate is limited by the amount of powder that undergoes CLCs during individual impacts, which is measured by the volume fraction of powder that undergoes CLCs in the unit time, k. In fact, we observe a linear change of k with the third power of the milling frequency, f, as shown in Fig. 3a.
Such dependence finds further evidence in the linear plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k versus ln
k versus ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f shown in Fig. 3b. Indeed, the slopes for the different datasets are quite similar to each other and compatible with a value of 3, namely 2.68 ± 0.23 for WC balls, 2.72 ± 0.44 for ZrO2 balls, 2.82 ± 0.28 for Fe balls and 2.99 ± 0.01 for mixed Fe and WC balls. This is not unexpected. A similar dependence has been already observed in several cases already reported in the literature, mostly regarding the formation of nanostructured metals and amorphous alloys by mechanical alloying.13,19 In all these cases, at least to a first approximation, the dependence of the apparent rate constant k on the third power of the milling frequency f can be related to the linear dependence of the impact frequency and impact velocity on f. Observing an exponent equal to 3 and a dependence on the ball mass strongly suggests that the local kinetics is governed by the kinetic energy that the ball transfers to powder compressed during the impact.13,19
f shown in Fig. 3b. Indeed, the slopes for the different datasets are quite similar to each other and compatible with a value of 3, namely 2.68 ± 0.23 for WC balls, 2.72 ± 0.44 for ZrO2 balls, 2.82 ± 0.28 for Fe balls and 2.99 ± 0.01 for mixed Fe and WC balls. This is not unexpected. A similar dependence has been already observed in several cases already reported in the literature, mostly regarding the formation of nanostructured metals and amorphous alloys by mechanical alloying.13,19 In all these cases, at least to a first approximation, the dependence of the apparent rate constant k on the third power of the milling frequency f can be related to the linear dependence of the impact frequency and impact velocity on f. Observing an exponent equal to 3 and a dependence on the ball mass strongly suggests that the local kinetics is governed by the kinetic energy that the ball transfers to powder compressed during the impact.13,19
It is worth noting that other scenarios can be, in principle, observed.20 Discriminating between such scenarios necessarily requires reducing the experimental uncertainties in the kinetic data. The problem does not concern exclusively the dependence of reaction rates on the milling frequency, but, more generally, the proper analysis of kinetic data. For instance, the uncertainties affecting our experimental kinetic curves do not allow the dependence of the interface area generation rate on the milling frequency to be reliably pointed out. Data are scattered and any attempt to finely tune the S0, Sfin, and r values appears as forcing. This is also true for the reaction probability between reactant molecules at the interface, Π. In this latter case, however, it is quite reasonable to use the same value for all the different cases investigated. Indeed, we do not expect that BM conditions affect the inherent chemical behaviour of the reactant species, at least to a first approximation.
5. Conclusions
The mechanical processing of benzoic acid and heavy water by BM results in the exchange of the acidic hydrogen of the benzoic acid with the deuterium made available from heavy water. The kinetic curves at different milling frequencies exhibit the same shape and a suitable scaling of the experimental reaction times can make the curves overlap. The scaling coefficients are proportional to the third power of the milling frequency, which can be interpreted as a signature of the isokinetic character of the mechanically induced deuteration process with the reaction extent being dependent on the total dose of mechanical energy transferred to the processed mixture. Further supporting evidence is that the scaling coefficients are also proportional to the mass of the milling balls.The experimental kinetic curves can be satisfactorily best fitted by the equations derived from a kinetic model that accounts for the statistical, deformational and chemical factors involved in mechanochemical transformations. The kinetic model suggests that the rate of the deuteration process is dominated by the amount of reactants effectively involved in mechanical loading processes during individual impacts. The rate constants we obtain exhibit a linear dependence on the third power of the milling frequency, which confirms the considerations made on a strictly phenomenological basis regarding the shape and overlapping of experimental kinetic curves. Furthermore, the kinetic model also suggests that the benzoic acid is deformed during impacts, resulting in the generation of the interface area between the two reactants.
The results of our kinetic study highlight the need for quality kinetic data to disentangle the different factors involved in mechanochemical reactions and gain deeper insight into the mechanistic features. It seems that the chemical factor is the most interesting quantity to study and only its accurate estimation can unveil truly mechanochemical effects and throw light on how mechanical forces ultimately affect molecular solids on the scale of individual molecules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Croatian Science Foundation for financial support through grant no. IP-2020-02-1419 and for supporting SL. MC performed her activity within the framework of the International PhD in Innovation Sciences and Technologies at the Università degli Studi di Cagliari, Italy.References
- V. V. Boldyrev and E. G. Avvakumov, Russ. Chem. Rev., 1971, 40, 847 CrossRef; P. Yu. Butyagin, Russ. Chem. Rev., 1971, 40, 901 CrossRef; V. V. Boldyrev, Experimental Methods in the Mechanochemistry of Solid Inorganic Materials, Nauka, Novosibirsk, 1983 Search PubMed; G. Heinicke, Tribochemistry, Akademie-Verlag, Berlin, 1986 Search PubMed; E. G. Avvakumov, Mechanical Methods for Activation of Chemical Processes, Nauka, Novosibirsk, 1986 Search PubMed; E. M. Gutman, Mechanochemistry of Materials, Cambridge International Science Publishing, Cambridge, 1998 Search PubMed.
- J. Benjamin, Metal Powder Rep., 1990, 45, 122 CrossRef CAS; C. C. Suryanarayana, Prog. Mater. Sci., 2001, 46, 1 CrossRef; P. Balaz, Mechanochemistry in Nanoscience and Minerals Engineering, Springer-Verlag Berlin Heidelberg, Berlin, 2008 Search PubMed.
- S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413 RSC; T. Friščić, Chem. Soc. Rev., 2012, 41, 3493 RSC; G.-W. Wang, Chem. Soc. Rev., 2013, 42, 7668 RSC; A. Stolle and B. RanuBall, Milling Towards Green Synthesis: Applications, Projects, Challenges, Royal Society of Chemistry, London, 2014 RSC; N. R. Rightmire and T. P. Hanusa, Dalton Trans., 2016, 45, 2352 RSC; J.-L. Do and T. Friščić, ACS Cent. Sci., 2017, 3, 13 CrossRef CAS PubMed; D. Tan and F. García, Chem. Soc. Rev., 2019, 48, 2274 RSC; T. Friščić, C. Mottillo and H. M. Titi, Angew. Chem., Int. Ed., 2020, 59, 1018 CrossRef PubMed.
- P. A. Thiessen, K. Meyer and G. Heinicke, Grundlagen der Tribochemie, Akademie Verlag, Berlin, 1967 CrossRef CAS; P. Yu. Butyagin, Z. Vsesoj. Obsc. D. I. Mendelejeva, 1970, 18, 90 CrossRef CAS; K. P. Thiessen, Z. Phys. Chem., 1979, 260, 403 CrossRef CAS; K. P. Thiessen and K. Sieber, Z. Phys. Chem., 1979, 260, 410 CrossRef; K. P. Thiessen and K. Sieber, Z. Phys. Chem., 1979, 260, 417 CrossRef; T. H. Courtney, Rev. Particulate Mater., 1994, 2, 63 Search PubMed; F. Kh. Urakaev and V. V. Boldyrev, Powder Tech., 2000, 107, 93 CrossRef; F. Kh. Urakaev and V. V. Boldyrev, Powder Tech., 2000, 107, 197 CrossRef; G. Cocco, F. Delogu and L. Schiffini, J. Mater. Synth. Process, 2000, 8, 167 CrossRef; F. Delogu and G. Cocco, J. Mater. Synth. Process, 2000, 8, 271 CrossRef; I. F. Vasconcelos and R. S. de Figuereido, J. Phys. Chem. B, 2003, 107, 3761 CrossRef; V. K. Smolyakov, O. V. Lapshin and V. V. Boldyrev, Int. J. Self-Propag. High-Temp. Synth., 2007, 16, 1 CrossRef; V. K. Smolyakov, O. V. Lapshin and V. V. Boldyrev, Int. J. Self-Propag. High-Temp. Synth., 2008, 17, 20 CrossRef; F. Delogu, Acta Mater., 2008, 56, 2344 CrossRef; T. Friscic, I. Halasz, P. J. Beldon, A. M. Belenguer, F. Adams, S. A. J. Kimber, V. Honkimaki and R. E. Dinnebier, Nat. Chem., 2013, 5, 66 CrossRef PubMed; F. Delogu and L. Takacs, Acta Mater., 2014, 80, 435 CrossRef; S. Humphry-Baker, F. Delogu, S. Garroni and C. A. Schuh, Nat. Mater., 2016, 15, 1280 CrossRef PubMed; S. Lukin, T. Stolar, M. Tireli, M. V. Blanco, D. Babić, T. Friščić, K. Užarevic and I. Halasz, Chem. – Eur. J., 2017, 23, 13941 CrossRef PubMed; F. Delogu and L. Takacs, J. Mater. Sci., 2018, 53, 13331 CrossRef; A. M. Belenguer, A. A. L. Michalchuk, G. I. Lampronti and J. K. M. Sanders, Beilstein J. Org. Chem., 2019, 15, 1226–1235 CrossRef PubMed; F. I. S. Silva, M. S. Pereira and I. F. Vasconcelos, Appl. Phys. A: Mater. Sci. Process., 2018, 124, 544 CrossRef; A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, J. Mater. Sci., 2018, 53, 13380–13389 CrossRef PubMed.
- D. L. Zhang, Prog. Mater. Science, 2004, 49, 537 CrossRef CAS; A. Stolle, T. Szuppa, S. E. S. Leonhardt and B. Ondruschka, Chem. Soc. Rev., 2011, 40, 2317 RSC; C. F. Burmeister and A. Kwade, Chem. Soc. Rev., 2013, 42, 7660 RSC; L. M. Tavares, KONA Powder Particle J., 2017, 34, 106 CrossRef.
- J. Uddin, J. O. Marston and S. T. Thoroddsen, Phys. Fluids, 2012, 24, 073104 CrossRef.
- C. L. Martin, D. Bouvard and S. Shima, J. Mech. Phys. Solids, 2003, 51, 667 CrossRef; R. Saurel, N. Favrie, F. Petitpas, M. H. Lallemand and S. L. Gavrilyuk, J. Fluid Mech., 2010, 664, 348 CrossRef.
- H. A. Makse, D. L. Johnson and L. M. Schwartz, Phys. Rev. Lett., 2000, 84, 4160 CrossRef CAS PubMed; E. B. Herbold, M. A. Homel, J. Lind, R. Crum, R. C. Hurley, B. J. Jensen, A. J. Iverson, C. T. Owens, C. A. Carlson and M. C. Akin, AIP Conf. Proc., 1979, 070015 Search PubMed; M. Pouragha, J. Duriez, A. Wautier, R. Wan, F. Nicot and F. Darve, Granular Matter, 2019, 21, 67 CrossRef; S. Ji and L. Liu, Computational Granular Mechanics and Its Engineering Applications, Science Press and Springer Nature, Beijing, 2020 Search PubMed.
- F. Delogu, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014115 CrossRef CAS; F. Delogu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205415 CrossRef; M. Gonzalez, P. Poorsolhjouy, A. Thomas, J. Liu and K. Balakrishnan, Mater. Res. Comm., 2018, 92, 131 Search PubMed; H. Fan, Q. Wang, J. A. Al-Awady, D. Raabe and M. Zaiser, Nat. Commun., 2021, 12, 1845 CrossRef PubMed.
- F. Delogu, Chem. Phys. Letter, 2012, 521, 125 CrossRef CAS; B. P. Johnson, X. Zhou, H. Ihara and D. D. Dlott, J. Phys. Chem. A, 2020, 124, 4646 CrossRef PubMed.
- M. Carta, F. Delogu and A. Porcheddu, Phys. Chem. Chem. Phys., 2021, 23, 14178–14194 RSC.
- L. Vugrin, M. Carta, F. Delogu and I. Halasz, Chem. Commun., 2023, 59, 1629–1632 RSC.
- L. Vugrin, M. Carta, S. Lukin, E. Meštrović, F. Delogu and I. Halasz, Faraday Discuss., 2023, 241, 217–229 RSC; F. Delogu, M. Monagheddu, G. Mulas, L. Schiffini and G. Cocco, Int. J. Non-Eq. Proc., 1998, 11, 235–242 Search PubMed; G. Cocco, F. Delogu and L. Schiffini, J. Mater. Synth. Proc., 2000, 8, 167–180 CrossRef CAS; F. Delogu, G. Mulas, L. Schiffini and G. Cocco, Mater. Sci. Eng., A, 2004, 382, 280–287 CrossRef; F. Delogu, Acta Mater., 2008, 56, 2344–2352 CrossRef.
- M. Carta, L. Vugrin, G. Miletić, M. J. Kulcsár, P. C. Ricci, I. Halasz and F. Delogu, Angew. Chem., Int. Ed., 2023, e202308046 CAS.
- A. C. Olivera, M. G. Coelho, R. F. Pires and M. R. Franco, J. Chem. Eng. Data, 2007, 52, 298–300 CrossRef.
- S. J. Khoun, Am. J. Anal. Chem., 2015, 6, 429–436 CrossRef.
- S. Lukin, K. Užarević and I. Halasz, Nat. Protoc., 2021, 16, 3492–3521 CrossRef CAS PubMed.
- S. Lukin, M. Tireli, T. Stolar, D. Barišić, M. V. Blanco, M. di Michiel, K. Užarević and I. Halasz, J. Am. Chem. Soc., 2019, 141, 1212–1216 CrossRef CAS PubMed.
- A. N. Streletskii, A. V. Leonov and P. Yu Butyagin, Colloid J., 2001, 63, 630–634 CrossRef CAS; F. Delogu, L. Schiffini and G. Cocco, Phil. Mag. A, 2001, 81, 1917–1937 Search PubMed; F. Delogu and G. Cocco, Mater. Sci. Eng., A, 2003, 343, 314–317 CrossRef; C. Deidda, F. Delogu and G. Cocco, J. Metast. Nanocryst. Mater., 2004, 20–21, 337–342 Search PubMed; F. Miai and F. Maurigh, Dekker Encycl. Nanosci. Nanotechnol., 2004, 1787–1795 Search PubMed; P. Yu Butyagin and A. N. Streletskii, Phys. Solid State, 2005, 47, 856–862 CrossRef; F. Delogu and G. Cocco, J. Alloys Compd., 2006, 420, 246–250 CrossRef; F. Delogu, Acta Mater., 2008, 56, 905–912 CrossRef; G. Mulas, F. Delogu, C. Pistidda and G. Cocco, J. Mater. Sci., 2008, 43, 5193–5198 CrossRef; F. Delogu and G. Mulas, Int. J. Hydrogen Energy, 2009, 34, 3026–3031 CrossRef; E. Napolitano, G. Mulas, S. Enzo and F. Delogu, Acta Mater., 2010, 58, 3798–3804 CrossRef; P. Meloni, G. Carcangiu and F. Delogu, Mater. Res. Bull., 2012, 47, 146–151 CrossRef; F. Delogu, Mater. Chem. Phys., 2012, 137, 297–302 CrossRef; F. Delogu, Metall. Mater. Trans. B, 2013, 44, 166–174 CrossRef; F. Delogu, Scripta Mater., 2013, 69, 223–226 CrossRef; F. Delogu, Mater. Chem. Phys., 2014, 147, 629–635 CrossRef; F. Delogu and L. Takacs, J. Mater. Sci., 2018, 53, 13331–13342 CrossRef; A. Porcheddu, A. Cincotti and F. Delogu, Int. J. Hydrogen Energy, 2021, 46, 967–973 CrossRef; F. Torre, M. Carta, P. Barra, A. Cincotti, A. Porcheddu and F. Delogu, Metall. Mater. Trans. B, 2021, 52, 830–839 CrossRef.
- E. Nwoye, S. Raghuraman, M. Costales, J. Batteas and J. R. Felts, Phys. Chem. Chem. Phys., 2023, 25, 29088–29097 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06147g |
| ‡ Equal contribution. |
| This journal is © the Owner Societies 2024 |