Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evidence of progressive Fe2+ to Fe3+oxidation in Fe2+-doped ZnO nanoparticles
F. F. H.
Aragón
 *ab,
L.
Villegas-Lelovsky
*ab,
L.
Villegas-Lelovsky
 cf,
J. G.
Parizaka
a,
E. G.
Zela
a,
R.
Bendezu
a,
R. O.
Gallegos
cf,
J. G.
Parizaka
a,
E. G.
Zela
a,
R.
Bendezu
a,
R. O.
Gallegos
 a,
D. G.
Pacheco-Salazar
a,
D. G.
Pacheco-Salazar
 a,
S. W.
da Silva
a,
S. W.
da Silva
 b,
R.
Cohen
b,
R.
Cohen
 d,
L. C. C. M.
Nagamine
d,
L. C. C. M.
Nagamine
 d,
J. A. H.
Coaquira
d,
J. A. H.
Coaquira
 b and
P. C.
Morais
b and
P. C.
Morais
 be
be
aUniversidad Nacional de San Agustín de Arequipa, Av Independencia SN, Arequipa, Peru. E-mail: ffharagon@gmail.com
bUniversity of Brasília, Institute of Physics, Brasília, DF 70919-970, Brazil
cDepartamento de Física, Centro de Ciências Exatas e de Tecnologia, Universidade Federal de São Carlos, São Carlos, SP 13565-905, Brazil
dInstituto de Física, Universidade de São Paulo, São Paulo, SP 05508-090, Brazil
eCatholic University of Brasília, Genomic Sciences and Biotechnology, Brasília, DF 71966-700, Brazil
fPhysics Department, IGCE, Paulista State University, CEP 13506-900, Rio Claro, SP, Brazil
First published on 8th February 2023
Abstract
Oxide-diluted magnetic semiconductors have received considerable attention in diverse scientific and technological fields because they combine the optoelectronic properties of the hosting semiconductor with the magnetic properties of the metal dopant. In this report, the role of Fe doping on the structural, vibrational, optical, hyperfine, and magnetic properties of Fe-doped ZnO nanoparticles (Zn1−xFexO) synthesized via a polymeric precursor method is presented. Our findings display that the crystallite size decreases from ∼23 nm (x = 0.000) to ∼8 nm (x = 0.200) as the Fe-content (x) is increased. From the XRD data analysis, our results suggest an isovalent solid solution between Fe2+ and Zn2+ ions for lower Fe-content (up to 0.075) and aliovalent solution (Fe3+ and Zn2+ ions) for higher Fe-content. Elliot's theory was used to assess the band gap energy of Eg ∼ 3.4 eV, and an exciton binding energy of Eb ∼ 66 meV for the undoped sample. The excitonic peak exhibits a broadening trend with increasing Fe-content, suggesting disorder enhancement in the ZnO matrix. Besides, FTIR data analysis suggests that the Zn–O bond length increases with Fe-content up to 0.075 and decreases above this value. The intensity ratio of the O–H and Zn–O modes shows a discontinuity as the Fe-content is increased. Room temperature Mössbauer spectra carried out for samples with x = 0.050, 0.075, and 0.200 show that the isomer shift and quadrupole splitting increase with the Fe-content, in agreement with the structural properties. Magnetic measurements suggest that the iron ions stabilize as Fe2+ in samples with low Fe-content and then as Fe3+ in samples with high Fe-content. Besides, the occurrence of short-range antiferromagnetic interactions was determined, which becomes stronger as the Fe-content is increased.
1. Introduction
Diluted magnetic oxide semiconductor (DMOS) has received considerable attention because it combines the optoelectronic properties of semiconductors (oxide semiconductors) with the magnetic properties of transition metals. In this regard, ZnO undoped and doped with transition metal ions (such as Fe, Ni, Co among others) and rare-earth ions (such as Ce, Er, Gd among others) have been used for several applications. Moreover, a wide range of methods have been used to produce Fe-doped ZnO nanostructures, among which we can point out solution combustion,1 sol–gel,2 and hydrothermal.3 The polymeric precursor method (Pechine's method) used in the present study, in addition to being a bottom-up synthesis route, is a highly reproducible approach, which is based on the formation of chelate between mixed cations and citric acid. The metal ions are chelated, and these chelates are then cross-linked with ethylene glycol to form a gel by esterification. After thermal treatment in the air (∼400 °C), a removal of all organic substances is accomplished. Subsequently, thermal annealing at high temperatures (>400 °C) improves the crystallinity of the as-synthesized nanoparticles.4 However, due to the high temperatures employed in this chemical route, while compared with other methods (such as hydrothermal and precipitation) the polymeric precursor method suffers from a lack of morphology control. Regarding their applications, one can highlight their use in wastewater treatment processes. In this scenario, Andia-Huaracha et al., reported the photocatalytic activity (PCA) of ZnO nanoparticles (NPs) synthesized via the polymeric precursor method and presenting mean crystallite size in the range of 23–150 nm.5 Moreover, the PCA tests of the ZnO NPs do not show a straightforward dependence on the NPs’ size, but it seems to be correlated with the density of defects.5 In addition, Rokhsat et al. reported the PCA of Fe-doped ZnO nanosheets on the p-nitrophenol degradation under visible light, revealing the high performance of the Fe-doped sample compared to the undoped one.3 On the other hand, based on the Langmuir isotherm analysis, ZnO nanocrystals decorated with regenerated microfibrillated cellulose scaffolds and containing 41 wt% ZnO were found to be very efficient in removing As(V) from water with a maximum capacity of 4.421 mg g−1, at neutral pH (7).6Importantly, in Fe-doped oxides, iron ions can exist in two regular oxidation states (Fe2+ and Fe3+), which could impact differently the structural properties of the hosting ZnO nanocrystal due to differences in their ionic radii. The latter may be strongly reflected in the physicochemical properties of the Fe-doped ZnO structure. As a result, determining the oxidation state of heterovalent elements (such as Fe) is critical for understanding how the doped system works. Importantly, the oxidation state of iron ions in Fe-doped ZnO can be strongly dependent on the synthesis process.7 However, several reports show that iron is usually found as high spin Fe2+-ions substituting Zn2+-ions.7–9 It is noteworthy the report of George et al. regarding the study of Fe-doped ZnO NPs, suggesting that the entry of isovalent Fe2+ replacing Zn2+ leads to minimally distorted ZnO lattice structure.9 Determination of the iron oxidation state and the impact on the Fe-doped crystalline environment can be performed by different experimental techniques, such as X-ray photoelectron spectroscopy (XPS), X-ray absorption near-edge structure (XANES), inner-shell electron energy-loss spectroscopy (ISEELS), and Mössbauer spectroscopy.8,10,11 The hyperfine parameters obtained from Mössbauer spectroscopy are commonly used to assess the oxidation state of iron in iron oxides. It is commonly known that the isomershift (IS) of Fe3+ in pure oxides is around 0.25 mm s−1 and 0.29 mm s−1 for the upper limit in tetrahedral coordination and lower limit for octahedral coordination, respectively. These values are lower than those expected for Fe2+, which are in the range of 1.05–1.20 mm s−1 for octahedral coordination and in the range of 0.90–1.05 mm s−1 for tetrahedral coordination. The Mössbauer spectroscopy, however, is unusual and costly for most laboratories and, for this reason, new methods such as XRD and FTIR could be used instead.
In the present report, the structural, optical, vibrational, hyperfine and magnetic properties of Fe-doped ZnO nanoparticles are assessed aiming to determine the effect of iron-ions while entering in the ZnO hosting matrix. Moreover, one is interested in finding out how the oxidation state of iron-ions is modulated through the entry of iron in the ZnO hosting matrix.
2. Samples description and experimental details
Undoped and Fe-doped ZnO nanoparticles were synthesized by the polymer precursor chemical method using zinc nitrate hexahydrate (Zn(NO3)2·6H2O), iron nitrate nonahydrate (Fe(NO3)3·9H2O), ethylene glycol (C2H4(OH)2), and citric acid (C6H8O7). To make the polymer precursor gel, the following steps were performed: citric acid (47.7%) and zinc nitrate hexahydrate (31.7%) were dissolved in ethylene glycol (20.6%) at 70 °C with magnetic stirring, then the temperature was raised to 120 °C to enhance citric acid and ethylene glycol polymerization. For iron doping, the amount of iron was controlled according to the atomic ratio Fe/(Fe + Zn), where x mol of iron (x mol of the iron nitrate nonahydrate) was mixed with (1 − x) × Eff mol of the ZnO resin, where Eff is the resin's efficiency. After promoting polymerization, the obtained liquid was pyrolyzed at 450 °C for 4 h. The final carbon-rich powder was thermally treated at 500 °C for 6 h. Homogeneous and energetically metastable powders were obtained. X-Ray diffraction (XRD) measurements at room temperature were performed using a Rigaku MiniFlex 600 X-ray diffractometer equipped with Cu Kα radiation (λ = 1.5418 Å) and scanning in the 2θ range of 20°–80°. The instrumental contribution was removed using a Si standard sample. UV-Vis spectra were collected using a Shimadzu UV-1800 UV/Visible Scanning Spectrophotometer, in a range of measurement from 190 to 1100 nm. Fourier-transform infrared spectroscopy (FTIR) measurements were carried out (samples pressed in KBr pellet) using a Bruker VERTEX 70 FT-IR spectrometer, scanning in the wavenumber range of 450–4000 cm−1. TEM images were performed with a JEOL microscope, model JEM-2100. Mössbauer measurements were carried out using a commercial spectrometer (WisselMössbauer spectrometer) equipped with a 57Co source, operating in the constant acceleration mode and scanning the velocity in the range of ±10 mm × s−1. Using the NORMOS software package, the Mössbauer spectra were curve fitted by minimizing the chi-square (χ2) parameter. Magnetic measurements were performed using a commercial SQUID magnetometer (Quantum Design), in the temperature range of 2–300 K, and applied magnetic fields up to ± 70 kOe.3. Results and discussions
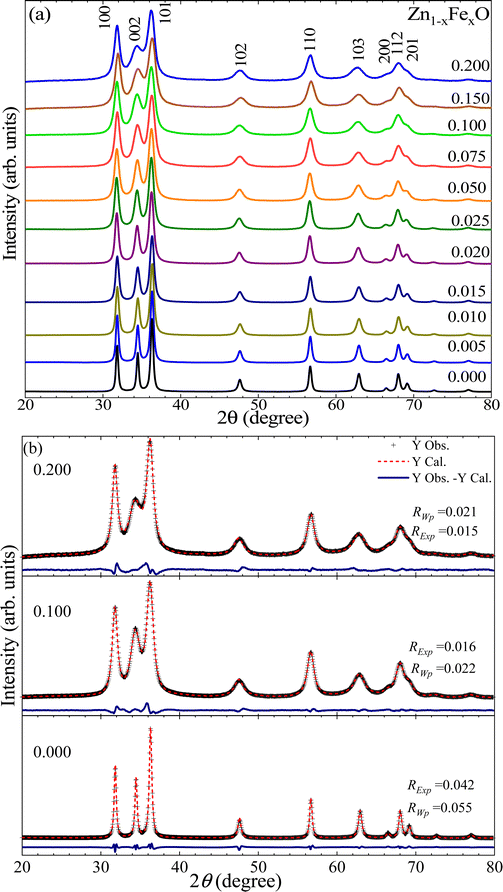
Fig. 1(a) shows the XRD patterns of the undoped and Fe-doped ZnO nanoparticles (Zn1−xFexO, with x from 0.000 to 0.200). According to the XRD data, the wurtzite crystal structure is identified as the crystalline phase in all samples, in agreement with the Inorganic Crystal Structure Database (ICSD) card No. 34477. Within the XRD equipment's limit, no secondary phase was detected, indicating that the materials obtained through the employed chemical process are single-phase in the Fe-content (x) range of 0.000–0.200. Besides, a broadening of the XRD peaks is also detected, which can be correlated with a decrease in the mean crystallite size (〈D〉) and/or an increase in residual strain (〈ε〉), which will be discussed later on in this report. It can also be seen that the (101) XRD peak has the highest intensity, indicating a high degree of crystallinity in the powder samples. To assess the structural parameters, the XRD patterns were analyzed using the Generalized Structure Analysis System (GSAS) software12 modeling the peaks with Lorentzian shape functions. Fig. 2(b) shows a typical refinement for the undoped (x = 0.000) and Fe-doped (x = 0.100, 0.200) samples, where the cross symbol (+) represents experimental data, the solid red line represents the theoretical XRD curve, and the solid blue line at the bottom of the panels represents the difference between them. According to the refinement quality parameter (S = RExp/RWp, where the R-factors RExp and RWp quantify the quality of the refinement) all performed refinements (S < 2) are acceptable (see Table 1).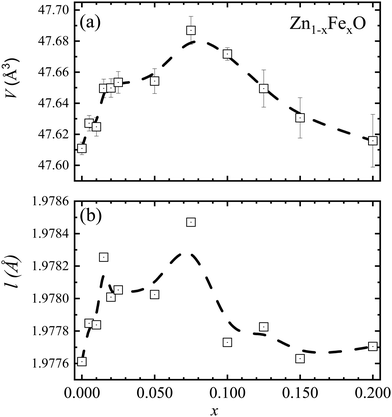 | ||
| Fig. 2 (a) Unit cell volume (V). (b) Bond length (l) as a function of the Fe-content (x). Data obtained from the XRD analysis. Dashed lines are guides to the eye. | ||
| Fe-content (x) | a (Å) | c (Å) | c/a | 〈D〉 (nm) | ρ (g cm−3) | S |
|---|---|---|---|---|---|---|
| 0.000 | 3.2493(1) | 5.2070(2) | 1.6025 | 23.3 | 5.68 | 1.31 |
| 0.005 | 3.2496(1) | 5.2078(2) | 1.6026 | 19.8 | 5.67 | 1.30 |
| 0.010 | 3.2493(1) | 5.2086(3) | 1.6030 | 17.5 | 5.67 | 1.27 |
| 0.015 | 3.2499(1) | 5.2101(3) | 1.6031 | 15.0 | 5.66 | 1.27 |
| 0.020 | 3.2494(1) | 5.2099(3) | 1.6034 | 13.6 | 5.66 | 1.27 |
| 0.025 | 3.2493(2) | 5.2104(4) | 1.6035 | 13.5 | 5.66 | 1.27 |
| 0.050 | 3.2498(2) | 5.2084(4) | 1.6027 | 11.9 | 5.64 | 1.34 |
| 0.075 | 3.2494(3) | 5.2135(5) | 1.6044 | 10.2 | 5.62 | 1.35 |
| 0.100 | 3.2479(1) | 5.2127(3) | 1.6049 | 10.0 | 5.60 | 1.36 |
| 0.125 | 3.2472(3) | 5.2159(6) | 1.6063 | 11.4 | 5.59 | 1.39 |
| 0.150 | 3.2465(4) | 5.2168(7) | 1.6069 | 8.9 | 5.57 | 1.41 |
| 0.200 | 3.2457(5) | 5.2199(9) | 1.6082 | 7.7 | 5.54 | 1.43 |
The lattice constants on the undoped ZnO NPs are a = b = 3.2493 ± 0.0001 Å and c = 5.2070 ± 0.0002 Å. The extracted unit cell volume is V = 47.611 ± 0.004 Å3. These findings are in excellent agreement with the values of a = b = 3.250 Å, c = 5.207 Å, and V = 47.63 Å3 reported in the literature.13 However, for Fe-doped ZnO NPs, interesting results are observed in regard to the unit cell volume (V), which displays an increasing trend as the Fe-content increases up to x =0.075 (see Fig. 2(a)), followed by a decreasing tendency. Taking into account that within the ZnO matrix the Zn2+-ions present four-fold coordination, that finding can be explained by two plausible scenarios. Firstly, at a lower Fe-content (up to x = 0.075), an entry of Fe2+-ions with an ionic radius equal to 0.63 Å, which is greater than the ionic radius of Zn2+(0.60 Å), explains the increase of the unit cell volume, as it is displayed in Fig. 2(a). This isovalent solid solution scenery is energetically more likely. Moreover, at higher Fe-content (above x = 0.075), the entry of trivalent iron-ions (Fe3+) with an ionic radius equals to 0.49 Å (four-fold coordination),14 may lead to a decrease in the unit cell volume (V), as it is displayed in Fig. 2(a). As a result of the aforesaid, and taking into account what has been reported in the literature, doping ions segregate on the nanoparticle surface, and segregation increases as the doping content increases.15 Therefore, an alternative and feasible scenario can be built using Fe2+-ions in the NP's core and Fe3+-ions onto the NP's surface, in accordance with the result reported by McLeod et al.,16 claiming that Fe-doping in bulk ZnO promotes isovalent cation substitution (Fe2+ → Zn2+). Meanwhile, Fe-doping near the surface induces both isovalent (Fe2+ → Zn2+) and aniovalent substitution (Fe3+ → Zn2+).17 Also, this fact may be related to the Kataoka et al. report, showing that Fe3+-ions predominate onto the surface of NPs.16 A second possible scenario is related to the unit cell volume dependence (see Fig. 2(a)) on the ionic radius of both the Fe3+-ion in six-fold coordination (0.65 Å) and in four-fold coordination (0.49 Å),14 respectively larger and smaller than the ionic radius of Zn2+-ions (0.60 Å). Within this second scenario, lower Fe-content (up to x = 0.075) favors the entry of Fe3+-ions in six-fold coordination, whereas higher Fe-content (above x = 0.075) favors the entry of Fe3+-ions in four-fold coordination, as represented by the data collected in Fig. 2(a). The second model picture could explain fairly well the observed experimental trends regarding the unit cell volume. However, the entry of iron-ions in positions other than the tetrahedral (four-fold coordination) is energetically more expensive, as this would imply iron-ions entering into interstitial positions (six-fold coordination), much more unlikely. Meanwhile, the entry of Fe3+-ions into regions with a high degree of crystalline disorder (like the surface) plus the coexistence of Fe3+/Fe2+ became more likely as the Fe-content increases, as it is suggested in the literature.16Fig. 1(b) displays the typical Rietveld refinement for x = 0.000, 0.100 and 0.200 in the Zn1−xFexO NPs, where the symbol (+) represents the experimental data, the solid red line the calculated XRD pattern data, and in the bottom, the solid blue line the difference between them. Fig. 2(b) shows the bond length (l) as a function of Fe-content (x), which is consistent with the unit cell volume trend shown in Fig. 2(a). Regarding the density, the value of the undoped sample is 5.68 g cm−3, which is very close to the theoretical value (5.67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g cm−3) for ZnO.18 However, a monotonic tendency toward lower density values with increasing Fe-content is observed (see Table 1); this tendency is linked to atomic weight losses brought on by the replacement of Zn (65.4 g mol−1) atoms with Fe (55.8 g mol−1) atoms.
g cm−3) for ZnO.18 However, a monotonic tendency toward lower density values with increasing Fe-content is observed (see Table 1); this tendency is linked to atomic weight losses brought on by the replacement of Zn (65.4 g mol−1) atoms with Fe (55.8 g mol−1) atoms.
To extract the mean crystallite size and residual strain, the corrected linewidths (β) of the Bragg diffraction peaks are correlated to the mean crystallite size (〈D〉) and residual strain (〈ε〉), through the Williamson–Hall plot (WHP) given by:
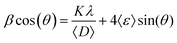 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) as a function of sin(θ), the values of 〈D〉 and 〈ε〉 can be estimated from the intercept and slope associated with the linear function fitting, respectively. The WHP for the undoped (x = 0.000) and Fe-doped (x = 0.050, 0.150) NPs are displayed in Fig. 3, clearly showing that the intercept and slope associated with eqn (1) increase as the Fe-content increases. These findings suggest a decreasing and increasing tendency in the mean crystallite size (∝ 〈D〉−1) and residual strain (∝ 〈ε〉), respectively (see Fig. 4). The decreasing tendency in the mean crystallite size (see Table 1) as the Fe-content increases is in agreement with previous report of Fe-doped ZnO.19
cos(θ) as a function of sin(θ), the values of 〈D〉 and 〈ε〉 can be estimated from the intercept and slope associated with the linear function fitting, respectively. The WHP for the undoped (x = 0.000) and Fe-doped (x = 0.050, 0.150) NPs are displayed in Fig. 3, clearly showing that the intercept and slope associated with eqn (1) increase as the Fe-content increases. These findings suggest a decreasing and increasing tendency in the mean crystallite size (∝ 〈D〉−1) and residual strain (∝ 〈ε〉), respectively (see Fig. 4). The decreasing tendency in the mean crystallite size (see Table 1) as the Fe-content increases is in agreement with previous report of Fe-doped ZnO.19
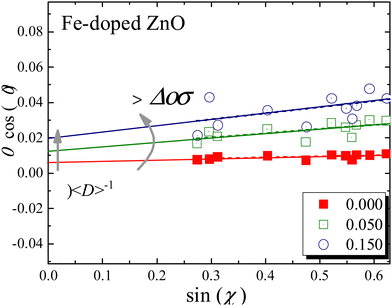 | ||
| Fig. 3 Williamson–Hall plot for the undoped (x = 0.000) and Fe-doped (x = 0.050, 0.150) NPs. Solid (red, green, and blue) lines are the best fit of the experimental data using eqn (1). | ||
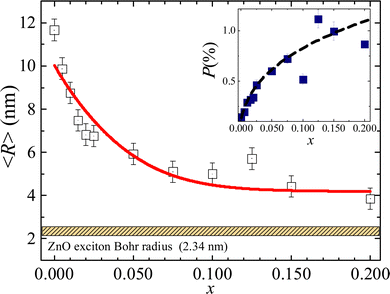 | ||
| Fig. 4 Crystallite radius as a function of the Fe-content (x). The inset shows the residual strain as a function of the Fe-content (x). Note the ZnO exciton Bohr radius value (2.34 nm) reported in ref. 22. The solid red line is the best fit of the experimental data using eqn (3). The dashed black line in the inset is only a guide to the eye. | ||
In the approach of spherical shape NPs the mean crystallite radius (〈R〉 = 〈D〉/2) obtained through the WHP is plotted as a function of the Fe-content (x) in Fig. 4. The observed monotonic decreasing trend of 〈R〉 versus x (see Fig. 4) could be correlated with a progressive iron-ions enrichment of the NP's surface, decreasing the surface energy in agreement with the Ostwald ripening equation given by:20
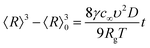 | (2) |
| 〈R〉3 = 〈R〉03 + k−1 exp(−Ax) | (3) |
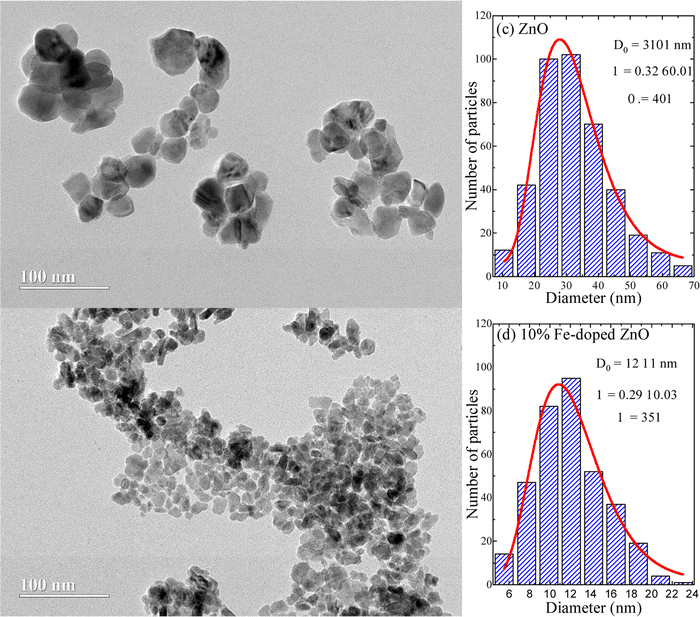
Fig. 5(a and b) depict the transmission electron microscopy (TEM) images of undoped and Fe-doped ZnO nanoparticles, respectively. Importantly, the morphological analysis (shape and physical size) of the crystallites shows a clear relationship between crystallite size and Fe-content. The latter suggests that the incorporation of iron ions suppresses the growth of ZnO nanoparticles to a large extent. As previously stated, this is strongly correlated with a progressive iron-ions enrichment of the NP's surface, resulting in a decrease in surface energy. To determine the mean physical size several particles (N) are counted. Fig. 5(c and d) show the histograms, which are curve-fitted using the lognormal distribution function, thus assessing the mean physical sizes (D0) of ∼31 ± 1 nm and ∼12 ± 1 nm, with polydispersity indexes (σ) of 0.32 ± 0.01 and 0.29 ± 0.03, for the undoped and 10% Fe-doped ZnO, respectively.
The optical properties of undoped and Fe-doped ZnO NPs were assessed using the UV-Visible absorbance as a function of wavelength. For this purpose, powder samples were dispersed in a liquid medium (distilled water) with a concentration of 3 µg mL−1. Fig. 6 shows the spectra for the undoped (x = 0.000) and Fe-doped (x from 0.005 to 0.200) ZnO NPs. As can be seen in Fig. 6, a clear and narrow excitonic peak located in the range of 3.0–3.5 eV is observed, which is correlated with the electron–hole pair bound formation. Aiming to determine the exact electronic bandgap and excitonic properties of the as-fabricated materials, Elliot's approach was used to model the absorbance versus energy curves. It is worth mentioning that this approach has been successfully used to analyze other systems, such as perovskites.23,24 However, to the best of our knowledge, this is the first time it is used to analyze the Zn1−xFexO system. Elliot's approach shows that the optical absorption coefficient (α) depends on the linear combination of the exciton (αexc) plus continues edge (αcont), given by the following relationship:24
| α = αexc + αcont | (4) |
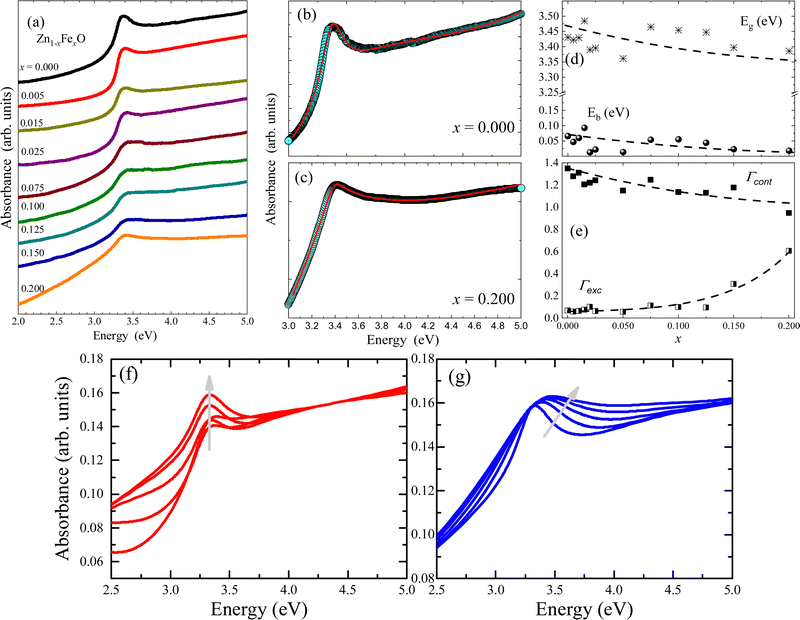 | ||
| Fig. 6 (a) Absorbance as a function of the optical excitation energy for Fe-undoped (x = 0.000) and Fe-doped (from x 0.005 to 0.200) ZnO NPs. (b and c) Experimental data (open symbols) of absorbance versus optical excitation energy and curve fittings (solid red lines) for the ZnO and Zn0.8Fe0.2O NP samples, respectively (curve fit using eqn (4)–(6)). (d) Fitted values of Eg and Ebversus Fe-content (x). (e) Fitted values of Γcont and Γexcversus Fe-content (x). Dashed lines in (d and e) are guides to the eye. (f and g) Represent theoretical simulations maintaining fix the excitonic (Γexc) and continuous (Γcont) broadening parameters, respectively. The gray arrows are guides to the eye. | ||
The first contribution in eqn (4) correlates with the exciton formation (electron–hole pair), whereas the second contribution accounts for the absorption into the free-carrier continuum. However, two key aspects need to be included in the description of the samples herein reported and related to the excitonic transitions. Firstly, the NPs size monotonically decreases with the Fe-content, as shown in Fig. 4. Secondly, the entry of the iron ions into the hosting ZnO crystal structure leads to local distortions in the neighboring iron-ions, thus increasing the polydispersity of the exciton peak. In this scenario, the excitonic transition broadening parameter (Γexc) is included in Elliot's method:
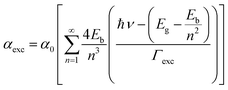 | (5) |
 | (6) |
Using eqn (4)–(6), typical fittings of the absorbance regarding the undoped (x = 0.000) and Fe-doped (x = 0.200) ZnO NPs are displayed in Fig. 6(b and c), respectively. For the undoped ZnO, values of Eg ∼ 3.4 eV and Eb ∼ 66 meV were obtained, in very good agreement with the reported values of Eg ∼ 3.37 eV and Eb ∼ 60 meV.25 However, as the Fe-content (x) increases, a slight and monotonic reduction trend in both Eg and Eb is observed, as shown in Fig. 6(d). Concerning the broadening parameters (see Fig. 6(e)), one observes opposite trends as the Fe-content (x) increases. The excitonic transition broadening parameter (Γexc) increases as the Fe-content increases, very likely evidencing an enhancement of the ZnO matrix disorder. Meanwhile, the continuous broadening parameter (Γcont) exhibits monotonic reduction as the Fe-content increases, which is associated with the decreasing of the free-carrier concentration, very likely connected with the removal of intrinsic defects. It is worth noting that reduction of free-carrier concentration leads to an increase in the resistivity, as reported in the literature for Fe-doped ZnO thin films.26 To see clearly the effect of the change of the Γexc and Γcont in the curves, the theoretical simulation of the absorbance by fixing Γexc and decreasing progressively Γcont is presented in Fig. 6(f), while the opposite behavior is addressed in Fig. 6(g) by fixing Γcont and increasing the Γexc contribution. It is clear that the continuous or excitonic contribution, prevail over each other depending on the case. In the first, the continuous part loses relevance while the excitonic peak emerges and exhibits its average width almost without variation as Γcont contribution is decreasing. In the second (Fig. 6(g)), the half-width excitonic peak broadens while the continuous part almost maintains its shape, the Γexc contribution increases.
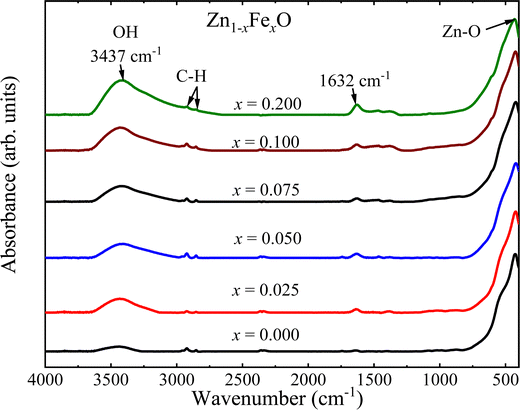
Fig. 7 shows the FTIR spectra of the undoped and Fe-doped ZnONPs, all of which exhibit the expected spectra of the ZnO structure.5 However, due to neighborhood modifications, iron-ions are located into the core or onto the surface of the ZnO NPs lead toFTIR spectra displaying considerable alterations. Before looking deeper into the details, it is worth noting the band at ∼3437 cm−1, observed in all spectra, which can be associated with the O–H stretching mode adsorbed from the environment.27 Moreover, bands at ∼2922 and ∼2852 cm−1 are respectively attributed to asymmetrical and symmetrical C–H stretching vibrations of CH2 groups.28 Finally, the band at ∼1632 cm−1 is attributed to the O–H bending mode.29 It is herein hypothesized that the above-mentioned mode could be adsorbed by the NPs’ surface from the reaction medium and by handling the samples in the air atmosphere. On the other hand, the inorganic vibrational frequency of the Zn–O is observed below 700 cm−1, which is specifically located at ∼423 cm−1 for the undoped ZnO NPs, slightly below the value (∼431 cm−1) reported in the literature.5 Furthermore, an additional vibrational mode, possibly associated with a secondary iron oxide phase has not been observed within the limit of detection of the FTIR equipment (expected for Fe2O3 in the range of 578–567 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30). The FTIR observation is in good agreement with the XRD data.
30). The FTIR observation is in good agreement with the XRD data.
To assess the effect caused by the entry of iron-ions into the ZnO matrix, the shift in the position of the Zn–O band in the FTIR spectra (400–700 cm−1) was monitored. In this regard, the spectra were fitted using two Lorentzian peaks, for both undoped and Fe-doped ZnO NPs, revealing for the former (x = 0.000) two peaks located at ∼423 cm−1 and ∼532 cm−1. The main mode shift (below 430 cm−1) is displayed in Fig. 8(a), from where one can see a clear tendency to down shift up to ∼7.5%, following a gradual increase as the Fe-doping increases. This finding could be related to the possibility of iron entering into the ZnO crystal structure using two different oxidation states, namely Fe2+ at lower and Fe3+ at higher doping, in agreement with the XRD analysis. The following frequency equation can be used to explain the experimental observation collected in Fig. 8(a):31
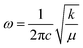 | (7) |
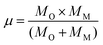 | (8) |
 | ||
Fig. 8 (a) Zn–O peak position as a function of Fe-content (x) as obtained from the FTIR data. (b) Bond length of the Zn–O extracted from the FTIR data using eqn (7)–(9). (c) Filled blue circles represent the experimental FTIR cubic band intensity ratio 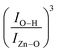 as a function of Fe-content, whereas solid red line is the best fit of the data using eqn (3) and (10). Dashed lines in (a and b) are guides to the eye. as a function of Fe-content, whereas solid red line is the best fit of the data using eqn (3) and (10). Dashed lines in (a and b) are guides to the eye. | ||
In eqn (8)MO is the oxygen mass and MM represents the mass of the metal atom (Zn or Fe). Regarding the force constant (k) appearing in eqn (7), it could be expressed by the phenomenological equation proposed by Singh et al.:31
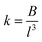 | (9) |
| Fe-content (x) | ω (cm−1) | µ (× 10−26 Kg) | k (N cm−1) | l (Å) |
|---|---|---|---|---|
| 0.0 | 423.2 | 2.1344 | 1.358 | 1.9779 |
| 1.0 | 427.1 | 2.1338 | 1.383 | 1.9660 |
| 1.5 | 423.8 | 2.1335 | 1.361 | 1.9764 |
| 2.5 | 419.9 | 2.1329 | 1.336 | 1.9888 |
| 5.0 | 415.1 | 2.1314 | 1.305 | 2.0047 |
| 7.5 | 416.9 | 2.1298 | 1.315 | 1.9992 |
| 10.0 | 421.5 | 2.1283 | 1.343 | 1.9852 |
| 12.5 | 421.9 | 2.1267 | 1.345 | 1.9845 |
| 15.0 | 419.6 | 2.1251 | 1.329 | 1.9922 |
| 20.0 | 425.8 | 2.1219 | 1.367 | 1.9736 |
Finally, the FTIR spectra shown in Fig. 7 provide extra information regarding the intensity ratio 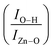 of the O–H band and the structural ZnO band. The experimental values (symbols) of the
of the O–H band and the structural ZnO band. The experimental values (symbols) of the 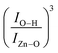 versus the Fe-content (x) are collected in Fig. 8(c), revealing a monotonic and exponential-like increase. This trend can be associated with the increase in surface area due to the monotonic reduction in particle size (see data in Fig. 4). In this scenario, one can suggest the following relationship:
versus the Fe-content (x) are collected in Fig. 8(c), revealing a monotonic and exponential-like increase. This trend can be associated with the increase in surface area due to the monotonic reduction in particle size (see data in Fig. 4). In this scenario, one can suggest the following relationship:
 | (10) |
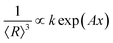 . Using eqn (3) into eqn (10) the solid red line in Fig. 8(c) represents the best fit of the experimental data. This finding displays a very good correlation between the XRD and the FTIR data.
. Using eqn (3) into eqn (10) the solid red line in Fig. 8(c) represents the best fit of the experimental data. This finding displays a very good correlation between the XRD and the FTIR data.
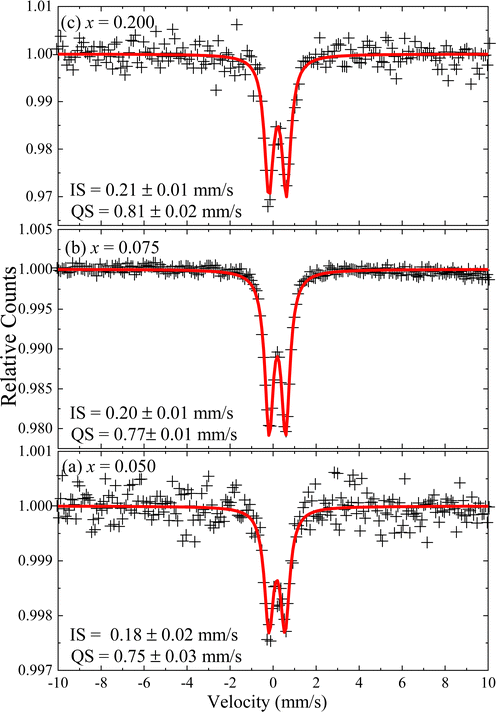
The oxidation state of the iron-ions in the doped samples was assessed by room temperature 57Fe Mössbauer spectroscopy. Samples with x = 0.050, x = 0.075 and x = 0.200 were selected for investigation. Fig. 9 shows the recorded spectra of selected samples, with symbols representing the experimental data while the solid red lines represent the best curve fitting using the NORMOS software package. The data analysis provided isomershift (IS) of 0.18 mm s−1 for the x = 0.050, while slightly increasing for the x = 0.075 (IS = 0.20 mm s−1) and x = 0.200 (IS = 0.21 mm s−1) samples. Meanwhile, the quadrupole splitting (QS) shows a similar trend, slightly increasing from 0.75 mm s−1 to 0.81 mm s−1 for the x = 0.050 and x = 0.200 samples, respectively. The obtained hyperfine parameters suggest the presence of Fe3+-ions in the Fe-doped ZnO NPs. However, as reported by Xiao et al.,32 the values of the hyperfine parameters (IS = 0.3 mm s−1 and QS = 0.83 mm s−1) obtained for Fe-doped (x in the range of 0.010–0.100) ZnO NPs correspond to Fe2+-ions occupying tetrahedral sites (ZnO4), which was supported by theoretical calculations of the electronic structure in Fe-doped ZnO matrix. Moreover, this result is in agreement with another report of Fe-doped ZnO wurtzite NPs, suggesting the presence of mainly Fe2+-ions and only traces of Fe3+-ions.8 As pointed out by Xiao et al.,32 it means that the hyperfine parameters of Fe-doped ZnO samples assessed through Mössbauer spectroscopy not directly correlates to the iron oxidation state, as it is the case of unperturbed iron oxide compounds. As Mössbauer spectroscopy directly probes the s-character charge on the nucleus of iron ions, our results suggest charge depletion of Fe2+-ions occupying tetrahedral sites, which is related to the shorter Fe–O bond lengths (∼2.00 Å) in Fe-doped ZnO NPs with respect to the Fe–O bond length of 2.16 Å for unperturbed iron oxide compounds.33 Therefore, reports in the literature support the hypothesis of the presence of Fe2+-ions in the Fe-doped ZnO NPs containing low Fe-content, as suggested by the XRD and FTIR data analysis herein reported. On the other hand, the observed slight increase of the QS as the Fe-content increases could be related to structural disorder increase due to the increase of Fe-content, which can favor the presence of Fe3+-ions, as observed in the samples herein investigated.
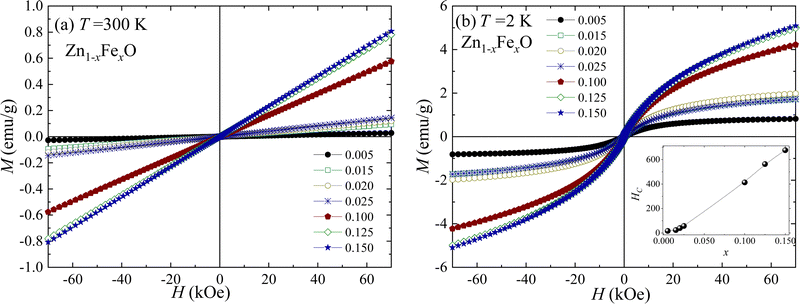
In order to assess the magnetic properties of the Fe-doped ZnO NPs magnetic measurements were performed on selected samples (i) at low (x = 0.005, 0.015, 0.020, and 0.025) and (ii) high (x = 0.100, 0.125, and 0.150) Fe-content. Fig. 10(a and b) depict the field dependence of the magnetization (M versus H) recorded at 300 and 2 K. As it is shown in Fig. 10(a), the magnetic response at 300 K exhibits paramagnetic behavior, evidenced by a linear behavior with no coercive field (HC ∼ 0.0 Oe). Differently, the magnetic response at 2 K (see Fig. 10(b)) displays an interesting behavior, with the expected shape of a paramagnetic loop. Data recorded at 2 K show an increasing coercivity (HC) as the Fe-content increases (see inset of Fig. 10(b)), thus evidencing the increase of the iron ions interaction with the increasing Fe-content. Additionally, the temperature dependence of the magnetic susceptibility (χ) was recorded in the range of 5–300 K while applying a magnetic field of 1 kOe. Fig. 11 displays the χ versus T curves for all selected samples, confirming the dominant paramagnetic behavior, in agreement with the M versus H curves shown in Fig. 10(a and b).
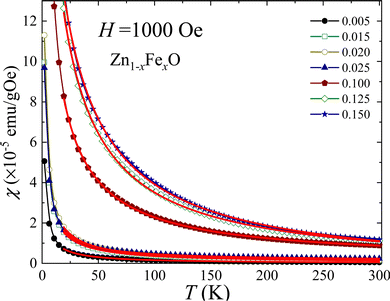 | ||
| Fig. 11 Temperature dependence of the magnetic susceptibility obtained for selected Fe-doped ZnO NPs. Symbols are experimental data and solid lines are the best fit using eqn (11). | ||
The Curie–Weiss law, given by eqn (11), was used to analyze the χ versus T curves shown in Fig. 10 in the temperature range of 20–300 K, where the Curie–Weiss law is minimally influenced by Fe–Fe interactions.
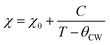 | (11) |
| Fe (x) | C (×10−5 emu K g−1 Oe−1) | θ cw (K) | χ 0 (×10−7 emu g−1 Oe−1) | µ eff (µB) |
|---|---|---|---|---|
| 0.005 | 16.7 | −4.03 | 0.002 | 5.10 |
| 0.015 | 36.0 | −4.65 | 2.099 | 4.32 |
| 0.020 | 43.1 | −5.05 | 1.317 | 4.10 |
| 0.025 | 35.7 | −4.23 | 11.72 | 3.33 |
| 0.100 | 242.0 | −10.7 | 10.14 | 4.32 |
| 0.125 | 443.0 | −15.6 | −32.61 | 5.21 |
| 0.150 | 533.0 | −19.0 | −55.91 | 5.22 |
From the Curie–Weiss law (see eqn (11)) the effective magnetic moment (μeff) was obtained for all samples. The expected values for the spin-only contribution of free Fe3+-ions and Fe2+-ions are 5.9µB and 5.2µB, respectively. As shown in Table 3, the obtained value of μeff = 5.10µB for x = 0.005 is very much close to the expected value for Fe2+-ions, suggesting the presence of Fe2+-ions at lower Fe-content, in good agreement with the XRD and FTIR assessed data. Meanwhile, the μeff value decreases as the Fe-content increases up to x = 0.025. However, in the higher end of Fe-content (x = 0.100, 0.125, and 0.150) the effective magnetic moment (μeff) increases, suggesting the onset of Fe3+-ions. Moreover, in the higher end of Fe-content, θCW shows negative and increasing values (see Table 3) as the Fe-content increases, suggesting the occurrence of a short-range antiferromagnetic (AFM) correlation between iron spins (↑↓⋯↑↓) dispersed in the hosting matrix. The onset of this AFM interaction is claimed to be responsible for the observed discrepancies between the effective magnetic moment (see Table 3) and the value for free Fe3+-ions. A similar behavior was reported for Fe-doped ITO.35
4. Conclusions
The present study reports on the successful synthesis of single phase Fe-doped ZnO samples presenting the wurtzite structure. The structural characterization, assessed by XRD measurements, reveals a major effect of iron-ion entry into the ZnO matrix, namely a decreasing tendency of crystallite size with increasing Fe-content. This behavior was modeled using the Ostwald ripening equation plus a phenomenological dependence of the surface energy with Fe-content. Moreover, the crystallite radii values are close to the ZnO exciton Bohr radius (2.34 nm), asymptotically approaching this value as the Fe-content increases. Additionally, UV-Vis characterization reveals an excitonic peak associated with both the band gap energy (Eg) and binding energy (Eb). Values of Eg and Eb were extracted from the absorbance data by modeling the absorption coefficient using a combination of excitonic peak plus continuous edge, through a modified Elliot's approach including an inverse lognormal distribution function. The FTIR measurements proved to be a valuable tool for determining the structural properties of Fe-doped ZnO, which is consistent with the change in bond length and increase in the surface area suggested by XRD data. Finally, our results show strong evidence of the entry of Fe2+-ions as a solid solution with Zn2+-ions at low Fe-content, whereas for high Fe-content the coexistence of Fe3+/Fe2+ is increased, in agreement with magnetic measurements.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research work was carried out with the financial support of the UNSA INVESTIGA (Grant No. IBA-IB-13-2020-UNSA). The LVL author thanks to CAPES for the postdoctoral fellowship (No. 88887.319028/2019-00).References
- M. L. Dinesha, G. D. Prasanna, C. S. Naveen and H. S. Jayanna, Structural and dielectric properties of Fe doped ZnO nanoparticles, Indian J. Phys., 2013, 87, 147–153 CrossRef CAS.
- M. A. Ciciliati, M. F. Silva, D. M. Fernandes, M. A. C. de Melo, A. A. W. Hechenleitner and E. A. G. Pineda, Fe-doped ZnO nanoparticles: Synthesis by a modified sol–gel method and characterization, Mater. Lett., 2015, 159, 84–86 CrossRef CAS.
- E. Rokhsat and A. Khayatian, Enhanced photocatalytic activity of Fe doped ZnO hierarchical nanosheets on the degradation of p-nitrophenol under visible light, Inorg. Nano-Met. Chem., 2018, 48, 203–209 CrossRef CAS.
- L. Dimesso, Pechini Processes: An Alternate Approach of the Sol–Gel Method, Preparation, Properties, and Applications, in Handbook of Sol-Gel Science and Technology, ed. L. Klein, M. Aparicio and A. Jitianu, Springer, Cham, 2016, pp. 1–22 DOI:10.1007/978-3-319-19454-7_123-1.
- S. C. Andia-Huaracha, L. M. Zapana-Cayo, F. F. H. Aragón, J. C. R. Aquino, J. A. H. Coaquira, C. D. Gonzales-Lorenzo, J. S. Ayala-Arenas, J. L. Solis, P. C. Morais and D. G. Pacheco-Salazar, Tuning the photocatalytic activity of ZnO nanoparticles by the annihilation of intrinsic defects provoked by the thermal annealing, J. Nanopart. Res., 2022, 24, 50 CrossRef CAS.
- P. R. Sharma, S. K. Sharma, R. Antoine and B. S. Hsiao, Efficient Removal of Arsenic Using Zinc Oxide Nanocrystal-Decorated Regenerated Microfibrillated Cellulose Scaffolds, ACS Sustainable Chem. Eng., 2019, 7, 6140–6151 CrossRef CAS.
- R. Wang, A. W. Sleight and M. A. Subramanian, An Unusual Iron Site in Iron-Doped Zinc Oxide, J. Solid State Chem., 1996, 125, 224–227 CrossRef CAS.
- J. Xiao, A. Kuc, S. Pokhrel, M. Schowalter, S. Parlapalli, A. Rosenauer, T. Frauenheim, L. Mädler, L. G. M. Pettersson and T. Heine, Evidence for Fe2+ in Wurtzite Coordination: Iron Doping Stabilizes ZnO Nanoparticles, Small, 2011, 7, 2879–2886 CrossRef CAS PubMed.
- S. George, S. Pokhrel, T. Xia, B. Gilbert, Z. Ji, M. Schowalter, A. Rosenauer, R. Damoiseaux, K. A. Bradley, L. Mädler and A. E. Nel, Use of a Rapid Cytotoxicity Screening Approach To Engineer a Safer Zinc Oxide Nanoparticle through Iron Doping, ACS Nano, 2010, 4, 15–29 CrossRef CAS PubMed.
- P. S. Miedema and F. M. F. de Groot, The iron L edges: Fe 2p X-ray absorption and electron energy loss spectroscopy, J. Electron Spectrosc. Relat. Phenom., 2013, 187, 32–48 CrossRef CAS.
- J. T. Luo, Y. C. Yang, X. Y. Zhu, G. Chen, F. Zeng and F. Pan, Enhanced electromechanical response of Fe-doped ZnO films by modulating the chemical state and ionic size of the Fe dopant, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 014116 CrossRef.
- B. Toby, EXPGUI, a graphical user interface for GSAS, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- A. Galdámez-Martinez, G. Santana, F. Güell, P. R. Martínez-Alanis and A. Dutt, Photoluminescence of ZnO Nanowires: A Review, Nanomaterials, 2020, 10, 857 CrossRef PubMed.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- R. H. R. Castro, P. Hidalgo, J. A. H. Coaquira, J. Bettini, D. Zanchet and D. Gouvêa, Surface Segregation in SnO2–Fe2O3 Nanopowders and Effects in Mössbauer Spectroscopy, Eur. J. Inorg. Chem., 2005, 2134–2138 CrossRef CAS.
- T. Kataoka, M. Kobayashi, Y. Sakamoto, G. S. Song, A. Fujimori, F.-H. Chang, H.-J. Lin, D. J. Huang, C. T. Chen, T. Ohkochi, Y. Takeda, T. Okane, Y. Saitoh, H. Yamagami, A. Tanaka, S. K. Mandal, T. K. Nath, D. Karmakar and I. Dasgupta, Electronic structure and magnetism of the diluted magnetic semiconductor Fe-doped ZnO nanoparticles, J. Appl. Phys., 2010, 107, 033718 CrossRef.
- J. A. McLeod, D. W. Boukhvalov, D. A. Zatsepin, R. J. Green, B. Leedahl, L. Cui, E. Z. Kurmaev, I. S. Zhidkov, L. D. Finkelstein, N. V. Gavrilov, S. O. Cholakh and A. Moewes, Local Structure of Fe Impurity Atoms in ZnO: Bulk versus Surface, J. Phys. Chem. C, 2014, 118, 5336–5345 CrossRef CAS.
- S. C. Abrahams and J. L. Bernstein, Remeasurement of the structure of hexagonal ZnO, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 1233–1236 CrossRef CAS.
- Y. Cherifi, A. Chaouchi, Y. Lorgouilloux, M. Rguiti, A. Kadri and C. Courtois, Electrical, dielectric and photocatalytic properties of Fe-doped ZnO nanomaterials synthesized by sol gel method, Process. Appl. Ceram., 2016, 10, 125–135 CrossRef CAS.
- A. Baldan, Review Progress in Ostwald ripening theories and their applications to the γ′-precipitates in nickel-base superalloys Part II Nickel-base superalloys, J. Mater. Sci., 2002, 37, 2379–2405 CrossRef CAS.
- D. G. Pacheco-Salazar, F. F. H. Aragón, L. Villegas-Lelovsky, A. Ortiz de Zevallos, G. E. Marques and J. A. H. Coaquira, Engineering of the band gap induced by Ce surface enrichment in Ce-doped SnO2 nanocrystals, Appl. Surf. Sci., 2020, 527, 146794 CrossRef CAS.
- R. T. Senger and K. K. Bajaj, Optical properties of confined polaronic excitons in spherical ionic quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 045313 CrossRef.
- Y. Yang, M. Yang, K. Zhu, J. C. Johnson, J. J. Berry, J. van de Lagemaat and M. C. Beard, Large polarization-dependent exciton optical Stark effect in lead iodide perovskites, Nat. Commun., 2016, 7, 12613 CrossRef CAS PubMed.
- S. Neutzner, F. Thouin, D. Cortecchia, A. Petrozza, C. Silva and A. R. SrimathKandada, Exciton-polaron spectral structures in two-dimensional hybrid lead-halide perovskites, Phys. Rev. Mater., 2018, 2, 064605 CrossRef CAS.
- N. Kamarulzaman, M. F. Kasim and R. Rusdi, Band Gap Narrowing and Widening of ZnO Nanostructures and Doped Materials, Nanoscale Res. Lett., 2015, 10, 346 CrossRef PubMed.
- P. L. Hadimani, S. S. Ghosh and A. Sil, Preparation of Fe doped ZnO thin films and their structural, magnetic, electrical characterization, Superlattices Microstruct., 2018, 120, 199–208 CrossRef CAS.
- G. Rytwo, R. Zakai and B. Wicklein, The Use of ATR-FTIR Spectroscopy for Quantification of Adsorbed Compounds, J. Spectrosc., 2015, 2015, 727595 Search PubMed.
- J. Y. Chen, H. Zhang, J. Ma, T. Tuchiya and Y. Miao, Determination of the degree of degradation of frying rapeseed oil using Fourier-transform infrared spectroscopy combined with partial least-squares regression, Int. J. Anal. Chem., 2015, 2015, 185367 Search PubMed.
- H. Sanaeishoar, M. Sabbaghan and F. Mohave, Synthesis and characterization of micro-mesoporous MCM-41 using various ionic liquids as co-templates, Microporous Mesoporous Mater., 2015, 217, 219–224 CrossRef CAS.
- Y. Wang, A. Muramatsu and T. Sugimoto, FTIR analysis of well-defined α-Fe2O3 particles, Colloids Surf., A, 1998, 134, 281–297 CrossRef CAS.
- H. Singh and K. L. Yadav, Structural, dielectric, vibrational and magnetic properties of Sm doped BiFeO3 multiferroic ceramics prepared by a rapid liquid phase sintering method, Ceram. Int., 2015, 41, 9285–9295 CrossRef CAS.
- J. Xiao, A. Kuc, S. Pokhrel, L. Mädler, R. Pöttgen, F. Winter, T. Frauenheim and T. Heine, Fe-Doped ZnO Nanoparticles: The Oxidation Number and Local Charge on Iron, Studied by 57Fe Mößbauer Spectroscopy and DFT Calculations, Chem. – Eur. J., 2013, 19, 3287–3291 CrossRef CAS PubMed.
- H. Fjellvåg, F. Grønvold, S. Stølen and B. Hauback, On the Crystallographic and Magnetic Structures of Nearly Stoichiometric Iron Monoxide, J. Solid State Chem., 1996, 124, 52–57 CrossRef.
- K. Das, I. Ahmedmir, R. Ranjan and H. B. Bohidar, Size-dependent magnetic properties of cubic-phase MnSe nanospheres emitting blue-violet fluorescence, Mater. Res. Express, 2018, 5, 056106 CrossRef.
- F. F. H. Aragón, J. A. H. Coaquira, S. W. da Silva, R. Cohen, D. G. Pacheco-Salazar and L. C. C. M. Nagamine, Fe content effects on structural, electrical and magnetic properties of Fe-doped ITO polycrystalline powders, J. Alloys Compd., 2021, 867, 158866 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |