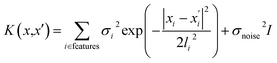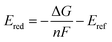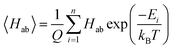Discovery of lead low-potential radical candidates for organic radical polymer batteries with machine-learning-assisted virtual screening†
Cheng-Han
Li
 and
Daniel P.
Tabor
and
Daniel P.
Tabor
 *
*
Department of Chemistry, Texas A&M University, College Station, TX 77842, USA. E-mail: daniel_tabor@tamu.edu
First published on 14th March 2022
Abstract
The discovery and development of new low reduction potential molecules that also have fast charge transfer kinetics is necessary for the further development of organic redox-active polymers in practical battery applications. Theoretical methods can aid in finding the lead radical candidates in large initial screening spaces, but low-cost (yet accurate) methods are needed to predict the functional properties of the materials. In this paper, we conduct a two-objective (potential and dimer electronic coupling) virtual screening campaign to identify lead low potential candidate molecules in an initial space of 660 candidate molecules. The screening is accelerated by employing a trained Gaussian Process regression model for the voltage screening task. The model takes a combination of core-group chemical fingerprints and low-cost semi-empirical quantum chemistry calculations as the features for the model. The top-10%-predicted lowest reduction potential molecules of the initial space are then screened further to identify the candidates with the highest predicted electronic coupling. From the screening campaign, a set of promising redox-active molecules and two Pareto-optimal molecules (both N-methylphthalimides) are identified.
1 Introduction
Nonconjugated redox-active polymers are promising alternatives to metal-based materials, particularly with their potential advantages as safe and environmentally-friendly alternatives to current metal-based batteries.1–6 In principle, these materials can be designed in a highly modular way, with potential several chemical modules, such as the side chain linker length, the chemistry of the polymer backbone, the topology of the polymer, the degree of polymerization, and the molecular identity of the functional redox-active group each serving as modules for targeted molecular engineering.7–10 This modularity has been specifically exploited for battery applications where critical properties including voltage, stability, and conductivity have been improved through targeted molecular engineering and synthesis.5–8,11–13 Indeed, these polymers are particularly appealing due to their relatively high synthetic accessibility.14 At the simplest level, one can think of the structural and overall dynamics of the polymers as being mostly tied to the chemistry and structure of the polymer and the electronic properties of the polymers as closely tied with the choice of the redox-active group, which is directly involved in the electron transfer reactions.8,14Several recent modeling efforts have focused on obtaining first-principles and physically intuitive models for predicting the conductivity of these materials.10,12,15 Sato et al. developed a diffusion-cooperative model for describing the electron kinetics in non-conjugated redox-active polymers.12 In parallel, Bello and Sing have developed models that leverage a coarse-grained framework for simulating the polymer dynamics.15 This access to longer timescales and length scales enabled the identification of different regimes of dominant charge transport mechanisms (e.g., intrachain vs. interchain hopping). In both models, the kinetics of individual electron hopping events is determined (or would be) by the molecular level details of the redox-active unit. Thus, obtaining a quantitative description that differentiates the performance of different proposed polymers from first principles requires that details about the molecular-level electron kinetics to be understood and accurately predicted.
Given the costs associated with simulating polymeric materials (with either atomistic molecular dynamics or coarse-grained simulations), one approach to computationally design new organic radical polymers is to focus on a “bottom-up” design, where a set of promising redox-active radical groups are first identified. From here, potential polymer backbones, structures, topologies, and electrolytes can be computationally (or experimentally) tested with the relatively small set of lead candidate radicals as part of the polymer repeat unit. Parallel studies of more generalized systems can help inform target properties (e.g. electronic couplings, reorganization energies, etc.) that would push the material performance to new limits. Thus, the focus of this article is on the discovery and molecular design of promising redox-active groups, specifically the low-potential (or anolyte) material. Though a large number of low potential molecular radicals have been employed as molecules or dissolved oligomers in organic redox flow batteries, the diversity of low potential molecules employed in polymer batteries is more limited (to mostly viologen species).16,17
Here, we conduct a two-objective, machine-learning-assisted virtual screening through a modularly-defined chemical space of anolyte candidates, seeking molecular redox-active groups estimated to have both low voltage and fast electron-transfer kinetics.4–6 Virtual screening workflows have been successfully employed for a number of molecular design problems, including organic functional materials18–21 and metal–organic complexes.22–24 For organic energy storage materials (primarily for use in flow batteries), the property objectives of previous screening campaigns have focused on finding molecules with optimal half cell potential, solubility, and (low) thermodynamic susceptibility to enumerated chemical decomposition reactions.25–29 In this paper, we simultaneously focus on the reduction potential and the molecular level property most likely to affect the conductivity – the electronic coupling. This property receives less attention in the flow battery literature due to the molecules being individually dissolved in solvent (electron transfer occurs at electrodes).30 However, there is substantial evidence that evaluating the electronic coupling can provide an “up or down” vote to the suitability of a radical core in polymeric batteries. Recently, Tan et al. conducted a comprehensive survey of the distribution of electronic coupling between radicals for four molecules, and found that the identity of the molecular core can substantially affect the localization of the radical and thus the effective electronic coupling between radical sites in the material.8 By screening for this property on a diverse set of molecular cores, we can determine the extent that these properties hold for other low potential cores.
Our work utilizes recent advances from the quantum chemistry community for calculating the electronic coupling between organic molecules. Until recently, electronic couplings between organic molecules have been often calculated with relatively low levels of electronic structure theory (e.g. HF/6-31G).12 Recently, Mao et al. developed the ALMO(MSDFT) family of methods for calculating electronic coupling (and hole coupling) between two molecules at a cost comparable to density functional theory (DFT).31 This method, which was benchmarked against EOM-CCSD methods, has also been shown to be relatively insensitive to the choice of the underlying density functional, making it a useful new tool for use in virtual screening protocols.
2 Computational methods
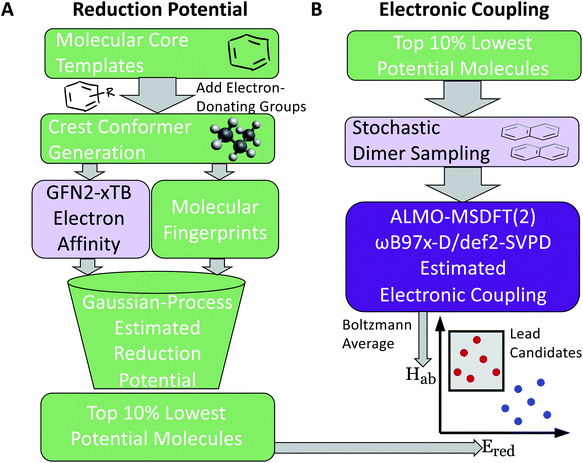
Our two-stage virtual screening workflow is shown in Fig. 1. As the electronic coupling evaluation requires more computational effort, due to the task requiring DFT calculations at numerous dimer geometries, the reduction potential screening is completed first to identify initial leads. We first generate a library of 660 candidates, then estimate their reduction potential. Lead candidates from this stage are then promoted to the more computationally intensive protocols that estimate their electronic coupling for the final stage of the screen.2.1 Candidate library construction
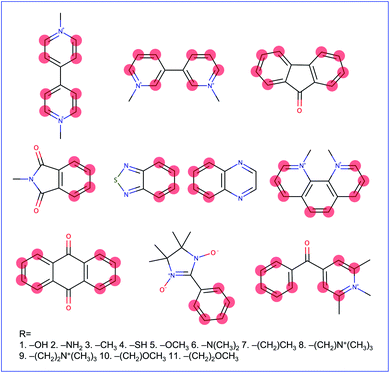
Molecular cores for the redox-active molecules in the library were chosen based on recent results in the literature that reported the synthesis or performance of low reduction potential molecules in a variety of battery applications (primarily organic redox flow batteries). We selected eight molecular cores from these reports (Fig. 2).32–39 In addition, 1,1′-dimethyl-[3,3′-bipyridine]-1,1′-diium (bipyridinium) and 1,10-dimethyl-1,10-phenanthroline-1,10-diium were included due to their similarity with methyl viologen, a commonly employed radical in both flow batteries and radical polymer batteries to date.7,19,40–42Electron-donating groups were introduced as substitution groups to build a library that should be rich in molecules with lower reduction potentials than the parent cores.16,17 Alkoxy and quaternary ammonium groups were included as they have strong precedent in the flow battery literature to increase the solubility and stability, in addition to the reduction potential effects.25,41,43 We systematically enumerated all the mono-substituted templates and selected some di-substituted species with priority on higher symmetry, which leads to a total of 660 candidates of low reduction potential molecules. A full list of the library is provided in the ESI† and Github repository. This library is small compared to the thousands (or millions) of molecules sometimes seen in virtual screening campaigns, but it is a targeted library that attempts to maximize synthetic accessibility of potential candidates. This library is also built to demonstrate the utility of workflows that focus on the transfer and adaptation of recent findings in one regime of organic materials design (flow batteries) to an area with some similar and some different demands (organic radical polymer batteries).
2.2 Gaussian-process estimation of reduction potentials
The following protocol was implemented to obtain estimates of the reduction potentials at a low computational cost. Molecular geometries for each molecule were initially generated from SMILES strings with Open Babel 3.1.1.44 The resulting structures were passed into the iMTD-GC45 workflow implemented in the CREST46 program to search for conformational minima. These conformers were further optimized at the GFN2-xTB47 level of theory in their “neutral” and reduced states with the implicit analytical linearized Poisson–Boltzmann48 (ALPB) acetonitrile model, using xtb 6.4.0.49 The electron affinity was obtained by subtracting the lowest energy of the reduced state from the lowest energy of the “neutral” state. An empirical EA energy shift, which was evaluated during the development of the GFN2-xTB method, was applied to correct the self-interaction error.50To accurately predict the reduction potential of redox-active molecules, several effects need to be taken into account. The energy of both the oxidized and reduced forms of the molecule can be influenced by the local solvation environment (solvation free energies), thermal corrections, and ion-pairing effect. Accounting for each of these effects, especially the solvation effects that may not closely cancel on each side of the reduction reaction, remains challenging to do in a low-cost computational manner.50–54 For the redox-active molecules in our library, we are interested in the redox pairs that differ by one charge at their cores. Considering the ion-pairing effect, the binding of the electrolyte cations toward the redox-active anions impedes the removal of the electron from the redox-active anions by the stabilizing electrostatic interactions. Different concentrations of electrolyte cations at equilibrium states will also shift the redox potential due to different ratios of the ion-paired and the free redox-active molecule populations.54 The focus of this paper is on optimization of the molecular component with other factors held fixed, but further considerations (including electrolytes and counter-ions) would need to be taken into consideration in the design of the final material. Recent investigations have tackled these problems with DFT,25,52–54 and machine learning models that predict the DFT redox potentials.55 Here, we leverage the capability of Gaussian Process (GP) regression models56,57 to calibrate electron affinity against experimental data of reduction potentials.
The GP regression model is a supervised machine learning model that is probabilistic in nature and importantly gives uncertainty measures of its predictions.58 GP models are regularly used in both computational material science and chemistry research.59 GP regression models can not only provide singular property predictions (such as in this work) with small training set sizes but also be scaled up using sparse GP regression models for generating potentials or forces that are useful for molecular dynamics simulations.60–62 The GP regression model treats each point for both training and prediction as a random variable and assumes these points follow multivariate Gaussian distribution. GP regression model incorporates the kernel as the prior to constrain the distribution. In property prediction models, prior work56,57 has demonstrated the superior performance of the GP regression model over a set of other ML models in molecular property prediction tasks by using the sum of squared exponential kernels along with a noise kernel:
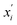 are the feature vectors of the i-th type of the selected features of data points x and x′, σi2 is the variance of the i-th feature kernel, li is the length scale of i-th feature kernel, and σnoise2 is the variance of the noise kernel.
are the feature vectors of the i-th type of the selected features of data points x and x′, σi2 is the variance of the i-th feature kernel, li is the length scale of i-th feature kernel, and σnoise2 is the variance of the noise kernel.
Our reduction potential prediction model combines semi-empirical quantum chemistry and low-data machine learning methods. For this task, a GP regression model was trained using the tools included in GPMol.57 The training set for the model is a set of experimental reduction potentials measured in acetonitrile selected from OROP set63 (a full list of molecules is included in the ESI†). Molecules in this set that have different counter-ions were not considered to avoid ion-pairing effects, though this could be considered in future design tasks.53,54 In addition, eight molecules that have experimental reduction potentials (Fig. 2) were added into the training set. It is necessary to add these data into our training set since the experimental conditions would affect the measured reduction potential. This is especially evident for quinoxaline, where a range of 1.35 V in reduction potential in different experimental conditions has been found.53 For these eight additional molecules, we found experimental literature values that were measured at similar experimental conditions, particularly with the same salt cation (Li in our case). This similarity would bear a resemblance to ion-pairing on the charged anions of the reduced redox-active molecules.54 All target values in the calibration set are adjusted to be their “absolute” reduction potential (by shifting values based on the reference electrode employed in the experiment):
Previous applications of GP models to regression tasks have used the full molecular fingerprints as features in the model. However, here we do not use the entire molecular fingerprint. Instead, we only pass the fingerprint and descriptor associated with the “core” group to the model (along with the electronic structure calculation of the estimated electron affinity). Building the model in this way has both chemical and mathematical advantages. The GP model incorporates the chemically-intuitive concept that reduction potentials of redox-active molecules with the same backbone generally remain in the same vicinity. The added functional groups are not treated on “equal footing” with the molecular cores, instead the quantum chemistry calculations are incorporated as the primary means to differentiate similar molecular cores that have different functionalizations. Using this prediction framework is further supported by the stratified nature of the plot of the GP-predicted potentials (when only the core is used) vs. the electronic affinities calculated by quantum chemistry (Fig. S2†) for a given core group. Prior library screens of reduction potentials have found that for a given core group, quantum chemistry (either DFT or semi-empirical methods) generally is able to capture a linear relationship.26–28 Mathematically, this simplification of the input features to the model reduces the variance of the model to avoid overfitting due to an over-reliance on a select number functional group results. After GP calibration, we then selected the top 10% of the lowest-electron affinity molecules and further evaluated their electronic coupling.
2.3 Electronic coupling calculations
As stated above, the fundamental electron transfer rate constant, which can be quantitatively described by Marcus–Hush theory,66–68 is a crucial factor that directly determines the upper bound of the kinetics of electron transfer between redox-active groups on the polymers.12 By accelerating the electron transfer kinetics between redox-active groups, it is possible to achieve a higher current density.12,15 In the nonadiabatic limit, it is desirable to increase the electronic coupling as this results in a higher probability of crossover of initial and final electron transfer states.8 One other important factor that affects the electron transfer rate constant is the reorganization energy. However, in these polymeric systems, the reorganization energy is dependent on the chemical environment, and the polymer structure, solvent, and morphology need to be accounted for to obtain reliable estimates of this value. Thus, this parameter would be more easily estimated further down in the molecular design process, where explicit polymer simulations are employed.To estimate the electronic coupling for the down-selected molecules, 100 dimer structures from optimized geometries for each molecule were generated (see Section S4† for details). Then, each dimer was further optimized using GFN2-xTB with the implicit ALPB acetonitrile model. Without the implicit solvent, charged species will often repel each other. The electronic coupling was calculated on these optimized dimer structures using the ALMO(MSDFT) method31 implemented in Q-Chem 5.3 (ref. 69) at the ωB97X-D/def2-SVPD level of theory. Since our molecular design objective is for non-conjugated radical polymer batteries, the maximum electronic coupling is not used. Instead, the Boltzmann-averaged electronic coupling was found:
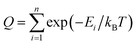 . The energies of each dimer were evaluated using the ALMO-EDA method70 with the IEF-PCM71,72 acetonitrile implicit solvent model.
. The energies of each dimer were evaluated using the ALMO-EDA method70 with the IEF-PCM71,72 acetonitrile implicit solvent model.
With further molecular engineering, it may be possible to engineer polymers that promote specific radical–radical orientations that maximize the electronic coupling. However, for near-term design tasks, the Boltzmann-averaged electronic coupling is a more realistic metric of the expected electronic couplings that the radical would experience.
3 Results and discussion
3.1 Performance of the Gaussian-process calibration reduction
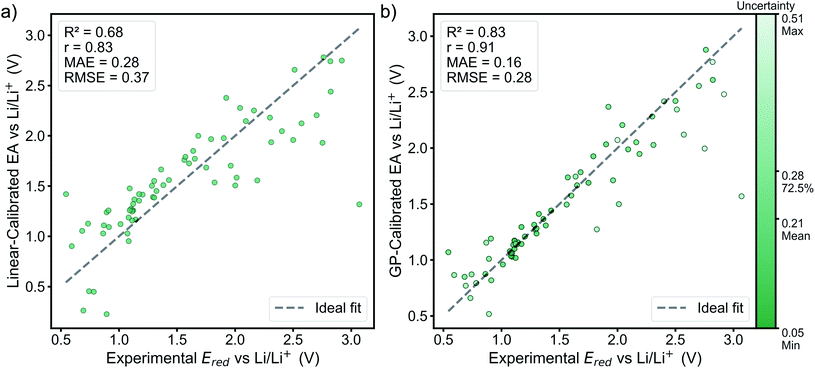
The performance of the GP model is evaluated in terms of absolute performance and by comparing to a linear model. Linear calibration models have generally been useful in estimating reduction potentials that involve simultaneous proton and electron transfer,26–28 but such calibration methods do not work as well for just electron transfer. The linear model is fitted by all the finding the best fit estimate of the experimental reduction potentials from the GFN2-xTB electron affinities. This model is directly compared with the leave-one-out cross-validation results of the GP model (implementation described above). The GP model performs better than the linear model on all of the statistics (Fig. 3).In the linear model, there is a single outlier with an experimental reduction potential near 3 V, quinoxaline. This outlier is due to the ion-pairing effect as mentioned above. Ideally, the GP model would learn this relationship without suffering from overfitting to the training set. Thus, using the same molecular descriptors for the substituted derivatives as their molecule templates can prevent the GP model from extrapolating on the unseen regime and let the GP model make the prediction based on the learned relationship with the GFN2-xTB electron affinity. By visualizing the bonds and atoms in a molecule that generate the bits with top importance in Fig. S4,† we can further interpret that the GP model is looking for the distinct functional groups and molecular environments that affect the reduction potential. This can be further supported by the fact that the average uncertainty is only about 0.024 V for the top-10% candidates, which shows the trained GP model is confident for its predictions. The candidates with higher uncertainty are all bipyridium and phenanthroline derivatives whose core molecular fingerprint is not included in the training data. The full list of calibrated reduction potentials with the uncertainty is included in the ESI.† The GP model also shows a higher certainty and converges at the lower reduction potential region, which helps predict the lowest reduction potential molecules from our candidates. Thus, the region of highest certainty directly matches the region of most interest for this work.
By combining estimates of the GFN2-xTB semi-empirical method and the GP model, we can achieve the prediction of experimental reduction potentials at a lower computational cost without conducting electronic structure calculations at a higher level of theory, such as DFT, which is often needed in organic materials screening. The strength of the GP model lies in the fact that after training the model with semi-empirical electron affinity and molecular fingerprints and descriptors, the GP model can calibrate the semi-empirical electron affinity with the functional group and structure of the molecule based on previous observations on the training data. The chemically intuitively strategy outlined above holds for this set of molecules.
3.2 Structure–property relationships and design rules for low reduction potential molecules
Fig. S1† shows the top 66 molecules with their GP-calibrated reduction potentials. Derivatives of N-methylphthalimide(phthalimide), 2,1,3-benzothiadiazole (benzothiadiazole), 9-fluorenone (fluorenone), and bipyridinium were found as the top candidates. Their molecule templates (unfunctionalized cores) were previously the lowest reduction potential compared to the other cores (except for the bipyridinium). For the same set of functional groups, the reduction potential of phthalimide derivatives is more strongly affected (in both directions) than the other derivatives, indicating that this core may warrant further functionalization investigations with other groups to push the potential even lower. Three derivatives of bipyridinium are also included in this top-10% set. The origin of their predicted low potential comes from the electronic structure calculations. The GFN2-xTB-predicted electron affinities of these molecules are about 1.65 eV lower than methyl viologen on average, which leads to the GP model predicting lower reduction potentials for each of them. Experimental results that explicitly contain these cores could be included in future training sets and would improve the regression model.Introducing the amino group as the substituent group provides the best effect in terms of lowering the reduction potential. The derivatives with the lowest reduction potential for four types of derivatives are all substituted with the amino group. To design a nonconjugated redox-active polymer, we also need to consider the side chain that links the redox-active group to the polymer backbone. The choice of the side chain can not only affect the structure of the entire polymer but also its character as a thin film electrode such as the degrees of the expulsion and uptake of counter-ions accompanied with solvent molecules, which will further modify the charge transport process of the redox-active group.11 Our results indicate that these functionalizations allow the molecule to maintain a low reduction potential while connecting redox-active groups with different side chains, consistent with chemical intuition. For example, as shown in Fig. S1,† introducing two –CH2 groups between each of the methoxy groups and the core of molecule 14, which leads to molecule 13, only slightly affects the reduction potential by 0.01 V.
3.3 Distribution of electronic coupling for the top-10% lowest reduction potential molecules
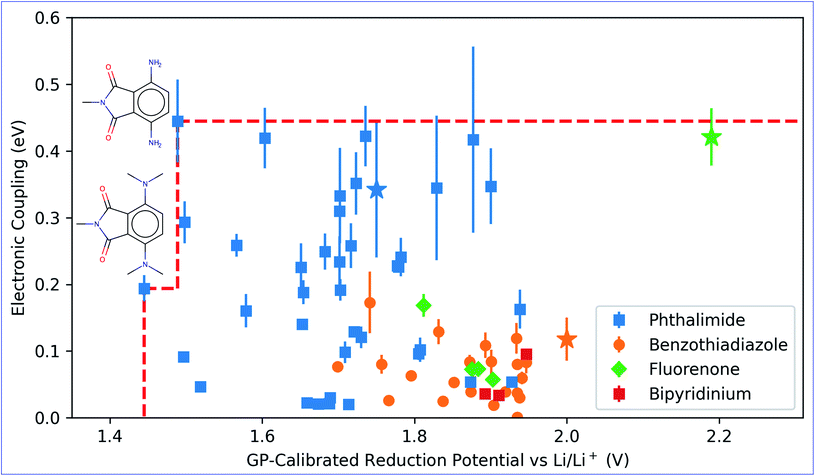
The charge transport process of the redox-active groups attached to the polymer backbones is often well-approximated by treating the problem as a series of electronic hopping events between the redox groups because of the localized nature of electrons on their redox centers.8,12,15 This picture may not completely hold when the mechanical effects brought by the structure of the polymer are taken into account. These mechanical effects have been important for TEMPO groups, where charge transfer is potentially inhibited due to the steric protection of its radical center.8 Thus, instead of finding the maximum possible electronic coupling that a pair of molecules can have together, we averaged over random dimer structures optimized in implicit acetonitrile. Note that even with the robustness of the ALMO(MSDFT) method, when applied at this higher-throughput (∼6600 calculations) scale, there are still some dimers conformations that have anomalously high estimated values of estimated electronic coupling (up to 6.8 eV). However, even if such high electronic coupling values were achievable at specific geometries, this is unlikely to be able to be engineered in a real material in the near term. Instead, it is most meaningful to examine the ensemble-averaged electronic coupling values. These are more likely to reflect the ability of these molecules to operate as the electroactive components of real batteries that can be currently synthesized. Therefore, outliers that fall outside of three standard deviations away from the mean of the sampling distribution were removed before Boltzmann-weighting calculations (see the discussion in Section S4†).By examining the distribution of electronic couplings (Fig. 4) among the lowest potential candidates, we can see that for the phthalimide cores, a wide range of calculated averaged electronic couplings are observed. In general, the highest average electronic couplings for molecules in this class (which is the largest class) are for molecules with relatively small functional groups attached. These findings may introduce additional design considerations for molecular radicals, as locality of the unfunctionalized radical core may provide an initial hint for the electronic coupling, but this must be confirmed by sampling the actual configurations that the molecules assume relative to each other.
3.4 Lead candidates and the two-objective Pareto-optimal front
The GP-calibrated reduction potentials and the Boltzmann-averaged electronic coupling are jointly plotted in Fig. 4 for the top-10% potential set. Also shown are the calculated electronic coupling values (using the same property prediction procedure) for molecule templates that were used to construct the library with their experimental reduction potentials. In general, our results shown that it is possible to obtain lower reduction potential from the derivatives of their molecule templates, but only a limited number derivatives of phthalimide and benzothiadiazole give higher expected electronic coupling. These trade-offs can be rationalized from steric arguments. The original molecular templates that lack substitution groups have more symmetrical and planar geometries. These geometries allow for closer packing when generating the random dimer structure and the electronic coupling is generally higher at closer approach. Three example cases of low-energy dimer configurations are provided in Fig. S5.† This picture is consistent with the view that larger degrees of monomer molecular orbitals overlap results in higher electronic coupling. This approach distance is closer than for the parent template molecules. We also note that for some of the –OH functionalized molecules, their lowest energy dimer configurations have a hydrogen-bonding, and these geometrical configurations lead to very little molecular orbital overlap and electronic coupling.Despite the general trade off between reduction potential and electronic coupling, two Pareto-optimal molecules22 were identified in Fig. 4, and both of them have phthalimide as their cores. Both Pareto-optimal molecules are substituted with amino groups and exhibit lower reduction potential. One of the Pareto-optimal molecules substituted with –N(CH2)2 results in the lowest reduction potential, while the other is substituted with –NH2 results in the highest expected electronic coupling due to less steric hindrance. The higher ends of the error bars on the Fig. 4 can also be thought of as targets that could be achieved in well engineered radical polymer, where higher electronic coupling is achievable through the resulting geometries dictated by the polymer structure.
4 Conclusions
With this work, we have identified lead candidates for the low potential components of organic radical polymer batteries that are predicted (at the molecular level) to have properties conducive to high electron conductivity. The workflow was enabled by leveraging a GP model that only required minimal training data to provide quantitative predictions of the experimental reduction potential. By selecting chemically-motivated features (the molecular core group fingerprint), we were able to reduce the risks of model over fitting while still providing quantitative predictions of the reduction potential, especially in the lowest potential regions, which were of the highest importance. The model also enabled the examination of much larger library (for a given timeframe), as the semi-empirical electronic structure calculations are much lower in cost than DFT calculations. This work demonstrates a potential strategy for rapidly identifying potential molecular modifications that would enable the translation of functional molecules from one field (molecular redox flow batteries) to a field with some common (and some new) property requirements.The phthalimide core had the highest number of low potential molecules in the library. This result is partially due to the parent molecule having the lowest reduction potential, but is also due to functionalization of phthalimide having the strongest effect on the reduction potential. The screening results predict that a small, but substantial number of molecules have both higher electronic coupling and lower reduction than the unfunctionalized parent molecules, suggesting that radical polymer batteries design requires further molecular engineering in all parts of the polymer. The set of lead radicals can be subjected to further tests, such as screens for stability against potential chemical reactions, and simulations of the structure and dynamics of radicals that contain these lead candidates as the radical component.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from Texas A&M University startup funding and the Robert A. Welch Foundation (Grant No. A-2049-20200401). Portions of this research were conducted with high-performance research computing resources provided by Texas A&M University HPRC. Preliminary results were supported by the Texas A&M Triads for Transformation (T3) program (Grant No. 02-247084). DPT acknowledges the Texas A&M Institute of Data Science Career Initiation Fellowship.Notes and references
- C. Friebe, A. Lex-Balducci and U. S. Schubert, ChemSusChem, 2019, 12, 4093–4115 CrossRef CAS.
- T. B. Schon, B. T. McAllister, P.-F. Li and D. S. Seferos, Chem. Soc. Rev., 2016, 45, 6345–6404 RSC.
- B. A. Helms and D. S. Seferos, Macromolecules, 2019, 52, 1349–1353 CrossRef CAS.
- Y. Lu and J. Chen, Nat. Rev. Chem., 2020, 4, 127–142 CrossRef CAS.
- J. Lopez, D. G. Mackanic, Y. Cui and Z. Bao, Nat. Rev. Mater., 2019, 4, 312–330 CrossRef CAS.
- J. Kim, J. H. Kim and K. Ariga, Joule, 2017, 1, 739–768 CrossRef CAS.
- T. P. Nguyen, A. D. Easley, N. Kang, S. Khan, S.-M. Lim, Y. H. Rezenom, S. Wang, D. K. Tran, J. Fan, R. A. Letteri, X. He, L. Su, C.-H. Yu, J. L. Lutkenhaus and K. L. Wooley, Nature, 2021, 593, 61–66 CrossRef CAS PubMed.
- Y. Tan, N. C. Casetti, B. W. Boudouris and B. M. Savoie, J. Am. Chem. Soc., 2021, 143, 11994–12002 CrossRef CAS.
- D. A. Wilcox, V. Agarkar, S. Mukherjee and B. W. Boudouris, Annu. Rev. Chem. Biomol. Eng., 2018, 9, 83–103 CrossRef PubMed.
- Y. Joo, V. Agarkar, S. H. Sung, B. M. Savoie and B. W. Boudouris, Science, 2018, 359, 1391–1395 CrossRef CAS PubMed.
- T. Ma, A. D. Easley, S. Wang, P. Flouda and J. L. Lutkenhaus, Cell Rep. Phys. Sci., 2021, 2, 100414 CrossRef CAS.
- K. Sato, R. Ichinoi, R. Mizukami, T. Serikawa, Y. Sasaki, J. Lutkenhaus, H. Nishide and K. Oyaizu, J. Am. Chem. Soc., 2018, 140, 1049–1056 CrossRef CAS.
- E. C. Montoto, Y. Cao, K. Hernández-Burgos, C. S. Sevov, M. N. Braten, B. A. Helms, J. S. Moore and J. Rodríguez-López, Macromolecules, 2018, 51, 3539–3546 CrossRef CAS.
- E. P. Tomlinson, M. E. Hay and B. W. Boudouris, Macromolecules, 2014, 47, 6145–6158 CrossRef CAS.
- L. Bello and C. E. Sing, Macromolecules, 2020, 53, 7658–7671 CrossRef CAS.
- M. Li, Z. Rhodes, J. R. Cabrera-Pardo and S. D. Minteer, Sustain. Energy Fuels, 2020, 4, 4370–4389 RSC.
- J. Winsberg, T. Hagemann, T. Janoschka, M. D. Hager and U. S. Schubert, Angew. Chem., Int. Ed., 2017, 56, 686–711 CrossRef CAS PubMed.
- E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, Ann. Rev. Mater. Res., 2015, 45, 195–216 CrossRef CAS.
- B. G. Abreha, S. Agarwal, I. Foster, B. Blaiszik and S. A. Lopez, J. Phys. Chem. Lett., 2019, 10, 6835–6841 CrossRef CAS.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120–1127 CrossRef PubMed.
- R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Matter, 2021, 4, 1654–1682 CrossRef CAS.
- J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, ACS Cent. Sci., 2020, 6, 513–524 CrossRef CAS PubMed.
- P. Friederich, G. dos Passos Gomes, R. De Bin, A. Aspuru-Guzik and D. Balcells, Chem. Sci., 2020, 11, 4584–4601 RSC.
- J. P. Janet, F. Liu, A. Nandy, C. Duan, T. Yang, S. Lin and H. J. Kulik, Inorg. Chem., 2019, 58, 10592–10606 CrossRef CAS PubMed.
- R. S. Assary, F. R. Brushett and L. A. Curtiss, RSC Adv., 2014, 4, 57442–57451 RSC.
- S. Er, C. Suh, M. P. Marshak and A. Aspuru-Guzik, Chem. Sci., 2015, 6, 885–893 RSC.
- K. Lin, R. Gómez-Bombarelli, E. S. Beh, L. Tong, Q. Chen, A. Valle, A. Aspuru-Guzik, M. J. Aziz and R. G. Gordon, Nat. Energy, 2016, 1, 16102 CrossRef CAS.
- D. P. Tabor, R. Gómez-Bombarelli, L. Tong, R. G. Gordon, M. J. Aziz and A. Aspuru-Guzik, J. Mater. Chem. A, 2019, 7, 12833–12841 RSC.
- H. A. Doan, G. Agarwal, H. Qian, M. J. Counihan, J. Rodríguez-López, J. S. Moore and R. S. Assary, Chem. Mater., 2020, 32, 6338–6346 CrossRef CAS.
- E. Martínez-González, H. G. Laguna, M. Sánchez-Castellanos, S. S. Rozenel, V. M. Ugalde-Saldivar and C. Amador-Bedolla, ACS Appl. Energy Mater., 2020, 3, 8833–8841 CrossRef.
- Y. Mao, A. Montoya-Castillo and T. E. Markland, J. Chem. Phys., 2019, 151, 164114 CrossRef PubMed.
- S. K. Cook and B. R. Horrocks, ChemElectroChem, 2017, 4, 320–331 CrossRef CAS PubMed.
- G. Kwon, S. Lee, J. Hwang, H.-S. Shim, B. Lee, M. H. Lee, Y. Ko, S.-K. Jung, K. Ku, J. Hong and K. Kang, Joule, 2018, 2, 1771–1782 CrossRef CAS.
- C. Zhang, Z. Niu, Y. Ding, L. Zhang, Y. Zhou, X. Guo, X. Zhang, Y. Zhao and G. Yu, Chem, 2018, 4, 2814–2825 CAS.
- W. Duan, J. Huang, J. A. Kowalski, I. A. Shkrob, M. Vijayakumar, E. Walter, B. Pan, Z. Yang, J. D. Milshtein, B. Li, C. Liao, Z. Zhang, W. Wang, J. Liu, J. S. Moore, F. R. Brushett, L. Zhang and X. Wei, ACS Energy Lett., 2017, 2, 1156–1161 CrossRef CAS.
- F. R. Brushett, J. T. Vaughey and A. N. Jansen, Adv. Energy Mater., 2012, 2, 1390–1396 CrossRef CAS.
- Y. Ding, Y. Li and G. Yu, Chem, 2016, 1, 790–801 CAS.
- W. Duan, R. S. Vemuri, J. D. Milshtein, S. Laramie, R. D. Dmello, J. Huang, L. Zhang, D. Hu, M. Vijayakumar, W. Wang, J. Liu, R. M. Darling, L. Thompson, K. Smith, J. S. Moore, F. R. Brushett and X. Wei, J. Mater. Chem. A, 2016, 4, 5448–5456 RSC.
- K. H. Hendriks, C. S. Sevov, M. E. Cook and M. S. Sanford, ACS Energy Lett., 2017, 2, 2430–2435 CrossRef CAS.
- T. Janoschka, S. Morgenstern, H. Hiller, C. Friebe, K. Wolkersdörfer, B. Häupler, M. D. Hager and U. S. Schubert, Polym. Chem., 2015, 6, 7801–7811 RSC.
- E. S. Beh, D. De Porcellinis, R. L. Gracia, K. T. Xia, R. G. Gordon and M. J. Aziz, ACS Energy Lett., 2017, 2, 639–644 CrossRef CAS.
- B. Hu, C. DeBruler, Z. Rhodes and T. L. Liu, J. Am. Chem. Soc., 2017, 139, 1207–1214 CrossRef CAS.
- T. Hagemann, J. Winsberg, B. Häupler, T. Janoschka, J. J. Gruber, A. Wild and U. S. Schubert, NPG Asia Mater., 2017, 9, e340 CrossRef CAS.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33 Search PubMed.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- H. Neugebauer, F. Bohle, M. Bursch, A. Hansen and S. Grimme, J. Phys. Chem. A, 2020, 124, 7166–7176 CrossRef CAS.
- S. Maier, B. Thapa and K. Raghavachari, Phys. Chem. Chem. Phys., 2020, 22, 4439–4452 RSC.
- J. E. Bachman, L. A. Curtiss and R. S. Assary, J. Phys. Chem. A, 2014, 118, 8852–8860 CrossRef CAS PubMed.
- E. V. Carino, C. E. Diesendruck, J. S. Moore, L. A. Curtiss, R. S. Assary and F. R. Brushett, RSC Adv., 2015, 5, 18822–18831 RSC.
- X. Qu and K. A. Persson, J. Chem. Theory Comput., 2016, 12, 4501–4508 CrossRef CAS PubMed.
- Y. Okamoto and Y. Kubo, ACS Omega, 2018, 3, 7868–7874 CrossRef CAS PubMed.
- B. Sanchez-Lengeling, L. M. Roch, J. D. Perea, S. Langner, C. J. Brabec and A. Aspuru-Guzik, Adv. Theory Simul., 2019, 2, 1800069 CrossRef.
- A. Jinich, B. Sanchez-Lengeling, H. Ren, R. Harman and A. Aspuru-Guzik, ACS Cent. Sci., 2019, 5, 1199–1210 CrossRef CAS.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, 2006 Search PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- A. Hajibabaei, M. Ha, S. Pourasad, J. Kim and K. S. Kim, J. Phys. Chem. A, 2021, 125, 9414–9420 CrossRef CAS PubMed.
- A. Hajibabaei and K. S. Kim, J. Phys. Chem. Lett., 2021, 12, 8115–8120 CrossRef CAS PubMed.
- A. Hajibabaei, C. W. Myung and K. S. Kim, Phys. Rev. B, 2021, 103, 214102 CrossRef CAS.
- E. Hruska, A. Gale and F. Liu, J. Chem. Theory Comput., 2022, 18, 1096–1108 CrossRef PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- R. Todeschini and V. Consonni, in Descriptors from Molecular Geometry, John Wiley & Sons, Ltd, 2003, ch. VIII.2, pp. 1004–1033 Search PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322 CrossRef CAS.
- N. Hush, J. Electroanal. Chem., 1999, 470, 170–195 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- Q. Ge, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2018, 148, 064105 CrossRef PubMed.
- D. M. Chipman, J. Chem. Phys., 2000, 112, 5558–5565 CrossRef CAS.
- E. Cancès and B. Mennucci, J. Chem. Phys., 2001, 114, 4744–4745 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Contains a list of the lowest potential molecules in the initial screening set, further details on the procedure for the Gaussian processor regression model training, and a description of the dimer generation procedure and statistical analysis of the calculated electronic couplings. The notebooks and code that were used to analyze the electronic coupling data and generate the plot are available at the following Github repo: https://github.com/Tabor-Research-Group/redox_mol_screening. See DOI: 10.1039/d2ta00743f |
| This journal is © The Royal Society of Chemistry 2022 |