Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Topology detection in cavity QED†
Beatriz
Pérez-González
 *a,
Álvaro
Gómez-León
b and
Gloria
Platero
*a,
Álvaro
Gómez-León
b and
Gloria
Platero
 a
a
aInstituto de Ciencia de Materiales de Madrid, ICMM-CSIC, Calle Sor Juana Inés de la Cruz, n°3, 28049 Madrid, Spain. E-mail: bperez03@ucm.es
bInstituto de Física Fundamental, IFF-CSIC, Calle Serrano 113b, 28006 Madrid, Spain
First published on 17th June 2022
Abstract
We explore the physics of topological lattice models immersed in c-QED architectures for arbitrary coupling strength with the photon field. We propose the use of the cavity transmission as a topological marker and study its behaviour. For this, we develop an approach combining the input–output formalism with a Mean-Field plus fluctuations description of the setup. We illustrate our results with the specific case of a fermionic Su–Schrieffer–Heeger (SSH) chain coupled to a single-mode cavity. Our findings confirm that the cavity can indeed act as a quantum sensor for topological phases, where the initial state preparation plays a crucial role. Additionally, we discuss the persistence of topological features when the coupling strength increases, in terms of an effective Hamiltonian, and calculate the entanglement entropy. Our approach can be applied to other fermionic systems, opening a route to the characterization of their topological properties in terms of experimental observables.
1 Introduction
Cavity Quantum Electro-Dynamics (c-QED) studies the interaction between light and matter at the most elementary level, either with real atoms1 or solid-state devices, like mesoscopic circuits.2 These hybrid systems have revealed themselves as an important tool for the control and manipulation of quantum systems,3 and in particular, they have become a essential landmark in the development of quantum technologies, such as quantum computing4,5 or quantum information processing.6–8 This is because the coherent interaction of the fermionic system and the photonic field allows for an efficient transfer of information between the two,9,10 provided that the coupling with the cavity is larger than the losses in the system. This is usually refered to as the strong-coupling regime in the literature of the field.The experiments in the field of c-QED with engineered solid-state devices have made formidable progress, especially studying different types of qubits (two-level systems) strongly coupled to resonators. Moving from the first realization of strong coupling11,12 back in 2004, many advances have been implemented in different directions, such as: single-qubit and two-qubit gates between two nearby qubits;13,14 coupling arbitrarily distant qubits with the resonator acting as a cavity bus;14–17 implementing quantum algorithms;18–20 or exploring the quantum nature of the photonic field.21–24 In conjunction with these achievements, there is an implicit quest for reducing the loss rates of the system to consolidate the strong-coupling condition, but also for increasing the coupling strength to make it comparable to the bare frequencies of the system. This leads to new regimes of interaction, known as ultrastrong and deep-strong coupling, that have also been recently measured25–28 and open up the way for different strategies in quantum technologies29–32 and to novel physical phenomena.33 In conclusion, it is clear that there is an enormous effort underway in harnessing the light-matter interaction under different choice of parameters, guided by both the exploration of fundamental phenomena and the prospects of designing outstanding technological applications.
In this context, a step further can be taken by considering the combination of quantum light and complex quantum materials with emergent properties, being topological systems an outstanding example of such systems.34–37 Topological phases of matter are characterized by a topological invariant which takes integer values, and whose associated physical properties are robust against a wide number of perturbations. A well-known example are topological insulators (TIs):38,39 they have mid-gap states which are exponentially localized at the boundaries and protected by the topological properties of the band structure. Topological insulators have their own plethora of applications in quantum technologies.40–45
In this work, we investigate the physics of fermionic topological systems in c-QED architectures and explore the cavity transmission for arbitrary coupling strength. Typical experiments probe the cavity through its transmited signal, and it is usually employed for readout and control of the state of the system.46,47 Our aim is to study the use of the cavity transmission as a topological marker, identifying the experimental signatures of non-trivial topology, and characterize the physics of the hybrid system. Specifically, we consider the case of a single-mode cavity interacting with a one-dimensional chain described by the SSH model,48–51 a canonical example of one-dimensional TIs consisting of a tight-binding Hamiltonian with an alternating hopping pattern. Despite its simplicity, this dimerized lattice structure captures the relevant features of non-trivial topology and gives rise to two distinct topological phases: the trivial phase, which corresponds to the usual two-band insulator, and the topological phase, hosting the aforementioned edge states.
For that purpose, we develop a formalism to calculate tc for arbitrary coupling in terms of the retarded photonic Green function (GF). We also obtain an analytical expression for the cavity transmission through a generalized input–output formalism, using a mean-field (MF) plus fluctuations analysis, and discuss its validity for different coupling strengths. We find that the transmission can be used to detect non-trivial topology in a fermionic system, with an appropriate state preparation depending on the regime considered. We also derive an effective Hamiltonian to investigate the topological changes produced by the hybridization between photons and fermions, and obtain the entanglement entropy for different partitions of the system.
2 Mean-field and fluctuations Hamiltonian
We consider a mesoscopic system interacting with a cavity. The system can be described by the following Hamiltonian H = H0 + V, where| H0 = Ωd†d + HS. | (1) |
| V = g(d† +d) Z, | (2) |
We apply a MF decoupling and write each operator in V as its average plus the fluctuations around it: ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) = 〈
= 〈![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 〉 + δ
〉 + δ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) , being δ
, being δ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) the fluctuations operator. This results in the following Hamiltonian for the cavity, fermionic system and its mutual interaction:
the fluctuations operator. This results in the following Hamiltonian for the cavity, fermionic system and its mutual interaction:
| H0 + V = HS + g(〈d†〉 + 〈d〉)Z + Ωd†d + g〈Z〉(d† +d) + g(δd† +δd)δZ | (3) |
The first and the second line in eqn (3) contain the fermionic and photonic MF Hamiltonians, HMF,S and HMF,Ω respectively. The third line in eqn (3) contains the term of second order in the fluctuations operators (which we will denote fluctuations Hamiltonian Hδ hereafter), while the scalar contribution has been neglected. Note that the MF Hamiltonians (that contain fluctuation operators only from one of the subsystems) have been rewritten in terms of the original operators using δ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) =
= ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) − 〈O〉.
− 〈O〉.
In the asymptotic limits of g → {0, ∞}, fluctuations are completely suppressed and the two systems effectively decouple, making the MF description exact. However, away from these limits, the effect of fluctuations is relevant. We shown below how their effect can be incorporated in the calculation.
For a complete characterization one needs to find self-consistent solutions to 〈Z〉, 〈d†〉 and 〈d〉, which can be easily obtained, to lowest order, from the MF Hamiltonian. For this, we rotate HMF,Ω with R = exp{−g〈Z〉 (d† − d)/Ω}, and find the following diagonal form:
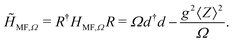 | (4) |
Eqn (4) indicates that, at the MF level, the solely effect of the topological system on the cavity photons is a global shift of all their energies. Importantly, the MF photonic Hamiltonian is diagonal now in the rotated basis, which means that eqn (4) allows to determine the average of the photon operators very easily, resulting in 〈d†〉 + 〈d〉 = − 2g〈Z〉/Ω. For this reason, we can write the MF fermionic Hamiltonian in terms of fermionic averages only:
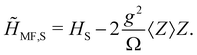 | (5) |
This simplifies the calculation of the self-consistency equation for 〈Z〉, which can now be obtained using an iterative numerical procedure.
For convenience, the fermionic operators will be expressed in the basis of Hubbard operators, defined as: 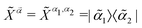 , with |
, with |![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) i〉 (αi = 1,…, N) being the eigenstates of the MF fermionic Hamiltonian,
i〉 (αi = 1,…, N) being the eigenstates of the MF fermionic Hamiltonian, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) MF,S|
MF,S|![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) i〉 =Ẽαi|
i〉 =Ẽαi|![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) i〉, and
i〉, and ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) = (α1, α2). We write the fluctuations Hamiltonian in terms of the fermionic Hubbard operators, and rotate the photonic operators with R as well. With R†d(†)R = d(†) − g〈Z〉/Ω, we finally obtain
= (α1, α2). We write the fluctuations Hamiltonian in terms of the fermionic Hubbard operators, and rotate the photonic operators with R as well. With R†d(†)R = d(†) − g〈Z〉/Ω, we finally obtain
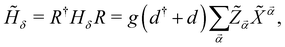 | (6) |
![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif)
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/char_e118.gif) = 〈
= 〈![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) 1|(Z − 〈Z〉)|
1|(Z − 〈Z〉)|![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) 2〉.
2〉. ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) δ has the same structure as V, however Z has been replaced by the fluctuations operator δZ = Z − 〈Z〉. Indeed,
δ has the same structure as V, however Z has been replaced by the fluctuations operator δZ = Z − 〈Z〉. Indeed, ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif)
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/char_e118.gif) measures the impact of fluctuations on the MF eigenstates, and vanishes when g → {0, ∞}, making
measures the impact of fluctuations on the MF eigenstates, and vanishes when g → {0, ∞}, making ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) δ negligable in these two asymptotic limits, as expected.
δ negligable in these two asymptotic limits, as expected.
Note that the effect of the interaction between subsystems is not only contained in ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) δ, but also in the MF Hamiltonians: both
δ, but also in the MF Hamiltonians: both ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) MF,Ω and
MF,Ω and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) MF,S are dressed by the interaction and include the backaction due to the presence of the other subsystem. Physically, one can see that if 〈Z〉 ≠ 0, the cavity photons introduce a term proportional to Z in the fermionic Hamiltonian (eqn (5)), that can affect the topological properties, while the photonic part acquires only a global shift in their bare energies (eqn (4)).
MF,S are dressed by the interaction and include the backaction due to the presence of the other subsystem. Physically, one can see that if 〈Z〉 ≠ 0, the cavity photons introduce a term proportional to Z in the fermionic Hamiltonian (eqn (5)), that can affect the topological properties, while the photonic part acquires only a global shift in their bare energies (eqn (4)).
3 Calculation of the cavity transmission
3.1 Connection with the photonic Green's function
To account for the measurement of the cavity transmission tc, we have to include the coupling of the cavity photons to the external modes.52 By means of input–output theory, we can obtain the input![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) in,l and output
in,l and output ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) out,l fields at each of the sides l = 1,2 of the cavity, and write the cavity transmission as the ratio tc = 〈
out,l fields at each of the sides l = 1,2 of the cavity, and write the cavity transmission as the ratio tc = 〈![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) out〉/〈
out〉/〈![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) in〉. Both the phase and the amplitude of tc = |tc|eiφ are modified by the interaction with the electronic system and can be experimentally measured. Importantly, the notation used for
in〉. Both the phase and the amplitude of tc = |tc|eiφ are modified by the interaction with the electronic system and can be experimentally measured. Importantly, the notation used for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) in,l (t) and
in,l (t) and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) out,l (t) denotes that to the input and output fields have to be transformed as well to the rotated frame with R (see ESI,† for further details on the input–output formalism).
out,l (t) denotes that to the input and output fields have to be transformed as well to the rotated frame with R (see ESI,† for further details on the input–output formalism).
First, we demonstrate a connection between the retarded photonic Green function G(t, t′) = −iθ(t − t′)〈[d(t), d†(t′)] 〉 and tc. The starting point is the Langevin equation for the cavity field d(t):4,52
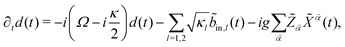 | (7) |
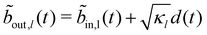 .
.
Now, it is only required to notice that G(t, t′), whose EoM yields
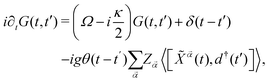 | (8) |
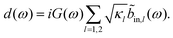 | (9) |
Then, using the previous expression and the input–output relation, one can easily see that
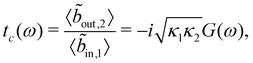 | (10) |
3.2 Analytical result for the cavity transmission
One can see in eqn (7) that, as the cavity photons couple to the fermionic system, the presence of the term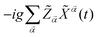 connects the topological properties of the later with the output photons detected at the ports of the transmission line. The equation of motion for the Hubbard operator yields:
connects the topological properties of the later with the output photons detected at the ports of the transmission line. The equation of motion for the Hubbard operator yields: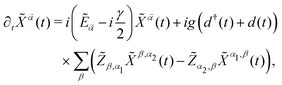 | (11) |
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) = Ẽα1 − Ẽα2, and the phenomenological spectral broadening γ is considered to be equal for all electronic transitions.
= Ẽα1 − Ẽα2, and the phenomenological spectral broadening γ is considered to be equal for all electronic transitions.
To close the system of equations and find an analytical solution for d(ω), a decoupling scheme is required. For this, we notice that contributions from fluctuations are small in the regimes g ≪ Ω, Ẽ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) and g ≫ Ω, Ẽ
and g ≫ Ω, Ẽ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) . Under these conditions, the MF description is accurate and we can rewrite the product d(†)(t)
. Under these conditions, the MF description is accurate and we can rewrite the product d(†)(t)![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif)
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) (t) as
(t) as
d(†)(t) ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) (t) ≈ 〈 (t) ≈ 〈![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 〉d(†)(t) + 〈d(†)〉 〉d(†)(t) + 〈d(†)〉![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) (t), (t), | (12) |
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) is obtained through the time evolution of the photonic and fermionic operator, separatedly. Note that by assuming that fluctuations are small, we are also neglecting extra correlation terms between the photonic and fermionic operators, which would only be relevant near resonances. For the same reason, the expected values 〈d(†)〉 and 〈
is obtained through the time evolution of the photonic and fermionic operator, separatedly. Note that by assuming that fluctuations are small, we are also neglecting extra correlation terms between the photonic and fermionic operators, which would only be relevant near resonances. For the same reason, the expected values 〈d(†)〉 and 〈![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 〉 can then be calculated using the MF Hamiltonians for the cavity and fermionic system, respectively. Importantly, the photonic averages in the rotated frame can be taken to be 〈d(†)〉 ∼ 0, since
〉 can then be calculated using the MF Hamiltonians for the cavity and fermionic system, respectively. Importantly, the photonic averages in the rotated frame can be taken to be 〈d(†)〉 ∼ 0, since ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) MF,Ω is of diagonal form. We will also neglect the contribution 〈
MF,Ω is of diagonal form. We will also neglect the contribution 〈![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 〉d†(t) for being small in the regime of interest,53 although this is not strickly necessary.
〉d†(t) for being small in the regime of interest,53 although this is not strickly necessary.
With these approximations, we can find a solution for the Hubbard and photonic operators, and together with the input–output relation, write an analytical expression for tc (see ESI†):
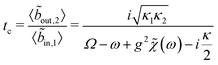 | (13) |
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) (ω) is the usual electronic susceptibility,
(ω) is the usual electronic susceptibility,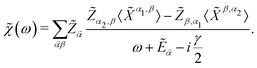 | (14) |
The statistical averages for the Hubbard operators found in eqn (14) can be approximated by their MF values: 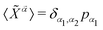 , being pα the occupation of state |
, being pα the occupation of state |![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) 〉 in the fermionic density matrix
〉 in the fermionic density matrix 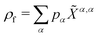 . Hence,
. Hence,![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) (ω) can be written as:
(ω) can be written as:
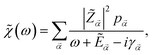 | (15) |
![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif)
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) | =
| = ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) α1,α2
α1,α2![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) α2,α1, and p
α2,α1, and p![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) = pα1 − pα2.
= pα1 − pα2.
Note that the decoupling scheme of eqn (12) is based on a perturbative approach on fluctuations rather than on the coupling strength. This allows to extend the validity of eqn (13), not only to the small-g regime as in the standard input–output theory within the linear approximation,53 but also to very-large-g (where the standard approach would fail). Additionally, working in the photonic rotated frame ensures that the calculation of the photonic averages yield the same results in both limits (d(†) = 0), and therefore ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) (ω) is formally equivalent to the usual electronic susceptibility derived for the small-g regime,53 with the difference that in this case all fermionic parameters are renormalized by the MF self-consistency equations (HS →
(ω) is formally equivalent to the usual electronic susceptibility derived for the small-g regime,53 with the difference that in this case all fermionic parameters are renormalized by the MF self-consistency equations (HS → ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) MF,S).
MF,S).
Correlations between photons and fermions are particularly important if there is a resonance between the cavity frequency and an electronic transition, in which case the decoupling of eqn (12) might not be valid. The validity of eqn (13) can then be compromised by the presence of highly-correlated hybrid states, and therefore the formalism presented above is specially tailored to capture the behaviour of the system in the dispersive regime, when Ω is far detuned from any electronic transition.
In general, G(ω) can always be calculated numerically using exact diagonalization of the total Hamiltonian H, including both the photon and matter Hilbert spaces. Hence, we can employ eqn (10), calculated by numerical means, to check the accuracy of the analytical result for tc obtained in eqn (13). Apart from the small- and very-large-g regimes, in which eqn (13) is specially well-suited, its validity for intermediate coupling strengths can also be tested by comparison with the exact numerical calculation, thus revealing the true effect of quantum fluctuations in the system. The results for tc at arbitrary g are presented in the following section. Further insight into the accuracy of eqn (13) can be obtained by means of an effective model, which will be also discussed thereupon, and the calculation of the entanglement entropy for different partitions of the system.
4 Results
4.1 SSH model and numerical solution for 〈Z〉
The theoretical framework developed so far is general and can be used for an arbitrary electronic system HS, with a general coupling operator Z. Now, we apply our formalism to a fermionic 1D topological system described by a tight-binding Hamiltonian with N sites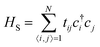 , where tij is the hopping amplitude and ci(c†i) is the destruction (creation) operator for a spinless fermion at site i. Particularizing for the SSH model, we define the inter- and intra-dimer hopping amplitudes t2i,2i+1 = t2i+1,2i ≡ t and t2i−1,2i = t2i,2i−1 ≡ t′ (in the following, we set t0 ≡ 1 as the energy scale for Ω and g).
, where tij is the hopping amplitude and ci(c†i) is the destruction (creation) operator for a spinless fermion at site i. Particularizing for the SSH model, we define the inter- and intra-dimer hopping amplitudes t2i,2i+1 = t2i+1,2i ≡ t and t2i−1,2i = t2i,2i−1 ≡ t′ (in the following, we set t0 ≡ 1 as the energy scale for Ω and g).
We choose to parametrize t and ′ through the dimerization constant δ: t = t0(1 − δ) and t′ = t0(1 + δ), with δ ∈ [ −1, 1]. The ratio between t and t' determines the phase of the system: the trivial phase happens for δ > 0, and the topological phase for δ < 0, with the corresponding pair of topologically protected edge states. Therefore, in finite samples, the non-trivial topological properties of the system manifest themselves in the appearance of topological edge states within the gap, and it is their presence that we wish to detect through the cavity transmission measurements.
The fact that this system can support two distinct topological phases stems from the presence of certain key symmetries, namely, time-reversal, particle-hole and chiral symmetry.54 The SSH model belongs to a wider class of materials known as symmetry-protected topological states,55 which implies that, in the absence of any of these symmetries, topological protection is lost. Therefore, it is important to analyze how the coupling to the cavity photons affects the symmetries and how this determines the fate of the edge states.
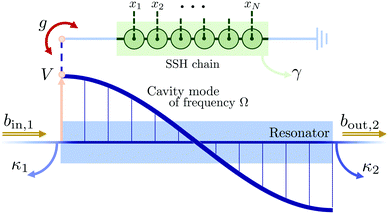
For the interaction between the cavity and the chain we consider the dipolar approximation, which couples the cavity electric field at a certain point of the axis of the resonator to the charge density at each site (see Fig. 1). The fermionic coupling operator is therefore the dipole operator 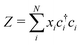 , being xi the position in the lattice.56 Hereafter we consider the origin of positions to be found at the middle of the chain, so that xN = −x1. The total voltage drop across the chain, which is determined by the design parameters of the resonator (impedance, frequency, total length), is proportional to the coupling strength. Ideally, one of the ends of the electronic system should be connected to the resonator at one antinode of the field, to maximize g.
, being xi the position in the lattice.56 Hereafter we consider the origin of positions to be found at the middle of the chain, so that xN = −x1. The total voltage drop across the chain, which is determined by the design parameters of the resonator (impedance, frequency, total length), is proportional to the coupling strength. Ideally, one of the ends of the electronic system should be connected to the resonator at one antinode of the field, to maximize g.
The first step is to find a solution for the order parameter 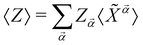 , which can be obtained through iteration of the self-consistent equation 〈Z〉 = Tr{Z
, which can be obtained through iteration of the self-consistent equation 〈Z〉 = Tr{Z![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) MF,S} until convergence. We assume the fermionic system is prepared in the ground state of
MF,S} until convergence. We assume the fermionic system is prepared in the ground state of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) MF,S,
MF,S,![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) MF,S = |
MF,S = |![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) 0〉 〈
0〉 〈![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) 0|. We also calculate the exact numerical result from the total Hamiltonian H = H0 + V (eqn (1) and (2)).
0|. We also calculate the exact numerical result from the total Hamiltonian H = H0 + V (eqn (1) and (2)).
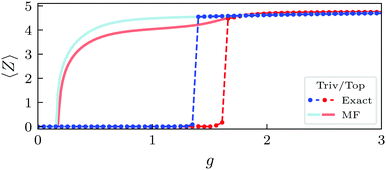
Fig. 2 shows 〈Z〉 as a function of g for the MF and exact cases, and provides us a precise value for the breakdown of the MF approximation. As expected, the MF calculation agrees with the exact value at small and large g. In the former case, 〈Z〉 = 0 indicates that the MF Hamiltonian coincides with the free Hamiltonian, and that the key symmetries of the model are unaffected by the coupling with the cavity. In the latter, the system polarizes (i.e.,〈Z〉 ≠ 0) indicating that the ground state of the system is modified and that certain symmetries change: the term 2g〈Z〉Z/Ω introduces an on-site energy in the chain and leads to the localization of the states. Furthermore, this breaks chiral symmetry, so we can anticipate that the interaction with the cavity will be detrimental for the edge states. To which extent and how they are affected will be studied in the following sections.
For intermediate values, fluctuations take over and lead to disagrement between the MF and the exact solution. The MF result indicates that the change in 〈Z〉 (i.e. the localization of the ground state) is continuous, corresponding to a second-order phase transition. However, the exact calculation shows a discontinuity at a critical value for g, which could indicate that is in fact a first-order transition.
4.2 Numerical results for tc for arbitrary coupling
In the small-g regime with 〈Z〉 = 0, the eigenstates |![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) i〉 of
i〉 of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) MF,S correspond to the eigenstates of the original electronic Hamiltonian HS, while
MF,S correspond to the eigenstates of the original electronic Hamiltonian HS, while ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) δ reduces to V. The calculation of the matrix elements
δ reduces to V. The calculation of the matrix elements ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif)
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) = 〈
= 〈![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) 1|Z|
1|Z|![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) 2〉 shows that in a finite system, the cavity can mediate transitions between all eigenstates of the chain, with the exception of the edge states in the topological phase, which exponentially suppress their coupling with the bulk states as a function of the chain length. In consequence, if the system is initially prepared in a bulk state, a measurement of tc will not reveal the presence of the edge states. The interaction with the electronic system will shift the cavity frequency equally for both the trivial and topological phase, which means that tc cannot be used as a topological marker in this regime, considering this state preparation. Only the initial preparation in an edge state would allow to detect topology: if the edge state is initially occupied in the topological phase, the transmission peak at ω = Ω should remain unaffected by the interaction (due to the suppressed coupling between edge and bulk states), as opposed to the behaviour of the trivial phase, in which changes in tc are expected (ESI†).
2〉 shows that in a finite system, the cavity can mediate transitions between all eigenstates of the chain, with the exception of the edge states in the topological phase, which exponentially suppress their coupling with the bulk states as a function of the chain length. In consequence, if the system is initially prepared in a bulk state, a measurement of tc will not reveal the presence of the edge states. The interaction with the electronic system will shift the cavity frequency equally for both the trivial and topological phase, which means that tc cannot be used as a topological marker in this regime, considering this state preparation. Only the initial preparation in an edge state would allow to detect topology: if the edge state is initially occupied in the topological phase, the transmission peak at ω = Ω should remain unaffected by the interaction (due to the suppressed coupling between edge and bulk states), as opposed to the behaviour of the trivial phase, in which changes in tc are expected (ESI†).
For g ≫ Ω, | ti,j|, we find instead that 〈Z〉 ≠ 0, due to the polarization of the system. However, the global shift in the energy of the cavity photons does not affect the measurement of tc, so we expect |tc| ≃ 1 again.
All these features are shown in Fig. 3, where we have calculated tc at ω = Ω = 10 (as in Fig. 2) for both phases, as a function of g, including from the small to the very-large g regime. One can see that the addition of fluctuations leads to a good agreement between the numerical (eqn (10)) and the analytical (eqn (13)) expression for tc, even for intermediate coupling strength. For small g, the peak of maximum transmission, initially found at ω = Ω, shifts due to the interaction for both phases. The edge states are transparent to the bulk states and their presence is not revealed in tc. However, eqn (10) and (13) predict that larger values of the coupling g bring essential differences between phases: while the trivial phase decays monotonically until reaching a minimum, the topological phase remains mostly unaffected, except for a notorius dip in |tc| for the intermediate regime (which corresponds to a change of sign in φ).
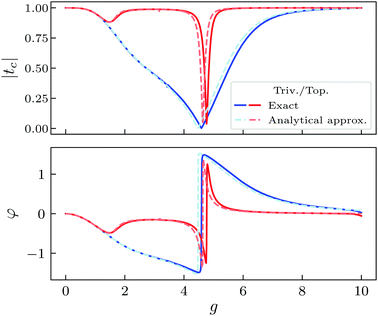 | ||
| Fig. 3 |tc(Ω)| and φ vs. g. Dashed lines correspond to the analytical approximation (eqn (13)), and solid lines to the exact solution (eqn (10)). The ground state of the chain is occupied. Parameters: ω = Ω = 10, δ = ±0.6, N = 20, γ = κ1 = κ2 = 0.01, nmax = 60. | ||
Thus, the effect of the topological edge states is not washed away by the chiral-symmetry breaking, and the difference between phases can still be detected. Finally, both phases display perfect transmission when g is sufficiently large, in accordance with the MF analysis. Importantly, the comparison between eqn (10) and (13) gives a perfect agreement between the exact and the analytical curves for arbitrary g, which means that eqn (13) captures the behaviour of the system for arbitrary coupling.
Note the important role of the fluctuations Hamiltonian in the calculation of the cavity transmission. If only the MF Hamiltonian was considered, the transmission would be trivially perfect tc ∼ 1 for all coupling strengths. This is precisely what we verify in the limits g → {0, ∞}, where the system effectively decouples and the MF description is accurate (see Fig. 3). The addition of Hδ as an effective interaction between subsystems allows to reproduce the exact result for the cavity transmission, despite the approximations employed in the derivation of eqn (13), i.e., neglecting correlations in the dynamics of photonic and fermionic operators (see eqn (??)). Similarly, the MF Hamiltonians include extra terms compared to the original unperturbed Hamiltonians, and therefore the calculation of the corresponding expected values are dressed by the interaction as well and depend on the parameters of both subsystems.
Regarding the numerical calculations, the exact diagonalization of the total Hamiltonian requires the truncation of the photons Hilbert space, which is of infinite dimension. We choose a maximum number of photons nmax by making sure that increasing the number of possible photons in the system does not affect the value of observables. The set of eigenvalues and eigenvectors are then used to calculate the exact Green's function, which provides the exact result for tc. The analytical result does not involve any truncation, and the sums are extended over the complete eigenvalues and eigenvectors of the MF fermionic Hamiltonian.
5 Effective Hamiltonian.
To explore in more detail the different interaction regimes, we derive an effective Hamiltonian using a Schrieffer–Wolff transformation in the basis of eigenstates of the MF Hamiltonian, where![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) δ is considered the perturbation to
δ is considered the perturbation to ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) S +
S + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) Ω.
Ω.
We propose the following ansatz for the transformation:
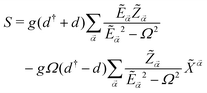 | (16) |
Then, the effective Hamiltonian 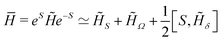 results in the following approximate form (ESI†):
results in the following approximate form (ESI†):
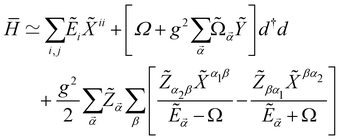 | (17) |
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif)
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) =
= ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif)
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) Ẽ
Ẽ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) /(Ẽ
/(Ẽ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) 2 − Ω2) and
2 − Ω2) and 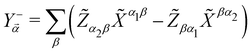 . To derive eqn (17) we have neglected the small correction provided by two-photon transitions in the rotated frame. Then,
. To derive eqn (17) we have neglected the small correction provided by two-photon transitions in the rotated frame. Then, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) includes a shift in the cavity frequency Ω, proportional to
includes a shift in the cavity frequency Ω, proportional to ![[capital Omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e133.gif)
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) , that depends on the state of the electronic system through Y
, that depends on the state of the electronic system through Y![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) −, as well as a correction to the MF electronic energies (second line).
−, as well as a correction to the MF electronic energies (second line).
The total frequency shift can be obtained from 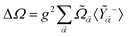 , where again the expected values are calculated to lowest order using the ground state of
, where again the expected values are calculated to lowest order using the ground state of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) S. In this case, we can give a simpler expression for ΔΩ:
S. In this case, we can give a simpler expression for ΔΩ:
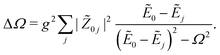 | (18) |
The cavity shift in plotted in Fig. 4 as a function of g for the same parameters as in Fig. 3. The dots correspond to the exact shift, obtained from the exact numerical tc (eqn (10)), compared to the predictions from the effective Hamiltonian (eqn (18), blue for the trivial and red for the topological phase) for arbitrary g. Additionally, ΔΩ obtained for 〈Z〉 = 0 (![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) → Z,
→ Z, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) MF,S → HS) has been included as well (dashed lines in light colors).
MF,S → HS) has been included as well (dashed lines in light colors).
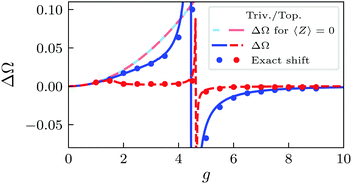 | ||
| Fig. 4 Plot of ΔΩ (eqn (18)) vs. g for both the trivial (blue) and topological (red) phase. The comparison with ΔΩ calculated with 〈Z〉 has been included in lighter colors. The dots corresponds to the exact shift (eqn (10)). Parameters: Ω = 10, δ = ±0.6, N = 20, nmax = 60. | ||
These results indicate that:
(i) the dependence of the MF electronic Hamiltonian on 〈Z〉 makes our result for the effective Hamiltonian ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) (eqn (17)) non-perturbative, since 〈Z〉 is a function of the other parameters as well. Indeed, eqn (18) shows an excellent agreement with the exact numerical data for arbitrary g.
(eqn (17)) non-perturbative, since 〈Z〉 is a function of the other parameters as well. Indeed, eqn (18) shows an excellent agreement with the exact numerical data for arbitrary g.
(ii) ΔΩ obtained for 〈Z〉 = 0 confirms that the employment of the MF + fluctuations approach allows to study the interaction between subsystems beyond small coupling for equilibrium configurations (i.e. ground state occupied): the predictions for this curve depart from those of the exact tc when the coupling is increased and the small-g regime breaks down. It also reinforces the idea that using tc as a topological marker is only possible beyond the small-g regime.
(iii) This break-down of the small-g regime and the onset of differences between both phases coincides with the critical value of g at which the exact 〈Z〉 signals the polarization of the topological phase (Fig. 2). Though 〈Z〉 obtained from the MF Hamiltonian does not reproduce that phase transition, the addition of fluctuations has an essential role in reproducing the exact results, for both the analytical tc (eqn (13)) and cavity shift ΔΩ (eqn (18)).
For larger values of g, the divergence in ΔΩ indicates the presence of a direct resonance between photons and fermions, which should lead to a drop in tc, as the minimum in Fig. 3 shows for both phases. Interestingly, ΔΩ changes sign after the divergence. Finally, for g ∼ Ω, ΔΩ → 0 for both phases, as expected: fluctuations are suppressed and the global shift in the energy of the photons predicted by the MF photonic Hamiltonian (eqn (4)) is not detected in tc.
The change in the eigenenergies of the system due to the interaction is not trivial. First, one has to take into account the polarization of the system and the appearance of the term 2g2〈Z〉Z/Ω in the MF Hamiltonian. However, the breaking of the symmetries that provide for topological protection is expected even for small g due to the term in the second line of eqn (17). Indeed, as g is increased, the topological edge states reduce their energy gradually, and eventually penetrate into the bulk band. Despite this, they play a crucial role: their presence can still be detected in tc even after their disappearance into the bulk, thus accounting for the differences in tc between phases. One can use this correction to the electronic MF eigenstates to measure the effect of fluctuations on the ground state of the MF electronic Hamiltonian. A numerical estimation of its magnitude reveals that it is very small, even in the intermediate regime. The fast suppression of fluctuations in the dispersive regime explains why there is such a nice agreement between the exact (eqn (10)) and analytical (eqn (13)) tc for arbitrary g shown in Fig. 3.
6 Entanglement entropy
Finally, to gain further insight into the topological features of the intermediate coupling regime, we explore the entanglement entropy in the system. The von Neumann entropy is defined as SA = −trAρA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρA, where ρA corresponds to the reduced density matrix of a subsystem A. When the system is divided in two partitions A ⊕ B, SA measures the amount of quantum correlation between them (note that SA = SB, with SB defined analogously). The entropy has been used in the study of quantum criticality and topology and has several contributions. In particular, in non-interacting systems one can find boundary contributions related with the Berry phase of the states and with the presence of edge modes.57 In the following, the reduced density matrices will be calculated exactly, using the eigenvalues and eigenvectors of the total Hamiltonian H = H0 + V, to include all correlation effects.
ρA, where ρA corresponds to the reduced density matrix of a subsystem A. When the system is divided in two partitions A ⊕ B, SA measures the amount of quantum correlation between them (note that SA = SB, with SB defined analogously). The entropy has been used in the study of quantum criticality and topology and has several contributions. In particular, in non-interacting systems one can find boundary contributions related with the Berry phase of the states and with the presence of edge modes.57 In the following, the reduced density matrices will be calculated exactly, using the eigenvalues and eigenvectors of the total Hamiltonian H = H0 + V, to include all correlation effects.
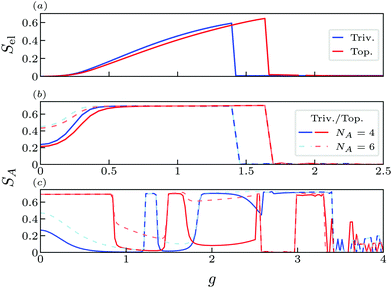
In our case, we can partition the system in two different ways. First, we consider a partition separating the fermionic chain and the cavity, and calculate Sfer by tracing out the photonic degrees of freedom (Fig. 5(a)). This produces a mixed state for the fermionic system. We can see that Sel grows with g and suddendly drops at a critical coupling strength value, which is different for the trivial and topological phase and reproduces the phase transition captured by the order parameter 〈Z〉 (see Fig. 2). However, the differences between both phases at finite coupling are not clarified for this partition.
The alternative partition requires to first integrate out the photonic degrees of freedom. The resulting density matrix for the fermionic chain encodes the role of photons and can be divided in two parts A = {1, 2,…,NA} and B = {NA + 1, NA + 2,…, N} (with NA ≠ N/2) of which the entropy can be calculated. This is interesting from a topological perspective, because the entanglement between these partitions has been already studied in non-interacting SSH chains and can differentiate between the trivial and the topological phase.57 In our case the fermionic reduced density matrix is dressed by photons, which makes the model more interesting from a fundamental perspective, as we are dealing with many-body topological models.
In Fig. 5(b) we plot the entanglement entropy for the system in its ground state. In general, the entropy increases as a function of g for both phases and saturates to log2, dropping to zero as the expectation value 〈Z〉 acquires a finite value. In that sense its behavior is similar to that of Fig. 5(a) and can be used to obtain information about the phase diagram for the order parameter. Interestingly, the saturation to log2 indicates that the ground state becomes a cat state for finite g, which is destroyed when the system polarizes (i.e., 〈Z〉 ≠ 0), turning into a fully localized state. However, it does not provide new insight into the topological characterization of the system, as it only differentiates between the two phases in the range of values comprised between their respective critical g.
In contrast, Fig. 5(c) considers the N/2-th state occupied (this is specially relevant to compare with half-filling in a non-interacting SSH chain). This state coincides with the edge state in the topological phase and with the top of the valence band in the trivial phase for the isolated chain. In this case the topological phase displays a quantized value SA = log2 for small g, independent of the partition, while for the trivial phase SA is smaller and changes for different partitions NA. The log2 value is a consequence of a maximally entangled cat state and its independence on the partition indicates that it is localized at the boundaries of the system (i.e., the bulk does not contribute and all entropy comes from the entanglement between the two edges57). Then, we can see that the topological boundary mode is present until the entropy drops, indicating the destruction of entanglement for the N/2-th state. This coincides with the first anti-crossing of the edge state with a bulk state as they penetrate in the bulk bands (see ESI†).
The persistence of the log(2) value for SA in the topological chain for small g means the interaction preserves the entanglement between ending sites created by the original topological boundary modes, though their energy and localization length does change due to the symmetry-breaking terms in the effective Hamiltonian. This can have important implications for designing quantum information protocols with c-QED structures in which correlation between distant sites of the fermionic system needs to be exploited, which in this case is naturally provided by the topological features of the chain. Importantly, the topological contribution to the entanglement does not dissappear after SA drops to zero at g ∼ 0.8, but migrates from one state to the other as the anti-crossing originated by the edge states entering the band take place in the energy spectrum (ESI†).
Interestingly, increasing g leads to a sucession of new log2 plateaus, indicating that boundary modes are linked with both the original trivial and the topological phases.58–60 Again, each abrupt change in SA coincides with an anti-crossing between the N/2-th and other states in the upper bands (see ESI†). Finally, when g approaches the divergence in Fig. 4 the entropy drops for both phases and the presence of boundary modes is completely washed out by the interaction with the cavity.
7 Conclusions
In this work, we have investigated the use of the cavity transmission tc as a topological marker for arbitrary coupling regimes in a hybrid system, composed of a quantum cavity coupled to a fermionic lattice with distinct topological phases. Both the amplitude |tc| and phase φ can be experimentally measured, carrying information about the fermionic system interacting with the cavity. For this purpose, we have developed a framework combining two perspectives: first, we have employed the retarded photonic Green function to obtain an exact result for tc for arbitrary coupling strengths; second, we have combined input–output formalism with a MF plus fluctuations analysis to derive an analytical expression whose validity can be extended beyond the small-g regime, where the standard input–output formalism would fail. Exploring how the interaction affects the topological properties of the fermionic system is also the aim of this work.To illustrate our results we have considered a topological SSH chain interacting via the dipolar coupling with the cavity. In topological systems, the bulk-boundary correspondence ensures that non-trivial properties of the bulk of the material translate into edge states within the gap of a finite sample with open ends, provided that certain symmetries are preserved. Therefore, we make use of the edge states and their signatures of their presence in the cavity transmission to characterize the topology of a finite size of N sites. We reproduce the expected results for small g, where it is well-known that the transmission allows for dispersive readout of the properties of the fermionic system. In the small coupling regime, detecting differences between phases with distinct topology is possible if the system is initialized in its edge state: while the cavity can mediate many transitions between the bulk states, the edge states remain isolated from them. In a experiment, one can benefit from these differences to test the formation of the topological edge states in the topological phase. One disadvantage of this regime of operation is that the measurement needs to be carried out before thermalization happens, but this could be avoided by filling the fermionic system to half-filling (however, in this case many systems require to account for particle interactions as well).
Beyond the small-g regime, differences between topological phases are enhanced, and importantly, they can be detected for the ground state as well, indicating that the measurement can be performed when the system has thermalized. This means that the presence of the edge states still has an impact on the cavity transmission, despite the chiral symmetry breaking induced by the coupling. In conclusion, if the coupling strength between the cavity and the SSH chain can be adiabatically increased, one should verify that the peak of maximum transmission is shifted towards higher energies for the trivial phase, while for the topological phase, its initial position at ω = Ω is rapidly restored (see Fig. 3 and 4). This is an unavoidable signature of the presence of the topological edge states. To study this intermediate regime in more depth, we have derived an effective Hamiltonian encoding the role of fluctuations to first order.
Finally, we have also studied the entanglement entropy between different partitions of the total system (Fig. 5), and how this quantity connects with the previous results. As expected, we verify the entanglement between photons and fermions increases as the coupling strength gets larger, which is crucial for many applications of c-QED architectures,61,62 up to a critical value at which it suddenly drops to zero. We also explored the entanglement between two assymetric partitions of the SSH chain, once the photonic degrees of freedom have been traced out. This sheds light on how the interaction affects the eigenstates of the chain, and how the entanglement created by the edge states is mantained for large values of the coupling, even after they have penetrated into the bulk bands.
Regarding the experimental implementations, crucial milestones have been achieved on different platforms that pave the way for the realization of the findings discussed in this work.
On one hand, quantum dots (QDs) offer a scalable, highly-tunable solid state platform, in which the control and manipulation of long arrays has already been reached,63–65 including the simulation of fundamental models.66,67 When placed inside cavities, different experiments have proven to fulfill the strong-coupling condition g > { κ, γ }, both in doble16,68–78 and triple QDs.17,79 The charge-photon coupling is achieved through dipolar coupling, with the architecture proposed in this article. The values of g that are reached with the current state-of-the-art techniques in QDs would only allow for topological detection in the small-g regime, occupying an edge state (ESI†). A typical value for the coupling strength in this setup is g < 0.1Ω. However, larger coupling strengths can be envisioned in future devices. The ongoing improvement of the experimental techniques of fabrication and properties of QDs, together with the design of resonators with higher impedances,68,75,80 is leading to the optimization of g versus the decoherence rates, specially charge noise.46,80
Another suitable option for implementation could be cold atoms, where the simulation of complex Hamiltonians with non-trivial topological properties has already been studied81 and implemented.82 They offer great versatility and control in c-QED experiments:83 atoms can be loaded deterministically inside the cavity, which allows to tailor the atom-field coupling on demand,84,85 as well as long coherence times.84,86 The condition g > {κ, γ} has also been achieved.84,86–94 For the model Hamiltonian, it is only required to notice that the hopping term can be written as 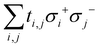 and the fermionic part of the interaction can be mapped to a Zeeman term that changes linearly with the position
and the fermionic part of the interaction can be mapped to a Zeeman term that changes linearly with the position 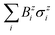 . This can also be extrapolated to trapped ions.95
. This can also be extrapolated to trapped ions.95
Larger coupling strengths have already been realized with superconducting qubits.96 The condition g > {γ, κ} is very well-stablished,97 but more significant is the achievement of further regimes of interaction in which the coupling to the resonator can reach values comparable to the energy of the qubit.25–28 Additionally, the SSH model considered in this work has also been realized using superconducting qubits98 Therefore, this would be a feasible platform to implement the topology detection discussed for arbitrary coupling strengths with the current techniques.
As an outlook, we believe our work provides a solid basis to study topological systems coupled to quantum cavities, while opening the way to complementary research. For example, including the role of electron interactions using a Hubbard term, or developing an effective Hamiltonian to study the resonant case in more depth. Besides, other interaction models for the cavity and fermionic system could be adressed in order to connect with experiments performed on different set-ups. Lastly, the employment of the entanglement entropy to study the effect of the interaction upon the fermionic system sets a precedent in the field, since it is usually used to characterize topology in non-interacting systems.
Author contributions
B. P. G. did the analytical and numerical analysis under the supervision of A. G. L. and G. P. All authors discussed and analyzed the results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. P. wants to acknowledge Prof. Giorgio Bennedek, to whom this issue is dedicated, for his scientific supervision and for hosting her for a stay at the university of Milano in her first steps of her scientific carrier. We thank M. Benito and S. Kohler for fruitful discussions. This work was supported by: Ministerio de Economía y Competitividad, through PID2020-117787GB-I00, Ministerio de Educación y Formación Profesional, under the program FPU, with reference FPU17/05297 (B. P.-G.), the Spanish project PGC2018-094792-B-100 (MCIU/AEI/FEDER, EU) (A. G.-L.). We also acknowledge support from CSIC Research Platform on Quantum Technologies PTI-001.References
- H. Walther, B. T. H. Varcoe, B.-G. Englert and T. Becker, Rep. Prog. Phys., 2006, 69, 1325–1382 CrossRef
.
- A. Cottet, M. C. Dartiailh, M. M. Desjardins, T. Cubaynes, L. C. Contamin, M. Delbecq, J. J. Viennot, B. Doucot and T. Kontos, J. Phys.: Condens. Matter, 2017, 29, 433002 CrossRef PubMed
.
- J. Li and M. Eckstein, Phys. Rev. Lett., 2020, 125, 217402 CrossRef CAS PubMed
.
- A. Blais, R.-S. Huang, A. Wallraff, S. M. Girvin and R. J. Schoelkopf, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 69, 062320 CrossRef
.
- T. Pellizzari, S. A. Gardiner, J. I. Cirac and P. Zoller, Phys. Rev. Lett., 1995, 75, 3788–3791 CrossRef CAS PubMed
.
- A. Blais, J. Gambetta, A. Wallraff, D. I. Schuster, S. M. Girvin, M. H. Devoret and R. J. Schoelkopf, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 032329 CrossRef
.
- A. Blais, J. Gambetta, A. Wallraff, D. I. Schuster, S. M. Girvin, M. H. Devoret and R. J. Schoelkopf, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 032329 CrossRef
.
- A. Blais, S. M. Girvin and W. D. Oliver, Nat. Phys., 2020, 16, 247–256 Search PubMed
.
- D. Matsukevich and A. Kuzmich, Science, 2004, 306, 663–666 CrossRef CAS PubMed
.
- J. I. Cirac, P. Zoller, H. J. Kimble and H. Mabuchi, Phys. Rev. Lett., 1997, 78, 3221–3224 CrossRef CAS
.
- I. Chiorescu, P. Bertet, K. Semba, Y. Nakamura, C. J. P. M. Harmans and J. E. Mooij, Nature, 2004, 431, 159–162 CrossRef CAS PubMed
.
- A. Wallraff, D. I. Schuster, A. Blais, L. Frunzio, R.-S. Huang, J. Majer, S. Kumar, S. M. Girvin and R. J. Schoelkopf, Nature, 2004, 431, 162–167 CrossRef CAS PubMed
.
- A. Fedorov, L. Steffen, M. Baur, M. P. da Silva and A. Wallraff, Nature, 2012, 481, 170–172 CrossRef CAS PubMed
.
- J. Majer, J. Chow, J. Gambetta, J. Koch, B. Johnson, J. Schreier, L. Frunzio, D. Schuster, A. Houck, A. Wallraff, A. Blais, M. Devoret, S. Girvin and R. Schoelkopf, Nature, 2007, 449, 443–447 CrossRef CAS PubMed
.
- M. A. Sillanpää, J. I. Park and R. W. Simmonds, Nature, 2007, 449, 438–442 CrossRef PubMed
.
- X. G. Borjans, F. Croot, X. Mi, M. J. Gullans and J. R. Petta, Nature, 2020, 577, 195–198 CrossRef PubMed
.
- A. J. Landig, J. V. Koski, P. Scarlino, C. Müller, J. C. Abadillo-Uriel, B. Kratochwil, C. Reichl, W. Wegscheider, S. N. Coppersmith, M. Friesen, A. Wallraff, T. Ihn and K. Ensslin, Nat. Commun., 2019, 10, 5037 CrossRef CAS PubMed
.
- L. DiCarlo, J. M. Chow, J. M. Gambetta, L. S. Bishop, B. R. Johnson, D. I. Schuster, J. Majer, A. Blais, L. Frunzio, S. M. Girvin and R. J. Schoelkopf, Nature, 2009, 460, 240–244 CrossRef CAS PubMed
.
- E. Lucero, R. Barends, Y. Chen, J. Kelly, M. Mariantoni, A. Megrant, P. O'Malley, D. Sank, A. Vainsencher, J. Wenner, T. White, Y. Yin, A. N. Cleland and J. M. Martinis, Nat. Phys., 2012, 8, 719–723 Search PubMed
.
- M. Mariantoni, H. Wang, R. C. Bialczak, M. Lenander, E. Lucero, M. Neeley, A. D. O'Connell, D. Sank, M. Weides, J. Wenner, T. Yamamoto, Y. Yin, J. Zhao, J. M. Martinis and A. N. Cleland, Nat. Phys., 2011, 7, 287–293 Search PubMed
.
- A. A. Houck, D. I. Schuster, J. M. Gambetta, J. A. Schreier, B. R. Johnson, J. M. Chow, L. Frunzio, J. Majer, M. H. Devoret, S. M. Girvin and R. J. Schoelkopf, Nature, 2007, 449, 328–331 CrossRef CAS PubMed
.
- K. W. Murch, S. J. Weber, K. M. Beck, E. Ginossar and I. Siddiqi, Nature, 2013, 499, 62–65 CrossRef CAS PubMed
.
- J. M. Fink, M. Göppl, M. Baur, R. Bianchetti, P. J. Leek, A. Blais and A. Wallraff, Nature, 2008, 454, 315–318 CrossRef CAS PubMed
.
- I. Schuster, A. Kubanek, A. Fuhrmanek, T. Puppe, P. W. H. Pinkse, K. Murr and G. Rempe, Nat. Phys., 2008, 4, 382–385 Search PubMed
.
- A. Baust, E. Hoffmann, M. Haeberlein, M. J. Schwarz, P. Eder, J. Goetz, F. Wulschner, E. Xie, L. Zhong, F. Quijandría, D. Zueco, J.-J. G. Ripoll, L. García-Álvarez, G. Romero, E. Solano, K. G. Fedorov, E. P. Menzel, F. Deppe, A. Marx and R. Gross, Phys. Rev. B, 2016, 93, 214501 CrossRef
.
- P. Forn-Díaz, J. Lisenfeld, D. Marcos, J. J. García-Ripoll, E. Solano, C. J. P. M. Harmans and J. E. Mooij, Phys. Rev. Lett., 2010, 105, 237001 CrossRef PubMed
.
- T. Niemczyk, F. Deppe, H. Huebl, E. P. Menzel, F. Hocke, M. J. Schwarz, J. J. Garcia-Ripoll, D. Zueco, T. Hümmer, E. Solano, A. Marx and R. Gross, Nat. Phys., 2010, 6, 772–776 Search PubMed
.
- F. Yoshihara, T. Fuse, S. Ashhab, K. Kakuyanagi, S. Saito and K. Semba, Nat. Phys., 2017, 13, 44–47 Search PubMed
.
- G. Romero, D. Ballester, Y. M. Wang, V. Scarani and E. Solano, Phys. Rev. Lett., 2012, 108, 120501 CrossRef CAS PubMed
.
-
J. Yu, F. A. Cárdenas-López, C. K. Andersen, E. Solano and A. Parra-Rodriguez, Charge qubits in the ultrastrong coupling regime, 2021, https://arxiv.org/abs/2105.06851 Search PubMed
.
- Y. Wang, J. Zhang, C. Wu, J. Q. You and G. Romero, Phys. Rev. A, 2016, 94, 012328 CrossRef
.
- T. H. Kyaw, S. Felicetti, G. Romero, E. Solano and L.-C. Kwek, Sci. Rep., 2015, 5, 8621 CrossRef CAS PubMed
.
- S. Felicetti and A. Le Boité, Phys. Rev. Lett., 2020, 124, 040404 CrossRef CAS PubMed
.
- C. A. Downing, T. J. Sturges, G. Weick, M. Stobińska and L. Martín-Moreno, Phys. Rev. Lett., 2019, 123, 217401 CrossRef CAS PubMed
.
- W. Nie and Y.-X. Liu, Phys. Rev. Res., 2020, 2, 012076(R) CrossRef
.
- M. C. Dartiailh, T. Kontos, B. Douçot and A. Cottet, Phys. Rev. Lett., 2017, 118, 126803 CrossRef PubMed
.
- O. Dmytruk, M. Trif and P. Simon, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 245432 CrossRef
.
- J. E. Moore, Nature, 2010, 464, 194–198 CrossRef CAS PubMed
.
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045–3067 CrossRef CAS
.
- M. He, H. Sun and Q. L. He, Front. Phys., 2019, 14, 43401 CrossRef
.
- T. W. Schmitt, M. R. Connolly, M. Schleenvoigt, C. Liu, O. Kennedy, J. M. Chávez-Garcia, A. R. Jalil, B. Bennemann, S. Trellenkamp, F. Lentz, E. Neumann, T. Lindström, S. E. de Graaf, E. Berenschot, N. Tas, G. Mussler, K. D. Petersson, D. Grützmacher and P. Schüffelgen, Nano Lett., 2022, 22, 2595–2602 CrossRef CAS PubMed
.
- Y. Ando, J. Phys. Soc. Jpn., 2013, 82, 102001 CrossRef
.
- F. M. D'Angelis, F. A. Pinheiro, D. Guéry-Odelin, S. Longhi and F. M. C. Impens, Phys. Rev. Res., 2020, 2, 033475 CrossRef
.
- F. Mei, G. Chen, L. Tian, S.-L. Zhu and S. Jia, Phys. Rev. A, 2018, 98, 012331 CrossRef CAS
.
- C. Dlaska, B. Vermersch and P. Zoller, Quantum Sci. Technol., 2017, 2, 015001 CrossRef
.
- X. Mi, J. V. Cady, D. M. Zajax, P. W. Deelman and J. R. Petta, Science, 2017, 355, 156–158 CrossRef CAS PubMed
.
- X. Mi, M. Benito, S. Putz, D. M. Zajac, J. M. Taylor, G. Burkard and J. R. Petta, Nature, 2018, 555, 599–603 CrossRef CAS PubMed
.
- W. P. Su, J. R. Schrieffer and A. J. Heeger, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 2099–2111 CrossRef CAS
.
- B. Pérez-González, M. Bello, A. Gómez-León and G. Platero, Phys. Rev. B, 2019, 99, 035146 CrossRef
.
- B. Pérez-González, M. Bello, G. Platero and A. Gómez-León, Phys. Rev. Lett., 2019, 123, 126401 CrossRef PubMed
.
- M. Bello, C. Creffield and G. Platero, Sci. Rep., 2016, 6, 22562 CrossRef CAS PubMed
.
-
C. Gardiner and P. Zoller, Quantum Noise: A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics, Springer-Verlag Berlin Heidelberg, 2004 Search PubMed
.
- S. Kohler, Phys. Rev. A, 2018, 98, 023849 CrossRef CAS
.
- S. Ryu, A. P. Schnyder, A. Furusaki and A. W. W. Ludwig, New J. Phys., 2010, 12, 065010 CrossRef
.
- T. Senthil, Annu. Rev. Condens. Matter Phys., 2015, 6, 299–324 CrossRef CAS
.
- A. Cottet, T. Kontos and B. Douçot, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205417 CrossRef
.
- S. Ryu and Y. Hatsugai, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 245115 CrossRef
.
- V. Gurarie, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 085426 CrossRef
.
- S. R. Manmana, A. M. Essin, R. M. Noack and V. Gurarie, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205119 CrossRef
.
- A. Gómez-León, Phys. Rev. B, 2016, 94, 035144 CrossRef
.
- H. Kimble, Nature, 2008, 453, 1023–1030 CrossRef CAS PubMed
.
- J. M. Raimond, M. Brune and S. Haroche, Rev. Mod. Phys., 2001, 73, 565–582 CrossRef
.
- D. M. Zajac, T. M. Hazard, X. Mi, E. Nielsen and J. R. Petta, Phys. Rev. Appl., 2016, 6, 054013 CrossRef
.
- C. Volk, A. M. J. Zwerver, U. Mukhopadhyay, P. T. Eendebak, C. J. van Diepen, J. P. Dehollain, T. Hensgens, T. Fujita, C. Reichl, W. Wegscheider and L. M. K. Vandersypen, Npj Quantum Inf., 2019, 5, 29 CrossRef
.
- W. I. L. Lawrie, H. G. J. Eenink, N. W. Hendrickx, J. M. Boter, L. Petit, S. V. Amitonov, M. Lodari, B. Paquelet Wuetz, C. Volk, S. G. J. Philips, G. Droulers, N. Kalhor, F. van Riggelen, D. Brousse, A. Sammak, L. M. K. Vandersypen, G. Scappucci and M. Veldhorst, Appl. Phys. Lett., 2020, 116, 080501 CrossRef CAS
.
- T. Hensgens, T. Fujita, L. Janssen, X. Li, C. J. Van Diepen, C. Reichl, W. Wegscheider, S. Das Sarma and L. M. K. Vandersypen, Nature, 2017, 548, 70–73 CrossRef CAS PubMed
.
- J. P. Dehollain, U. Mukhopadhyay, V. P. Michal, Y. Wang, B. Wunsch, C. Reichl, W. Wegscheider, M. S. Rudner, E. Demler and L. M. K. Vandersypen, Nature, 2020, 579, 528–533 CrossRef CAS PubMed
.
- A. Stockklauser, P. Scarlino, J. V. Koski, S. Gasparinetti, C. K. Andersen, C. Reichl, W. Wegscheider, T. Ihn, K. Ensslin and A. Wallraff, Phys. Rev. X, 2017, 7, 011030 Search PubMed
.
- A. Stockklauser, P. Scarlino, J. V. Koski, S. Gasparinetti, C. K. Andersen, C. Reichl, W. Wegscheider, T. Ihn, K. Ensslin and A. Wallraff, Phys. Rev. X, 2017, 7, 011030 Search PubMed
.
- X. Mi, J. M. Cady, D. M. Zajac, P. W. Deelman and J. R. Petta, Science, 2017, 355(6321), 156–158 CrossRef CAS PubMed
.
- L. E. Bruhat, T. Cubaynes, J. J. Viennot, M. C. Dartiailh, M. M. Desjardins, A. Cottet and T. Kontos, Phys. Rev. B, 2018, 98, 155313 CrossRef CAS
.
- D. J. van Woerkom, P. Scarlino, J. H. Ungerer, C. Müller, J. V. Koski, A. J. Landig, C. Reichl, W. Wegscheider, T. Ihn, K. Ensslin and A. Wallraff, Phys. Rev. X, 2018, 8, 041018 CAS
.
- B. Wang, T. Lin, H. Li, S. Gu, M. Chen, G. Guo, H. Jiang, X. Hu, G. Cao and G. Guo, Sci. Bull., 2021, 66, 332–338 CrossRef CAS
.
- D. Najer, I. Söller, P. Sekatski, V. Dolique, M. C. Löbl, D. Riedel, R. Schott, S. Starosielec, S. R. Valentin, A. Wieck, N. Sangouard, A. Ludwig and R. J. Warbutton, Nature, 2019, 5, 622–627 CrossRef PubMed
.
- N. Samkharadze, G. Zheng, N. Kalhor, D. Brousse, A. Sammak, U. C. Mendes, A. Blais, G. Scappucci and L. M. K. Vandersypen, Science, 2018, 359(6380), 1123–1127 CrossRef CAS PubMed
.
- X. Mi, M. Benito, S. Putz, D. M. Zajac, J. M. Taylor, G. Burkard and J. R. Petta, Nature, 2018, 555, 590–603 CrossRef PubMed
.
- T. Cubaynes, M. R. Delbecq, M. C. Dartiailh, R. Assouly, M. M. Desjardins, L. C. Contamin, L. E. Bruhat, Z. Leghtas, F. Mallet, A. Cottet and T. Kontos, npj Quantum Inf., 2019, 5, 47 CrossRef
.
- N. Samkharadze, G. Zheng, N. Kalhor, D. Brousse, A. Sammak, U. C. Mendes, A. Blais, G. Scappucci and L. M. K. Vandersypen, Science, 2018, 359, 1123–1127 CrossRef CAS PubMed
.
- A. J. Landig, J. V. Koski, P. Scalino, U. C. Mendes, A. Blais, C. Reichl, W. Wegscheider, A. Wallraff, K. Ensslin and T. Ihn, Nature, 2018, 560, 179–184 CrossRef CAS PubMed
.
- D. J. van Woerkom, P. Scarlino, J. H. Ungerer, C. Müller, J. V. Koski, A. J. Landig, C. Reichl, W. Wegscheider, T. Ihn, K. Ensslin and A. Wallraff, Phys. Rev. X, 2018, 8, 041018 CAS
.
- D.-W. Zhang, Y.-Q. Zhu, Y. X. Zhao, H. Yan and S.-L. Zhu, Adv. Phys., 2018, 67, 253–402 CrossRef
.
- M. Atala, M. Aidelsburger, J. T. Barreiro, D. Abanin, T. Kitagawa, E. Demler and I. Bloch, Nat. Phys., 2013, 9, 795–800 Search PubMed
.
- H. Ritsch, P. Domokos, F. Brennecke and T. Esslinger, Rev. Mod. Phys., 2013, 85, 553–601 CrossRef CAS
.
- K. M. Fortier, S. Y. Kim, M. J. Gibbons, P. Ahmadi and M. S. Chapman, Phys. Rev. Lett., 2007, 98, 233601 CrossRef PubMed
.
- S. Nußmann, M. Hijlkema, B. Weber, F. Rohde, G. Rempe and A. Kuhn, Phys. Rev. Lett., 2005, 95, 173602 CrossRef PubMed
.
- S. Nußmann, K. Murr, M. Hijlkema, B. Weber, A. Kuhn and G. Rempe, Nat. Phys., 2005, 1, 122–125 Search PubMed
.
- A. D. Boozer, A. Boca, R. Miller, T. E. Northup and H. J. Kimble, Phys. Rev. Lett., 2006, 97, 083602 CrossRef CAS PubMed
.
- A. Boca, R. Miller, K. M. Birnbaum, A. D. Boozer, J. McKeever and H. J. Kimble, Phys. Rev. Lett., 2004, 93, 233603 CrossRef CAS PubMed
.
- P. Maunz, T. Puppe, I. Schuster, N. Syassen, P. Pinkse and G. Rempe, Nature, 2004, 428, 50–52 CrossRef CAS PubMed
.
- J. McKeever, A. Boca, A. D. Boozer, R. Miller, J. R. Buck, A. Kuzmich and H. J. Kimble, Science, 2004, 303, 1992–1994 CrossRef CAS PubMed
.
- J. Ye, D. W. Vernooy and H. J. Kimble, Phys. Rev. Lett., 1999, 83, 4987–4990 CrossRef CAS
.
- J. McKeever, J. R. Buck, A. D. Boozer and H. J. Kimble, Phys. Rev. Lett., 2004, 93, 143601 CrossRef CAS PubMed
.
- J. A. Sauer, K. M. Fortier, M. S. Chang, C. D. Hamley and M. S. Chapman, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 69, 051804 CrossRef
.
- J. McKeever, J. R. Buck, A. D. Boozer, A. Kuzmich, H.-C. Nägerl, D. M. Stamper-Kurn and H. J. Kimble, Phys. Rev. Lett., 2003, 90, 133602 CrossRef CAS PubMed
.
- V. Bužek, G. Drobný, M. S. Kim, G. Adam and P. L. Knight, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 56, 2352–2360 CrossRef
.
- X. Gu, A. F. Kockum, A. Miranowicz, Y. X. Liu and F. Nori, Phys. Rep., 2017, 718-719, 1–102 CrossRef CAS
.
- D. I. Schuster, A. A. Houck, J. A. Schreier, A. Wallraff, J. M. Gambetta, A. Blais, L. Frunzio, J. Majer, B. Johnson, M. H. Devoret, S. M. Girvin and R. J. Schoelkopf, Nature, 2007, 445, 515–518 CrossRef CAS PubMed
.
- I. S. Besedin, M. A. Gorlach, N. N. Abramov, I. Tsitsilin, I. N. Moskalenko, A. A. Dobronosova, D. O. Moskalev, A. R. Matanin, N. S. Smirnov, I. A. Rodionov, A. N. Poddubny and A. V. Ustinov, Phys. Rev. B, 2021, 103, 224520 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01806c |
| This journal is © the Owner Societies 2022 |