Dielectric-constant effects on the exciton dissociation and photovoltaic conversion efficiency of water-soluble green conducting polymers

Abstract

While the best strategy to design semiconducting polymers for organic photovoltaics (OPVs) is still debated, several reports link the performance of some such polymers to a high dielectric constant, with polythiophenes at the forefront of those studies. The use of the dielectric constant as a figure of merit to design OPVs will represent a game-changing strategy towards high photoconversion efficiency (PCE) if it is rigorously proven by a theoretical model on a specific OPV polymer with tunable susceptibility. Water-soluble poly[2-(3-thienyl)-ethoxy-4-butyl-sulfonate] (PTEB) is the ideal platform to test such a hypothesis, due to its properties that are tunable in liquid environments and are highly dependent on the pH of the aqueous solutions used to disperse it, in addition to offering a unique avenue toward fully water-processed, environmentally green OPVs. Here, we characterize a set of PTEB samples, assemble bulk heterojunction (BHJ) OPVs out of them, and develop a mean-field theory model explaining why the tunability of the optoelectronic properties of PTEB persists in the solid state, which is assigned to the different polarizability of the terminations of PTEB pendant groups that are stable in basic and acidic environments. Dielectric constants decreasing from ε_r = 4.5 (in layers spun from solutions at pH = 4) to ε_r = 2.9 (at pH = 10) are measured and shown to affect the operation of PTEB OPVs with bathocuproine (BCP) as an acceptor, increasing their PCE from 0.44% up to 2.8% at the highest value of ε_r. Even if these figures are still relatively low over OPV polymers soluble in nonpolar solvents, they are the highest obtained to date for PTEB and, to the best of our knowledge, also for any other water-soluble polythiophenes, except for polythiophene particles previously processed in nonpolar solvents.

---

1. Introduction

Organic photovoltaics (OPVs) prepared from earth abundant and environmentally benign elements possess light weight, flexibility, and simplicity in terms of device manufacturing that are desirable towards the implementation of environmentally friendly solutions at zero-carbon emissions.^1,2 OPVs may find their use for in-motion applications requiring solar cells with high flexibility and light weight, for example on electrical vehicles,³ as backup power sources to be placed on wind turbine blades,⁴ and for recharging personal electronic devices.⁵ The photoactive layers of OPVs are made of polymers, small organic molecules, or their combination.^6,7 To date, photoconversion efficiencies (PCEs) approaching 20% have been reported for binary organic photovoltaics by enhancing the crystallization of their active layer via non-fullerene acceptors,⁸ additives⁹ and crystallization regulators¹⁰ as well as the use of step-by-step modulation of crystalline features.¹¹ OPVs do not require any precious metals such as ruthenium, a frequent ingredient of dye solar cell sensitizers.¹² Indium, determining the cost of indium–tin oxide (ITO) electrodes, can also be replaced in OPVs with graphene^13,14 or carbon nanotube¹⁵ electrodes. Furthermore, OPVs do not require any environmentally problematic element such as lead, ubiquitous in perovskite solar cells,¹⁶ and cadmium, that is frequent in quantum-dot photovoltaics.¹⁷

The use of green solvents in OPV manufacturing is vital so as not to lose all of their advantages in terms of environmental friendliness over competing technologies and has been the subject of unique attention.¹⁸ Although some high-efficiency OPV architectures that have been proposed to date utilize relatively benign solvents, such as o-xylene,^8,11 water is the solvent of choice for any green manufacturing process,¹⁹ which also limits the processing costs. It is imperative to envisage specific OPV architectures that are water-based. This poses compatibility challenges in the fabrication of multiple layers by spin-coating,²⁰ and the issue of low stability of certain organic polymers in an aqueous environment needs to be tackled.²¹ To this end, a number of reports^22–25 have heralded the use of water-dispersible surfactant-based polymer micelles, surfactant-stripped nanoparticles, Janus nanoparticles and mini-emulsions to fabricate OPVs from water-dispersed particles of nonpolar-soluble polymers. However, these types of fabrication processes are dubiously green, even if they reached up to 11% PCE.²⁵ In fact, while the final OPV preparation stage is claimed to be water-based, the initial stages of preparation always require highly volatile, environmentally problematic, nonpolar organic solvents in large amounts.²³ For example, Janus nanoparticle preparation²⁴ and surfactant-stripped preparation²⁶ use tetrahydrofuran that is highly explosive and potentially carcinogenic for kidneys,²⁷ while mini-emulsions necessitate considerable amounts of chloroform,²⁴ which presents reproductive toxicity and easily decomposes, in the presence of light, into extremely toxic phosgene and hydrogen chloride.²⁸ Therefore, these methods, albeit partially water-based, do not seem to offer the much-needed environmental friendliness that will make OPVs a green form of energy conversion for the future. Vohra et al.²⁹ reported open-circuit voltages up to 1.3 V from the poly[3-(6′-N,N,N-trimethyl ammonium)-hexylthiophene] bromide donor combined with a water-soluble fullerene acting as the acceptor, and Laval et al.³⁰ reported an open-circuit voltage of 0.69 V with the poly[(thiophene)-alt-(6,7-difluoro-2-(2-hexyldecyloxy)quinoxaline)] donor and a C₆₁ derivative as the acceptor, but the PCE was 0.24% and 1.02% respectively. A strategy for steadier PCE improvement in all-water OPV manufacturing processes, and related materials, is therefore in high demand.³¹

Water-soluble poly[2-(3-thienyl)-ethoxy-4-butylsulfonate] sodium (PTEBS) is a commercial, highly water-soluble and water-compatible organic photoconducting polymer that has found critical applications as a polyelectrolyte,³² in biosensing,^33,34 and for solar cell fabrication. The photoluminescence (PL) of PTEBS has been shown to be quenched in the presence of oxygen in the solvent, and by specific electron acceptors, such as methoxy-propyloxy-sulfonate-phenylenevinylene and TiO₂,^33,35 which is a strong indication that the dissociation of excitons photogenerated in PTEBS may also occur in the solid state. As far as PTEBS-based photovoltaics are concerned, Qiao et al.^35–38 reported bilayer dye-sensitized TiO₂ solar cells in which PTEBS plays the multifunctional role of both a sensitizer and electrolyte, with PCE up to 0.17%. The same authors reported³⁹ bulk heterojunction (BHJ) OPV devices where PTEBS (acting as an electron donor) was intermixed with single-walled carbon nanotubes (acting as acceptors). BHJ architectures are critical in achieving high PCEs in OPVs because of the very short exciton lifetimes and limited diffusion lengths (l_D ∼10 nm) in organic materials,^21,40 which requires donors and acceptors to be mixed at the nanoscale for optimal electron–hole pair dissociation, whereas planar p–n junctions are sufficient in solar cells from inorganic materials, where l_D can exceed 10 μm. With PTEBS being a commercially available material,⁴¹ these figures could indicate strong potential for its use in OPVs if this water-soluble polymer is properly understood and utilized.

One critical property of PTEBS rests in the tunability of the optical properties in liquid environment, which appear to be dependent on the presence of oxygen³³ as well as the pH of the aqueous solution used to disperse it. For example, it has been shown that, at a given polymer concentration, the color of aqueous solutions of PTEBS may vary from pale yellow to orange and dark red.⁴² This phenomenon has been explained in terms of different degrees of π-electron stacking,⁴³ cation exchange and self-doping,^44,45 as well as different polarizability of the terminations of the pendant groups attached, with this polymer sitting at the equilibrium configuration between a sodium salt (i.e., PTEBS) at basic pH and a proton salt (i.e., poly[2-(3-thienyl)-ethoxy-4-butylsulfonate], or PTEB) at acidic pH.³⁷ If either or both the last two explanations are assumed, PTEB/PTEBS will represent the ideal playground for investigating the role of dielectric constant in promoting high PCE in OPVs. While the best strategy to design photoconducting polymers for OPVs is still debated, several^46–49 reports link the performance of multiple polythiophenes as photoactive OPV materials to a high dielectric constant. The use of dielectric constant as a figure of merit to design polymers for OPVs will represent a game changer towards designing OPVs at high PCE, if it is rigorously proven by a theoretical model on a specific polymer with tunable susceptibility. Specifically, if the dielectric constant (ε_r) of PTEB/PTEBS is controlled by different terminations³⁷ we will expect it to decrease at increasing pH as protonated groups are expected to be more electronegative, and therefore more polar, than the PTEBS sodium salt. Conversely, if ε_r was controlled by self-doping related to cation exchange, we would expect it to decrease at decreasing pH, as self-doping occurs in an acidic environment, and free electrons produced by doping^44,45 will screen the dipoles and decrease the susceptibility of the material at long wavelengths and low frequencies.⁴⁹

In this paper, we will thoroughly investigate a set of commercial PTEBS samples with multiple characterization tools, including ultraviolet-visible (UV-vis), photoluminescence (PL), and electron spin resonance (ESR) spectroscopy as well as capacitive resonance dielectric function measurements. We anticipate that the dielectric function of PTEBS decreases at increasing dielectric function, consistent with different polarizability from different pendant groups in the sodium salt (PTEBS) and the corresponding proton salt – a phenomenon we will be able to explain in the framework of a mean-field theory model. Furthermore, we will report the discovery of favorable dissociation of the excitons from PTEBS in the presence of bathocuproine (BCP) as witnessed by PL quenching. Due to this observation, we will also assemble and report bulk heterojunction (BHJ) OPVs incorporating PTEBS in the solid state, and their efficiency will be successfully correlated with the polymer's dielectric constant.

2. Experimental

The flow chart of our process is shown in Fig. 1, and includes both liquid-phase and solid-state experiments, as well as device fabrication and testing. Collectively, the goal of the experiments is to determine the tunability of the solid-state dielectric properties of solution-processed PTEBS thin films, the link between the long-wavelength dielectric constant of the films and the pH of the starting solutions, and the photovoltaic properties of OPVs based on such films.

Fig. 1 Flow-chart of the experiments described in this work, in which the pH of PTEBS solutions was varied from 2 to 10, with reproducible change in solution color at pH = 2, and subsequent solution characterization, fabrication of thin solid films by spin-coating and their characterization with a focus on dielectric function measurements, as well as organic photovoltaic device fabrication and testing.

2.1. Preparation of PTEBS solutions

24 mg of sodium poly[2-(3-thienyl)-ethoxy-4-butylsulfonate] (PTEBS) (American Dye Source, Inc.) was dissolved in 6 ml of deionized water and stirred at 50 °C overnight. It was then separated into 6 different vials (4 mg ml⁻¹) and buffer solutions of pH 2, 4, 6, 8, 10 were added to 5 of the vials. Deionized water was added to the remaining vial to maintain equal concentration. The solutions were drop-cast on aluminium foil, and polystyrene dissolved in chlorobenzene was drop-cast on top of it and covered the PTEBS layer. Solutions were separated into 2 vials per pH. Bathocuproine (BCP) (Sigma-Aldrich, CAS Number: 4733-39-5) was added to one of those vials and stirred at 50 °C overnight to obtain PTEBS : BCP solution with a 1 : 1 weight ratio. These solutions were used for UV-vis spectrophotometry, ESR and PL spectroscopy, as well as OPV device fabrication.

2.2. Fabrication of OPV devices

OPV devices were fabricated with the architecture shown in Fig. 1 onto 1′′ × 1′′ indium tin oxide (ITO) coated glass substrates (90 Ω/□ sheet resistance). Prior to device fabrication, substrates were patterned by masking the central 1/2 × 1-in part of the substrate with Kapton™ tape and removing the unmasked area of the coating in an ITO etchant bath (LCE-200, Solexir) at 50 °C on a hot plate. Patterned substrates were thoroughly rinsed in sequential water, acetone and isopropanol baths. The nickel oxide (NiO_x) bath used to deposit the electron-blocking layer was prepared using the method described by Ezugwu et al.⁵⁰ Briefly, 1.3 g of nickel sulfate hydrate (NiSO₄·6H₂O Sigma-Aldrich, 10 101-97-0) was dissolved in 15 ml of deionized water along with 0.2 g of polyvinylpyrrolidone, acting as a surfactant, and 3 mg magnesium sulfate MgSO₄ as a doping agent. A droplet of 30% aqueous ammonia (Sigma-Aldrich, 1336-21-6) was added to the mixture until a clear and blue coloured solution was formed, signalling the formation of Mg-doped nickel hydroxide.⁵⁰ The pH of the mixture was kept in the range of 12.0–12.5 at 70 °C for 16 h of processing. The substrates were treated in a Novascan PSD-UV3 ozone-generating system for an exposure time of 15 min immediately prior to receiving the solution. The above-mentioned solution was spun on the substrates at 1000 rpm in a Laurell WS-650 spin-coater. The substrates were then baked at 300 °C for 30 min in air on a hot plate to obtain a NiO_x thin layer of about 50 nm, as measured by a Filmetrics F20 optical thin film profilometer.

Using the same apparatus, the PTEBS : BCP solutions prepared at varying pH were spin-coated at 150 nm thickness on top of the Mg-doped NiO_x. Samples were then annealed for 20 min on a hotplate at 120 °C in a glovebox (VAC Nexus, <10 ppm O level) with a built-in thermal evaporator in it. The device samples were subsequently transferred into the evaporator (Nano 36, K.J. Lesker Co) where subsequent C₆₀ hole-blocking layers (50 nm, Alfa Aesar 42007) and an anode layer made from stacked calcium (20 nm, Alfa Aesar, 14457) and aluminum (80 nm, Alfa Aesar, 42257) thin films were thermally evaporated on top of NiO_x : PTEBS : BCP through a shadow mask enabling four OPV devices on the same chip, thus completing the architecture in Fig. 1.

2.3. Sample and device characterization

2.3.1. Characterization of the solutions. UV-vis spectra of PTEBS solutions were recorded in transmission mode at 120 nm min⁻¹ using a Perkin Elmer Lambda 19 dual-beam spectrometer with the wavelength range from 200 nm to 800 nm and 1 ± 0.15 nm wavelength resolution. The samples for UV-vis analysis were diluted with deionized water to a concentration of 0.1 mg ml⁻¹. Scans were performed in a quartz cuvette cell used for UV-vis with 2 polished sides and a 190 nm–2.5 μm clear window, where 3 ml of each solution were transferred for measurement. An identical reference cuvette with pure deionized water was used on the second spectrometer beam to calibrate the spectra.

Solutions were further diluted for PL measurements. 3 mL of PTEBS (0.1 mg ml⁻¹) and PTEBS : BCP (0.1 : 0.1 mg ml⁻¹) solutions at varying pH were placed in a quartz cuvette (4-side polished, 3.5 mL capacity). PL emission spectra (330–825 nm wavelength range, 5 nm step and 0.3 nm accuracy) were recorded on a Horiba Fluorolog QM-75-22 apparatus with a 75 W xenon arc lamp as the excitation source filtrated through a monochromator. A fixed excitation wavelength λ = 430 nm was used. ESR spectra of PTEBS solutions were recorded on a JEOL JES-FA200 X-band (9.3 GHz) spectrometer at 100 kHz magnetic field modulation. Solutions at pH 2 were not measurable due to strong dielectric losses and high conductivity of the self-doped polymer. 30 μL of PTEBS solutions at pH 4, 7, 8, 10 were placed in 1.5 × 100 mm capillary tubes, and then inserted in 1 mm diameter, thin-wall, Suprasil™ EPR capillary tubes for measurement (Norrell, Inc.). The ESR spectra were acquired at 1 mW microwave power and room temperature, with a modulation width of 0.25 mT and a time constant of 30 ms. Additional measurements were performed at higher microwave power to rule out the sample saturation. The spin densities were estimated from the built-in Mn²⁺ marker situated in the TE-100 resonant cavity of the spectrometer, and an additional measurement of a (2,2,6,6-tetramethylpiperidin-1-yl)oxidanyl (TEMPO) radical in aqueous solution, containing a known number of spins.⁵⁰ Uncertainty on the spin density measurements is estimated to be 35% with this method.

2.3.2. Characterization of thin solid films. The long-wavelength dielectric constant of the PTEBS thin films was measured on thin films deposited on Al foil, forming a capacitor with a liquid top contact made by Galinstan™ and contained in a 2 mm diameter O-ring. This capacitor was used under a probe station (Signatone S725 probes) to realize an RLC circuit along with a function generator, a 10 kΩ resistor, a 70-mH inductor, and a digital scanning oscilloscope (Hantek) for signal detection. For dielectric measurements, the PTEBS thin films (pH 4, 6, 7, 8 and 10) were spun at 400 rpm and were 1.2-μm thick. The ratio between the voltage across the thin-film capacitor and the voltage at the function generator was measured in the f = 210–690 kHz range to determine the circuit's resonance frequency, which is then used to calculate the dielectric constant of the thin film layers under the assumption of a plate capacitor.

2.3.3. Testing of OPV solar cells. An SRC-1000-RTD-Qz reference solar cell (NREL calibrated) was used for irradiance calibration. The reference solar cell and OSC devices (pH 4 to 10) were placed under a Sciencetech AAA (ASTM E927-19) AM 1.5 solar simulator at 1 sun, with up to 1-in target area, placed in a dark environment. Current voltage (J–V) characteristics of each device were recorded using a Keithley 2400 source meter interfaced with a computer-controlled IEEE488 acquisition card in the −0.75 V to 0.75 V voltage range. The fill factor and PCE of each device were calculated from the maximum power conditions and the mean and standard deviation was estimated from the four devices on each chip (see sect. 2.2). External quantum efficiency (EQE) was measured in the 325–800 nm wavelength range on a Sciencetech PTS-2 apparatus using the aforementioned E927-19 solar simulator as a bias light source. Light from a 150-W xenon arc lamp photomodulated at 35 Hz was passed through a 1/4 m Czerny–Turner monochromator and was used as the pulsed photon source. The EQE system's response was calibrated through the abovementioned SRC-1000-RTD-Qz solar cell, and the photocurrents were recorded on a Keithley 2401 source meter.

3. Results and discussion

3.1. Characterization of polymer solutions

UV-vis spectra from PTEB/PTEBS solutions buffered at different pH values are shown in panel a of Fig. 2, from which the strong difference in visible properties from pH = 2 to pH = 4–10, already evident from the photo in Fig. 1, can be elucidated. At a first glance, all of the UV-vis spectra look very similar to each other, and this is confirmed by the similarity of the Tauc plots (Fig. 2b) and Tauc band gaps E_g (Fig. 2c) which are all within an error bar (E_g = 2.00 ± 0.25 eV at pH = 2 and E_g = 2.04 ± 0.25 eV at pH = 10). The peak energies for π–π* transitions (Fig. 2c) are also all within an error bar. In order to understand the colour variability of the solutions, one must consider the excess absorption photon energy region below the band gap (Fig. 2b, inset). It is apparent that the darker solution at pH = 2 has a significantly stronger excess absorption, consistent with previous findings in the literature,^44,45 which was assigned to self-doping of polythiophenes. Stronger excess absorption upon acidification was also observed by Tran-Van et al.⁴⁵ and was assigned to free carriers within the band gap. Free carriers may affect the optical properties of solids in the infrared and low-photon energy visible range, which explains the dark-brown colour of our most acidic solution. The physical meaning of the UV-vis optical properties can be therefore summarized as in Fig. 2d, elucidating that E_g remains constant regardless of the pH, but the Fermi level (E_F) is significantly downshifted at lower pH, consistent with the possibility of degenerate doping at pH 2, where the free carrier concentration is significantly higher.

Fig. 2 (a) UV-vis absorption spectra of PTEBS solutions at varying pH (0.1 mg mL⁻¹). It can be observed that the spectra are coincident, except for pH = 2 at low photon energy, where (b) the Tauc plots evidence a significantly higher excess absorption (dotted square box); (c) optical bandgaps (E_g, calculated from panel b) and peak energies which are independent of the pH; and (d) diagram showing the shifts of the Fermi level (E_F) of PTEBS at low pH due to self-doping, which is responsible for the higher excess absorption shown in panel b, and thus explains the different colour of the solution, at pH = 2.

Further evidence of free carriers and self-doping can be achieved by ESR. The ESR signals of good-quality polythiophenes were assigned⁴⁴ to free electrons due to their g-values close to 2.0023, the Landé constant. This is also evident from the ESR spectra presented in panel a of Fig. 3 (the sample at pH 2 was not measurable, arguably due to strong dielectric screening and metallic behavior, consistent, in fact, with degenerate self-doping). The signal intensity (proportional to the free carrier concentration) decreases at increasing pH, consistent with stronger self-doping upon acidification. The corresponding spin concentrations are reported in Fig. 3b. Basically, from the spin concentrations, it can be calculated that there is 1 to 3.5 unpaired electrons per polymer chain (about 3500 repeating units) at pH 10 and 4, respectively. This is a relatively low concentration, which seems to indicate that free carriers and self-doping will play a marginal role in determining the dielectric constant, as we will be able to confirm below.

Fig. 3 (a) Room-temperature ESR spectra of PTEBS solutions at varying pH from 4 to 10, which confirm the presence of free carriers due to self-doping; (b) spin density of PTEBS solution as a function of the pH, calculated from the ESR spectra in panel a. The spin density decreases as the environment shifts towards basic pH due to lower self-doping. The sample in water at pH = 2 was not measurable due to high dielectric screening from conduction electrons suggesting a spin density much larger than 10¹⁹ g⁻¹, consistent with degenerate self-doping.

3.2. Excitonic properties and exciton dissociation in the presence of BCP

Panel a in Fig. 4 shows the PL spectra of PTEBS (400 nm excitation) in water with and without the addition BCP. Spectra were recorded at pH ranging from 2 to 10 (pure PTEBS at pH = 2 exhibits negligible PL, consistent with degenerate self-doping inferred from UV-vis and ESR measurements). We have discovered (Fig. 4b) that the PL spectra of PTEBS in water are significantly quenched with the addition of BCP, but only for acidic pH values. PL quenching can be taken as an indication that excitons formed in PTEBS dissociate in the presence of BCP, either due to electron or hole transfer to the added type of molecule, which requires the corresponding energy levels to align. From an inspection of the electron energy spectra of PTEBS and BCP^36,51 (Fig. 4c) the highest occupied molecular orbital (HOMO) of BCP (−7.0 eV) is significantly lower than its PTEBS counterpart (−5.0 eV) which indicates that hole transfer is unlikely. Conversely, the lowest unoccupied molecular orbital (LUMO) of PTEBS (−3.0 eV) sits just above the BCP LUMO (−3.5 eV) which may potentially lead to electron transfer. We are therefore inclined to assign the observed PL quenching to electron transfer (Fig. 4d). However, the experimental observation that such quenching only occurs at specific values of pH requires an explanation, which we are proposing to assign to the intriguing behavior of this polymer in acidic and basic environments.

Fig. 4 (a) PL emission spectra of PTEBS and PTEBS : BCP solutions (1 : 1 weight ratio) at varying pH from p4 to 10; (b) PL quenching rate calculated as the intensity ratio as a function of pH. The quenching rate decreases as the pH of the solution increases; (c) energy-band diagram with the HOMO and LUMO levels of PTEBS and BCP. Electron transfer from the conduction band of PTEBS into BCP is possible, while hole transfer from the valence band of PTEBS into BCP is forbidden; (d) band diagram of PTEBS to BCP showing electron and hole transfer processes.

Specifically, our PL results can be understood by assuming that the pH of the solution affects the pendant group on the polymer. For example, as far as PTEBS is concerned, it is well known³⁷ that modifying the pH of the solution alters the equilibrium

−(C₆H₁₂O)HSO₃ + NaOHD ⇆ −(C₆H₁₂O)SO₃·Na + H₂O, (1)

and such a shift indicates that the polymer transitions from a sodium salt (PTEBS) at basic pH to a proton salt at acidic pH, which can be named as poly[2-(3-thienyl)-ethoxy-4-butylsulfonate] (PTEB) acid. When these aqueous solutions are used to prepare films by spin coating, which eliminates the solvent, such films are expected to have very different properties depending on the specific pendant group carried: either –(C₆H₁₂O)SO₃·Na as in pristine PTEBS, or –(C₆H₁₂O)HSO₃, with the former more likely produced at high pH, from basic solutions, and the second one more likely from low pH, in acidic environments.

In addition to understanding the thin-film properties, equilibrium (1) offers a consistent interpretation of the data from Fig. 2–4. For example, as far as Fig. 3 is concerned, the ESR spectra offer clear evidence that acidic aqueous environments increase the concentration of free carriers along the polymer backbone. This effect may be associated with the presence of -(C₆H₁₂O)SO₃⁻ pendant groups at low pH if we admit that it leads to small charge transfer effects that will even slightly move the polymer's Fermi level. Due to the one-dimensional nature of the polymer, this will have profound effects in the density of states at the Fermi energy⁵² even without altering the shape of the electronic bands.

Furthermore, as far as optical properties are concerned, it is well known⁵³ that the optical band gap of polythiophenes (and, more generally, their optical properties in the visible photon energy range) are controlled by π–π* optoelectronic transitions, with π-electrons only delocalized in the thiophene rings at the polymer backbone. This is especially true in PTEBS and related materials, where carbon atoms in the pendant groups are sp³ hybridized and do not contain any π-electrons. The hydrophilic terminations (–SO₃·Na or –HSO₃) at the end of the pendant have little direct effect on the optical properties of the polymer. Therefore, the observed band gap is not directly affected by the solution pH. However, there is a strong indirect effect of the pendants on the π-electron system at the polymer backbone, through the local electric field they produce, because the –SO₃·Na, and –HSO₃ terminations have a very different electron polarizability, which in turn has a dramatic impact on the polymer's static dielectric constant due to the limited capability of π-electrons to screen any external perturbation, albeit small. This is evident from the experiments that will be presented in the next section.

3.3. Polymer thin-film dielectric constant

Fig. 5 reports the solid-state dielectric function of pure PTEB thin films obtained from capacitive resonant circuit measurements, which are shown in Fig. 5a. The circuit response, defined as the ratio between the frequency dependent voltage [V_C (ω)] and the zero-frequency DC voltage [V₀], is given bywhere R and L are the resistance and inductance of the used circuit (see Experimental) and C_f is the polymeric film capacitance, which is linked to the dielectric function as ε_r = C_fd/ε₀A, where A and d are the film's area and thickness, respectively. As the resonant frequency increases at increasing pH, it is clear that ε_r is the lowest at the highest pH of the starting solution, a trend shown in Fig. 5b. From this, it can be inferred that the effects of the pH of the starting solution persist even after the solvent is removed in a dried polymeric thin film. We propose that this is an effect of the local field from different pendant groups, which in turn affects in different ways the π-electron system that is responsible for the optoelectronic properties, depending on the type of the end termination, –SO₃·Na, or –HSO₃. Different terminations have different dipole moments,⁵⁴ and, therefore, may polarize the π-electrons in a different way. For example, Fanchini et al.^55,56 have shown that different nitrogenated terminations, para-cyanogenic and nitrile, led to different polarization of small π-electron domains, to the point of leading to substantially different vibrational properties.

Fig. 5 (a) Frequency-dependent transfer functions of thin solid films of PTEBS processed from solutions at different pH; (b) dielectric constant of PTEBS thin solid films as a function of the pH of the starting solution, derived from the transfer functions in panel a; and (c) PTEB/PTEBS with different pendant groups in acidic and basic environments, with –HSO₃ and –SO₃·Na end terminations, respectively. The two types of end terminations have different dipole moments which induce different π-electron polarizations due to different local field intensities.

These effects can be understood^55,56 in the framework of mean-field theory, where the π-electrons are situated in a spherical cavity in which the local electric field E_loc is the resultant of both the external field (E₀) and the depolarization field (E₁ = –P/3ε₀):

E_loc = E₀ + E₁ = E₀ – P/3ε₀ (3)

In turn, the polarization P is the consequence of the magnitude of the dipole moments p_j = α_jE_loc offered by the different terminations [i.e., j = –SO₃·Na, or –HSO₃ with their respective polarizations, α(SO₃·Na) or α(HSO₃)] because all the other constituents of the polymer are significantly less polar. We can therefore adopt at the mesoscopic level a mean-field theory model,⁵⁷ in which

P = N × [fα(SO₃·Na) + (1 – f)α(HSO₃)] × E_loc = 3ε₀β_el × E_loc. (4)

E_loc is the same irrespective of the termination, because –HSO₃ and SO₃·Na are attached to identical pendant groups. In the rightmost term of eqn (4), we have introduced the electronic polarizability, β_el, which is linear in the concentrations N_j of each pendant group and, therefore, linked to the total concentration (N) of monomer groups within the thin solid film, by N(SO₃·Na) = N × f and N(HSO₃) = N × (1 – f), respectively. Thus, f in eqn (4) is the residual fraction of sodium-containing pendant groups, which, in consideration of equilibrium (1), is expected to be the largest for thin films spun at the highest pH. In contrast, sodium in acidic solutions tends to be present as NaOH, which will segregate upon spin-coating. Therefore, films prepared at the lowest pH are expected to mostly contain [(C₄HS)–(C₆H₁₂O)–(HSO₃)]_n (instead of pristine PTEBS, [(C₄HS)(C₆H₁₂O)(SO₃·Na)]_n) and, possibly, segregated NaOH, if this is not expelled from the film during the spinning process.

The different terminations of the polymer's pendant group in the solid state may explain the tunability of the films' dielectric constant, depending on the pH of the solution used to prepare them, as we must expect α(HSO₃) > α(SO₃·Na) due to the lower electronegativity of Na over H. Because of self-consistency, eqn (3) can be replaced into (4), thus solving for the dielectric susceptivity χ = P/E₀, from which the dielectric function, ε_r = 1 + χ can be determined. This results in (ε_r − 1)/(ε_r + 2) = β_el as in the Clausius–Mossotti relationship,⁵⁸ which gives

with β_el(f) = f × β_el(SO₃·Na) + (1 – f) × β_el(HSO₃). The blue line in Fig. 5b is a plot of eqn (5) at β_el(SO₃·Na) = 0.40 and β_el(HSO₃) = 0.54, which indicates that our mean-field model offers a fairly accurate description of the root causes for the dependence of the dielectric constant of PTEB/PTEBS thin films on the pH of the solution used to prepare them by spin-coating. Collectively our work indicates that small static perturbations in the pendant group lead to strong effects, in terms of polarization, on the π-electron system, with excitons on the polymer backbone that are strongly affected by the environment in which they diffuse. In the next section, we will elucidate how different values of ε_r from layers spun from solutions at different pH may explain the different PL quenching (sect 3.2) as well as the different photoconversion efficiency from OPVs incorporating those layers.

3.4. Dielectric-constant effects on exciton dissociation

The pH-dependent quenching of the PL in the presence of BCP can be explained in the framework of a Wannier–Mott model⁴⁹ for weakly bound excitons in the polymer. Within this model, the exciton energy can be expressed aswhere n is the exciton principal quantum number, μ_eh is the electron–hole exciton reduced mass, m₀ is the mass of the free electron and R_H = 13.6 eV is the Rydberg energy for the hydrogen atom. From the measured dielectric constants of PTEBS spun at varying solution pH, a strong increase of E^x₁(ε_r) from 0.33 eV at pH = 4 to 0.75 eV at pH = 10 can be estimated from eqn (6) as also plotted in Fig. 6. Since we are not aware of any estimates of electron and hole effective masses in PTEBS, we assume m_e ≫ m_h ≈ m₀ consistent with estimates⁵⁹ in other polythiophenes, which normally behave as p-type. Because the HOMO–LUMO band gap of PTEBS measured by UV-vis (Fig. 2c) is minimally affected by the pH, the dependence of the electron energy on the pH is mainly affected by E^x₁(ε_r).

Fig. 6 (a) Energy-band diagram of the PTEB/PTEBS : BCP system at low (acidic, left) and high (basic, right) pH. Excitonic levels closer to the valence band can be observed at acidic pH, thus enabling electron transfer to the BCP LUMO from the fundamental excitonic level (n = 1) while electron transfer from the fundamental excitonic level is prevented at basic pH, due to the high energy difference between such an excitonic level and the valence band, situating the excitonic level below the LUMO of BCP; and (b) energy-band diagram of OPV solar cells based on the PTEB/PTEBS : BCP bulk heterojunction, incorporating the concepts from panel a, where the functions of NiO_x and C₆₀ thin films as electron- and hole-blocking layers, respectively, are also highlighted.

For samples prepared at high pH, where E^x₁(ε_r) is large, the PTEBS electron energy

E^e_n = E_LUMO − E^x_n(ε_r) (7)

can be as low as 3.75 eV below the vacuum level for n = 1, which is larger than the LUMO level of BCP (E_BCP = 3.5 eV, Fig. 6). At high pH, this makes impossible the electron transfer from PTEBS to BCP in the fundamental (n = 1) excitonic state. Therefore, even though it is still a possible to transfer electrons into BCP from higher excitations of PTEBS (i.e., n ≥ 2, where E^ex₁(ε_r) ≤ 0.19 eV according to eqn 6) it is apparent that low-dielectric constant layers spun from basic solutions are not the most ideal ones for OPV fabrication.

Conversely, for samples prepared at low pH, the PTEBS electron energy sits at a minimum of E^e_n = 3.3 eV, which is lower than E_BCP and enables exciton dissociation and electron transfer to BCP even at the lowest excitation. This phenomenon explains the PL quenching of the samples, with diminished PL intensity of PTEBS : BCP solutions in water, as well as the increased photoconversion efficiency of OPV devices in the solid state. Therefore, the successful quenching of the PTEBS luminescence by BCP is chiefly due to E^e₁ ≥ E_BCP, with other effects (e.g. charge transfer from excitons at n > 1) being negligible. In other terms, this indicates that the dielectric properties of PTEB/PTEBS have a profound effect on the exciton Bohr radius.

The dielectric-constant effect on the excitonic energy levels of PTEB/PTEBS can be more immediately understood from its impact on the exciton's Bohr radius⁴⁹

where a_H = 0.053 nm is the Bohr radius for the hydrogen atom. From eqn (8), it is readily observed that the larger the ε_r, the larger the r^x_n and, therefore, the more delocalized the exciton, which increases the probability of the electron to transfer towards a nearby BCP molecule when this is added to PTEB/PTEBS within the active layer of a device. Conversely, smaller values of r^x_n indicate that the electron and hole components of the exciton are, on average, closer. This increases their probability of radiative recombination, with the photo-absorbed energy being lost as luminescence. Relatively small values of r^x_n also result in little quenching of the PL intensity in the presence of BCP, as previously demonstrated in Fig. 4.

Although a model linking the dielectric constant of the donor polymer to the OPV dielectric constant was previously proposed by Koster et al.⁴⁹ our present work goes significantly beyond this model in the following aspects: (a) our model explains, through mean field theory, that, in OPV semiconducting polymers, small modifications in the pendant groups (such as their transition from sodium salts to proton salts) have a dramatic impact on the dielectric constant and the polarization of the π-electron system and associated excitons; (b) differently from the model by Koster et al.,⁴⁹ which only considers the electron hole-pair binding energy, our model considers environment-dependent excitons at multiple quantum numbers to explain the dependence of the EQE spectra on the dielectric constant; and (c) our model is be backed by experimental data on a polymer (PTEB/PTEBS) with tunable dielectric constant. In summary, the profound effects of the polymer's dielectric constant on the exciton dissociation are assigned to:

i) Exciton delocalization promoted by more polar environments [eqn (8)], and

ii) Exciton energy decrease, inversely proportional to the square of the dielectric constant, favouring electron transfer to acceptor molecules at a given LUMO energy level [eqn (6)].

Although the differences of dielectric constants in the system investigated in this study are about 55% maximum, from ε_r = 2.9 to 4.5 (Fig. 5b), it is worth noting that the electron transfer process probability is highly superlinear in distance. For example, it will decrease as the inverse sixth power of the distance if a Förster resonance energy transfer is assumed⁶⁰ and will decrease exponentially under the assumption of Dexter energy transfer.⁶¹ This indicates that a 55% increase in dielectric constant may produce increases in dissociation rates by one order of magnitude,⁶⁰ or even more. Furthermore, the observed variation of ε_r in PTEB/PTEBS is among the highest ever measured without modifying the conformation of polythiophene rings. Therefore, using PTEB/PTEBS as a case study of a specific polymer with tunable susceptibility, our paper offers a rigorous proof, in the framework of the Wannier–Mott theory of excitons, of the dielectric constant effects on the exciton dissociation efficiency, which was observed in this work as well as several other reports.⁴⁸

3.5. Dielectric-constant effects on the photoconversion efficiency of OPV solar cells

The observed dielectric-constant effects also extend to the photoconversion efficiency of OPVs incorporating the PTEB/PTEBS:BCP system, as depicted in Fig. 1, and in analogy to what was previously shown in other organic photovoltaic systems by other groups.⁴⁸ The band diagram for these devices is shown in Fig. 6b (referring to devices spun from solutions in which PTEBS was dispersed in acidic water). The additional incorporation within the device of a doped NiO_x layer at the bottom of PTEB/PTEBS : BCP and a thermally evaporated C₆₀ layer at the top (functioning as electron-blocking and hole-blocking layers, respectively) enables the operation of these devices as solar cells. Specifically, previous studies from our group^50,62 have shown that our hydrothermally grown p-type NiO_x on ITO has its valence band sitting about 4.8 eV below the vacuum level and a 3.1 eV band gap, leading to a conduction band at about 1.7 eV, which offers a sufficient barrier for electrons not to recombine in ITO, while not preventing hole diffusion. Conversely, it is known⁶³ that thermally evaporated C₆₀ layers have a conduction band at 3.7 eV, aligning well with polythiophenes and calcium/aluminum (Ca/Al) bilayers, while its valence band (6.1 eV) is too high for holes to cross it thus effectively functioning as a hole-blocking layer. Although BCP also features a very high HOMO level (7.0 eV), it does not form a continuous layer, which explains the need for the C₆₀ top layer. As all of the device components are either fabricated by physical vapor deposition (ITO, C₆₀, and Ca/Al) or solution processed from aqueous solutions (NiO_x and PTEB/PTEBS : BCP) and do not contain toxic elements (e.g., Cd in quantum dots and Pb in organic perovskites) our architecture is of great promise towards the manufacturing of green and environmentally friendly organic photovoltaics.

AM 1.5, 1-sun current–voltage (J–V) characteristics of our devices are reported in panel a of Fig. 7, where the excellent correlation between the OPV efficiency and the pH of the PTEB/PTEBS : BCP starting solution can be appreciated. EQE scans of the same devices (Fig. 7b) are also reported. The root cause for the observed correlation between dielectric-constant effects and device PCEs is apparent from the EQE spectra in Fig. 7b, where it can be noticed that the decrease in device J–V curves (panel a) and PCE (panel c) is associated with a decrease of EQE in the long-wavelength region, while EQE at wavelength λ < 450 nm remains substantially unchanged up to pH 8. This is very consistent with more spread-out excitonic levels at lower dielectric constant in accordance with eqn (6) and Fig. 6a. Larger E^x_n at lower ε_r causes the impossibility of ground-state (n = 1) excitons excited by long-wavelength photons to diffuse and dissociate into BCP. Therefore, our EQE data also validate our model of dielectric-constant effects on the exciton dissociation and OPV photoconversion efficiency. There are multiple shoulder peaks in the EQE curves in Fig. 7b. While the origin of these shoulders is consistent with multiple excitonic peaks at different energies E^x_n (n = 1, 2, …) this is just a hypothesis that needs to be the subject of future investigations. This is also corroborated by the fact that the most relevant factor of influence leading to high PCE appears to be the short-circuit current and fill-factor (Fig. 7c). Specifically, the short-circuit current is related to the integrated EQE spectrum weighted over AM 1.5 illumination, which also controls the maximum electrical power delivered by the device and the fill-factor. Conversely, the device open-circuit voltage (V_OC) appears to be marginally dependent on ε_r and, therefore, the pH of the PTEB/PTEBS : BCP starting solution. This is also consistent with our model, as well as a band energy offset model^64,65 frequently invoked to explain the origin of V_OC in OPVs, which proposes that V_OC is controlled by the energy difference between the donor's HOMO (i.e., 5.0 eV in PTEBS) and the acceptor's LUMO (i.e., 3.7 eV in BCP) minus a fixed correlation energy.⁶⁶ Therefore, as none of these parameters is linked to E^x_n, V_OC is expected to be independent of the polymer's dielectric constant.

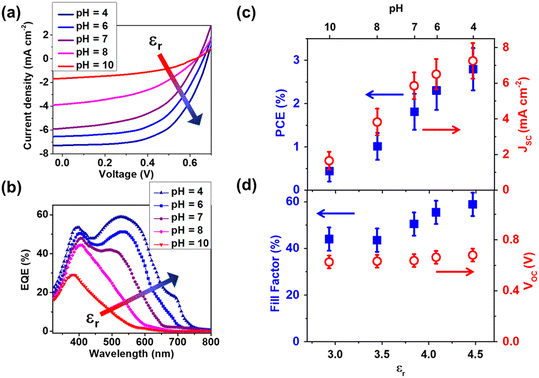Fig. 7 (a) Current–voltage characteristics of OPV solar cells at different pH of the processed water solutions based on PTEB/PTEBS : BCP active layers as in Fig. 1 and 6b; (b) EQE spectra of the same devices, where the quantum efficiency is seen to decrease at increasing pH in the long wavelength range, consistent with diminished electron transfer to BCP from the fundamental excitonic level (n = 1) of PTEBS at increasing pH and decreasing dielectric constant ε_r; (c) PCE and short-circuit current (J_sc) of the same OPVs, where it can be seen that the PCE increase up to 2.7% at the highest ε_r is due to higher EQE at long wavelengths while (d) the open circuit voltage (V_OC) of the OPVs is limitedly influenced by ε_r and the pH of the starting solution. Conversely, the fill factor only shows a moderate increaser with ε_r as it is influenced by both V_OC and J_sc.

It is also worth noting that, although the maximum PCE attained in our devices (2.8%) is still relatively low compared to nearly 20% in counterparts processed from nonpolar solvents such as o-xylene,^8,67 ours are already the most efficient fully water-processed OPVs obtained to date, with the exception of those requiring polymer nanoparticles and mini-emulsions^23–27 which require organic solvents (and quite often toxic ones) in addition to water at the earlier stages of fabrication. It is also remarkable that our devices are relatively stable in dry air, at least for a few hours (see the ESI†). Of course, we expect that stability in the presence of humidity will be more of an issue. It is also possible that our devices can be made more stable over extended times by encapsulating them with the same technology that is extensively used to improve the lifetime of commercial organic light-emitting devices. It is also critical to remark that our devices are assembled from relatively low-cost and widely commercially available photoconducting polymer, PTEBS, and a commercial and easy-to-synthesize acceptor, BCP. It is expected that more sophisticated polymer donors and non-fullerene molecular acceptors can be used to dramatically improve the PCE of OPV devices implementing our architecture.⁶⁷

4. Conclusion

Our work is extremely significant from three very different perspectives: in terms chemistry, engineering and physics. As far as chemistry is concerned, we have discovered that bathocuproine, a water-soluble organic molecule that is very commonly used in organic light-emitting device technology, is a pH-tunable quencher for the PL of PTEB/PTEBS, with extremely high PL quenching efficiency for acidic pH values (4–7). This effect can be understood from the transformation of the polymer's pendant group from a sodium-salt (PTEBS, basic pH) to a proton-salt (PTEB, acidic pH). Through a mean-field theory model, we have shown that the sodium-to-proton salt transition has a profound impact on the thiophene's π-electron polarizability and, therefore, the polymer's dielectric constant. A higher polymer dielectric constant in its acidic environment suggests a decrease in the exciton energy (E^x_n) which is inversely proportional to ε_r², thus favoring the transfer of electrons to BCP and its photoreduction, with photooxidation of PTEB.

From an engineering perspective, our discovery that the tunability of the dielectric constant of PTEB/PTEBS persists in the solid state, as measured in Fig. 5, is a powerful tool towards the optimization of the efficiency of bulk-heterojunction OPVs based on PTEB/PTEBS : BCP active layers. Specifically, we have found that the PCE increases up to a maximum of 2.8% in devices at pH 4, which is a record for devices based on commercial PTEBS, a widely available semiconducting polymer of relatively low cost. Ours are the most efficient fully water-processed OPVs to date, thanks to effective exciton dissociation by BCP, and will pave the way for improving the efficiency of dielectric-constant designed green OPVs with more sophisticated polymers and acceptors. For example, the presence of multiple π-electron systems and highly polar pendant groups in a semiconducting polymer is expected to increase their dielectric constant. Our findings will be pivotal to designing green OPVs that can be processed from environmentally friendly aqueous solvents, such as water.

From a physics perspective, our paper is pivotal because it elucidates for the first time, thanks to a rigorous model based on Wannier–Mott excitons, the root cause for the dependency of the OPV efficiency on the dielectric constant of their p-type constituent, which was previously conjectured in a number of different experimental reports.^9,46–48 PTEBS is the ideal case study for validating our model because of its widely tunable long-wavelength dielectric constant, from ε_r = 2.9 to 4.5. Nonetheless, our model is general enough to be applicable to a wide range of bulk heterojunction OPVs. Within our model, the p-type polymer's dielectric constant determines the Bohr radius of the excitons, and therefore their degree of delocalization. It is thus demonstrated that a larger value of ε_r results in more likely exciton dissociation, and faster dissociation rates, as well as reduced radiative recombination. As short exciton lifetime is known to be the bottleneck limiting the PCE of OPVs, all of these effects concur towards more efficient organic solar cells. In addition, higher values of ε_r also result in an upshift (i.e., decrease) of the exciton energy levels, which favours the electron transfer to acceptor molecules at a given LUMO energy level. The use of dielectric constant as a figure of merit to design new photoactive polymers will represent a game-changing strategy towards more competitive OPVs with higher photoconversion efficiencies.

Data availability

Data for this article, including experimental logs, are available on University of Western Ontario's Microsoft OneDrive with source files accessible from MS Power Point.

Author contributions

X. Wei: investigation, data curation, validation, writing – original draft, and visualization. D. Williams: investigation. G. Fanchini: investigation, methodology, data curation, supervision, project administration, funding acquisition, and writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) through the Discovery Grant (RGPIN-2020-06669) and Research Tools and Instruments (RTI) programs, as well as the Canada Foundation for Innovation (CFI). The authors would like to thank Wei Zhu, Matheus Adam and Dr. Lyudmila Goncharova for their valuable help with the PL measurements. DW acknowledges a MITACS Globalink internship.

References

1. M. Riede, D. Spoltore and K. Leo, Organic Solar Cells—The Path to Commercial Success, Adv. Energy Mater., 2020, 11(1), 2002653,  DOI:10.1002/aenm.202002653.
2. G. V. Bulavko and A. A. Ishchenko, Organic bulk heterojunction photovoltaic structures: design, morphology and properties, Russ. Chem. Rev., 2014, 83(7), 575–599,  DOI:10.1070/RC2014v083n07ABEH004417.
3. Z. Hu, J. Wang, X. Ma, J. Gao, C. Xu and K. Yang, et al., A critical review on semitransparent organic solar cells, Nano Energy, 2020, 78, 105376,  DOI:10.1016/j.nanoen.2020.105376.
4. K. Schulte, P. Kaparaju and S. Stegen, Concept design of a solar wind turbine blade, Smart Innov Syst Technol., 2020, vol. 203, pp. 265–274,  DOI:10.1007/978-981-15-8783-2_22.
5. C. Li, W. Jia, Q. Tao and M. Sun, Solar cell phone charger performance in indoor environment, 2011 IEEE 37th Annual Northeast Bioengineering Conference (NEBEC), IEEE, Troy, NY, 2011 Ar 1–3, pp. 1–2,  DOI:10.1109/nebc.2011.5778623.
6. S. Günes, H. Neugebauer and S. Sariciftci, Conjugated Polymer-Based organic solar cells, Chem. Rev., 2007, 107(4), 1324–1338,  DOI:10.1021/cr050149z.
7. B. Kan, Y. Kan, L. Zuo, X. Shi and K. Gao, Recent progress on all-small molecule organic solar cells using small-molecule nonfullerene acceptors, InfoMat, 2020, 3(2), 175–200,  DOI:10.1002/inf2.12163.
8. H. Bai, R. Ma, W. Su, T. A. D. Peña, T. Li and L. Tang, et al., Green-Solvent Processed Blade-Coating Organic Solar Cells with an Efficiency Approaching 19% Enabled by Alkyl-Tailored Acceptors, Nanomicro Lett., 2023, 15, 241,  DOI:10.1007/s40820-023-01208-0.
9. P. Li, Y. Zhang, T. Yu, Q. Zhang, J. Masse and Y. Yang, et al., Unveiling photovoltaic performance enhancement mechanism of polymer solar cells via synergistic effect of binary solvent additives, Sol. RRL, 2020, 4(10), 2000239,  DOI:10.1002/solr.202000239.
10. J. Fu, P. W. K. Fong, H. Liu, C. Huang, X. Lu and S. Lu, et al., 19.31% binary organic solar cell and low non-radiative recombination enabled by non-monotonic intermediate state transition, Nat. Commun., 2023, 14, 1760,  DOI:10.1038/s41467-023-37526-5.
11. B. Zou, W. Wu, T. A. D. Peña, R. Ma, Y. Luo and Y. Hai, et al., Step-by-Step modulation of crystalline features and exciton kinetics for 19.2% efficiency Ortho-Xylene processed organic solar cells, Nanomicro Lett., 2024, 16, 30,  DOI:10.1007/s40820-023-01241-z.
12. M. K. Nazeeruddin, P. Péchy, T. Renouard, S. M. Zakeeruddin, R. Humphry-Baker and P. Comte, et al., Engineering of efficient panchromatic sensitizers for nanocrystalline TIO2-Based solar cells, J. Am. Chem. Soc., 2001, 123(8), 1613–1624,  DOI:10.1021/ja003299u.
13. F. Sharifi, R. Bauld, M. S. Ahmed and G. Fanchini, Transparent and conducting Graphene-RNA-Based nanocomposites, Small, 2011, 8(5), 699–706,  DOI:10.1002/smll.201101537.
14. R. Bauld, F. Sharifi and G. Fanchini, Solution processed graphene thin films and their applications in organic solar cells, Int. J. Mod. Phys. B, 2012, 26(21), 1242004,  DOI:10.1142/s0217979212420040.
15. G. Fanchini, S. Miller, B. Parekh and M. Chhowalla, Optical Anisotropy in Single-Walled Carbon Nanotube Thin Films: Implications for Transparent and Conducting Electrodes in Organic Photovoltaics, Nano Lett., 2008, 8(8), 2176–2179,  DOI:10.1021/nl080563p.
16. J. Y. Kim, J. Lee, H. S. Jung, H. Shin and N. Park, High-Efficiency Perovskite solar cells, Chem. Rev., 2020, 120(15), 7867–7918,  DOI:10.1021/acs.chemrev.0c00107.
17. Z. Yang, J. Z. Fan, A. H. Proppe, F. P. G. De Arquer, D. Rossouw and O. Voznyy, et al., Mixed-quantum-dot solar cells, Nat. Commun., 2017, 8, 1325,  DOI:10.1038/s41467-017-01362-1.
18. S. Zhang, L. Ye, H. Zhang and J. Hou, Green-solvent-processable organic solar cells, Mater. Today, 2016, 19(9), 533–543,  DOI:10.1016/j.mattod.2016.02.019.
19. Green manufacturing: Fundamentals and Applications, ed. D. A. Dornfeld, Springer, New York, 2013.
20. S. Subianto, N. Dutta, M. Andersson and N. R. Choudhury, Bulk heterojunction organic photovoltaics from water-processable nanomaterials and their facile fabrication approaches, Adv. Colloid Interface Sci., 2016, 235, 56–69,  DOI:10.1016/j.cis.2016.05.013.
21. R. Bauld, L. M. Fleury, M. Van Walsh and G. Fanchini, Correlation between density of paramagnetic centers and photovoltaic degradation in polythiophene-fullerene bulk heterojunction solar cells, Appl. Phys. Lett., 2012, 101(10), 103306,  DOI:10.1063/1.4749813.
22. F. J. M. Colberts, M. M. Wienk and R. A. J. Janssen, Aqueous nanoparticle polymer solar cells: Effects of surfactant concentration and processing on device performance, ACS Appl. Mater. Interfaces, 2017, 9(15), 13380–13389,  DOI:10.1021/acsami.7b00557.
23. A. Holmes, H. Laval, M. Guizzardi, V. Maruzzo, G. Folpini and N. Barbero, et al., Water-based solar cells over 10% efficiency: designing soft nanoparticles for improved processability, Energy Environ. Sci., 2024, 17(3), 1107–1116,  10.1039/d3ee03744d.
24. A. Holmes, H. Laval, E. Deniau, M. Schmutz, S. Blanc and G. Wantz, et al., Water-based organic solar cells from Janus nanoparticles: Closing the performance gap with reference cells, Sol. Energy Mater. Sol. Cells, 2024, 266, 112656,  DOI:10.1016/j.solmat.2023.112656.
25. C. Xie, S. Liang, G. Zhang and S. Li, Water−Processed Organic Solar Cell with Efficiency Exceeding 11%, Polymer, 2022, 14(19), 4229,  DOI:10.3390/polym14194229.
26. C. Xie, T. Heumüller, W. Gruber, X. Tang, A. Classen and I. Schuldes, et al., Overcoming efficiency and stability limits in water-processing nanoparticular organic photovoltaics by minimizing microstructure defects, Nat. Commun., 2018, 9, 5335,  DOI:10.1038/s41467-018-07807-5.
27. T. Katahira, K. Teramoto and S. Horiguchi, Experimental studies on the acute toxicity of tetrahydrofuran in animals, Sangyo Igaku., 1982, 24(4), 373–378,  DOI:10.1539/joh1959.24.373.
28. C. McDowell and G. C. Bazan, Organic solar cells processed from green solvents, Curr. Opin. Green Sustainable Chem., 2017, 5, 49–54,  DOI:10.1016/j.cogsc.2017.03.007.
29. V. Vohra, S. Shimizu and Y. Takeoka, Water-Processed Organic Solar Cells with Open-Circuit Voltages Exceeding 1.3V, Coatings, 2020, 10(4), 421,  DOI:10.3390/coatings10040421.
30. H. Laval, A. Holmes, M. A. Marcus, B. Watts, G. Bonfante and M. Schmutz, et al., Toward High Efficiency Water Processed Organic Photovoltaics: Controlling the Nanoparticle Morphology with Surface Energies, Adv. Energy Mater., 2023, 13(26), 2300249,  DOI:10.1002/aenm.202300249.
31. X. Du, Q. Zeng, H. Zhang and B. Yang, Hybrid Solar Cells from Aqueous Polymers and Colloidal Nanocrystals, Chin. J. Chem., 2017, 35(5), 551–561,  DOI:10.1002/cjoc.201600733.
32. F. Schosseler, P. Vallat, N. Kutsevol, J. Catala and M. Rawiso, Optical properties of conjugated hydrophobic weak polyelectrolytes: Effects of pH, temperature and ionic strength, Mol. Cryst. Liq. Cryst., 2016, 639(1), 2–18,  DOI:10.1080/15421406.2016.1254506.
33. E. L. Cabarcos and S. A. Carter, Characterization of the photoluminescence quenching of mixed Water-Soluble conjugated polymers for potential use as biosensor materials, Macromolecules, 2005, 38(10), 4409–4415,  DOI:10.1021/ma050153c.
34. E. López-Cabarcos, J. R. Retama, V. Sholin and S. A. Carter, Controlling the photoluminescence of water-soluble conjugated poly[2-(3-thienyl)ethyloxy-4-butylsulfonate] for biosensor applications, Polym. Int., 2007, 56(5), 588–592,  DOI:10.1002/pi.2140.
35. Q. Qiao, Y. Xie and J. T. McLeskey, Organic/Inorganic Polymer Solar Cells Using a Buffer Layer from All-Water-Solution Processing, J. Phys. Chem. C, 2008, 112(26), 9912–9916,  DOI:10.1021/jp7115615.
36. Q. Qiao, L. Su, J. Beck and J. T. McLeskey, Characteristics of water-soluble polythiophene: TiO2 composite and its application in photovoltaics, J. Appl. Phys., 2005, 98(9), 094906,  DOI:10.1063/1.2130517.
37. J. T. McLeskey and Q. Qiao, Hybrid solar cells from water-soluble polymers, Int. J. Photoenergy, 2006, 2006, 20951,  DOI:10.1155/ijp/2006/20951.
38. Q. Qiao and J. T. McLeskey, Water-soluble polythiophene/nanocrystalline TiO₂ solar cells, Appl. Phys. Lett., 2005, 86(15), 153501,  DOI:10.1063/1.1900300.
39. J. A. Rud, L. S. Lovell, J. W. Senn, Q. Qiao and J. T. Mcleskey, Water soluble polymer/carbon nanotube bulk heterojunction solar cells, J. Mater. Sci., 2005, 40, 1455–1458,  DOI:10.1007/s10853-005-0582-2.
40. M. T. Sajjad, A. Ruseckas and I. D. Samuel, Enhancing exciton diffusion length provides new opportunities for organic photovoltaics, Matter, 2020, 3(2), 341–354,  DOI:10.1016/j.matt.2020.06.028.
41. American Dye Source, ADS2000P, American Dye Source, Quebec, CA, [cited 2024 July 25], available from: https://adsdyes.com/products/polythiophene/ads2000p/.
42. Q. Qiao, J. Beck and J. T. McLeskey, Photovoltaic devices from self-doped polymers, in: Optics and Photonics 2005, ed. P. A. Lane, SPIE, San Diego, California, US, 2005 July 31–Aug 4, p. 59380E,  DOI:10.1117/12.615052.
43. X. Chen, G. Wang, X. Zeng, W. Li and M. Zhou, Unveiling the Role of Water on π–π Stacking Through Microwave Spectroscopy of (Thiophene)2-(Water)1–2 Clusters, J. Am. Chem. Soc., 2023, 146(2), 1484–1490,  DOI:10.1021/jacs.3c10887.
44. A. Patil, Y. Ikenoue, N. Basescu, N. Colaneri, J. Chen, F. Wudl and A. Heeger, Self-doped conducting polymers, Synth. Met., 1987, 20(2), 151–159,  DOI:10.1016/0379-6779(87)90554-6.
45. F. Tran-Van, M. Carrier and C. Chevrot, Sulfonated polythiophene and poly(3,4-ethylenedioxythiophene) derivatives with cations exchange properties, Synth. Met., 2004, 142(1–3), 251–258,  DOI:10.1016/j.synthmet.2003.09.013.
46. S. Chen, S. Tsang, T. Lai, J. R. Reynolds and F. So, Dielectric effect on the photovoltage loss in organic photovoltaic cells, Adv. Mater., 2014, 26(35), 6125–6131,  DOI:10.1002/adma.201401987.
47. N. Cho, C. W. Schlenker, K. M. Knesting, P. Koelsch, H. Yip, D. S. Ginger and A. K. Jen, High-Dielectric constant Side-Chain polymers show reduced Non-Geminate recombination in heterojunction solar cells, Adv. Energy Mater., 2014, 4(10), 1301857,  DOI:10.1002/aenm.201301857.
48. P. Li, Investigations on photovoltaic efficiency, stability, and mechanism of organic solar cells [dissertation on the Internet], Université du Québec, Québec, CA, 2021, [cited 2024 July 25], available from: https://espace.inrs.ca/id/eprint/12072/.
49. L. J. A. Koster, S. E. Shaheen and J. C. Hummelen, Pathways to a New Efficiency Regime for Organic Solar Cells, Adv. Energy Mater., 2012, 2(10), 1246–1253,  DOI:10.1002/aenm.201200103.
50. A. E. Ezugwu, V. Wong, P. Bazylewski and G. Fanchini, On the role of different paramagnetic centers in conducting nickel oxide thin films, in SPIE OPTO, ed. D. J. Rogers, D. C. Look and F. H. Teherani, SPIE, San Francisco, California, US, 2019 Feb 2–7, p. 109191G,  DOI:10.1117/12.2509171.
51. C. Chen, S. Zhang, S. Wu, W. Zhang, H. Zhu and Z. Xiong, et al., Effect of BCP buffer layer on eliminating charge accumulation for high performance of inverted perovskite solar cells, RSC Adv., 2017, 7, 35819–35826,  10.1039/c7ra06365b.
52. M. Fox, Optical properties of solids, Oxford University Press, Oxford, GB, 2nd edn, 2010.
53. J. C. Costa, R. J. Taveira, C. F. Lima, A. Mendes and L. M. Santos, Optical band gaps of organic semiconductor materials, Opt. Mater., 2016, 58, 51–60,  DOI:10.1016/j.optmat.2016.03.041.
54. J. B. Derr, J. Tamayo, E. M. Espinoza, J. A. Clark and V. I. Vullev, Dipole-induced effects on charge transfer and charge transport. Why do molecular electrets matter?, Can. J. Chem., 2018, 96(9), 843–858,  DOI:10.1139/cjc-2017-0389.
55. G. Fanchini, A. Tagliaferro, G. Messina, S. Santangelo, A. Paoletti and A. Tucciarone, Vibrational properties and microstructure of reactively sputtered hydrogenated carbon nitrides, J. Appl. Phys., 2002, 91(3), 1155–1165,  DOI:10.1063/1.1425424.
56. G. Fanchini, A. Tagliaferro and S. Ray, Electronic and vibrational structures of amorphous carbon nitrides, Diamond Relat. Mater., 2003, 12(2), 208–218,  DOI:10.1016/s0925-9635(03)00024-4.
57. C. Kittel, Introduction to solid state physics, Wiley, Hoboken, US, 8th edn, 2005.
58. J. D. Jackson, Classical electrodynamics, Wiley, New York US, 3rd edn, 1998.
59. A. Abutaha, P. Kumar, E. Yildirim, W. Shi, S. Yang, G. Wu and K. Hippalgaonkar, Correlating charge and thermoelectric transport to paracrystallinity in conducting polymers, Nat. Commun., 2020, 11, 1737,  DOI:10.1038/s41467-020-15399-2.
60. FRET – Förster Resonance Energy Transfer, ed. I. Medintz and N. Hildebrandt, Wiley-VCH Verlag GmbH, Weinheim, GER, 2014.
61. D. L. Dexter, A theory of sensitized luminescence in solids, J. Chem. Phys., 1953, 21(5), 836–850,  DOI:10.1063/1.1699044.
62. A. E. Ezugwu, Defect-Related Magnetic Properties of Nanostructured Nickel Oxide Thin Films for Solar Cell Applications [master's thesis on the Internet], University of Western Ontario, London, CA, 2018 [cited 2024 July 25], available from: https://ir.lib.uwo.ca/etd/5445.
63. K. Schulze, C. Uhrich, R. Schüppel, K. Leo, M. Pfeiffer and E. Brier, et al., Efficient Vacuum-Deposited organic solar cells based on a new Low-Bandgap oligothiophene and fullerene C60, Adv. Mater., 2006, 18(21), 2872–2875,  DOI:10.1002/adma.200600658.
64. C. J. Brabec, A. Cravino, D. Meissner, N. S. Sariciftci, T. Fromherz and M. T. Rispens, et al., Origin of the open circuit voltage of plastic solar cells, Adv. Funct. Mater., 2001, 11(5), 374–380,  DOI:10.1002/1616-3028(200110)11:5<374::AID-ADFM374>3.0.CO;2-W.
65. B. P. Rand, D. P. Burk and S. R. Forrest, Offset energies at organic semiconductor heterojunctions and their influence on the open-circuit voltage of thin-film solar cells, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(11), 115327,  DOI:10.1103/physrevb.75.115327.
66. A. Cravino, Origin of the open circuit voltage of donor-acceptor solar cells: Do polaronic energy levels play a role?, Appl. Phys. Lett., 2007, 91(24), 243502,  DOI:10.1063/1.2817930.
67. G. Zhang, F. R. Lin, F. Qi, T. Heumüller, A. Distler and H. Egelhaaf, et al., Renewed prospects for organic photovoltaics, Chem. Rev., 2022, 122(18), 14180–14274,  DOI:10.1021/acs.chemrev.1c00955.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lf00269e

---