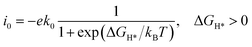Curvature-switched activity of carbon nanotube-supported single atom catalysts for the hydrogen evolution reaction†
Wenshan
Zhao
,
Shenyu
Shen
,
YiRu
Zhao
,
Tiantian
Wu
 *,
Shujiang
Ding
*,
Shujiang
Ding
 and
Yaqiong
Su
and
Yaqiong
Su
 *
*
School of Chemistry, Engineering Research Center of Energy Storage Materials and Devices of Ministry of Education, National Innovation Platform (Center) for Industry-Education Integration of Energy Storage Technology, Xi'an Jiaotong University, Xi'an 710049, China. E-mail: tianwu@xjtu.edu.cn; yqsu1989@xjtu.edu.cn
First published on 30th May 2024
Abstract
The hydrogen evolution reaction (HER) is an essential process for hydrogen production through water splitting. Atom-doped carbon nanotubes (CNTs) exhibit significant potential in promoting the electrocatalytic HER. By performing density functional theory (DFT) calculations, we have screened HER performance over a series of single atom transition metals (TM = Mo, Rh, Fe, Cr, Co, Zn, Mn, Cu, Ni, Pd) anchored on CNTs (n, n) (n = 5, 10) and graphene (seen as a CNT with the smallest curvature), and found the volcano curves between the adsorption free energy of H* (ΔGH*) and the current density for the HER, yielding the RhN4 catalyst at the peak of the volcano and even with a current density higher than that of Pt when the curvature is smaller than (10, 10). Then, more detailed DFT calculations were conducted to investigate the effect of curvature of CNTs on tuning the HER activity of RhN4@CNT (n, n) (n = 5–10) catalysts, where ΔGH* decreased with the decrease of the curvature, suggesting CNT-supported single atom catalysts having curvature-switched HER activity. The improved HER activity at a higher curvature arose from the more upshifted d-band center. Creating one single vacancy (5-1DB defect) could further enhance the HER activity of RhN4@CNTs. Our work provides a novel approach to designing HER catalysts with tunable activity and stability.
1. Introduction
The depletion of traditional fossil fuels and the environmental pressure are driving the rapid advancement of sustainable energy. As a clean energy, hydrogen energy has attracted increasing attention during the global energy transition.1,2 Water electrolysis is an effective and feasible method for hydrogen (H2) generation, in which the hydrogen evolution reaction (HER) is a crucial step.3 It is well-known that platinum (Pt) is the most common catalyst used due to its excellent catalytic activity and stability during the HER,4 while the high price of Pt seriously limits its application.5–8 Thus, the pursuit of novel cost-effective catalysts stands as a paramount objective in the progression of the HER.Transition metals (TMs), anchored on graphene or carbon nanotubes (CNTs), have attracted much attention due to their flexible structural plasticity, strong stability and unique electronic properties.9,10 Various single atom TMs based on nitrogen-doped graphene for the HER have been reported both experimentally and theoretically.11–15 Despite the notable advantages exhibited by graphene-supported single-atom catalysts, there remains room for improvement in the precise adjustment of catalytic activity. CNTs possess a distinctive three-dimensional structure, enabling facile adjustment of the electronic properties of TMs by manipulating the curvature to achieve higher catalytic activity or selectivity.16–18 Sun et al.19 have reported the curvature-dependent selectivity in CO2 reduction on cobalt-porphyrin nanotubes (CoPorNTs), revealing that the Carbon Reduction Reaction (CRR) tends to produce CO at lower-bent nanotubes and CH4 at higher-bent ones. Cao et al.20 have achieved outstanding HER catalytic activity by modulating the d-band center of Co4N@CoSA/N-CNT/CC, which was regulated effectively by the confined Co4N nanoparticles in the N-CNTs. Hence, changing the curvature is a potential approach to adjusting the d-band center of the single atom TM doped on graphene/CNTs.
Moreover, carbon nanotubes inherently possess imperfections during their formation. Various defects, including Stone–Wales defects and single vacancy, can be induced or manifest as native defects inevitably.21–24 These defects may influence the physical and chemical properties of catalysts featuring metals on carbon nanotubes. Ajayan et al.22 have suggested a stable single vacancy defect in CNTs (n, n), formatted by the recombination of three dangling bonds (DBs). The optimal point vacancy defect on CNTs reorganized into a pentagon and a dangling bond, referred to as the 5-1DB defect. Sun et al.25 have reported tunable defective and carbonylated plasma-treated CNTs (E-CNTs), indicating that the defective carbons on CNTs exhibited the largest contribution rates of the nucleophilic reaction. Evidently, the structure and defects of CNTs are the main factors affecting the catalytic activity. However, the effect of defects on the catalytic HER performance of CNT-supported single atom TMs remains unclear.
Herein, we employed density functional theory (DFT) calculations to thoroughly screen a range of TMs (TM = Mo, Rh, Fe, Cr, Co, Zn, Mn, Cu, Ni, Pd) anchored on graphene and CNTs for HER catalytic activity and found that TMs loaded on graphene perform better for hydrogen adsorption compared to those on CNT substrates. It was also observed that the carbon-based RhN4 site shows the highest HER activity. Then we systematically investigated the curvature effect on the catalytic performance of RhN4@CNTs (n, n) (n = 5–10) in the HER. Finally, we explored the influence of 5-1DB defects of CNTs on the HER activity. Our work provides a profound comprehension of the curvature effect on the HER catalyzed by RhN4@CNTs, and proposes a rational material design scheme for CNT-supported catalysts with tuneable activity in experimental endeavors.
2. Computational methods
All the calculations are carried out by using density functional theory (DFT) methods implemented in the Vienna Ab Initio Simulation Package (VASP)26,27 with the revised Perdew–Burke–Ernzerhof (PBE) functional28 based on the generalized-gradient approximation. A plane-wave basis was set with a cut-off energy of 400 eV.29,30 For the structural optimizations of TMN4@C, the Monkhorst–Pack k-point mesh of 3 × 3 × 1 is used for the Brillouin zone integration. And for TMN4@CNTs, the k-point grid is 1 × 1 × 5. The effect of core–valence interactions is described by the projector augmented wave (PAW) method.30 The energy and force convergence criteria were set to 10−4 eV per atom and −0.05 eV Å−1, respectively. Vibrational frequencies are calculated over the Γ point to obtain zero-point energies (ZPEs), thermal corrections, and entropy contributions.CNTs (n, n) (n = 5–10) with different curvatures were constructed as the basis to build RhN4@CNT (n, n) (n = 5–10) and de-RhN4@CNT (n, n) (n = 5–10) structures.
The adsorption energy (ΔEH*) of hydrogen on RhN4@CNTs was calculated by using the equation
| ΔEH* = Ecat+H − Ecat − 1/2EH2 |
The catalytic activity of the HER can be evaluated using ΔGH*, which can describe the adsorption strength of H on the catalysts.
| ΔGH* = ΔEH* + ΔEZPE ± TΔSH + ΔGpH |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 Pa (∼1 bar) of H2 at the temperature of 298.15 K. ΔGpH is the correction of the H+ free energy by the concentration, which can be evaluated as ΔGpH = 2.303 × kBT × pH eV, here the value of pH was assumed to be zero.
325 Pa (∼1 bar) of H2 at the temperature of 298.15 K. ΔGpH is the correction of the H+ free energy by the concentration, which can be evaluated as ΔGpH = 2.303 × kBT × pH eV, here the value of pH was assumed to be zero.
To predict HER activity, the theoretical exchange current density (i0)31 was calculated by using the equation
where k0 is set to 200 s−1 per site and taken from ref. 31. kB is the Boltzmann constant and T is set to 298.15 K.
3. Results and discussion
3.1 Screening of HER catalytic performance on TMN4@C/CNTs
Generally, the Gibbs free energy ΔGH* is considered to be an appropriate descriptor of HER reactivity, which shows the adsorption strength of H atom on the catalyst.33 It is worth noting that strong adsorption does not imply high catalytic activity. Adsorption that is too strong will make it difficult to desorb the product, while too weak adsorption indicates the challenge of H adsorption at the catalytic site. For the HER, superior catalytic activity can be achieved when ΔGH* is close to 0 eV.34–36 This condition facilitates a rapid proton/electron-transfer step and an expedited hydrogen desorption process.36 Graphene can be approximated as carbon nanotubes with an extremely low curvature. Therefore, a 4 × 4 graphene model was selected to load TM atoms, together with the CNTs (n, n) (n = 5, 10), screening for high-performance single-atom catalysts. As shown in Fig. 1a, the Gibbs free energies of H adsorption on TMN4@C and TMN4@CNTs (n, n) (n = 5, 10) (TM = Mo, Rh, Fe, Cr, Co, Zn, Mn, Cu, Ni, Pd) were calculated. The computational results demonstrated that graphene-based single atom catalysts exhibit a stronger hydrogen adsorption capability than those on CNTs, while TMs on CNTs (10, 10) with less curvature show lower ΔGH* than those on CNTs (5, 5). Thus, DFT calculations suggest that reducing the curvature of CNTs can enhance the adsorption of H atom on catalysts. Moreover, the HER catalytic performance of Rh metal is most outstanding. The configurations of H adsorption and relaxed binding energies (Eb) are shown in Fig. S1 and S2 and Tables S1 and S2 of the ESI.† The volcano curves between the adsorption free energy of H* (ΔGH*) and the current density for the HER were found, yielding the RhN4@CNTs (10, 10) and RhN4@C catalysts at the peak of the volcano with a current density higher than Pt, as shown in Fig. 1c and d. Metals at the top of the volcano perform well with an optimal H-binding energy. Thus, the results revealed that Rh metal anchored on both graphene and CNTs has adequate ΔGH* and high exchange current density (i0) to adsorb and desorb H atom, which was screened out to further construct the single-atom catalyst on CNTs with different curvatures. | ||
| Fig. 1 DFT-calculated Gibbs free energies and volcano plots of the exchange current density. (a) Gibbs free energy of H adsorption (ΔGH*) on TMN4@C and TMN4@CNTs (n, n) (n = 5, 10), TM = Mo, Ru, Rh, Fe, Cr, Co, Ag, Zn, Mn, Cu, Ni, Pd. (b)–(d) Volcano plot between exchange current density (i0) and ΔGH* in TMN4@CNTs (n, n) (n = 5, 10) and TMN4@C. Data for the Pt (111) surface were obtained from ref. 32. | ||
In addition to the high HER activity, the RhN4 catalyst has been found to have high thermodynamic stability, which is analysed by investigating the binding energy (Eb) and the cohesive energy (Ecoh) of Rh via the following formulae:
| Eb = Etotal − ERh − Esub |
| Ecoh = ERh-bulk/n − ERh-single |
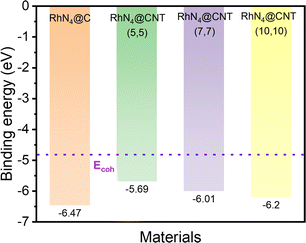 | ||
| Fig. 2 The calculated cohesive energy of Rh and the binding energy (Eb) of RhN4@C and RhN4@CNTs (n, n) (n = 5, 7, 10). | ||
3.2 HER catalytic activity of RhN4@CNTs (n, n) (n = 5–10)
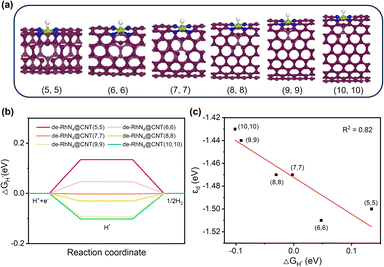
The Rh metal single-atom catalyst exhibited appropriate interactions with H, showcasing the potential for efficient catalysis of the HER while maintaining thermodynamic stability. Thus, the geometric models of RhN4@CNTs with different nanotube diameters were constructed to study the effect of curvature on the HER performance (Fig. 3a). The optimized structural parameters and associated key structural parameters are shown in Fig. S3 and Table S3.† As shown in Fig. 3b, ΔGH* declined and approached nearly zero when n = 10, which illustrated that a decrease in carbon nanotube curvature is conducive to enhanced hydrogen adsorption on the catalytic surface.As a valid descriptor for the HER, the d-band center was also calculated to analyze the adsorption properties of catalytic materials. The position of the d-band center influences the activity of the catalytic reaction. The distance between the d-band center and Fermi level can predict the performance of catalysts during the processes of adsorption and dissociation in the HER. The proximity of the d-band center to the Fermi level facilitates more efficient electron transfer, thereby enhancing the adsorption strength of the adsorbate and improving the catalytic activity.37 As shown in Fig. 3c, it is found that the d-band centers have a correlation with ΔGH* (R2 = 0.99), indicating that the d-band center was a highly effective descriptor for RhN4@CNT catalysts. Crucially, there is also a correlation between the curvature and the position of the d-band center. When n = 10, the d-band center exhibited the smallest value, which was the closest proximity to the Fermi level, resulting in the lowest ΔGH*. The decrease in the curvature led to the tailoring of εd, bringing it closer to the Fermi level. As a result, the catalyst exhibited stronger hydrogen adsorption affinity. Therefore, adjusting the curvature can be an approach to set εd in a carbon nanotube-based single atom catalyst to regulate the adsorption strength.
The effect of curvature on the catalytic performance was further analyzed by state density, as shown in Fig. 4. The PDOS of RhN4@CNTs (n, n) (n = 5–10) revealed a noteworthy involvement of the d orbitals of Rh atom in the DOS at the Fermi level, indicating robust hybridization between the d states of Rh atom and the p states of C and N atoms. With the decreasing of curvature, the DOS of C at 2p states below the Fermi level is expanded, and the 4d states of Rh overlaps more with the 2p states of C, suggesting the enhanced electron interaction among C, N and Rh. The enlarged diagram showed that as the curvature decreased, the d-band center moved closer to the Fermi level, resulting in the enhancement of hydrogen adsorption on RhN4@CNTs. Hence, by modulating the curvature of carbon nanotubes, the control of the material's d-band center can be achieved, subsequently regulating the catalytic reaction activity.
3.3 The 5-1DB defect on RhN4@CNTs
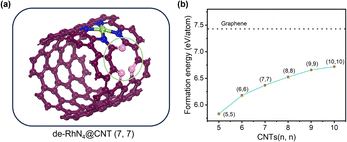
Perfect carbon nanotubes show remarkable performance in the fields of mechanics, thermodynamics and chemistry. However, in the process of generating carbon nanotubes, various structural defects will inevitably be formed such as single vacancy and Stone–Wales defects.38 In contrast to the common perception, the defects did not negatively affect the performance of the CNTs. Instead, it can improve the chemical properties of CNTs and make new functions possible.39–41 For armchair carbon nanotubes (n, n), 5-1DB is a common defect resulting from the absence of a single carbon atom.22 This single point defect leads to the creation of three dangling bonds (DBs) which are unstable. Through the recombination of three DBs, a five-ring structure and a DB are formed, which is called the 5-1DB defect. In order to explore the effect of the defect on RhN4@CNTs during the HER, a 5-1DB defect was created, as shown in Fig. 5. And the formation energy of the defects on CNTs was calculated. Although the defect formation energy for RhN4@CNTs (n, n) (n = 5–10) increased monotonically with decreasing curvature, it remains lower than that on graphene, indicating that creating one 5-1DB defect on CNTs is more facile than on graphene. Therefore, the consideration of the presence of defects on CNTs is indispensable for assessing the impact on catalytic reactions.3.4 HER catalytic activity of de-RhN4@CNTs (n, n) (n = 5–10)
As shown in Fig. 6a, the geometric models of de-RhN4@CNTs (n, n) (n = 5–10) were constructed, containing a 5-1DB defect neighboring the single atomic site. The Gibbs free energy calculation (Fig. 6b) revealed that ΔGH* decreased as the curvature of the CNTs reduced. Compared to the catalysts without any defect (Fig. 3b), a 5-1DB defect on the CNTs caused a lower ΔGH*. For the HER on RhN4@CNTs, ΔGH* approached zero when n = 10, while for that on de-RhN4@CNTs, ΔGH* was close to zero as n = 7. Thus, the 5-1DB defect greatly reduced the ΔGH* of H adsorption, leading to a stronger interaction between hydrogen and catalysts. The presence of individual 5-1DB defect on CNTs is conducive to promoting the HER. As the curvature decreased, the d-band center upshifted more closer to the Fermi level, and a linear relationship (R2 = 0.82) existed between ΔGH* and εd, as shown in Fig. 6c.Subsequently, to deeply understand the optimal intrinsic activity of the HER on de-RhN4@CNTs, PDOS and the d-band centers were computed. The PDOS of de-RhN4@CNTs (n, n) (n = 5–10) also revealed strong hybridization between the d states of Rh atom and the p states of C and N atoms (Fig. 7). Strong electron transfer still existed between C atoms, N atoms and Rh atoms. Compared with the perfect carbon nanotubes, the 5-1DB defect changed the local electron density distribution on de-RhN4@CNTs, which affected the shape and position of the electronic state, so that the peak of the 2p states of C was less sharp in the enlarged image on the right of Fig. 7. Given the close association between the d-band center and the electronic structure of transition metals, alterations in the electronic structure induced by defects may lead to uncertainty in the position of the d-band center. The d-band center of metallic Rh in the de-RhN4@CNTs was similar when n = 5, 6, n = 7, 8, n = 9, 10, respectively. From the overall trend in the data of εd, it was still observed that the d-band center moved closer to the Fermi level with a decrease in curvature.
The 5-1DB defect introduced local curvature and distortion, resulting in changes of the local electronic structure of carbon nanotubes. To analyze the change of electron distribution in the 5-1DB defect, the charge density difference of RhN4@CNTs (7, 7) and de-RhN4@CNTs (7, 7) with H atom adsorption were calculated (Fig. 8). The 5-1DB defect enriched the charge density on the nearby C atoms, increasing the charge density of the adsorption site region. Furthermore, the charge density of Rh atoms also increased, which enhanced the interaction between Rh metal and the H atom, directly. Bader charge showed that the atomic charges of Rh in de-RhN4@CNTs (7, 7) (+7.67e) are more positive than those in RhN4@CNTs (7, 7) (+7.53e). Therefore, the 5-1DB defect facilitated the adsorption of hydrogen on de-RhN4@CNTs.
4. Conclusions
In this work, we have performed computational screening of a series of TMs (TM = Mo, Rh, Fe, Cr, Co, Zn, Mn, Cu, Ni, Pd) anchored on graphene and CNTs for catalyzing the HER, with Rh showcasing the best HER activity. Then, we explored the effects of curvature and 5-1DB defect on the HER catalytic activity of the RhN4@CNTs (n, n) (n = 5–10). Our results indicate a linear relationship between the d-band center and curvature of CNTs, so that the H adsorption of RhN4@CNTs can be regulated precisely by altering the curvature. The interaction of Rh metal with H atom increases as the curvature of the carbon nanotubes decreases. The 5-1DB defect affects the local electronic structure near the active site, which is conducive to tuning the binding between Rh metal and H atom and further regulating HER activity. The improved HER activity is explained by the upshift of the d-band center. Thus, the adjustment of curvature or the formation of the 5-1DB defect can regulate the binding energy of H atom on RhN4@CNTs and further affects the catalytic activity. Our findings shed light on the design of efficient carbon nanotube-supported catalysts and contribute to the innovative advancements in catalyst development.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the “Young Talent Support Plan” of Xi'an Jiaotong University. The simulations were conducted on the supercomputing facilities provided by Xi'an and Hefei Advanced Computing Center.References
- J. A. Turner, Science, 2004, 305, 972–974 CrossRef CAS PubMed.
- Y. Yan, L. Thia, B. Y. Xia, X. Ge, Z. Liu, A. Fisher and X. Wang, Adv. Sci., 2015, 2, 1500120 CrossRef PubMed.
- J. K. Norskov and C. H. Christensen, Science, 2006, 312, 1322–1323 CrossRef CAS PubMed.
- S. Bai, C. Wang, M. Deng, M. Gong, Y. Bai, J. Jiang and Y. Xiong, Angew. Chem., Int. Ed. Engl., 2014, 53, 12120–12124 CrossRef CAS PubMed.
- S. Sultan, J. N. Tiwari, A. N. Singh, S. Zhumagali, M. Ha, C. W. Myung, P. Thangavel and K. S. Kim, Adv. Energy Mater., 2019, 9, 1900624 CrossRef.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- A. Bharti and G. Cheruvally, J. Power Sources, 2017, 360, 196–205 CrossRef CAS.
- H. Yin, S. Zhao, K. Zhao, A. Muqsit, H. Tang, L. Chang, H. Zhao, Y. Gao and Z. Tang, Nat. Commun., 2015, 6, 6430 CrossRef CAS PubMed.
- X. Zhang, A. Chen, Z. Zhang, M. Jiao and Z. Zhou, J. Mater. Chem. A, 2018, 6, 11446–11452 RSC.
- Y. Li, D. Bahamon, M. Sinnokrot and L. F. Vega, npj Comput. Mater., 2022, 8, 229 CrossRef CAS.
- Z. Chen, H. Qing, R. Wang and R. Wu, Energy Environ. Sci., 2021, 14, 3160–3173 RSC.
- H. Cao, Q. Wang, Z. Zhang, H.-M. Yan, H. Zhao, H. B. Yang, B. Liu, J. Li and Y.-G. Wang, J. Am. Chem. Soc., 2023, 145, 13038–13047 CrossRef CAS PubMed.
- J. Guo, J. Liu, X. Mao, S. Chu, X. Zhang, Z. Luo, J. Li, B. Wang, C. Jia and D. Qian, J. Phys. Chem. Lett., 2022, 13, 5195–5203 CrossRef CAS PubMed.
- S. Aralekallu, L. K. Sannegowda and V. Singh, Int. J. Hydrogen Energy, 2023, 48, 16569–16592 CrossRef CAS.
- K. Munoz-Becerra, F. J. Recio, R. Venegas and J. H. Zagal, Curr. Opin. Electrochem., 2023, 42, 101387 CrossRef CAS.
- W. Liu, K. Guo, Y. Xie, S. Liu, L. Chen and J. Xu, Sci. Rep., 2023, 13, 9926 CrossRef CAS PubMed.
- N. Ma, Y. Zhang, Y. Wang, J. Zhao, B. Liang, Y. Xiong, S. Luo, C. Huang and J. Fan, J. Colloid Interface Sci., 2024, 654, 1458–1468 CrossRef CAS PubMed.
- M. De Volder, S. Park, S. Tawfick and A. J. Hart, Nat. Commun., 2014, 5, 4512 CrossRef CAS PubMed.
- G. Zhu, Y. Li, H. Zhu, H. Su, S. H. Chan and Q. Sun, ACS Catal., 2016, 6, 6294–6301 CrossRef CAS.
- C. Bo, H. Minghao, C. Yan, J. Peng, L. Baocang, Z. Bo, W. Xi, G. Rui, S. Xiaolei, D. Yaping and Z. Jun, NPG Asia Mater., 2021, 13, 1 CrossRef.
- R. Jussane, R. Baierle, A. Fazzio and R. Mota, Nano Lett., 2005, 5, 197–200 CrossRef PubMed.
- P. M. Ajayan, V. Ravikumar and J. C. Charlier, Phys. Rev. Lett., 1998, 81, 1437–1440 CrossRef CAS.
- L. G. Zhou and S. Q. Shi, Appl. Phys. Lett., 2003, 83, 1222–1224 CrossRef CAS.
- A. V. Krasheninnikov, K. Nordlund, M. Sirviö, E. Salonen and J. Keinonen, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245405 CrossRef.
- C. Sun, H. Wang, T. Jiang, X. Zhao, M. Yao, X. Wang, Y. Zhu, D. Wang, Z. Li, Y. Hou, L. Lei and B. Yang, Sep. Purif. Technol., 2024, 337, 126454 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. K. Norskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and J. K. Norskov, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef CAS.
- T. F. Jaramillo, K. P. Jorgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102 CrossRef CAS PubMed.
- R. Subbaraman, D. Tripkovic, D. Strmcnik, K.-C. Chang, M. Uchimura, A. P. Paulikas, V. Stamenkovic and N. M. Markovic, Science, 2011, 334, 1256–1260 CrossRef CAS PubMed.
- B. Hinnemann, P. G. Moses, J. Bonde, K. P. Jorgensen, J. H. Nielsen, S. Horch, I. Chorkendorff and J. K. Norskov, J. Am. Chem. Soc., 2005, 127, 5308–5309 CrossRef CAS PubMed.
- F. Li, G.-F. Han, H.-J. Noh, J.-P. Jeon, I. Ahmad, S. Chen, C. Yang, Y. Bu, Z. Fu, Y. Lu and J.-B. Baek, Nat. Commun., 2019, 10, 4060 CrossRef PubMed.
- Y.-Y. Ma, C.-X. Wu, X.-J. Feng, H.-Q. Tan, L.-K. Yan, Y. Liu, Z.-H. Kang, E.-B. Wang and Y.-G. Li, Energy Environ. Sci., 2017, 10, 788–798 RSC.
- B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240 CrossRef CAS.
- M. Dhawan, R. S. Dondapati and S. Sharma, International Conference on Computational Science, 2018, pp. 209–212 Search PubMed.
- K. Sharma, K. K. Saxena and M. Shukla, Procedia Eng., 2012, 38, 3373–3380 CrossRef CAS.
- J. Kumar, Ansh and M. Shrivastava, ACS Omega, 2020, 5, 31281–31288 CrossRef CAS PubMed.
- A. V. Stepanov, J. Surf. Invest.: X-Ray, Synchrotron Neutron Tech., 2013, 7, 218–222 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta01719f |
| This journal is © The Royal Society of Chemistry 2024 |