Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Extensive reference set and refined computational protocol for calculations of 57Fe Mössbauer parameters†
Golokesh
Santra
 ,
Frank
Neese
,
Frank
Neese
 * and
Dimitrios A.
Pantazis
* and
Dimitrios A.
Pantazis
 *
*
Max-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: dimitrios.pantazis@kofo.mpg.de
First published on 23rd August 2024
Abstract
Mössbauer spectroscopy is a powerful technique for probing the local electronic structure of iron compounds, because it reports in an element-selective manner on both the oxidation state and coordination environment of the Fe ion. Computational prediction of the two main Mössbauer parameters, isomer shift (δ) and quadrupole splitting (ΔEQ), has long been targeted by quantum chemical studies, and useful protocols based on density functional theory have been proposed. Here we present an extensive curated reference set of Fe compounds that is considerably larger and more diverse than literature precedents. We make a distinction between low-temperature and high-temperature experimental subgroups. This set is employed for optimizing a refined computational protocol utilizing the scalar version of the exact 2-component (X2C) Hamiltonian with the finite nucleus approximation. Attention is devoted to having an accurate and flexible all-electron basis set for Fe. We assess the performance of several DFT methods that cover all representative families and rungs of functionals and find that hybrid functionals with ca. 25–30% exact exchange offer the best accuracy for isomer shifts. The work establishes a refined general protocol of wide applicability that achieves good performance for the prediction of isomer shifts in a wider variety of systems than before, but the limitations of DFT for quadrupole splittings are also highlighted. Finally, comparison of calculated values with high-temperature experimental results shows that the use of an empirical correction factor is required to account for the second-order Doppler shift and to achieve the same quality of correlation as with the low-temperature data.
1. Introduction
After the discovery of the Mössbauer effect in 1958,1–3 Mössbauer spectroscopy has emerged as a powerful analytic tool in solid state physics, chemistry, metallurgy, biological- and geo-sciences as well as in industrial and materials science applications. This spectroscopic technique is based on the phenomenon of recoilless resonant absorption of gamma-ray photons by an atomic nucleus and it can successfully probe minute changes in the nuclear energy levels originating from hyperfine interactions of the active center with surrounding electrons. Over the years, the Mössbauer effect has been observed for nearly 90 γ-ray transitions in 72 isotopes of 42 different elements.4 However, 57Fe Mössbauer spectroscopy is the most common due to the importance of iron in homogeneous and heterogeneous catalysis as well as the abundance of different spin and oxidation states of this element in biologically relevant systems.5–9The two most important parameters encoded in a Mössbauer spectrum are the isomer shift (δ) and the quadrupole splitting (ΔEQ). The isomer shift of a metal center is directly related to the electron density at the nucleus, while ΔEQ is proportional to the electric field gradient (EFG), which originates from a nonsymmetrical distribution of electrons in the valence shell as well as charges on the neighboring ligands.
The isomer shift of 57Fe measures the shift in the energy of the γ-ray absorption relative to a standard, usually iron foil. The isomer shift is sensitive to the electron density at the nucleus, and indirectly probes changes in iron–ligand bond lengths, covalency and nature of its bonds, and shielding due to the 3d orbital occupation pattern. As a result, it can successfully probe oxidation and spin states, and the coordination environment of Fe. This shift between an absorber (A) and a source (S) comes from the difference in the electrostatic interactions between electronic and nuclear charge distributions, which originates from the difference in their electron densities as well as the change in the nuclear radius upon gamma transition. Considering the nucleus to be a uniformly charged sphere, the mathematical expression for the Mössbauer isomer shift is
δ = α(![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) Ae − Ae − ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) Se) Se) | (1) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) e denotes the “effective” electron density, i.e., the weighted average of the electron density within the finite volume the nucleus; α is the isomer shift “calibration constant” and can be expressed with the following form
e denotes the “effective” electron density, i.e., the weighted average of the electron density within the finite volume the nucleus; α is the isomer shift “calibration constant” and can be expressed with the following form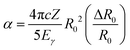 | (2) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) Ae all terms in eqn (1) are constant. In the standard computational approach, the “effective” electron density is usually approximated by the contact density, ρ(0). Although for lighter elements like 57Fe this approximation produces negligible error, for heavier nuclei this error is nontrivial.10 Considering this approximation, eqn (1) can be written in a simple form as
Ae all terms in eqn (1) are constant. In the standard computational approach, the “effective” electron density is usually approximated by the contact density, ρ(0). Although for lighter elements like 57Fe this approximation produces negligible error, for heavier nuclei this error is nontrivial.10 Considering this approximation, eqn (1) can be written in a simple form as| δ = a[ρ(0) − C] + b | (3) |
Over the years, linear regression analysis has been extensively applied for the calculation of isomer shifts using semi-empirical, Hartree–Fock (HF), density functional theory (DFT), and wave function based ab initio methods like the domain based local pair-natural orbital coupled-cluster theory (DLPNO-CCSD).11,13–34 All these studies have demonstrated good correlation between theory and experiment. Despite its simplicity, this approach is fairly reliable and efficient and is known to predict isomer shifts with an accuracy of up to ∼0.1 mm s−1.27 Accurate computation of the contact density is challenging and depends on factors like the choice of the quantum chemical method, the basis set, and the proper treatment of relativistic effects. An ideal basis set which can adequately describe the contact density of Fe has to be sufficiently large in the region where a cusp in the electron density will occur. The known nonrelativistic HF limit for ρ(0) is ∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 903.987 a.u.−3, whereas with a good basis set one can only obtain up to 11
903.987 a.u.−3, whereas with a good basis set one can only obtain up to 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 a.u.−3.16,19 Although in terms of absolute contact density this error is negligible, compared to the variation of the electron density over the chemical range (∼10 a.u.−3) it is nontrivial.
820 a.u.−3.16,19 Although in terms of absolute contact density this error is negligible, compared to the variation of the electron density over the chemical range (∼10 a.u.−3) it is nontrivial.
The relativistic effects on the electron density at the nucleus are large for iron, increasing ρ(0) by a factor of 1.3 compared to the nonrelativistic electron density of 57Fe.17,19 On the other hand, Saue and co-workers have shown that for the calculation of Mössbauer isomer shifts spin–orbit coupling can be safely ignored while using the eXact 2-Component (X2C) Hamiltonian35–38 and a finite nucleus model,39 therefore the consideration of scalar relativistic effects is sufficient.40 As already demonstrated,11 the contributions from the core 1s and 2s orbitals remain nearly constant to the absolute contact density at the iron nucleus. The major contribution to the variation of the contact density due to its electronic configuration and ligand environment arise from the valence and subvalence regions. Hence, these inner valence and outer valence orbitals of iron matter the most for obtaining a correct calibration.11,19
The other important parameter in a Mössbauer spectrum is the quadrupole splitting (ΔEQ), which arises from the interaction of the nuclear quadrupole moment of the excited state with the EFG at the nucleus. Quadrupole splittings can also be used as a sensitive probe for the coordination environment of iron centers. The quadrupole splitting is obtained from the EFGs using the expression
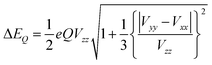 | (4) |
Another important factor is the absence of an accurate value of the 57Fe nuclear quadrupole moment (NQM). As the NQM is impossible to determine experimentally, the only possible way to obtain those values is via linear regression analysis using the experimental ΔEQ values and the theoretical EFGs. Therefore, a wide range of values between 0.1 to 0.3b can be found in the literature. In the present study, we have used Q = 0.160b for the calculation of quadrupole splittings.17
Over the years, several benchmark studies on 57Fe Mössbauer parameters have been performed by employing scalar relativistic Hamiltonians like ZORA (zero-order regular approximation),41 DKH2 (second-order Douglas–Kroll–Hess),42–48 and X2C (exact two-component).18,19,21,22,40,49 Although changing the Hamiltonian had little effect on the overall correlation of experimental δ and calculated contact densities of iron,18,22 a detailed evaluation of a variety of density functional methods and basis sets with the scalar relativistic X2C Hamiltonian against a large and diverse dataset is still absent. Another potential constraint of previous studies is related to the set of iron complexes considered for benchmarking quantum-chemistry methods. These datasets are either composed of limited number of compounds, a mixture of molecular and solid-state systems, a specific type of ligand, or only a limited number of spin and oxidation states of iron. The main objectives of the present study are:
(a) To construct a complete database of Fe complexes with well-established Mössbauer parameters, which is curated so that it includes most of the known spin and oxidation state of iron and is representative of the wide range of chemical types encountered in iron coordination chemistry;
(b) To conduct a thorough benchmark study of basis sets and DFT functionals against our new database in order to develop a refined computational protocol based on the popular X2C Hamiltonian.
2. Reference set
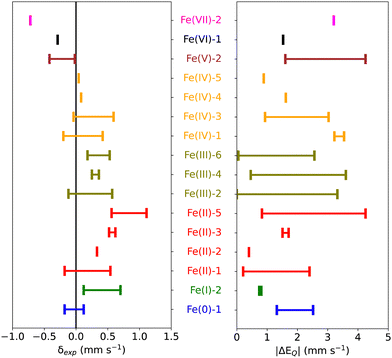
Starting from 155 iron-containing systems with one Fe center, 116 unique entries were sorted out depending on the nature of ligands, spin and oxidation states of the Fe center, and distribution of the experimental isomer shift (δexp) and quadrupole splitting (ΔEQ) values. Among these, 101 are molecular iron complexes, where 80 experimental isomer shifts were recorded at low temperature (4.2–80 K) and the remaining 21 were recorded at – or close to – room temperature. In the following, we shall focus on the subset of 80 molecular iron-complexes for which low-T δexp values are known. We call this dataset MPMIC80 (Mössbauer Parameters of 80 Molecular Iron Complexes). Among these complexes, δexp ranges from −0.72 to 1.11 mm s−1, and the absolute quadrupole splitting (|ΔEQ|) values range from 0.0 to 4.25 mm s−1 (see Fig. 1). The complexes in our dataset cover the known oxidation and spin states of iron. For detailed information on spin, oxidation states, δexp, |ΔEQ|, and corresponding references see Table S1 in the ESI.†3. Methodology
All the calculations were carried out using a development version of ORCA.50 All molecular iron complexes were optimized at the gas-phase using the scalar relativistic X2C Hamiltonian,51 the TPSSh52,53 functional, the D3BJ dispersion corrections,54,55 and the x2c-TZVPall basis sets.56 During optimization, the DefGrid2 integration grid, TightSCF convergence criteria, RIJCOSX approximation,57 and picture change effects58–61 were included. Using two selected complexes, we validated that DefGrid2 is already fully converged for optimizations with the above-mentioned methodology (see Table S3, ESI†). For the scalar relativistic calculations of Mössbauer parameters, we used the x2c-TZVPPall56 basis set for the ligand atoms, we employed first-order picture change effects and the finer DefGrid3 integration grids throughout.In the present study the performance of 10 different basis sets for iron is evaluated: CP(PPP),11 x2c-TZVPPall,56 x2c-TZVPPall-s,62 aug-cc-pVTZ-J (or aVTZ-J),63 DKH-def2-TZVPP (exponents from def2-TZVPP64 were recontracted for scalar-relativistic DKH243–47,65 Hamiltonian), ANO-RCC-VTZP,66 s-decontracted x2c-TZVPPall, s-decontracted aug-cc-pVTZ-J, s-decontracted aug-cc-pVTZ-J(-dfg), and aug-cc-pVTZ-Jmod.67 The last basis set was proposed by Gómez-Piñeiro et al. for the calculations of Cu(II) core properties, where the aug-cc-pVTZ-J was modified by decontracting the s functions and removing the three innermost primitives.67 On the other hand, the outermost d-, f- and g-primitives are removed from s-decontracted aug-cc-pVTZ-J to obtain the s-decontracted aug-cc-pVTZ-J(-dfg) basis set. For the ligand atoms, x2c-TZVPPall56 was used throughout. 15 different density functionals from all five rungs of Jacob's ladder68 were calibrated: SVWN5,69,70 BP86,71,72 PBE,73 BLYP,72,74 TPSS,53 PBE0,75 B1LYP,76 B3LYP,74,77,78 TPSSh,52,53 TPSS0,79 M06,80 LC-BLYP,81 CAM-B3LYP,82 ωB97X,83 and B2PLYP.84 For the PT2 part of the double hybrid functionals, we correlated all core electrons and employed both relaxed and unrelaxed densities. The ORCA sample input files for the calculation of Mössbauer properties and the modified basis sets are provided in the ESI.† In a previous study, the accuracy of selected DFT functionals was evaluated on a small set of 20 iron-containing compounds.18 The structures were optimized there using the TPSS functional and def2-TZVP85 basis set. Following the same protocol for purposes of comparison, the complexes of MPMIC80 were also reoptimized and the nonrelativistic Mössbauer parameters were calculated by employing the B3LYP functional, CP(PPP)11 basis set for iron, and def2-TZVP64 for the ligand atoms.
4. Results and discussion
4.1. Isomer shifts (ISs) for the MPMIC80 set
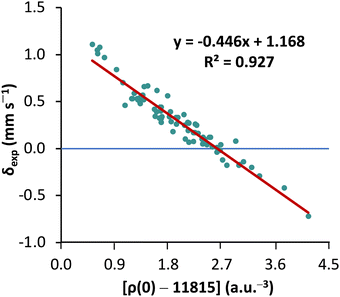
First, to orient ourselves, linear regression analysis was performed for the calculated nonrelativistic electron densities using the originally proposed protocol18 against the experimental isomer shifts of MPMIC80. The coefficient of determination (R2), a and b values obtained from the linear fit were 0.927, −0.446, and 1.168, respectively (see Fig. 2).These results are worse than literature expectations,18,22 owing to the considerably expanded reference set of compounds in the present study. The mean absolute error and standard deviation of calculated isomer shift (δcal) with respect to δexp are 0.07 and 0.09 mm s−1, respectively. Closer inspection reveals that the calculated isomer shifts of all nine Fe(ii) complexes with quintet spin multiplicity (2S + 1 = 5) deviate significantly from the experimental data. This stresses the necessity of reconsidering the linear correlation parameters obtained from more restricted reference sets.
| Basis set for Fe | a | b | C | R 2 | MADc (mm s−1) | Max. dev.d (mm s−1) | St. dev.e (mm s−1) |
|---|---|---|---|---|---|---|---|
| a With first-order picture change effect and finite nucleus model. For the results obtained with the point nucleus model and picture change effect, see Table S4 in the ESI. b a and b are the fitting coefficients obtained from the linear fit of eqn (3). C is a constant, which is very close to the calculated ρ(0) value. The units of a, b, and C are a.u.3 mm s−1, mm s−1, and a.u.−3, respectively. R2 is the coefficient of determination from the linear fit. c Mean absolute deviations of the calculated ISs with respect to the experimental ISs, where the former ones are obtained by using eqn (3). d Maximum deviation of the calculated ISs from the experimental ISs. e Standard deviation of the calculated ISs. | |||||||
| CP(PPP) | −0.30 | 0.9704 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 362 362 |
0.956 | 0.054 | 0.191 | 0.070 |
| x2c-TZVPPall | −0.22 | 1.0294 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 651 651 |
0.820 | 0.108 | 0.346 | 0.142 |
| x2c-TZVPPall-s | −0.22 | 0.8917 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 652 652 |
0.806 | 0.113 | 0.356 | 0.147 |
| aug-cc-pVTZ-J | −0.41 | 1.3456 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511 511 |
0.956 | 0.054 | 0.181 | 0.070 |
| ANO-RCC-VTZP | −0.18 | 0.8903 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 631 631 |
0.414 | 0.184 | 0.752 | 0.255 |
| DKH-def2-TZVPP | −0.30 | 1.0315 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 076 |
0.956 | 0.055 | 0.190 | 0.070 |
| s-decontracted x2c-TZVPPall | −0.31 | 1.1020 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 688 |
0.955 | 0.054 | 0.197 | 0.071 |
| s-decontracted aug-cc-pVTZ-J | −0.29 | 1.1073 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 930 |
0.958 | 0.053 | 0.180 | 0.069 |
| s-decontracted aug-cc-pVTZ-J (-dfg) | −0.29 | 1.1051 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 930 |
0.958 | 0.053 | 0.181 | 0.069 |
| aug-cc-pVTZ-Jmod67 | −0.29 | 1.1015 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804 804 |
0.958 | 0.053 | 0.180 | 0.069 |
| Exp.12 | −0.31 ± 0.04 | ||||||
Our evaluation included first some standard basis sets. With the default x2c-TZVPPall basis set the calculated ρ(0) values, which are reflected in the very large value of C in eqn (3), are significantly smaller than the fully relativistic electron density 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 a.u.−3.86 The coefficient of determination (R2) obtained from linear regression analysis is very low and the value of “a” is far from the experimentally determined value (see Table 1). As a result, the MAD of the calculated isomer shifts from the experimental ones is also high (0.108 mm s−1). This is to be expected because of the lack of enough tight s basis functions in the x2c-TZVPPall basis set of Fe, which has been proven to be critical to obtain correct ρ(0) values.11 For the same reason, shifting from the default x2c-TZVPPall to Weigend's segmented contracted relativistic basis set for NMR shielding constants (x2c-TZVPPall-s),62 which has no additional s-space flexibility, does not result in any improvement.
070 a.u.−3.86 The coefficient of determination (R2) obtained from linear regression analysis is very low and the value of “a” is far from the experimentally determined value (see Table 1). As a result, the MAD of the calculated isomer shifts from the experimental ones is also high (0.108 mm s−1). This is to be expected because of the lack of enough tight s basis functions in the x2c-TZVPPall basis set of Fe, which has been proven to be critical to obtain correct ρ(0) values.11 For the same reason, shifting from the default x2c-TZVPPall to Weigend's segmented contracted relativistic basis set for NMR shielding constants (x2c-TZVPPall-s),62 which has no additional s-space flexibility, does not result in any improvement.
The CP(PPP) basis set was originally proposed precisely for the prediction of Mössbauer parameters, albeit in a non-relativistic context.11 Nevertheless, we test it and is a clear improvement also using the X2C Hamiltonian, underlining the leading importance of core flexibility for these properties. However, even though the calculated contact densities are better than those obtained with x2c-TZVPPall, those are still significantly smaller than 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 a.u.−3. Next, we test the aug-cc-pVTZ-J basis set, which was optimized by Sauer and coworkers for the calculation of electron paramagnetic resonance (EPR) hyperfine coupling constants.63 Interestingly, we get a good R2 value from the linear fit and the MAD is close to what was obtained with CP(PPP). However, the calculated ρ(0) values are very small and consequently the “a” value obtained from linear fit significantly deviates from the experimental calibration constant α = −0.31 ± 0.04. The probable reason behind this unusually small contact densities could be the presence of contracted s functions in aug-cc-pVTZ-J, which restricts the core flexibility of Fe. Due to the lack of sufficiently tight s-primitives, the ρ(0) values calculated using the relativistically contracted ANO-family basis set for iron, ANO-RCC-VTZP,66 has very poor linear correlation (R2 = 0.414) with the experimental isomer shifts. As a result, the fitted parameter “a” deviates significantly from the experimentally determined value (see Table 1).
070 a.u.−3. Next, we test the aug-cc-pVTZ-J basis set, which was optimized by Sauer and coworkers for the calculation of electron paramagnetic resonance (EPR) hyperfine coupling constants.63 Interestingly, we get a good R2 value from the linear fit and the MAD is close to what was obtained with CP(PPP). However, the calculated ρ(0) values are very small and consequently the “a” value obtained from linear fit significantly deviates from the experimental calibration constant α = −0.31 ± 0.04. The probable reason behind this unusually small contact densities could be the presence of contracted s functions in aug-cc-pVTZ-J, which restricts the core flexibility of Fe. Due to the lack of sufficiently tight s-primitives, the ρ(0) values calculated using the relativistically contracted ANO-family basis set for iron, ANO-RCC-VTZP,66 has very poor linear correlation (R2 = 0.414) with the experimental isomer shifts. As a result, the fitted parameter “a” deviates significantly from the experimentally determined value (see Table 1).
Another standard basis set we have tested for Fe is DKH-def2-TZVPP, where the exponents of def2-TZVPP64 were recontracted for the DKH2 Hamiltonian with a looser contraction.43–47,65 Although the calculated ρ(0) values are still not close to the fully relativistic density, the R2 and “a” obtained from the linear regression analysis are considerably improved. Additionally, the mean absolute error and standard deviation of δcal relative to δexp are significantly better than those obtained with the x2c-TZVPPall basis set. The importance of flexibility in the s-functions is highlighted when we look at the correlation between the calculated ρ(0) and experimental isomer shifts with the s-decontracted x2c-TZVPPall, which is clearly better than standard x2c-TZVPPall. By using s-decontracted aug-cc-pVTZ-J the calculated contact densities of the iron centre are very close to the fully relativistic value 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 a.u.−3. Moreover, we also achieve a very good correlation between ρ(0) and δexp (R2 = 0.958).
070 a.u.−3. Moreover, we also achieve a very good correlation between ρ(0) and δexp (R2 = 0.958).
Finally, we test two more modifications of aug-cc-pVTZ-J: (a) fully decontracted s functions and removal of the three innermost s-primitives (i.e., aug-cc-pVTZ-Jmod),67 (b) fully decontracted s-functions and removal of the outermost d-, f-, and g-primitives (denoted s-decontracted aug-cc-pVTZ-J(-dfg)). The first one was recommended for the prediction of Cu(II) hyperfine coupling constants in a scalar relativistic approach,67 whereas the second modification might be useful for large Fe-complexes where linear dependencies in the basis set may arise if diffuse functions are included. These modified basis sets yield effectively indistinguishable results. However, the calculated ρ(0) values with s-decontracted aug-cc-pVTZ-J(-dfg) are closer to the fully relativistic electron density (i.e., 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 a.u.−3) than those obtained with aug-cc-pVTZ-Jmod (see Table 1). With s-decontracted aug-cc-pVTZ-J and its two modifications, the mean absolute errors and the R2 and “a” values obtained from the linear regression analysis are the same. We note that using a set of 12 iron clusters, Kurian and Filatov also found that the computed isomer shift values are only marginally affected by the addition (or subtraction) of the tightest primitive functions to a sizable, uncontracted basis set.88 Unlike that study, however, here we find that the performance of contracted basis sets is noticeably worse compared to the large decontracted ones for the MPMIC80 set.
070 a.u.−3) than those obtained with aug-cc-pVTZ-Jmod (see Table 1). With s-decontracted aug-cc-pVTZ-J and its two modifications, the mean absolute errors and the R2 and “a” values obtained from the linear regression analysis are the same. We note that using a set of 12 iron clusters, Kurian and Filatov also found that the computed isomer shift values are only marginally affected by the addition (or subtraction) of the tightest primitive functions to a sizable, uncontracted basis set.88 Unlike that study, however, here we find that the performance of contracted basis sets is noticeably worse compared to the large decontracted ones for the MPMIC80 set.
For each basis set, the mean absolute error of the isomer shifts calculated using the point nucleus model is slightly higher than those obtained with the Gaussian finite nucleus model (see Table 1 and Table S4 in the ESI†). Except for the aug-cc-pVTZ-J and its modifications, the linear fitting parameters of other basis sets are quite similar regardless of whether a point nucleus or finite nucleus model is used.
Our conclusion regarding basis set selection for the calculation of the Mössbauer isomer shifts is that within the X2C approach with the Gaussian finite nucleus model a basis set with very tight s functions is necessary. Among the standard and non-standard basis sets evaluated here, s-decontracted versions of aug-cc-pVTZ-J and aug-cc-pVTZ-J(-dfg) are equally good and are among the best choices. For the next step, we benchmark different DFT methods in combination with s-decontracted aug-cc-pVTZ-J, CP(PPP), and DKH-def2-TZVPP.
| Basis set for Fe | Methods | a | b | C | R 2 | MADb (mm s−1) | Max. dev.c (mm s−1) | St. dev.d (mm s−1) |
|---|---|---|---|---|---|---|---|---|
| a a and b are the fitting coefficients obtained from the linear fit of eqn (3). C is a constant, which is very close to the calculated ρ(0) value. The units of a, b, and C are a.u.3 mm s−1, mm s−1, and a.u.−3, respectively. R2 is the coefficient of determination from the linear fit. b Mean absolute deviations of the calculated ISs with respect to the experimental ISs, where the former ones are obtained by using eqn (3). c Maximum deviation of the calculated ISs from the experimental ISs. d Standard deviation of the calculated ISs. | ||||||||
| s-decontracted aug-cc-pVTZ-J | SVWN5 | −0.32 | 0.8946 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 831 |
0.913 | 0.071 | 0.296 | 0.098 |
| BP86 | −0.32 | 0.9957 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 960 |
0.922 | 0.067 | 0.270 | 0.093 | |
| PBE | −0.32 | 0.9970 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 933 933 |
0.921 | 0.067 | 0.267 | 0.094 | |
| BLYP | −0.32 | 1.0974 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 954 954 |
0.917 | 0.070 | 0.275 | 0.096 | |
| TPSS | −0.32 | 1.0045 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 917 917 |
0.935 | 0.060 | 0.243 | 0.085 | |
| PBE0 | −0.28 | 1.1225 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 920 920
|
0.965 | 0.050 | 0.148 | 0.063 | |
| B1LYP | −0.28 | 1.1358 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936 936 |
0.961 | 0.054 | 0.150 | 0.066 | |
| B3LYP | −0.29 | 1.1073 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 930 |
0.958 | 0.053 | 0.180 | 0.069 | |
| TPSSh | −0.30 | 1.1976 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 913 913 |
0.954 | 0.052 | 0.227 | 0.072 | |
| TPSS0 | −0.28 | 1.1425 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 908 908
|
0.967 | 0.049 | 0.122 | 0.060 | |
| M06 | −0.31 | 0.9446 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010 010 |
0.936 | 0.065 | 0.277 | 0.084 | |
| LC-BLYP | −0.29 | 1.0845 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951 951 |
0.950 | 0.062 | 0.168 | 0.075 | |
| CAM-B3LYP | −0.27 | 1.2024 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939 939 |
0.960 | 0.055 | 0.137 | 0.067 | |
| ωB97X | −0.27 | 1.1689 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 034 034 |
0.958 | 0.055 | 0.147 | 0.068 | |
| B2PLYP | −0.24 | 1.1367 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916 916 |
0.939 | 0.066 | 0.183 | 0.083 | |
| CP(PPP) | SVWN5 | −0.33 | 1.1214 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 272 272 |
0.910 | 0.072 | 0.295 | 0.100 |
| BP86 | −0.33 | 0.8681 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 388 388 |
0.919 | 0.068 | 0.270 | 0.095 | |
| PBE | −0.33 | 1.1551 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371 |
0.917 | 0.068 | 0.266 | 0.096 | |
| BLYP | −0.33 | 1.1620 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 382 |
0.914 | 0.070 | 0.275 | 0.098 | |
| TPSS | −0.33 | 1.1673 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 358 |
0.932 | 0.061 | 0.253 | 0.087 | |
| PBE0 | −0.29 | 1.0344 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 359 359 |
0.965 | 0.049 | 0.157 | 0.063 | |
| B1LYP | −0.29 | 1.1515 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 367 367 |
0.963 | 0.051 | 0.159 | 0.064 | |
| B3LYP | −0.30 | 0.9704 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 362 362 |
0.956 | 0.054 | 0.191 | 0.070 | |
| TPSSh | −0.32 | 0.9775 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 355 |
0.952 | 0.053 | 0.237 | 0.073 | |
| TPSS0 | −0.29 | 1.1373 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 349 349 |
0.966 | 0.049 | 0.127 | 0.062 | |
| M06 | −0.32 | 1.0447 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 427 427 |
0.934 | 0.065 | 0.277 | 0.085 | |
| LC-BLYP | −0.30 | 1.2454 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 379 379 |
0.951 | 0.061 | 0.177 | 0.074 | |
| CAM-B3LYP | −0.29 | 1.0531 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 370 |
0.961 | 0.054 | 0.134 | 0.066 | |
| ωB97X | −0.28 | 1.1687 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 450 |
0.959 | 0.055 | 0.147 | 0.068 | |
| B2PLYP | −0.25 | 1.1856 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 350 |
0.940 | 0.066 | 0.176 | 0.082 | |
| DKH-def2-TZVPP | SVWN5 | −0.33 | 0.9272 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010 010 |
0.909 | 0.074 | 0.305 | 0.101 |
| BP86 | −0.33 | 0.9640 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 094 094 |
0.919 | 0.069 | 0.277 | 0.095 | |
| PBE | −0.33 | 1.1343 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 086 086 |
0.919 | 0.069 | 0.273 | 0.095 | |
| BLYP | −0.33 | 1.0651 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 089 089 |
0.914 | 0.072 | 0.280 | 0.098 | |
| TPSS | −0.33 | 1.1151 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078 |
0.934 | 0.061 | 0.247 | 0.086 | |
| PBE0 | −0.29 | 1.0853 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078 |
0.964 | 0.051 | 0.156 | 0.063 | |
| B1LYP | −0.29 | 1.1600 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 080 |
0.962 | 0.054 | 0.161 | 0.065 | |
| B3LYP | −0.30 | 1.0315 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 076 |
0.956 | 0.055 | 0.190 | 0.070 | |
| TPSSh | −0.32 | 0.9873 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 076 |
0.953 | 0.053 | 0.220 | 0.072 | |
| TPSS0 | −0.29 | 1.0877 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072 072 |
0.967 | 0.049 | 0.127 | 0.060 | |
| M06 | −0.32 | 1.2105 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 105 |
0.934 | 0.067 | 0.282 | 0.086 | |
| LC-BLYP | −0.30 | 1.0128 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087 087 |
0.945 | 0.065 | 0.163 | 0.078 | |
| CAM-B3LYP | −0.29 | 1.2614 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081 081 |
0.957 | 0.058 | 0.138 | 0.069 | |
| ωB97X | −0.28 | 1.2380 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087 087 |
0.957 | 0.056 | 0.146 | 0.069 | |
| B2PLYP | −0.25 | 1.1934 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 070 |
0.938 | 0.66 | 0.178 | 0.083 | |
Unlike the different basis sets, using different density functionals does not have much influence on the calculated contact densities. Based on the R2 and mean absolute errors, climbing the rungs of “Jacob's ladder” improves accuracy gradually from the 1st to the 4th rung. As in earlier findings, hybrid functionals demonstrate a significant improvement over the performance of pure GGA and meta-GGA approaches.26,27,33,88,89 The inferior correlations obtained with pure density functionals can be attributed to their incorrect behavior near the nucleus.90 The only exception is the extensively parametrized hybrid functional M06, which offers accuracy similar to the pure meta-GGA functionals. Among the hybrid functionals, range separation offers no benefit over the global hybrid variants, and it does more harm than good when there is no short-range HF-exchange involved (e.g., in LC-BLYP). Contrary to what Römelt et al.18 found with the scalar-relativistic ZORA Hamiltonian41,91,92 on a much smaller dataset, the performance of the double hybrid functional for the extensive MPMIC80 set is inferior to standard hybrids like PBE0 and TPSS0.
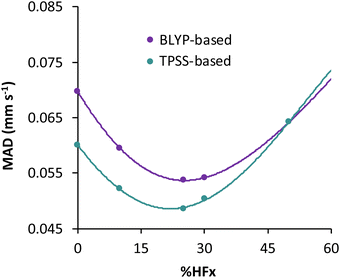
For the TPSS exchange- and correlation-based hybrid functionals, increasing the percentage of exact exchange from 10% to 25% improves its accuracy. Therefore the question may arise, what is the optimum percentage of exact exchange for predicting the isomer shifts in MPMIC80? To investigate this, we chose the BLYP and TPSS functionals and their hybrid counterparts with varying percentage of exact (Hartree–Fock, HF) exchange (i.e., %HFx) while employing the s-decontracted aug-cc-pVTZ-J basis set for iron. Polynomial fitting of MADs with respect to the %HFx suggest minima near 30% for the BLYP-based and near 25% for the TPSS-based functionals (see Fig. 3 and Table S6 in the ESI†). The MAD gap between the BLYP- and TPSS-based functionals decreases with the increase of exact exchange. We obtained the lowest mean absolute error with TPSS0 (25% HFx) among all functionals, and it starts to increase rapidly with higher percentage of exact exchange. For the present dataset the fitting parameter “a” from linear regression has strong dependence on the exact exchange, but it is not sensitive to specific exchange and correlation combinations (Fig. S1, ESI†). Finally, we note that despite having 27% HF exchange, the M06 functional gives inferior electron densities and hence its performance for isomer shifts is inferior to other hybrid functionals (Table 2).
As the GGA exchange and correlation parts of B2PLYP (i.e., B88 and LYP) work fine for our dataset, the origin of the poor performance of the double hybrid functional could be either the PT2 correlation part or the amount of exact exchange used. We note that for the calculation of Cu(II) hyperfine coupling constants, the use of relaxed densities for the PT2 part was recommended.67 Following the same protocol and using the s-decontracted aug-cc-pVTZ-J basis set for Fe improves the “a” value of the linear fit from −0.24 to −0.27. However, R2 and mean absolute error are worse than the unrelaxed density calculations, allowing us to rule out the first possible source of error (see Table S7, ESI†). Hence, the high fraction of exact exchange (53%) used in the B2PLYP seems to be the principal reason behind its poorer performance compared to standard hybrid DFT functionals.
Earlier studies have shown that spin-component scaled double hybrids are more accurate than simple double hybrids like B2PLYP for calculating the energetics and spectral properties of transition metal complexes.93–96 The contact densities computed using the DSD-PBEP86 functional and the s-decontracted aug-cc-pVTZ-J basis set for iron, along with the relaxed PT2 density, were fitted to the experimental isomer shifts. This resulted in the fitting parameter a = −0.26 with R2 = 0.895 (see Fig. S2, ESI†). The relatively high percentage (68%) of HF exchange used in DSD-PBEP86 could be the reason behind its marginally poorer performance than B2PLYP. However, for most of the quintet FeII and sextet FeIII complexes of our dataset, the isomer shifts calculated using DSD-PBEP86 are closer to the experimental values than δcal using TPSS0 or B2PLYP (see Table S11, ESI†). We note in passing that a double hybrid calculation with relaxed density is approximately three times more expensive and requires more memory allocation than a similar calculation with unrelaxed density. The “unrelaxed” PT2 density corresponds to simple PT2 expectation value density, whereas the “relaxed” one incorporates orbital relaxation.
In conclusion, hybrid functionals incorporating ca. 25–30% exact exchange offer the best linear correlation and accuracy for predicting isomer shifts. Among all methods tested, our best picks are TPSS0 and PBE0, combined with the s-decontracted aug-cc-pVTZ-J basis set for Fe.
With respect to the literature, we note that using 15 iron-containing compounds and the CP(PPP) basis set for Fe, an R2 = 0.972 was obtained from the linear regression analysis of the nonrelativistic electron densities calculated with B3LYP against experimental isomer shifts.11 The reported standard deviation for the theoretical prediction of isomer shifts was 0.09 mm s−1. Later, with a slightly larger and more diverse set, B3LYP offered a marginally better correlation (R2 = 0.980) and a standard deviation of 0.09 mm s−1, while using a larger dataset, Pápai and Vankó found R2 = 0.975 and MAD = 0.06 mm s−1 for B3LYP.30 However, Kurian and Filatov found a better correlation with experimental results using BH&HLYP instead of B3LYP, which might be a result of employing a small dataset.88 Using a dataset comprising 69 iron compounds, Comas-Vilà and Salvador showed that replacing the density at the iron nucleus with the density integrated in a sphere of radius 0.06 au surrounding the iron center can provide excellent correlation (R2 = 0.976) when using the conventional def2-TZVP basis set.89 In a recent study, using 20 molecular Fe complexes, Gallenkamp et al. found the best performance with TPSSh and PBE0 (R2= 0.978 and 0.976) with mean absolute errors of 0.05 and 0.06 mm s−1, respectively.33 With a set of 21 iron-complexes, using the scalar-relativistic ZORA Hamiltonian and ZORA-def2-TZVP basis set for Fe, hybrid, and double hybrid functionals offered similar accuracy (R2 = 0.970 and Standard deviation = 0.08 mm s−1).18 Employing the DKH2 Hamiltonian and custom-defined basis sets for Fe did not offer any further improvement in the performance of hybrid functionals.22 Although our best pick, TPSS0 with the s-decontracted aug-cc-pVTZ-J basis set for Fe, has a slightly smaller R2 value, the standard deviation is better than what was reported previously. The smaller R2 can be attributed to using a dataset that is more than three times larger than what was used in ref. 18 and 22, Perdew and coworkers argue that highly parameterized density functional methods are often significantly inferior to the functionals developed by constraint satisfaction while calculating the electron densities.97 Among the 128 functionals tested in their work, PBE0 is one of the best for calculating electron density distributions compared to the all-electron coupled cluster singles and doubles (CCSD-full) densities. PBE0 and TPSS0 should therefore yield reliable electron densities and, hence, good performance for Mössbauer isomer shift computations.
4.2. High-temperature isomer shifts
It is well known that the Mössbauer parameters are temperature-dependent, and this behavior originates from the temperature dependence of the Lamb–Mössbauer factor f. With increasing temperature, the second-order Doppler shift (SODS) appears owing to significant thermal motions of the source and absorber nuclei, which leads to a lower isomer shift.5,9 The SODS-corrected chemical isomer shift of a Mössbauer spectrum is sometimes referred to in literature as the center shift (CS),98 which has the following expression| CS = δ + SODS | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mm s−1 to the measured isomer shift, it can be as large as 0.1 mm s−1 at room temperature. A fair comparison between computational and experimental isomer shifts is therefore guaranteed only at temperatures of a few Kelvin (K). Since the influence of the temperature may exceed the uncertainties from density functional methods and basis sets, comparison with experimental data obtained above 80 K needs special treatment before comparing them with the calculated counterparts. In multiple occasions, Noodleman and co-workers have proposed a linear SODS correction of the experimentally recorded isomer shifts by 0.12 mm s−1 for a temperature decrease from 300 K to 4.2 K.25,99–101 However, Friesner and co-workers recommended to avoid such empirical corrections in a benchmark study because of the nontrivial temperature dependence of the 57Fe Mössbauer parameters.27
mm s−1 to the measured isomer shift, it can be as large as 0.1 mm s−1 at room temperature. A fair comparison between computational and experimental isomer shifts is therefore guaranteed only at temperatures of a few Kelvin (K). Since the influence of the temperature may exceed the uncertainties from density functional methods and basis sets, comparison with experimental data obtained above 80 K needs special treatment before comparing them with the calculated counterparts. In multiple occasions, Noodleman and co-workers have proposed a linear SODS correction of the experimentally recorded isomer shifts by 0.12 mm s−1 for a temperature decrease from 300 K to 4.2 K.25,99–101 However, Friesner and co-workers recommended to avoid such empirical corrections in a benchmark study because of the nontrivial temperature dependence of the 57Fe Mössbauer parameters.27
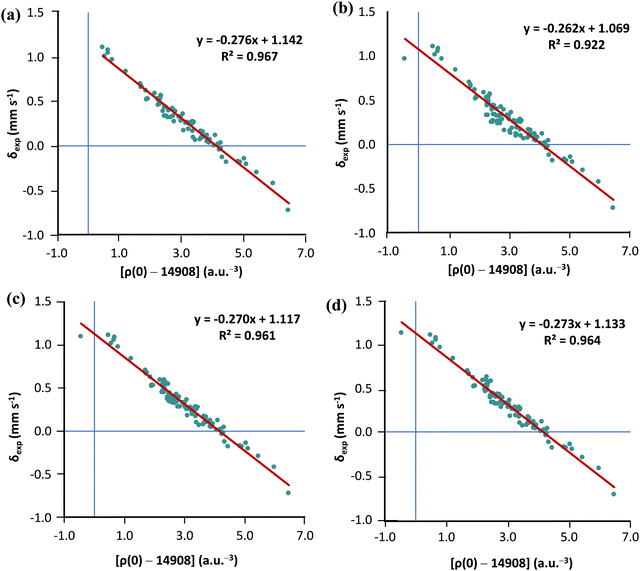
As we already have a curated subset of molecules (21 Fe-complexes) with high-T experimental isomer shirts, we can examine whether the solution proposed by Noodleman is transferable (see Table S2 in the ESI†). For this purpose, we chose the TPSS0 functional with the s-decontracted aug-cc-pVTZ-J basis set for iron. Considering the 80 low-temperature isomer shifts, linear regression analysis of ρ(0) vs. δexp gives R2 = 0.967. Adding the 21 high-T isomer shifts to the MPMIC80 and refitting the linear equation we obtain a significantly lower R2 value of 0.922. However, if Noodleman's correction is applied to the 21 high-T isomer shifts, linear regression analysis for the mixed set of 101 compounds almost recovers the correlation obtained with the original MPMIC80 set (see Fig. 4a–c). The same trend is observed with PBE0/s-decontracted aug-cc-pVTZ-J(Fe) and B3LYP/CP(PPP)(Fe) (see Fig. S3 and S4, ESI†).
Now, refitting a high-T isomer shift correction factor against 21 complexes we get the value 0.16 mm s−1. However, using a larger IS correction factor only marginally improves correlation compared to Noodleman's correction (see Fig. 4c and d).
4.3. Quadrupole splittings in the MPMIC80 set
Similar to isomer shifts, we start with the non-relativistic quadrupole splitting calculation using TPSSh functional and CP(PPP) basis set for Fe. Relative to the experimental |ΔEQ|, non-relativistically obtained quadruple splittings yield mean absolute deviation and root-mean-square deviation 0.331 and 0.443 mm s−1, respectively. Although deviation from |ΔEQ,exp| is distributed among all the oxidation states of Fe, the largest error was obtained for iron(III) phthalocyanine chloride and octaethylporphyrinato-iron(II) (i.e., molecules #35 and #65 from the MPMIC80 dataset; see Fig. S5, ESI†).The mean absolute and root-mean-square errors of calculated |ΔEQ| with respect to the experimental |ΔEQ| for ten different basis sets evaluated using B3LYP functional, finite nucleus model, and first-order picture change effect are listed in Table 3. Among the six standard basis sets, DKH-def2-TZVPP and x2c-TZVPPall are the best and the worst performer, respectively. Unlike what we observed for isomer shifts, x2c-TZVPPall-s basis set, developed for NMR shielding constants, offers a noticeably better accuracy than x2c-TZVPPall. Decontraction of the s primitives does more harm than good for x2c-TZVPPall.
| Basis set for Fe | MAD (mm s−1) | RMSD (mm s−1) |
|---|---|---|
| a For the results with point nucleus model, see Table S8 in the ESI. b With CP(PPP) basis set for Fe and def2-TZVP for the ligand atoms. | ||
| CP(PPP) | 0.312 | 0.451 |
| x2c-TZVPPall | 0.357 | 0.504 |
| x2c-TZVPPall-s | 0.299 | 0.436 |
| aug-cc-pVTZ-J | 0.352 | 0.495 |
| DKH-def2-TZVPP | 0.241 | 0.381 |
| ANO-RCC-VTZP | 0.283 | 0.421 |
| s-decontracted x2c-TZVPPall | 0.361 | 0.514 |
| s-decontracted aug-cc-pVTZ-J | 0.347 | 0.487 |
| s-decontracted aug-cc-pVTZ-J (-dfg) | 0.349 | 0.489 |
| aug-cc-pVTZ-Jmod67 | 0.347 | 0.487 |
| Non-relativisticb | 0.331 | 0.443 |
Next, for the evaluation of DFT methods to calculate |ΔEQ| values three basis sets were chosen: CP(PPP), DKH-def2-TZVPP, and s-decontracted aug-cc-pVTZ-J. The MAD and RMSD statistics for each the method and basis set combinations are listed in Table 4. (For the error statistics obtained using the s-decontracted aug-cc-pVTZ-J(-dfg) basis set for Fe, see Table S9 in the ESI†).
| Basis set for Fe | Methods | MAD (mm s−1) | RMSD (mm s−1) |
|---|---|---|---|
| s-decontracted aug-cc-pVTZ-J | SVWN5 | 0.319 | 0.495 |
| BP86 | 0.274 | 0.450 | |
| PBE | 0.280 | 0.457 | |
| BLYP | 0.272 | 0.450 | |
| TPSS | 0.269 | 0.437 | |
| PBE0 | 0.374 | 0.523 | |
| B1LYP | 0.404 | 0.557 | |
| B3LYP | 0.347 | 0.487 | |
| TPSSh | 0.261 | 0.410 | |
| TPSS0 | 0.383 | 0.525 | |
| M06 | 0.544 | 0.949 | |
| LC-BLYP | 0.432 | 0.562 | |
| CAM-B3LYP | 0.474 | 0.632 | |
| ωB97X | 0.493 | 0.649 | |
| B2PLYP | 0.648 | 0.857 | |
| CP(PPP) | SVWN5 | 0.348 | 0.516 |
| BP86 | 0.308 | 0.473 | |
| PBE | 0.319 | 0.484 | |
| BLYP | 0.303 | 0.475 | |
| TPSS | 0.305 | 0.463 | |
| PBE0 | 0.326 | 0.457 | |
| B1LYP | 0.346 | 0.480 | |
| B3LYP | 0.312 | 0.451 | |
| TPSSh | 0.251 | 0.405 | |
| TPSS0 | 0.353 | 0.489 | |
| M06 | 0.500 | 0.891 | |
| LC-BLYP | 0.371 | 0.487 | |
| CAM-B3LYP | 0.409 | 0.553 | |
| ωB97X | 0.419 | 0.546 | |
| B2PLYP | 0.587 | 0.779 | |
| DKH-def2-TZVPP | SVWN5 | 0.451 | 0.602 |
| BP86 | 0.398 | 0.545 | |
| PBE | 0.408 | 0.557 | |
| BLYP | 0.396 | 0.542 | |
| TPSS | 0.396 | 0.534 | |
| PBE0 | 0.258 | 0.399 | |
| B1LYP | 0.258 | 0.392 | |
| B3LYP | 0.241 | 0.381 | |
| TPSSh | 0.291 | 0.431 | |
| TPSS0 | 0.270 | 0.412 | |
| M06 | 0.423 | 0.813 | |
| LC-BLYP | 0.270 | 0.381 | |
| CAM-B3LYP | 0.301 | 0.440 | |
| ωB97X | 0.305 | 0.423 | |
| B2PLYP | 0.466 | 0.635 | |
For all these basis sets, GGA and meta-GGA functionals offer better accuracy than the LDA functional. Importantly, and unlike what we observed for the isomer shifts, hybrid functionals produce larger errors than GGA and meta-GGA functionals. Range separation leads to deterioration rather than improvement. The only exception is when the DKH-def2-TZVPP functional is used, in which case hybrid functionals are better performers than the 2nd and 3rd rung functionals. Interestingly, using either the CP(PPP) or the s-decontracted aug-cc-pVTZ-J basis set for Fe combined with TPSSh functional provides noticeably lower mean absolute error than TPSS0.
Once again, B2PLYP is the worst performer among all functionals tested. While using the s-decontracted aug-cc-pVTZ-J basis set for Fe, employing relaxed density for PT2 correlation improve its accuracy (MAD goes down from 0.648 to 0.485 mm s−1). A large percentage of exact exchange in B2PLYP also contributes a significant share to its large mean absolute error. Analyzing the results obtained from varying percentage of exact exchange in PBE-, BLYP-, and TPSS-based hybrid functionals, it is evident that beyond 10% the mean absolute error in calculated |ΔEQ| compared to experiment increases rapidly (see Table S10 in the ESI†). However, pure GGA and meta-GGA functionals are also good and cheaper alternatives. This observation agrees with the recommendation of Nemykin and Hadt for using the pure GGA functional BPW91 over B3LYP to predict quadrupole splittings in ferrocenes accurately.26 Overall, the quadrupole splittings are harder to reproduce systematically with equally high level of reliability as the isomer shifts and remain a challenge that will have to be addressed more satisfactorily in future studies.
So far, we have used the 57Fe nuclear quadrupole moment Q = 0.16b to calculate the quadrupole splitting values. A reasonable question is whether there is anything to be gained by refitting the quadrupole moment of the 57Fe nucleus against the MPMIC80 set. Using the s-decontracted aug-cc-pVTZ-J basis set for iron, we selected nine representative functionals for this purpose and plotted the experimental QSs following eqn (4). The new Q(57Fe) value is determined from the slope of the linear fit to the plot (see Table 5). With TPSS-based hybrid functionals, increasing the percentage of HF-exchange gradually decreases the fitted Q(57Fe).
| Functionals | Calculated Q(57Fe)a | MAD (mm s−1) | RMSD (mm s−1) |
|---|---|---|---|
a Slope of the linear fit to the plot of experimental QS vs.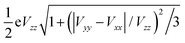 . .
|
|||
| BP86 | 0.165 | 0.268 | 0.446 |
| PBE | 0.166 | 0.271 | 0.452 |
| TPSS | 0.167 | 0.254 | 0.429 |
| TPSSh | 0.155 | 0.248 | 0.405 |
| B3LYP | 0.141 | 0.272 | 0.408 |
| PBE0 | 0.139 | 0.285 | 0.424 |
| TPSS0 | 0.141 | 0.303 | 0.435 |
| TPSS30 | 0.137 | 0.328 | 0.456 |
| TPSS50 | 0.125 | 0.429 | 0.569 |
Using the nuclear quadrupole moment thus obtained, we reevaluated the quadrupole splittings and calculated the MAD and RMSD errors against the experimental ΔEQ values (see Table 5). It can be seen that refitting the 57Fe NQMs only marginally improves the performance of pure GGA and mGGA functionals. This improvement is negligible for the hybrid functionals at a small fraction of HF exchange, and increasing the %HFx also increases the performance gap.
5. Conclusions
We have presented the largest and most extensive molecular dataset, namely MPMIC80, for the calculation of 57Fe Mössbauer isomer shifts and quadruple splittings. This new set of complexes covers most of the known spin and oxidation states of iron, a diverse set of ligands, and with each complex having one unique iron center and low-temperature experimentally determined Mössbauer parameters. After an extensive survey of density functional methods and basis sets with the aid of the MPMIC80 data set, we can conclude the following:• Irrespective of the choice of basis sets and density functional methods, use of finite nucleus model and picture change effect is recommended with the scalar relativistic X2C-Hamiltonian.
• Tight s-primitives are necessary for the calculation of contact densities close to the fully relativistic limit (ρ = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 a.u.−3). Consequently, standard basis sets that are either general-purpose or have been optimized for other properties (e.g., for NMR chemical shifts) are inappropriate poor choices for these calculations, whereas the s-decontracted version of aug-cc-pVTZ-J is a solid choice.
070 a.u.−3). Consequently, standard basis sets that are either general-purpose or have been optimized for other properties (e.g., for NMR chemical shifts) are inappropriate poor choices for these calculations, whereas the s-decontracted version of aug-cc-pVTZ-J is a solid choice.
• For isomer shifts, 25–30% is the optimum percentage of exact (HF) exchange for hybrid functionals with scalar relativistic X2C Hamiltonian. Best accuracy was found with the TPSS0 and PBE0 functionals with s-decontracted aug-cc-pVTZ-J. Range separation has no benefit over global hybrid functionals.
• Double hybrid functionals are not recommended. The performance of B2PLYP is worse than any hybrid functional, which is most likely the result of the high percentage of exact exchange used.
• Refitting the original 80 isomer shifts and 21 high-T isomer shifts adjusted to 4.2 K by a linear correction against the calculated contact densities almost fully recovers the R2 value obtained with the low-temperature MPMIC80.
• Quadruple splitting values are less systematically predicted with DFT. Unlike isomer shifts, pure GGA, meta-GGA, and hybrid functionals with small fraction of HF exchange (∼10%) are preferred for these calculations, but there is considerable room for improvement.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The authors gratefully acknowledge support from the Max Planck Society. G. S. thanks Dr Daniel SantaLucia (Max Planck Institute for Chemical Energy Conversion) and Dr Georgi Stoychev (FAccTs GmbH, Germany) for helpful discussions. G. S. and D. A. P. thank Dr Sergio A. V. Jannuzzi (Max Planck Institute for Chemical Energy Conversion) for pointing out a recently reported FeVII complex. Open Access funding provided by the Max Planck Society.References
- R. L. Mössbauer, Kernresonanzfluoreszenz von Gammastrahlung in Ir191, Z. Phys., 1958, 151, 124–143 CrossRef.
- R. L. Mössbauer, Kernresonanzabsorption von Gammastrahlung in Ir191, Naturwissenschaften, 1958, 45, 538–539 CrossRef.
- R. L. Mössbauer, Kernresonanzabsorption von γ-Strahlung in Ir191, Z. Naturforsch., A: Phys. Sci., 1959, 14, 211–216 Search PubMed.
- P. Gütlich, C. Schröder and V. Schünemann, Mössbauer spectroscopy—an indispensable tool in solid state research, Spectrosc. Eur., 2012, 24, 21–32 Search PubMed.
- P. Gütlich, E. Bill and A. X. Trautwein, Mössbauer spectroscopy and transition metal chemistry: fundamentals and applications, Springer Berlin, Heidelberg, 2010 Search PubMed.
- P. Gütlich, R. Link and A. X. Trautwein, Mössbauer Spectroscopy and Transition Metal Chemistry, Springer, Berlin, Heidelberg, 1978 Search PubMed.
- L. J. Que, Physical Methods in Bioinorganic Chemistry: Spectroscopy and Magnetism, University Science Books, Sausalito, 2000 Search PubMed.
- E. Münck and A. Stubna, Mössbauer Spectroscopy: Bioinorganic, Comprehensive Coordination Chemistry II, Elsevier, 2003, vol. 2, pp. 279–286 Search PubMed.
- N. N. Greenwood and T. C. Gibb, Mössbauer spectroscopy, Springer, Dordrecht, 2012 Search PubMed.
- S. Knecht, S. Fux, R. van Meer, L. Visscher, M. Reiher and T. Saue, Mössbauer spectroscopy for heavy elements: a relativistic benchmark study of mercury, Theor. Chem. Acc., 2011, 129, 631–650 Search PubMed.
- F. Neese, Prediction and interpretation of the 57Fe isomer shift in Mössbauer spectra by density functional theory, Inorg. Chim. Acta, 2002, 337, 181–192 CrossRef.
- J. Ladrière, A. Meykens, R. Coussement, M. Cogneau, M. Boge, P. Auric, R. Bouchez, A. Benabed and J. Godard, Isomer shift calibration of 57Fe by life-time variations in the electron-capture decay of 52Fe, J. Phys., Colloq., 1979, 40, C2-20–C2-22 Search PubMed.
- K. J. Duff, Calibration of the isomer shift for 57Fe, Phys. Rev. B: Condens. Matter Mater. Phys., 1974, 9, 66–72 CrossRef CAS.
- A. Trautwein, F. E. Harris, A. J. Freeman and J. P. Desclaux, Relativistic electron densities and isomer shifts of 57Fe in iron-oxygen and iron-fluorine clusters and of iron in solid noble gases, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 11, 4101–4105 CrossRef CAS.
- R. Reschke, A. Trautwein and J. P. Desclaux, Limitation of semi-empirical mo-calculations in deriving charge densities ρ(0) in iron-oxygen compounds, J. Phys. Chem. Solids, 1977, 38, 837–841 CrossRef CAS.
- W. C. Nieuwpoort, D. Post and P. T. V. Duijnen, Calibration constant for 57Fe Mössbauer isomer shifts derived from ab initio self-consistent-field calculations on octahedral FeF6 and Fe(CN)6 clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 91–98 CrossRef CAS.
- S. Sinnecker, L. D. Slep, E. Bill and F. Neese, Performance of Nonrelativistic and Quasi-Relativistic Hybrid DFT for the Prediction of Electric and Magnetic Hyperfine Parameters in 57Fe Mössbauer Spectra, Inorg. Chem., 2005, 44, 2245–2254 CrossRef CAS PubMed.
- M. Römelt, S. Ye and F. Neese, Calibration of Modern Density Functional Theory Methods for the Prediction of 57Fe Mössbauer Isomer Shifts: Meta-GGA and Double-Hybrid Functionals, Inorg. Chem., 2009, 48, 784–785 CrossRef PubMed.
- F. Neese and T. Petrenko, Quantum Chemistry and Mössbauer Spectroscopy, in Mössbauer Spectroscopy and Transition Metal Chemistry: Fundamentals and Applications, ed. P. Gütlich, E. Bill and A. X. Trautwein, Springer Science & Business Media, 2011, pp. 137–199 Search PubMed.
- M. Sparta, D. Bykov and F. Neese, Calculating Mössbauer parameters using the local pair natural orbital coupled-cluster method, Möessbauer Eff. Ref. Data J., 2014, 37, 69–77 Search PubMed.
- R. Bjornsson, F. Neese and S. DeBeer, Revisiting the Mössbauer Isomer Shifts of the FeMoco Cluster of Nitrogenase and the Cofactor Charge, Inorg. Chem., 2017, 56, 1470–1477 CrossRef CAS PubMed.
- D. Datta, M. Saitow, B. Sandhöfer and F. Neese, 57Fe Mössbauer parameters from domain based local pair-natural orbital coupled-cluster theory, J. Chem. Phys., 2020, 153, 204101 CrossRef CAS PubMed.
- A. Banerjee, Q. Liu, J. Shanklin and M. Z. Ertem, Predicting Mössbauer Parameters of Nonheme Diiron Complexes with Density Functional Theory, Inorg. Chem., 2023, 62, 11402–11413 CrossRef CAS PubMed.
- Y. Zhang, J. Mao and E. Oldfield,
57Fe Mössbauer Isomer Shifts of Heme Protein Model Systems:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Electronic Structure Calculations, J. Am. Chem. Soc., 2002, 124, 7829–7839 CrossRef CAS PubMed.
Electronic Structure Calculations, J. Am. Chem. Soc., 2002, 124, 7829–7839 CrossRef CAS PubMed. - W.-G. Han, T. Liu, T. Lovell and L. Noodleman, DFT calculations of 57Fe Mössbauer isomer shifts and quadrupole splittings for iron complexes in polar dielectric media: Applications to methane monooxygenase and ribonucleotide reductase, J. Comput. Chem., 2006, 27, 1292–1306 CrossRef CAS PubMed.
- V. N. Nemykin and R. G. Hadt, Influence of Hartree−Fock Exchange on the Calculated Mössbauer Isomer Shifts and Quadrupole Splittings in Ferrocene Derivatives Using Density Functional Theory, Inorg. Chem., 2006, 45, 8297–8307 CrossRef CAS PubMed.
- A. D. Bochevarov, R. A. Friesner and S. J. Lippard, Prediction of 57Fe Mössbauer Parameters by Density Functional Theory: A Benchmark Study, J. Chem. Theory Comput., 2010, 6, 3735–3749 CrossRef CAS PubMed.
- G. M. Sandala, K. H. Hopmann, A. Ghosh and L. Noodleman, Calibration of DFT Functionals for the Prediction of 57Fe Mössbauer Spectral Parameters in Iron–Nitrosyl and Iron–Sulfur Complexes: Accurate Geometries Prove Essential, J. Chem. Theory Comput., 2011, 7, 3232–3247 CrossRef CAS PubMed.
- J. Gubler, A. R. Finkelmann and M. Reiher, Theoretical 57Fe Mössbauer Spectroscopy for Structure Elucidation of [Fe] Hydrogenase Active Site Intermediates, Inorg. Chem., 2013, 52, 14205–14215 CrossRef CAS PubMed.
- M. Pápai and G. Vankó, On Predicting Mössbauer Parameters of Iron-Containing Molecules with Density-Functional Theory, J. Chem. Theory Comput., 2013, 9, 5004–5020 CrossRef PubMed.
- S. F. McWilliams, E. Brennan-Wydra, K. C. MacLeod and P. L. Holland, Density Functional Calculations for Prediction of 57Fe Mössbauer Isomer Shifts and Quadrupole Splittings in β-Diketiminate Complexes, ACS Omega, 2017, 2, 2594–2606 CrossRef CAS PubMed.
- M. Malischewski, K. Seppelt, J. Sutter, D. Munz and K. Meyer, A Ferrocene-Based Dicationic Iron(IV) Carbonyl Complex, Angew. Chem., Int. Ed., 2018, 57, 14597–14601 CrossRef CAS PubMed.
- C. Gallenkamp, U. I. Kramm, J. Proppe and V. Krewald, Calibration of computational Mössbauer spectroscopy to unravel active sites in FeNC catalysts for the oxygen reduction reaction, Int. J. Quantum Chem., 2021, 121, e26394 CrossRef CAS.
- V. N. Nemykin, D. E. Nevonen, L. S. Ferch, M. Shepit, D. E. Herbert and J. van Lierop, Accurate Prediction of Mössbauer Hyperfine Parameters in Bis-Axially Coordinated Iron(II) Phthalocyanines Using Density Functional Theory Calculations: A Story of a Single Orbital Revealed by Natural Bond Orbital Analysis, Inorg. Chem., 2021, 60, 3690–3706 CrossRef CAS PubMed.
- W. Kutzelnigg and W. Liu, Quasirelativistic theory equivalent to fully relativistic theory, J. Chem. Phys., 2005, 123, 241102 CrossRef PubMed.
- W. Liu and D. Peng, Exact two-component Hamiltonians revisited, J. Chem. Phys., 2009, 131, 031104 CrossRef PubMed.
- T. Saue, Relativistic Hamiltonians for Chemistry: A Primer, ChemPhysChem, 2011, 12, 3077–3094 CrossRef CAS PubMed.
- D. Peng and M. Reiher, Exact decoupling of the relativistic Fock operator, Theor. Chem. Acc., 2012, 131, 1081 Search PubMed.
- D. Andrae, Finite nuclear charge density distributions in electronic structure calculations for atoms and molecules, Phys. Rep., 2000, 336, 413–525 CrossRef CAS.
- E. D. Hedegård, S. Knecht, U. Ryde, J. Kongsted and T. Saue, Theoretical 57Fe Mössbauer spectroscopy: isomer shifts of [Fe]-hydrogenase intermediates, Phys. Chem. Chem. Phys., 2014, 16, 4853–4863 RSC.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic regular two-component Hamiltonians, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- A. Wolf, M. Reiher and B. A. Hess, The generalized Douglas–Kroll transformation, J. Chem. Phys., 2002, 117, 9215–9226 CrossRef CAS.
- C. van Wüllen, Relation between different variants of the generalized Douglas–Kroll transformation through sixth order, J. Chem. Phys., 2004, 120, 7307–7313 CrossRef PubMed.
- M. Reiher and A. Wolf, Exact decoupling of the Dirac Hamiltonian. II. The generalized Douglas–Kroll–Hess transformation up to arbitrary order, J. Chem. Phys., 2004, 121, 10945–10956 CrossRef CAS PubMed.
- M. Reiher, Relativistic Douglas–Kroll–Hess theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 139–149 CAS.
- M. Reiher, Douglas–Kroll–Hess Theory: a relativistic electrons-only theory for chemistry, Theor. Chem. Acc., 2006, 116, 241–252 Search PubMed.
- T. Nakajima and K. Hirao, The higher-order Douglas–Kroll transformation, J. Chem. Phys., 2000, 113, 7786–7789 CrossRef CAS.
- M. Douglas and N. M. Kroll, Quantum electrodynamical corrections to the fine structure of helium, Ann. Phys., 1974, 82, 89–155 CAS.
- H. Zhu, C. Gao, M. Filatov and W. Zou, Mössbauer isomer shifts and effective contact densities obtained by the exact two-component (X2C) relativistic method and its local variants, Phys. Chem. Chem. Phys., 2020, 22, 26776–26786 RSC.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- W. Liu, Big picture of relativistic molecular quantum mechanics, Natl. Sci. Rev., 2015, 3, 204–221 CrossRef.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- P. Pollak and F. Weigend, Segmented Contracted Error-Consistent Basis Sets of Double- and Triple-ζ Valence Quality for One- and Two-Component Relativistic All-Electron Calculations, J. Chem. Theory Comput., 2017, 13, 3696–3705 CrossRef CAS PubMed.
- B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, An improved chain of spheres for exchange algorithm, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS PubMed.
- F. Neese, A. Wolf, T. Fleig, M. Reiher and B. A. Hess, Calculation of electric-field gradients based on higher-order generalized Douglas–Kroll transformations, J. Chem. Phys., 2005, 122, 204107 CrossRef PubMed.
- R. Mastalerz, G. Barone, R. Lindh and M. Reiher, Analytic high-order Douglas-Kroll-Hess electric field gradients, J. Chem. Phys., 2007, 127, 074105 CrossRef PubMed.
- G. Barone, R. Mastalerz, M. Reiher and R. Lindh, Nuclear Quadrupole Moment of 119Sn, J. Phys. Chem. A, 2008, 112, 1666–1672 CrossRef CAS PubMed.
- J. Autschbach, D. Peng and M. Reiher, Two-Component Relativistic Calculations of Electric-Field Gradients Using Exact Decoupling Methods: Spin–orbit and Picture-Change Effects, J. Chem. Theory Comput., 2012, 8, 4239–4248 CrossRef CAS PubMed.
- Y. J. Franzke, R. Treß, T. M. Pazdera and F. Weigend, Error-consistent segmented contracted all-electron relativistic basis sets of double- and triple-zeta quality for NMR shielding constants, Phys. Chem. Chem. Phys., 2019, 21, 16658–16664 RSC.
- E. D. Hedegård, J. Kongsted and S. P. A. Sauer, Optimized Basis Sets for Calculation of Electron Paramagnetic Resonance Hyperfine Coupling Constants: aug-cc-pVTZ-J for the 3d Atoms Sc–Zn, J. Chem. Theory Comput., 2011, 7, 4077–4087 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. A. R. Wolf, Markus and Hess, Bernd Artur, The generalized Douglas–Kroll transformation, J. Chem. Phys., 2002, 117, 9215–9226 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, New Relativistic ANO Basis Sets for Transition Metal Atoms, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS PubMed.
- R. J. Gómez-Piñeiro, D. A. Pantazis and M. Orio, Comparison of Density Functional and Correlated Wave Function Methods for the Prediction of Cu(II) Hyperfine Coupling Constants, ChemPhysChem, 2020, 21, 2667–2679 CrossRef PubMed.
- J. P. Perdew and K. Schmidt, Jacob's ladder of density functional approximations for the exchange–correlation energy, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
- P. A. M. Dirac, Note on Exchange Phenomena in the Thomas Atom, Math. Proc. Cambridge Philos. Soc., 1930, 26, 376–385 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: the PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable adiabatic connection models free from adjustable parameters, Chem. Phys. Lett., 1997, 274, 242–250 CrossRef CAS.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, Accurate Calculation of the Heats of Formation for Large Main Group Compounds with Spin-Component Scaled MP2 Methods, J. Phys. Chem. A, 2005, 109, 3067–3077 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, A long-range correction scheme for generalized-gradient-approximation exchange functionals, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- S. Grimme, Semiempirical hybrid density functional with perturbative second-order correlation, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- J. V. Mallow, A. J. Freeman and J. P. Desclaux, Relativistic electron densities and isomer shifts in transition-metal ions, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 1884–1892 CrossRef CAS.
- L. Visscher and K. G. Dyall, Dirac-Fock atomic electronic structure calculations using different nuclear charge distributions, Atom. Data Nucl. Data Tables, 1997, 67, 207–224 CrossRef CAS.
- R. Kurian and M. Filatov, DFT Approach to the Calculation of Mössbauer Isomer Shifts, J. Chem. Theory Comput., 2008, 4, 278–285 CrossRef CAS PubMed.
- G. Comas-Vilà and P. Salvador, Accurate 57Fe Mössbauer Parameters from General Gaussian Basis Sets, J. Chem. Theory Comput., 2021, 17, 7724–7731 CrossRef PubMed.
- R. van Leeuwen and E. J. Baerends, Exchange-correlation potential with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 49, 2421–2431 CrossRef CAS PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic total energy using regular approximations, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, The zero-order regular approximation for relativistic effects: The effect of spin–orbit coupling in closed shell molecules, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- S. Dohm, A. Hansen, M. Steinmetz, S. Grimme and M. P. Checinski, Comprehensive Thermochemical Benchmark Set of Realistic Closed-Shell Metal Organic Reactions, J. Chem. Theory Comput., 2018, 14, 2596–2608 CrossRef CAS PubMed.
- M. A. Iron and T. Janes, Evaluating Transition Metal Barrier Heights with the Latest Density Functional Theory Exchange–Correlation Functionals: The MOBH35 Benchmark Database, J. Phys. Chem. A, 2019, 123, 3761–3781 CrossRef CAS PubMed.
- J. M. L. Martin and G. Santra, Empirical Double-Hybrid Density Functional Theory: A ‘Third Way’ in Between WFT and DFT, Isr. J. Chem., 2020, 60, 787–804 CrossRef CAS.
- M. Drosou, C. A. Mitsopoulou, M. Orio and D. A. Pantazis, EPR Spectroscopy of Cu(II) Complexes: Prediction of g-Tensors Using Double-Hybrid Density Functional Theory, Magnetochemistry, 2022, 8, 36 CrossRef CAS.
- M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Density functional theory is straying from the path toward the exact functional, Science, 2017, 355, 49–52 CrossRef CAS PubMed.
- J. Bland, A Mössbauer Spectroscopy and Magnetometry Study of Magnetic Multilayers and Oxides, PhD, University of Liverpool, 2002 Search PubMed.
- K. H. Hopmann, A. Ghosh and L. Noodleman, Density Functional Theory Calculations on Mössbauer Parameters of Nonheme Iron Nitrosyls, Inorg. Chem., 2009, 48, 9155–9165 CrossRef CAS PubMed.
- W.-G. Han and L. Noodleman, Structural model studies for the high-valent intermediate Q of methane monooxygenase from broken-symmetry density functional calculations, Inorg. Chim. Acta, 2008, 361, 973–986 CrossRef CAS PubMed.
- T. Liu, T. Lovell, W.-G. Han and L. Noodleman, DFT Calculations of Isomer Shifts and Quadrupole Splitting Parameters in Synthetic Iron−Oxo Complexes:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Applications to Methane Monooxygenase and Ribonucleotide Reductase, Inorg. Chem., 2003, 42, 5244–5251 CrossRef CAS PubMed.
Applications to Methane Monooxygenase and Ribonucleotide Reductase, Inorg. Chem., 2003, 42, 5244–5251 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00431k |
| This journal is © the Owner Societies 2024 |