Fragmentation dynamics of CH3Clq+ (q = 2,3): theory and experiment
Pragya
Bhatt
*a,
K. R.
Maiyelvaganan
 b,
M.
Prakash
b,
M.
Prakash
 b,
J.
Palaudoux
c,
C. P.
Safvan
b,
J.
Palaudoux
c,
C. P.
Safvan
 a and
M.
Hochlaf
a and
M.
Hochlaf
 *d
*d
aInter University Accelerator Centre, Aruna Asaf Ali Marg, New Delhi – 110067, India. E-mail: pbpragya@gmail.com
bDepartment of Chemistry, Faculty of Engineering and Technology, SRM Institute of Science and Technology, SRM Nagar, Kattankulathur-603203, Chennai, TN, India
cSorbonne Université, CNRS, Laboratoire de Chimie Physique – Matière et Rayonnement, LCP-MR, F-75005, Paris, France
dUniversité Gustave Eiffel, COSYS/IMSE, 5 Bd Descartes 77454, Champs sur Marne, France. E-mail: majdi.hochlaf@univ-eiffel.fr
First published on 12th October 2022
Abstract
A combined theoretical and experimental study of the dissociation of the di- and trication of the CH3Cl molecule has been performed. Experimentally, these multi-charged ions were produced after interactions of a CH3Cl effusive jet with a mono-energetic beam of H+ or Ar9+ projectile ions. Theoretically, we mapped the multi-dimensional potential energy surfaces of CH3Cl2+, H2CClH2+ and CH3Cl3+ species in their electronic ground and electronically excited states using post-Hartree–Fock configuration interaction methods. In addition to the obvious bond-breaking ionic fragments (i.e. H+ + CH2Cl+, H+ + CH2Cl2+ and CH3+ + Cl+), the formation of H2+ (+CHCl+ or CHCl2+), H3+ (+CCl+) and HCl+ (+CH2+) was observed upon bond rearrangement after ion impact of CH3Cl. The interaction strength of the incident projectiles is found to affect the relative yields on the observed dissociation channels, however, it has no effect on the kinetic energy releases of the fragmentation pathways. For the observed dissociation channels, plausible formation mechanisms were proposed. These reaction pathways take place on the ground and/or electronic excited potential energy surfaces of the doubly and triply charged CH3Cl ions, where spin–orbit and vibronic couplings are in action. Moreover, this work suggests that the mechanisms undertaken may depend on the multiply charged ion preparation by valence or inner-shell single photon photoionization, fast ion beam impact or ultrafast intense laser ionization.
I Introduction
The formation, dissociation and isomerization of hydrocarbons have been a subject of numerous studies for many decades.1–3 Of these, the ionization and dissociation of chloromethane (CH3Cl) has attracted wide attention as it is one of the most abundant chlorine containing molecules in Earth's atmosphere. Recently, CH3Cl became the first organohalogen to be detected in the interstellar space.4A number of studies have been performed on the chloromethane molecule under intense laser fields,5–9 both valence and core photoionization,2,10–17 ion impact,3,18 electron impact19,20 and double-charge-transfer spectroscopy.21 For instance, Ma et al.6 treated in 2017 the Coulomb explosion and fast H-atom rearrangement after intense laser field ionization of CH3Cl. They have determined the kinetic energy releases (KERs) and the yields of two body dissociation channels of di- and tri-cations of CH3Cl. Back in 1981, Monce et al.18 measured the dissociation energies for the fragments of CH3Cl2+ under 1 MeV ion impact. Siegmann et al.3 reported the fragmentation patterns of CH3Cl in collisions with swift ions and have measured the corresponding KERs. Aitken et al.19 have studied the electron impact ionization of oriented CH3Cl molecules. Rejoub et al.20 used electrons from threshold up to 1000 eV to measure the partial ionization yields of CH3Cl using coincidence measurements. These works allowed identifying H+, H2+, H3+, C+, CH2+, CH3+, and Cl+ fragments and their respective kinetic energy spectra were recorded. Nevertheless, the relative yields of the different dissociation channels were not determined using projectile ion impact.
Concerning photoionization studies and the subsequent fragmentation of the doubly charged CH3Cl species, several works were carried. Back in 1990, Ruhl et al.2 have used single photon ionization of the CH3X (X = Cl, OH, SH, NH2, CN, CHO) molecules to study the dissociation of their doubly charged ions using the electron-ion-ion coincidence technique. They have determined the KERs for different fragmentation channels of CH3Cl dication and their relative intensities. They were the first in reporting the production of H3+ from methyl compounds and some evidences for rearrangement processes via ylide dications prior to charge separation. In 1994, Thissen et al.16 have used photoexcitation near Cl (2p) to measure the total photo-electron yield using charge transfer mass spectrometry. Later on, Miron et al.8 have used electron-ion coincidence technique in combination with high resolution spectroscopy to disentangle the complex competing decay processes leading either to HCl+ or to Cl+ after Cl (2p) CH3Cl excitation. This work was complimented later by Céolin et al.15 who have measured the partial ion yields around the Cl (2p) and C (1s) core level thresholds in CH3Cl. Interestingly, they have reported that the vibrational population of the intermediate state does not affect the H-atom isomerization processes. They have further showed that the formation of H2+ and H3+ is suppressed above C (1s) threshold; however, their formation increases above the Cl (2p) threshold. More recently, Kokkonen et al.10,11 have recorded the photoions in coincidence with energy selected electrons to study the resonant Auger decay after removal of an electron from Cl (2p). They have also performed qualitative theoretical simulations to study the formation of HCl+. Using the photo-electron-photo-electron coincidence technique Hult Roos et al.13 have measured the vertical double ionization energies for methyl halides. For CH3Cl, a vertical double ionization of 31.5 eV was determined.
Theoretically, Duflot et al.22,23 have done a detailed study on the CH3Cl2+ isomers and of its fragmentation channels, where they mapped the ground potential energy surface. Indeed, they characterized the stable isomers and the transition states leading to the major products at the Complete Active Space Self Consistent Field level of theory. Mainly, two isomers are found: a C3v form (denoted as CH3Cl2+) and a planar isomer (denoted as H2CClH2+) (Fig. 1). They also determined the KERs associated with the fragmentations of CH3Cl2+. Moreover, Walt et al.5 have done ab initio calculations to obtain the KERs for CH3X2+ (X = F, Cl, Br, I) decomposition into CH3+ + X+. Recently, Palaudoux and Hochlaf24 have performed multi configuration interaction ab initio calculations to study the formation of H3+ after dissociation of CH3Cl2+. They have suggested a new multi-step mechanism for H3+ formation where the three H-atoms in CH3Cl approach each other along with singlet-triplet spin–orbit and internal conversions. This mechanism is in contrast to the H-migration and H2 roaming mechanisms prior to H3+ formation in alcohol molecules as suggested by Ekanayake et al.25 Prior to that Grant et al.21 determined the double ionization energy of CH3Cl using the second order algebraic diagrammatic construction Green's function method and Roithova et al.26 investigated the potential energy surface of the reaction between CHCl2+ and H2 using the Coupled Cluster approach. Nevertheless, none of previous theoretical works investigated the electronic excited states of CH3Cl2+ and their possible role on the further evolution of this ion till dissociation.
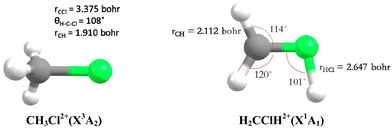 | ||
| Fig. 1 C 3v (left) and planar (right) stable forms of chloromethane doubly charged ions as computed by Duflot et al.22,23 and confirmed presently at the RCCSD(T)/aug-cc-pVTZ level. | ||
Despite of the large number of studies on the CH3Cl2+ unimolecular decompositions, a detailed analysis of the fragmentation channels of CH3Cl2+ considering the involved electronic states have not been performed so far. In particular, nothing is known on the possible role of the electronic excited states of CH3Cl2+ since these previous works were treating only the corresponding ground state. The further evolution of the CH3Cl3+ trication is also missing. In the present work, we have performed a systematic study on the fragmentation dynamics of CH3Clq+ (q = 2,3) formed after energetic ion impact of CH3Cl, where both ionic species resulting from the decomposition of CH3Cl2+ or CH3Cl3+ were detected in coincidence. Moreover, we mapped the potential energy surfaces of the electronic states of these ions along suitable coordinates using post Hartree–Fock configuration interaction approaches. Using the previous and present experimental data, our computational results are used to propose the unimolecular reaction pathways undertaken by the CH3Cl2+ dication leading to the CH3+, Cl+, H+, CH2Cl+, H3+, CCl+, CH2+ and HCl+ products and by the CH3Cl3+ trication forming the H+ + CH2Cl2+ and the H2+ + CHCl2+ ion pairs.
II. Methodologies
a. Experiment
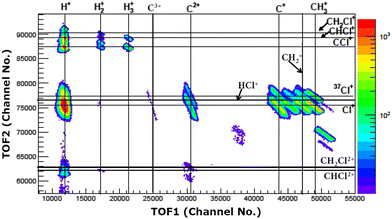
The experiments were carried out at the low-energy ion-beam facility at Inter-University Accelerator Centre, New Delhi, India. The details of the experimental setup were published in ref. 27. Briefly, a mono-energetic beam of the projectile ions interacts with an effusive jet of a target gas kept at room temperature. The projectile ions (0.25 MeV H+, 0.45 MeV Ar9+, 2.25 MeV Ar9+) are generated using an electron-cyclotron-resonance ion source. The target gas used was CH3Cl (purity > 99.5%, Sigma Aldrich). The experiments were performed in a high vacuum chamber to maintain single collision conditions. The pressures of the experimental chamber with and without gas load were 6 × 10−7 Torr and 8 × 10−8 Torr, respectively. The recoil ions and the ejected electrons produced in these collision experiments are guided using a homogeneous electric field (4.7 kV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m−1) toward their respective detectors. The mass resolution (Δm/m) of our TOF mass spectrometer is found to be about 0.0057. The recoil ions after passing through a time-of-flight spectrometer were detected using dual-micro-channel plates equipped with a delay-line position sensitive detector; the ejected electrons were detected using a channeltron. Then, the multi-ion coincidence technique was used to detect the recoil ions with reference to an ejected electron. The typical data acquisition time ranges from 22 hours to 48 hours in order to collect sufficient statistics. A typical TOF spectrum generated in collisions of 0.45 MeV Ar9+ with CH3Cl is shown in Fig. 2 and a double ion coincidence spectrum is presented in Fig. 3.
m−1) toward their respective detectors. The mass resolution (Δm/m) of our TOF mass spectrometer is found to be about 0.0057. The recoil ions after passing through a time-of-flight spectrometer were detected using dual-micro-channel plates equipped with a delay-line position sensitive detector; the ejected electrons were detected using a channeltron. Then, the multi-ion coincidence technique was used to detect the recoil ions with reference to an ejected electron. The typical data acquisition time ranges from 22 hours to 48 hours in order to collect sufficient statistics. A typical TOF spectrum generated in collisions of 0.45 MeV Ar9+ with CH3Cl is shown in Fig. 2 and a double ion coincidence spectrum is presented in Fig. 3.
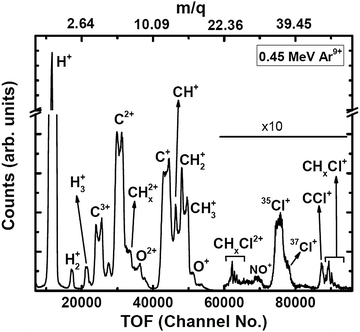 | ||
| Fig. 2 TOF spectrum (raw) of ions generated in 0.45 MeV Ar9+ collisions with CH3Cl. Oxygenated species are originating from NO gas used in a trial run just before starting the experiments on CH3Cl. | ||
The detection efficiency is almost constant for all ions as the impact energy on the microchannel plate is 2.6 keV for singly charged ions, and even larger for higher charge states. Thus corrections for efficiency for the light ions used in this experiment are not envisaged.
After measuring the time and position information of the recoil ions in coincidence with an electron, the momenta and the kinetic energies of the recoil ions are obtained. The KER for a given dissociation channel is determined by summing the kinetic energies of the corresponding recoil (fragment) ions.
b. Theoretical computations
In order to deduce the energetics of the CH3Clq+ (q = 2,3) molecular systems, we performed geometry optimizations of CH3Cl, its di- and trications and the charged fragments observed presently. These optimizations were done without constraints (in C1 point group) and followed by frequency computations to attest the minimal nature of the structures (all > 0 frequencies). These computations were done using the (partially spin restricted) coupled-cluster singles and doubles plus perturbative triples (R)CCSD(T) method28–31 in conjunction with the aug-cc-pVXZ (X = T,D) basis sets32–34 of Dunning and co-workers. For the dissociation energies, the (R)CCSD(T)/aug-cc-pVTZ and the (R)CCSD(T)/aug-cc-pVQZ methods lead to close results i.e. ∼0.1 eV energetics differences. Both set of data are accurate enough compared to the present measurements.We also performed one dimensional cuts of the 10D potential energy surfaces (PESs) of CH3Cl2+ and of CH3Cl3+ by varying one internal coordinate, allowing giving an insight into the evolution of these electronic states not far from the Franck–Condon region accessed after either double or triple ionization of CH3Cl. We thus computed the one dimensional evolutions of the lowest electronic states of CH3Cl2+ of singlet and triplet spin multiplicities and the isomerization processes between CH3Cl2+ and H2CClH2+. We also calculated the lowest doublet and quartet potentials of CH3Cl3+ by lengthening one CH or the CCl distances. These computations were carried out at the Complete Active Space Self Consistent field (CASSCF)35,36 followed by the internally contracted Multi Reference Configuration Interaction (MRCI)37–39 methods as implemented in the MOLPRO program suite.40 For C and Cl(H) atoms, the spdf (spd) cc-pV5Z subset were used. The CASSCF active space comprised all valence orbitals and all electronic states having the same spin multiplicity were averaged together. At the MRCI level, all configurations with coefficients larger than 0.005 in the CI expansion of the CASSCF wave functions were taken into account as a reference resulting in more than 6 × 108 uncontracted configuration state functions (CSFs) per Cs point group symmetry to be treated. All valence electrons were correlated. Moreover, we used the CASSCF wavefunctions to evaluate the spin–orbit coupling matrix elements in Cartesian coordinates, where these wavefunctions were used as the multi-electron basis for the two-step spin–orbit coupling calculations41,42 at the level of Breit–Pauli Hamiltonian.43
For the spin–orbit free energies, the accuracy of the relative energy position of the PESs and the dissociation limits is expected to be better than ∼0.1 eV. Nevertheless, the inclusion of spin–orbit splittings should lead to ∼0.1–0.2 eV levy for molecular species of interest and for > 0.3 eV for heavy atoms such as Cl and its ions. Obviously, this affects the relative energy positions of the PESs and the corresponding dissociation channels. But one should be aware that the error bars of the experimental determinations of the ionization energies, appearance energies and the KERs of the products issued from the CH3Clq+ (q = 2,3) unimolecular decomposition reactions are as large as ±0.5–1 eV i.e. distinctly larger than the accuracy of the present computations. In the following, we will therefore rely on the spin–orbit free energies, except if explicitly specified.
III. Experimental results
We have studied the interaction of the energetic projectile ions (0.25 MeV H+, 0.45 MeV Ar9+, 2.25 MeV Ar9+) with a CH3Cl molecule. The following channels are observed for two body dissociation of the CH3Clq+ (q = 2,3) molecular ions formed in these collisions:| CH3Cl2+ → CH3+ + Cl+ | (1) |
| CH3Cl2+ → H+ + CH2Cl+ | (2) |
| CH3Cl3+ → H+ + CH2Cl2+ | (3) |
| CH3Cl2+ → H2+ + CHCl+ | (4) |
| CH3Cl3+ → H2+ + CHCl2+ | (5) |
| CH3Cl2+ → H3+ + CCl+ | (6) |
| CH3Cl2+ → CH2+ + HCl+ | (7) |
a. Kinetic energy releases
We have measured the KERs for the dissociation channels of di- and tri-cations of CH3Cl (see, eqn (1)–(7)). The KER distributions (KERD) for different dissociation channels obtained under the impact of all three projectile ions used in present experiments are similar. For a typical example, the KERDs for the dissociation channels produced under 0.45 MeV Ar9+ impact are presented in Fig. 4 and for the channels involving rearrangement of atoms are given in Fig. 5. These figures show that whatever the dissociation channel the KERs present a unique peak. This peak has an asymmetric shape with a sharp increase for low energy KERs and then more or less a long tail for high energy KERs. The latter are probably due to the steepness of the associated potential energy curves at small inter-nuclear distances (leading to a large spread in the KER). A detailed comparison of our experimental KERs with those earlier reported in the literature is presented in the discussion section.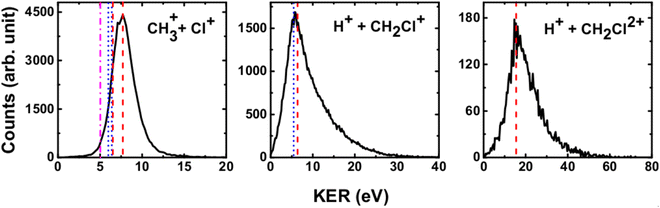 | ||
| Fig. 4 Present experimental KER distributions (black curve) for the dissociation channels of CH3Clq+ (q = 2,3) under 0.45 MeV Ar9+ along with our theoretical calculations (red dashed lines) and those reported in the literature: Duflot et al.23 (blue dashed line), Walt et al.5 (dashed dotted magenta line). See text for more details. | ||
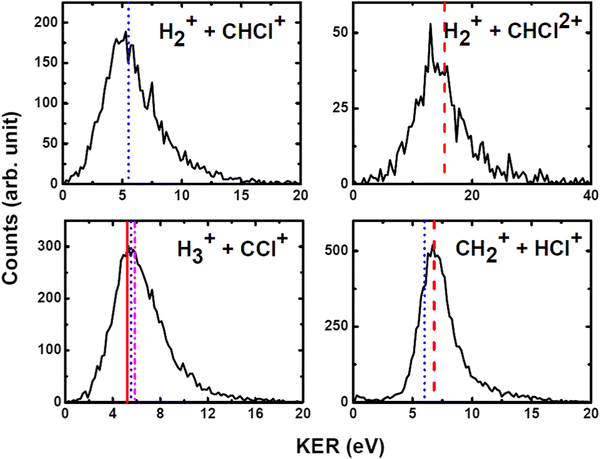 | ||
| Fig. 5 Measured KER distributions (black curve) for the bond rearrangement channels observed in the dissociation of CH3Clq+ (q = 2,3) under 0.45 MeV Ar9+ along with our theoretical calculations (red dashed line). The vertical lines correspond to the theoretical calculations for KERs reported in the literature: Palaudoux and Hochlaf24 (red solid line), Duflot et al.23 (blue dashed line), Walt et al.5 (dashed dotted magenta line). See text for more details. | ||
b. Relative yields of dissociation channels
We have measured the relative yields of the dissociation channels of CH3Clq+ (q = 2,3) by integrating the area under each coincidence island shown in Fig. 3 separately and dividing it by the total counts of all the two body dissociation channels observed in the present experiments (cf.Table 1). Coincidence islands for different two-body dissociation channels (Fig. 3) are extracted after correcting for false coincidences using the conservation of momentum in the centre of mass frame of the parent molecular ion. The statistical uncertainties in measuring these yields are ∼3% and ∼5% for the dissociation channels given in eqn (1)–(3) and for bond rearrangement channels (eqn (4)–(7)), respectively. These errors correspond to the standard deviations.| Dissociation channel | Experimental yield (%) | |||||
|---|---|---|---|---|---|---|
| Present | Literature | |||||
| H+/E = 0.25 MeV/v = 3.16 a.u./q/v = 0.32 | Ar9+/E = 2.25 MeV/v = 1.50 a.u./q/v = 6.0 | Ar9+/E = 0.45 MeV/v = 0.67 a.u./q/v = 13.42 | Intense laser6 | Photo-ionization at hν = 40.8 eV2 | ||
| 800 nm | 400 nm | |||||
| H+ + CH2Cl+ | 23.6 | 27.3 | 44.2 | 27.2 | 6.1 | 13 |
| H2+ + CHCl+ | 2.0 | 1.7 | 2.8 | 4.6 | 1.3 | 6 |
| H3+ + CCl+ | 9.1 | 7.1 | 4.3 | 10.8 | 1.3 | 9 |
| CH2+ + HCl+ | 6.2 | 4.4 | 5.5 | 6.3 | 6.6 | 2 |
| CH3+ + Cl+ | 59.1 | 59.5 | 43.1 | 51.1 | 84.6 | 70 |
| H+ + CH2Cl2+ | 0 | 100.0 | 86.0 | 86.1 | 86.3 | 0 |
| H2+ + CHCl2+ | 0 | 0 | 14.0 | 13.9 | 13.7 | 0 |
Table 1 shows that the most dominant dissociation channel at 0.25 MeV H+ and 2.25 MeV Ar9+ impact corresponds to the CCl bond breaking upon formation of CH3Cl2+ (eqn (1)); the CH bond breaking of this dication (eqn (2)) is also observed abundantly. Interestingly, the relative yield between both channels depends on the interaction strengths (q/v) (Table 1). Indeed, the relative yields for the dominant dissociation channels (CH3+ + Cl+ and H+ + CH2Cl+) are comparable for q/v = 0.32, 6.0, whereas, the yields for these two dissociation channels are completely different at the highest interaction strength (q/v = 13.42) used here as compared to those observed at lower q/v values. Further, for 0.45 MeV Ar9+ impact, the relative yields for the channels H+ + CH2Cl+ and CH3+ + Cl+ are almost the same suggesting that the probabilities of breaking of the C–H and the C–Cl bonds are almost equal. Moreover, Table 1 shows that the other dissociation channels (eqn (3)–(7)) present relative yields of less than 10%, which also strongly depend on the experimental conditions. For instance, the H+ + CH2Cl2+ (eqn (3)) ion pair is only observed while using Ar9+ as projectile. The H2+ + CHCl2+ trication dissociation channel is not observed with H+ projectile and with low Ar9+ interaction (q/v = 6.0). Obviously this is due to different CH3Clq+ (q = 2,3) formation/unimolecular decomposition mechanisms in each case.
The relative yields reported earlier in the literature under intense laser fields and photo-ionization of CH3Cl have also been compiled in Table 1. It can be seen that the trend of the yields of the dissociation channels of CH3Cl2+ is similar in case of 800 nm laser multiphoton ionization and our results at 0.25 MeV H+ and 2.25 MeV Ar9+. However, the relative yields under 400 nm laser multiphoton ionization, 40.8 eV photons ionization and our experiments are entirely different. Again, these results indicate that the formation of different dissociation channels depends on the mechanisms of excitation of the parent molecular ion and in turn on the electronic states populated under the given experimental conditions. For example, in case of intense laser fields experiments, Ma et al.6 have observed that the sequential ionization is the dominant source of excitation in CH3Cl.
For ion impact where the velocity of the projectile ions is comparable to that of the orbital velocity of the electrons, the electron capture is the dominant source of excitation; however, if the velocity of the incident projectile is high enough the ionization becomes the dominant process. In classical limit (v = 1 a.u. = 2.18 × 108 cm s−1), it has been observed that the electron capture takes place dominantly; however, ionization is most prominent process for higher velocities of the projectile (v > 1 a.u.). In the present experiments, both electron capture and ionization phenomena are relevant for the formation of di- and trications of CH3Cl under our energies of impact. Considering these details, we may suggest that the similar trend of relative yields at 0.25 MeV H+ and at 2.25 MeV Ar9+ is due to the ionization being the dominant process. However, in case of 0.45 MeV Ar9+, the process of electron capture from the continuum of CH3Cl may be dominantly in action.
Further, to compare our results with those of Ma et al.,6 we have neglected a trication channel (CH3+ + Cl2+) from Ma et al., which is not present in our experiments. It is interesting to note that the yields of the two observed channels are similar in case of trication dissociation under ion impact and under two different intense laser fields as reported by Ma et al.6 We suggest this is due to the increased Coulomb repulsion in case of CH3Cl trication which may result in prompt dissociation of the trication. Our theoretical calculations also suggest that the potential energy curves of the trication are mostly repulsive (see below).
It is to be noted here that the CH2+ + HCl+ channel is slightly merged with the CH3+ + Cl+ channel due to the mass resolution of our spectrometer. However, other dissociation channels reported in this work are well resolved. The overlapping part is neglected in measuring the relative yield for CH2+ + HCl+ channel. Therefore, the cross sections for this channel will be higher than the values reported in Table 1; the CH3+ + Cl+ yield will reduce accordingly. It is not possible to determine exactly this quantity. Nevertheless, we have estimated crudely that the yields for the CH2+ + HCl+ channel may get increased by about 10% at the most, while the corresponding decrease in the yield of the CH3+ + Cl+ channel will be only 1%. Yields for the other channels would remain unchanged.
To explicitly observe the effect of the interaction strength on the bond rearrangement process, the relative yields of the dissociation channels involving bond rearrangement are separately reported in Table 2. It is observed, under all projectile ions used in the present experiments, that the yields for the formation of H3+ (eqn (6)) and HCl+ (eqn (7)) are higher compared to that of H2+ formation. Also, Table 2 shows that the yield for the H3+ formation channel reduces at highest q/v used in present experiments, whereas the yields for those involving H2+ or HCl+ formation increase. The role of electron capture and ionization processes in these dissociations channels will be an interesting study for our future experiments.
| Dissociation channel | Experimental yield (%) | |||||
|---|---|---|---|---|---|---|
| Present | Literature | |||||
| H+/E = 0.25 MeV/v = 3.16 a.u./q/v = 0.32 | Ar9+/E = 2.25 MeV/v = 1.50 a.u./q/v = 6.0 | Ar9+/E = 0.45 MeV/v = 0.67 a.u./q/v = 13.42 | Intense laser6 | Photoionization at hν = 40.8 eV2 | ||
| 800 nm | 400 nm | |||||
| H2+ + CHCl+ | 11.7 | 12.9 | 22.2 | 21.2 | 14.1 | 35.3 |
| H3+ + CCl+ | 52.5 | 53.8 | 34.2 | 49.8 | 14.1 | 52.9 |
| CH2+ + HCl+ | 35.7 | 33.3 | 43.6 | 29.0 | 71.7 | 11.8 |
Ma et al.6 have concluded for rearrangement of H-atoms, the height of the potential barriers is more important in determining the relative yields in comparison to the number of the potential barriers. In case of photoionization at 40.8 eV, Ruhl et al.2 have proposed that the dissociation of CH3Cl dications into the fragments in their ground states may occur statistically in respect of their initial energetic requirement.
IV. Theoretical results
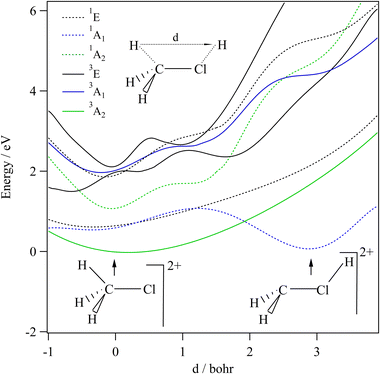
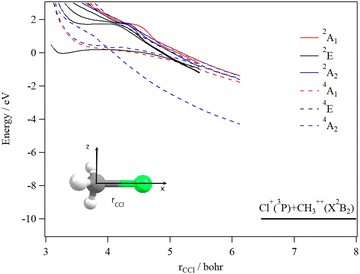
We started our investigations by computing the energetics of the CH3Cl2+ doubly charged ion. After geometry optimizations, minimal structures were located for CH3Cl2+(X3A2) and H2CClH2+(X1A′) on line with previous works. At the (R)CCSD(T)/aug-cc-pVQZ level, we deduce an adiabatic double ionization energy (ADIE) of CH3Cl of ∼30.7 eV. This value agrees with the recent experimental ADIE determination of 30.6 eV by Hult Roos et al.13 The H2CClH2+(X1A′) isomer is computes at ∼2.7 eV lower than CH3Cl2+(X3A2). This energy difference is larger than that found by Duflot et al. (i.e. ∼1.8 eV).22,23 Our value should be viewed as more accurate. For the fragmentation channels, we compute the CH3+(X1A′) + Cl+(3P) dissociation limit at ∼26.1 eV, CH2+(X2A1) + HCl+(X2Π) at ∼26.9 eV and CH2Cl+(X1A1) + H+(1S) at ∼26.6 eV with respect to neutral CH3Cl(X1A1) minimal energy.We also investigated the intramolecular isomerization of CH3Cl2+ into H2CClH2+. Fig. 6 gives the one dimensional evolutions of the lowest singlet and triplet electronic states of CH3Cl2+ along the distance d, where we moved the H atom from the left to the right. For d close to 0 bohr, the CH3Cl2+ can be found and for d close to 3 bohr the H2CClH2+ isomer is formed. The curves on this figure do not correspond to the minimal isomerization energy paths but they connect the electronic states of the C3v isomer to the trans planar form. Fig. 6 shows that the electronic ground state of CH3Cl2+ is of X3A2 nature and its of X1A′ for H2CClH2+, corresponding to the lowest 1A1 singlet state of CH3Cl2+. Also, this figure reveals a high density of electronic states favoring the mixing of the wavefunctions of these electronic states by vibronic interactions (e.g. between 1E and 1A1) and spin–orbit conversions between the singlets and the triplets. For instance, the spin–orbit coupling between the lowest 3A2 and lowest 1A1 electronic states at their respective crossing (i.e. d ∼ 1.9 bohr) is calculated to be ∼290 cm−1.
The CH3Cl2+(1A′) → H2CCl2+ (1A′) isomerization process was already investigated by Duflot et al.22 while the reaction is taking place in the lowest singlet potential. Indeed, these authors identified a reaction coordinate as a combination of in-plane CClH bending mode and H migrating atom out of the plane of the molecule. At the CASSCF level, a transition state was located at ∼0.73 eV, which is in close agreement with the potential barrier we found along the 1A1 potential energy surface as depicted in Fig. 6. Nevertheless, Duflot et al.22 were not able to determine a reaction path and hence a transition state of the triplet reaction. This agrees with the present computations. For instance, Fig. 6 shows that the triplets have potential wells in the CH3Cl2+ configurations and not in the H2CClH2+ side. So no transition states can be found in the ground nor in the electronic excited potentials.
During the CH3Cl2+ → H2CClH2+ isomerization, the CH3Cl2+(X3A2) dication needs to be converted into the lowest singlet PES before reaching the H2CClH2+(X1A′) valley. The isomerization occurs along a coordinate, which involves the d distance and most likely a H2CCl out-of-plane coordinates (leading to planarity of this part of the molecule as in H2CClH2+). The reaction occurs along the triplet potential of CH3Cl2+ and then the H2CClH2+ isomer is formed after a spin–orbit conversion at the crossing between these triplet and singlet states i.e. for d distances of about 1.9 bohr. This is strongly favored since the corresponding spin–orbit integral is large (of ∼290 cm−1). Moreover, the H2CClH2+(X1A′) minimum may be reached from the electronic excited states of CH3Cl2+ (for internal energies > 0.7 eV). Multi step mechanisms are expected involving the vibronic and spin–orbit interactions between the electronic states of Fig. 6 mentioned above. For instance, large amplitude motions on the second 3E state of CH3Cl2+ should induce isomerization to form the corresponding state of H2CClH2+. After vibronic interaction between the first and second 3E states, the spin–orbit conversion of H2CClH2+ (13E) ions forms the H2CClH2+ (X1A′) ions.
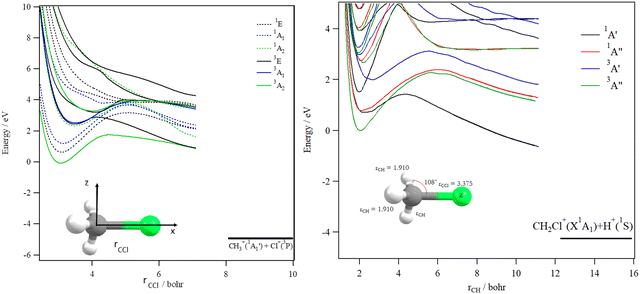
The decomposition of the CH3Cl2+ dication leads to the CH3+ + Cl+ ions, which are produced after cleavage of the CCl bond. For illustration, Fig. 7 shows the spd(f) cc-pV5Z MRCI one dimensional cuts of the electronic states of CH3Cl2+ along the CCl coordinate and where the remaining internal coordinates are kept fixed at their equilibrium values in CH3Cl(X1A1) [RCCl = 3.45 bohr, RCH = 2.084 bohr, HCH = 116°]. This figure presents also the one dimensional evolution of the CH3Cl2+ electronic states by stretching one CH bond whereas the other internal coordinates are kept fixed at their equilibrium values in CH3Cl2+ ground state.
Several deep potential wells are computed for CH3Cl2+ dication along the CH or the CCl distances (Fig. 7). For instance, this is the case for the X3A2, 1E, 1A1, 1A2, 3E and 3A1 electronic states, for which large potential barriers are separating the dissociation asymptotes from the corresponding potential wells. Thus, long-lived CH3Cl2+ dications may be found there. The other dicationic electronic states are repulsive in nature. The identification of these states corresponds to that already discussed by Grant et al.21 and by Hult Roos et al.13
Upon CH3Cl2+ → H2CClH2+ isomerization, the electronic states of the H2CClH2+ species can be populated. Fig. 8 shows the evolution of the H2CClH2+ electronic states along the central CCl bond, where the remaining internal coordinates are kept fixed at their equilibrium values in H2CClH2+ ground state. By lengthening the CCl bond, we form the CH2+ + HCl+ fragments. This figure reveals that the ground potential exhibits a potential well of >2 eV, which is separated from the lowest dissociation channel to which it correlates adiabatically by a potential barrier. We may locate long-lived H2CClH2+ ions in this potential well. Besides, the upper states are mostly repulsive in nature or presenting shallow potential wells.
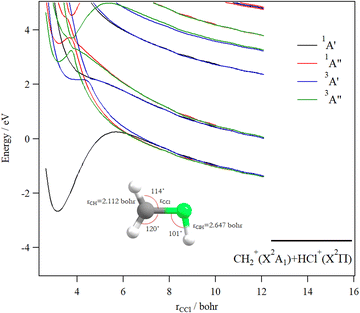
Fig. 9 shows the one dimensional cuts of the 10D-PESs of the lowest doublet and quartet states of the CH3Cl3+ trication. Although some shallow potential wells can be observed, no stable structures were found in the lowest doublet or quartet PESs. Indeed, these potentials are mainly repulsive and lead to the [H + CH2Cl]3+ and [Cl + CH3]3+ fragmentation channels. Moreover, this figure reveals a high density of electronic states that favors their mutual interactions, which should lead to the population of the lowest doublet PES by vibronic (between states having the same spin-multiplicity) and/or spin–orbit (between states of different spin multiplicities) interactions.
We evaluated the vertical triple ionization energy (VTIE) of CH3Cl as the difference between the energies of the tricationic lowest doublet state and that of the neutral CH3Cl species where both species were taken at the CH3Cl (X1A1) equilibrium geometry. At the (R)CCSD(T)/aug-cc-pVTZ level, VTIE is equal to 61.4 eV. At the same level of theory, we locate the H+ + CH2Cl2+ channel at 46.2 eV, the H2+ + CHCl2+ channel at 46.0 eV and the CH32+ + Cl+ channel at 51.2 eV, respectively. This results in KERs of ∼15.4 eV for both channels upon dissociating CH3Cl3+ on the lowest doublet PES.
V. Discussion
The current theoretical computations are of higher level than those carried out previously. For instance, the computations by Duflot et al.22,23 were done at the CASSCF and CIPSI levels of theory with relatively small basis sets for the description of the atoms. However, we performed extensive and much larger computations using the (R)CCSD(T) and MRCI techniques in conjunction with large basis sets. Also, Duflot et al.22,23 computations consisted on the determination of stationary points on the lowest singlet and triplet potential energy surfaces, whereas we mapped a large number of potential energy surfaces of diverse di- and tricationic electronic states and probed their evolutions till reaching the dissociations, in particular their crossings and avoided crossings. Therefore, our calculations are comparatively more accurate and more informative to derive the appearance energies and the related KERs and the subsequent dissociation mechanisms.In ion collisions with a molecule, we do not have control over the energy deposited into the molecular system and all energetically accessible states may be populated. This results a priori in more than one KER value. However, due to the experimental resolution of the present setup we record a broad distribution for the KERs (see Fig. 4 and 5). To compare our experimental data with the earlier reported experimental and theoretical results, the peak values of the KERDs of the present measurements are reported in Table 3. The errors involved in the measurement of KERs are ≤0.6 eV in case of dications and ≤2.3 eV in case of trications of CH3Cl. Table 3 lists also the theoretical results from the present calculations and those earlier reported in the literature. These theoretical data are shown in Fig. 4 and 5 as vertical lines.
| Dissociation channel | KER (eV) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Experiment | Theory | ||||||||
| This work | Ref. 2 | Ref. 5 | Ref. 6 | ||||||
| 0.25 MeV H+ | 0.45 MeV Ar9+ | 2.25 MeV Ar9+ | This work | Ref. 23 | Ref. 5 | ||||
| a Ref. 24. b See text for details. | |||||||||
| H+ + CH2Cl+ | 6.3 | 5.8 | 6.2 | 5.2 | 3.9 | 6.4 | 5.55 | ||
| H2+ + CHCl+ | 5.8 | 5.2 | 5.6 | 2.8 | 3.6 | — | 5.52 | ||
| H3+ + CCl+ | 5.7 | 5.6 | 5.8 | 3.4 | 4.27 | 3.6 | 5.2a | 5.55 | 5.87 |
| CH2+ + HCl+ | 6.9 | 6.7 | 6.8 | — | 4.6 | 6.7 | 6.01 | ||
| CH3+ + Cl+ | 7.9 | 7.7 | 7.7 | 5.4 | 4.3 | 4.6 | 6.4/7.7b | 5.96/6.38 | 5.0 |
| H+ + CH2Cl2+ | — | 16.5 | 18.5 | 8.3 | 15.4 | ||||
| H2+ + CHCl2+ | — | 14.1 | — | 7.7 | 15.4 | ||||
| CH32+ + Cl+ | — | — | — | 4.0 | 10.2 | ||||
The dissociation pathway followed by a molecular ion is sensitive to the initial ionization process. In ion-molecule interaction, the velocity of the incident projectile plays a key role in determining the dominant mode of electron removal from the target molecule.44 At 0.45 MeV Ar9+ (v = 0.67 a.u.), the dominant mode of electron removal from CH3Cl is expected to be electron capture; however, ionization is the dominant source of electron removal by the other two projectiles (2.25 MeV Ar9+ (v = 1.5 a.u.) and 0.25 MeV H+ (v = 3.16 a.u.)).
a. CH3Cl2+ → Cl+ + CH3+
Fig. 7 shows that the electronic ground state of CH3Cl2+ connects directly to the lowest dissociation limit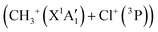 . Along this potential, a potential barrier of about 1.8 eV is calculated. The energy difference between the energy at the maximum and this dissociation limit is ∼6.4 eV, which corresponds to our computed KER for this channel. In a rather crude approximation of measurement of dissociation energies of the Cl+ and CH3+ fragment ions, Monce at al.18 have suggested a KER value of 6.6 eV for this dissociation channel under 1 MeV H+, He+ and O+ ion impact. This is in good agreement with our data. The KER of 5.4 ± 1.0 eV obtained after single photon ionizing CH3Cl by Ruhl et al.2 is also in reasonable agreement with our theoretical result. The theoretical KER values of Duflot et al.22 agree relatively well with our results (see Table 3). Nevertheless, these KERs are lower by ∼1 eV than the present experimental result for the KER distribution for this channel (of ∼7.7eV; Table 3). It is higher by ∼1 eV with that measured by Siegmann et al.3 in 200 keV He+ collisions with CH3Cl. The KER values of 4.3 and 4.6 eV measured under intense laser fields5,6 are comparatively off from our experimental and theoretical determinations.
. Along this potential, a potential barrier of about 1.8 eV is calculated. The energy difference between the energy at the maximum and this dissociation limit is ∼6.4 eV, which corresponds to our computed KER for this channel. In a rather crude approximation of measurement of dissociation energies of the Cl+ and CH3+ fragment ions, Monce at al.18 have suggested a KER value of 6.6 eV for this dissociation channel under 1 MeV H+, He+ and O+ ion impact. This is in good agreement with our data. The KER of 5.4 ± 1.0 eV obtained after single photon ionizing CH3Cl by Ruhl et al.2 is also in reasonable agreement with our theoretical result. The theoretical KER values of Duflot et al.22 agree relatively well with our results (see Table 3). Nevertheless, these KERs are lower by ∼1 eV than the present experimental result for the KER distribution for this channel (of ∼7.7eV; Table 3). It is higher by ∼1 eV with that measured by Siegmann et al.3 in 200 keV He+ collisions with CH3Cl. The KER values of 4.3 and 4.6 eV measured under intense laser fields5,6 are comparatively off from our experimental and theoretical determinations.
Dealing with the dissociation of the CH3Cl2+ electronic excited states, it may happen directly along the PESs of the corresponding electronic states and/or after vibronic couplings (occurring at the crossings and the avoid crossings of the electronic states having the same spin multiplicity), Jahn–Teller interactions (for the doubly degenerate electronic states) and spin–orbit conversions (between the singlets and the triplets), in competition with the isomerization processes mentioned in previous section. For illustration, the electronically excited CH3Cl2+ (1E and 1A1) dications may decompose directly forming the 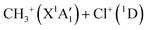 products or may be converted by spin–orbit interaction into the CH3Cl2+(3E) dications (for energies >2.4 eV). Fig. 7 shows that the population of the first excited state (i.e. the lowest 1E) followed by spin–orbit conversion to the lowest 3E state leads also to the CH3+ + Cl+ products in their electronic ground states. The crossing between these singlet and triplet states occurs at ∼3.1 eV above CH3Cl2+(X3A2). This results in a KER of 7.7 eV in close agreement with the present 7.7–7.9 eV measured values as can be seen in Table 3. Therefore, we may assume that the singlet states of CH3Cl2+ are populated first in the present experiment. Singlet CH3Cl2+ are then converted into CH3Cl2+(3E) ions. Afterwards, the formation of the Cl+ + CH3+ fragments in their electronic ground states follows the 3E state potential till dissociation.
products or may be converted by spin–orbit interaction into the CH3Cl2+(3E) dications (for energies >2.4 eV). Fig. 7 shows that the population of the first excited state (i.e. the lowest 1E) followed by spin–orbit conversion to the lowest 3E state leads also to the CH3+ + Cl+ products in their electronic ground states. The crossing between these singlet and triplet states occurs at ∼3.1 eV above CH3Cl2+(X3A2). This results in a KER of 7.7 eV in close agreement with the present 7.7–7.9 eV measured values as can be seen in Table 3. Therefore, we may assume that the singlet states of CH3Cl2+ are populated first in the present experiment. Singlet CH3Cl2+ are then converted into CH3Cl2+(3E) ions. Afterwards, the formation of the Cl+ + CH3+ fragments in their electronic ground states follows the 3E state potential till dissociation.
The appearance energy (AE) of the Cl+ + CH3+ ion pair through the fragmentation of CH3Cl2+ was measured 32.5 ± 0.5 eV.45 By combining the CH3Cl ADIE (of ∼30.7 eV) and the potential barrier we compute for CH3Cl2+(X3A2) (of ∼1.8 eV, Fig. 7), we obtain an AE of 32.5 eV for the CH3Cl2+ → Cl+ + CH3+ process while the reaction is occurring along the ground state potential. This value is in excellent agreement with the experimental value obtained by Thissen using photoelectron photoion photoion coincidence (PEPIPICO) technique.45 Whereas we deduce a much larger AE (of 33.8 eV) when the reaction starts on the lowest singlet (i.e. the lowest 1E state). The latter AE is also distinctly larger than the measured value. Again, this strongly suggests that the reaction takes place along the ground CH3Cl2+ potential prior to fragmentations in Thissen's experiments.45
b. CH3Cl2+ → H+ + CH2Cl+
The CH3Cl2+ dication may lose a proton and produces the CH2Cl+ and H+ ions. Fig. 7 shows that the ground state potential possesses a barrier of ∼2.3 eV, which results in a KER of 6.4 eV. The present computed KER is close to the presently measured ones of 6.3–6.2 eV. Thus, this assumes that the reaction occurs on the ground state potential, which is of triplet spin-multiplicity. Nevertheless, only the lowest singlet dicationic potential correlates adiabatically to the CH2Cl+(X1A1) + H+(1S) channel. Some spin–orbit conversion should occur at large separations between CH2Cl+ and H+(1S) converting triplet CH3Cl2+ into singlet CH3Cl2+. The KER measured by Ruhl et al.2 is in reasonable agreement with our experimental value, within the experimental uncertainties of both sets of data. However, the KERs for this channel obtained under intense laser field by Ma et al.6 are considerably lower than our experimental ones (cf.Table 3). In addition, a second reaction pathway may be proposed where we assist to a cleavage of the ClH bond after CH3Cl2+ → H2CClH2+ intramolecular isomerization processes. Again all couplings mentioned above are expected to play a role. Nevertheless, we have no indication from experiments for its occurrence presently.We deduce an AE of ∼33.0 eV for the CH2Cl+ and H+ ion pair production assuming that the reaction takes place solely along the lowest triplet PES. This value is reduced to 31.0 eV if the reaction follows the lowest singlet potential first and then the lowest triplet leading to CH2Cl+ and H+ in their electronic ground states. The latter computed AE is in excellent agreement with that measured by Thissen45 of 31.0 eV ± 0.5 eV using PEPIPICO method. This strongly suggests thus the primary population of the singlet state of CH3Cl2+ in these experiments.
c. CH2+ + HCl+
The formation of the CH2+ + HCl+ ion pair is observed. Obviously, we cannot propose a direct mechanism for the production of these species from the CH3Cl2+ dication. Instead, this dication may isomerize first to the trans planar H2CClH2+ form. Then the reaction proceeds by cleavage of the CCl bond of H2CClH2+. Fig. 8 presents the one-dimensional cuts of the potentials of H2CClH2+ along the CCl distance. This figure shows that the ground state of this species possesses a potential barrier towards dissociation to form CH2+ + HCl+ of ∼2.9 eV. Therefore, these ions can be produced carrying ∼6.7 eV KER in excellent agreement with the present experimental measurements (of 6.7–6.9 eV). The associated AE is ∼32.6 eV i.e. close to the 32.0 ± 1.0 eV AE determined by Thissen.45 This suggests that this reaction occurs on the lowest singlet potential upon double ionizing the CH3Cl molecule.Although previous works dealing with this channel suggested a multi-step mechanism for this channel, it is the first time that both calculated and experimental KERs coincide. Indeed, the calculations of Duflot et al.23 imply that there are two possible pathways for the isomerization followed by fragmentation to produce HCl+. Their calculated KER value is however smaller than our experimental and theoretical determinations. Also, the measured KER for this channel by Ma et al.6 is lower than ours. In a photoionization study of CH3Cl after fast resonant Auger decay in Cl by Kokkonen et al.,10 the formation of a stable HCl+ was also reported. However, their qualitative simulation could not find convergence to this isomerization channel.
d. H2+ + CHCl+
The formation of H2+ + CHCl+ is due to a bond arrangement upon double ionizing CH3Cl. This ion pair can be produced either by dissociating CH3Cl2+ or after isomerization from H2CClH2+. In the former case, both H atoms approach each other to form the H2+ ion, whereas in the latter we have a H atom migration in addition to this H2+ formation. For this channel, we measure KERs of ∼5.2 to 5.6 eV in good agreement with Duflot et al.23 computed KER. This validates thus the mechanism they proposed. The present experimental KER values are however higher than those reported under double photoionization2 and intense laser field ionization.6e. H3+ + CCl+
Recently, a detailed theoretical study for the production of this channel was done by some of us.24 Upon dissociating the CH3Cl dication, a multistep mechanism is in action for the formation of H3+ where the three H-atoms in CH3Cl2+ approach each other simultaneously while CCl+ goes away. A KER value of 5.2 eV has been calculated in this multi-step process as the energy difference between the X3A2/11A1 crossing and the lowest dissociation limit of the dissociated fragments. This theoretical KER value is in good agreement with our experimental data. This confirms the occurrence of such multistep mechanism for the formation of H3+ from CH3Cl2+ in the present experiments. This also rules out the possibility of roaming of H2 upon ionization in this case as proposed in Ekanayake et al.25 for other organic compounds. Besides, the KER value measured by Walt et al.5 under intense laser field is lower than our theoretical and experimental values.f. Trication channels
In the dissociation of CH3Cl3+, we have experimentally observed H+ + CH2Cl2+ and H2+ + CHCl2+ channels. To the best of our knowledge, the KER distributions shown in Fig. 4 and 5 and those reported in Table 3 are the only available data on the dissociation of CH3Cl3+. The experimental KERs for these two channels are in reasonable agreement, under the experimental uncertainties, with our theoretical calculations. Nevertheless, the KER values reported in the literature by Ma et al.6 are considerably lower than our experimental and theoretical values.The CH3Cl3+ ions once formed from neutral CH3Cl by ion impact do not decompose by C–Cl bond breaking. Indeed, the CH32+ + Cl+ channel is not observed experimentally in spite of the fact that the CCl bond cleavage is the major channel for the dication decomposition. Our calculations also suggest that this channel is less favorable thermodynamically. Instead, we observe in majority the H+ + CH2Cl2+ and the H2+ + CHCl2+ products. This may suggest some state selectivity upon fragmenting CH3Cl3+ ions as recently evidenced by some of us for SO22+ unimolecular decomposition forming the less favorable thermodynamically SO2+ + O46 and O2+ + S+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 ion pairs in addition to the obvious SO+ + O+ ion pair.46 Such experiments on polyatomic triply charged ions are still challenging in particular upon valence triple ionization because of the low abundance of triple ionization compared to single and double ionization processes.48
47 ion pairs in addition to the obvious SO+ + O+ ion pair.46 Such experiments on polyatomic triply charged ions are still challenging in particular upon valence triple ionization because of the low abundance of triple ionization compared to single and double ionization processes.48
In sum, the multiple ionization of CH3Cl and the subsequent fragmentation of the multiply charged CH3Clq+ (q = 2,3) ions was investigated by electron impact, ions impact, single photon valence and inner shell ionization and intense laser multiple photon ionization. All these processes are different and may lead to various population of the multicharged ions electronic sates and thus to different energetics. For instance, the experimental KERs reported by Ma et al.6 shown in Table 3 obtained after intense laser fields interaction with CH3Cl are considerably smaller than our experimental values and those determined using single photon ionization.2 This may be due to the effect of the intense laser field which causes the sequential ionization of the electrons during the dissociation and the fragments are produced from Coulomb explosion at a bond length larger than the equilibrium bond length of the neutral molecule. Generally, one needs to be aware of such considerations and the comparison of the theoretical data and the experimental ones should be done with care.
VI. Conclusion
We used a combined theoretical and experimental methodology to investigate the evolution of the CH3Cl2+ and CH3Cl3+ ions formed by ion collision of CH3Cl with energetic H+ and Ar9+ ion beams. Several dissociation channels were characterized. Globally, we have good agreement between our computed KERs and AEs with those either measured presently or in previous experimental works. Therefore, our theoretical data allowed to elucidate the mechanisms of the formation of the ion pairs, where fragmentations occur on the ground potentials and/or from the electronic excited states of these multiply charged ions. Nevertheless, we observed some discrepancies between the experimental data to compare with. This is mainly related to the ionization processes in action to form the CH3Cl2+ and CH3Cl3+ ions. As expected, valence double or triple single photon ionization should lead to the population of a bench of CH3Cl2+ and CH3Cl3+ electronic states that may be different from those reached by intense lasers or inner shell ionization followed by Auger processes or by fast ion beams impact. Strictly speaking, the full understanding of the dynamics of CH3Cl upon double or triple ionization requires further experiments to separate the relative yields in terms of ionization and electron capture processes. Such experiments can be done using threefold and fourfold electron–ion coincidence measurements, which fully connect the electrons to the ion pairs coming from the same events. This should give a full picturing of the state-to-state decomposition of the CH3Cl2+ and CH3Cl3+ ions. For other molecular systems, such experiments combined with advanced theoretical treatments allowed elucidating the unimolecular state-to-state reaction pathways undertaken by the doubly changed molecular ions formed by valence double photoionization of the corresponding neutral.46,47,49,50Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of Centre National de la Recherche Scientifique (CNRS)/Institut National des Sciences de l’Univers (INSU) with Institut de Chimie (INC)/Institut de Physique (INP) co-funded by Commissariat à l’Energie Atomique (CEA) and Centre National d’Etudes Spatiales (CNES). The authors also thank N. Das, A. Kumar and A. Duley for help during the experiments. The authors thank the staff of LEIBF at Inter University Accelerator Centre, New Delhi, India for smooth operation of the ion beam during the experiments. K. R. M. thanks the SRM Institute of Science and Technology (SRM IST) for the research fellowship. M. P. thanks the Department of Science and Technology (DST) – SERB India (Grant: ECR/2017/000891) for providing financial support. M. P. thanks also SRM-IST for providing the supercomputing facility.References
- J. H. D. Eland, Int. J. Mass Spectrom. Ion Phys., 1969, 2, 471 CrossRef CAS.
- E. Ruhl, S. D. Price, S. Leach and J. H. D. Eland, Int. J. Mass Spectrom. Ion Process., 1990, 97, 175 CrossRef CAS.
- B. Siegmann, U. Werner and R. Mann, Nucl. Instrum. Methods Phys. Res. B, 2005, 233, 182 CrossRef CAS.
- E. C. Fayolle, K. I. Öberg and J. K. Jørgensen, et al. , Nat. Astron., 2017, 1, 703 CrossRef.
- S. G. Walt, N. Bhargava Ram, A. Von Conta, O. I. Tolstikhin, L. B. Madsen, F. Jensen and H. J. Worner, J. Phys. Chem. A, 2015, 119, 11772 CrossRef CAS PubMed.
- P. Ma, C. Wang, X. Li, X. Yu, X. Tian, W. Hu, J. Yu, S. Luo and D. Ding, J. Chem. Phys., 2017, 146, 244305 CrossRef PubMed.
- P. D. Grugan, N. Ekanayake, S. White, S. Y. Luo, P. Ruan and B. C. Walker, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 165601 CrossRef.
- C. Miron, P. Morin, D. Céolin, L. Journel and M. Simon, J. Chem. Phys., 2008, 128, 154314 CrossRef PubMed.
- Handbook of High-resolution Spectroscopy, ed. M. Quack and F. Merkt, John Wiley & Sons, Ltd, 2011, ISBN: 978-0-470-74959-3 Search PubMed.
- E. Kokkonen, M. Vapa, K. Bucar, K. Jänkälä, W. Cao, M. Zitnik and M. Huttula, Phys. Rev. A, 2016, 94, 033409 CrossRef.
- E. Kokkonen, K. Jänkälä, M. Patanen, W. Cao, M. Hrast, K. Bučar, M. Žitnik and M. Huttula, J. Chem. Phys., 2018, 148, 174301 CrossRef CAS PubMed.
- D. M. P. Holland, I. Powis, G. Öhrwall, L. Karlsson and W. von Niessen, Chem. Phys., 2006, 326, 535 CrossRef CAS.
- A. Hult Roos, J. H. D. Eland, D. Koulentianos, R. J. Squibb, L. Karlsson and R. Feifel, Chem. Phys., 2017, 491, 42 CrossRef CAS.
- J. Harvey, R. P. Tuckett and A. Bodi, J. Phys. Chem. A, 2012, 116, 9696 CrossRef CAS PubMed.
- D. Céolin, M. N. Piancastelli, R. Guillemin, W. C. Stolte, S.-W. Yu, O. Hemmers and D. W. Lindle, J. Chem. Phys., 2007, 126, 084309 CrossRef PubMed.
- R. Thissen, M. Simon and M.-J. Hubin-Franskin, J. Chem. Phys., 1994, 101, 7548 CrossRef CAS.
- A. F. Lago, A. C. F. Santos and G. G. B. de Souza, J. Chem. Phys., 2004, 120, 9547 CrossRef CAS PubMed.
- M. N. Monce, A. K. Edwards, R. M. Wood, M. F. Steuer, A. V. Shah and P. Tabor, J. Chem. Phys., 1981, 74, 2860 CrossRef CAS.
- C. G. Aitken, D. A. Blunt and P. W. Harland, Int. J. Mass Spectrom. Ion Process., 1995, 149, 279 CrossRef.
- R. Rejoub, B. G. Lindsay and R. F. Stebbings, J. Chem. Phys., 2002, 117, 6450 CrossRef CAS.
- P. Grant, F. M. Harris and D. E. Parry, Int. J. Mass Spectrom., 1999, 192, 111 CrossRef.
- D. Duflot, J.-M. Robbe and J.-P. Flament, J. Chem. Phys., 1995, 103, 10571 CrossRef CAS.
- D. Duflot, J.-M. Robbe and J.-P. Flament, Int. J. Mass Spectrom. Ion Process., 1997, 171, 215 CrossRef CAS.
- J. Palaudoux and M. Hochlaf, ACS Earth Space Chem., 2019, 3, 980 CrossRef CAS.
- N. Ekanayake, T. Severt, M. Nairat, N. P. Weingartz, B. M. Farris, B. Kaderiya, P. Feizollah, B. Jochim, F. Ziaee, K. Borne, R. P. Kanaka, K. D. Carnes, D. Rolles, A. Rudenko, B. G. Levine, J. E. Jackson, I. Ben-Itzhak and M. Dantus, Nat. Commun., 2018, 9, 5186 CrossRef PubMed.
- J. Roithova, J. Hrusak and Z. Herman, J. Phys. Chem. A, 2003, 107, 7355 CrossRef CAS.
- A. Kumar, J. Rajput, T. Sairam, M. Jana, L. Nair and C. Safvan, Int. J. Mass Spectrom., 2014, 374, 44 CrossRef CAS.
- C. Hampel, K. A. Peterson and H. J. Werner, Chem. Phys. Lett., 1992, 190, 1 CrossRef CAS.
- P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219 CrossRef CAS.
- P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 2000, 112, 3106 CrossRef CAS.
- M. J. O. Deegan and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- R. A. Kendall, J. Chem. Phys., 1998, 96, 6796 CrossRef.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1998, 82, 5053 CrossRef.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1998, 89, 5803 CrossRef.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514 CrossRef CAS.
- K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101 CrossRef CAS PubMed.
- MOLPRO (version 2015) is a ab initio package written by H. J. Werner and P. J. Knowles. Further details at https://www.molpro.net.
- R. Llusar, M. Casarrubios, Z. Barandiarán and L. Seijo, J. Chem. Phys., 1996, 105, 5321 CrossRef CAS.
- T. Zeng, D. G. Fedorov, M. W. Schmidt and M. Klobukowski, J. Chem. Phys., 2011, 134, 214107 CrossRef PubMed.
- A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823 CrossRef CAS.
- C. Illescas and A. Riera, Phys. Rev. A, 1999, 60, 4546 CrossRef CAS.
- R. Thissen, unpublished results as given in ref. 23.
- M. Jarraya, M. Wallner, G. Nyman, S. Ben Yaghlane, M. Hochlaf, J. H. D. Eland and R. Feifel, Sci. Rep., 2021, 11, 17137 CrossRef CAS PubMed.
- M. Wallner, M. Jarraya, E. Olsson, V. Ideböhn, R. J. Squibb, S. Ben Yaghlane, G. Nyman, J. H. D. Eland, R. Feifel and M. Hochlaf, Sci. Adv., 2022, 8, eabq5411 CrossRef CAS PubMed.
- A. Hult Roos, J. H. D. Eland, J. Andersson, R. J. Squibb, D. Koulentianos, O. Talaee and R. Feifel, Sci. Rep., 2018, 8, 16405 CrossRef PubMed.
- R. Linguerri, E. Olsson, G. Nyman, M. Hochlaf, J. H. D. Eland and R. Feifel, Inorg. Chem., 2021, 60, 17966 CrossRef CAS PubMed.
- V. Ideböhn, A. J. Sterling, M. Wallner, E. Olsson, R. J. Squibb, U. Miniotaite, E. Forsmalm, M. Forsmalm, S. Stranges, J. M. Dyke, F. Duarte, J. H. D. Eland and R. Feifel, Phys. Chem. Chem. Phys., 2022, 24, 786 RSC.
| This journal is © the Owner Societies 2022 |