The role of filament length, finite-extensibility and motor force dispersity in stress relaxation and buckling mechanisms in non-sarcomeric active gels

Abstract

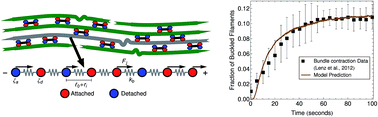
After relaxing some assumptions we apply a single-chain mean-field mathematical model recently introduced [RSC Adv. (2014)] to describe the role of molecular motors in the mechanical properties of active gels. The model allows physics that are not available in models postulated on coarser levels of description. Moreover it proposes a level of description that allows the prediction of observables at time scales too difficult to achieve in multi-chain simulations for realistic filament lengths and densities. We model the semiflexible filaments that compose the active gel as bead-spring chains; molecular motors are accounted for by using a mean-field approach, in which filaments undergo transitions of one motor attachment state depending on the state of the probe filament. The level of description includes the end-to-end distance and attachment state of the filaments, and the motor-generated forces, as stochastic state variables which evolve according to a proposed differential Chapman–Kolmogorov equation. The motor-generated forces are drawn from a stationary distribution of motor stall forces. We consider bead-spring chains with multiple beads, explore the effect of finite-extensibility of the strands and incorporate into the model motor force distributions that have been measured experimentally. The model can no longer be solved analytically but is amenable to numerical simulation. This version of the model allows a more quantitative description of buckling dynamics [Lenz et. al. PRL, 2012, 108, 238107] and the dynamic modulus of active gels. The effect of finite extensibility of the filament strands on the dynamic modulus was also found to be in agreement with the microrheology experiments of Mizuno et. al., [Science, 2007, 315, 370–373].