Statics and diffusive dynamics of surfaces driven by p-atic topological defects

Abstract

Inspired by epithelial morphogenesis, we consider a minimal model for the shaping of a surface driven by p-atic topological defects. We show that a positive (negative) defect can dynamically generate a (hyperbolic) cone whose shape evolves diffusively, and predict that a defect of charge + 1/p leads to a final semi-cone angle β which satisfies the inequality 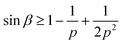. By exploiting the fact that for axisymmetric surfaces, the extrinsic geometry is tightly coupled to the intrinsic geometry, we further show that the resulting stationary shape of a membrane with negligible bending modulus and embedded polar order is a deformed lemon with two defects at antipodal points. Finally, we close by pointing out that our results may be relevant beyond epithelial morphogenesis in such contexts as shape transitions in macroscopic closed spheroidal surfaces such as pollen grains.