Equilibrium states corresponding to targeted hyperuniform nonequilibrium pair statistics

Abstract

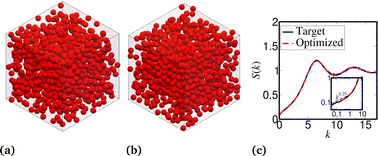
The Zhang–Torquato conjecture [G. Zhang and S. Torquato, Phys. Rev. E, 2020, 101, 032124.] states that any realizable pair correlation function g₂(r) or structure factor S(k) of a translationally invariant nonequilibrium system can be attained by an equilibrium ensemble involving only (up to) effective two-body interactions. To further test and study this conjecture, we consider two singular nonequilibrium models of recent interest that also have the exotic hyperuniformity property: a 2D “perfect glass” and a 3D critical absorbing-state model. We find that each nonequilibrium target can be achieved accurately by equilibrium states with effective one- and two-body potentials, lending further support to the conjecture. To characterize the structural degeneracy of such a nonequilibrium–equilibrium correspondence, we compute higher-order statistics for both models, as well as those for a hyperuniform 3D uniformly randomized lattice (URL), whose higher-order statistics can be very precisely ascertained. Interestingly, we find that the differences in the higher-order statistics between nonequilibrium and equilibrium systems with matching pair statistics, as measured by the “hole” probability distribution, provide measures of the degree to which a system is out of equilibrium. We show that all three systems studied possess the bounded-hole property and that holes near the maximum hole size in the URL are much rarer than those in the underlying simple cubic lattice. Remarkably, upon quenching, the effective potentials for all three systems possess local energy minima (i.e., inherent structures) with stronger forms of hyperuniformity compared to their target counterparts. Our methods are expected to facilitate the self-assembly of tunable hyperuniform soft-matter systems.