Singularity identification for the characterization of topology, geometry, and motion of nematic disclination lines

Abstract

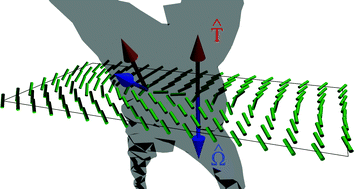
We introduce a characterization of disclination lines in three dimensional nematic liquid crystals as a tensor quantity related to the so called rotation vector around the line. This quantity is expressed in terms of the nematic tensor order parameter Q, and shown to decompose as a dyad involving the tangent vector to the disclination line and the rotation vector. Further, we derive a kinematic law for the velocity of disclination lines by connecting this tensor to a topological charge density as in the Halperin-Mazenko description of defects in vector models. Using this framework, analytical predictions for the velocity of interacting line disclinations and of self-annihilating disclination loops are given and confirmed through numerical computation.