Multicomponent diffusion of interacting, nonionic micelles with hydrophobic solutes
Abstract
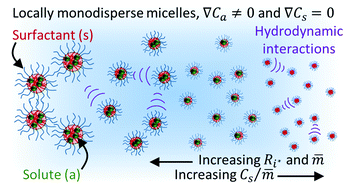
Ternary diffusion coefficient matrices [D] were measured using the Taylor dispersion method, for crowded aqueous solutions of decaethylene glycol monododecyl ether (C12E10) with either decane or limonene solute. The matrix [D], for both systems, was found to be highly non-diagonal, and concentration dependent, over a broad domain of solute to surfactant molar ratios and micelle volume fractions. A recently developed theoretical model, based on Batchelor's theory for gradient diffusion in dilute, polydisperse mixtures of interacting spheres, was simplified by neglecting local polydispersity, and effectively used to predict [D] with no adjustable parameters. Even though the model originates from dilute theory, the theoretical results were in surprisingly good agreement with experimental data for concentrated mixtures, with volume fractions up to ϕ ≈ 0.47. In addition, the theory predicts eigenvalues D− and D+ that correspond to long-time self and gradient diffusion coefficients, respectively, for monodisperse spheres, in reasonable agreement with experimental data.


 Please wait while we load your content...
Please wait while we load your content...
