A perturbation solution to the full Poisson–Nernst–Planck equations yields an asymmetric rectified electric field†
Abstract
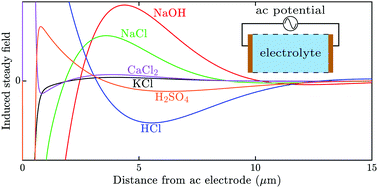
We derive a perturbation solution to the one-dimensional Poisson–Nernst–Planck (PNP) equations between parallel electrodes under oscillatory polarization for arbitrary ionic mobilities and valences. Treating the applied potential as the perturbation parameter, we show that the second-order solution yields a nonzero time-average electric field at large distances from the electrodes, corroborating the recent discovery of Asymmetric Rectified Electric Fields (AREFs) via numerical solution to the full nonlinear PNP equations [Hashemi et al., Phys. Rev. Lett., 2018, 121, 185504]. Importantly, the first-order solution is analytic, while the second-order AREF is semi-analytic and obtained by numerically solving a single linear ordinary differential equation, obviating the need for full numerical solutions to the PNP equations. We demonstrate that at sufficiently high frequencies and electrode spacings the semi-analytical AREF accurately captures both the complicated shape and the magnitude of the AREF, even at large applied potentials.


 Please wait while we load your content...
Please wait while we load your content...