Complementary first and second derivative methods for ansatz optimization in variational Monte Carlo
Abstract
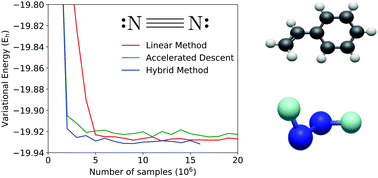
We present a comparison between a number of recently introduced low-memory wave function optimization methods for variational Monte Carlo in which we find that first and second derivative methods possess strongly complementary relative advantages. While we find that low-memory variants of the linear method are vastly more efficient at bringing wave functions with disparate types of nonlinear parameters to the vicinity of the energy minimum, accelerated descent approaches are then able to locate the precise minimum with less bias and lower statistical uncertainty. By constructing a simple hybrid approach that combines these methodologies, we show that all of these advantages can be had at once when simultaneously optimizing large determinant expansions, molecular orbital shapes, traditional Jastrow correlation factors, and more nonlinear many-electron Jastrow factors.


 Please wait while we load your content...
Please wait while we load your content...
