Growth of form in thin elastic structures

Abstract

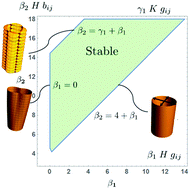
Heterogeneous growth plays an important role in the shape and pattern formation of thin elastic structures ranging from the petals of blooming lilies to the cell walls of growing bacteria. Here we address the stability and regulation of such growth, which we modeled as a quasi-static time evolution of a metric, with fast elastic relaxation of the shape. We consider regulation via coupling of the growth law, defined by the time derivative of the target metric, to purely local properties of the shape, such as the local curvature and stress. For cylindrical shells, motivated by rod-like E. coli, we show that coupling to curvature alone is generically linearly unstable to small wavelength fluctuations and that additionally coupling to stress can stabilize these modes. Interestingly, within this framework, the longest wavelength fluctuations can only be stabilized with the mean curvature flow. Our approach can readily be extended to gain insights into the general classes of stable growth laws for different target geometries.