Hard sphere packings within cylinders†
Abstract
Arrangements of identical hard spheres confined to a cylinder with hard walls have been used to model experimental systems, such as fullerenes in nanotubes and colloidal wire assembly. Finding the densest configurations, called close packings, of hard spheres of diameter σ in a cylinder of diameter D is a purely geometric problem that grows increasingly complex as D/σ increases, and little is thus known about the regime for D > 2.873σ. In this work, we extend the identification of close packings up to D = 4.00σ by adapting Torquato–Jiao's adaptive-shrinking-cell formulation and sequential-linear-programming (SLP) technique. We identify 17 new structures, almost all of them chiral. Beyond D ≈ 2.85σ, most of the structures consist of an outer shell and an inner core that compete for being close packed. In some cases, the shell adopts its own maximum density configuration, and the stacking of core spheres within it is quasiperiodic. In other cases, an interplay between the two components is observed, which may result in simple periodic structures. In yet other cases, the very distinction between the core and shell vanishes, resulting in more exotic packing geometries, including some that are three-dimensional extensions of structures obtained from packing hard disks in a circle.
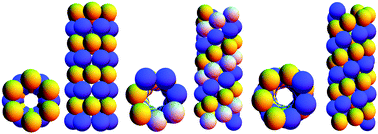

 Please wait while we load your content...
Please wait while we load your content...