Diffusion of eccentric microswimmers
Abstract
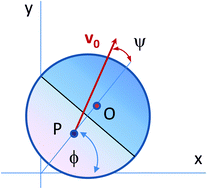
We model the two-dimensional diffusive dynamics of an eccentric artificial microswimmer in a highly viscous medium. We assume that the swimmer's propulsion results from an effective force applied to a center distinct from its center of mass, both centers resting on a body's axis parallel to its average self-propulsion velocity. Moreover, we allow for angular fluctuations of the velocity about the body's axis. We prove, both analytically and numerically, that the ensuing active diffusion of the swimmer is suppressed to an extent that strongly depends on the model parameters. In particular, the active diffusion constant undergoes a transition from a quadratic to a linear dependence on the self-propulsion speed, with practical consequences on the interpretation of the experimental data. Finally, we extend our model to describe the diffusion of chiral eccentric swimmers.

 Please wait while we load your content...
Please wait while we load your content...