Response of adherent cells to mechanical perturbations of the surrounding matrix

Abstract

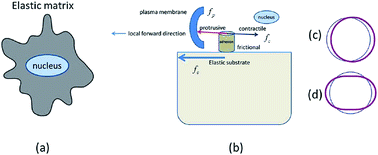
We present a generic and unified theory to explain how cells respond to perturbations of their mechanical environment such as the presence of neighboring cells, slowly applied stretch, or gradients of matrix rigidity. Motivated by experiments, we calculate the local balance of forces that give rise to a tendency for the cell to locally move or reorient, with a focus on the contribution of feedback and homeostasis to cell contractility (manifested by a fixed displacement, strain or stress) that acts on the adhesions at the cell boundary. These forces can be either reinforced or diminished by elastic stresses due to mechanical perturbations of the matrix. Our model predicts these changes and how their balance with local protrusive forces that act on the cell's leading edge either increase or decrease the tendency of the cell to locally move (toward neighboring cells or rigidity gradients) or reorient (in the direction of slowly applied stretch or rigidity gradients).