Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Voltage breakdown analyses in anion exchange membrane water electrolysis – the contributions of catalyst layer resistance on overall overpotentials
Emily K.
Volk
 a,
Elliot
Padgett
a,
Elliot
Padgett
 b,
Melissa E.
Kreider
b,
Melissa E.
Kreider
 b,
Stephanie
Kwon
b,
Stephanie
Kwon
 *c and
Shaun M.
Alia
*c and
Shaun M.
Alia
 *b
*b
aAdvanced Energy Systems Graduate Program, Colorado School of Mines, Golden, Colorado 80401, USA
bChemistry and Nanoscience Center, National Renewable Energy Laboratory, Golden, Colorado 80401, USA. E-mail: shaun.alia@nrel.gov
cDepartment of Chemical and Biological Engineering, Colorado School of Mines, Golden, Colorado 80401, USA. E-mail: kwon@mines.edu
First published on 29th December 2025
Abstract
Despite many recent advances, overpotentials remain high for anion exchange membrane water electrolyzers (AEMWEs). Voltage breakdown analyses (VBA) can help decouple the origins of overpotentials and facilitate design decisions to improve cell performance, but studies investigating how to adapt and apply VBA to AEMWEs are lacking. Specifically, catalyst layer resistances and their contributions to overpotentials are not consistently quantified in water electrolysis and are rarely quantified for AEMWEs. This work presents a systematic methodology for VBA tailored to AEMWEs, including an approach to Tafel analysis in the absence of a reference electrode and under conditions where both the oxygen evolution reaction and hydrogen evolution reaction exhibit significant overpotentials. Catalyst layer resistance contributions are diagnosed via changes in the catalyst layer thickness, transport layer porosity, ionomer content, and electrolyte concentration. In this study, we explain discrepancies between inherent catalytic kinetics and device level performance and identify catalyst layer design strategies to reduce catalyst layer resistances.
Anion exchange membrane water electrolysis (AEMWE) is an emerging technology poised to overcome materials and performance limitations of traditional electrolysis devices, such as proton exchange membrane water electrolyzers (PEMWEs) and liquid alkaline water electrolyzers (LAWE).1 Recent studies have demonstrated the feasibility of AEMWEs operating over extended periods (up to 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hours) at high current densities.2–6 Overpotentials for AEMWEs, however, have remained high compared to those for PEMWEs,1,7 highlighting the need for further development and optimization at the device level to enhance the commercial viability of AEMWEs.
000 hours) at high current densities.2–6 Overpotentials for AEMWEs, however, have remained high compared to those for PEMWEs,1,7 highlighting the need for further development and optimization at the device level to enhance the commercial viability of AEMWEs.
Voltage breakdown analysis (VBA) is an approach to decouple the kinetic, ohmic, and transport contributions to measured cell overpotentials in electrochemical devices.8–11 This analysis can help identify key areas for future device development and potentially resolve discrepancies between inherent catalytic trends predicted from half-cell, rotating disc electrode (RDE) measurements and the corresponding catalyst performance in single-cell membrane electrode assemblies (MEAs). For example, prior studies have shown that catalyst layer resistance (RCL), related to resistances to the flow of ions or electrons through the catalyst layer, significantly contributes to overall overpotentials in PEMWEs, impacting catalyst utilization and potentially limiting cell kinetics at the device level.12 In AEMWEs, however, the contributions of RCL are yet to be quantified, diagnosed, or decoupled, posing a barrier to optimizing these systems for high device-level performance. Here, we focus on the oxygen evolution reaction (OER) as it provides a well-established system for examining how the catalyst layer composition and structure influence anode performance in AEMWEs. The strategies and insights discussed, however, can be readily extended to study the increasingly critical hydrogen evolution reaction (HER), which is part of our ongoing and future works.13
Fig. 1 shows the activities towards the oxygen evolution reaction (OER) for four different representative metal oxides (IrO2, NiFe2O4, Co3O4, and Mn2O3) measured in RDE and MEA; detailed methods are described in the SI. Activities were overall lower in RDE compared to the MEAs due to the differences in the operating temperature (23 °C for RDE and 80 °C for MEA, respectively). In RDE, the four catalyst materials exhibited significantly different OER activities and kinetic signatures (Tafel slope and exchange current density; Fig. 1a).14 When the same catalysts were tested in a standard MEA setup, however, their performance became similar (Fig. 1b).14 This discrepancy, at least in part, can be attributed to differences in test design. In RDE testing, thin, near-monolayer catalyst layers enable high catalyst utilization, while electrode rotation is used to minimize mass transfer limitations of reactants and products,15–17 though this can be complicated for a gas-evolution reaction. It also allows isolation of a single electrode reaction (i.e., OER at the anode or hydrogen evolution reaction (HER) at the cathode). In contrast, MEA tests inherently include contributions from both half-cell reactions (i.e., OER and HER). Moreover, electrode structures can vary significantly based on the catalyst particle size, catalyst–ionomer interactions, ink properties, and agglomeration behavior, while transport occurs through complex interconnected networks and interfaces of the catalyst layer (CL), membrane, and porous transport layers (PTLs).1 MEAs are also often operated at a higher temperature, influencing catalytic kinetics and catalyst conductivity in oxides. In this work, we aim to demonstrate how device-level challenges can be isolated by deconstructing the cell voltage to decouple the various sources of overpotentials.
Fig. 2 shows the results of applying our proposed VBA for four anode catalysts. First, the thermodynamic potential is calculated under the relevant conditions using the Nernst equation, as shown by grey shaded areas in Fig. 2,
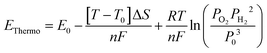 | (1) |
Here, T is the temperature, ΔS is the entropy change of the reaction (ΔS = 2SH2 + SO2 − 2SH2O), n is the number of moles of electrons involved in the electrochemical reaction (4 mol e− for the OER), F is Faraday's constant, R is the gas constant, PO2 and PH2 are the partial pressures of O2 and H2, respectively, and T0 and P0 are the standard temperature and atmospheric pressure, respectively.
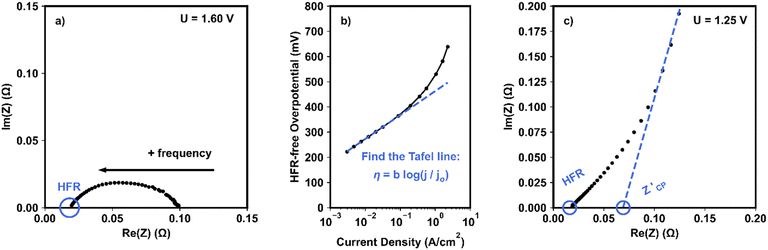
Next, ohmic losses (ηOhmic; shown by orange shaded areas in Fig. 2) can be calculated using electrochemical impedance spectroscopy (EIS) measurements (Fig. 3). These losses arise from resistive losses in the cell, including the membrane and interfacial contact resistances. A characteristic Nyquist plot for EIS measurements collected at faradaic potentials (here, 1.6 V) is shown in Fig. 3a. In EIS, an AC voltage is applied at increasing frequencies (designated by the right-to-left arrow in Fig. 3a). It is standard to determine these ohmic losses from the high frequency resistance (HFR; circled in Fig. 3a). For an accurate VBA, the HFR should be measured at each potential in the polarization curve, as it can vary slightly with applied potential. Ohmic losses are then calculated as follows:
| ηOhmic = J × (HFR) | (2) |
Kinetic losses (ηkinetic; shown by the green shaded areas in Fig. 2) can be quantified using Tafel analysis of HFR-free overpotentials, as illustrated in Fig. 3b. The polarization curve data used for Tafel analysis should be collected using chronopotentiometry or chronoamperometry methods, holding at each current or potential step for at least 1–2 minutes to minimize errors associated with the cell stabilization time. Polarization curve data should also contain sufficient points in the kinetic region (typically >5 points in a linear region, often between 5 and 50 mA cm−2). From these data, the apparent Tafel slope and exchange current density can be extracted from the linear region of the HFR-corrected data, and a Tafel line can be extrapolated across the full current density (as shown in Fig. 3b).
We note that in the AEMWE, both the HER and the OER are expected to have high overpotentials and to follow Tafel kinetics.18,19 This contrasts with the PEMWE, where the acidic HER is generally assumed to proceed without significant kinetic limitations. Best practices would utilize a reference electrode to separate HER and OER kinetics; most studies, however, utilize a two-electrode MEA configuration in which full cell potentials are measured and reported.1 This can introduce discrepancies between the potential applied and the actual potential experienced at the electrode. Consequently, the extracted kinetic parameters (Tafel slope and exchange current density) are only “apparent” and not directly comparable to those obtained from half-cell measurements. Nevertheless, in the absence of a reference electrode, an “effective” Tafel analysis can still be reasonably performed, which we demonstrate through the following analysis.
For a two-electrode cell in which both electrodes follow Tafel kinetics, the total overpotential (ηtot) can be approximated as the sum of the individual kinetic contributions from each electrode:
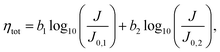 | (3) |
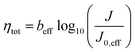 | (4) |
This relationship, which maintains the form of the Tafel equation, shows that a standard Tafel analysis can be employed for the case where both the OER and the HER are significant and yields an “effective” Tafel slope and exchange current density which are defined by beff (=b1 + b2) and 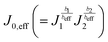 . These parameters can then be used to determine full-cell kinetic overpotentials as discussed above.
. These parameters can then be used to determine full-cell kinetic overpotentials as discussed above.
Catalyst layer resistances (RCL) arise from disruptions in the ionic and electronic transport networks within the CL. These contributions can be quantified using non-faradaic EIS, i.e., measurements performed at a potential where no charge transfer reactions occur (1.25 V in this work). CLR contributions can be determined by leveraging the transmission line theory of porous electrodes.12,20–22 In this approach, the electrode is modeled using a transmission line equivalent circuit in which parallel capacitive and kinetic elements, representing small local sections of the electrochemical surface, are connected by resistive elements that represent the ionically and electronically conductive regions of the electrode. A uniform porous CL behaving as an RC transmission line is expected to exhibit an approximately 45° line in Nyquist plots, although deviation from this behavior can arise when the electrode structure is nonuniform (e.g., in the presence of bottlenecked or tapered pores).20,23
An illustrative example of non-faradaic impedance spectroscopy for an AEMWE with a NiFe2O4 anode CL is shown in Fig. 3c. In this figure, the characteristic 45° region lies between approximately 20 and 80 Ω-cm2 on the real axis; this region is directly proportional to the RCL.12,21,22RCL can then be calculated using a transmission line model, as has been shown previously,24,25 or approximated using a linear fit of the constant phase region as follows:
 | (5) |
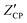 is the x-intercept of the constant phase region with the real axis.
is the x-intercept of the constant phase region with the real axis.
Previous work from our group demonstrated a method to estimate RCL contributions to overpotential (ηCLR) for PEMWEs from the RCL and Tafel slope.12 Here, we apply this approximation to the AEMWE, calculating ηCLR as follows:
ηCLR = −b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(u) log10(u) | (6) |
 | (7) |
α (=1.1982) is a scaling parameter determined previously.12Jint is the transition current density between the region dominated by the Tafel limit and the region dominated by the semi-infinite pore limit12 and is given by
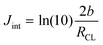 | (8) |
These equations demonstrate that catalyst layer utilization decreases as current increases, RCL increases, and the Tafel slope decreases.
Thus far, we have demonstrated how to decouple ohmic, kinetic, and RCL contributions to overpotentials by evaluating ηOhmic, ηKinetic and ηCLR; together, these contributions account for most of the losses observed in Fig. 2. However, some additional losses remain that are not captured by these terms and are commonly referred to as residual losses (ηresidual). These ηresidual values are generally attributed, at least in part, to mass transport limitations through the CL.26
Interestingly, the estimated ηkinetic values were found to be very similar for the four catalysts tested, as shown by green shaded areas in Fig. 2. In contrast, the largest differences were observed for ηCLR and ηresidual (purple and white areas in Fig. 2). These variable RCL values may stem from differences in CL structures, influenced by variations in the particle size, agglomeration tendencies, and interactions with anion exchange polymers. These factors also affect the degree of catalyst utilization and the transport of evolved O2(g), potentially contributing to the observed trends in ηCLR and ηresidual. We further hypothesize that poor catalyst utilization contributes to ηkinetic and suggest that diagnosing and reducing RCL and ηkinetic will also decrease and drive trends closer to those predicted from half-cell, RDE testing (in Fig. 1a).
In the following paragraphs, we outline strategies to improve performance by addressing the key factors contributing to RCL. We note that in AEMWEs, RCL can arise from (1) the anode CL, (2) the cathode CL, and (3) the PTL. Specifically, the HER overpotentials are non-negligible in AEMWEs and thus the cathode RCL may be significant, which is in sharp contrast to PEMWEs and consistent with the above discussions on Tafel kinetics. The PTL, often made of OER-active Ni or stainless steel and flooded with a supporting electrolyte, could also exhibit its own transmission line impedance as we have shown in our previous work.4 Here, we focus on the anode CL, as the OER is still expected to be the limiting half-reaction. To isolate the relevant effects, all other variables were held constant while only the anode CL parameters were varied, and the resulting trends were examined with respect to RCL.
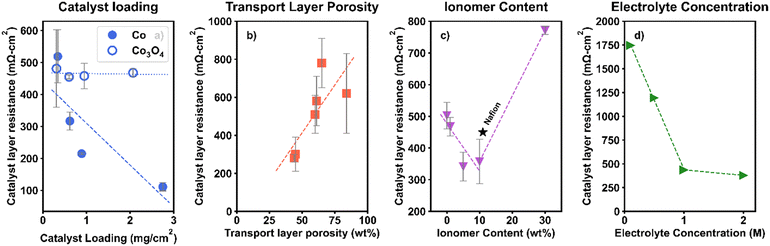
Fig. 4 shows the results of changing key catalyst layer design and operational variables (catalyst loading, PTL porosity, ionomer content, and electrolyte concentration) on RCL. We note that these variables had a negligible impact on the high frequency resistance (HFR; Fig. S1, SI) and RCL trends generally followed the electrochemical performance trends (Fig. S2, SI).
In Fig. 4a, the results of changing Co and Co3O4 loading on RCL are shown, adapted from our previous work.26 A direct relationship between catalyst loading and RCL would indicate a significant through-plane electronic or ionic RCL, where a thicker CL induces increased resistance due to the inherent conductivity limitations or contact issues. Neither Co nor Co3O4 loading showed this relationship, indicating that CLs with these materials in the loading ranges tested do not have a through-plane limitation. Instead, for Co, there was an inverse relationship between RCL and catalyst loading and for Co3O4, there was no clear trend between RCL and catalyst loading. The disparities in trends between these two materials are likely related to their different inherent conductivities; as we have shown previously, for catalysts with high conductivity, increased loading leads to improved kinetics and decreased RCL and for catalysts with low conductivity, there is minimal variance in RCL with loading (<200 mΩ cm2 difference).26
When changing the PTL morphology for Co3O4 CLs, shown in Fig. 4b, we found a direct relationship between PTL porosity and RCL. Low porosity PTLs (smaller gaps between PTL fibers) led to the smallest RCL and high porosity PTLs (large gaps between fibers) led to the largest RCL. This trend underscores the importance of optimizing the PTL microstructure to promote effective ionic and electronic transport within the catalyst layer.
These observed trends (i.e., an inverse relationship between RCL and catalyst loading and a direct relationship between RCL and PTL porosity) may indicate the presence of a pseudo in-plane electronic resistance, similar to phenomena previously reported for PEMWE CLs.12 In the PEM case, this was due to the distances electrons must travel along the CL (on the membrane) to reach contact points with the conductive PTL in a catalyst coated membrane (CCM) configuration. While this is not directly analogous to the catalyst coated substrate (CCS) approach commonly used for AEMWE, the mechanism is likely not ionic, due to the high ionic conductivity provided by the 1 M KOH supporting electrolyte (discussed further below). Instead, we propose an explanation related to electronic limitations; at low catalyst loadings and high PTL porosities (shown here to have high RCL), there are potentially large gaps between catalyst particles and poor coverage of the CL on the PTL, leading to a lower effective area for electron conduction. As loading increases and PTL porosity decreases, the catalyst layer becomes more uniform and there is better coverage across the PTL pores, increasing the effective conduction area and lowering resistance. Furthermore, the catalyst on the membrane-facing surface of the PTL is likely kept in better electronic contact than the catalyst within the PTL pores during MEA compression. The improved PTL coverage at high loading/low PTL porosity may therefore lead to better contact within the CL, contributing to decreasing RCL.
We assumed the anode-side PTL to be incompressible, such that it did not undergo any mechanical deformation that could affect CL compressibility. Moreover, for PTLs of differing thicknesses, it was not possible to precisely match gasket thicknesses, preventing exact equivalence in compression across all samples. Although not specifically investigated in this study, variations in CL compressibility with different PTL thicknesses or morphologies could potentially influence overall performance and RCL values, representing a topic for future study.
Ionic contributions to RCL were probed via changes in the ionomer content and electrolyte concentration. Fig. 4c shows the results of changing the ionomer content on RCL, adapted from our previous work.27 Here, high RCL at low ionomer content suggests insufficient ionic transport pathways. This result is consistent with the similar RCL for a CL constructed with 10 wt% Nafion, a non-anion conducting polymer (i.e., one that provides no anionic conductivity; black star in Fig. 4c). RCL improved as the ionomer content was increased to 5 and 10 wt%, suggesting that these quantities are sufficient to provide ionic transport networks. At 30 wt%, however, RCL increased significantly, suggesting segregation of catalyst particles and the ionomer phase, disrupting the catalyst–catalyst contact and electron transport, as has been seen previously.27,28 This can be seen clearly in SEM images of the catalyst layer at different ionomer contents, as shown in our previous work.27 Note that the ionomer content can also affect the CL structure and porosity,27 which may lead to differences in RCL caused by electronic resistances. It is therefore important to couple the assessment of RCL with other diagnostic techniques, such as cross-sectional microscopy, where possible. A comprehensive discussion on the influence of the ionomer content and electrolyte concentration on AEMWE performance is available in the literature.27,29,30
While the present study focuses on a single ionomer chemistry, we note that the identity of the ionomer can also influence RCL. For example, CLs prepared with 10 wt% Versogen versus 10 wt% Nafion exhibited differences in apparent porosity and in the homogeneity of the catalyst–ionomer distribution, and these differences were linked to catalyst–ionomer agglomeration tendencies in inks.27 Furthermore, strong binding of certain ionomers to catalytic active sites may also affect CL accessibility, and previous studies have shown that catalyst–ionomer interactions vary significantly with both the catalyst and the ionomer type.31
Ionic conductivity limitations were further probed by changing the electrolyte concentration with the fixed ionomer content (10 wt% PiperION), as shown in Fig. 4d. RCL decreased with increasing electrolyte concentration up to 1 M KOH, but there was a minimal change upon increasing to 2 M. This suggests that there is an ionic conductivity limitation that is benefited by the supporting electrolyte, but 1 M KOH is sufficient to overcome it, likely due to the increased ionic conductivity at higher concentrations.
The trends presented here are based on data collected for CLs in a supporting electrolyte environment. Overall, these trends are expected to persist for AEMWEs operated with pure-water feed; however, such systems require a dedicated study. For example, ion transport through the ionomer phase becomes more critical in a pure-water environment, potentially impacting RCL. Readers are referred to recent discussions on pure-water AEMWE operation for additional context.32–34
In summary, our VBA demonstrated that the intrinsic activity of catalyst materials does not solely determine the kinetic losses in device-level testing. Instead, we propose that RCL may also contribute to non-ideal kinetics at the device level and suggest that by improving CL design, it may be possible to bridge the gaps between intrinsic kinetics measured in half-cell, RDE testing and performance in MEAs. The calculated RCL values were found to range from 100 to 2000 mΩ cm2, emphasizing the importance of quantifying and diagnosing these resistances. We provide a discussion of the likely origins of RCL in AEMWEs and methods to diagnose and reduce these contributions. Specifically, we find that catalyst loadings must be optimized for each catalyst type based on the composition and inherent conductivity and that CLs should be constructed with low PTL porosities, intermediate ionomer contents (5–10 wt%), and supporting electrolytes (≥1 M KOH) to help decrease RCL and increase cell performances.
Conflicts of interest
There are no conflicts to declare.Data availability
The data presented in this manuscript were generated as part of the HydroGEN Energy Materials Network. While the data are not publicly available today, these data sets are currently going through approvals and will be available through the HydroGEN Data Hub, https://datahub.h2awsm.org/ in the near future.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5ya00310e.
Acknowledgements
This work was authored by the National Renewable Energy Laboratory for the U.S. Department of Energy (DOE) under contract no. DE-AC36-08GO28308. Funding was provided by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy Hydrogen Fuel Cell Technologies Office, through the HydroGEN Energy Materials Network. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.References
- E. K. Volk, M. E. Kreider, S. Kwon and S. M. Alia, Recent Progress in Understanding the Catalyst Layer in Anion Exchange Membrane Electrolyzers – Durability, Utilization, and Integration, EES. Catal., 2023, 2, 109–137, 10.1039/D3EY00193H.
- B. Motealleh, Z. Liu, R. I. Masel, J. P. Sculley, Z. Richard Ni and L. Meroueh, Next-Generation Anion Exchange Membrane Water Electrolyzers Operating for Commercially Relevant Lifetimes, Int. J. Hydrogen Energy, 2021, 46(5), 3379–3386, DOI:10.1016/j.ijhydene.2020.10.244.
- A. Caprì, I. Gatto, C. Lo Vecchio, S. Trocino, A. Carbone and V. Baglio, Anion Exchange Membrane Water Electrolysis Based on Nickel Ferrite Catalysts, ChemElectroChem, 2023, 10(1), e202201056, DOI:10.1002/celc.202201056.
- M. E. Kreider, A. R. Maldonado Santos, A. L. Clauser, M. E. Sweers, L. Hu, E. K. Volk, A.-L. Chan, J. D. Sugar and S. M. Alia, Porous Transport Layers for Anion Exchange Membrane Water Electrolysis: The Impact of Morphology and Composition, ACS Electrochem., 2025, 1(6), 897–909, DOI:10.1021/acselectrochem.4c00207.
- L. Osmieri, H. Yu, R. P. Hermann, M. E. Kreider, H. M. Meyer, A. J. Kropf, J. H. Park, S. M. Alia, D. A. Cullen, D. J. Myers and P. Zelenay, Aerogel-Derived Nickel-Iron Oxide Catalysts for Oxygen Evolution Reaction in Alkaline Media, Appl. Catal., B, 2024, 348, 123843, DOI:10.1016/j.apcatb.2024.123843.
- M. Mandal, Recent Advancement on Anion Exchange Membranes for Fuel Cell and Water Electrolysis, ChemElectroChem, 2021, 8(1), 36–45, DOI:10.1002/celc.202001329.
- H. N. Dinh; S. M. Alia; B. S. Pivovar; F. M. Toma; A. Z. Weber; D. Ding; G. Groenewold; A. McDaniel; A. Ambrosini; T. Ogitsu and B. Wood, HydroGEN Overview: A Consortium on Advanced Water Splitting Materials, Annual Merit Review DOE project (AOP WBS#): 2.7.0.518 (HydroGEN 2.0) & 2.7.0.513 (Node Support); 2022. https://www.hydrogen.energy.gov/docs/hydrogenprogramlibraries/pdfs/review21/p148_dinh_2021_o-pdf.pdf?sfvrsn=b10ed0e0_0 (accessed 2023-02-21).
- Z. Kang, H. Wang, Y. Liu, J. Mo, M. Wang, J. Li and X. Tian, Exploring and Understanding the Internal Voltage Losses through Catalyst Layers in Proton Exchange Membrane Water Electrolysis Devices, Appl. Energy, 2022, 317, 119213, DOI:10.1016/j.apenergy.2022.119213.
- M. Rogler, M. Suermann, R. Wagner, S. Thiele and J. Straub, Advanced Method for Voltage Breakdown Analysis of PEM Water Electrolysis Cells with Low Iridium Loadings, J. Electrochem. Soc., 2023, 170(11), 114521, DOI:10.1149/1945-7111/ad0b74.
- Z. Kang, S. M. Alia, M. Carmo and G. Bender, In-Situ and in-Operando Analysis of Voltage Losses Using Sense Wires for Proton Exchange Membrane Water Electrolyzers, J. Power Sources, 2021, 481, 229012, DOI:10.1016/j.jpowsour.2020.229012.
- M. Bernt, A. Siebel and H. A. Gasteiger, Analysis of Voltage Losses in PEM Water Electrolyzers with Low Platinum Group Metal Loadings, J. Electrochem. Soc., 2018, 165(5), F305, DOI:10.1149/2.0641805jes.
- E. Padgett, G. Bender, A. Haug, K. Lewinski, F. Sun, H. Yu, D. A. Cullen, A. J. Steinbach and S. M. Alia, Catalyst Layer Resistance and Utilization in PEM Electrolysis, J. Electrochem. Soc., 2023, 170(8), 084512, DOI:10.1149/1945-7111/acee25.
- W. Y. Noh, S. J. Kazmouz, S. Lee, J.-K. Peng, T. J. Shin and M. Shviro, Decoupling Electrode Kinetics to Elucidate Reaction Mechanisms in Alkaline Water Electrolysis, Energy Environ. Sci., 2025, 18(18), 8679–8696, 10.1039/D5EE03044G.
- E. K. Volk, S. Kwon and S. M. Alia, Catalytic Activity and Stability of Non-Platinum Group Metal Oxides for the Oxygen Evolution Reaction in Anion Exchange Membrane Electrolyzers, J. Electrochem. Soc., 2023, 170(6), 064506, DOI:10.1149/1945-7111/acd605.
- W. G. Cochran, The Flow Due to a Rotating Disc, Math. Proc. Cambridge Philos. Soc., 1934, 30(3), 365–375, DOI:10.1017/S0305004100012561.
- M. J. Eddowes, Numerical Methods for the Solution of the Rotating Disc Electrode System, J. Electroanal. Chem. Interfacial Electrochem., 1983, 159, 1–22 CrossRef CAS.
- F. Opekar and P. Beran, Rotating Disk Electrodes, J. Electroanal. Chem. Interfacial Electrochem., 1976, 69(1), 1–105, DOI:10.1016/S0022-0728(76)80129-5.
- S. Anantharaj, S. Noda, V. R. Jothi, S. Yi, M. Driess and P. W. Menezes, Strategies and Perspectives to Catch the Missing Pieces in Energy-Efficient Hydrogen Evolution Reaction in Alkaline Media, Angew. Chem., Int. Ed., 2021, 60(35), 18981–19006, DOI:10.1002/anie.202015738.
- N.-T. Suen, S.-F. Hung, Q. Quan, N. Zhang, Y.-J. Xu and H. M. Chen, Electrocatalysis for the Oxygen Evolution Reaction: Recent Development and Future Perspectives, Chem. Soc. Rev., 2017, 46(2), 337–365, 10.1039/C6CS00328A.
- J. Huang, Y. Gao, J. Luo, S. Wang, C. Li, S. Chen and J. Zhang, Editors’ Choice—Review—Impedance Response of Porous Electrodes: Theoretical Framework, Physical Models and Applications, J. Electrochem. Soc., 2020, 167(16), 166503, DOI:10.1149/1945-7111/abc655.
- R. de Levie, On Porous Electrodes in Electrolyte Solutions: I. Capacitance Effects, Electrochim. Acta, 1963, 8(10), 751–780, DOI:10.1016/0013-4686(63)80042-0.
- A. Lasia, Impedance of Porous Electrodes, ECS Trans., 2008, 13(13), 1, DOI:10.1149/1.3004025.
- H. Keiser, K. D. Beccu and M. A. Gutjahr, Abschätzung Der Porenstruktur Poröser Elektroden Aus Impedanzmessungen, Electrochim. Acta, 1976, 21(8), 539–543, DOI:10.1016/0013-4686(76)85147-X.
- G. Wang, L. Osmieri, A. G. Star, J. Pfeilsticker and K. C. Neyerlin, Elucidating the Role of Ionomer in the Performance of Platinum Group Metal-Free Catalyst Layer via in Situ Electrochemical Diagnostics, J. Electrochem. Soc., 2020, 167(4), 044519, DOI:10.1149/1945-7111/ab7aa1.
- K. C. Neyerlin, W. Gu, J. Jorne, A. Clark and H. A. Gasteiger, Cathode Catalyst Utilization for the ORR in a PEMFC: Analytical Model and Experimental Validation, J. Electrochem. Soc., 2007, 154(2), B279, DOI:10.1149/1.2400626.
- M. E. Kreider, H. Yu, L. Osmieri, M. R. Parimuha, K. S. Reeves, D. H. Marin, R. T. Hannagan, E. K. Volk, T. F. Jaramillo, J. L. Young, P. Zelenay and S. M. Alia, Understanding the Effects of Anode Catalyst Conductivity and Loading on Catalyst Layer Utilization and Performance for Anion Exchange Membrane Water Electrolysis, ACS Catal., 2024, 10806–10819, DOI:10.1021/acscatal.4c02932.
- E. K. Volk, A. L. Clauser, M. E. Kreider, D. D. Soetrisno, S. Khandavalli, J. D. Sugar, S. Kwon and S. M. Alia, Role of the Ionomer in Supporting Electrolyte-Fed Anion Exchange Membrane Water Electrolyzers, ACS Electrochem., 2024, 1(2), 239–248, DOI:10.1021/acselectrochem.4c00061.
- P. Mardle, B. Chen and S. Holdcroft, Opportunities of Ionomer Development for Anion-Exchange Membrane Water Electrolysis, ACS Energy Lett., 2023, 3330–3342, DOI:10.1021/acsenergylett.3c01040.
- E. Cossar, F. Murphy, J. Walia, A. Weck and E. A. Baranova, Role of Ionomers in Anion Exchange Membrane Water Electrolysis: Is Aemion the Answer for Nickel-Based Anodes, ACS Appl. Energy Mater., 2022, 5(8), 9938–9951, DOI:10.1021/acsaem.2c01604.
- A. P. L. Thévenot, T. Reiter, T. Ngo Thanh, L. Titze, C. Cazzaniga, F. Dionigi and P. Strasser, Ionomer Interphase Layers Enable Efficient Anion-Exchange Membrane Water Electrolyzer Operation at Low pH, Energy Fuels, 2025, 39(17), 8203–8210, DOI:10.1021/acs.energyfuels.5c00396.
- M.-A. Ha, E. K. Volk, O. Leitner, A. Isakov, H. J. González Vélez, S. Alia and R. Larsen, Complex Degradation Mechanisms Accessible to Anion Exchange Membrane Ionomers on Model Catalysts, NiO and IrO2, ACS Electrochem., 2025, 1(8), 1339–1351, DOI:10.1021/acselectrochem.5c00040.
- M. Muhyuddin, C. Santoro, L. Osmieri, V. C. A. Ficca, A. Friedman, K. Yassin, G. Pagot, E. Negro, A. Konovalova, G. Lindquist, L. Twight, M. Kwak, E. Berretti, V. D. Noto, F. Jaouen, L. Elbaz, D. R. Dekel, P. Mustarelli, S. W. Boettcher, A. Lavacchi and P. Atanassov, Anion-Exchange-Membrane Electrolysis with Alkali-Free Water Feed, Chem. Rev., 2025, 125(15), 6906–6976, DOI:10.1021/acs.chemrev.4c00466.
- Y. Zheng, A. Serban, H. Zhang, N. Chen, F. Song and X. Hu, Anion Exchange Ionomers Enable Sustained Pure-Water Electrolysis Using Platinum-Group-Metal-Free Electrocatalysts, ACS Energy Lett., 2023, 8(12), 5018–5024, DOI:10.1021/acsenergylett.3c01866.
- S. Hou, A. Sekar, Y. Zhao, M. Kwak, J. Oh, K. K.-Y. Li, P. Wu, R. T. Hannagan, V. Cartagena, A. C. Ekennia, H. Duan, M. J. Zachman, J. Frechette, G. M. Su, B. Lakshmanan, Y. Yan, T. F. Jaramillo and S. W. Boettcher, Durable, Pure Water–Fed, Anion-Exchange Membrane Electrolyzers through Interphase Engineering, Science, 2025, 390(6770), 294–298, DOI:10.1126/science.adw7100.
| This journal is © The Royal Society of Chemistry 2026 |