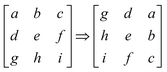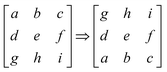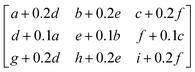Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Advanced fault detection in PV panels using deep neural networks: leveraging transfer learning and electroluminescence image processing
Ihtesham
Ibn Malek
 and
Hafiz
Imtiaz
and
Hafiz
Imtiaz
 *
*
Department of Electrical and Electronic Engineering, Bangladesh University of Engineering and Technology, Dhaka-1205, Bangladesh. E-mail: shanto.bin.malek@gmail.com; hafiz.imtiaz@eee.buet.ac.bd
First published on 9th December 2025
Abstract
Photovoltaic (PV) systems are susceptible to different types of faults, such as electrical, physical, and environmental issues, which can significantly impact power generation and system reliability. Physical faults, such as cracks, delamination, shading, dirt accumulation, and temperature fluctuations, can reduce module efficiency by altering irradiance levels. To address these challenges, accurate and timely fault detection is essential for ensuring optimal PV system performance and longevity. In this work, we propose a novel machine learning (ML) approach for fault detection using unlabeled electroluminescence (EL) images of PV panels. First, we label the dataset through k-means clustering, applied to features extracted using transfer learning (TL) from a pre-trained VGG-16 model's convolutional and pooling layers. k-Means clustering categorizes the images into three classes based on Silhouette scores, with all healthy panels grouped together. We employ Principal component analysis (PCA) to reduce dimensionality, revealing that 64 principal components account for 95% of the variance in the data. Finally, we train and evaluate classical ML models, including random forest (RF) for binary classification and logistic regression (LR) for three-class classification, achieving accuracies of 97.54% and 89.44%, respectively. We empirically demonstrate that data augmentation further improves the performance of the three-class classification, with RF emerging as the best classifier at 91.5% accuracy. Additionally, we note that the convolutional neural network (CNN) model, which is comparatively lightweight and computationally efficient, saw an increase in accuracy from 98% to 99.5% with data augmentation for binary classification, while the semi-supervised learning approach for the three-class problem achieved an average accuracy of 92.25%. By combining TL, k-means clustering, and data augmentation, our proposed approach enhances fault detection accuracy, reduces reliance on manual labeling, and improves PV system reliability. The proposed method advances automated fault detection techniques and supports the broader adoption of renewable energy systems.
1 Introduction
The global shift towards renewable energy sources has intensified the adoption of photovoltaic (PV) power systems, positioning them as a viable alternative to conventional fossil fuel-based and nuclear power plants.1–3 The increasing focus on climate change and energy security has positioned PV technology as an environmentally responsible option, leveraging solar energy with minimal carbon output.4,5 Unlike traditional power generation methods, PV systems offer significant advantages, including reduced operational costs, decentralized energy production, and improved energy accessibility in remote areas.6,7 Additionally, PV systems enhance grid stability by integrating distributed energy resources, thereby reducing dependency on centralized power generation.8,9 However, the transition to PV-based energy systems also introduces new technical challenges,10 particularly in maintaining system reliability and efficiency in diverse environmental conditions.11,12Despite the numerous benefits of PV systems, their operational efficiency is often compromised by various types of faults that affect energy output and system longevity. These faults can be broadly classified into electrical, physical, and environmental categories – each posing unique challenges to fault detection and diagnosis.13,14 Electrical faults, such as open circuits, short circuits, and degradation of wiring connections, can lead to severe power losses, increased safety risks, and potential system failures.15 Physical faults, including micro-cracks, delamination, and corrosion, gradually degrade PV module performance, reducing their lifespan. Meanwhile, environmental faults, such as shading, soiling, and temperature fluctuations, cause efficiency losses by affecting the irradiance levels received by the PV panels.16 Among these, physical and environmental faults are particularly critical, as they often remain undetected in early stages, resulting in irreversible damage and increased maintenance costs over time.17 Therefore, precise and timely fault detection is crucial for ensuring the durability and optimal performance of PV installations.18 To address these challenges, researchers have explored various fault detection methodologies, ranging from traditional model-based approaches to advanced data-driven techniques.19 Model-based methods, such as equivalent circuit modeling and analytical techniques, provide theoretical insights into PV system behavior but require extensive parameter tuning, making them less adaptable to real-world variations.20
Real-time monitoring methods, including infrared thermography and electroluminescence (EL) imaging, offer practical means of identifying physical defects but often demand specialized equipment and favorable environmental conditions for accurate assessment.21 Similarly, output signal analysis techniques, such as wavelet transforms and statistical methods, have demonstrated promising results in detecting anomalies in PV performance. However, they lack robustness when dealing with large-scale and complex PV arrays.22 Recent advancements in machine learning (ML) have revolutionized PV fault detection by enabling automated and high-accuracy classification of faults based on historical data and real-time measurements.23 Traditional ML techniques, such as support vector machines (SVMs) and decision trees (DTs), have been applied to fault diagnosis with varying levels of success, achieving detection accuracies of up to 99.5% for electrical faults.13 Additionally, thermography-based fault classification has demonstrated 93.4% accuracy,21 while wavelet transform approaches using radial basis function networks have reached 97% efficiency in identifying faults within a 1kW PV system.22 Among ML-based approaches, deep learning models,24 notably convolutional neural networks (CNNs), have demonstrated superior performance in detecting physical and environmental faults by analyzing image-based datasets.25 However, a persistent challenge in applying CNN-based models to PV fault detection is the reliance on well-labeled datasets, as mislabeling in training data significantly impacts model accuracy and generalization.26
Existing research has highlighted the limitations of supervised learning approaches in PV fault detection, emphasizing the need for improved dataset quality and labeling techniques. Manual annotation of PV fault images is labor-intensive and error-prone, while the scarcity of publicly available labeled datasets restricts model scalability. To mitigate these challenges, some studies have explored unsupervised clustering methods to enhance dataset organization; however, their applicability to large-scale PV datasets remains an open question.26 Additionally, semi-supervised learning (SSL) has emerged as a promising approach, combining limited labeled data with a large amount of unlabeled data to improve model performance.27
Recent studies have further advanced PV fault detection by integrating deep learning, IoT, and enhanced monitoring strategies. For instance, Aljafari et al.28 proposed a 1D-CNN combined with an IoT platform for grid-connected PV systems, achieving fault detection accuracies of 98.15% under normal conditions and 93.12% under cyberattacks, leveraging optimally placed sensors and a temperature-dependent PV model for real-time monitoring. Similarly, Awedat et al.29 enhanced U-Net architectures with Residual Blocks, Atrous Spatial Pyramid Pooling (ASPP), and Attention Mechanisms to improve feature extraction, contextual understanding, and fault localization from thermal images, addressing environmental noise and subtle anomalies. Moreover, Satpathy et al.30 investigated electrical fault tolerance of various PV array configurations using MATLAB simulations, prototype experiments, and a low-cost monitoring system with optimal sensor placement and web-based alerts, demonstrating practical real-time fault detection and highlighting the robustness of series-parallel configurations. These studies collectively emphasize the effectiveness of combining deep learning with advanced monitoring and real-time IoT-enabled systems, highlighting the growing trend towards practical, accurate, and scalable PV fault detection frameworks. In addition,31 proposed SPF-Net, combining InceptionV3-Net with U-Net for PV fault detection, achieving a validation accuracy of 98.34% and an F1 score of 0.94.32 applied ResNet architectures on EL images for crack detection, with ResNet34–152 yielding F1-scores between 86.63% and 88.89%.33 introduced an OpenCV-based automated method for hotspot detection using grayscale conversion, histogram analysis, and adaptive thresholding, providing efficient and scalable PV panel monitoring. These studies further demonstrate the effectiveness of deep learning and image processing for accurate PV fault detection.
Furthermore, while transfer learning (TL) has proven effective in other domains of image classification, its integration with clustering methodologies for PV fault detection remains a field to contribute.34 Addressing these gaps is essential for developing scalable and automated fault detection frameworks that can adapt to real-world PV deployment scenarios.
An additional but often overlooked aspect of PV fault detection is the impact of domain-specific variations on classification performance. Factors such as environmental heterogeneity, panel aging effects, and variations in PV module technologies introduce inconsistencies in fault characteristics, leading to reduced model reliability.35 Standard ML models often struggle with generalization when trained on limited or specific datasets from various PV installations, necessitating adaptive learning techniques and domain adaptation strategies to enhance robustness.36 By incorporating augmentation mechanisms, ML-based fault detection models can achieve higher consistency and accuracy across diverse PV environments, thereby improving their practical applicability.37
In this work, we present a machine learning-based approach for detecting physical and environmental faults in PV systems using electroluminescence (EL) imaging. Our approach addresses the challenge of working with unlabeled panel images by combining TL, k-means clustering to improve both dataset quality and classification performance. Feature extraction is performed using the convolutional and pooling layers of a pre-trained VGG-16 model. The extracted features are then clustered into three categories using k-means clustering, creating labeled data for supervised learning. To further refine the dataset, principal component analysis (PCA)38–40 is applied, reducing dimensionality while preserving essential information. The labeled dataset is then used to train classical machine learning models for both binary and three-class classification tasks with data augmentation. Note that, a CNN model is trained separately for binary classification, while a SSL approach is used to improve performance in the three-class problem. By integrating k-means clustering for dataset labeling and leveraging TL for feature extraction, our approach enhances fault detection accuracy and increases the reliability of PV systems. Addressing key challenges such as automated data labeling, domain adaptation, and scalability, this work contributes to advancing intelligent fault detection methods for real-world PV applications.
2 Proposed methodology
We aim to classify physical and environmental faults in PV panels. These faults can be due to physical damage, such as cracks, or environmental issues, such as shading. A critical challenge in this task is the need to effectively handle large datasets, as traditional machine learning techniques41 often struggle with the complexity of image-based data. Misclassifications can lead to power losses, especially when faulty panels are misidentified as normal. Given the significant impact of faults on the power output of PV systems, it is essential to use robust algorithms capable of identifying these faults accurately. CNNs are particularly well-suited for this task due to their powerful feature extraction capabilities, making them ideal for image-based fault detection in PV panels.Fig. 1 illustrates the comprehensive workflow of this study. Initially, EL images are captured from the PV panels, which are then transferred to a computer system for data acquisition. In the next step, the acquired data undergo a labeling process, where the features extracted from the images through TL are clustered using the k-means algorithm. Data augmentation methods are then employed to synthetically expand the dataset, improving the model's capacity to generalize. In the training phase, convolutional layers within a CNN extract meaningful features from the enriched dataset, while pooling layers condense spatial information to enhance computational efficiency. Ultimately, the fully connected layers interpret these extracted features and classify the image, determining its condition based on learned representations.
2.1 Transfer learning enhanced k-means clustering
To improve the efficiency of image classification, we employed transfer learning by leveraging the pre-trained Visual Geometry Group (VGG16) model available in Keras, originally trained on the ImageNet dataset. VGG16 consists of 13 convolutional layers, 5 max-pooling layers, and 16 weighted layers.42 The rationale for selecting VGG16 lies in its proven ability to extract high-level spatial features from images, significantly reducing the computational complexity associated with training a deep learning model from scratch. By utilizing the convolutional and pooling layers of VGG16, we extracted meaningful representations from input images, facilitating a faster and more accurate classification process.Once the feature representations were obtained from the VGG16 model, we applied k-means clustering to group the images based on similarity. k-Means clustering is an iterative, centroid-based clustering algorithm that partitions a dataset into k clusters.43 The process begins by initializing k cluster centroids, followed by assigning each data point to the closest centroid using Euclidean distance. The centroids are progressively revised through successive iterations, with their positions recalculated as the average of the data points assigned to each cluster. This iterative process continues until convergence, ensuring that data points within the same cluster exhibit high similarity.26
By integrating TL with k-means clustering, we improved clustering accuracy and effectively identified patterns within the dataset. This method enabled the unsupervised labeling of images, leading to a refined classification of photovoltaic (PV) panel conditions, as illustrated in Fig. 2.
 | ||
| Fig. 2 k-Means clustering followed by transfer learning for feature extraction. The pre-trained VGG16 model extracts deep features, which are subsequently clustered using k-means. | ||
The overall workflow involves modifying the VGG16 model to extract feature vectors from the fully connected ‘fc2’ layer. Prior to clustering, the images were preprocessed by resizing them to 224 × 224 pixels to match the input dimensions of VGG16. These images were then passed through the model to obtain deep feature representations, which were subsequently clustered using the k-means algorithm. The optimal number of clusters was determined using silhouette analysis, which evaluates clustering quality based on the silhouette score. The best-performing value of k was selected by identifying the highest silhouette score, and k-means ++ was utilized to initialize cluster centroids more effectively.
For clarity in interpretation, images assigned to cluster 0 were labeled as “Normal,” whereas those in clusters 1 and 2 were labeled as “Faulty.”
2.2 Image augmentation
To enhance dataset diversity and improve the model's generalization capability, image augmentation techniques were applied.44 These augmentations were performed dynamically during training to mitigate overfitting and increase robustness against real-world variations.45 The transformations employed are detailed below:We clarify that all the 3 × 3 matrices described above serve only as didactic representations to illustrate the augmentation operators mathematically. The full-resolution EL images were actually used for augmentation, as shown in the Results section, and these represent the real transformations applied to the dataset.
The augmentation process was implemented using Keras’ ImageDataGenerator class, which dynamically generated augmented images during training. Each image underwent transformations such as rotation, zoom, and flip with specified probabilities, increasing dataset variability. Images were resized to a standard resolution, and pixel values were scaled to remain within the bounds of [0,1]. For each original image, up to five augmented images were generated and stored alongside the original dataset. These augmentations enhanced the model's capacity to generalize across a wide range of real-world scenarios, reducing overfitting and improving classification performance on unseen data.
2.3 Convolutional neural network
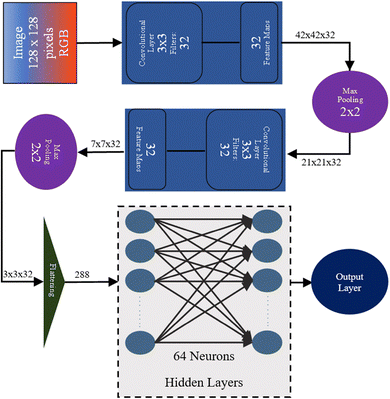
This section details the use of CNNs to classify solar PV panel images into two categories: healthy and faulty. To simplify the classification problem, all panels exhibiting physical or environmental faults are grouped into a single class labeled as faulty. This results in a binary classification task aimed at distinguishing operational PV panels from defective ones.The dataset used for training and evaluation consists of labeled RGB images, each resized to a uniform dimension of 128 × 128 pixels. The CNN model in Fig. 3 extracts meaningful features from these images using multiple convolutional layers.46 Initially, 32 convolutional filters of size 3 × 3 are applied to detect spatial features, such as edges and textures. Following this, a max-pooling layer with a window size of 2 × 2 is employed to reduce the spatial dimensions while retaining the most critical features. This downsampling reduces the image size to 21 × 21 × 32, optimizing computational efficiency. A second convolution and max-pooling sequence is then applied, further refining feature extraction before flattening the output into a one-dimensional feature vector comprising 288 elements. These extracted features are then fed into fully connected dense layers for final classification.
The network architecture is outlined in Table 1. Each layer processes its input by computing a weighted sum of activations from the preceding layer, which is then transformed through an activation function. The rectified linear unit (ReLU) activation function, as defined in eqn (1), is used for the input and hidden layers to introduce non-linearity:
| y = max(0, x) | (1) |
| Parameters | Values |
|---|---|
| Algorithm | Backpropagation |
| Activation function | ReLU (input/hidden layers), sigmoid (output layer) |
| Layers | 2 hidden layers with 64 units each |
| Loss function | Binary cross-entropy |
| Optimizer | Adam |
| Data split | Train: 70%, validation: 20%, test: 10% |
| Batch size | 50 |
| Epochs | 100 |
| Tuning | Dropout |
| Augmentation | 5 types |
Here, negative inputs are mapped to zero, while positive inputs are retained, aiding efficient gradient propagation. The output layer employs a sigmoid activation function to map the network's final predictions to a probability range between 0 and 1, suitable for binary classification, as defined in eqn (2):
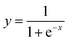 | (2) |
The model's performance is evaluated using the binary cross-entropy loss function, formulated in eqn (3), where y represents the actual class label, ŷ is the predicted probability, and N is the total number of samples:
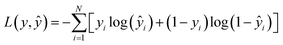 | (3) |
The network is optimized using the Adaptive Moment Estimation (Adam) optimizer, which dynamically adjusts learning rates for faster convergence. The dataset is partitioned into training, validation, and test sets in a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 ratio. The training process employs a batch size of 50 and runs for 100 epochs. To enhance generalization and prevent overfitting, dropout layers with rates of 10% and 20% are introduced in the initial and subsequent hidden layers. In addition, techniques for data augmentation are employed to expand the training dataset.
10 ratio. The training process employs a batch size of 50 and runs for 100 epochs. To enhance generalization and prevent overfitting, dropout layers with rates of 10% and 20% are introduced in the initial and subsequent hidden layers. In addition, techniques for data augmentation are employed to expand the training dataset.
The CNN model is implemented using TensorFlow and is structured to efficiently extract hierarchical features from images. The network consists of an initial convolutional layer with 32 filters of size 3 × 3, followed by a ReLU activation function. A max-pooling layer with a 2 × 2 window is then used to reduce spatial dimensions and computational cost. This sequence of convolution followed by pooling is repeated to extract progressively abstract features.
Following feature extraction, the output is flattened into a one-dimensional vector and passed through dense layers consisting of 64 neurons with ReLU activation. To regularize the model, dropout layers with rates of 10% and 20% are included before the final output layer. The model outputs a binary classification prediction using a single neuron with a sigmoid activation function. The network is compiled with binary cross-entropy as the loss function and the Adam optimizer, while accuracy is used as the primary evaluation metric.
2.4 Semi-supervised learning
Semi-supervised learning is a powerful approach that leverages a small amount of labeled data in conjunction with a large pool of unlabeled data to improve model performance.47 The process typically consists of two main stages: an initial supervised training phase followed by a pseudo-labeling phase,48 as illustrated in Fig. 4.In the first stage, a CNN is trained on a small subset of labeled data to learn essential patterns from the dataset. Once trained, this model is then employed to create pseudo labels for the much larger unlabeled dataset. These pseudo-labeled samples are subsequently combined with the original labeled data to train a more robust CNN model in the second stage. Finally, the trained model is evaluated on a separate test set to classify unseen samples accurately. By utilizing the vast amount of unlabeled data in this iterative manner, SSL helps mitigate the limitations of data scarcity and enhances classification performance.
3 Experimental results and discussions
This section presents the results of the data labeling, data augmentation, feature extraction, and performance evaluation of classical machine learning models, CNN, and semi-supervised learning techniques.3.1 Data labeling
In the process of detecting faults in solar PV panels, images are essential for identifying potential issues such as cracks or shaded regions. Fig. 5a illustrates the various conditions of solar panels: healthy panels, panels with visible cracks (physical faults), and panels with shaded regions (environmental faults). Faulty panels are those with either cracks or shading, while healthy panels are categorized separately. This classification approach results in a binary image classification problem for distinguishing between physical and environmental faults. For our analysis, we used a dataset comprising 2000 unlabeled images of solar panels to detect faults, as referenced in ref. 49. | ||
| Fig. 5 (a) EL images of PV panels under different conditions: healthy panel, panel with cracks, and panel with shading. (b) Silhouette scores for various cluster numbers (k). | ||
For fault classification in PV arrays, the model adopts a neural network-based architecture combined with a supervised learning approach. This approach requires both feature extraction and labeled data to make accurate predictions. In the case of detecting physical and environmental faults, features are extracted from images using convolutional layers and kernel filters, which play a crucial role in identifying key patterns in the images. Effective preprocessing and feature extraction are essential to enhance classification performance.
Given the absence of labels in the training dataset, we initially applied an unsupervised method for labeling, specifically using k-means clustering. The pre-trained VGG16 model was leveraged for feature extraction, with the goal of generating two clusters. However, a two-cluster solution did not yield optimal results, leading us to explore the most suitable number of clusters for better performance. The Silhouette method50 was utilized to assess the quality of clustering for various values of k. The Silhouette scores, shown in Fig. 5b, indicate the highest score for k = 6, suggesting that this clustering option may provide the most distinct separation of the data.
Despite the higher Silhouette score at k = 6, a smaller number of clusters would simplify the classification task. Given this trade-off, we opted for k = 3, which provides a reasonable balance between clustering quality and simplicity. In this configuration, the dataset was divided into three clusters: one representing healthy panels, and the other two encompassing both cracked and shaded defective panels, which were manually corrected. As a result, the final classification was achieved with two distinct categories: healthy panels and faulty panels. The labeled images, along with their corresponding labels, are shown in Fig. 6.
Although the Silhouette analysis indicated that k = 6 yields the highest cluster separation with k = 3 being a close second, the resulting groups for k = 6 did not correspond to meaningful physical categories when visually examined. Several clusters contained mixed samples of cracked and shaded panels, indicating that a purely mathematical optimum did not guarantee physically interpretable groupings. To ensure label reliability, each cluster, whether in the k = 3 or k = 6 configuration, was manually validated by visually reviewing the electroluminescence patterns in the images. This validation step confirmed whether a panel was healthy, cracked, or shaded, and helped eliminate inconsistencies introduced by unsupervised clustering. The manual inspection revealed that the three-cluster configuration produced cleaner, more stable groups that aligned with actual physical conditions.
To further examine the reliability of the automatically generated labels, we assessed the cluster-condition consistency through manual inspection. As shown in Table 2, the k = 3 configuration exhibits high purity: summing the correctly labeled panels along the diagonal (568 + 406 + 875 = 1849) out of 2000 yields a cluster purity of 92.45%. This confirms that the pseudo-labels derived from VGG16 features are sufficiently accurate for downstream supervised training and do not introduce significant label noise. These validated labels were subsequently used to train the CNN model for physical and environmental fault classification.
| Cluster no. | Healthy | Cracked | Shaded |
|---|---|---|---|
| First cluster | 568 | 0 | 0 |
| Second cluster | 0 | 406 | 93 |
| Third cluster | 0 | 58 | 875 |
3.2 Feature extraction and augmentation
The features were extracted from the labeled image data using the convolutional and pooling layers of the pre-trained VGG16 model, resulting in a total of 4096 (=212) features. Since visualizing all these features is challenging, PCA was applied to reduce the dimensionality. The results of PCA are shown in Fig. 7, where the individual variance ratios (VRs) are depicted on the primary Y-axis, while the cumulative variance is shown on the secondary Y-axis.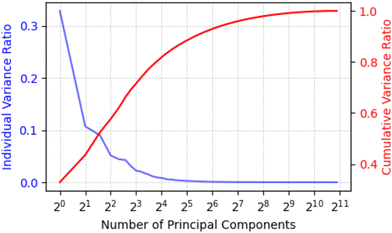 | ||
| Fig. 7 PCA VRs: individual VR on the primary Y-axis and cumulative variance on the secondary Y-axis. | ||
From the PCA analysis, we observed that the individual variance ratios drop significantly beyond the first 26 = 64 components. In other words, selecting these 64 components captures ∼95% of the total variance, ensuring that the most informative features from the VGG16 embeddings are preserved. The purpose of choosing 26 components is therefore to reduce dimensionality while retaining the essential signal for downstream reconstruction and analysis, balancing efficiency with information retention. The graph reveals that nearly 26 features contribute significantly to the data, as the individual VR tends to zero beyond this point, and the cumulative variance reaches approximately 95%. To further reduce the dimensionality and capture the most significant components, we selected principal components (PCs) at 21, 23, 25, and 27 for image reconstruction. This was done by taking the corresponding number of PCs, performing an inverse transformation, and reconstructing the images from the reduced set of components. The reconstructed images based on these selected PCs are shown in the upper row of Fig. 8.
 | ||
| Fig. 8 Image reconstruction using the selected PCs at 21, 23, 25, and 27 (upper row) and image augmentation techniques (lower row). | ||
Additionally, five augmentation methods were applied to the images to enhance the dataset and improve the robustness of the model. These methods included random rotation of the images, flipping the images vertically, and zooming with random zooming transformations. The brightness levels of the images were adjusted through brightness adjustment, and shearing transformations were applied to introduce random shearing effects. These augmentations introduced variability into the dataset, helping the model generalize better during training. The results of these augmentations are shown in lower row of Fig. 8. These augmented images demonstrate the diversity introduced to the dataset, which is expected to help improve the model's generalization capabilities.
3.3 Classical ML models performances
The performance of various classical machine learning models, trained on labeled data with extracted features for both binary and three-class classification tasks, is shown in Table 3. The models evaluated include Logistic Regression (LR), DT, SVM, K-Nearest Neighbors (KNN), and Random Forest (RF).51 For the binary classification, RF achieved the highest accuracy of 97.54%, followed by KNN with 96.65%. Both models also excelled in precision, recall, and F1-score, indicating their overall robustness in handling the binary classification task. LR, while having a slightly lower accuracy of 96.13%, demonstrated competitive precision and recall values.| Model | Binary | 3-Class | ||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | Accuracy | Precision | Recall | F1-Score | |
| LR | 0.9613 | 0.94 | 0.93 | 0.94 | 0.8944 | 0.95 | 0.93 | 0.94 |
| DT | 0.9560 | 0.94 | 0.92 | 0.93 | 0.8169 | 0.94 | 0.89 | 0.92 |
| SVM | 0.9560 | 0.94 | 0.92 | 0.93 | 0.8539 | 0.94 | 0.93 | 0.93 |
| KNN | 0.9665 | 0.92 | 0.98 | 0.95 | 0.8415 | 0.92 | 0.98 | 0.95 |
| RF | 0.9754 | 0.96 | 0.97 | 0.96 | 0.8820 | 0.95 | 0.96 | 0.96 |
In the three-class classification scenario, LR performed the best in terms of accuracy at 89.44%, though this is notably lower than its binary classification performance. Other models, like DT and KNN, showed lower accuracy, with DT scoring 81.69% and KNN achieving 84.15%. The precision, recall, and F1-score values are also generally lower in the three-class case compared to the binary classification. A closer inspection reveals that, in the three-class classification task, LR performed better than expected, but RF and SVM showed decreased performance compared to their binary classification counterparts. This is due to the added complexity of the three-class classification task.
This highlights that the three-class task tends to reduce overall accuracy and precision, with the models having to deal with an additional class and more variability in the data. To improve model performance for three-class classifications, data augmentation techniques were applied, and the results are shown in Fig. 9, where an increase in accuracy and precision is observed on the primary y-axis, and recall values are shown on the secondary y-axis. It is evident that all models, except LR, show increased accuracy after augmentation. Furthermore, precision and recall increased for all models except KNN, suggesting that data augmentation helped improve the generalization ability of most models. After applying data augmentation, the RF model demonstrated the most significant improvement, achieving an accuracy of 91.5% in the three-class classification, up from 88.2% without augmentation. RF consistently outperformed other models in binary classification tasks, while LR showed relatively balanced performance across both binary and three-class classifications. The results of the data augmentation process further support these findings, where an improvement in model robustness is evident.
3.4 Performance of CNN for binary-classification
The CNN model's performance is assessed using a confusion matrix, shown in Fig. 10. This matrix offers important insights into the model's classification accuracy. Notably, the CNN model accurately classified 56 panels as healthy, and 140 faulty panels were correctly identified, demonstrating its effectiveness in distinguishing between healthy and faulty panels. However, there were 4 misclassified panels, indicating that there is room for improvement. These misclassifications could stem from various factors, such as ambiguity in the images or limitations in the model's capacity to distinguish subtle differences between panel conditions. These errors underscore the need for further refinement in the model, such as additional training data or tuning of hyperparameters.In terms of model robustness, a critical indicator is the validation accuracy during training. A well-performing model generally demonstrates higher validation accuracy than training accuracy, indicating its ability to generalize well to unseen data. In our case, this trend is observed, with the validation accuracy consistently surpassing the training accuracy across most epochs. This is a positive sign, as it suggests that the model is not overfitting to the training data and is instead learning to generalize better.
Furthermore, Fig. 11a presents a plot that shows the accuracy of the CNN model over the number of epochs. It is evident that the model reached a peak accuracy of 98% at both the 54th and 95th epochs, highlighting its ability to learn effectively from the data. While it might seem tempting to improve accuracy further by increasing the number of hidden layers or epochs, doing so may lead to overfitting, where the model performs well on the training data but struggles to generalize to new, unseen data. Therefore, it's important to balance model complexity to avoid overfitting while still achieving optimal performance. Based on this accuracy trend, the current architecture seems well-tuned for the task at hand. Fig. 11b presents the loss curve of the CNN model. The validation loss is consistently lower than the training loss throughout the epochs, showing that the model generalizes well. This trend is consistent with the accuracy curve in Fig. 11a, reflecting stable and effective learning as the model optimizes over time.
 | ||
| Fig. 11 Training results of the model: (a) accuracy versus number of epochs; (b) loss versus number of epochs, for both training and validation. | ||
The CNN model shows strong performance with accurate fault detection in solar panels, with only minor misclassifications. The confusion matrix and accuracy plot both provide clear insights into its effectiveness and potential areas for improvement. The model's behavior indicates it is learning well, as evidenced by its consistent validation accuracy and high peak accuracy, while avoiding overfitting. Additionally, its relatively low-density architecture makes it lightweight and computationally efficient.
Finally, data augmentation was applied to further enhance the model's accuracy, as observed with the improvement in classical machine learning model performance. Given that healthy panel images constitute almost half of the number of faulty panel images, five augmentation methods were applied to the healthy panel images, and two augmentation methods were applied to the faulty panels. This balanced the dataset and boosted the performance from 98% to 99.5% as shown in Fig. 12a. This indicates that data augmentation plays a crucial role in enhancing the model's ability to generalize, particularly in cases where the dataset is imbalanced, and it demonstrates the power of augmenting the data to achieve higher accuracy in real-world applications.
 | ||
| Fig. 12 Performance evaluation of the proposed model: (a) confusion matrix for healthy and faulty classes; (b) ROC curve of the classifier. | ||
To further ensure the robustness of this result, we explicitly confirmed that all augmented samples were restricted to the training split only, with strict separation between augmented data and both the validation and test sets, thereby preventing any possibility of data leakage or artificially inflated accuracy. The validation accuracy consistently remained higher than the training accuracy throughout training, indicating strong generalization and absence of overfitting. Additionally, the confusion matrix in Fig. 12a shows that misclassifications remained minimal across both classes, confirming stability of the classifier. Because the test and validation sets share the same distribution and no augmented images enter either split, the validation confusion matrix at the best epoch was numerically identical to the test confusion matrix, demonstrating consistent performance across unseen data. The ROC curve in Fig. 12b further supports this conclusion: the model's curve (orange) lies well above the navy dashed line representing a random classifier, achieving an area under the curve (AUC) of 99.05%, indicating near-perfect discrimination between the two classes. To further verify robustness, we conducted five independent runs of 10 epochs each. These runs differ due to randomness in weight initialization, data shuffling, and dropout layers. A t-test yielded t = 0.731, p = 0.518, showing no statistically significant difference between runs. This demonstrates the stability and reliability of the reported performance. The performance gain is therefore attributable to the targeted augmentation strategy used to correct class imbalance, rather than to training randomness or accidental data leakage.
The computational profile of the proposed method was also evaluated. Full model training required approximately 1168.18 seconds with a peak memory usage of 25.17 MB, which corresponds to one-time offline training and therefore does not affect deployment. For real-time PV monitoring, the relevant factor is inference time, which is significantly lower; a single forward pass completes within tens to hundreds of milliseconds on standard embedded hardware. Given its modest memory footprint and fast inference characteristics, the proposed CNN architecture is suitable for embedded PV inspection systems requiring real-time operation.
3.5 Performance of semi-supervised learning
The performance of the semi-supervised learning approach is evaluated. The model was trained with a combination of labeled and unlabeled data, where 10% of the data was used for testing, 30% for training, and the remaining 60% was treated as unlabeled data for pseudo-labeling. The average accuracy of the model was evaluated as a function of the percentage of labeled data. As shown in Fig. 13, the model achieved its maximum accuracy of 92.25% when 30% of the data was labeled. This highlights the effectiveness of SSL, where the inclusion of unlabeled data through pseudo-labeling helps improve the model's generalization ability. We note that pseudo-labels were assigned only to unlabeled samples for which the model predicted class probabilities above a confidence threshold of 0.95, while low-confidence samples were excluded to mitigate error propagation. The model was iteratively retrained after adding high-confidence pseudo-labeled data, and the remaining unlabeled samples were re-evaluated in subsequent iterations, ensuring reliability of the pseudo-labeling process.In Fig. 14, the confusion matrix for the SSL model is presented, with the iteration that gives the maximum accuracy of 92.5% at 30% labeled data. The diagonal values reflect the correct predictions for each class, while the off-diagonal values indicate the instances of misclassification. Specifically, the model shows strong performance in classifying the Healthy and Shaded classes, with only a few misclassifications. The Cracked class, however, experiences a higher number of misclassifications, particularly with the Other faults class. This is primarily due to inherent similarities in the EL patterns of Cracked and Shaded panels. The test sample labels were manually verified and corrected, ensuring that labeling errors do not contribute to these misclassifications. Despite this challenge, the iterative pseudo-labeling process and high-confidence filtering ensure robust overall performance, even when a large portion of the training data is unlabeled, as reflected in the final SSL accuracy of 92.25%.
3.6 Comparative analysis
Table 4 compares various classification methods and results across several studies in the field of PV panel image classification. In particular, our work demonstrates a significant advantage in both dataset labeling and accuracy when compared to the other approaches.| Study | Classes | Samples | Training portion (%) | Data labeling | Feature extraction | Classification method | Accuracy |
|---|---|---|---|---|---|---|---|
| Akram et al.52 | 2 | 3217 | Manual | CNN | 93.02% | ||
| Deitsch et al.53 | 2 | 1968 | CNN | 88.42% | |||
| Demirci et al.54 | 2 | 2624 | DFB | SVM | 94.52% | ||
| Et-taleby et al.55 | 2 | 2624 | 75% | VGG16 | SVM | 99.49% | |
| Al-Otum56 | 4 | 2624 | 70% | CNN | 88.60% | ||
| Ozturk et al.57 | 2 | 1720 | 80% | CNN | 95% | ||
| Abdelsattar et al.58 | 2 | 3102 | 80% | CNN | Mobilenetv2 | 99.95% | |
| Tella et al.59 | 4 | 2624 | — | CNN | Resnet18 | 73.02% | |
| Karakan60 | 3 | 5836 | 75% | CNN | SqueezeNet | 97.82% | |
| This-work | 2 | 2000 | 70% | k-Means, TL | CNN | 99.5% | |
| 3 | — | SSL | 92.5% | ||||
Our approach utilizes k-means clustering for automated data labeling combined with transfer learning techniques. Unlike many of the previous studies that rely on manual labeling, this hybrid approach allows for efficient handling of large datasets and reduces the need for labor-intensive manual annotation, which is often a bottleneck in machine learning workflows. The k-means clustering method automatically labels the dataset, while transfer learning helps to transfer knowledge from pre-trained models, thus improving performance even with a relatively smaller dataset.
Regarding accuracy, as seen in the table, our method achieves an impressive accuracy of 99.5% on a dataset with 2 classes, which is higher than many other approaches listed. For instance, the closest competitor is the study by ref. 58, which achieved 99.95%, but this study used a larger training dataset (3102 samples compared to our 2000 samples). Additionally, our method uses only 70% of the dataset for training, further demonstrating the robustness of our approach despite a comparatively smaller training portion.
Finally, while several studies listed in the table used relatively smaller datasets, ranging from 1720 to 3217 samples, our work leverages a substantial sample size of 2000, with 70% of the data used for training. This provides a balance between dataset size and computational efficiency, ensuring robust model performance even with a more modest training portion compared to some of the other works, such as ref. 58, which utilized 80% of the dataset.
Given the infrequency of physical and environmental faults in solar PV panels, we propose that periodic monitoring—such as weekly image assessments—should be adequate for early detection of any emerging issues.
4 Conclusions
The early detection of faults in PV systems is essential for maintaining their efficiency, safety, and longevity. In this study, we developed a comprehensive fault classification model that integrates machine learning techniques to address physical and environmental faults in solar panels. By utilizing CNN, we were able to accurately differentiate between normal and faulty states. For physical and environmental fault detection, we leveraged k-means clustering enhanced by transfer learning using the pre-trained Visual Geometry Group model to effectively label and classify image data. This combination of advanced algorithms allowed for precise feature extraction and improved clustering accuracy. Features were extracted from the second-to-last fully connected layer of VGG16, providing high-level representations suitable for classification. While the proposed method demonstrates strong performance on labeled datasets and controlled test conditions, its application in real photovoltaic system deployments may face certain limitations, such as variations in lighting, panel orientation, soiling, and environmental conditions, as well as practical constraints due to high-resolution imaging and computational requirements. Future work should explore robustness under diverse real-world conditions, strategies to optimize computational efficiency for field deployment, and a layer-wise ablation study to further optimize feature extraction. Although challenges persist, particularly in differentiating faults under varying conditions, the integration of these methods demonstrates a notable enhancement in the reliability of fault detection. Our approach not only strengthens the operational resilience of photovoltaic systems but also supports the larger objectives of sustainability and the adoption of renewable energy solutions.Author contributions
Ihtesham Ibn Malek: conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing – original draft, writing – review & editing. Hafiz Imtiaz: conceptualization, investigation, methodology, supervision, validation, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper.Abbreviations
| CNN | Convolutional Neural Network |
| DNN | Deep Neural Network |
| EL | Electroluminescence |
| KNN | k-Nearest Neighbors |
| LR | Logistic Regression |
| ML | Machine Learning |
| PV | Photovoltaic |
| RF | Random Forest |
| SSL | Semi-Supervised Learning |
| SVM | Support Vector Machine |
| TL | Transfer Learling |
| VGG | Visual Geometry Group |
| VR | Variance Ratio |
Data availability
All relevant data that support the findings of this study are presented in the manuscript. Source data for this article, including the images collected in September 2022, were publicly available at the GitHub repository https://github.com/tayebiarasteh/PV_defect_detection. However, the repository has since been made private by the owner. As such, the dataset has been uploaded as supplementary information (SI). The SI contains unlabelled images of solar PV panels. See DOI: https://doi.org/10.1039/d5ya00239g.Acknowledgements
The authors acknowledge the facility and support provided by the Department of Electrical and Electronic Engineering at Bangladesh University of Engineering and Technology. The authors also thank Dr Shaikh Anowarul Fattah, under whose graduate course this project was originated.Notes and references
- Q. Hassan, P. Viktor, T. J. Al-Musawi, B. M. Ali, S. Algburi, H. M. Alzoubi, A. K. Al-Jiboory, A. Z. Sameen, H. M. Salman and M. Jaszczur, Renewable Energy Focus, 2024, 48, 100545 CrossRef.
- R. Hafezi and M. Alipour, Affordable and clean energy, Springer, 2021, pp. 1085–1099 Search PubMed.
- K. E. Gan, O. Taikan, T. Y. Gan, T. Weis, D. Yamazaki and H. Schüttrumpf, Energy Technol., 2023, 11, 2300275 CrossRef.
- N. S. M. N. Izam, Z. Itam, W. L. Sing and A. Syamsir, Energies, 2022, 15, 2790 CrossRef CAS.
- M. Tawalbeh, A. Al-Othman, F. Kafiah, E. Abdelsalam, F. Almomani and M. Alkasrawi, Sci. Total Environ., 2021, 759, 143528 CrossRef CAS PubMed.
- A. Chaurey and T. C. Kandpal, Renewable Sustainable Energy Rev., 2010, 14, 2266–2278 CrossRef.
- I. Javid, A. Chauhan, S. Thappa, S. Verma, Y. Anand, A. Sawhney, V. Tyagi and S. Anand, J. Cleaner Prod., 2021, 309, 127304 Search PubMed.
- P. Basak, S. Chowdhury, S. H. Nee Dey and S. Chowdhury, Renewable Sustainable Energy Rev., 2012, 16, 5545–5556 CrossRef.
- C. D. Iweh, S. Gyamfi, E. Tanyi and E. Effah-Donyina, Energies, 2021, 14, 5375 CrossRef.
- I. I. Malek and S. A. Fattah, 2024 13th International Conference on Electrical and Computer Engineering (ICECE), 2024, pp. 603–608.
- I. I. Malek, M. Z. Islam, M. Hasan, M. S. Rahman and A. H. Chowdhury, 2020 11th International Conference on Electrical and Computer Engineering (ICECE), 2020, pp. 331–334.
- M. S. Rahman, M. Hasan, M. Z. Islam, I. I. Malek and A. H. Chowdhury, 2021 5th International Conference on Electrical Information and Communication Technology (EICT), 2021, pp. 1–5.
- B. Basnet, H. Chun and J. Bang, J. Sens., 2020, 2020, 6960328 Search PubMed.
- N.-C. Yang and H. Ismail, Mathematics, 2022, 10, 285 CrossRef.
- A. Y. Appiah, X. Zhang, B. B. K. Ayawli and F. Kyeremeh, Int. J. Photoenergy, 2019, 2019, 6953530 CrossRef.
- M. Aghaei, A. Fairbrother, A. Gok, S. Ahmad, S. Kazim, K. Lobato, G. Oreski, A. Reinders, J. Schmitz and M. Theelen, et al. , Renewable Sustainable Energy Rev., 2022, 159, 112160 CrossRef CAS.
- H. Al Mahdi, P. G. Leahy, M. Alghoul and A. P. Morrison, Solar, 2024, pp. 43–82 Search PubMed.
- M. W. Akram, G. Li, Y. Jin and X. Chen, Appl. Energy, 2022, 313, 118822 CrossRef.
- D. S. Pillai, F. Blaabjerg and N. Rajasekar, IEEE J. Photovolt., 2019, 9, 513–527 Search PubMed.
- R. Venkateswari and N. Rajasekar, Int. Trans. Electr. Energy Syst., 2021, 31, e13113 Search PubMed.
- V. B. Kurukuru, A. Haque and M. A. Khan, 2019 IEEE Industry Applications Society Annual Meeting, 2019, pp. 1–6.
- V. S. B. Kurukuru, F. Blaabjerg, M. A. Khan and A. Haque, Energies, 2020, 13, 308 CrossRef.
- A. Et-taleby, Y. Chaibi, M. Benslimane and M. Boussetta, Statistics, Opt. Inf. Comput., 2023, 11, 168–177 CrossRef.
- I. I. Malek, S. M. S. H. Hasib and M. F. Shadiq, International Conference on Data Science, Artificial Intelligence and Applications (ICDSAIA 2025), Cham, 2026, pp. 1–17.
- R. H. F. Alves, G. A. de Deus Junior, E. G. Marra and R. P. Lemos, Renewable Energy, 2021, 179, 502–516 CrossRef.
- A. M. Ikotun, A. E. Ezugwu, L. Abualigah, B. Abuhaija and J. Heming, Inf. Sci., 2023, 622, 178–210 Search PubMed.
- S. Li, P. Kou, M. Ma, H. Yang, S. Huang and Z. Yang, IEEE Access, 2024, 12, 27331–27343 Search PubMed.
- B. Aljafari, P. R. Satpathy, S. B. Thanikanti and N. Nwulu, Energy Rep., 2024, 12, 2156–2178 CrossRef.
- K. Awedat, G. Comert, M. Ayad and A. Mrebit, Mach. Learn. Appl., 2025, 20, 100636 Search PubMed.
- P. R. Satpathy, B. Aljafari, S. B. Thanikanti and S. R. K. Madeti, Renewable Energy, 2023, 206, 960–981 CrossRef.
- R. A. M. Rudro, K. Nur, M. F. A. Al Sohan, M. Mridha, S. Alfarhood, M. Safran and K. Kanagarathinam, Energy Rep., 2024, 12, 1580–1594 CrossRef.
- M. Abdelsattar, A. AbdelMoety and A. Emad-Eldeen, Sci. Rep., 2025, 15, 24356 CrossRef CAS.
- M. Abdelsattar, A. AbdelMoety and A. Emad-Eldeen, Mansoura Eng. J., 2025, 50, 2 Search PubMed.
- R. Fang, K. Wang, J. Li, X. Yuan and Y. Wang, Adv. Eng. Inf., 2024, 61, 102684 Search PubMed.
- M. Aghaei, M. Kolahi, A. Nedaei, N. Venkatesh, S. M. Esmailifar, A. Moradi Sizkouhi, A. Aghamohammadi, A. Oliveira, A. Eskandari and P. Parvin, et al. , Prog. Photovoltaics Res. Appl., 2025, 33, 381–409 Search PubMed.
- X. Luo and D. Zhang, Sustainable Energy Technol. Assess., 2022, 52, 102326 CrossRef.
- X. Wang, Y. Shen, H. Song and S. Liu, Energies, 2025, 18, 747 CrossRef.
- I. I. Malek, K. Sarkar and A. Zubair, Nanoscale Adv., 2024, 6, 5112–5132 RSC.
- I. I. Malek, H. Imtiaz and S. Subrina, Sol. Energy, 2024, 278, 112737 Search PubMed.
- I. I. Malek, H. Imtiaz and S. Subrina, arXiv, 2025, preprint, arXiv:2505.18693 DOI:10.48550/arXiv.2505.18693.
- H. Zhu, L. Lu, J. Yao, S. Dai and Y. Hu, Sol. Energy, 2018, 176, 395–405 CrossRef.
- K. Simonyan and A. Zisserman, arXiv, 2014, preprint, arXiv:1409.1556 DOI:10.48550/arXiv.1409.1556.
- A. K. Dubey, U. Gupta and S. Jain, Int. J. Computer Assisted Radiol. Surgery, 2016, 11, 2033–2047 Search PubMed.
- S.-A. Rebuffi, S. Gowal, D. A. Calian, F. Stimberg, O. Wiles and T. A. Mann, Adv. Neural Inf. Process. Syst., 2021, 34, 29935–29948 Search PubMed.
- C. Liu, Y. Dong, W. Xiang, X. Yang, H. Su, J. Zhu, Y. Chen, Y. He, H. Xue and S. Zheng, Int. J. Comput. Vis., 2025, 133, 567–589 CrossRef.
- K. O'shea and R. Nash, arXiv, 2015, preprint, arXiv:1511.08458 DOI:10.48550/arXiv.1511.08458.
- Y. Ouali, C. Hudelot and M. Tami, arXiv, 2020, preprint, arXiv:2006.05278 DOI:10.48550/arXiv.2006.05278.
- G. Li, X. Li, Y. Wang, Y. Wu, D. Liang and S. Zhang, European Conference on Computer Vision, 2022, pp. 457–472.
- S. T. Arasteh, Multi-label defect detection for Solar Cells from images of the modules, using Deep Learning, 2023, https://github.com/tayebiarasteh/PV_defect_detection, GitHub.
- L. Lovmar, A. Ahlford, M. Jonsson and A.-C. Syvänen, BMC Genomics, 2005, 6, 1–6 Search PubMed.
- I. I. Malek, K. Sarkar and A. Zubair, 2024 13th International Conference on Electrical and Computer Engineering (ICECE), 2024, pp. 741–746.
- M. W. Akram, G. Li, Y. Jin, X. Chen, C. Zhu, X. Zhao, A. Khaliq, M. Faheem and A. Ahmad, Energy, 2019, 189, 116319 CrossRef.
- S. Deitsch, V. Christlein, S. Berger, C. Buerhop-Lutz, A. Maier, F. Gallwitz and C. Riess, Sol. Energy, 2019, 185, 455–468 CrossRef.
- M. Y. Demirci, N. Besli and A. Gümüsçü, Expert Syst. Appl., 2021, 175, 114810 CrossRef.
- A. Et-taleby, Y. Chaibi, A. Allouhi, M. Boussetta and M. Benslimane, Sustainable Energy, Grids Networks, 2022, 32, 100946 CrossRef.
- H. M. Al-Otum, Adv. Eng. Inf., 2023, 58, 102147 Search PubMed.
- E. Ozturk, E. Ogliari, M. Sakwa, A. Dolara, N. Blasuttigh and A. M. Pavan, Energy Convers. Manage., 2024, 319, 118866 CrossRef.
- M. Abdelsattar, A. AbdelMoety, M. A. Ismeil and A. Emad-Eldeen, IEEE Access, 2025, 13, 4136–4157 Search PubMed.
- H. Tella, A. Hussein, S. Rehman, B. Liu, A. Balghonaim and M. Mohandes, Case Stud. Therm. Eng., 2025, 66, 105749 CrossRef.
- A. Karakan, Sustainability, 2025, 17, 1141 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |