Floquet engineering of topological phase transitions in intrinsic ferrovalley semiconductor via circularly and elliptically polarized light
Wenpeng
Wang
,
Xinge
Zhang
 ,
Yuping
Tian
,
Yuping
Tian
 ,
Haoyue
Bai
,
Shaozhi
Li
,
Wei-Jiang
Gong
,
Haoyue
Bai
,
Shaozhi
Li
,
Wei-Jiang
Gong
 and
Xiangru
Kong
and
Xiangru
Kong
 *
*
College of Sciences, Northeastern University, Shenyang 110819, China. E-mail: kongxiangru@neu.edu.cn
First published on 5th November 2025
Abstract
Floquet engineering provides a non-contact approach to dynamically tailor electronic band structures and induce topological phase transitions via time-periodic optical fields. However, experimental limitations such as dissipation and the underexplored role of anisotropic driving have hindered its application in two-dimensional magnetic semiconductors. Recently, monolayer 2H RuCl2 has been identified as a promising ferrovalley material exhibiting large out-of-plane magnetic anisotropy and tunable first- and second-order topological phases. In this work, we construct a Wannier-based tight-binding model and apply Floquet–Bloch theory to monolayer 2H RuCl2 under circularly, elliptically, and linearly polarized light. We examine both off-resonant and on-resonant driving schemes by considering different scales of light frequency. In the off-resonant scheme, we demonstrate that both the amplitude and ellipticity of light can trigger band inversion at the K′ valley, leading to a topological phase transition into a quantum anomalous Hall (QAH) phase with a quantized Hall conductance and Chern number C = 1. In the on-resonant scheme, the hybridization of Floquet replica bands reveals even richer topological phase transitions driven by light frequency, amplitude, and ellipticity. Notably, we observe a Floquet-induced QAH phase with high Chern number C = 3, suggesting that intrinsic ferrovalley semiconductors such as RuCl2 serve as an ideal platform for Floquet band engineering in future topological quantum devices.
I. Introduction
Since the advent of quantum theory, the interaction between light and matter has remained a central theme in fundamental physics and continues to be an active and evolving research area.1–5 The use of external fields to control topological phases has more recently become an essential focus within condensed matter physics and materials science research.6,7 When subjected to periodic external drives, these systems are commonly described as Floquet systems. Their dynamical behavior is then characterized by quasienergy levels and associated eigenstates, which parallel the static energy spectra and eigenfunctions found in periodic lattice arrangements.8–11 Floquet engineering, as a dynamic modulation strategy, enables the renormalization of band structures through time-periodic drives, such as laser fields, and can induce novel topological phases that are absent under periodic lattice potential.1,5,12–14 Due to its non-contact feature, Floquet engineering has been instrumental in manipulating topological states within cold atom systems,3,15–18 solid-state materials,19–30 and photonic platforms.31–33 These transitions between topological phases induced by light are significant not only for fundamental research but also show substantial potential for enabling high-speed electronic devices and topological quantum devices.Two-dimensional (2D) materials, owing to their unique low-dimensional nature and highly tunable electronic structures, have become ideal platforms for realizing Floquet topological phase transitions. A classic example is the laser-induced quantum Hall state in graphene under circularly polarized light (CPL), which drives topological transport properties and exhibits quantized Hall conductance.20,25,34–39 However, the experimental observation of Floquet states has long been hindered by ultrafast dissipation and decoherence effects.25,40,41 Recently, the formation of Floquet states under linearly polarized laser pulses has been successfully detected using a combination of angle-resolved photoemission spectroscopy (ARPES) and femtosecond pump–probe techniques.40–42 Research efforts currently concentrate overwhelmingly on elucidating topological properties in non-magnetic compounds, aiming to solidify foundational theoretical models. Meanwhile, although studies of 2D intrinsic magnetic materials under periodic optical excitation commonly employ isotropic CPL, the potential of anisotropic modulation methods—such as elliptically polarized light (EPL)—remains profoundly underexplored.
In recent years, the valley degree of freedom has garnered significant attention as a novel electronic degree of freedom. In 2D materials, valley polarization can be engineered through interlayer sliding,43–45 strain engineering,46–48 electric or magnetic fields,11,49–53 and multi-field coupling.54 By spontaneously breaking time-reversal symmetry in momentum space without any external field, the energy degeneracy is lifted, thus resulting in band splitting and valley polarization that induce ferrovalley states in ferroelectric or ferromagnetic materials.55,56 Such materials are collectively termed as ferrovalley materials. In monolayer 2H RuCl2, its intrinsic inversion symmetry breaking, coupled with strong spin-valley locking, which breaks time-reversal symmetry, stabilizes it as a highly robust intrinsic ferrovalley semiconductor.46 More importantly, previous studies have demonstrated that strain can induce phase transitions in monolayer RuCl2 from a second-order topological ferrovalley semiconductor to a half-valley metal and even to a quantum anomalous Hall state under equilibrium conditions.46,57 This material exhibits out-of-plane magnetic anisotropy energy of 678 µeV per Ru atom,58 while simultaneously demonstrating robust second-order topological insulation, significant valley polarization positioning it as a promising candidate for valleytronic devices and magnetic memory applications.59
In our work, we systematically study the topological phase transitions of the monolayer RuCl2 in both the off-resonant and on-resonant schemes. We consider various types of light fields, including circular, elliptical, and linear polarization. Our results demonstrate that the monolayer RuCl2 enables fully optical control of topological phase transitions, where light polarization, frequency, and amplitude serve as multidimensional tuning parameters. Furthermore, we constructed a visualization diagram (Fig. S12) for the experimental demonstration of Floquet band engineering via TrARPES, which employed to probe the Floquet states in RuCl2. This study opens new avenues for the development of Floquet topological electronics based on 2D magnetic materials.
II. Computational method
First-principles calculations were performed within the framework of density functional theory (DFT)60,61 using the Vienna ab initio Simulation Package (VASP).62,63 The strong correlation effects of Ru-4d electrons were addressed via the rotationally invariant PBE+U64,65 scheme for structural optimization and electronic structure calculations, with an effective on-site Hubbard correction of Ueff = 2.0 eV applied.46,66,67 Existing research has demonstrated that topological states can be controlled by tuning Ueff.68 Therefore, calculations were performed for different Ueff values in the monolayer RuCl2 system. The results demonstrate that Ueff serves as an effective parameter for modulating the topological states of monolayer RuCl2. In order to demonstrate that calculations were conducted for a range of Ueff values, further regulation was achieved by combining an external periodic optical field, with detailed results presented in SI section titled “Topological phase transition versus different Ueff and Floqute engineering at Ueff = 2.5 eV”. A plane-wave basis set cut-off energy of 500 eV was employed for structural relaxation, with ionic optimization continuing until the Hellmann–Feynman forces on each atom were reduced below 0.01 eV Å−1, and the energy convergence criterion was set to 10−6 eV. Integration over the Brillouin zone (BZ) utilized a Γ-centered 11 × 11 × 1 Monkhorst–Pack k-point mesh,69 while the Berry curvature integration employed a significantly denser 801 × 801 × 1 grid. A large vacuum layer of 25 Å was applied along the z/c-direction to eliminate artificial interactions between adjacent periodic images.To explore the excited states under a periodic optical field, we first derive a tight-binding Hamiltonian (TBH) using maximally localized Wannier functions (MLWFs), constructed via the Wannier90 package.70 The MLWFs are constructed by projecting Ru-d and Cl-p orbitals, thereby capturing the fundamental low-energy electronic behavior. Utilizing the time-dependent Wannier-derived TBH,
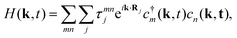 | (1) |
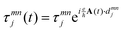 . Here, dmnj represents displacement vector, and τmnj is the hopping amplitude from orbital m in the 0-cell to orbital n in the j-cell. The on-site energy for the mth orbital is given by τmm0, Rj is the lattice vector, while c†(k) and c(k) are creation and annihilation operators. Under the dipole approximation, a laser field be considered with the direction of incidence perpendicular to RuCl2 which can be described as A(t) = A(η
. Here, dmnj represents displacement vector, and τmnj is the hopping amplitude from orbital m in the 0-cell to orbital n in the j-cell. The on-site energy for the mth orbital is given by τmm0, Rj is the lattice vector, while c†(k) and c(k) are creation and annihilation operators. Under the dipole approximation, a laser field be considered with the direction of incidence perpendicular to RuCl2 which can be described as A(t) = A(η![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt), r
sin(ωt), r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt), 0). Here, η = +1(−1) denotes the right (left)-handed polarized light, and A is the amplitude of light. The polarization of light can be changed by setting r. For example, when r = 1.0, CPL be used, which preserves spatial inversion symmetry; when r in (0.0, 1.0), the polarization model is EPL; when r = 0, the light becomes linearly polarized light (LPL), which exhibits significant anisotropy due to broken spatial inversion symmetry. A d + 1 dimensional system under a time-periodic potential can be effectively characterized by a static Hamiltonian, as dictated by the Floquet–Bloch theory:71,72
cos(ωt), 0). Here, η = +1(−1) denotes the right (left)-handed polarized light, and A is the amplitude of light. The polarization of light can be changed by setting r. For example, when r = 1.0, CPL be used, which preserves spatial inversion symmetry; when r in (0.0, 1.0), the polarization model is EPL; when r = 0, the light becomes linearly polarized light (LPL), which exhibits significant anisotropy due to broken spatial inversion symmetry. A d + 1 dimensional system under a time-periodic potential can be effectively characterized by a static Hamiltonian, as dictated by the Floquet–Bloch theory:71,72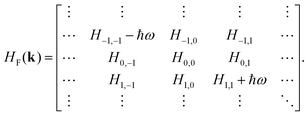 | (2) |
Here, each matrix element can be obtained by:
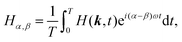 | (3) |
Periodic optical driving is classified as off-resonant or on-resonant according to how the driving frequency (the light frequency of the external periodic potential) compares with the band gap and the system bandwidth. When the frequency exceeds the band gap yet remains below the bandwidth, it produces off-resonant Floquet band engineering; in contrast, if the frequency is higher than the bandwidth, hybridization of Floquet replica bands leads to on-resonant Floquet band engineering. Here, we selected polarized light with light frequency ħω = 10 eV as the off-resonant external optical field, which significantly exceeds the projected bandwidth of any orbital in 2H RuCl2, while choosing light with ħω below 0.35 eV for the on-resonant external optical field. Subsequently, the topological properties of the system in both driving schemes, including edge states, Berry curvature, Wannier charge centers (WCCs), anomalous Hall conductance (AHC) and Chern numbers, are systematically calculated using the WannierTools in subsequent sections.73
III. Results and discussion
A. Off-resonant Floquet band engineering
The monolayer RuCl2 forms a typical sandwich structure: a single Ru atomic sheet lies between two Cl sheets in a symmetric fashion. First-principles structural optimization yields a lattice constant a = 3.49 Å. The ground state is characterized by out-of-plane ferromagnetism and ferrovalley behavior.57 Reversing the magnetization results in a reversal of the ferrovalley polarization, as seen in Fig. 1(b) and (c). This manipulation is evidenced by the Berry curvature profiles in Fig. 1, showing larger curvature concentrated around valleys with a smaller gap.By this way, we can explore how the light's polarization influences the topological properties. Similarly to 2H VSe2 with hexagonal structure,55 we use a four-band k·p model including magnetic interaction to study how light can induce band inversions near K and K′ valleys. The basis functions are chosen as ψτ1 = |dz2〉 and 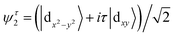 , in which τ = +1(−1) denotes the K and K′ valleys. Therefore, the total effective Hamiltonian of the system is given as
, in which τ = +1(−1) denotes the K and K′ valleys. Therefore, the total effective Hamiltonian of the system is given as
| H(k) = I2 ⊗ H0(k) + HSOC(k) + Hex(k), | (4) |
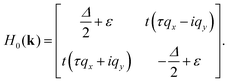 | (5) |
Here, Δ denotes the band gap, while t is the effective nearest-neighbor hopping parameter. The quantity ε stands for the correction energy relative to the Fermi level. The momentum q = (qx, qy) is defined with respect to the valleys K/K′. The terms HSOC and Hex correspond to the spin–orbit coupling and the magnetic exchange interaction, respectively, and can be expressed as:74
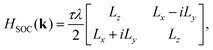 | (6) |
| Hex(k) = I2 ⊗ (B·σ), | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, 0, cos
θ, 0, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). Using the Peierls substitution k → k + A(t), this system can be described by a time-dependent Hamiltonian H(k,t). In the high-frequency regime, we retain only the first-order term of the Magnus expansion,75–77 since in this limit it already provides sufficient accuracy:
θ). Using the Peierls substitution k → k + A(t), this system can be described by a time-dependent Hamiltonian H(k,t). In the high-frequency regime, we retain only the first-order term of the Magnus expansion,75–77 since in this limit it already provides sufficient accuracy: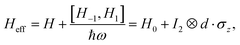 | (8) |
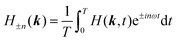 is the nth Fourier coefficients of H(k), the second term d can be seen as the light-induced coupling strength
is the nth Fourier coefficients of H(k), the second term d can be seen as the light-induced coupling strength 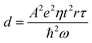 .
.
Under the irradiation of CPL, the Floquet bands in the two systems with opposite directions of magnetization will exhibit opposite responses to the same chirality of CPL, as shown in Fig. 1(b) and (c). This is because the energy dispersion satisfies the relation E+M(k) = E−M(−k), in which M indicates the magnetization. By gradually increasing the light amplitude (eA/ħ = 0.0, 0.1, 0.3 Å−1), we observe that the band gap at both K and K′ valleys gradually decreases due to light-induced band renormalization. Especially, when the light amplitude reaches eA/ħ = 0.3 Å−1, the band gap at K or K′ valley will close completely, as shown in Fig. 1(b) and (c). Besides, the first-principles calculation confirms that the states near Fermi level mostly contributed from the d orbitals of Ru atoms, as shown in Fig. S1, which is consistent with previous research.46 When the magnetization is aligned along the +z direction (Fig. 1(b)), an increase in the amplitude of the optical field leads to distinct orbital evolutions at the K and K′ valleys. Specifically, the d-orbital characteristics at the K valley remain stable. In contrast, the orbital-resolved electronic structures at the K′ valley undergo a significant transition: initially, the maximum of the valence minimum of the valence bands is dominated by Ru-dz2 orbitals, while the minimum of the conduction bands is dominated by the dx2−y2 orbital of the Ru atom. As the light amplitude increases, this configuration evolves into a state where the conduction band minimum is dominated by the Ru-dx2−y2 orbital, and the valence band maximum is dominated by a combination of Ru-dz2 orbitals. Conversely, when the magnetization is oriented along the −z direction, the orbital-projected band structures at the K′ valley remain stable, while a band inversion occurs at the K valley (Fig. S1).
The light-induced semimetal phase indicates the possible band inversions could exist in Floquet band engineering in a monolayer RuCl2. To avoid redundancy, all subsequent calculations are performed in the FM configuration with magnetization aligned along the +z direction. We further investigate the influence of light chirality on the electronic band structures and topological phase transitions, such as left- and right-handed circularly polarization (L- and R-CPL). Fig. 2(a) and (b) illustrate the evolution of band gaps versus the light amplitude eA/ħ at the K and K′ valleys under the irradiation of L-CPL and R-CPL, respectively. Under the irradiation of L-CPL, in the low-field regime eA/ħ < 0.315 Å−1, the band gap at both valleys decrease monotonically with increasing light amplitude. The system will preserve a second-order topological insulator but with a trivial Chern number C = 0. At the critical point eA/ħ = 0.315 Å−1, the gap at K′ valley closes while the valley still maintains a gap of 376 meV.
This gap closure event triggers a topological phase transition, in which the Chern number abruptly changes from C = 0 to C = +1. The evolution of WCCs in Fig. S2 demonstrate the process of topological phase transition and the change of Chern numbers. Fig. 2(c)–(e) show the corresponding edge states under L-CPL at eA/ħ = 0.1, 0.44, and 0.6 Å−1. At eA/ħ = 0.44 Å−1, a single chiral edge mode connecting the conduction and valence bands emerges, consistent with the phase C = +1. In contrast, at eA/ħ = 0.1 and 0.6 Å−1, no gapless edge states appear, confirming the trivial phases with C = 0. As the light amplitude continues to increase, the gap at K′ valley reopens and expands, while the gap at K valley shrinks progressively. When eA/ħ = 0.585 Å−1, the gap at K valley fully closes, returning the system to a trivial phase C = 0.
Under the irradiation of R-CPL, a similar evolution of band gaps at both valleys is observed, but with shifted critical points as shown in Fig. 2(b). The topological nontrivial phase C = +1 is induced in the range of eA/ħ = 0.41 to 0.52 Å−1, where the band gap at K′ valley closes first, followed by the gap at K valley. As shown in Fig. S3, similar topological phase transitions induced by R-CPL could be observed in the evolution of both edge states and Berry curvature, exhibiting the same change of Chern number C = 0 → +1 → 0 as the case under the irradiation of L-CPL. Notably, a process of band inversion occurs under the irradiation of R-CPL, which is shown in Fig. S4. Compared with the case under the irradiation of L-CPL, the case under R-CPL demonstrates that the ferrovalley properties in the monolayer RuCl2 could respond slightly different to the chirality of CPL. With the reversal of magnetization in the monolayer RuCl2, the sign of Chern number is expected to be reserved under the irradiation of CPL (see Fig. 1(c)), which demonstrates the tunability in the propagating direction of chiral edge state by Floquet engineering.
However, under the irridation of EPL, there will be subtle yet critical differences arise in modifing the topological properties due to the inherent anisotropy of EPL.78–81 The role of EPL's ellipticity is considered to investigate the EPL-induced topological phases in monolayer RuCl2. As shown in Fig. 3(a), there will be band inversions in the monolayer RuCl2 as the ellipticity of EPL increases. Specifically, at r = 0.1, the K′ valley exhibits a gap of approximately 60 meV. As r increases, the gap at K′ valley gradually decreases and fully closes at r = 0.5. Further increasing r to 0.9 reopens the gap to about 100 meV, forming a characteristic gap-closing and reopening process that signifies a topological phase transition. However, as shown in Fig. S5, the band gap at K valley remains insulating regardless of changing in r. Consequently, the topological phase transition is primarily governed by the evolution of band gap at K valley. This reveals that EPL could provide another parameter to induce the topological properties in the monolayer ferrovalley semiconductor. The edge states evolve significantly with ellipticity. At r = 0.1, no chiral edge states are present, indicating a trivial phase; whereas at r = 0.9, distinct unidirectional chiral edge modes emerge, confirming the transition to a Chern insulator, as seen in Fig. 3(c) and (d). We also compute the AHC as a function of r, as shown in Fig. 3(b). At r = 0.1, the AHC plateau remains at zero, corresponding to the topological trivial phase. As r increases to 0.9, the AHC jumps to e2/ħ, indicating the emergence of a Chern insulating phase. The evolution of WCCs in Fig. S6(b)–(d) also confirms the the process of EPL-induced topological phase transition. This results are fully consistent with the evolution of band inversion and edge states, comprehensively verifying the controllable topological phase transitions induced by tuning the ellipticity of EPL. Moreover, we also track the band gap at K′ valley under different ellipticity of EPL versus the light amplitude eA/ħ as shown in Fig. S6(a), which illustrates the K′ valley gap evolution as the ellipticity varies from r = 0.0 to 0.9, exhibiting a typical gap-closing and reopening process. Specifically, we computed the Berry curvature for ellipticities of 0.1 and 0.9 (Fig. S4), and found that the band inversion process is accompanied by a reversal of the Berry curvature at the K valley. Ellipticity r solely affects the specific position of band closure at the K′ valley during the variation of energy bands with light amplitude.
When the ellipticity is exactly zero, the light field reduces to LPL 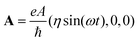 , we get d = 0, which indicates the coupling matrix elements between linear polarization and the system integrate to zero over momentum space. Due to the fixed direction of the electric field vector, linear polarization cannot sufficiently break time-reversal symmetry, and thus cannot trigger gap closing or induce a topological phase transition. The corresponding band structures and WCCs are shown in Fig. S7. As shown in Fig. S7(a), the gaps at both K and K′ valleys remain open with increasing light amplitude, and no gap closing occurs. The calculated WCCs at eA/ħ = 0.1, 0.3, and 0.45 Å−1 as shown in Fig. S7(b)–(d) confirm that the system remains in a topologically trivial phase throughout. These results verify that LPL cannot induce topological phase transitions, consistent with theoretical predictions.40,82 In additional, for the case of in-plane magnetization in the off-resonant scheme, under the irradiation of CPL and EPL, there is similar process of topological phase transitions as presented in Fig. S14 and S15 of SI.
, we get d = 0, which indicates the coupling matrix elements between linear polarization and the system integrate to zero over momentum space. Due to the fixed direction of the electric field vector, linear polarization cannot sufficiently break time-reversal symmetry, and thus cannot trigger gap closing or induce a topological phase transition. The corresponding band structures and WCCs are shown in Fig. S7. As shown in Fig. S7(a), the gaps at both K and K′ valleys remain open with increasing light amplitude, and no gap closing occurs. The calculated WCCs at eA/ħ = 0.1, 0.3, and 0.45 Å−1 as shown in Fig. S7(b)–(d) confirm that the system remains in a topologically trivial phase throughout. These results verify that LPL cannot induce topological phase transitions, consistent with theoretical predictions.40,82 In additional, for the case of in-plane magnetization in the off-resonant scheme, under the irradiation of CPL and EPL, there is similar process of topological phase transitions as presented in Fig. S14 and S15 of SI.
B. On-resonant Floquet band engineering
In the preceding section, the Floquet band engineering in the off-resonant scheme requires the light frequency is larger than the bandwidth or at least the band gap of the insulating system. The behavior of Floquet band engineering will mainly be focused in the original copy of Floquet bands, which can be effectively described by using a high-frequency expansion of the effective Hamiltonian. As the driving frequency becomes smaller than the size of band gap (ħω ≤ ECB − EVB), the interactions or hybridizations between the Floquet replica bands will dominate the behaviors of on-resonant Floquet band engineering. This will introduce a more intricate scheme of light-induced topological phase diagram. To comprehensively map the tunable topological phases of monolayer RuCl2, we systematically investigate the system's behavior under light irradiation in the on-resonant scheme, focusing on driving frequencies below 0.35 eV, which is below the band gap at K valley.In the on-resonant driving scheme, there will be multiple Floquet replica bands in the band gap of K and K′ valleys. The interaction between Floquet replica bands will become unneglectable in engineering the topological phase transitions. As shown in Fig. S8, the Floquet bands under light frequency ħω = 0.05, 0.15, 0.25, 0.35 eV but without the light amplitude demonstrates that there will exist overlap between the Floquet replica bands at K′ valley under lower light frequency and such overlap at K valley under higher energy. This is due to the band gap at K′ valley is smaller than that at K valley. Usually, there will be light-induced band gap in the overlaps between Floquet replica bands with finite light amplitude, which indicates the possible topological phase transitions. As the light-induced band gap at K′ valley is relatively small, so we track the light-induced band gap at K valley in Fig. 4 to demonstrate the light-induced phase diagrams under the irradiation of L-CPL and EPL.
As shown in Fig. 4(a), when the light frequency is below 0.09 eV, the increasing light amplitude will not induce any band inversions as there is no overlap between the Floquet replica bands as shown in Fig. S8(a). However, when the light frequency is in the range of 0.13 to 0.22 eV, a small but finite light amplitude will induce a topological nontrivial phase with Chern number C = 1. This kind of topological phase transition happens at the K′ valley as indicated in Fig. S8(b). As indicated by the vertical dotted line in Fig. 4(a), the increasing light amplitude will induce the topological nontrivial phase into topological trivial phase with Chern number C = 0, and then again into a topological nontrivial phase with Chern number C = 3. When the light frequency of L-CPL is above 0.22 eV, a topological trivial phase will be induced into a topological nontrivial phase with Chern number C = 3 by both the increasing amplitude or the increasing light frequency with finite light amplitude. As in the case of EPL-induced topological phase transitions as shown in Fig. 4(b), both the light amplitude and light ellipticity will induce the topological trivial phase with Chern number C = 0 into a topological nontrivial phase with Chern number C = 1. Notably, within a certain range where the photon energy ħω exceeds 0.295 eV, an increase in the ellipticity drives a transition of the Chern number from C = 1 to C = 3 in the monolayer RuCl2.
Here, to further analyze the specific process of topological phase transitions, we perform detailed calculations along two representative directions in the phase diagram as shown in Fig. 4(a). First, by fixing the light frequency at ħω = 0.20 eV as indicated by the vertical dotted line, there will two successive band inversions that appear from K′ valley to K valley. As shown in Fig. 5(a), as the light amplitude increases from eA/ħ = 0.040 Å−1, the gap at K′ valley gradually decreases and closes at eA/ħ = 0.047 Å−1, then reopens, completing a typical gap-closing and reopening process. The evolution of edge states and WCCs, as shown in Fig. 5(b) and (c) and Fig. S11(a) and (b), confirms that the gap closure at K′ valley induces a topological phase transition from a Chern number C = 1 to C = 0, which indicated by the red stars in Fig. 4(a). However, as the light amplitude increases, the band gap at K′ valley will increase as shown in Fig. S9(a)–(c), but the band gap at K valley will exhibit the process of band inversions, which is explicitly shown in Fig. 5(d). At eA/ħ = 0.30 Å−1, the K valley maintains a gap of about 21 meV (Fig. 5(d)), but as the light amplitude increases to eA/ħ = 0.350 Å−1, the gap fully closes and then reopens at eA/ħ is above 0.35 Å−1, which is shown by the yellow stars in Fig. 4(a). The evolution of edge states in Fig. 5(e) and (f) and the evolution of WCCs in Fig. S11(c) and (d) indicates there exists a topological phase transition from Chern number C = 0 to C = 3. The L-CPL induced high Chern number indicates the L-CPL could engineering the number of chiral edge states in ferrovalley semiconductor.
With specific light amplitude, the CPL-induced topological phase transition could be investigated by the tuning the light frequency as indicated by the horizontal dotted line with eA/ħ = 0.3 Å−1. Under this condition, the gap at K′ valley remains open, and the topological phase transition is mainly driven by the evolution of band gap at K valley, as shown in Fig. S9(f)–(j). Specifically illustrated in Fig. 6(a), the increasing light frequency ħω will result in the band inversion at K valley with ħω = 0.22 eV. The calculations of edge states in Fig. 6(b) and (c) and the evolution of WCCs in Fig. 6(e) and (f) confirm the process of topological phase transition induced by light frequency. As there exists a light-induced global band gap, the calculation of AHC in Fig. 6(d) demonstrates that the system is in a trivial phase with a zero plateau (C = 0) at ħω = 0.15 eV, while the system transitions into a topologically nontrivial phase with a Hall plateau of 3e2/ħ (C = 3) at ħω = 0.30 eV.
Beyond the irradiation of CPL, we further investigate the behavior of EPL-induced Floquet bands in the on-resonant driving scheme. As shown in Fig. 4(b), the ellipticity of EPL will enable a more flexible mechanism for engineering topological phase transitions in valleytronic semiconductor. As indicated by the horizontal dotted line in Fig. 4(b), by choosing the ellipticity at r = 0.3, there will exist a topological phase transition, as shown by the red stars in Fig. 4(b). By tracking the light-induced band gap versus the light frequency at K valley in Fig. 7(a) and Fig. S10(g)–(l), there is a typical feature of band inversion. The results reveal that there will be band crossing at ħω = 0.20 eV. The calculation of edge states in Fig. 7(b) and (c) and the evolution of WCCs in Fig. S11(e) and (f) confirm the existence of topological chiral edge state.
Additionally, to directly reveal the role of EPL's ellipticity in engineering the topological phase transition, the light frequency is chosen as ħω = 0.25 eV as indicated by the vertical dotted line in Fig. 4(b). Also by tracking the band gap at K valley in Fig. 7(d) and Fig. S10(a)–(f), the increasing light ellipticity will induce a band inversion around the light ellipticity r = 0.3. The process of topological phase transition could be confirmed by the evolution of edge states in Fig. 7(e) and (f) and WCCs in Fig. S11(g) and (h), which indicates the trivial phase with Chern number C = 0 could be induced into a topological nontrivial phase with C = 1. Similarly, as for the Floquet engineering in monolayer RuCl2 with in-plane magnetization under the on-resonant scheme, the topological phase transitions with Chern number 3 could also emerge as detailed in Fig. S16 of SI.
Therefore, in the on-resonant driving scheme, the monolayer ferrovalley semiconductor such as monolayer RuCl2 exhibits multiple stage of topological phase transitions under the irridation of CPL and EPL. As demonstrated in Fig. 4, the light frequency, light amplitude and ellipticity of CPL and EPL could provide multiple dimensions to engineering the Floquet topological phases. Especially, the tunability of the light-induced Chern number demonstrates that the ferrovalley semiconductor could also provide as platform to manipulation of the chiral edge states. In our work, the proposed mechanism provides a more flexible and versatile approach for Floquet engineering, allowing for precise engineering of topological phases, multiple stage of transitions in Chern number. Such capabilities offer a theoretical foundation for designing optical logic nanodevices and topological quantum devices.
IV. Conclusion
This work systematically investigates Floquet-engineered topological phase transitions in the ferrovalley semiconductor monolayer RuCl2. Different types of periodic light field including CPL, EPL and LPL, and both the off-resonant and on-resonant schemes are considered to investigate the light-induced behaviors. Our results demonstrate that light frequency, field amplitude, and ellipticity can result in a light-induced QAH phase with a tunable Chern number, corroborated by calculations of edge states, WCCs, and AHC. In particular, we present light-induced phase diagrams in the on-resonant scheme, supporting the view that this intrinsic ferrovalley semiconductor is a promising platform for engineering light-induced topological phases. This study provides theoretical guidance for applications in the design of optical-logic nanodevices and topological quantum devices.Conflicts of interest
There are no conflicts to declare.Data availability
Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5tc03354c.The data that support the findings of this study are available on request from the corresponding author, upon reasonable request.
Acknowledgements
This work was financially supported by the Fundamental Research Funds for the Central Universities (No. N25LPY025), the LiaoNing Revitalization Talents Program (Grant No. XLYC1907033) and the Natural Science Foundation of Liaoning province (Grant No. 2023-MS-072). X. K. acknowledges the start up funding from Northeastern University, China. S. L. was supported by the National Natural Science Foundation of the People's Republic of China (Grand No. 12204236).References
- T. Oka and S. Kitamura, Floquet Engineering of Quantum Materials, Annu. Rev. Condens. Matter Phys., 2019, 10(1), 387–408 CrossRef.
- M. S. Rudner and N. H. Lindner, Band structure engineering and non-equilibrium dynamics in Floquet topological insulators, Nat. Rev. Phys., 2020, 2(5), 229–244 CrossRef CAS.
- A. De La Torre, D. M. Kennes, M. Claassen, S. Gerber, J. W. McIver and M. A. Sentef, Colloquium: Nonthermal pathways to ultrafast control in quantum materials, Rev. Mod. Phys., 2021, 93(4), 041002 CrossRef CAS.
- F. Zhan, R. Chen, Z. Ning, D.-S. Ma, Z. Wang, D.-H. Xu and R. Wang, Perspective: Floquet engineering topological states from effective models towards realistic materials, Quantum Front., 2024, 3(1), 21 CrossRef.
- C. Bao, P. Tang, D. Sun and S. Zhou, Light-induced emergent phenomena in 2D materials and topological materials, Nat. Rev. Phys., 2021, 4(1), 33–48 CrossRef.
- H. Hübener, U. De Giovannini, C. Schäfer, J. Andberger, M. Ruggenthaler, J. Faist and A. Rubio, Engineering quantum materials with chiral optical cavities, Nat. Mater., 2021, 20(4), 438–442 CrossRef PubMed.
- D. N. Basov, R. D. Averitt and D. Hsieh, Towards properties on demand in quantum materials, Nat. Mater., 2017, 16(11), 1077–1088 CrossRef CAS PubMed.
- J. H. Shirley, Solution of the Schrödinger Equation with a Hamiltonian Periodic in Time, Phys. Rev., 1965, 138(4B), B979–B987 CrossRef.
- H. Sambe, Steady States and Quasienergies of a Quantum-Mechanical System in an Oscillating Field, Phys. Rev. A:At., Mol., Opt. Phys., 1973, 7(6), 2203–2213 CrossRef.
- F. H. M. Faisal and J. Z. Kaminski, Floquet-Bloch theory of high-harmonic generation in periodic structures, Phys. Rev. A:At., Mol., Opt. Phys., 1997, 56(1), 748–762 CrossRef CAS.
- F. D. M. Haldane, Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”, Phys. Rev. Lett., 1988, 61(18), 2015–2018 CrossRef CAS PubMed.
- N. H. Lindner, G. Refael and V. Galitski, Floquet topological insulator in semiconductor quantum wells, Nat. Phys., 2011, 7(6), 490–495 Search PubMed.
- T. Kitagawa, E. Berg, M. Rudner and E. Demler, Topological characterization of periodically-driven quantum systems, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82(23), 235114 CrossRef.
- J.-I. Inoue and A. Tanaka, Photoinduced transition between conventional and topological insulators in two-dimensional electronic systems, Phys. Rev. Lett., 2010, 105(1), 017401 CrossRef PubMed.
- G. Jotzu, M. Messer, R. Desbuquois, M. Lebrat, T. Uehlinger, D. Greif and T. Esslinger, Experimental realization of the topological Haldane model with ultracold fermions, Nature, 2014, 515(7526), 237–240 CrossRef CAS.
- C. V. Parker, L.-C. Ha and C. Chin, Direct observation of effective ferromagnetic domains of cold atoms in a shaken optical lattice, Nat. Phys., 2013, 9(12), 769–774 Search PubMed.
- K. Jiménez-García, L. J. LeBlanc, R. A. Williams, M. C. Beeler, C. Qu, M. Gong, C. Zhang and I. B. Spielman, Tunable Spin-Orbit Coupling via Strong Driving in Ultracold-Atom Systems, Phys. Rev. Lett., 2015, 114(12), 125301 CrossRef PubMed.
- L. Jiang, T. Kitagawa, J. Alicea, A. R. Akhmerov, D. Pekker, G. Refael, J. Ignacio Cirac, E. Demler, M. D. Lukin and P. Zoller, Majorana Fermions in Equilibrium and in Driven Cold-Atom Quantum Wires, Phys. Rev. Lett., 2011, 106(22), 220402 CrossRef PubMed.
- Y. H. Wang, H. Steinberg, P. Jarillo-Herrero and N. Gedik, Observation of floquet-bloch states on the surface of a topological insulator, Science, 2013, 342(6157), 453–457 CrossRef CAS PubMed.
- M. A. Sentef, M. Claassen, A. F. Kemper, B. Moritz, T. Oka, J. K. Freericks and T. P. Devereaux, Theory of Floquet band formation and local pseudospin textures in pump-probe photoemission of graphene, Nat. Commun., 2015, 6(1), 7047 CrossRef CAS PubMed.
- S. Fan, S. Huang, Z. Chen, F. Zhan, X.-Y. Ding, D.-S. Ma and R. Wang, Circularly polarized light irradiated ferromagnetic mnbi2te4: A possible ideal weyl semimetal, Phys. Rev. B, 2024, 110, 125204 CrossRef CAS.
- E. J. Sie, J. W. McIver, Y.-H. Lee, L. Fu, J. Kong and N. Gedik, Valley-selective optical Stark effect in monolayer WS2, Nat. Mater., 2015, 14(3), 290–294 CrossRef CAS PubMed.
- F. Mahmood, C.-K. Chan, Z. Alpichshev, D. Gardner, Y. Lee, P. A. Lee and N. Gedik, Selective scattering between Floquet–Bloch and Volkov states in a topological insulator, Nat. Phys., 2016, 12(4), 306–310 Search PubMed.
- M. Reutzel, A. Li, Z. Wang and H. Petek, Coherent multidimensional photoelectron spectroscopy of ultrafast quasiparticle dressing by light, Nat. Commun., 2020, 11(1), 2230 Search PubMed.
- S. Aeschlimann, S. A. Sato, R. Krause, M. Chávez-Cervantes, U. De Giovannini, H. Hübener, S. Forti, C. Coletti, K. Hanff, K. Rossnagel, A. Rubio and I. Gierz, Survival of Floquet–Bloch States in the Presence of Scattering, Nano Lett., 2021, 21(12), 5028–5035 CrossRef CAS PubMed.
- S. Park, W. Lee, S. Jang, Y.-B. Choi, J. Park, W. Jung, K. Watanabe, T. Taniguchi, G. Young Cho and G.-H. Lee, Steady Floquet–Andreev states in graphene Josephson junctions, Nature, 2022, 603(7901), 421–426 CrossRef CAS PubMed.
- S. Zhou, C. Bao, B. Fan, H. Zhou, Q. Gao, H. Zhong, T. Lin, H. Liu, P. Yu, P. Tang, S. Meng, W. Duan and S. Zhou, Pseudospin-selective Floquet band engineering in black phosphorus, Nature, 2023, 614(7946), 75–80 CrossRef CAS PubMed.
- S. Ito, M. Schüler, M. Meierhofer, S. Schlauderer, J. Freudenstein, J. Reimann, D. Afanasiev, K. A. Kokh, O. E. Tereshchenko, J. Güdde, M. A. Sentef, U. Höfer and R. Huber, Build-up and dephasing of Floquet–Bloch bands on subcycle timescales, Nature, 2023, 616(7958), 696–701 CrossRef CAS PubMed.
- Y. Kobayashi, C. Heide, A. C. Johnson, V. Tiwari, F. Liu, D. A. Reis, T. F. Heinz and S. Ghimire, Floquet engineering of strongly driven excitons in monolayer tungsten disulfide, Nat. Phys., 2023, 19(2), 171–176 Search PubMed.
- S. Zhou, C. Bao, B. Fan, F. Wang, H. Zhong, H. Zhang, P. Tang, W. Duan and S. Zhou, Floquet engineering of black phosphorus upon below-gap pumping, Phys. Rev. Lett., 2023, 131(11), 116401 CrossRef CAS PubMed.
- M. C. Rechtsman, J. M. Zeuner, Y. Plotnik, Y. Lumer, D. Podolsky, F. Dreisow, S. Nolte, M. Segev and A. Szameit, Photonic Floquet topological insulators, Nature, 2013, 496(7444), 196–200 CrossRef CAS PubMed.
- Y.-G. Peng, C.-Z. Qin, D.-G. Zhao, Y.-X. Shen, X.-Y. Xu, M. Bao, H. Jia and X.-F. Zhu, Experimental demonstration of anomalous Floquet topological insulator for sound, Nat. Commun., 2016, 7(1), 13368 CrossRef CAS PubMed.
- S. Mukherjee, A. Spracklen, M. Valiente, E. Andersson, P. Öhberg, N. Goldman and R. R. Thomson, Experimental observation of anomalous topological edge modes in a slowly driven photonic lattice. Nat. Commun., 8(1), 2017 Search PubMed.
- J. P. Dahlhaus, B. M. Fregoso and J. E. Moore, Magnetization Signatures of Light-Induced Quantum Hall Edge States, Phys. Rev. Lett., 2015, 114(24), 246802 CrossRef PubMed.
- T. Oka and H. Aoki, Photovoltaic Hall effect in graphene, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 79(8), 169901 CrossRef.
- T. Kitagawa, T. Oka, A. Brataas, L. Fu and E. Demler, Transport properties of nonequilibrium systems under the application of light: Photoinduced quantum hall insulators without landau levels, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 235108 CrossRef.
- Z. Gu, H. A. Fertig, D. P. Arovas and A. Auerbach, Floquet Spectrum and Transport through an Irradiated Graphene Ribbon, Phys. Rev. Lett., 2011, 107(21), 216601 CrossRef PubMed.
- G. Usaj, P. M. Perez-Piskunow, L. E. F. Foa Torres and C. A. Balseiro, Irradiated graphene as a tunable Floquet topological insulator, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90(11), 115423 CrossRef.
- J. W. McIver, B. Schulte, F.-U. Stein, T. Matsuyama, G. Jotzu, G. Meier and A. Cavalleri, Light-induced anomalous Hall effect in graphene, Nat. Phys., 2020, 16(1), 38–41 Search PubMed.
- M. Merboldt, M. Schüler, D. Schmitt, J. Philipp Bange, W. Bennecke, K. Gadge, K. Pierz, H. Werner Schumacher, D. Momeni, D. Steil, S. R. Manmana, M. A. Sentef, M. Reutzel and S. Mathias, Observation of Floquet states in graphene, Nat. Phys., 2025, 21(7), 1093–1099 Search PubMed.
- J. Madéo and K. M. Dani, Floquet states in graphene revealed at last, Nat. Phys., 2025, 21(7), 1040–1041 Search PubMed.
- D. Choi, M. Mogi, U. De Giovannini, D. Azoury, B. Lv, Y. Su, H. Hübener, A. Rubio and N. Gedik, Observation of Floquet–Bloch states in monolayer graphene, Nat. Phys., 2025, 21(7), 1100–1105 Search PubMed.
- R. Peng, T. Zhang, Z. He, Q. Wu, Y. Dai, B. Huang and Y. Ma, Intrinsic layer-polarized anomalous hall effect in bilayer Mnbi2te4, Phys. Rev. B, 2023, 107, 085411 CrossRef CAS.
- W. Xun, C. Wu, H. Sun, W. Zhang, Y.-Z. Wu and P. Li, Coexisting Magnetism, Ferroelectric, and Ferrovalley Multiferroic in Stacking-Dependent Two-Dimensional Materials, Nano Lett., 2024, 24(11), 3541–3547 CrossRef CAS PubMed.
- T. Zhang, X. Xu, B. Huang, Y. Dai, L. Kou and Y. Ma, Layer-polarized anomalous Hall effects in valleytronic van der Waals bilayers, Mater. Horiz., 2023, 10(2), 483–490 RSC.
- K. Sheng, B. Zhang, H.-K. Yuan and Z.-Y. Wang, Strain-engineered topological phase transitions in ferrovalley 2h-rucl2 monolayer, Phys. Rev. B, 2022, 105, 195312 CrossRef CAS.
- J. Zhao, Y. Qi, C. Yao and H. Zeng, Strain-driven valley-dependent berry phase effects and topological transitions in janus svgen2 monolayer, Appl. Phys. Lett., 2024, 124(9), 093103 CrossRef CAS.
- Y. Qi, C. Yao, J. Zhao and H. Zeng, Strain-induced tunable valley polarization and topological phase transition in svsin2 monolayer, J. Mater. Chem. C, 2024, 12, 4417–4425 RSC.
- J. Lee, K. F. Mak and J. Shan, Electrical control of the valley Hall effect in bilayer MoS2 transistors, Nat. Nanotechnol., 2016, 11(5), 421–425 CrossRef CAS PubMed.
- M. Sui, G. Chen, L. Ma, W.-Y. Shan, D. Tian, K. Watanabe, T. Taniguchi, X. Jin, W. Yao, D. Xiao and Y. Zhang, Gate-tunable topological valley transport in bilayer graphene, Nat. Phys., 2015, 11(12), 1027–1031 Search PubMed.
- Z. Zhu, A. Collaudin, B. Fauque, W. Kang and K. Behnia, Field-induced polarisation of Dirac valleys in bismuth, Nat. Phys., 2012, 8(1), 89–94 Search PubMed.
- Y. P. Shkolnikov, E. P. De Poortere, E. Tutuc and M. Shayegan, Valley splitting of AlAs two-dimensional electrons in a perpendicular magnetic field, Phys. Rev. Lett., 2002, 89(22), 226805 CrossRef CAS PubMed.
- A. Gomez-Leon and G. Platero, Floquet-Bloch theory and topology in periodically driven lattices, Phys. Rev. Lett., 2013, 110(20), 200403 CrossRef CAS PubMed.
- Y. Ikeda, S. Kitamura and T. Morimoto, Floquet engineering of electric polarization with two-frequency drive, Prog. Theor. Exp. Phys., 2022, 2022(4), 04A101 CrossRef.
- W.-Y. Tong, S.-J. Gong, X. Wan and C.-G. Duan, Concepts of ferrovalley material and anomalous valley Hall effect, Nat. Commun., 2016, 7(1), 13612 CrossRef CAS PubMed.
- P. Li, B. Liu, S. Chen, W.-X. Zhang and Z.-X. Guo, Progress on two-dimensional ferrovalley materials, Chin. Phys. B, 2024, 33(1), 017505 CrossRef CAS.
- X. Zhang, Y. Jiang, Y. Tian, B. Zhang, L. Li, W.-J. Gong and X. Kong, Strain-engineering quantized spin hall conductivity in sliding multiferroic rucl 2 bilayers, J. Mater. Chem. C, 2025, 13(7), 3352–3361 RSC.
- R. Li, N. Mao, X. Wu, B. Huang, Y. Dai and C. Niu, Robust Second-Order Topological Insulators with Giant Valley Polarization in Two-Dimensional Honeycomb Ferromagnets, Nano Lett., 2023, 23(1), 91–97 CrossRef CAS PubMed.
- W. Xie, L. Zhang, Y. Yue, M. Li and H. Wang, Giant valley polarization and perpendicular magnetocrystalline anisotropy energy in monolayer mX2 (m = Ru,Os; x = Cl,Br), Phys. Rev. B, 2024, 109, 024406 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- Y. Ma, Y. Wu, J. Tong, L. Deng, X. Yin, L. Zhou, X. Han, F. Tian and X. Zhang, Distinct ferrovalley characteristics of the Janus RuClX (X = F, Br) monolayer, Nanoscale, 2023, 15(18), 8278–8288 RSC.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 57(3), 1505–1509 CrossRef CAS.
- S.-D. Guo, W.-Q. Mu and B.-G. Liu, Valley-polarized quantum anomalous Hall insulator in monolayer RuBr2, 2D Mater., 2022, 9(3), 035011 CrossRef CAS.
- H. Huan, Y. Xue, B. Zhao, G. Gao, H. Bao and Z. Yang, Strain-induced half-valley metals and topological phase transitions in mbr2 monolayers (m = Ru, Os)., Phys. Rev. B, 2021, 104, 165427 CrossRef CAS.
- H. Sun, S.-S. Li, W.-X. Ji and C.-W. Zhang, Valley-dependent topological phase transition and quantum anomalous valley hall effect in single-layer ruclbr, Phys. Rev. B, 2022, 105, 195112 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, An updated version of wannier90: A tool for obtaining maximally-localised Wannier functions, Comput. Phys. Commun., 2014, 185(8), 2309–2310 CrossRef CAS.
- X. Kong, W. Luo, L. Li, M. Yoon, T. Berlijn and L. Liang, Floquet band engineering and topological phase transitions in 1T′ transition metal dichalcogenides, 2D Mater., 2022, 9(2), 025005 CrossRef.
- X. Kong, B. Zhang, W.-J. Gong and L. Li, Tunable light-induced topological edge states in strain engineering of bismuthene monolayers, J. Mater. Chem. C, 2024, 12(34), 13325–13331 RSC.
- Q. Wu, S. Zhang, H.-F. Song, M. Troyer and A. A. Soluyanov, WannierTools: An open-source software package for novel topological materials, Comput. Phys. Commun., 2018, 224, 405–416 CrossRef CAS.
- Y. Tian, X. Kong, L. Li, B. Zhang and W.-J. Gong, Quantized anomalous Hall conductivity induced by Floquet and strain engineering in second-order topological insulators, Phys. Rev. B, 2025, 111(23), 235406 CrossRef CAS.
- M. Bukov, L. D'Alessio and A. Polkovnikov, Universal High-Frequency Behavior of Periodically Driven Systems: from Dynamical Stabilization to Floquet Engineering, Adv. Phys., 2015, 64(2), 139–226 CrossRef.
- N. Marzari and D. Vanderbilt, Maximally-localized generalized Wannier functions for composite energy bands, Phys. Rev. B:Condens. Matter Mater. Phys., 1997, 56(20), 12847–12865 CrossRef CAS.
- S. Blanes, F. Casas, J. A. Oteo and J. Ros, The Magnus expansion and some of its applications, Phys. Rep., 2009, 470(5–6), 151–238 CrossRef.
- R. Seshadri and D. Sen, Engineering Floquet topological phases using elliptically polarized light, Phys. Rev. B, 2022, 106(24), 245401 CrossRef CAS.
- K. Kitayama, Y. Tanaka, M. Ogata and M. Mochizuki, Floquet Theory of Photoinduced Topological Phase Transitions in the Organic Salt α-(BEDT-TTF)2 I3 Irradiated with Elliptically Polarized Light, J. Phys. Soc. Jpn., 2021, 90(10), 104705 CrossRef.
- H. Chnafa, M. Mekkaoui, A. Jellal and A. Bahaoui, Effect of Strain on Band Engineering in Gapped Graphene, Eur. Phys. J. B, 2021, 94(1), 39 CrossRef CAS.
- A. Diaz-Fernandez, Inducing anisotropies in Dirac fermions by periodic driving, J. Phys.: Condens. Matter, 2020, 32(49), 495501 CrossRef CAS PubMed.
- Z. Li, H. Cao and S. Meng, Light-induced above-room-temperature Chern insulators in group-IV Xenes, npj Comput. Mater., 2025, 11(1), 160 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |








