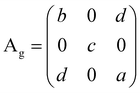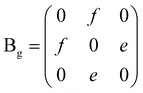Open Access Article
Open Access ArticleAntipolar and short- and long-range magnetic ordering in quasi-two-dimensional AgCrP2S6
Chaitanya B. Auti *a,
Atul G. Chakkar
*a,
Atul G. Chakkar a,
Shantanu Semwal
a,
Shantanu Semwal b,
Sebastian Selter
b,
Sebastian Selter c,
Yuliia Shemerliuk
c,
Yuliia Shemerliuk c,
Bernd Büchner
c,
Bernd Büchner cd,
Saicharan Aswartham
cd,
Saicharan Aswartham c,
Koushik Pal
c,
Koushik Pal b and
Pradeep Kumar
b and
Pradeep Kumar *a
*a
aSchool of Physical Sciences, Indian Institute of Technology, Mandi-175005, India. E-mail: autichaitanya5@gmail.com; pkumar@iitmandi.ac.in
bDepartment of Physics, Indian Institute of Technology Kanpur, Kanpur 208016, India
cInstitute for Solid State Research, Leibniz IFW Dresden, Helmholtzstr. 20, 01069 Dresden, Germany
dInstitute of Solid State and Materials Physics and Würzburg-Dresden Cluster of Excellence ct.qmat, Technische Universität Dresden, 01062 Dresden, Germany
First published on 23rd December 2025
Abstract
AgCrP2S6 serves as a versatile system to probe dynamics of the quasiparticle excitations as well as multiple phase transitions with lowering temperature linked with the polar, lattice and spin degrees of freedom. Here, we report in-depth temperature- and polarization-dependent Raman scattering measurements on single crystals of quasi-2D zigzag antiferromagnetic AgCrP2S6, along with first principles-based phonon calculations. We observed multiple phase transitions triggered by the short- and long-range ordering of spins at ∼90 K and 20 K, respectively, within the Cr sublattice, where spins are arranged in a 1D chain, as evident from the distinct anomalies in the phonon-mode self-energy parameters and intensity. Contrary to the conventional belief, we proposed the possibility of quasi-antipolar ordering at ∼200 K and with further lowering in temperature an antipolar ordering at ∼140 K attributed to the Ag ions, which is conjectured to be forbidden owing to the heaviness of Ag ions. The quasi-antipolar and antipolar orderings are gauged via a distinct renormalization of the parameters of phonons, which exist at all the temperatures. Additionally, a large number of modes appeared with the decrease in temperature, in the range of ∼200–140 K, where antipolar ordering started settling in. The emergence of a large number of phonon modes below ∼200 K, nearly double that at room temperature, suggests the lowering of symmetry from high-temperature C2h to low-temperature C2 or Cs.
1. Introduction
Two-dimensional (2D) van der Waals (vdW) materials have attracted significant attention due to their distinct properties that are advantageous for potential applications in next-generation electronics and advanced physics.1,2 A significant domain of modern research focuses on magnetic vdW materials that exhibit intriguing physical properties. The intrinsic 2D nature of these materials provides unique opportunities to explore novel magnetic ground states, magnetic excitations, and their interactions with other quasiparticle excitations.3–6 These tunable properties are of great interest not only for fundamental studies but also for potential applications in advanced fields such as spintronics, optoelectronics, and nanoelectronics.7,8Recently, 2D metal thiophosphates (MTPs) have drawn significant interest because of their intriguing characteristics including magnetism down to monolayer, ferroelectricity, and multiferroicity. The MPS3 (M = Mn, Fe, Ni, Co, and V) family of layered materials presents a rich array of isostructural compounds that form 2D vdW antiferromagnets.6,9,10 2D MPS3 materials exhibit a wide range of band gaps (∼0.24–3.5 eV), which make them highly promising for applications in catalysis, spintronics, and energy conversion.11 Colombet et al. reported that heterocharge substitution also yields numerous stable compounds, which provide an extra degree of freedom in the atomic arrangement.12,13 One such member of this family is AgCrP2S6, which exhibits an antiferromagnetic transition temperature (TN) at ∼20 K.14 The non-magnetic Ag atom and the magnetic Cr atom are arranged in zigzag strips. The Ag+ ion is bigger in size than the Cr3+ ion; as a result, the layer above the Ag atoms significantly bends outward (see SI Fig. S1-(a)15). Consequently, a deformation occurs in the P2S6 octahedra to accommodate the cations of different sizes. Therefore, to reduce this strain energy, the cations organize themselves in a zigzag chain, and this arrangement functions as a one-dimensional chain of magnetic atoms with a spin value of S = 3/2 (see SI Fig. S1-(d)15). The layers are arranged in an AAA stacking, resulting in a quasi-2D structure.16,17
Magnetic fluctuations in 2D structures are influenced by the symmetry of order parameters, namely, the Ising, XY, and Heisenberg types.9 One-dimensional (1D) spin S = 3/2 Heisenberg antiferromagnetic Hamiltonian is given as follows:18
Raman spectroscopy is a promising technique for studying the presence of magnons, phase transitions, and various quasiparticle excitations, including spin–phonon and electron–phonon coupling, in 2D magnetic materials.20–24 Recently, heterocharge MTPs moved into focus due to their low-dimensional magnetism, multiferroicity, and Haldane phase.25,26 Understanding these singular behaviour in MTPs will provide valuable insights for potential applications in spin-based logic gate devices and non-volatile memory storage devices, opening up the possibility of fabricating heterostructures for multifunctional device applications.27,28 Motivated by the rich underlying physics in these low-dimensional systems, we conducted an in-depth investigation of the AgCrP2S6 single crystal using Raman scattering measurements as well as first-principles calculations of the phonons. The current literature lacks information on the temperature-dependent characteristics of phonon and magnetic dynamics, suggesting a potential for uncovering novel insights into the vibrational and magnetic properties of materials.
In this work, we elucidated the phonon excitations and crystal symmetry of AgCrP2S6 using comprehensive temperature- and polarization-dependent Raman spectroscopy measurements along with the first-principles calculations of phonons. We observed significant hardening of the low-energy phonon modes, attributed to the strong phonon–phonon anharmonic interactions, or an increase in bonding stiffness, indicating structural instability in the material. Based on the temperature-dependent phonon-mode analysis, we observed a signature of antiferromagnetic transition at TN ∼ 20 K. Interestingly, we observed anomalies in mode frequency, linewidth, and intensity around temperatures ∼90 K, ∼140 K, and ∼200 K. These transitions are attributed to the possible short-range ordering of the spins and polar ordering in the system, respectively. We also examined the interactions between quasiparticle excitations and electronic and/or magnetic continuums, i.e., Fano asymmetry in the phonon line shape, as a function of temperature. Polarization-dependent measurements show the two-fold symmetry of all the observed modes in line with the group theoretical predictions. Quite surprisingly, we also observed a systematic rotation of the polarization major axis of the phonon modes as a function of temperature. This opens up the possibility of tuning the scattered light in this quasi 2D magnet via symmetry control.
2. Experimental and computational details
2.1. Experimental details
The single-crystal samples of AgCrP2S6 were prepared using a chemical vapor transport technique, as described in ref. 29. Temperature-dependent Raman scattering and photoluminescence (PL) measurements (see the SI for PL measurements15) were carried out from 6 to 300 K with ±0.1 K precision with a closed-cycle refrigerator (Montana) and a Horiba LabRAM HR-evolution Raman spectrometer in the backscattering configuration. A 633 nm laser was used to excite the Raman spectra. The laser power was kept very low (<0.5 mW) to prevent local heating. A 50× (NA = 0.5) long-working-distance objective was used to focus the incident laser light on the sample. Scattered light was collected using a Peltier-cooled charge-coupled detector. To unveil the symmetry of phonon modes, polarization-dependent measurements were performed at temperatures of 6 K, 60 K, 120 K, and 170 K. A half-wave plate was placed near the laser entrance to manually rotate the incident polarization onto the sample, while the scattered polarization analyzer remained fixed.2.2. Computational details
We performed first-principles density functional theory (DFT) calculations using the Vienna ab initio simulation package30,31 and utilized pseudo potentials generated using the projected augmented wave (PAW)32 method. The valence electron configurations used are 4p64d105s1, 3d54s1, 3s23p3, and 3s23p4 for Ag, Cr, P and S, respectively. We used Gaussian smearing for treating the partial occupancies for each orbital with an energy broadening of 0.05 eV and treated the exchange–correlation energies of the electrons within the GGA-Perdew–Burke–Ernzerhof (PBE) functional.33 The cutoff for the kinetic energy was set to 450 eV for all calculations. The primitive cell structure of AgCrP2S6 contained 20 atoms (2 Ag, 2 Cr, 4 P and 12 S atoms); we considered the antiferromagnetic (AFM) arrangement of Cr atoms and used the DFT-D3 method of Grimme34 to include the vdW interactions in the structure. The lattice parameters were fully optimized using a k-point grid of 9 × 9 × 9, and the energy convergence criterion was set to 10−8 eV. After full optimization, the energies are converged and the force on each atom is of the order of 10−4 eV A−1 or less. The lattice parameters and volume for the optimized structure were a = 5.888 A, b = 10.647 A, c = 6.704 A and 403.848 A3, respectively. The changes in a, b, c and volume are 0.09%, 0.24%, −0.6% and 0.3%, respectively, when compared with the experimental lattice parameters.The phonon calculations were performed using the finite-difference method as implemented in Phonopy.35,36 We used a 2 × 2 × 2 supercell containing 160 atoms, considering the AFM arrangement of Cr atoms and including the vdW interactions. The tabulated frequencies and symmetry labels of all the modes at Γ-point are provided in Table S2.
3. Results and discussion
3.1 Crystal structure and phonon modes
AgCrP2S6 exhibits a monoclinic symmetry having the space group P2/a (#13) and the point group C2h (2/m). The unit cell of the AgCrP2S6 bulk single crystal consists of 60 phonon modes at the Γ-point of the Brillouin zone, with the following irreducible representations:37 Γtotal = 14Ag + 14Au + 16Bg + 16Bu. There are 30 Raman active (ΓRaman= 14Ag + 16Bg) modes and 27 infrared active (ΓIR = 13Au + 14Bu) modes (for more details, see Table 1). The Raman spectra is recorded using 633 nm laser excitation, and 48/27 Raman modes are observed at 6 K/300 K, which are labelled as P1–P48 at 6 K, as shown in Fig. S2. To extract the self-energy parameters of phonon modes, i.e., peak frequency (ω), full width at half maximum (FWHM), and intensity, spectra are fitted using a sum of Lorentzian functions. We also recorded the spectra in the higher frequency range of 700–1400 cm−1 and observed some very weak higher order modes, as shown in SI Fig. S9.15 Fig. 1(a) and (b) show the temperature evolution of the Raman spectrum of AgCrP2S6 in the temperature range of 6 to 300 K from 15 to 350 cm−1 and 350 to 700 cm−1 (magnified spectra in the smaller spectral range are shown in SI Fig. S6–S815). | ||
| Fig. 1 Temperature evolution of the Raman spectrum in the temperature range of 6 to 300 K, ranging from (a) 15–350 cm−1 and (b) 350–700 cm−1. The observed phonon modes are labelled as P1–P48. | ||
All higher frequency modes ranging from ∼250 cm−1 soften with the increase in temperature, showing a normal anharmonic phonon behaviour; while some lower frequency range modes show anomalous hardening, and others show a softening and get broadened with the increase in temperature. In the M2P2S6 material family, the higher frequency (above ∼250 cm−1) modes are assigned to the vibration due to P2S6 octahedra; therefore, these modes are similar in all M2P2S6 compounds, and the lower frequency (below ∼250 cm−1) Raman modes are assigned to the heavy metal ion.38 The particular M atom determines the cutoff frequency that separates the high- and low-frequency regimes. Phonon dispersion along with the atom-resolved phonon density of state (phdos) is shown in Fig. 2a and b, respectively. From the atom-resolved phdos shown in Fig. 2b, we can see that in the high-frequency region (500 cm−1 to 650 cm−1), the contributions to the phonon dispersion are mainly due to the P and S atoms due to smaller masses of these atoms. In the middle region (150 cm−1 to 500 cm−1), we see the P contribution waning and being taken over by the S atoms and rising contribution due to Cr seen around 350 cm−1, 300 cm−1, and 200 cm−1. Finally, in the lower frequency region (20 cm−1 to 150 cm−1), we see the contributions of S, P and Cr decreasing and the Ag contributions increasing with large Ag localization having peaks around 60 cm−1 and 20 cm−1 to 40 cm−1. All prominent phonon-mode intensities reduce drastically from the lowest recorded temperature to the highest temperature, as shown in Fig. 1(a) and (b). The most intense phonon mode P19 could be a mode associated with the anionic complex [P2S6]4−, which is almost twice as intense as the other prominent modes P11, P33, and P47. Many phonon modes as P4, P5, P9, P15, P16, P17, P20, P23, P25, P29, P31, P32, P34, P35, P36, P40, P41, P42, P44, and P48 disappear with the increase in temperature (see Fig. S3, which shows disappeared phonon modes). Mode P31 (∼469.5 cm−1 at 6 K) shows an asymmetric line shape (see Fig. 4(c)), as discussed in detail in Section 3.4.
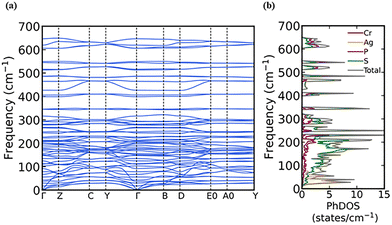 | ||
| Fig. 2 (a) Phonon dispersion and (b) atom-resolved phonon density of states based on the AFM arrangement of AgCrP2S6 and including the vdW forces. | ||
3.2 Temperature dependence of the phonon modes
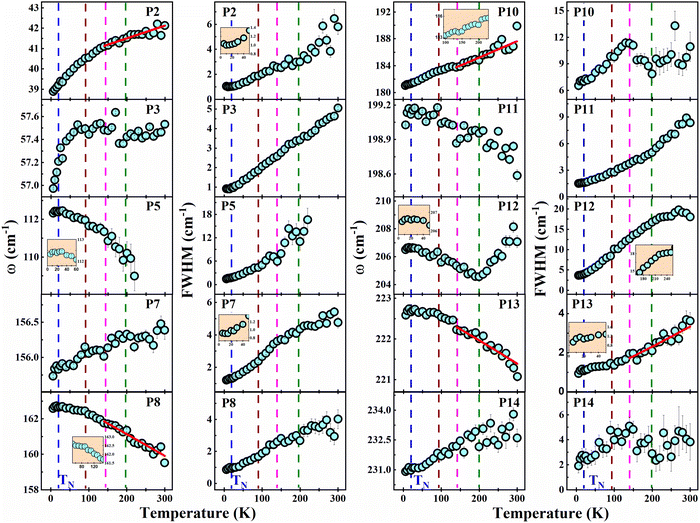
Generally, mode frequencies are expected to exhibit softening with the increase in temperature.39 Fig. 3 shows the temperature dependence of frequency and the FWHM of some of the prominent phonon modes labelled as P2, P3, P5, P7, P8, and P10–P14 (for more phonon modes, see SI Fig. S415). Some intriguing features are observed: (i) for the lower frequency range ω ≤ 250 cm−1, some of the phonon modes P2, P3, P7, P10, P12, and P14 show abnormal hardening with the increase in temperature. (ii) A rapid decrease in the intensity of the phonon modes P10 and P14 with the increase in temperature (see Fig. 4(a)). (iii) Many phonon modes disappear with the increase in temperature (see SI Fig. S315). Interestingly, the mode P7 shows abnormal hardening with the increase in temperature and approaches towards P8 (ωP8 = 159.5 cm−1 at room temperature). The mode P10 approaches P11 with a sharp increase in frequency ΔωP10 ∼ 12 cm−1. However, P13 and P14 diverge from each other with the increase in temperature (see Fig. 4(b)). P2 and P3 both show abnormal hardening with the increase in temperature. These modes may be associated with the heavy metal ion Ag+.16 The possible reasons associated with the anomalous frequency change are discussed in detail in Section 3.3.We note that at room temperature, several phonon modes are relatively broad (see Fig. 1(a), (b) and Fig. S6–S815), evolving into much sharper modes at low temperatures. While such behaviour is consistent with anharmonic phonon–phonon interactions, the relatively large linewidth changes observed for low-frequency modes such as P2, P3, P7, P11, and P12 of ∼75% (|(ω6K − ω300K)|/ω300K) (see Fig. 3) may also suggest a possible contribution from additional temperature-dependent lattice fluctuations and the presence of Ag+ cation disorders at high temperatures.
It is noteworthy that several phonon modes P5, P6, P8, P13, P19, P21, P24, P28, P33, P39, and P47 show a change in the slope of their frequency shifts ∼90 K (see Fig. 3 and Fig. S415). The mode P3 exhibits a sharp frequency increase up to ∼90 K, remaining nearly constant thereafter. The FWHM of modes P13, P28, P45, and P47 also shows slope changes at ∼90 K, indicating a clear anomaly. In addition, the mode P10 shows a slight kink at ∼140 K, while the modes P13, P19, and P21 display discontinuities in frequency at this temperature. The FWHM of phonon modes P6, P10, and P14 exhibits a jump at ∼140 K, while modes P8, P19, and P47 show a change in slope, indicating an anomaly at this temperature. Around 200 K, mode P2 displays a discontinuity in frequency, and modes P8, P19, P21, and P39 show slope changes in their frequency shifts. Mode P12 exhibits an unusual hardening behaviour above 200 K, with its frequency increasing from ∼204.5 to ∼209 cm−1 with the increase in temperature from 200 K to ∼300 K, marking a clear anomaly near 200 K. Additionally, the FWHM of modes P6 and P10 shows a jump, and that of modes P7, P12, P19, and P21 shows slope changes around this temperature; the lifetime of the phonons is strongly influenced in the vicinity of this temperature. Moreover, many phonon modes start appearing below ∼200 K and continue to emerge till ∼140 K (see SI Fig. S315), consistent with the anomalies observed in the modes which survive at all the temperatures.
Interestingly, the intensity change of all the phonon modes with temperature is nearly uniform except for the modes P10 and P14, whose intensity decreases sharply with the increase in temperature by ∼10 times compared to its intensity at 6 K, as shown in Fig. 4(a). Phonon modes P2 and P3 show very interesting intensity variation; their intensity increases with the increase in temperature up to ∼90 K, after which it decreases, indicating an anomaly at ∼90 K. We note that a similar intensity behaviour is also reported for the low-frequency modes in a sister compound, i.e. CuCrP2S6, which suggests that the lattice dynamics of off-centre Cu+ cations within the intralayer is not quenched, indicating that an order–disorder type of structural transition is responsible for the emergence of defect dipoles associated with Cu ions.43 It is observed that the intensity of the modes P7, P10, P11, P13, P14 and P19 shows a sharp decrease with the increase in temperature and remains nearly constant after 200 K, clearly showing an anomaly at ∼200 K (see Fig. 4(a) and Fig. S515).
Our observations clearly favour the possibility of structural instability, with singular changes in self-energy parameters of the prominent modes, which survive at all the temperatures. We note that the symmetry of the newly emerged modes at low temperatures (see Fig. S12 and S1315) is also similar to the modes at high temperatures. This reflects that the symmetry of the modes is the same, but their number becomes nearly double, i.e. going to the lower symmetry (C2 or Cs) as the temperature is decreased. Our observation of emergence of new modes in the temperature interval of ∼140–200 K and modes showing distinct anomalies at these temperatures suggest a symmetry-lowering structural transition from a high-temperature C2h point group to C2 or Cs point groups at these temperatures.21
3.3 Discussion on anomalous hardening of the phonon modes
Anomalous hardening of the low-frequency phonon modes P2, P3, P7, P10, P12 and P14 may be associated with the anharmonic effects, which comes into the picture due to (i) strong phonon–phonon anharmonic interactions and (ii) lattice thermal contraction or structural instability, which are discussed as follows:
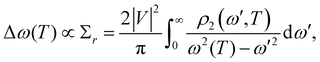 | (1) |
Now to understand the impact of anharmonicity on the frequency and FWHM of the phonon modes in the temperature range of ∼140 to 300 K, we used an anharmonic three-phonon model, given as follows:39,51
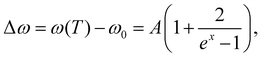 | (2) |
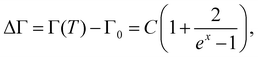 | (3) |
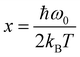 . A and C represent the self-energy constant that describes the strength of phonon–phonon interactions involving three phonon processes. Anharmonic model fit to the experimental data for the case of frequency and FWHM is shown by solid red lines in the temperature range of 140–300 K. Fig. 3 illustrates the prominent modes fitted (frequency and FWHM) using eqn (2) and (3), respectively. The optimal parameters are shown in Table S3. The self-energy constant (A) associated with the modes P2 and P10 is positive, indicating that the term ω > ω′ is dominant in eqn (1) for these modes, while for all other phonon modes, it is negative.
. A and C represent the self-energy constant that describes the strength of phonon–phonon interactions involving three phonon processes. Anharmonic model fit to the experimental data for the case of frequency and FWHM is shown by solid red lines in the temperature range of 140–300 K. Fig. 3 illustrates the prominent modes fitted (frequency and FWHM) using eqn (2) and (3), respectively. The optimal parameters are shown in Table S3. The self-energy constant (A) associated with the modes P2 and P10 is positive, indicating that the term ω > ω′ is dominant in eqn (1) for these modes, while for all other phonon modes, it is negative.
3.4 Fano resonance
We observed that the phonon mode P31 exhibits an asymmetric line shape, which can be attributed to the interaction between the discrete phonon and an underlying magnetic or electronic continuum. In AgCrP2S6, an electronic origin of the continuum can be ruled out, since the optical band gap lies far above the Raman excitation energy (∼1.32 eV at 6 K), making the electronic contribution negligible. Therefore, the continuum responsible for the Fano asymmetry is most likely magnetic in nature. This suggests that the asymmetric profile of the P31 mode originates from magnetic fluctuations within the Cr sublattice, indicative of a spin–phonon coupling mechanism. Such asymmetry is well described by the Breit–Wigner–Fano (BWF) function as54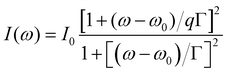 , where ω0 and Γ are the frequency and FWHM of the uncoupled phonon, respectively. q is the asymmetry parameter that characterizes the coupling strength between the phonon and the continuum, quantified by the parameter 1/|q|. Microscopically 1/|q| ∝ |VE|, where |VE| tells the interaction between the discrete state and the continuum. Therefore, limit 1/|q| → 0 corresponds to weak coupling, which causes the peak to be symmetric and reduces to a Lorentzian line shape; and limit 1/|q| → ∞ represents strong coupling that causes the peak to be more asymmetric. Fig. 4(c-i) show the temperature evolution of the asymmetric mode P31 in the temperature range of 6–300 K. Fig. 4(c-ii) and (c-iii) show the temperature dependence of the frequency and FWHM of mode P31 in the temperature range of 6–200 K. For mode P31, as the temperature increases, the frequency decreases and the FWHM increases, with a change in slope for both parameters occurring around TN (∼20 K). Fig. 4(c-iv) shows the temperature dependence of the coupling strength (1/|q|), and it decreases with the increase in temperature with a jump around TN (∼20 K). This suggests that the coupling between phonon and underlying magnetic continuum is strongly affected by long-range magnetic ordering.
, where ω0 and Γ are the frequency and FWHM of the uncoupled phonon, respectively. q is the asymmetry parameter that characterizes the coupling strength between the phonon and the continuum, quantified by the parameter 1/|q|. Microscopically 1/|q| ∝ |VE|, where |VE| tells the interaction between the discrete state and the continuum. Therefore, limit 1/|q| → 0 corresponds to weak coupling, which causes the peak to be symmetric and reduces to a Lorentzian line shape; and limit 1/|q| → ∞ represents strong coupling that causes the peak to be more asymmetric. Fig. 4(c-i) show the temperature evolution of the asymmetric mode P31 in the temperature range of 6–300 K. Fig. 4(c-ii) and (c-iii) show the temperature dependence of the frequency and FWHM of mode P31 in the temperature range of 6–200 K. For mode P31, as the temperature increases, the frequency decreases and the FWHM increases, with a change in slope for both parameters occurring around TN (∼20 K). Fig. 4(c-iv) shows the temperature dependence of the coupling strength (1/|q|), and it decreases with the increase in temperature with a jump around TN (∼20 K). This suggests that the coupling between phonon and underlying magnetic continuum is strongly affected by long-range magnetic ordering.
4. Polarization dependence of the phonon modes
To determine the symmetry and to understand the angle-dependent characteristics of the phonon modes, we carried out in-depth polarization-dependent Raman measurements at four temperatures: 6 K, 60 K, 120 K, and 170 K, as shown in Fig. 5, for few selected modes (for more phonon modes, see SI Fig. S10 and S1115). The angular dependence of the phonon mode intensity is given by eqn (4) and (5), considering the complex element of the Raman tensor (see Section S1 in the SI for polarization intensity analysis details15):
IAg = |b|2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(θ + θ0)cos2 cos2(θ + θ0)cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 + |c|2 θ0 + |c|2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(θ + θ0)sin2 sin2(θ + θ0)sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 + 2|b||c|cos(θ + θ0)cos θ0 + 2|b||c|cos(θ + θ0)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 θ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ + θ0)sin sin(θ + θ0)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 θ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕbc ϕbc
| (4) |
IBg = |f|2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(θ + 2θ0), sin2(θ + 2θ0),
| (5) |
In Fig. 5 (SI Fig. S10 and S1115), the solid red line shows the fitted curves using eqn (4) and (5).
Fig. 5 shows the polar plot for the intensity of the modes P7, P8, P13, P19, and P47 at four different temperatures. The mode P7 shows the quasi-isotropic behaviour at 6 K, and it approaches a two-fold symmetry at 60 K; and it shows a complete two-fold symmetry at higher temperatures of 120 and 170 K with maxima around 20 and 200 degrees. The mode P8 shows the two-fold symmetry at all four temperatures, with maxima around 40 and 220 degrees. The mode P47 shows the quasi-isotropic behaviour at 6 and 60 K, while it becomes two-fold at 120 and 170 K with maxima around 20 and 200 degrees. The modes that disappeared at higher temperatures also exhibit a twofold symmetry, as shown in SI Fig. S12 and S13.15 This reflects that the symmetry of these modes is also Ag/Bg or A/B consistent with the group theoretical arguments. Interestingly, mode P13 shows the quasi-isotropic behaviour with maxima around 40 and 220 degrees at 6 and 60 K, while at higher temperatures of 120 and 170 K, it shows the maxima around 90 and 270 degrees. Moreover, the modes P19 and P33 (see Fig. S11) show maxima at ∼140 and 320 degrees at 6 and 60 K, while at higher temperatures, it shows maxima at ∼0 and 180 degrees. Such rotation in the polar plots likely originates from subtle structural changes or distortions that modify the Raman tensor elements at lower temperatures. The magneto-optical Kerr effect can be ruled out as the primary cause, since the observed rotation is not uniform across all phonon modes and occurs well above the magnetic ordering temperature, where long-range magnetic order is absent. The possibility of birefringence-induced rotation is also less probable, as the effect is strongly mode-selective and does not show the uniform angular dependence characteristic of optical birefringence. Instead, a more probable origin could be strain-induced local anisotropy or temperature-driven structural distortion, both of which can locally modify the polarizability tensor and give rise to the observed rotation in certain phonon modes. We note that a similar rotation has also been reported recently in other 2D magnetic systems.5,55 The microscopic understanding of these rotations and changes in the symmetry from quasi-isotropic behaviour to twofold symmetry as a function of temperature calls for a detailed theoretical study to uncover the mechanisms underlying these changes.
5. Conclusion
In conclusion, we performed comprehensive temperature- and polarization-dependent Raman measurements on single-crystal AgCrP2S6 along with the first-principles-based calculations of phonons. Our results have shown that this quasi-2D van der Waals material, AgCrP2S6, with 1D spin chains demonstrated a possibility of quasi-antipolar and antipolar phase transitions in contrast to the conventional view so far adopted in the literature, therefore putting forward that even the heavy ion (Ag)-based system may show antiferroelectric ordering. Our findings also pave the way forward for potentially controlling and manipulating these orderings as a function of layer and making them useful for potential applications. We also observed the signature of a long-range magnetic ordering at low temperatures, and all these transitions are marked by the distinct renormalization of the phonon modes as well as the emergence of multiple phonon modes with the decrease in temperature. Our findings indicated that this material may also be tuned as a potential multiferroic material similar to its sister compounds. Additionally, polarization-dependent measurements elucidate the role of anisotropy in the system, shedding light on the crystal symmetry. Our findings offer critical insights into the phonon dynamics of this quasi-2D magnetic compound, providing a deeper understanding of its underlying mechanisms.Author contributions
Chaitanya B. Auti: writing, review and editing, writing – original draft, investigation, data curation, formal analysis, methodology. Atul G. Chakkar: data curation, formal analysis, writing – review & editing. Shantanu Semwal: data curation, formal analysis, writing – review & editing. Sebastian Selter: formal analysis, writing – review & editing. Yuliia Shemerliuk: formal analysis, writing – review & editing. Bernd Büchner: formal analysis, writing – review & editing. Saicharan Aswartham: formal analysis, writing – review & editing. Koushik Pal: data curation, formal analysis, writing – review & editing. Pradeep Kumar: formal analysis, funding acquisition, supervision, validation, methodology, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
All the data that support the findings of this study are included within the article and supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5tc03093e.Acknowledgements
P. K. thanks SERB (project no. CRG/2023/002069) for the financial support and IIT Mandi for the experimental facilities.References
- C. Liu, H. Chen, S. Wang, Q. Liu, Y.-G. Jiang, D. W. Zhang, M. Liu and P. Zhou, Two-dimensional materials for next-generation computing technologies, Nat. Nanotechnol., 2020, 15, 545 CrossRef CAS.
- L. Liao, E. Kovalska, J. Regner, Q. Song and Z. Sofer, Two-Dimensional van der Waals Thin Film and Device, Small, 2024, 20, 2303638 CrossRef CAS.
- T. T. Mai, K. F. Garrity, A. McCreary, J. Argo, J. R. Simpson, V. Doan-Nguyen, R. V. Aguilar and A. R. H. Walker, Magnon–phonon hybridization in 2D antiferromagnet MnPSe3, Sci. Adv., 2021, 7, eabj3106 CrossRef CAS.
- S. Liu, A. Granados del Águila, D. Bhowmick, C. K. Gan, T. Thu Ha Do, M. A. Prosnikov, D. Sedmidubský, Z. Sofer, P. C. M. Christianen and P. Sengupta, Direct observation of magnon–phonon strong coupling in two-dimensional antiferromagnet at high magnetic fields, Phys. Rev. Lett., 2021, 127, 097401 CrossRef CAS PubMed.
- A. G. Chakkar, D. Kumar and P. Kumar, Broken weak and strong spin rotational symmetries and tunable interactions between phonons and the continuum in Cr2Ge2Te6, Phys. Rev. B, 2024, 109, 134406 CrossRef CAS.
- N. Khan, D. Kumar, V. Kumar, Y. Shemerliuk, S. Selter, B. Büchner, K. Pal, S. Aswartham and P. Kumar, The interplay of topology and antiferromagnetic order in two-dimensional van der Waals crystals of (NixFe1−x)2P2S6, 2D Mater., 2024, 11, 035018 CrossRef CAS.
- H. Li, S. Ruan and Y.-J. Zeng, Intrinsic van der Waals Magnetic Materials from Bulk to the 2D Limit: New Frontiers of Spintronics, Adv. Mater., 2019, 31, 1900065 Search PubMed.
- S. Kumari, D. K. Pradhan, N. R. Pradhan and P. D. Rack, Recent developments on 2D magnetic materials: challenges and opportunities, Emergent Mater., 2021, 4, 827 CrossRef CAS.
- P. Joy and S. Vasudevan, Magnetism in the layered transition-metal thiophosphates MPS3 (M= Mn, Fe, and Ni), Phys. Rev. B, 1992, 46, 5425 CrossRef CAS PubMed.
- A. R. Wildes, S. J. Kennedy and T. J. Hicks, True two-dimensional magnetic ordering in MnPS3, J. Phys.: Condens. Matter, 1994, 6, L335 CrossRef CAS.
- R. Samal, G. Sanyal, B. Chakraborty and C. S. Rout, Two-dimensional transition metal phosphorous trichalcogenides (MPX3): a review on emerging trends, current state and future perspectives, J. Mater. Chem. A, 2021, 9, 2560 RSC.
- P. Colombet, A. Leblanc, M. Danot and J. Rouxel, Structural aspects and magnetic properties of the lamellar compound Cu0.50Cr0.50PS3, J. Solid State Chem., 1982, 41, 174 CrossRef CAS.
- S. Lee, P. Colombet, G. Ouvrard and R. Brec, A new chain compound of vanadium(III): Ag12V12PS3 structure, metal ordering, and magnetic properties, Mater. Res. Bull., 1986, 21, 917 CrossRef CAS.
- H. Mutka, C. Payen and P. Molinié, One-Dimensional Heisenberg Antiferromagnet with Spin S = 3/2. Experiments on AgCrP2S6, Europhys. Lett., 1993, 21, 623 CrossRef CAS.
- See SI at https://doi.org/10.1039/d5tc03093e for analysis of polarization dependent intensity; temperature-dependent photoluminescence; crystal structure; fitted Raman spectrum; temperature dependent frequency, FWHM, intensity of phonon modes; magnified temperature dependent Raman spectrum; polarization dependence of phonon modes; schematic for polarization configuration; mode visualization, and related tables. The SI also contains ref. ref. 56–67.
- M. A. Susner, M. Chyasnavichyus, M. A. McGuire, P. Ganesh and P. Maksymovych, Metal Thio- and Selenophosphates as Multifunctional van der Waals Layered Materials, Adv. Mater., 2017, 29, 1602852 CrossRef PubMed.
- R. Brec, Review on structural and chemical properties of transition metal phosphorous trisulfides MPS3, Solid State Ionics, 1986, 22, 3 CrossRef CAS.
- C. Payen, P. Molinie, P. Colombet and G. Fillion, Powder and single crystal susceptibility of the quasi-1D Heisenberg antiferromagnetic chain compounds AgVP2S6 (S = 1) and AgCrP2S6 (S = 3/2), J. Magn. Magn. Mater., 1990, 84, 95 CrossRef CAS.
- E. Park, J. P. Philbin, H. Chi, J. J. Sanchez, C. Occhialini, G. Varnavides, J. B. Curtis, Z. Song, J. Klein, J. D. Thomsen, M.-G. Han, A. C. Foucher, K. Mosina, D. Kumawat, N. Gonzalez-Yepez, Y. Zhu, Z. Sofer, R. Comin, J. S. Moodera, P. Narang and F. M. Ross, Anisotropic 2D van der Waals Magnets Hosting 1D Spin Chains, Adv. Mater., 2024, 36, 2401534 CrossRef CAS PubMed.
- K. Kim, S. Y. Lim, J.-U. Lee, S. Lee, T. Y. Kim, K. Park, G. S. Jeon, C.-H. Park, J.-G. Park and H. Cheong, Suppression of magnetic ordering in XXZ-type antiferromagnetic monolayer NiPS3, Nat. Commun., 2019, 10, 345 CrossRef PubMed.
- M. A. Susner, R. Rao, A. T. Pelton, M. V. McLeod and B. Maruyama, Temperature-dependent Raman scattering and X-ray diffraction study of phase transitions in layered multiferroic CuCrP2S6, Phys. Rev. Mater., 2020, 4, 104003 CrossRef CAS.
- R. Rao, R. Selhorst, B. S. Conner and M. A. Susner, Ferrielectric-paraelectric phase transitions in layered CuInP2S6 and CuInP2S6–In4/3P2S6 heterostructures: a Raman spectroscopy and x-ray diffraction study, Phys. Rev. Mater., 2022, 6, 045001 CrossRef CAS.
- V. Kumar, D. Kumar, B. Singh, Y. Shemerliuk, M. Behnami, B. Büchner, S. Aswartham and P. Kumar, Fluctuating fractionalized spins in quasi-two-dimensional magnetic V0.85PS3, Phys. Rev. B, 2023, 107, 094417 CrossRef CAS.
- B. Singh, D. Kumar, V. Kumar, M. Vogl, S. Wurmehl, S. Aswartham, B. Büchner and P. Kumar, Fractional spin fluctuations and quantum liquid signature in Gd2ZnIrO6, Phys. Rev. B, 2021, 104, 134402 CrossRef CAS.
- X. Wang, Z. Shang, C. Zhang, J. Kang, T. Liu, X. Wang, S. Chen, H. Liu, W. Tang, Y.-J. Zeng, J. Guo, Z. Cheng, L. Liu, D. Pan, S. Tong, B. Wu, Y. Xie, G. Wang, J. Deng, T. Zhai, H.-X. Deng, J. Hong and J. Zhao, Electrical and magnetic anisotropies in van der Waals multiferroic CuCrP2S6, Nat. Commun., 2023, 14, 840 CrossRef CAS.
- P. T. Orban, S. M. Bernier, T. Berry, M. A. Siegler and T. M. McQueen, Random-exchange Heisenberg behavior in the electron-doped quasi-one-dimensional spin-1 chain compound AgVP2S6, Phys. Rev. B, 2024, 110, 054423 CrossRef CAS.
- X. Wang, C. Zhu, Y. Deng, R. Duan, J. Chen, Q. Zeng, J. Zhou, Q. Fu, L. You, S. Liu, J. H. Edgar, P. Yu and Z. Liu, van der Waals engineering of ferroelectric heterostructures for long-retention memory, Nat. Commun., 2021, 12, 1109 CrossRef CAS PubMed.
- Y. Ma, Y. Yan, L. Luo, S. Pazos, C. Zhang, X. Lv, M. Chen, C. Liu, Y. Wang, A. Chen, Y. Li, D. Zheng, R. Lin, H. Algaidi, M. Sun, J. Z. Liu, S. Tu, H. N. Alshareef, C. Gong, M. Lanza, F. Xue and X. Zhang, High-performance van der Waals antiferroelectric CuCrP2S6-based memristors, Nat. Commun., 2023, 14, 7891 CrossRef CAS PubMed.
- S. Selter, Y. Shemerliuk, B. Büchner and S. Aswartham, Crystal Growth of the Quasi-2D Quarternary Compound AgCrP2S6 by Chemical Vapor Transport, Crystals, 2021, 11, 500 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59, 1758 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B, 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, Implementation strategies in phonopy and phono3py, J. Phys.: Condens. Matter, 2023, 35, 353001 Search PubMed.
- A. Togo, First-principles phonon calculations with phonopy and phono3py, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef.
- D. L. Rousseau, R. P. Bauman and S. P. S. Porto, Normal mode determination in crystals, J. Raman Spectrosc., 1981, 10, 253 CrossRef CAS.
- M. Bernasconi, G. Marra, G. Benedek, L. Miglio, M. Jouanne, C. Julien, M. Scagliotti and M. Balkanski, Lattice dynamics of layered MPX3 (M = Mn, Fe, Ni, Zn; X = S, Se) compounds, Phys. Rev. B, 1988, 38, 12089 CrossRef CAS PubMed.
- M. Balkanski, R. F. Wallis and E. Haro, Anharmonic effects in light scattering due to optical phonons in silicon, Phys. Rev. B, 1983, 28, 1928 CrossRef CAS.
- D. J. Lockwood and M. G. Cottam, The spin–phonon interaction in FeF2 and MnF2 studied by Raman spectroscopy, J. Appl. Phys., 1988, 64, 5876 CrossRef CAS.
- A. Ghosh, M. Palit, S. Maity, V. Dwij, S. Rana and S. Datta, Spin–phonon coupling and magnon scattering in few-layer antiferromagnetic FePS3, Phys. Rev. B, 2021, 103, 064431 CrossRef CAS.
- B. Zhang, Y. Hou, Z. Wang and R. Wu, First-principles studies of spin–phonon coupling in monolayer Cr2Ge2Te6, Phys. Rev. B, 2019, 100, 224427 CrossRef CAS.
- K. Cho, S. Lee, R. Kalaivanan, R. Sankar, K. Y. Choi and S. Park, Tunable ferroelectricity in van der Waals layered antiferroelectric CuCrP2S6, Adv. Funct. Mater., 2022, 32, 2204214 Search PubMed.
- M. A. Susner, B. S. Conner, E. Rowe, R. Siebenaller, A. Giordano, M. V. McLeod, C. R. Ebbing, T. J. Bullard, R. Selhorst and T. J. Haugan, Structural, Magnetic, and Optical Properties of the van der Waals Antiferromagnet AgCrP2Se6, J. Phys. Chem. C, 2024, 128, 4265 CrossRef CAS.
- I. Zamaraite, A. Dziaugys, J. Banys and Y. Vysochanskii, Dielectric and electrical properties of AgCrP2S6 and Cu0.2Ag0.8CrP2S6 layered crystals, Ferroelectrics, 2017, 515, 13 CrossRef CAS.
- D. Fausti, A. A. Nugroho, P. H. van Loosdrecht, S. A. Klimin, M. N. Popova and L. N. Bezmaternykh, Raman scattering from phonons and magnons in RFe3(BO3)4, Phys. Rev. B, 2006, 74, 024403 CrossRef.
- S. Kamba, Soft-mode spectroscopy of ferroelectrics and multiferroics: a review, APL Mater., 2021, 9, 020704 CrossRef CAS.
- J. Tang, B. J. Lawrie, M. Cheng, Y.-C. Wu, H. Zhao, D. Kong, R. Lu, C.-H. Yao, Z. Gai and A.-P. Li, Raman Fingerprints of Phase Transitions and Ferroic Couplings in van der Waals Multiferroic CuCrP2S6, J. Phys. Chem. Lett., 2025, 16, 4336 CrossRef CAS.
- M. Cardona and T. Ruf, Phonon self-energies in semiconductors: anharmonic and isotopic contributions, Solid State Commun., 2001, 117, 201 CrossRef CAS.
- B. Singh, G. A. Cansever, T. Dey, A. Maljuk, S. Wurmehl, B. Büchner and P. Kumar, Orbiton–phonon coupling in Ir5+(5d4) double perovskite Ba2YIrO6, J. Phys.: Condens. Matter, 2019, 31, 065603 CrossRef PubMed.
- P. G. Klemens, Anharmonic Decay of Optical Phonons, Phys. Rev. B, 1966, 148, 845 CrossRef CAS.
- Y. S. Lee, T. W. Noh, J. H. Park, K. B. Lee, G. Cao, J. E. Crow, M. K. Lee, C. B. Eom, E. J. Oh and I.-S. Yang, Temperature-dependent Raman spectroscopy in BaRuO3 systems, Phys. Rev. B, 2002, 65, 235113 Search PubMed.
- J. Scott, Soft-mode spectroscopy: experimental studies of structural phase transitions, Rev. Mod. Phys., 1974, 46, 83 Search PubMed.
- U. Fano, Effects of configuration interaction on intensities and phase shifts, Phys. Rev., 1961, 124, 1866 CrossRef CAS.
- B. Huang, J. Cenker, X. Zhang, E. L. Ray, T. Song, T. Taniguchi, K. Watanabe, M. A. McGuire, D. Xiao and X. Xu, Tuning inelastic light scattering via symmetry control in the two-dimensional magnet CrI3, Nat. Nanotechnol., 2020, 15, 212 CrossRef CAS PubMed.
- R. Loudon, The Raman effect in crystals, Adv. Phys., 1964, 13, 423 Search PubMed.
- J. Kim, J.-U. Lee and H. Cheong, Polarized Raman spectroscopy for studying two-dimensional materials, J. Phys.: Condens. Matter, 2020, 32, 343001 CrossRef CAS.
- V. Funk, K. Wagner, E. Wietek, J. D. Ziegler, J. Förste, J. Lindlau, M. Förg, K. Watanabe, T. Taniguchi and A. Chernikov, Spectral asymmetry of phonon sideband luminescence in monolayer and bilayer WSe2, Phys. Rev. Res., 2021, 3, L042019 CrossRef CAS.
- A. Boziki, M. I. Dar, G. Jacopin, M. Gratzel and U. Rothlisberger, Molecular origin of the asymmetric photoluminescence spectra of CsPbBr3 at low temperature, J. Phys. Chem. Lett., 2021, 12, 2699 Search PubMed.
- J. Diouri, J. P. Lascaray and M. E. Amrani, Effect of the magnetic order on the optical-absorption edge in Cd1−xMnxTe, Phys. Rev. B, 1985, 31, 7995 CrossRef CAS.
- Y. P. Varshni, Temperature dependence of the energy gap in semiconductors, Physica, 1967, 34, 149 Search PubMed.
- R. Pässler, Basic model relations for temperature dependencies of fundamental energy gaps in semiconductors, Phys. Status Solidi B, 1997, 200, 155 Search PubMed.
- P. Lautenschlager, M. Garriga, S. Logothetidis and M. Cardona, Interband critical points of GaAs and their temperature dependence, Phys. Rev. B, 1987, 35, 9174 CrossRef CAS.
- C. Yu, Z. Chen, J. J. Wang, W. Pfenninger, N. Vockic, J. T. Kenney and K. Shum, Temperature dependence of the band gap of perovskite semiconductor compound CsSnI3, J. Appl. Phys., 2011, 110, 063526 CrossRef.
- S. Wang, J. Ma, W. Li, J. Wang, H. Wang, H. Shen, J. Li, J. Wang, H. Luo and D. Li, Temperature-dependent band gap in two-dimensional perovskites: thermal expansion interaction and electron–phonon interaction, J. Phys. Chem. Lett., 2019, 10, 2546 Search PubMed.
- S. Rudin, T. Reinecke and B. Segall, Temperature-dependent exciton linewidths in semiconductors, Phys. Rev. B, 1990, 42, 11218 Search PubMed.
- M. Leroux, N. Grandjean, B. Beaumont, G. Nataf, F. Semond, J. Massies and P. Gibart, Temperature quenching of photoluminescence intensities in undoped and doped GaN, J. Appl. Phys., 1999, 86, 3721 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |