Open Access Article
Open Access ArticleOSC-Net: a multi-fidelity machine learning model for organic solar cells
Haizhou
Yang
 a,
Adam
Wold
b,
Junlin
Ou
c,
Jeromy J.
Rech
a,
Adam
Wold
b,
Junlin
Ou
c,
Jeromy J.
Rech
 b,
Wei
You
b,
Wei
You
 *d and
Yi
Wang
*d and
Yi
Wang
 *e
*e
aDepartment of Biomedical Engineering, University of Michigan, Ann Arbor, MI 48109, USA
bDepartment of Chemistry, University of North Carolina at Asheville, Asheville, NC 28804, USA
cDepartment of Engineering Technology, Middle Tennessee State University, Murfreesboro, TN 37132, USA
dDepartment of Chemistry, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA. E-mail: wyou@unc.edu
eDepartment of Mechanical Engineering, University of South Carolina, Columbia, SC 29208, USA. E-mail: yiwang@cec.sc.edu
First published on 4th November 2025
Abstract
Organic solar cells (OSCs) have emerged as a promising renewable energy technology, offering advantages such as lightweight design, semitransparency, flexibility, and cost-effectiveness. Power conversion efficiency (PCE) is a key device performance parameter for OSCs, defined as the ratio of the electrical power output generated by the device to the incident solar power input. Despite significant advances, the development of high-performance OSCs remains a labor-intensive process, heavily dependent on expert experience, involving extensive synthesis, characterization, and iterative optimization. Data-driven methods offer a promising alternative for accelerating material discovery, but their effectiveness is often limited by the scarcity of high-quality experimental data. To overcome this challenge, we propose OSC-Net, a multi-fidelity machine learning framework that integrates a large volume of computational data with a smaller set of high-accuracy experimental measurements. This approach enables accurate prediction of key device performance parameters, including PCE, while simultaneously tackling the challenges associated with experimental data scarcity and uncertainty quantification, enabling efficient screening of OSC materials. Importantly, the predictive capability of OSC-Net was verified against published experimental data, confirming its accuracy and reliability. By leveraging both data sources, OSC-Net achieves superior predictive performance compared to conventional single-fidelity models. Furthermore, the uncertainty quantification captures variability in the model, enhancing the reliability of predictions. Finally, OSC-Net was employed for large-scale high-throughput screening, successfully identifying promising candidates with high predicted PCEs that were validated against literature-reported experimental data. Thus, OSC-Net presents a feasible approach for rapid and accurate inference of device performance parameters with limited experimental datasets, enabling efficient OSC material discovery.
1 Introduction
Organic solar cells (OSCs) have gained significant traction as a promising renewable energy technology due to their unique attributes, including light weight, flexibility, and cost-effectiveness.1–4 These characteristics make OSCs highly appealing for a variety of innovative applications such as wearable electronics, building-integrated photovoltaics, and portable power solutions.5,6 Power conversion efficiency (PCE) is a key device performance parameter for evaluating OSCs, defined as the ratio of the electrical power output generated by the device to the incident solar power input, typically expressed as a percentage. Recent advancements in OSCs have led to notable improvements in PCE, driven by optimizations in device architectures, active-layer materials, and fabrication processes.7–11 Nevertheless, the development of OSCs remains labor-intensive and heavily reliant on expert intuition, involving extensive synthesis, characterization, and iterative optimization. This is primarily due to (1) the intrinsic complexity of organic materials, which complicates the design and selection of donor and acceptor components; (2) the limited understanding of the complex relationship between material properties, fabrication parameters, and their effects on device performance parameters, such as PCE;12 and (3) the time-intensive nature of experimentally evaluating OSCs, involving material design and engineering, device fabrication, and performance characterization, which can take days to weeks and thus limit high-throughput material screening. These challenges highlight the need for efficient computational approaches to predict device performance parameters based on material properties, enabling faster material discovery.In recent years, advanced machine learning methods have emerged as powerful tools to identify relationships between materials properties and OSC device performance for accelerating OSC research.8,13–15 By leveraging either computational data, such as density functional theory (DFT) calculations and the Scharber model,16 experimental data, or both, machine learning techniques enable the discovery of hidden patterns and critical trends governing OSC performance. For example, Aspuru-Guzik et al.17 employed a Gaussian process model trained on 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 computational data points from the Harvard Clean Energy Project database,18 which comprises data derived from DFT calculations and the Scharber model. This model successfully predicted PCE and identified 838 potential high-performing candidate molecules. Similarly, Sun et al. used a convolutional neural network to extract features from molecular structures for PCE prediction,19 also leveraging computational data from the same database. However, computational data, particularly PCE values derived from the Scharber model,16 often suffer from limited accuracy due to simplified assumptions and descriptors. This restricts the predictive accuracy of machine learning models and the reliability of the candidates they identify for achieving high efficiency. To overcome these limitations, recent efforts have focused on training machine learning models using experimental data. Several studies have explored the use of machine learning methods to predict device performance based on single-component properties, either donor or acceptor, by learning their relationships to experimental outcomes.20–23 However, since OSC device performance is critically dependent on the interaction between both donor and acceptor materials, it is necessary to develop models that simultaneously account for both donor and acceptor materials in relation to device performance; indeed, some research studies have explored this direction.24–31 For example, Sun et al. collected a dataset of 1719 donor materials and evaluated different molecular representations as inputs to ML models, finding that fingerprints exceeding 1000 bits achieved the highest prediction accuracy.24 Wu et al. collected 565 donor–acceptor combinations and developed five machine-learning models for PCE inference, identifying that boosted regression trees and random forest models outperformed others in prediction accuracy.25 Similarly, Zhang et al. curated a dataset of 2078 D/A combinations and trained a graph neural network using a newly designed polymer fingerprint representation as input features.31 Despite progress in leveraging machine learning for material discovery, challenges such as limited datasets, low prediction accuracy, and insufficient uncertainty quantification still exist. These issues are particularly critical given the complex relationship between material properties and device performance for an OSC, and the substantial uncertainties inherent in the material synthesis process.
000 computational data points from the Harvard Clean Energy Project database,18 which comprises data derived from DFT calculations and the Scharber model. This model successfully predicted PCE and identified 838 potential high-performing candidate molecules. Similarly, Sun et al. used a convolutional neural network to extract features from molecular structures for PCE prediction,19 also leveraging computational data from the same database. However, computational data, particularly PCE values derived from the Scharber model,16 often suffer from limited accuracy due to simplified assumptions and descriptors. This restricts the predictive accuracy of machine learning models and the reliability of the candidates they identify for achieving high efficiency. To overcome these limitations, recent efforts have focused on training machine learning models using experimental data. Several studies have explored the use of machine learning methods to predict device performance based on single-component properties, either donor or acceptor, by learning their relationships to experimental outcomes.20–23 However, since OSC device performance is critically dependent on the interaction between both donor and acceptor materials, it is necessary to develop models that simultaneously account for both donor and acceptor materials in relation to device performance; indeed, some research studies have explored this direction.24–31 For example, Sun et al. collected a dataset of 1719 donor materials and evaluated different molecular representations as inputs to ML models, finding that fingerprints exceeding 1000 bits achieved the highest prediction accuracy.24 Wu et al. collected 565 donor–acceptor combinations and developed five machine-learning models for PCE inference, identifying that boosted regression trees and random forest models outperformed others in prediction accuracy.25 Similarly, Zhang et al. curated a dataset of 2078 D/A combinations and trained a graph neural network using a newly designed polymer fingerprint representation as input features.31 Despite progress in leveraging machine learning for material discovery, challenges such as limited datasets, low prediction accuracy, and insufficient uncertainty quantification still exist. These issues are particularly critical given the complex relationship between material properties and device performance for an OSC, and the substantial uncertainties inherent in the material synthesis process.
In this study, we established a comprehensive database comprising 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 329 computational entries from ref. 17 and 1782 experimental data points collected from the literature and our laboratory database. Building on this resource, we introduced a multi-fidelity machine learning framework (OSC-Net) to predict device performance parameters, including PCE, with uncertainty quantification, thereby enabling high-throughput screening of OSC materials. Different from previous efforts, this work presents several novelties: (1) a multi-fidelity approach is implemented using a two-step training strategy to integrate data of different fidelity levels. Specifically, the proposed model is pre-trained on a large volume of computational data, which is relatively low in accuracy, and fine-tuned with a smaller but more accurate set of experimental data. Importantly, the predictive capability of OSC-Net is verified against published experimental data, confirming its reliability and practical relevance for OSC material discovery. This represents a pioneering study to investigate the feasibility of a multi-fidelity approach for screening high performance OSC materials. (2) Uncertainty associated with the machine learning model prediction is quantified to provide confidence intervals for PCE predictions. These confidence intervals offer valuable guidance for material discovery and design. (3) Our curated experimental dataset includes both fullerene and non-fullerene acceptors, paired with a broad range of conjugated polymer donors in binary blends, including many of the champion devices throughout history to date. The donor selection spans various levels of synthetic complexity and includes specialized subgroups with subtle alterations to the chemical structures, such as the PBnDT-TAZ series, facilitating analysis of structure–property–performance relationships. Additionally, to account for batch-to-batch variability, a common challenge in OSC materials, we incorporate replicate data from different laboratories, enhancing the ability of the model to quantify experimental uncertainty.
329 computational entries from ref. 17 and 1782 experimental data points collected from the literature and our laboratory database. Building on this resource, we introduced a multi-fidelity machine learning framework (OSC-Net) to predict device performance parameters, including PCE, with uncertainty quantification, thereby enabling high-throughput screening of OSC materials. Different from previous efforts, this work presents several novelties: (1) a multi-fidelity approach is implemented using a two-step training strategy to integrate data of different fidelity levels. Specifically, the proposed model is pre-trained on a large volume of computational data, which is relatively low in accuracy, and fine-tuned with a smaller but more accurate set of experimental data. Importantly, the predictive capability of OSC-Net is verified against published experimental data, confirming its reliability and practical relevance for OSC material discovery. This represents a pioneering study to investigate the feasibility of a multi-fidelity approach for screening high performance OSC materials. (2) Uncertainty associated with the machine learning model prediction is quantified to provide confidence intervals for PCE predictions. These confidence intervals offer valuable guidance for material discovery and design. (3) Our curated experimental dataset includes both fullerene and non-fullerene acceptors, paired with a broad range of conjugated polymer donors in binary blends, including many of the champion devices throughout history to date. The donor selection spans various levels of synthetic complexity and includes specialized subgroups with subtle alterations to the chemical structures, such as the PBnDT-TAZ series, facilitating analysis of structure–property–performance relationships. Additionally, to account for batch-to-batch variability, a common challenge in OSC materials, we incorporate replicate data from different laboratories, enhancing the ability of the model to quantify experimental uncertainty.
The rest of the paper is organized as follows. Section 2 introduces the methodology of the proposed multi-fidelity machine learning model, including database, model architecture, and uncertainty quantification methods. The results and discussion are presented in Sections 3 and 4, respectively. Finally, conclusions and future work are presented in Section 5.
2 Methodology
The proposed OSC-Net framework focuses on bulk heterojunction (BHJ) OSCs, in which the active layer consists of a nanoscale interpenetrating network formed by blending two organic semiconductors, a donor and an acceptor. This nanostructured morphology enables efficient exciton dissociation and facilitates charge separation and transport throughout the device. OSC-Net aims to predict key device performance parameters, along with their associated uncertainties, based on the chemical identity of the donor and acceptor materials, as well as their blending ratio for high-throughput material screening. Specifically, OSC-Net takes the fingerprints (FPs) of donor and acceptor materials, along with their relative ratio, as inputs to predict three critical device performance parameters as responses, including the open-circuit voltage (VOC), which represents the maximum voltage a solar cell can produce, the short-circuit current density (JSC), which is the current when the voltage across the device is zero, and the fill factor (FF), which quantifies how closely the maximum power output approaches its theoretical maximum. These device performance parameters are sufficient for calculating the PCE, so the PCE itself is not included as a direct model output. The PCE can be expressed mathematically as: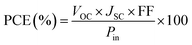 | (1) |
The OSC-Net structure features a combination of an encoder as the feature extractor and a multilayer perceptron (MLP) as the predictor head, as shown in the blue block in Fig. 1. The model first encodes the fingerprint features of the donor and acceptor materials. The resulting encoded features, along with the donor/acceptor ratio, are passed into the MLP that predicts the three target performance parameters and their corresponding uncertainties.
The development of the OSC-Net framework involves two main stages: training and testing, as illustrated in Fig. 1. In the training stage shown in Fig. 1(a), a two-step training strategy is employed to incorporate data with different fidelity levels, accuracies, and associated costs, specifically, computational and experimental data in this study. Initially, a large amount of computational data, derived from DFT calculations and the Scharber model, was used to pre-train the OSC-Net. This step allows the OSC-Net to capture the general trend of the input–output relationships present in low-fidelity computational data. A relatively smaller but highly accurate set of high-fidelity experimental data was then utilized for fine-tuning the model above, allowing the model to progressively align with the response surface of the experimental data. This sequential strategy, inspired by transfer learning,32 effectively enables the OSC-Net to leverage data from different fidelities, accuracies and costs to create a unified, robust multi-fidelity machine learning model for predicting device performance.33–36
In the testing stage, shown in Fig. 1(b), the fine-tuned model above can rapidly predict the performance parameters given any input materials, which normally takes sub-seconds per prediction and, therefore, can be used for high-throughput material screening.
2.1 OSC database
The dataset consists of 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 329 computational entries from ref. 17 and 1782 experimental data points collected from the literature and our laboratory database. All computational data used PCDTBT as the donor and various non-fullerene acceptors constructed from a library of 107 fragments—13 cores, 49 spacers, and 45 terminal groups (see ref. 17). For each acceptor, DFT was used to compute the HOMO energy, LUMO energy, and HOMO–LUMO gap, and the PCE was then predicted via the Scharber model. Note that a fixed donor/acceptor weight ratio of 0.4 (corresponding to 1
329 computational entries from ref. 17 and 1782 experimental data points collected from the literature and our laboratory database. All computational data used PCDTBT as the donor and various non-fullerene acceptors constructed from a library of 107 fragments—13 cores, 49 spacers, and 45 terminal groups (see ref. 17). For each acceptor, DFT was used to compute the HOMO energy, LUMO energy, and HOMO–LUMO gap, and the PCE was then predicted via the Scharber model. Note that a fixed donor/acceptor weight ratio of 0.4 (corresponding to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5) is applied to every computational sample. Fig. 2 illustrates the distribution of PCE values for both the computational and experimental datasets. The data are categorized into three groups: low (0–5%), moderate (5–10%), and high (above 10%) PCE values. For the computational dataset, the median PCE value is 1.06%, and the average is 1.85%, with the data split as follows: 45
1.5) is applied to every computational sample. Fig. 2 illustrates the distribution of PCE values for both the computational and experimental datasets. The data are categorized into three groups: low (0–5%), moderate (5–10%), and high (above 10%) PCE values. For the computational dataset, the median PCE value is 1.06%, and the average is 1.85%, with the data split as follows: 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 in the low category, 4779 in the moderate category, and 98 in the high category.
990 in the low category, 4779 in the moderate category, and 98 in the high category.
In the experimental dataset, the median PCE is 4.88%, and the average is 5.56%, with 914 data points in the low category, 663 in the moderate category, and 205 in the high category. The experimental dataset includes a wide selection of conjugated polymers as donors, with both fullerene and non-fullerene small molecule acceptors. Instances involving the same donor and acceptor material, reported with varying device performance values from different data sources, are all included, allowing for uncertainty quantification.
For the computational dataset, 90% was randomly selected for pretraining, 5% for validation during pretraining, and the remaining 5% for testing. Similarly, for the experimental dataset, 80% was randomly chosen for fine-tuning, while 10% was chosen for validation and the remaining 10% for testing. Various representations of material have been proposed for machine learning-based analysis, including images, SMILES, fingerprints, energy levels, and more.8 In this study, fingerprints are used to represent molecules, serving as the input for the machine learning model to enhance prediction accuracy.24 Specifically, each donor or acceptor material is converted into a 4096-bit binary array to generate Morgan fingerprints.
2.2 OSC-Net architecture
This section describes the architecture of OSC-Net. As shown in Fig. 3, the network comprises an encoder and an MLP, and is designed to predict three key device performance parameters (VOC, JSC, and FF) using the donor and acceptor Morgan fingerprints (see Section 2.1) alongside the D/A ratio as inputs. The encoder compresses fingerprint information into feature maps in the latent space. It consists of three pooling layers, each followed by two convolutional layers with ReLU activation. The convolutional layer, using a kernel size of 2 × 1 and a stride of 1, compresses the fingerprint data to produce feature maps. Maximum pooling layers, with a 2 × 1 kernel and a stride of 2, further reduce the dimensions of the feature maps. The number of kernels in each layer, corresponding to the number of channels, is annotated above the corresponding blocks in Fig. 3. The MLP, taking feature maps from the encoder and the D/A ratio as inputs, predicts the device performance parameters and their corresponding uncertainties. This MLP has four layers with 4097, 512, 128, and 3 neurons, respectively.The model was pre-trained on computational dataset for 500 epochs and subsequently fine-tuned on the experimental dataset, over 7000 epochs. The number of epochs for both stages was determined through iterative experimentation, guided by the convergence behavior of the training and validation losses. The large-scale, low-fidelity computational dataset was primarily used to establish the overall trend of the response surface, and thus required fewer training epochs. In contrast, the smaller but higher-fidelity experimental dataset necessitated a longer fine-tuning phase to allow the model to adapt gradually and fully exploit the available data. The Adam optimizer was utilized with an initial learning rate of 1 × 10−3 and a decaying schedule was employed to reduce the learning rate every 10 epochs if validation performance stagnated. The batch size was set to 20 and 5 for pre-training and fine-tuning, respectively, chosen empirically to balance memory constraints and convergence speed. The training process used mixed precision training via Automatic Mixed Precision (AMP), enabling gradient scaling to mitigate underflow issues in the lower-precision computations. Validation was performed periodically throughout training, with a routine that assessed model performance on a separate validation set. Based on these evaluations, the learning rate scheduler dynamically adjusted learning rates to optimize training progress. The loss curves for both training and validation datasets were monitored across epochs to track convergence trends. The training employed the mean squared error (MSE) loss, which is defined as:
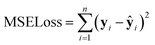 | (2) |
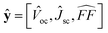 denotes their predicted values. The training was performed on an NVIDIA GeForce RTX 3080 GPU, utilizing PyTorch 1.13.0 for model implementation. The model training took approximately 11 hours for completion.
denotes their predicted values. The training was performed on an NVIDIA GeForce RTX 3080 GPU, utilizing PyTorch 1.13.0 for model implementation. The model training took approximately 11 hours for completion.
2.3 Uncertainty quantification
The OSC-Net, serving as an approximate data-driven model, is inherently subject to uncertainties in its predictions. These uncertainties can be broadly classified into two categories: aleatoric and epistemic uncertainty.37–41 Aleatoric uncertainty accounts for the inherent noise in data caused by randomness, which cannot be reduced even with extensive training data. The evaluation of materials for OSCs typically involves several steps, including material design and engineering, device engineering, and performance evaluation. Each of these steps may introduce noise into the data, making it essential to quantify aleatoric uncertainty to account for these effects. However, given the limited size of our dataset, particularly the experimental entries, modeling aleatoric uncertainty would compromise the predictive accuracy of OSC-Net, which is the primary focus of this work. Moreover, the PCE values in our database are generally averaged over multiple devices to capture variability in performance. For these reasons, we chose not to explicitly model aleatoric uncertainty in this study.Epistemic uncertainty, on the other hand, arises from a lack of knowledge or information about the underlying processes, models, or parameters.42 It reflects uncertainty that could potentially be reduced with additional data or improved modeling. In this study, the relationship between input features and OSC device performance is highly complex and may not be fully captured by the current model structure, highlighting the importance of quantifying epistemic uncertainty to account for potential model-driven variability. Several techniques have been developed to quantify epistemic uncertainty in machine learning models, including Bayesian neural networks, Monte Carlo dropout, ensemble methods, and Gaussian processes.37,43–45 In this work, a deep ensemble approach is utilized to estimate the epistemic uncertainty in OSC-Net. Specifically, an ensemble of M = 5 models is explicitly constructed, and a statistical variance is computed from their predictions ŷj, where j = 1, …, M. Mathematically, the epistemic uncertainty, denoted as σe2 = [σe−VOC2, σe−JSC2, σe−FF2] is defined as:
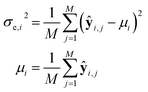 | (3) |
3 Results
This section first presents the inference results of the pre-trained OSC-Net, trained exclusively on computational data to predict device performance parameters. Next, the inference results of the fine-tuned OSC-Net are introduced, which was fine-tuned using experimental data based on the pre-trained OSC-Net. These fine-tuning results are also compared to those from an identical model architecture trained solely on experimental data. Finally, the fine-tuned OSC-Net is applied for high-throughput screening to identify promising high-performance donor–acceptor material pairs.3.1 Inference results using pre-trained OSC-Net
Fig. 4 presents scatter plots illustrating the performance of the pre-trained OSC-Net in predicting device performance parameters for both (a) computational and (b) experimental test datasets, both of which were not used during training. In these plots, light-colored error bars represent the 95% confidence interval for epistemic uncertainty (ŷi − 1.96σe,i, ŷi + 1.96σe,i). The corresponding statistical metrics, including Pearson correlation coefficients, mean square errors (MSEs), uncertainty estimates, and confidence interval (CI) accuracy are summarized in Table 1. The CI accuracy, defined as the percentage of ground truth values yi falling within the 95% confidence interval range (ŷi − 1.96σe,i, ŷi + 1.96σe,i), reflects the performance of both the model prediction and its uncertainty quantification. Training and validation loss curves from the pre-training stage are shown in Fig. S1 of the SI.| r value | MSE | σ e | CI accuracy | ||
|---|---|---|---|---|---|
| Computational data | V OC | 0.987 | 0.007 | 0.041 | 73.976 |
| J SC | 0.985 | 0.256 | 0.272 | 86.523 | |
| FF | N/A | 0.000 | 0.016 | 100.000 | |
| PCE | 0.981 | 0.129 | 0.249 | 89.565 | |
| Experimental data | V OC | −0.162 | 1.396 | 0.212 | 0.000 |
| J SC | 0.625 | 112.872 | 0.764 | 4.444 | |
| FF | −0.241 | 256.956 | 0.009 | 0.000 | |
| PCE | 0.437 | 25.285 | 0.973 | 42.222 | |
For the computational dataset, the pre-trained OSC-Net demonstrates strong predictive performance across four device performance parameters (VOC, JSC, FF, and PCE). The model achieves low MSE values of 0.007, 0.256, 0, and 0.129, respectively, and high Pearson correlation coefficients of 0.987, 0.985, N/A, and 0.981, respectively. It is worth noting that, in the computational dataset, FF values are constant at 65%, making prediction trivial and resulting in an MSE of 0. Consequently, the correlation coefficient for FF cannot be computed due to zero standard deviation. For the experimental dataset, the model performs less effectively, yielding higher MSE values of 1.396, 112.872, 256.956, and 25.285 for VOC, JSC, FF, and PCE, respectively, and lower correlation coefficients of −0.162, 0.625, −0.241, and 0.437, respectively. The epistemic uncertainty in experimental datasets is substantially greater than that in computational datasets. Furthermore, the CI accuracy is substantially higher for the computational dataset.
3.2 Inference results using fine-tuned OSC-Net
Fig. 5 presents scatter plots comparing the predictive performance of (a) the fine-tuned OSC-Net, trained on both computational and experimental data, and (b) single fidelity OSC-Net (SF-OSC-Net), a machine learning model with the same architecture as OSC-Net but trained exclusively on experimental data. As mentioned previously, in the plots, light green error bars represent the 95% confidence intervals for epistemic uncertainty. Statistical metrics, including Pearson correlation coefficients, MSEs, and uncertainty measures, are summarized in Table 2. The training and validation loss curves from the fine-tuning stage are provided in Fig. S2 of the SI.| r value | MSE | σ e | CI accuracy | ||
|---|---|---|---|---|---|
| Fine-tuned OSC-Net | V OC | 0.740 | 0.005 | 0.031 | 61.111 |
| J SC | 0.907 | 6.726 | 0.824 | 47.778 | |
| FF | 0.774 | 69.386 | 2.107 | 40.000 | |
| PCE | 0.921 | 2.680 | 0.465 | 38.889 | |
| SF-OSC-Net | V OC | 0.729 | 0.005 | 0.023 | 54.444 |
| J SC | 0.901 | 7.185 | 0.601 | 34.444 | |
| FF | 0.769 | 70.111 | 1.590 | 31.111 | |
| PCE | 0.920 | 2.711 | 0.338 | 31.111 | |
Both OSC-Net and SF-OSC-Net share nearly identical architectures and training procedures, except that OSC-Net was trained on both computational and experimental data, whereas SF-OSC-Net used only experimental data. While there are clear trends across all device parameters (VOC, JSC, FF, and PCE), OSC-Net consistently outperforms SF-OSC-Net, exhibiting an average 2.5% reduction in MSE and higher correlation coefficients. The OSC-Net exhibits slightly higher uncertainties than SF-OSC-Net, and achieves better CI accuracy, with an average improvement of approximately 9.2%.
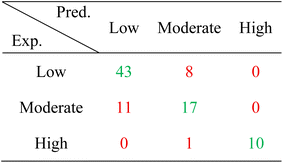
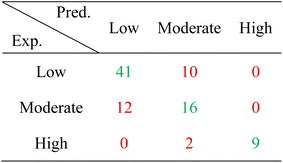
As mentioned previously, the PCE data were divided into three groups, low (0–5%), moderate (5–10%), and high (above 10%). Classification performance was evaluated by assigning class labels based on the predicted PCE values and comparing them with the corresponding ground truth labels. Tables 3 and 4 present the confusion matrices for predicting the PCE groups using OSC-Net and SF-OSC-Net, respectively. The diagonal elements of each matrix (highlighted in green) indicate correctly classified instances. Overall, OSC-Net demonstrated a higher classification accuracy compared to SF-OSC-Net, achieving 73.3% versus 71.1%. These results underscore that incorporating multi-fidelity data through OSC-Net leads to more accurate and robust predictions than relying solely on experimental data, validating the effectiveness of the multi-fidelity approach.
3.3 High-throughput screening
Next, we conducted a high-throughput screening of all possible donor–acceptor combinations in our databases, using the trained OSC-Net model. Both donors and acceptors were presented in our databases (see Section 2.1), although most of the specific pairings had not been previously evaluated. The screening considered 1289 unique donor materials, 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 unique acceptor materials, and 11 different donor-to-acceptor ratios ranging from 0.10 to 0.60 in increments of 0.05, resulting in a total of 728
385 unique acceptor materials, and 11 different donor-to-acceptor ratios ranging from 0.10 to 0.60 in increments of 0.05, resulting in a total of 728![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587
587![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915 potential device configurations. The distribution of the predicted PCE is presented in Fig. 6. Among the combinations evaluated, 768
915 potential device configurations. The distribution of the predicted PCE is presented in Fig. 6. Among the combinations evaluated, 768![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 achieved a PCE exceeding 10%, and 4870 achieved a PCE above 15%.
664 achieved a PCE exceeding 10%, and 4870 achieved a PCE above 15%.
Table 5 compares the key device performance parameters (VOC, JSC, FF, and PCE) of several top-performing blends identified by OSC-Net with corresponding experimental data reported in recent literature published within the last three years.46–50 None of these blends were included in the training databases, and the predicted PCEs closely agree with the experimental values, with percentage differences (PDs) within 3%. Minor discrepancies can be attributed to variations in processing conditions, film morphology, additives, active-layer thickness, polymer molecular weight, and other factors not currently considered by OSC-Net. Finally, Table 6 lists five high-performance donor–acceptor configurations predicted by OSC-Net to exhibit the highest PCEs across all tested configurations. To the best of our knowledge, these combinations have not yet been reported in the literature. The chemical structures of these top-performing donor–acceptor pairs are summarized in Fig. S3 and S4 in the SI.
| # | Donor | Acceptor | D/A ratio | V OC | J SC | FF (%) | PCE | Source | PCE PD (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | D18 | DTY-6 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 (0.45) 1.2 (0.45) |
0.860 | 26.766 | 76.419 | 17.591 | OSC-Net | 2.85 |
| 0.876 | 26.2 | 78.5 | 18.1 | Ref. 46 | |||||
| 2 | D18-Cl | N3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.9 (0.35) 1.9 (0.35) |
0.850 | 26.778 | 76.968 | 17.526 | OSC-Net | 0.78 |
| 0.848 | 27.18 | 75.45 | 17.39 | Ref. 47 | |||||
| 3 | D18 | AQx-2 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 (0.45) 1.2 (0.45) |
0.856 | 27.379 | 74.895 | 17.553 | OSC-Net | 1.92 |
| 0.868 | 26.1 | 76.0 | 17.22 | Ref. 48 | |||||
| 4 | D18 | N3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.9 (0.35) 1.9 (0.35) |
0.848 | 26.140 | 77.67 | 17.217 | OSC-Net | 1.27 |
| 0.83 | 27.2 | 75.3 | 17.0 | Ref. 49 | |||||
| 5 | D18 | Y6-BO | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.9 (0.35) 1.9 (0.35) |
0.859 | 26.317 | 75.971 | 17.174 | OSC-Net | 1.55 |
| 0.876 | 26.2 | 73.7 | 16.91 | Ref. 50 |
| # | Donor | Acceptor | D/A ratio | V OC | J SC | FF (%) | PCE |
|---|---|---|---|---|---|---|---|
| 1 | PL1 | A-WSSe-Cl | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 (0.45) 1.2 (0.45) |
0.860 | 26.536 | 77.811 | 17.762 |
| 2 | D18-Cl | SY1 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 (0.4) 1.5 (0.4) |
0.871 | 27.141 | 74.420 | 17.600 |
| 3 | PM6-Ir1 | SY2 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 (0.45) 1.2 (0.45) |
0.856 | 26.329 | 77.851 | 17.544 |
| 4 | D18-Cl | BP4T-4F | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 (0.4) 1.5 (0.4) |
0.842 | 27.413 | 75.771 | 17.483 |
| 5 | D18 | Bu-OD-4F | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 (0.45) 1.2 (0.45) |
0.856 | 26.366 | 76.410 | 17.236 |
4 Discussion
The pre-trained OSC-Net demonstrates better performance on computational data than on experimental data, which aligns with expectations since it was trained on computational data. Our hypothesis is that the relationship between molecular fingerprints and device performance parameters in computational and experimental datasets would be highly correlated. The pre-trained OSC-Net is designed to learn this relationship effectively for the computational dataset. At the same time, it captures the general trend of the relationship for the experimental dataset, as evidenced by the correlation coefficients for the experimental dataset, which, although not high, still have measurable values. These observations suggest that the pre-trained OSC-Net has the potential to benefit subsequent fine-tuning. However, the small correlation coefficients may not fully reflect the benefits of pretraining with computational data, as the Pearson correlation coefficient only accounts for linear relationships. More evidence will be present in the discussion about fine-tuning.During inference with the pre-trained OSC-Net, the epistemic uncertainty is notably higher for the experimental dataset than for the computational dataset. This is because the experimental dataset contains more complex materials and falls outside the range of the computational dataset, effectively making inference for the experimental data an extrapolation task. Additionally, larger gaps between the predicted values and the ground truth are associated with higher uncertainty levels. This observation validates the effectiveness of the uncertainty quantification framework, which accurately captures uncertainties associated with each model prediction. When the model is less confident in its predictions, it assigns relatively large uncertainty values to reflect this lack of confidence, indicating the robustness of the framework in handling uncertain predictions.
The pre-trained OSC-Net achieves higher CI accuracy on computational data compared to experimental data. This difference highlights the challenges posed by extrapolation, which impacts both the model prediction and its uncertainty quantification. Despite the CI accuracy for experimental data being lower than that for the computational dataset, the pretrained model still provides a valuable foundation that benefits the subsequent fine-tuning process.
The enhanced performance of OSC-Net over SF-OSC-Net can be attributed to its pretraining on computational datasets, which serves as a bridge to the ultimate goal, capturing the experimental response surface. This pretraining makes fine-tuning more efficient compared to training a model from scratch. However, the performance enhancement is constrained by the limitations of the computational dataset, including use of a single donor material, outdated acceptor material properties and a relatively simple computational approach for evaluating device performance parameters, which results in lower accuracy relative to the experimental data. The slightly higher uncertainties observed in OSC-Net, compared to SF-OSC-Net, result in higher CI accuracy, suggesting that larger and more precise uncertainty estimates accurately capture the variability in the model.
The higher CI accuracy and classification accuracy of OSC-Net over SF-OSC-Net aligns with the CI accuracy achieved during the pretraining stage. These findings demonstrate that OSC-Net is a superior modeling approach in both predictive accuracy and uncertainty quantification for inferring device performance parameters in OSCs.
It is important to note that device performance is influenced by multiple factors beyond donor and acceptor materials and their ratios, including solvents, additives, processing conditions, annealing temperature, layer thicknesses, electrode materials, interfacial layers, etc. In the current OSC-Net framework, only the most significant contributors, donor, acceptor, and D/A ratio, are explicitly modeled, while the other factors are treated as sources of uncertainty. We employ uncertainty quantification to implicitly capture the effect of these unaccounted factors, providing confidence intervals for predictions.
Beyond material synthesis, device optimization (e.g. donor–acceptor pairing, solvent selection, D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratio, additive choice) remains one of the most time-consuming tasks for developing ideal OSC devices. Leveraging the fine-tuned OSC-Net model, we conducted a high-throughput screening of 728
A ratio, additive choice) remains one of the most time-consuming tasks for developing ideal OSC devices. Leveraging the fine-tuned OSC-Net model, we conducted a high-throughput screening of 728![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587
587![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915 potential donor–acceptor combinations, the vast majority of which have not been previously reported. Several of the top-performing blends predicted by OSC-Net were validated against experimental data from the literature, with percentage differences (PDs) within 3%, confirming the accuracy and robustness of the model. In addition, a list of previously unreported high-efficiency configurations was provided to facilitate future experimental investigation by the community. Among the identified candidates, donor materials such as D18 and PM6, along with their derivatives, consistently ranked among the top-performing candidates, demonstrating strong robustness and adaptability across diverse pairings. Similarly, many asymmetric Y6 derivatives, such as Bu-OD-4F, BP4T-4F, A-WSSe-Cl, and SY1, also exhibited outstanding performance. Although these asymmetric acceptors often present greater synthetic complexity than their symmetric counterparts, their superior efficiencies in prediction justify further synthesis and experimental investigation. These findings highlight the potential of OSC-Net to accelerate the identification of high-efficiency material pairings, thereby reducing the experimental burden and material costs associated with device optimization. As new donor and acceptor materials are synthesized, they can be readily integrated into the OSC-Net framework to guide the selection of promising pairings for optimal performance.
915 potential donor–acceptor combinations, the vast majority of which have not been previously reported. Several of the top-performing blends predicted by OSC-Net were validated against experimental data from the literature, with percentage differences (PDs) within 3%, confirming the accuracy and robustness of the model. In addition, a list of previously unreported high-efficiency configurations was provided to facilitate future experimental investigation by the community. Among the identified candidates, donor materials such as D18 and PM6, along with their derivatives, consistently ranked among the top-performing candidates, demonstrating strong robustness and adaptability across diverse pairings. Similarly, many asymmetric Y6 derivatives, such as Bu-OD-4F, BP4T-4F, A-WSSe-Cl, and SY1, also exhibited outstanding performance. Although these asymmetric acceptors often present greater synthetic complexity than their symmetric counterparts, their superior efficiencies in prediction justify further synthesis and experimental investigation. These findings highlight the potential of OSC-Net to accelerate the identification of high-efficiency material pairings, thereby reducing the experimental burden and material costs associated with device optimization. As new donor and acceptor materials are synthesized, they can be readily integrated into the OSC-Net framework to guide the selection of promising pairings for optimal performance.
5 Conclusion and future work
This paper introduces a novel multi-fidelity machine learning framework, OSC-Net, designed to predict device performance parameters with uncertainty quantification, enabling high-throughput screening of OSC materials. A comprehensive database was first constructed, comprising 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 329 computational data points and 1782 experimental data points collected from existing literature. OSC-Net was then developed to incorporate datasets of varying fidelity. The model uses fingerprints of donor and acceptor materials, along with their relative ratios, as inputs to predict device performance parameters and their associated uncertainties, facilitating efficient screening of OSC materials. Compared to previous contributions, the main contributions of this study are: (1) multi-fidelity framework – a two-step pre-training and fine-tuning strategy was implemented to integrate datasets of different fidelities effectively, (2) uncertainty quantification – epistemic uncertainties are quantified, providing confidence intervals for model predictions and (3) curated experimental dataset – both fullerene and non-fullerene acceptors, paired with a broad range of conjugated polymer donors in binary blends, are included.
329 computational data points and 1782 experimental data points collected from existing literature. OSC-Net was then developed to incorporate datasets of varying fidelity. The model uses fingerprints of donor and acceptor materials, along with their relative ratios, as inputs to predict device performance parameters and their associated uncertainties, facilitating efficient screening of OSC materials. Compared to previous contributions, the main contributions of this study are: (1) multi-fidelity framework – a two-step pre-training and fine-tuning strategy was implemented to integrate datasets of different fidelities effectively, (2) uncertainty quantification – epistemic uncertainties are quantified, providing confidence intervals for model predictions and (3) curated experimental dataset – both fullerene and non-fullerene acceptors, paired with a broad range of conjugated polymer donors in binary blends, are included.
Our results demonstrate that (1) the pre-trained OSC-Net exhibits strong predictive performance for computational datasets, achieving low MSE values of 0.007, 0.256, 0, and 0.129, and high Pearson correlation coefficients of 0.987, 0.985, N/A, and 0.981 for VOC, JSC, FF, and PCE, respectively. (2) For experimental datasets, the pre-trained OSC-Net successfully captures the general input–output trends, demonstrating moderate correlation coefficients and CI accuracy, which enhance the subsequent fine-tuning process. (3) The fine-tuned OSC-Net consistently outperforms SF-OSC-Net, achieving lower MSE values (an average reduction of 2.5%), higher correlation coefficients, higher CI accuracy (an average increase of 9.2%), and higher classification accuracy (an increase of 2.2%). These results confirm that pretraining improves the efficiency of the fine-tuning process, leading to a more accurate model. (4) The fine-tuned OSC-Net provides more accurate uncertainty quantification compared to SF-OSC-Net, as evidenced by improved CI accuracy. This indicates that OSC-Net better captures the variability in the model, leading to more trustworthy predictions. (5) The fine-tuned OSC-Net was applied to a large-scale high-throughput screening, successfully identifying promising candidates with predicted PCEs exceeding 15%. Several of these candidates agree well with reported experimental data, and a list of previously unreported high-efficiency configurations is provided for future investigation. These findings confirm that OSC-Net is a robust computational tool for accurately predicting OSC device performance with uncertainty quantification, enabling the discovery of high-performance OSC materials in scenarios with limited high quality experimental data.
Future research will focus on generating higher-quality computational data for pretraining and expanding experimental datasets for fine-tuning. Subsequently, OSC-Net will be applied to the material design process to identify optimal donor and acceptor materials for OSC devices, followed by experimental validation.
Author contributions
H. Y., Y. W., and W. Y. conceived and designed the study. H. Y., A. Q., and J. R. collected the OSC database. H. Y. and J. O. developed OSC-Net and performed model training. H. Y., J. R., Y. W., and W. Y. wrote the initial draft of the manuscript. All authors contributed to its review and approval.Conflicts of interest
There are no conflicts to declare.Data availability
The source code for OSC-Net development can be found at https://github.com/yhz37/OSC-Net. The data supporting this article are collected from references, which are included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ta08724d.Acknowledgements
This work was financially supported by the Office of Naval Research (ONR) under award no. N000142412107. A. W. was supported by the McCullough Institute for Conservation, Land Use, and Environmental Resiliency at UNC Asheville.References
- J. Yi, G. Zhang, H. Yu and H. Yan, Advantages, challenges and molecular design of different material types used in organic solar cells, Nat. Rev. Mater., 2023, 9, 46–62 CrossRef.
- H. Imahori, T. Umeyama and S. Ito, Large π-aromatic molecules as potential sensitizers for highly efficient dye-sensitized solar cells, Acc. Chem. Res., 2009, 42, 1809–1818 CrossRef.
- S. Günes, H. Neugebauer and N. S. Sariciftci, Conjugated polymer-based organic solar cells, Chem. Rev., 2007, 107, 1324–1338 CrossRef.
- M. Riede, D. Spoltore and K. Leo, Organic Solar Cells—The Path to Commercial Success, Adv. Energy Mater., 2021, 11, 2002653 CrossRef CAS.
- K. Fukuda, K. Yu and T. Someya, The Future of Flexible Organic Solar Cells, Adv. Energy Mater., 2020, 10, 2000765 CrossRef CAS.
- Y. Li, X. Huang, H. K. M. Sheriff and S. R. Forrest, Semitransparent organic photovoltaics for building-integrated photovoltaic applications, Nat. Rev. Mater., 2022, 8, 186–201 CrossRef.
- T. Webb, S. J. Sweeney and W. Zhang, Device Architecture Engineering: Progress toward Next Generation Perovskite Solar Cells, Adv. Funct. Mater., 2021, 31, 2103121 CrossRef CAS.
- A. Mahmood and J. L. Wang, Machine learning for high performance organic solar cells: current scenario and future prospects, Energy Environ. Sci., 2021, 14, 90–105 RSC.
- C. Chen, et al., Molecular interaction induced dual fibrils towards organic solar cells with certified efficiency over 20%, Nat. Commun., 2024, 15, 1–10 Search PubMed.
- Z. Zheng, et al., Tandem Organic Solar Cell with 20.2% Efficiency, Joule, 2022, 6, 171–184 CrossRef CAS.
- X. Xiao, et al., Strategies to achieve efficiencies of over 19% for organic solar cells, Cell Rep. Phys. Sci., 2025, 6, 102390 CrossRef CAS.
- S. Xiao, Q. Zhang and W. You, Molecular Engineering of Conjugated Polymers for Solar Cells: An Updated Report, Adv. Mater., 2017, 29, 1601391 CrossRef.
- X. Rodríguez-Martínez, E. Pascual-San-José and M. Campoy-Quiles, Accelerating organic solar cell material's discovery: high-throughput screening and big data, Energy Environ. Sci., 2021, 14, 3301–3322 RSC.
- M. Seifrid, et al., Beyond molecular structure: critically assessing machine learning for designing organic photovoltaic materials and devices, J. Mater. Chem. A, 2024, 12, 14540–14558 RSC.
- D. R. Ahmed and F. F. Muhammadsharif, A Review of Machine Learning in Organic Solar Cells, Processes, 2025, 13, 393 CrossRef CAS.
- M. C. Scharber, et al., Design Rules for Donors in Bulk-Heterojunction Solar Cells—Towards 10% Energy-Conversion Efficiency, Adv. Mater., 2006, 18, 789–794 CrossRef CAS.
- S. A. Lopez, B. Sanchez-Lengeling, J. de Goes Soares and A. Aspuru-Guzik, Design Principles and Top Non-Fullerene Acceptor Candidates for Organic Photovoltaics, Joule, 2017, 1, 857–870 CrossRef CAS.
- J. Hachmann, et al., Lead candidates for high-performance organic photovoltaics from high-throughput quantum chemistry – the Harvard Clean Energy Project, Energy Environ. Sci., 2014, 7, 698–704 RSC.
- W. Sun, et al., The Use of Deep Learning to Fast Evaluate Organic Photovoltaic Materials, Adv. Theory Simul., 2019, 2, 1800116 CrossRef.
- J. Sun, et al., Accelerating the generation and discovery of high-performance donor materials for organic solar cells by deep learning, J. Mater. Chem. A, 2024, 12, 21813–21823 RSC.
- J. Sun, et al., Accelerating the discovery of acceptor materials for organic solar cells by deep learning, npj Comput. Mater., 2024, 10, 1–11 CrossRef.
- Y. Morishita, M. Yarimizu, M. Kaneko and A. Muraoka, Machine learning approach for predicting high JSC donor molecules in fullerene-typed organic solar cells, Chem. Phys. Lett., 2024, 857, 141719 CrossRef CAS.
- S. Nagasawa, E. Al-Naamani and A. Saeki, Computer-Aided Screening of Conjugated Polymers for Organic Solar Cell: Classification by Random Forest, J. Phys. Chem. Lett., 2018, 9, 2639–2646 CrossRef CAS PubMed.
- W. Sun, et al., Machine learning–assisted molecular design and efficiency prediction for high-performance organic photovoltaic materials, Sci. Adv., 2019, 5, eaay4275 CrossRef CAS.
- Y. Wu, J. Guo, R. Sun and J. Min, Machine learning for accelerating the discovery of high-performance donor/acceptor pairs in non-fullerene organic solar cells, npj Comput. Mater., 2020, 6, 1–8 CrossRef.
- M. H. Lee, Insights from Machine Learning Techniques for Predicting the Efficiency of Fullerene Derivatives-Based Ternary Organic Solar Cells at Ternary Blend Design, Adv. Energy Mater., 2019, 9, 1900891 CrossRef.
- H. Sahu, W. Rao, A. Troisi and H. Ma, Toward Predicting Efficiency of Organic Solar Cells via Machine Learning and Improved Descriptors, Adv. Energy Mater., 2018, 8, 1801032 CrossRef.
- H. Sahu and H. Ma, Unraveling Correlations between Molecular Properties and Device Parameters of Organic Solar Cells Using Machine Learning, J. Phys. Chem. Lett., 2019, 10, 7277–7284 CrossRef CAS PubMed.
- A. Mahmood, Y. Sandali and J. L. Wang, Easy and fast prediction of green solvents for small molecule donor-based organic solar cells through machine learning, Phys. Chem. Chem. Phys., 2023, 25, 10417–10426 RSC.
- C. R. Zhang, et al., Designing Donors and Nonfullerene Acceptors for Organic Solar Cells Assisted by Machine Learning and Fragment-Based Molecular Fingerprints, Sol. RRL, 2025, 9, 2400846 CrossRef CAS.
- S. Zhang, et al., Deep Learning-Assisted Design of Novel Donor–Acceptor Combinations for Organic Photovoltaic Materials with Enhanced Efficiency, Adv. Mater., 2025, 37, 2407613 CrossRef PubMed.
- D. Buterez, J. P. Janet, S. J. Kiddle, D. Oglic and P. Lió, Transfer learning with graph neural networks for improved molecular property prediction in the multi-fidelity setting, Nat. Commun., 2024, 15, 1–18 Search PubMed.
- H. Yang, S. H. Hong, Y. Qian and Y. Wang, Multi-fidelity surrogate-based optimization for microfluidic concentration gradient generator design, Eng. Comput., 2023, 40, 772–792 CrossRef.
- H. Yang and Y. Wang, A sparse multi-fidelity surrogate-based optimization method with computational awareness, Eng. Comput., 2023, 39(5), 3473–3489 CrossRef.
- H. Yang, S. H. Hong and Y. Wang, A sequential multi-fidelity surrogate-based optimization methodology based on expected improvement reduction, Struct. Multidiscip. Optim., 2022, 65, 1–17 CrossRef.
- H. Yang, S. H. Hong, G. Wang and Y. Wang, Multi-fidelity reduced-order model for GPU-enabled microfluidic concentration gradient design, Eng. Comput., 2022, 1–19, DOI:10.1007/s00366-022-01672-z.
- E. Hüllermeier and W. Waegeman, Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods, Mach. Learn., 2021, 110, 457–506 CrossRef.
- A. Kendall and Y. Gal, What uncertainties do we need in bayesian deep learning for computer vision?, ed. I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Advances in Neural Information Processing Systems, Curran Associates, Inc., 2017, vol. 30 Search PubMed.
- J. Gawlikowski, et al., A survey of uncertainty in deep neural networks, Artif. Intell. Rev., 2023, 56, 1513–1589 CrossRef.
- H. Yang, J. Ou and Y. Wang, Neural-physics multi-fidelity model with active learning and uncertainty quantification for GPU-enabled microfluidic concentration gradient generator design, Comput. Methods Appl. Mech. Eng., 2023, 417, 116434 CrossRef.
- H. Yang, B. K. Nallamothu, C. A. Figueroa and K. Garikipati, Attention-based multi-fidelity machine learning model for fractional flow reserve assessment, Comput. Methods Appl. Mech. Eng., 2024, 432, 117338 CrossRef.
- M. Abdar, et al., A review of uncertainty quantification in deep learning: Techniques, applications and challenges, Inf. Fusion, 2021, 76, 243–297 CrossRef.
- B. Lakshminarayanan, A. Pritzel and C. Blundell, Simple and scalable predictive uncertainty estimation using deep ensembles, ed. I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Advances in Neural Information Processing Systems, Curran Associates, Inc., 2017, vol. 30 Search PubMed.
- Y. Gal and Z. Ghahramani, Dropout as a bayesian approximation: Representing model uncertainty in deep learning, in International Conference on Machine Learning, PMLR, 2016, pp. 1050–1059 Search PubMed.
- M. A. Ganaie, M. Hu, A. K. Malik, M. Tanveer and P. N. Suganthan, Ensemble deep learning: A review, Eng. Appl. Artif. Intell., 2022, 115, 105151 CrossRef.
- Z. Zhong, et al., Non-Halogen Solvent Processed Binary Organic Solar Cells with Efficiency of 19% and Module Efficiency Over 15% Enabled by Asymmetric Alkyl Chain Engineering, Adv. Energy Mater., 2023, 13, 2302273 CrossRef CAS.
- H. Kang, et al., 1,8,9-Trihydroxyanthracene as a Green Solid Additive for Operational Stability in Organic Solar Cells, Sol. RRL, 2023, 7, 2201084 CrossRef CAS.
- Y. Jiang, et al., Suppressing electron-phonon coupling in organic photovoltaics for high-efficiency power conversion, Nat. Commun., 2023, 14, 1–12 Search PubMed.
- Y. Tang, et al., Identifying and Amplifying the Spontaneously Formed Photo-Charge Contribution in Opaque and Semitransparent Organic Photovoltaics, Adv. Energy Mater., 2024, 14, 2303799 CrossRef CAS.
- H. Liu, et al., Hybrid Linking Sites Constructed Non-Fully Conjugated Asymmetric Dimerized Giant Molecule Acceptors for Organic Solar Cells with an Efficiency of ≈20%, Angew. Chem., 2025, 137, e202503721 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |