 Open Access Article
Open Access ArticleX-ray analysis of Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O: disentangling elemental contributions in a prototypical high-entropy oxide
Maryia
Zinouyeva
 *a,
Martina
Fracchia
*a,
Martina
Fracchia
 bc,
Giulia
Maranini
b,
Mauro
Coduri
bc,
Giulia
Maranini
b,
Mauro
Coduri
 bc,
Davide
Impelluso
bc,
Davide
Impelluso
 a,
Nicholas B.
Brookes
a,
Nicholas B.
Brookes
 d,
Lorenzo
Grilli†
d,
Lorenzo
Grilli†
 a,
Kurt
Kummer
a,
Kurt
Kummer
 d,
Francesco
Rosa
d,
Francesco
Rosa
 a,
Matteo
Aramini
e,
Giacomo
Ghiringhelli
a,
Matteo
Aramini
e,
Giacomo
Ghiringhelli
 af,
Paolo
Ghigna
af,
Paolo
Ghigna
 bc and
Marco
Moretti Sala
bc and
Marco
Moretti Sala
 *a
*a
aDipartimento di Fisica, Politecnico di Milano, Piazza Leonardo da Vinci 32, I-20133 Milano, Italy. E-mail: maryia.zinouyeva@polimi.it; marco.moretti@polimi.it
bDepartment of Chemistry, University of Pavia, V.le Taramelli, 12, I-27100 Pavia, Italy
cINSTM, National Inter-University Consortium for Materials Science and Technology, Via G. Giusti 9, I-50121 Florence, Italy
dESRF, The European Synchrotron, 71 Avenue des Martyrs, CS 40220, F-38043 Grenoble, France
eDiamond Light Source, Harwell Science and Innovation Campus, Didcot, OX11 0DE, UK
fCNR-SPIN, Dipartimento di Fisica, Politecnico di Milano, I-20133 Milano, Italy
First published on 25th November 2025
Abstract
We employ several X-ray based techniques, including X-ray diffraction, X-ray absorption spectroscopy and resonant inelastic X-ray scattering, to disentangle the contributions of individual chemical species to the structural, electronic and magnetic properties of high-entropy oxides. In the benchmark compound Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O and related systems, we unambiguously resolve a sizable Jahn–Teller distortion at the Cu sites, more pronounced in the absence of Ni2+ and Mg2+, suggesting that these ions promote positional order, whereas Cu2+ ions act to destabilize it. Moreover, we detect magnetic excitations and estimate the strength of the interactions between pairs of different magnetic elements. Our results provide valuable insights into the role of various chemical species in shaping the physical properties of high-entropy oxides.
1 Introduction
High-entropy materials are single-phase compounds characterized by significant configurational disorder, wherein multiple chemical species randomly occupy equivalent crystallographic sites. Configurational disorder disrupts periodicity and symmetry, significantly influencing a material's physical properties. Among high-entropy materials, high-entropy oxides (HEOs) stand out for their exceptional characteristics,1 such as tunable room-temperature superionic conductivity,2 colossal dielectric constants,3 and high lithium-storage capacity.4,5 In HEOs, configurational disorder facilitates the formation of a single-phase material from the multi-phase mixture of different chemical species through a temperature-dependent entropic contribution −TΔSc < 0, which offsets the enthalpic contributions ΔHmix to the Gibbs free energy of mixing ΔGmix = ΔHmix − TΔSc; specifically, the spontaneous formation of a homogeneous solid solution occurs when the latter is negative. So, for entropy-stabilized oxides (ESOs), i.e., HEOs where the enthalpic contribution is positive and the entropic contribution satisfies TΔSc > ΔHmix, there exists a critical temperature Tc = ΔHmix/ΔSc below which the homogeneous solid solution cannot spontaneously form. Since where χi is the molar fraction of the i-th chemical species and N is their total number, configurational entropy is maximized in equimolar systems, for which χi = 1/N and ΔSc = R
where χi is the molar fraction of the i-th chemical species and N is their total number, configurational entropy is maximized in equimolar systems, for which χi = 1/N and ΔSc = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N.
N.
Rocksalt Mg0.2Ni0.2Co0.2Zn0.2Cu0.2O (hereafter referred to as 5HEO) is a prototypical HEO.6 It is obtained from an equimolar mixture of MgO, CoO, NiO, CuO and ZnO, which, however, do not share a common crystal structure; indeed, MgO, CoO and NiO possess a rocksalt crystal structure, while CuO and ZnO have tenorite and wurtzite crystal structures, respectively, such that their incorporation into the rocksalt structure comes with a positive enthalpy of mixing. Rost et al.6 showed that (i) a single-phase crystal of 5HEO forms only at an equilibration temperature Tc ≈ 1150 K or above; since ΔSc = 13.4 J (mol K)−1 for N = 5, such a critical temperature corresponds to an enthalpy of mixing of approximately 15.4 kJ mol−1; (ii) the transition from the multi- to the single-phase solid solution is reversible with temperature; (iii) the critical temperature is minimized for the equimolar composition when the amount of an individual chemical species is changed and the others are kept even, and (iv) the quaternary compounds never form a single phase at Tc or below. Moreover, (v) the authors' estimate of 10 kJ mol−1 for the enthalpy of mixing solely based on the tenorite-to-rocksalt (22.2 kJ mol−1 (ref. 7)) and the wurtzite-to-rocksalt (24.5 kJ mol−1 (ref. 8)) transition enthalpies for CuO and ZnO, respectively, is compatible with the experimental estimate in (iii). These observations were taken as evidence that the formation of the homogeneous solid solution is driven by entropy, i.e., 5HEO is an ESO. However, (iii) suggests that the enthalpy of mixing is very little dependent on the actual composition of the material, implying that the enthalpy of mixing of all the chemical species is very similar. This is in contradiction to the hypothesis used in (v), where the enthalpy of mixing of MgO, CoO and NiO is neglected. Indeed, Coduri et al. found that the relative concentration of MgO, CoO and NiO affects the stability of the rocksalt structure in samples with the same configurational entropy, suggesting that the nature of chemical species with the rocksalt structure also plays a role.9 A similar conclusion can be drawn from the observation of Fracchia et al. that Ni0.6Cu0.2Zn0.2O is stable in the rocksalt structure at relatively low temperatures;10,11 here, configurational entropy is lower, so that the critical temperature should be higher than that of 5HEO if CuO and ZnO were the sole chemical species contributing to the enthalpy of mixing. The most plausible scenario is that the latter hypothesis should be relaxed. Recently, experimental12–15 and theoretical16–19 studies have provided evidence for Jahn–Teller distortions at the sites occupied by Cu in 5HEO. Their very presence points to deviations of the crystal structure from the perfect rocksalt, which should definitely be taken into account for a quantitative understanding of the energetics of the system. Indeed, distortions of the sites occupied by Cu are necessarily shared with neighboring sites, which are randomly occupied by various chemical elements that may respond very differently to perturbation. Interestingly, this could explain the dependence of the stability of the rocksalt structure on the relative concentration of various chemical species; unfortunately, structural probes did not reveal distortions of the octahedral environment around any of the metal ions, with the exception of Cu2+. Such a picture is complicated by the tendency of 5HEO to form the guggenite phase rather than simply demixing into single binary oxides below the critical temperature.20 All the above findings prompted us to adopt a different approach, focusing on potential spectroscopic signatures of putative distortions on the electronic structure of various metal ions individually.
Another intriguing feature of 5HEO is that, despite configurational disorder, it displays a long-range magnetic order below approximately 113 K.21 Indeed, neutron powder diffraction studies revealed a magnetic structure analogous to that of NiO and CoO,22 with antiferromagnetically coupled ferromagnetic (111) planes.21 Notably, spin waves have been observed at temperatures significantly higher than the Néel temperature, suggesting the persistence of short-range magnetic correlations also in the paramagnetic state.21 Magnetic susceptibility measurements23 and Monte Carlo simulations24 indicate that the long-range magnetic order is strongly dependent on the concentration of magnetic ions, again pointing to the nature of chemical species playing a role in shaping the HEO's physical properties. Unfortunately, the contribution of individual metal ions to the collective magnetic behavior could not be singled out, another challenge that we address in this paper.
We performed X-ray diffraction (XRD), including pair distribution function (PDF) analysis, as well as soft- and hard-X-ray absorption spectroscopy (XAS) and resonant inelastic X-ray scattering (RIXS) measurements, on 5HEO and five sister compounds. RIXS is a powerful probe of the electronic and magnetic excitations in solids and benefits from its intrinsic chemical sensitivity, which is particularly welcome in the context of HEOs to isolate the contributions of various metal ions. Our results directly evidence a sizable distortion of the Cu2+ sites and provide hints of the associated energy scale. Moreover, unlike structural probes, RIXS provides indications that the sites occupied by Co and Ni are also distorted, and we point to the different roles played by various metal ions in accommodating these distortions. Finally, we determine almost all of the relevant magnetic interactions among pairs of magnetic ions, which are essential ingredients for a quantitative understanding of the magnetic properties of HEOs.
2 Experimental method
The six powder samples studied in this work are listed in Table 1, together with their crystal structure and cell parameters.| Chemical composition | Label | Structure | Cell parameter(s) (Å) | FWHM ratio |
|---|---|---|---|---|
| Mg0.25Co0.25Ni0.25Zn0.25O | noCu | Cubic | a = 4.2301 ± 0.00012 | 1.0 |
| Mg0.20Co0.20Ni0.20Cu0.20Zn0.20O | 5HEO | Cubic | a = 4.2365 ± 0.00006 | 1.1 |
| Mg0.25Ni0.25Cu0.25Zn0.25O | noCo | Cubic | a = 4.2293 ± 0.00008 | 1.3 |
| Mg0.25Co0.25Ni0.25Cu0.25O | noZn | Cubic | a = 4.2258 ± 0.00018 | 1.8 |
| Co0.25Ni0.25Cu0.25Zn0.25O | noMg | Tetragonal | a = 3.0138 ± 0.00052, c = 4.2106 ± 0.00097 | |
| Mg0.25Co0.25Cu0.25Zn0.25O | noNi | Tetragonal | a = 3.0311 ± 0.00039, c = 4.1936 ± 0.00062 |
The samples were prepared using the Pechini method, a variant of the sol–gel method. A starting solution was obtained by dissolving a stoichiometric amount of nitrate salts of each cation in distilled water, with an excess of citric acid. The solution was stirred and heated at 100 °C overnight to form a gel, which was subsequently treated at 280 °C for two hours and then at 900 °C for another two hours to remove the organic components. The resulting fine powders primarily consisted of mechanically blended oxide precursors. These powders were pelletized and annealed at 1000 °C for 12 hours to complete solid solution formation and then quenched at room temperature.
XRD patterns were recorded in Bragg–Brentano geometry using a Bruker D2 diffractometer equipped with Cu radiation and a Ni filter collecting data over a 2θ angular range from 15° to 90°. Rietveld refinements were performed with GSAS-II software to verify the crystal structure and determine the lattice parameters.25 The full-width-at-half-maximum (FWHM) was computed using the software WINPlotR.26 XRD patterns for PDF analysis were collected at the beamline ID15A of ESRF – The European Synchrotron (Grenoble, France) at an incident wavelength of λ = 0.1240 Å (≈100 keV), using a Pilatus 2M CdTe detector (Dectris) placed 380 mm away from the specimen.27 The powders were packed into quartz capillaries (Hilgenberg) with 0.5 mm diameter and rotated during the acquisition to improve the orientational average of the grains. PDF data were described according to the G(r) formalism,28 which indicates the probability of finding a couple of atoms separated by a certain distance r. G(r) was determined experimentally via sine Fourier transform of the structure factor S(Q):
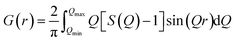 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ), 2θ is the angle between the incoming and outgoing X-rays and λ is the X-ray wavelength. G(r) curves were computed using the software PDFGetX3 (ref. 29) subtracting the contribution of the quartz capillary and limiting the integration of diffraction data to a maximum value of Q of 24 Å−1. PDF peaks were fitted using the direct analysis approach30 using Gaussian functions, as implemented in the Fityk software.31
θ/λ), 2θ is the angle between the incoming and outgoing X-rays and λ is the X-ray wavelength. G(r) curves were computed using the software PDFGetX3 (ref. 29) subtracting the contribution of the quartz capillary and limiting the integration of diffraction data to a maximum value of Q of 24 Å−1. PDF peaks were fitted using the direct analysis approach30 using Gaussian functions, as implemented in the Fityk software.31
Hard XAS at the Co, Ni, and Cu K edges was carried out at beamline I20 of Diamond Light Source (Didcot, United Kingdom) on 5HEO and at beamline XAFS of ELETTRA (Trieste, Italy) on all the other samples. In both cases, the spectra were acquired at room temperature. X-ray absorption spectroscopy (XAS) experiments at the I20 beamline of Diamond Light Source were performed using a Si(111) four-bounce monochromator. X-rays were focused via dedicated mirrors, achieving a beam size (FWHM) at a sample position of ∼400 µm (H) × 300 µm (V). Rhodium-coated harmonic rejection mirrors were used to remove high-energy harmonics. The absorption spectra were either recorded with fluorescence detection via a 64-element monolithic Ge detector combined with an Xspress4 readout system, after calibration of the monochromator with transmission measurement of a piece of Cu foil. An ion chamber operated at 15% absorption was used to measure the photon flux delivered to the samples. For each measurement, an appropriate amount of sample was mixed with cellulose, pressed into a pellet, and measured in air.
The extended X-ray absorption fine structure (EXAFS) spectra were collected in transmission mode at the Elettra synchrotron. The spectra were acquired at room temperature at the Co, Ni, and Cu K edges using ion chambers as detectors. The samples were prepared as describe above. The ring current and energy were 200 mA and 2.4 GeV, respectively. A Si(111) double-crystal monochromator was used ensuring high-order harmonic rejection by detuning the second crystal. A water-cooled, Pt-coated silicon mirror was used to obtain vertical collimation of the beam. The energy calibration was ensured by simultaneously acquiring the spectra of Co, Ni and Cu metal foil, respectively, using a third ion chamber. The XANES part of the spectra was analyzed by means of the Athena code.32 Spectra were first processed by subtracting a smooth pre-edge background fitted with a straight line and then normalized to unity at 300 eV above the edge jump, where the EXAFS can be neglected. The data analysis has been performed using the EXCURVE program.33 Phases and amplitudes were calculated using the muffin-tin approximation in the framework of the Hedin–Lundqvist and Von Bart approximations for the exchange and ground state potentials, respectively:33 this includes the effects of inelastic losses due to the electron inelastic scattering (photoelectron mean free path). The fittings have been made in the k space, using a k3 weighting scheme, and full multiple scattering calculations within the cluster used in the fits. The stability of the fits was checked by testing different weighting schemes and verifying that the fitting parameters were recovered within the errors. The passive amplitude reduction factor was kept fixed to 0.8, which is a sensible value in the Hedin–Lundqvist approximation. The accuracy of the phase shifts and amplitudes was tested by fitting the spectra of pure metal oxides at their K edge and recovering the crystallographic distances within 0.01 Å. To avoid unnecessary correlations between the parameters and to keep the number of fitted parameters below the number of EXAFS independent points, which in the present case was estimated to be Nidp ≈ 2ΔkΔR/π ≈ 25, a single energy shift parameter was used for all the shells, and the coordination numbers were fixed to their crystallographic values.
Soft XAS and RIXS measurements were carried out at beamline ID32 of ESRF – The European Synchrotron (Grenoble, France).34 The spectra were collected at the Co, Ni, and Cu L3 edges with energy resolutions of approximately 40, 46, and 50 meV, respectively, using scattering angles of 90° and 150° with π polarization of the incident photons. Measurements were performed at 30, 300, and 600 K. The RIXS spectra were normalized to the integrated intensity of the crystal-field excitations, specifically in the energy range from 0.5 to 3.5 eV at the Ni and Co L3 edges and from 0.5 to 2 eV at the Cu L3 edge.
3 Results and discussion
3.1 Long-range crystal structure – XRD
To start with, we characterized the crystal structure of the investigated samples by means of XRD. The corresponding patterns are displayed in Fig. 1, while the results of Rietveld refinements are summarized in Table 1. Four samples (5HEO, noCu, noCo, and noZn) are consistent with the prototype rocksalt crystal structure (space group: Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Among them, noCu and 5HEO display sharp peaks, whereas noCo and noZn show a general peak broadening of all reflections except for those related to the hhh family.35 The broadening of a diffraction peak reflects a limited structural coherence perpendicular to the corresponding plane. We can exclude that the broadening arises from the limited size effect as the specimens were treated at 1000 °C and the grain size was submicrometric. These broadenings are therefore deemed as indirect evidence of structural disorder. Such broadening is then quantified as the ratio between the full-width-at-half-maximum (FWHM) of the 200 and 111 reflections (see Table 1): this is the smallest for noCu and increases in 5HEO, noCo and noZn, yet without inducing a structural transition. A transition from the cubic to the tetragonal crystal structure (space group: I4/mmm), instead, occurs in noMg and noNi, as evidenced by the splitting and asymmetric broadening of all peaks but those corresponding to the hhh reflections. The absence of asymmetries in the hhh reflections points towards the formation of homogeneous solid solutions, as compositional fluctuations would affect all XRD reflections. Our results are in line with the available literature20,36 even in case of specimens produced with a different synthetic approach. This suggests that the observed distortions are intrinsic properties of the materials.
m). Among them, noCu and 5HEO display sharp peaks, whereas noCo and noZn show a general peak broadening of all reflections except for those related to the hhh family.35 The broadening of a diffraction peak reflects a limited structural coherence perpendicular to the corresponding plane. We can exclude that the broadening arises from the limited size effect as the specimens were treated at 1000 °C and the grain size was submicrometric. These broadenings are therefore deemed as indirect evidence of structural disorder. Such broadening is then quantified as the ratio between the full-width-at-half-maximum (FWHM) of the 200 and 111 reflections (see Table 1): this is the smallest for noCu and increases in 5HEO, noCo and noZn, yet without inducing a structural transition. A transition from the cubic to the tetragonal crystal structure (space group: I4/mmm), instead, occurs in noMg and noNi, as evidenced by the splitting and asymmetric broadening of all peaks but those corresponding to the hhh reflections. The absence of asymmetries in the hhh reflections points towards the formation of homogeneous solid solutions, as compositional fluctuations would affect all XRD reflections. Our results are in line with the available literature20,36 even in case of specimens produced with a different synthetic approach. This suggests that the observed distortions are intrinsic properties of the materials.
3.2 Short-range crystal structure – PDF
The broadening observed in XRD patterns suggest a certain degree of structural disorder, eventually resulting in a structural transition in some of the samples. Insights on the short-range, i.e., local structure can, instead, be obtained by performing a PDF analysis. Fig. 2 shows the experimental PDF curves in G(r) notation for 5HEO, noCu and noMg, where the latter two have been chosen as references for cubic and tetragonal crystal structures, respectively. The atom pairs associated with the PDF peaks are identified in Table 2, along with the corresponding interatomic distances for 5HEO, noCu and noMg. We assume that O–O pairs do not contribute to the PDF peaks due to the low scattering factor of oxygen compared to metal ions. The PDF curves in Fig. 2 of noCu, 5HEO and noMg are similar, but with appreciable differences, particularly in terms of peak position and broadening at large interatomic distances. The values detected by direct analysis of PDF peaks up to about 5 Å are compared in Table XII in the SI. Since the broadening of the peaks mostly depends on the degree of structural disorder, we conclude that noCu is more ordered compared to 5HEO and, notably, noMg, which appears to be the most disordered, in agreement with previous high-resolution powder diffraction measurements.20 The fact that the PDF signal of tetragonal noMg being similar to that of cubic noCu and 5HEO at short interatomic distances is not surprising because the PDF peak resolution is limited by thermal vibration and termination ripples. Rather, the impact of tetragonal distortion is evident at large interatomic distances (above 20 Å), where the curve of noMg is markedly different from the others.3.3 Short-range crystal structure – XANES and EXAFS
Structural characterization techniques evidence a certain degree of structural disorder in some of the samples. Unfortunately, the information they provide is averaged over all metal sites. With the aim of characterizing the short-range crystal structure around the various chemical species individually, we acquired hard XAS spectra at the Co, Ni and Cu K edges for noCu, 5HEO and noMg, respectively (Fig. 3). The XANES data for the Cu, Co and Ni K edges are reported in panels (a), (d) and (g), respectively. We here note that the edge energy position is sensitive to the metal oxidation state, and possible variations thereof. In the present case, no variation of the edge energy is detected in all the cases. In addition, comparison with the CoO, NiO and CuO spectra used as standards (not shown here), confirms that the oxidation state is +2 for all the transition metals.The XANES spectra in Fig. 3 show a clear trend. If we compare each of the spectra of the HEO with the corresponding spectra of the noMg sample, we note a decrease in the definition of the spectral features. On the other hand, a comparison with the spectra of the noCu samples (which of course is not possible at the Cu K edge) shows an increase in the definition. These trends are also apparent in the EXAFS part of the spectra shown in panels (b), (e) and (h), along with the corresponding Fourier transforms (FT) in panels (c), (f) and (i), as it is highlighted by the magnitude of the EXAFS FT peaks, particularly evident for the second coordination shell at ca. 3 Å. Reminding here that the broadening of the XAS structures is related to the disorder around the photoabsorber, we can conclude that these effects can be explained by the different amount of disorder in different samples, which is increased by removing Mg and decreased by removing Cu. The disorder is static, as all the spectra have been collected at the same temperature and can be explained by the local Jahn–Teller distortion around Cu. This conclusion can be made quantitative by looking at the EXAFS fitted parameters, as shown in Tables 3 and 4 for the data at the Cu K edge and Tables in the SI for the data at the other edges. The general increase in the EXAFS Debye–Waller factors removing Mg and their decrease by removing Cu are evident, in perfect agreement with the above discussion.
| Shell | Atom (Å) | N | R (Å) | σ (Å2) | b (Å3) | c (Å4) |
|---|---|---|---|---|---|---|
| 1 | O | 6 | 2.01(1) | 0.013(2) | 0.00300(9) | |
| 2 | M | 12 | 3.009(6) | 0.011(1) | ||
| 3 | O | 8 | 3.26(1) | 0.005(2) | ||
| 4 | M | 6 | 4.21(1) | 0.016(2) | ||
| 5 | O | 24 | 3.97(4) | 0.015(5) | ||
| 6 | M | 24 | 5.19(2) | 0.015(2) | ||
| 7 | M | 12 | 5.5(2) | 0.03(2) |
| Shell | Atom (Å) | N | R (Å) | σ (Å2) | b (Å3) | c (Å4) |
|---|---|---|---|---|---|---|
| 1 | O | 6 | 1.95(2) | 0.025(2) | −0.04(4) | 0.0039(2) |
| 2 | M | 12 | 2.987(9) | 0.016(2) | ||
| 3 | O | 8 | 3.25(2) | 0.006(2) | ||
| 4 | M | 6 | 3.70(3) | 0.029(7) | ||
| 5 | O | 24 | 4.1(1) | 0.04(6) | ||
| 6 | M | 24 | 4.69(4) | 0.025(4) | ||
| 7 | M | 12 | 5.54(3) | 0.015(3) |
The EXAFS oscillations and their FT were fitted adopting a rocksalt structure for all the samples, even though noMg possesses a tetragonal crystal structure. The reason behind this choice is twofold: on one hand, we keep the number of fitting parameters as low as possible, in order to avoid unnecessary correlations between them; on the other hand, the change in the bond lengths due to the tetragonal distortion is 0.03 Å at the most, i.e., comparable with the experimental resolution of EXAFS, and, as a matter of fact, the first peak in the FT of noMg is never split. The fit to the EXAFS oscillations and their FT are shown by the thin lines in Fig. 3, and the extracted average Co–O, Ni–O and Cu–O bond lengths are shown in Fig. 4. We note that the Co–O bond length remains practically unchanged and identical within the error bars to the Ni–O bond length in 5HEO, while the Cu–O and Ni–O bond lengths undergo opposite changes, with the former decreasing and the latter increasing in the tetragonal crystal structure. We interpret this and the above observations as an effect of Jahn–Teller distortions, resulting in a smaller average Cu–O distance.20 It is peculiar, though, that the change in the Cu–O bond length has no or little impact on the Co–O bond length but strong on the Ni–O bond length, indicating that Ni exhibits a greater propensity than Co to adjust to the distortions introduced by Cu2+. It can be attributed to the fact that Ni2+ is Jahn–Teller inactive, and there is no or little energy cost associated with the distortion of the Ni local environment. Otherwise, in a regular octahedral environment, the Ni–O atom pair should be shorter than Co–O and Cu–O, according to Shannon's ionic radii.37
 | ||
| Fig. 4 Average Co–O, Ni–O and Cu–O bond lengths for noCu, 5HEO and noMg, as extracted from Cu, Ni and Co K edge EXAFS, respectively. | ||
3.4 Crystal-field excitations and Jahn–Teller distortions
The interpretation of XRD and hard XAS data based on the Jahn–Teller distortion at the Cu sites is rather speculative at this stage and necessitates further investigation. RIXS can be extremely helpful in this respect because it directly probes d–d excitations. For a TM ion in octahedral symmetry, the crystal field splits the d orbitals into an eg (dx2−y2 and d3z2−r2) doublet and a t2g (dxy, dyz and dzx) triplet; for lower symmetries, these degeneracies are further lifted. The so-called d–d excitations are transitions between crystal-field split states, and their energy is therefore directly linked to the strength and symmetry of the crystal field interaction.38Fig. 5(a) shows the collected RIXS spectra at the Cu L3 edge (approximately 930 eV, see the inset in panel (c)) at 30 K for the five samples containing Cu. In analogy with the literature on insulating and superconducting cuprates,38–41 the peaks in the energy range from 0.5 to 2 eV are assigned to d–d excitations, and the weak, but extended spectral weight above 2 eV is attributed to charge-transfer excitations. Similarly, we could tentatively assign the peak at approximately 0.1 eV to magnetic excitations, albeit the lack of long-range configurational order necessitates a degree of caution. In this section, we focus on d–d excitations, while magnetic excitations will be discussed in the following.
In Cu2+ with a 3d9 electronic configuration, a single hole occupies the d orbitals. The RIXS cross-section for d–d excitations in Cu2+ is well described by a single-ion model,38 which is exploited here to assign features in the RIXS spectra based on their intensities. To do so, we fit the region of the spectra between 0.5 and 2 eV to three Gaussian curves whose integrated spectral weight is constrained to the calculated one using the actual experimental conditions and performing the powder average, see Fig. 5(b). The best fit is obtained assuming that the ground state has dx2−y2 symmetry, implying an elongation of the CuO6 octahedra. Nevertheless, we cannot fully rule out that the CuO6 octahedra are instead subject to compression, stabilizing the d3z2−r2 orbital as the ground state. While RIXS measurements on single crystals could help determine the sign of distortion, the presence of a significant deviation from ideal octahedral symmetry is beyond any doubt.
The peak corresponding to the d3z2−r2 excited state is centered at approximately 0.9 eV. This value is much lower than the least distorted layered cuprate (1.7 eV in La2CuO4 (ref. 38)), still it implies that the symmetry of the Cu sites is lower than octahedral and points to a sizable distortion of the CuO6 octahedron in all samples, though with appreciable differences (see Table 5). Namely, the energy of the d3z2−r2 excited state and its full width at half maximum (FWHM) in the noNi sample are higher than those in other compounds, indicating that the distortion of the Cu sites is larger and more broadly distributed in this sample than in other compounds, and suggesting that the presence of Ni in other systems reduces positional disorder. A similar, though less effective, role is played by Mg. These findings are consistent with XRD, PDF and hard XAS investigations.
| d3z2−r2 | dxy | dxz/yz | ΔECu | ΔENi | |
|---|---|---|---|---|---|
| 5HEO | 0.904 ± 0.007 (0.430 ± 0.014) | 1.341 ± 0.002 (0.205 ± 0.004) | 1.527 ± 0.004 (0.366 ± 0.006) | 90.5 ± 6.6 | 43.5 ± 6.4 |
| noCo | 0.888 ± 0.005 (0.374 ± 0.012) | 1.338 ± 0.002 (0.208 ± 0.004) | 1.517 ± 0.004 (0.375 ± 0.006) | 86.7 ± 6.8 | 44.5 ± 2.7 |
| noCu | 44.4 ± 2.6 | ||||
| noMg | 1.023 ± 0.011 (0.550 ± 0.020) | 1.389 ± 0.003 (0.240 ± 0.004) | 1.580 ± 0.004 (0.415 ± 0.007) | 114.8 ± 2.7 | 52.1 ± 4.0 |
| noNi | 1.173 ± 0.017 (0.760 ± 0.044) | 1.431 ± 0.004 (0.281 ± 0.006) | 1.637 ± 0.005 (0.456 ± 0.009) | 96.4 ± 16.4 | |
| noZn | 0.920 ± 0.007 (0.434 ± 0.014) | 1.362 ± 0.002 (0.210 ± 0.004) | 1.529 ± 0.004 (0.387 ± 0.006) | 107.3 ± 2.7 | 51.7 ± 1.6 |
| CuO | 2.162 ± 0.029 (0.748 ± 0.062) | 1.699 ± 0.001 (0.189 ± 0.004) | 2.042 ± 0.003 (0.392 ± 0.007) | 145.8 ± 1.5 |
Finally, we look at the changes in the RIXS spectra as a function of temperature. A similar behavior is observed for all compounds, so we report in Fig. 5(c) only the data for 5HEO as an example. We note that d–d excitations soften and broaden in energy as the temperature is increased; the softening can be attributed to thermal expansion, as an increase in the Cu–O distance weakens the crystal-field interaction, while the broadening is likely caused by lattice vibrations, which induce fluctuations in the bond length and hence a distribution of Cu sites with varying crystal-field interactions, a phenomenon previously observed in NiO42 and CuO.43
Our experimental findings provide unambiguous evidence that the Cu sites are affected by a sizable Jahn–Teller distortion, which breaks the cubic symmetry of the CuO6 octahedron, and back up previous measurements using structural probes.12–15 While we cannot estimate the variation of the Cu–O bond lengths with respect to the ideal octahedral situation, we can estimate the energy change involved in the distortion by comparing the RIXS spectra of rocksalt 5HEO and tenorite CuO, as shown in Fig. 6(a). The spectra are remarkably different and, specifically, the average energy of d–d excitations is significantly lower in 5HEO than in CuO, consistent with a larger Cu–O bond length. The fit to the CuO spectrum following the same procedure described above puts the d3z2−r2 excited state at an energy of approximately 2.2 eV, in perfect agreement with previous estimates,43i.e., approximately 1.3 eV higher than that in 5HEO. It should be possible, though beyond the scope of this work, to extract a more accurate estimate of the enthalpy of mixing from the observed reconstruction of the electronic structure.
Next, we also look for signatures of distortions at the Ni and Co sites. Fig. 7(a) and (d) show the low-temperature Ni L3 edge RIXS spectra with energies of the incident photons corresponding to the main (MP) and satellite (ST) peaks in the XAS profile at approximately 852 and 854 eV, respectively. In analogy with NiO,44–46 the energy range from 1 to 3.5 eV is covered by d–d excitations, while charge-transfer excitations emerge above 3.5 eV; single and double spin excitations appear below 0.1 eV. Notably, the RIXS spectra at the MP look very much alike for all samples. In contrast, the RIXS spectra excited at the ST peak show differences; in particular, we observe that the RIXS spectrum of noCu is significantly sharper than the spectra of other compounds. Fig. 8(a), instead, shows the low-temperature Co L3 edge RIXS spectra with an energy of the incident photons corresponding to the main peak of the XAS profile at 779 eV. Here, d–d and charge-transfer excitations are dominant down to the lowest energies because of the multiplet structure of Co2+.47–49 As a result, if present, magnetic excitations cannot be easily identified. Similar to Ni, the Co L3 edge RIXS spectra also overlap for all the samples, with the exception of noCu, which again shows sharper features.
Both Ni (see Fig. 7(b), (c), (e) and (f)) and Co (see Fig. 8(b) and (c)) L3 edge RIXS spectra of 5HEO and noCu broaden with temperature, progressively eliminating their differences. Consequently, there appears to be a potential parallel between the broadening of the RIXS spectra induced by temperature and the incorporation of Cu in the crystal structure. Since the FWHM of the peaks reflects a distribution of bond lengths,42 we conclude that the bond length in noCu is more uniformly distributed than in other compounds. Unfortunately, we cannot rule out the possibility that noCu itself exhibits distortions, nor can we quantify the crystal-field splitting associated with the distortions at TM sites other than Cu. These remain as subjects of research for future investigations.
Similar to the case of CuO, we try to highlight potential variations in the electronic structure of rocksalt 5HEO compared to that of pristine rocksalt NiO and CoO in Fig. 6(b) and (c), respectively. Unlike the case of CuO, the spectra of NiO are not markedly different from those of 5HEO, the major changes being related to the intensity, not the energy, of various excited states. The comparison between 5HEO and CoO, instead, shows little, but appreciable differences in the energy of d–d excitations, especially in the very low energy region, where the double structure in 5HEO merges into a single peak in CoO at approximately 0.1 eV (note that the excitation at approximately 0.5 eV is related to Co3+ impurities). This suggests that the electronic structure of Ni2+ ions does not change significantly when NiO is incorporated in 5HEO, implying a negligible enthalpy of mixing, while the electronic reconstruction of Co2+ ions is appreciable. We did not perform measurements on MgO and ZnO because no d–d excitations are expected for systems with nominal d0 and d10 electronic configurations, respectively. However, it might be interesting to test this hypothesis experimentally.
3.5 Magnetic excitations and interactions
We now focus on the low-energy region of the RIXS spectra to investigate the magnetic dynamics in 5HEO and related compounds. Fig. 9(a) compares the Cu L3 edge RIXS spectra of all samples at 30 K, where the feature at 0.1 eV is better appreciated. The magnetic nature of this excitation can be attributed by drawing an analogy with cuprates,50 and here it was confirmed by two additional experimental observations: (i) Fig. 9(b) shows that its intensity progressively decreases with increasing temperature from below to well above the Néel temperature of 5HEO; (ii) the RIXS spectra in Fig. 9(d)–(h) were fit to two energy-resolution-limited Gaussian curves (black solid lines) representing the quasi-elastic and phonon peaks and a Pearson curve (colored solid line with a shaded area) representing the magnetic excitation. The results are summarized in the left panel of Fig. 9(n) and in Table 5 and show that the energy of excitation is consistently higher in noMg and noZn than in other compounds; since Mg2+ and Zn2+ are nonmagnetic, the effect can be qualitatively accounted for by noting that their removal from the crystal structure increases the energy cost of flipping a Cu spin, consistent with the magnetic origin of the feature. This argument is better developed below to provide further information. Also, for magnetic excitations, the peak is broader in the noNi sample than in other compounds, again suggesting that Ni2+ reduces positional disorder in the system.Having confirmed that the origin of the low-energy excitation is magnetic, we discuss its local or collective nature. In single crystalline materials, this is usually tested by checking the dispersion of magnetic excitation, but for powder samples the test could be less conclusive. In our case, however, powder averaging is not very effective because of the small momentum available in the soft X-ray energy range, and the experiment might still be meaningful. With this in mind, we repeated the RIXS measurements for 2θ = 150°. The spectra are shown in Fig. 9(i)–(m), and the results of the fitting are summarized in the right panel of Fig. 9(n). Within the experimental uncertainties, we find that the energy of the magnetic excitations does not depend on |q|, so we conclude that they should be better thought of as local spin excitations rather than collective spin-waves. This result seems reasonable for a system with large configurational disorder, which prevents the magnetic excitations from propagating coherently over long distances.
We also identify magnetic excitations in Ni L3 edge RIXS spectra taken at the ST peak (see Fig. 10), in analogy with NiO.44–46 Their intensity is strong at low temperatures (Fig. 10(b)). As shown in Fig. 10(d)–(h), the RIXS spectra were fit to a resolution-limited Gaussian curve (black solid line) representing the quasi-elastic peak and two antisymmetrized Lorentzian curves (colored solid line with a shaded area) representing the single and double magnetic excitations.46Fig. 10(i) and Table 5 report the energy of the single spin excitation. In Fig. 10(c), we directly compare the Cu and Ni L3 edge RIXS spectra of 5HEO and observe that the energy of the single magnetic excitation measured at the Ni resonance is significantly lower than that measured at the Cu resonance. In our view, this can be explained as follows: configurational disorder prevents excitations from developing long-range coherence, while the chemical selectivity of RIXS probes only those localized at the resonant metal ions, each characterized by different magnetic interactions.
Based on the above considerations, we use a cluster composed of a central metal ion M coordinated to six (next-nearest neighboring) metal ions through 180° bonds and adopt an Ising-like Hamiltonian to model its magnetism and explain the dependence of spin excitation energy on the molar fraction of various elements, as probed by RIXS at various absorption edges. We introduce the spins of the central and of the surrounding metal ions, SM and Sj, respectively, and their magnetic (super-exchange) interactions JM,j. We neglect the magnetic coupling of the central metal ion to its twelve nearest neighbor metal ions through 90° bonds, as it is expected to be very weak;24 then, the energy cost associated with a ΔSM = 1 spin excitation of the central metal ion in the magnetically ordered phase is given by
 | (2) |
| ΔEM = 9χCoJM,Co + 6χNiJM,Ni + 3χCuJM,Cu | (3) |
Such a simple model captures two key features of our experimental observations: it explains the dependence of the spin excitation energy on (i) the chemical composition of various samples and (ii) the absorption edge used for RIXS measurements, which selects the central (resonant) metal ion. Specifically, the spin excitation energy in samples with a nonmagnetic ion removed, i.e., noMg and noZn, is larger than that in 5HEO by a factor 5/4 = 1.25, according to eqn (3), irrespective of the central (resonant) metal ion. Indeed, inspection of Table 5 shows that the ratios between the experimental values of the spin excitation energies for noMg (noZn) and 5HEO are 1.27 (1.19) and 1.20 (1.19) at the Cu and Ni edges, respectively. We pushed the analysis of the data using the model even further and used it to estimate the magnetic interactions between pairs of magnetic ions by fitting the calculated spin excitation energies to the values observed in our experiment. We simultaneously fit the results from Cu and Ni edge RIXS measurements as they are coupled through the magnetic interaction term JNi,Cu = JCu,Ni and obtain the values of magnetic interactions reported in Table 6. We note that the values of magnetic interactions are not necessarily consistent with the theoretical predictions24 but are compatible with available experimental estimates for related systems (e.g., La2CuO4 (ref. 51) and NiO45) with similar bond geometries. Discrepancies, instead, can possibly be attributed to different bond lengths, although we find a larger JNi,Ni magnetic coupling despite the larger Ni–O–Ni distance in 5HEO (4.23 Å) than in NiO (4.17 Å). Unfortunately, we did not find estimates of the magnetic interactions between other pairs of magnetic ions, for which RIXS or inelastic neutron scattering studies of oxides like La2Cu1−xCoxO4,52 La2Ni1−xCoxO4 (ref. 53) and La2Cu1−xNixO4 (ref. 54) would be particularly useful.
For the sake of completeness, we predict the spin excitation energies that could potentially be measured by means of Co L3 edge RIXS if one were capable of isolating the magnetic signal from the low-energy d–d excitations (e.g., by improving the energy resolution or analyzing the polarization of the scattered beam). All the magnetic interactions have been determined in this work, except for JCo,Co; using the literature value of 2.4 meV for CoO,56,57 we predict ΔECo ≈ 13.6 meV for 5HEO, 17.0 meV for noMg and noZn, 12.0 meV for noNi and 10.5 meV for noCu.
4 Conclusions
We conducted a thorough investigation of the structural, electronic, and magnetic properties of 5HEO and related compounds. We probed their long-range crystal structure by means of XRD and concluded that noCu is perfectly cubic, noNi and noMg are tetragonal, and noZn and noCo, while remaining cubic, show signs of considerable structural disorder. The short-range crystal structure has been probed using PDF, XANES and EXAFS on 5HEO, noCu and noMg, where the latter two have been chosen as references for cubic and tetragonal crystal structures, respectively. It turns out that noMg has the largest structural disorder, with Ni accommodating the distortion induced by Jahn–Teller active Cu2+ ions and the Co–O bond length being very little affected.Since all quaternary samples contain 25% of Cu2+, Cu content alone does not account for the emergence of tetragonal symmetry in noMg and noNi. To further assess the role of various chemical species, we employed RIXS. RIXS measurements at the Cu L3 edge revealed Jahn–Teller distortions at the Cu sites through the splitting of d–d excitations. Also, their broadening confirms a high degree of short-range disorder in noNi and noMg, suggesting that Ni2+ and Mg2+ mitigate positional disorder. Consistently, RIXS spectra at the Co and Ni L3 edges suggest that Cu2+ promotes positional disorder. In addition to that of Ni, we could here appreciate an effect on the electronic structure of Co, which was invisible to the analysis of EXAFS data.
Finally, we identified low-energy features in Cu and Ni L3 edge RIXS spectra, which we interpreted as local magnetic excitations. We estimated most of the magnetic interactions between pairs of magnetic Cu2+, Ni2+ and Co2+ ions, the most relevant ingredients for a comprehensive understanding of the magnetic properties of 5HEO. Our findings provide valuable insights into the influence of various chemical species on the formation and magnetic properties of 5HEO and related HEO systems.
Author contributions
M. F., M. C., P. G. and M. M. S. conceived the experiment. M. Z., M. F., M. C., G. M. and M. M. S. analyzed the data. M. F. and G. M. synthesized the samples. M. Z., M. F., G. M., D. I., N. B., L. G., K. K., F. R., M. A. and M. M. S. performed the experiments. M. F., M. C., G. G., P. G. and M. M. S. supervised the project. All authors contributed to the interpretation. M. Z. and M. M. S. wrote the manuscript with input from all authors.Conflicts of interest
There are no conflicts to declare.Data availability
RIXS data are available at https://doi.org/10.15151/ESRF-ES-1335198610. XRD, XANES, EXAFS and PDF data are available at https://doi.org/10.5281/zenodo.15784409.Supplementary information: all EXAFS fitting parameters (Tables I–XI) and detailed information extracted from PDF data analyses (Table XII). See DOI: https://doi.org/10.1039/d5ta05324b.
Acknowledgements
We acknowledge ESRF – The European Synchrotron for provision of synchrotron radiation facilities under proposal numbers HC-6743 and HC-5356, and we would like to thank the whole technical and scientific staff of ID32 for their excellent support. The work presented here was partly funded by the European Union – NextGenerationEU – “PNRR – M4C2, investimento 1.1 – Fondo PRIN 2022” – “Superlattices of relativistic oxides” (ID: 2022L28H97 and CUP D53D23002260006). The authors acknowledge the ESRF for provision of beamtime on ID15A (exp CH-5675) and thank Dr Stefano Checchia for support. They also acknowledge the Elettra synchrotron facility for provision of beamtime (beamline XAFS, experiment 20212199), thank Dr Luca Olivi for the kind support and the Diamond Light Source for the provision of in-house beamtime (beamline I20). M. F., M. C., G. M. and P. G. acknowledge support from the Ministero dell'Università e della Ricerca (MUR) and the University of Pavia through the program “Dipartimenti di Eccellenza 2023–2027”.Notes and references
- M. Fracchia, M. Coduri, P. Ghigna and U. Anselmi-Tamburini, J. Eur. Ceram. Soc., 2024, 44, 2 CrossRef.
- D. Bérardan, S. Franger, A. Meena and N. Dragoe, J. Mater. Chem. A, 2016, 4, 24 RSC.
- D. Bérardan, S. Franger, D. Dragoe, A. K. Meena and N. Dragoe, Phys. Status Solidi RRL, 2016, 10, 4 Search PubMed.
- A. Sarkar, L. Velasco, D. Wang, Q. Wang, G. Talasila, L. de Biasi, C. Kübel, T. Brezesinski, S. S. Bhattacharya and H. Hahn, et al. , Nat. Commun., 2018, 9, 1 CrossRef.
- N. Qiu, H. Chen, Z. Yang, S. Sun, Y. Wang and Y. Cui, J. Alloys Compd., 2019, 777, 767–774 CrossRef CAS.
- C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J.-P. Maria, Nat. Commun., 2015, 6, 1 CrossRef.
- J. Bularzik, P. Davies and A. Navrotsky, J. Am. Ceram. Soc., 1986, 69, 6 CrossRef.
- P. K. Davies and A. Navrotsky, J. Solid State Chem., 1981, 38, 2 CrossRef.
- M. Coduri, L. R. Magnaghi, M. Fracchia, R. Biesuz and U. Anselmi-Tamburini, Chem. Mater., 2024, 36, 2 CrossRef.
- M. Fracchia, M. Coduri, M. Manzoli, P. Ghigna and U. A. Tamburini, Nat. Commun., 2022, 13, 1 Search PubMed.
- M. Fracchia, M. Coduri, S. Bonati, C. Dejoie, P. Ghigna and U. Anselmi-Tamburini, J. Eur. Ceram. Soc., 2025, 45, 7 CrossRef.
- D. Berardan, A. Meena, S. Franger, C. Herrero and N. Dragoe, J. Alloys Compd., 2017, 704, 693–700 CrossRef CAS.
- C. M. Rost, Z. Rak, D. W. Brenner and J.-P. Maria, J. Am. Ceram. Soc., 2017, 100, 6 CrossRef.
- M. Fracchia, P. Ghigna, T. Pozzi, U. A. Tamburini, V. Colombo, L. Braglia and P. Torelli, J. Phys. Chem. Lett., 2020, 11, 9 CrossRef PubMed.
- J. Sushil, A. Kumar, A. Gautam and M. I. Ahmad, Mater. Chem. Phys., 2021, 259, 124014 CrossRef CAS.
- Z. Rak, C. Rost, M. Lim, P. Sarker, C. Toher, S. Curtarolo, J.-P. Maria and D. Brenner, J. Appl. Phys., 2016, 120, 095105 CrossRef.
- Z. Rák, J.-P. Maria and D. Brenner, Mater. Lett., 2018, 217, 300–303 CrossRef.
- G. Anand, A. P. Wynn, C. M. Handley and C. L. Freeman, Acta Mater., 2018, 146, 119–125 CrossRef CAS.
- J. Kaufman and K. Esfarjani, J. Mater. Res., 2021, 36, 1615–1623 CrossRef CAS.
- M. Coduri, M. Fracchia, S. Checchia, M. Manzoli, C. Dejoie, P. Ghigna and U. Anselmi-Tamburini, Small, 2025, 21, 5 CrossRef.
- J. Zhang, J. Yan, S. Calder, Q. Zheng, M. A. McGuire, D. L. Abernathy, Y. Ren, S. H. Lapidus, K. Page and H. Zheng, et al. , Chem. Mater., 2019, 31, 10 Search PubMed.
- W. Roth, Phys. Rev., 1958, 110, 6 CrossRef.
- M. P. Jimenez-Segura, T. Takayama, D. Bérardan, A. Hoser, M. Reehuis, H. Takagi and N. Dragoe, Appl. Phys. Lett., 2019, 114, 12 CrossRef.
- Z. Rák and D. Brenner, J. Appl. Phys., 2020, 127, 18 CrossRef.
- B. H. Toby and R. B. Von Dreele, Appl. Crystallogr., 2013, 46, 2 Search PubMed.
- T. Roisnel and J. Rodríquez-Carvajal, Mater. Sci. Forum, 2001, 378–381, 118–123 CAS.
- G. B. Vaughan, R. Baker, R. Barret, J. Bonnefoy, T. Buslaps, S. Checchia, D. Duran, F. Fihman, P. Got and J. Kieffer, et al. , Synchrotron Radiat., 2020, 27, 2 CrossRef PubMed.
- S. J. Billinge, Philos. Trans. R. Soc., A, 2019, 377, 20180413 CrossRef CAS.
- P. Juhás, T. Davis, C. L. Farrow and S. J. Billinge, Appl. Crystallogr., 2013, 46, 2 Search PubMed.
- M. Coduri, M. Brunelli, M. Scavini, M. Allieta, P. Masala, L. Capogna, H. E. Fischer and C. Ferrero, Z. Kristallogr. - Cryst. Mater., 2012, 227, 272–279 CrossRef CAS.
- M. Wojdyr, Appl. Crystallogr., 2010, 43, 1126–1128 CrossRef CAS.
- B. Ravel and M. Newville, Synchrotron Radiat., 2005, 12, 4 CrossRef.
- M. C. Feiters, R. W. Strange and N. Binsted, International Tables for Crystallography, International Union of Crystallography, Chester, England, 2020, pp. 744–751 Search PubMed.
- N. B. Brookes, F. Yakhou-Harris, K. Kummer, A. Fondacaro, J. Cezar, D. Betto, E. Velez-Fort, A. Amorese, G. Ghiringhelli, L. Braicovich, R. Barrett, G. Berruyer, F. Cianciosi, L. Eybert, P. Marion, P. van der Linden and L. Zhang, Nucl. Instrum. Methods Phys. Res., Sect. A, 2018, 903, 175–192 CrossRef CAS.
- D. Berardan, A. Meena, S. Franger, C. Herrero and N. Dragoe, J. Alloys Compd., 2017, 704, 693–700 CrossRef CAS.
- W. Mnasri, D. Bérardan, S. Tusseau-Nenez, T. Gacoin, I. Maurin and N. Dragoe, J. Mater. Chem. C, 2021, 9, 42 RSC.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767 CrossRef.
- M. M. Sala, V. Bisogni, C. Aruta, G. Balestrino, H. Berger, N. Brookes, G. De Luca, D. Di Castro, M. Grioni and M. Guarise, et al. , New J. Phys., 2011, 13, 4 Search PubMed.
- G. Ghiringhelli, N. B. Brookes, E. Annese, H. Berger, C. Dallera, M. Grioni, L. Perfetti, A. Tagliaferri and L. Braicovich, Phys. Rev. Lett., 2004, 92, 117406 CrossRef CAS.
- A. M. Oleś, K. Wohlfeld and G. Khaliullin, Condens. Matter, 2019, 4, 2 Search PubMed.
- F. Barantani, M. K. Tran, I. Madan, I. Kapon, N. Bachar, T. Asmara, E. Paris, Y. Tseng, W. Zhang and Y. Hu, et al. , Phys. Rev. X, 2022, 12, 2 Search PubMed.
- D. Ishikawa, M. W. Haverkort and A. Q. Baron, J. Phys. Soc. Jpn., 2017, 86, 9 Search PubMed.
- S. Huotari, L. Simonelli, C. J. Sahle, M. M. Sala, R. Verbeni and G. Monaco, J. Phys.: Condens. Matter, 2014, 26, 16 Search PubMed.
- G. Ghiringhelli, A. Piazzalunga, C. Dallera, T. Schmitt, V. N. Strocov, J. Schlappa, L. Patthey, X. Wang, H. Berger and M. Grioni, Phys. Rev. Lett., 2009, 102, 027401 CrossRef CAS PubMed.
- D. Betto, Y. Y. Peng, S. B. Porter, G. Berti, A. Calloni, G. Ghiringhelli and N. B. Brookes, Phys. Rev. B, 2017, 96, 020409 CrossRef.
- A. Nag, H. C. Robarts, F. Wenzel, J. Li, H. Elnaggar, R.-P. Wang, A. C. Walters, M. García-Fernández, F. M. F. de Groot, M. W. Haverkort and K.-J. Zhou, Phys. Rev. Lett., 2020, 124, 067202 CrossRef CAS.
- S. Shi and V. Staemmler, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 52, 12345–12354 CrossRef CAS.
- M. Magnuson, S. Butorin, J.-H. Guo and J. Nordgren, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 65, 20 CrossRef.
- K. Tomiyasu and S. Itoh, J. Phys. Soc. Jpn., 2006, 75, 8 CrossRef.
- L. Braicovich, J. van den Brink, V. Bisogni, M. M. Sala, L. J. P. Ament, N. B. Brookes, G. M. De Luca, M. Salluzzo, T. Schmitt, V. N. Strocov and G. Ghiringhelli, Phys. Rev. Lett., 2010, 104, 077002 CrossRef CAS.
- Y. Peng, G. Dellea, M. Minola, M. Conni, A. Amorese, D. Di Castro, G. De Luca, K. Kummer, M. Salluzzo and X. Sun, et al. , Nat. Phys., 2017, 13, 12 Search PubMed.
- C. S. Dash, S. Yuvaraj, R. Jothiramalingam, S. Iqbal, R. R. Isaac, A. A. Bahajjaj, M. Sundararajan, M. Sukumar and L. Rajadurai, Effect of Co 2+ substituted La 2 CuO 4 nanoparticles: Structural, morphological, optical and magnetic behaviour, 2024, PREPRINT (Version 1) available at Research Square, DOI:10.21203/rs.3.rs-4195720/v1.
- G. Amow, P. Whitfield, I. Davidson, R. Hammond, C. Munnings and S. Skinner, Ceram. Int., 2004, 30, 7 CrossRef.
- S. T. Ting, P. Pernambuco-Wise, J. E. Crow, E. Manousakis and J. Weaver, Phys. Rev. B:Condens. Matter Mater. Phys., 1992, 46, 11772–11778 CrossRef CAS PubMed.
- M. T. Hutchings and E. J. Samuelsen, Phys. Rev. B, 1972, 6, 3447–3461 CrossRef CAS.
- P. M. Sarte, R. A. Cowley, E. E. Rodriguez, E. Pachoud, D. Le, V. García-Sakai, J. W. Taylor, C. D. Frost, D. Prabhakaran, C. MacEwen, A. Kitada, A. J. Browne, M. Songvilay, Z. Yamani, W. J. L. Buyers, J. P. Attfield and C. Stock, Phys. Rev. B, 2018, 98, 024415 CrossRef CAS.
- P. M. Sarte, M. Songvilay, E. Pachoud, R. A. Ewings, C. D. Frost, D. Prabhakaran, K. H. Hong, A. J. Browne, Z. Yamani, J. P. Attfield, E. E. Rodriguez, S. D. Wilson and C. Stock, Phys. Rev. B, 2019, 100, 075143 CrossRef CAS.
Footnote |
| † Current address: Institut für Experimentalphysik, Freie Universität Berlin, Arnimallee 14, D-14195 Berlin-Dahlem, Germany. |
| This journal is © The Royal Society of Chemistry 2026 |













