Metal-ion mediated mesopore engineering in hierarchical porous carbons for enhanced high-rate volumetric capacitance
Jie
Du
a,
Xinkun
Zhao
b,
Xin
Chen
a,
Tianxiang
Sun
a,
Bona
Dai
c,
Jiaxin
Li
a,
Tangming
Mo
d,
Bo
Cui
*a,
Qinglei
Liu
 *a and
Di
Zhang
a
*a and
Di
Zhang
a
aThe State Key Lab of Metal Matrix Composites, School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, P. R. China. E-mail: liuqinglei@sjtu.edu.cn; cuibo13@sjtu.edu.cn
bChina Academy of Launch Vehicle Technology, Beijing 100076, China
cInstrumental Analysis Center, Shanghai Jiao Tong University, Shanghai 200240, P. R. China
dSchool of Mechanical Engineering, Guangxi University, Nanning 530004, P. R. China
First published on 7th November 2025
Abstract
Hierarchical porous carbons (HPCs) have emerged as promising materials for energy storage, due to their ability to simultaneously deliver high capacitance and fast ion transport kinetics. However, precisely tailoring mesoporous structures of HPCs, which are critical to balance material density and capacitive performance, remains a challenge. Herein, we present a scalable mesopore engineering strategy for renewable biopolymer alginate derived HPCs, enabling precise control over mesopore sizes and contents. Combining solid-state nuclear magnetic resonance, small-angle X-ray scattering, and nitrogen adsorption analyses, we unravel the “structural inheritance” mechanism of mesopore evolution from the crosslinked metal ion–alginate frameworks. The results reveal that the crosslinking degree, determined by metal ion size, governs the formation of small mesopores (ca. 5 nm) in the resulting metal–alginate derived porous carbons (metal–ADCs). Electrochemical characterization studies demonstrate that these 5 nm mesopores optimize the trade-off between material density and ion transport: Cu–ADC with 25% 5 nm mesopores achieves 33 F cm−3 at 500 mV s−1, outperforming other metal–ADCs by 20–70%. This work uncovers the structural evolution mechanism in alginate-derived HPCs and establishes a definitive structure–performance relationship, while the scalable mesopore engineering protocol provides a transformative roadmap for designing next-generation energy storage materials with optimized volumetric performance.
1. Introduction
Hierarchical porous carbons (HPCs) have gained significant attention in energy storage applications due to their unique pore structures. According to the IUPAC classification, pores are categorized into micropores (<2 nm), mesopores (2–50 nm) and macropores (>50 nm).1 Abundant micropores endow HPCs with a high specific surface area (SSA) and numerous ion storage sites, ensuring substantial energy storage capacity at low charge–discharge rates.2,3 In comparison, mesopores play a critical role in balancing volumetric capacitance and rate performance, as they facilitate rapid ion transport without compromising the material density like macropores do.4 Notably, our recent study has demonstrated that small mesopores (ca. 5 nm) promote ultrafast ion transport kinetics in different electrolytes through a prefilled and concerted ion transport mechanism.5 This insight underscores the importance of constructing porous carbon structures that integrate efficient ion storage with rapid ion transport, which is a pivotal research focus in the field.6However, precise regulation of mesopore parameters and engineering of highly interconnected hierarchical porous structures remain critical challenges. Currently, fabrication strategies for HPCs are primarily categorized into two approaches: template-assisted synthesis and direct synthesis.7,8 Template-derived carbons exhibit well-defined mesopores but are often plagued by poor pore connectivity, which impairs ion transport efficiency.9 Additionally, high fabrication costs limit their scalability for large-scale production.7,10 In contrast, direct synthesis using biomass or polymer precursors enables efficient carbonization, which inherits precursor structures and generates hierarchical pores for rapid ion transport. However, this approach struggles to achieve precise regulation of pore structures.6,11–14 Specifically, biomass-derived porous carbons typically exhibit hierarchical porous structures with broad pore size distributions and may even form macropores up to several micro-meters. This structural characteristic reduces material utilization and results in low-density carbons with compromised volumetric performance.11,15–17 Thus, a critical challenge lies in balancing material density with efficient ion transport pathways.18 Furthermore, existing methods lack the capability to fine-tuning hierarchical pore size distributions, thereby leaving a critical research gap in optimizing the mesopore size and content. Therefore, precisely regulating hierarchical pore structures and exploring how mesopore characteristics affect rate performance, particularly high-rate volumetric performance, hold substantial significance for the development of advanced supercapacitors.
Alginate, a natural polysaccharide extracted from brown algae, ranks as the second most abundant renewable biopolymer resource in marine environments and has demonstrated substantial application potential for the development of functional materials.19–21 Compared to cellulose, the widely used terrestrial renewable polymer alginate possesses a unique metal-ion crosslinking capability, which enables the fabrication of gels with tunable mechanical strength and thus holds irreplaceable value in fields such as the high-end food industry and biomedicine.22,23 Notably, this unique metal-ion crosslinking behaviour also offers a promising innovative avenue for the development of functional carbon materials.24,25
Our prior work demonstrated that alginate forms small, uniformly sized interconnected mesopores via phase separation during Ca2+ crosslinking,5,26 which mitigates the random pore formation typical of direct synthesis. Beyond Ca2+, alginate crosslinks with diverse metal ions, expanding opportunities to fabricate HPCs with tailored pore structures. However, the mechanisms by which metal ions influence mesopore formation, and how metal–alginate crosslinked structures evolve and are inherited by porous carbons, remain unclear. Thus, exploring how metal ions drive pore structure evolution is essential, as it guides rational synthesis and regulation of the hierarchical porous structure and provides possibilities for establishing a clear correlation between the pore structure and performance. This, in turn, provides critical insights for designing high-efficiency structures optimized for both volumetric and rate performance, thereby addressing a long-standing challenge in energy storage applications.
In this study, we report a metal-ion mediated mesopore pre-construction strategy leveraging alginate's differential crosslinking with various metal ions (Cu2+, Zn2+, Ca2+, Sr2+, Ba2+, and Sn2+) and investigate how mesopore parameters in hierarchical structures affect energy storage performance, particularly the volumetric capacitance. Using multiple characterization techniques (transmission electron microscopy (TEM), solid-state nuclear magnetic resonance (ss-NMR), small-angle X-ray scattering (SAXS), N2 adsorption, etc.), we systematically elucidate how the metal ion size dictates the cross-linking degree, which subsequently governs mesopore evolution. We found that mesopores are preserved from dried alginate gels to carbons via a “structural inheritance” mechanism. This strategy enables precise pre-control of mesopore structures in the precursor stage, mitigating random pore formation in direct synthesis. Synthesized metal–alginate derived porous carbons (metal–ADCs) with tailored mesopore sizes and tunable mesopore contents were employed to study how mesopore structures affect energy storage performance. Results show that small mesopores (5 nm) optimally balance the carbon density and ion transport, maximizing the gravimetric and volumetric capacitance and resolving the long-standing trade-off in energy storage materials. These findings reveal metal-ion mediated mesopore “structural inheritance” and establish a precursor-engineering strategy for designing high-performance HPCs with enhanced volumetric capacitance, promoting their practical application in next-generation energy storage.
2. Experimental section
2.1 Synthesis of metal–Alg and metal–ADCs
Sodium alginate (SA, Meryer, China, M29285) was dissolved in deionized (DI) water under continuous stirring for 24 h until fully dissolved, creating solutions with concentrations of 3 wt%. Separately, different metal chloride salts (CuCl2, ZnCl2, CaCl2, SrCl2, BaCl2 and SnCl2·2H2O) were dissolved in 500 mL of DI water and stirred for 30 min to prepare 0.15 mol L−1 solutions. Subsequently, the sodium alginate sol was added dropwise to the metal salt solutions. The mixtures were continuously stirred for 24 hours to complete the crosslinking reaction, forming metal–alginate (metal–Alg) beads.The gel beads were rinsed 3 times with deionized water to remove surface-adhered excess metal ions, followed by drying using two methods. For direct oven drying: the gel beads were placed in a clean Petri dish and oven-dried at 60 °C for 24 h to obtain oven-dried metal–Alg. For freeze drying: the cleaned gel beads were frozen in liquid nitrogen for 30 min, then transferred to a freeze dryer for freeze-drying over 72 h to obtain freeze-dried metal–Alg.
Metal–alginate-derived carbons (metal–ADCs) were synthesized via a two-step carbonization–activation process. Briefly, dried metal–Alg gels were first carbonized under a nitrogen atmosphere at 600 °C for 3 h. The resulting carbonized intermediates were then subjected to acid washing with 5 M HCl at 60 °C for 12 h, followed by thorough rinsing with deionized water until neutral pH was achieved. After drying, the intermediates were mixed with KOH solution at a carbon-to-KOH weight ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. The mixtures were evaporated to dryness, then heated at 750 °C for 1 h under nitrogen flow. The final products were washed extensively with 5 M HCl and DI water until neutral pH was achieved, then dried and denoted as X–ADC, where X represents the crosslinking metal ion species (Cu, Zn, Ca, Sr, Ba, or Sn).
4. The mixtures were evaporated to dryness, then heated at 750 °C for 1 h under nitrogen flow. The final products were washed extensively with 5 M HCl and DI water until neutral pH was achieved, then dried and denoted as X–ADC, where X represents the crosslinking metal ion species (Cu, Zn, Ca, Sr, Ba, or Sn).
2.2 Characterization of materials
X-ray diffraction (XRD) patterns were collected using a Rigaku Ultima IV powder diffractometer with Cu Kα radiation (λ = 1.5406 Å). Raman spectra were acquired on a Renishaw inVia reflex spectrometer with a 532 nm laser excitation source. Surface morphologies and microstructures were examined via scanning electron microscopy (SEM, RISE-MAGNA) and transmission electron microscopy (TEM, TALOS F200X). Thermogravimetric analysis (TGA) of metal–Alg precursors was performed using a Netzsch STA449 F3 thermal analyzer under an argon atmosphere (flow rate: 20 mL min−1). Metal elemental compositions were determined by inductively coupled plasma optical emission spectrometry (ICP-OES, Thermo Fisher iCAP7600). Fourier transform infrared (FTIR) spectra were recorded on a Thermo Fisher Nicolet 6700 spectrometer. Nitrogen adsorption isotherms were measured at −196 °C using an Autosorb-IQ3 adsorption analyzer, with specific surface areas calculated via the Brunauer–Emmett–Teller (BET) method and pore size distributions derived from density functional theory (QSDFT, slit/cylinder pores, equilibrium model). Small-angle X-ray scattering (SAXS) measurements were performed using a Xeuss 3.0 system (Xenocs) equipped with a GeniX3D Cu Ultra Low Divergence microfocus X-ray source (λ = 1.54 Å) and an Eiger2 R 1M detector (Dectris). Solid-state nuclear magnetic resonance (ss-NMR) experiments were conducted with a Bruker AVANCE NEO 600WB spectrometer operated at the frequency of 600.43 MHz for 1H and 150.99 MHz for 13C, using a MASDVT600W2 BL3.2X/Y/H probe. The spinning rate for the magic angle spinning (MAS) unit was set as 10 or 15 kHz. 1H MAS spectra were obtained by one pulse sequence. 1D 1H DQ filtered MAS and 2D 1H DQ/SQ experiments were conducted using the back-to-back (BABA) recoupling sequence for the excitation and reconversion of DQCs. For all the 13C CP TOSS spectra, a ramped 1H-pulse amplitude was applied during the contact time, tc = 2000 µs to circumvent spin modulation under Hartmann–Hahn conditions.2.3 Electrochemical measurements
The electrochemical performances were measured on a multi-channel electrochemical workstation (BioLogic VMP3) in two-electrode symmetric systems assembled as Swagelok cells. For the preparation of working electrodes, the activated carbon samples were mixed with carbon black and polytetrafluoroethylene (PTFE) at a mass ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. The freestanding electrode was pressed under a pressure of 10 MPa for 1 min, then punched into circular pieces with a diameter of 7 mm. All of the tested electrodes were around 150 µm. The mass loading of active materials was 3–5 mg cm−2. For the symmetric supercapacitors, two electrodes with identical size and active material mass were assembled with a matching separator; electrochemical tests were measured in 6 M aqueous KOH and 1 M TEABF4 (tetraethylammonium tetrafluoroborate) in ACN (acetonitrile).
10. The freestanding electrode was pressed under a pressure of 10 MPa for 1 min, then punched into circular pieces with a diameter of 7 mm. All of the tested electrodes were around 150 µm. The mass loading of active materials was 3–5 mg cm−2. For the symmetric supercapacitors, two electrodes with identical size and active material mass were assembled with a matching separator; electrochemical tests were measured in 6 M aqueous KOH and 1 M TEABF4 (tetraethylammonium tetrafluoroborate) in ACN (acetonitrile).
Cyclic voltammetry (CV) scans were carried out at scan rates ranging from 2 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mV s−1. Galvanostatic cycling was performed at current densities ranging from 0.1 to 100 A g−1, with the potential limits identical to those in the CV scans. Electrochemical impedance spectroscopy (EIS) was performed at various potentials relative to the reference electrodes with frequencies ranging from 100 kHz to 0.01 Hz with a sinusoidal voltage of 5 mV.
000 mV s−1. Galvanostatic cycling was performed at current densities ranging from 0.1 to 100 A g−1, with the potential limits identical to those in the CV scans. Electrochemical impedance spectroscopy (EIS) was performed at various potentials relative to the reference electrodes with frequencies ranging from 100 kHz to 0.01 Hz with a sinusoidal voltage of 5 mV.
The specific capacitance of the samples was calculated from the CV curves using the following integral formula:
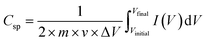 | (1) |
The energy density (E) and power density (P) were calculated using the following equations:
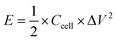 | (2) |
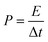 | (3) |
The kinetic parameter b was calculated according to the following equation:27–29
| i(v) = a × vb | (4) |
| i(V) = k1v + k2v1/2 | (5) |
The Warburg coefficient σ and ion diffusion coefficient D can be calculated using the following formulas30–32
| D = 1/2 × (RT/Aσn2F2C)2 | (6) |
| Zre = Rs + Rct + σω−1/2 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), C is the electrolyte concentration (mol mL−1), σ is the Warburg coefficient (Ω cm2 s−1/2), Zre is the real part of Nyquist plot, and ω is the angular frequency (rad s−1).
485 C mol−1), C is the electrolyte concentration (mol mL−1), σ is the Warburg coefficient (Ω cm2 s−1/2), Zre is the real part of Nyquist plot, and ω is the angular frequency (rad s−1).
3. Results and discussion
3.1 Impact of crosslinking degree on mesopores in metal–ADCs
In our preliminary investigations, synthesis process optimization was conducted on calcium-rich alginate-based seaweed (Undaria). It was found that the carbonization temperature, activation temperature, and activator (KOH) dosage could modify the pore structures of the resulting carbon materials to some extent but failed to enable effective regulation of mesopore sizes and contents (Fig. S1). It suggests that the mesopore formation is inherently linked to the crosslinked structural characteristics of precursors.26 Here, we standardized the preparation conditions as carbonization at 600 °C, activation at 750 °C, and a KOH to carbon ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
To elucidate the formation mechanism of hierarchical pore structures, samples synthesized from freeze-dried and oven-dried calcium alginate precursors were systematically compared. Microstructural evolution and pore structure transformation of acid-washing and activated products were characterized using scanning electron microscopy (SEM) and nitrogen adsorption analysis (Fig. S2). Pore size distribution profiles reveal that the acid-washed freeze-dried samples retained abundant mesopores, indicating that mesopores are pre-formed within the calcium–alginate crosslinked precursor. However, the loose architecture of freeze-dried precursors induced mesopore collapse during activation, which induced further etching of the activator to carbon walls,33 resulting in micropore-dominant carbons (Fig. S2c). In contrast, oven-dried precursors maintained a compact structure after carbonization, enabling the formation of high-surface-area micropores while preserving interconnected mesopores after activation (Fig. S2f and Table S1). These results underscore the pivotal role of the metal–alginate crosslinking structure in hierarchical meso-/microporous structure production.
A series of metal–alginate (metal–Alg) gels with different crosslinking degrees were synthesized (Fig. 1a) by reacting with various metal ions (Cu2+, Zn2+, Ca2+, Sr2+, Ba2+, and Sn2+), followed by carbonization activation to prepare HPCs (Fig. S3). These metal ions were selected as they are all divalent, exhibit identical crosslinking modes with alginate, and do not exert any obvious catalytic graphitization effect on the final carbon materials—thus ensuring the similarity in the chemical structures of the resulting carbons. The oven-dried metal–Alg gels exhibit distinct weight-loss profiles in their thermogravimetric analysis (TGA) curves (Fig. 1b), indicating significant variations in crosslinking degrees. Inductively coupled plasma (ICP) analysis was used to quantify metal ion loadings in the gels, enabling the calculation of metal-to-alginate molar ratios (Fig. 1c). Notably, the highest molar ratio was obtained for Cu2+ ions, suggesting a stronger crosslinking ability with alginate chains. Fourier transform infrared (FTIR) spectroscopy was used to characterize the functional group vibrations in the metal–Alg gels (Fig. 1d). Symmetric/asymmetric stretching of –COO– at 1410/1590 cm−1 confirms metal-carboxyl coordination between metal ions and carboxyl groups.34 Based on peak intensities, the order of crosslinking degree was Cu2+ > Zn2+ > Ca2+ ≈ Sr2+ > Ba2+ > Sn2+. Additionally, O–H stretching vibrations at 3200–3600 cm−1, associated with hydrogen bonding in the gels, also show intensity variations consistent with the crosslinking degree trend.35
Using the metal–Alg gels with different crosslinking degrees as precursors, we synthesized a series of metal–ADCs featuring varied total mesopore volumes and 5 nm mesopore contents. Nitrogen adsorption analysis (Fig. S4 and 1e) reveals a direct proportionality between 5 nm mesopore content and the crosslinking degree. Specifically, the 5 nm mesopore content in Cu–ADC reaches 25% (Table S2) due to their superior crosslinking capability. Transmission electron microscopy (TEM) and High-Angle Annular Dark-Field Scanning Transmission Electron Microscopy (HAADF-STEM) were used to characterize the pore structures of metal–ADCs (Fig. 1f, g, S5 and S6). The HAADF-STEM mode provided an extended depth of field, thereby facilitating clearer visualization of the three-dimensional structure of the samples. Comparison of STEM-BF and STEM-HAADF images jointly verified the presence of uniformly distributed, interconnected ∼5 nm mesopores in Cu–ADC (Fig. 1f). In contrast, Sn–ADC exhibited a denser carbon matrix morphology (Fig. 1g).
In comparison, both Ca–ADC and Sr–ADC, besides containing dispersed 5 nm mesopores, also possess some larger mesopores in the 10–20 nm range (Fig. S6). These observations confirm the differences in pore structures as measured by nitrogen adsorption. And XRD and Raman spectroscopy results (Fig. S7) confirm that the metal–ADCs derived from these metal–alginates exhibit comparable graphitization degrees and highly similar chemical structures. These features render them ideal comparative samples for studying pore structure–property relationships in energy storage.
To gain deeper insights into the molecular architecture of metal–Alg gels, solid-state nuclear magnetic resonance (ss-NMR) spectroscopy was utilized to characterize 1H and 13C signals. Owing to the paramagnetic interference induced by Cu2+, the Cu–Alg could not be characterized by NMR. We herein characterized Zn–, Ca–, Sr–, Ba–, and Sn–Alg gels, with Na–Alg, the pristine water-soluble alginate polymer, as the reference sample. As shown in Fig. 2a, the narrow 1H peak can be ascribed to the mobile water molecules, whereas the broad baseline signal stems from water bound to rigid polymer chains.36 A broader peak reflects increased system heterogeneity, indicating restricted proton mobility—a direct consequence of heightened crosslinking degree or structural disorder.37,38 The 1H spectrum of Zn–Alg exhibits the widest baseline (∼26 ppm), confirming its robust crosslinking, while Sn– and Na–Alg display narrower peaks, denoting weaker network formation and greater chain mobility. The observed ion crosslinking strength follows the order of Zn2+ > Ca2+ ≈ Sr2+ > Ba2+ > Sn2+ > Na+, which is consistent with the ion–alginate affinity sequences reported in earlier studies.39–42 This trend also aligns with ionic radius patterns: smaller, higher-charge cations exhibit stronger carboxyl coordination ability, a behavior consistent with hard–soft acid–base theory described in previous literature.36,43–45 Although Cu2+ could not be characterized by NMR, its smaller ionic radius (72 pm vs. 74 pm for Zn2+) and observed higher crosslinking degree also align well with this trend.
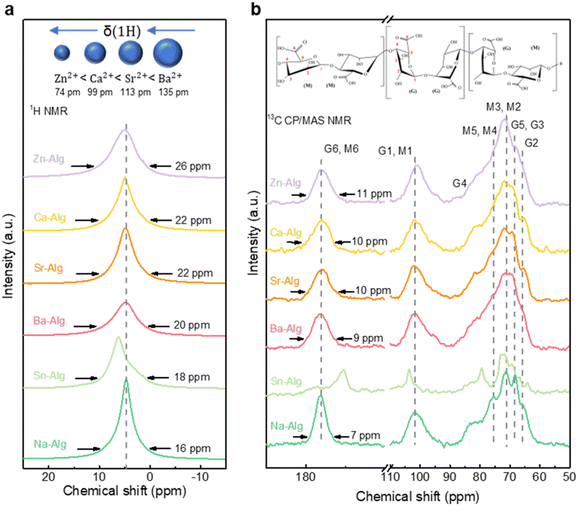 | ||
| Fig. 2 1H MAS (a) and 13C CP TOSS (b) ss-NMR spectra of the metal–Alg gels. The spectra at the bottom represent the reference Na–Alg sample, serving as a comparison for the metal–Alg spectra. | ||
The line shapes and resonance frequencies of 13C spectra directly reveal the carbon element's positions on the MG chains, enabling the investigation on structural changes in the crosslinked metal–Alg gels.36,46 The signal at 170–180 ppm corresponds to carboxyl carbons (G6 and M6), where metal ions coordinate with carboxylic groups within the crosslinked alginate network. The coordination strength influences the characteristic shifts and broadening of 13C peaks in this region (Fig. 2b). Similar to its 1H spectral width variation, Zn–Alg exhibits the broadest carboxyl carbon signals, reflecting stronger and more diverse COO−–Zn2+ coordination. Conversely, Ca–, Sr–, Ba–, and Na–Alg display narrower peaks with minimal shifts, indicating weaker coordination, consistent with the 1H and FTIR spectral results. Notably, the 13C peaks of Sn–Alg deviate significantly from other metal–Alg samples, suggesting a distinct crosslinking mode beyond just coordination degree. This uniqueness explains the different pore size distribution of Sn–ADC compared to other metal–ADC materials.
The 1H DQ filtered NMR is a homonuclear correlation technique that enables the observation of dipolar couplings between protons in solid-state systems.47–49 To explore the molecular chain structures and the spatial relationships between different protons within gel networks, both one-dimensional (Fig. S8) and two-dimensional (Fig. S9) 1H DQ filtered experiments were performed. In the 1D 1H DQ filtered spectrum of Sn–Alg, three distinct chemical shift regions emerged at approximately 2–4 ppm, 4–6 ppm, and 6–9 ppm. The signals in the 2–4 ppm range originated from non-crosslinked alginate backbone protons, while those in the 4–6 ppm region corresponded to backbone protons near metal ions. Signals at 6–9 ppm were attributed to highly acidic protons, including those from carboxylic acid (–COOH) groups and residual H2O species.36,50,51 This spectral pattern indicated a lower crosslinking degree in Sn–Alg and a looser local molecular network structures. Conversely, the spectra of alginate crosslinked with Zn2+, Ca2+, Sr2+ and Ba2+ ions were dominated by signals in the 4–6 ppm range, which corresponded to C–H protons adjacent to metal coordination sites. These characteristics suggested stronger crosslinking interactions, leading to more rigid and compact network structures.
The 2D 1H DQ/SQ correlation spectra further provide valuable spatial information through the identification of both diagonal (autocorrelation) and off-diagonal (cross-correlation) peaks (Fig. S9).47 In Sn–Alg, strong autocorrelation signals in the 6–9 ppm region indicate local aggregation or clustering of acidic protons. Conversely, other metal–alginate gels show significant cross-peaks between 2–4 ppm and 4–6 ppm regions, implying that protons from non-crosslinked and crosslinked segments are in close spatial proximity, which reflects the compactness of the crosslinked network. Comparison of the overall 2D 1H DQ/SQ spectral patterns reveals that Zn–Alg, in particular, exhibits a more complex and rigid spatial structure, further supporting its higher degree of crosslinking and structural integrity.
3.2 Formation mechanism of the hierarchical porous structure in metal–ADCs
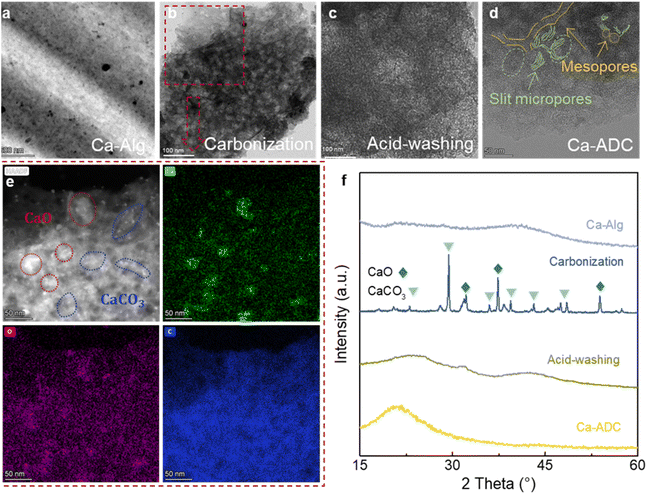
Focusing on calcium–alginate crosslinking, we systematically investigated the evolution of material compositions and pore structures during the synthesis of HPCs. Ca–Alg was selected as a representative sample because Ca–ADC exhibits a complex and broad pore structure distribution, encompassing abundant micropores, 5 nm mesopores, and a distinct population of larger mesopores, making it more representative. Using TEM and X-ray Diffraction (XRD), we studied the composition transformations across different key stages: the as-synthesized Ca–Alg gel, intermediates after carbonization and acid-washing, and the final activated Ca–ADC. As illustrated in Fig. 3a, the crosslinked Ca–Alg initially generates a spatial network-like structure. During carbonization, the organic matrix converts to amorphous carbon, while Ca2+ reacts with residual oxygen functionalities to form CaO and CaCO3 nanoparticles (Fig. 3b and e), as recognized from the XRD pattern (Fig. 3f). Acid-washing removes these inorganic phases, generating carbon voids (Fig. 3c). After activation, Ca–ADC exhibits a typical XRD pattern of activated carbon, with an obvious peak at around 22° (corresponding to the (002) plane of graphite, Fig. 3f), as well as a highly interconnected mesopore–micropore hierarchical porous structure (Fig. 3d and S6). From the TEM and HAADF images, interconnected mesoporous channels and slit-like micropores formed by KOH activation33 are observed.N2 adsorption analysis of other metal–alginate gels (Fig. S10) also confirms the universal presence of ∼5 nm mesopores. Similarly, metal species in other metal–Alg precursors transform into corresponding metal/metal oxides/metal carbonates during pyrolysis (Fig. S11 and S12). However, these intermediates typically form particles larger than 5 nm (even reach 50 nm in the Sr sample) that do not correspond to the interconnected mesopore channels. This spatial discrepancy conclusively demonstrates that 5 nm mesopores originate from the inheritance of a metal–alginate crosslinked framework rather than the removal of inorganic intermediates.
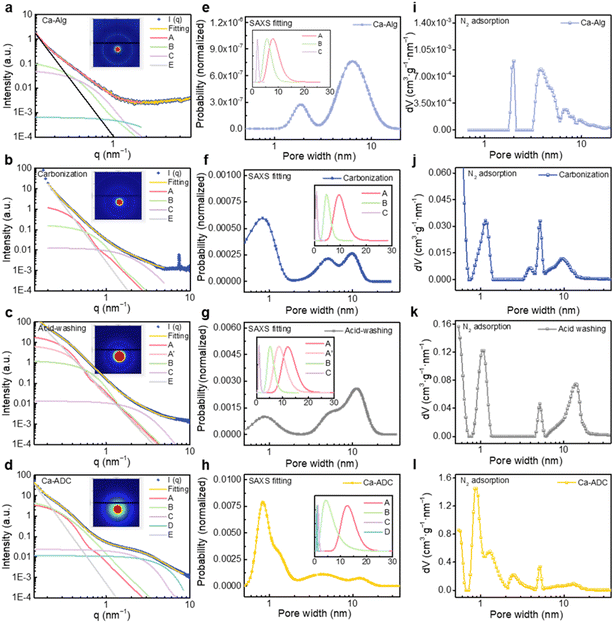
Small-angle X-ray scattering (SAXS) was utilized to characterize pore structures by probing scattering signals from electron density fluctuations, enabling fine-scale analysis of pore structures.52–56 The SAXS profiles of four key samples during Ca–ADC synthesis were measured, and the stepwise evolution of meso- and micropores was analyzed in conjunction with N2 adsorption analysis (Fig. 4 and S13). Peak deconvolutions of SAXS spectra (Fig. 4a) reveal the presence of 5–10 nm mesopores within the Ca–Alg matrix (Fig. 4e), consistent with the TEM-observed network-like morphology. These mesopore features were progressively retained in carbonized and acid-washed intermediates (Fig. 4f and g). While the subsequent activation process preserved preexisting mesopores and generated abundant micropores, yielding the final hierarchical porous structure in Ca–ADC (Fig. 4h).
Pore size distributions derived from SAXS deconvolutions (Fig. 4e–h) show remarkable consistency with N2 adsorption results (Fig. 4i–l), validating the reliability of SAXS-based pore structure analysis. These findings confirm the “structural inheritance” of mesopores, which originate from the crosslinked spatial framework of the precursor and are substantially retained in Ca–ADC. Thus, we conclude that the evolution of the pore structure proceeds as shown in Fig. S14: following crosslinking of alginate with metal ions, the molecular chains self-assemble and aggregate into network-like organic frameworks with three-dimensionally interconnected pores; upon carbonization, the polymer chains are converted into a carbon matrix, and these three-dimensional channels persist as mesopores in the resulting porous carbons. This finding further validates the rationality of the strategy to tune the mesoporous structure by manipulating the metal–alginate crosslinking. By integrating the carbonization-activation process with mesopore pre-engineering using metal–alginate gels, porous carbons with distinct pore structure parameters and highly interconnected hierarchical pores can be rationally designed and fabricated.
3.3 Impact of mesopores on energy storage performance
Finally, based on the resulting HPCs with distinct total mesopore volume and 5 nm mesopore contents, we investigated the impact of mesopore content on the gravimetric and volumetric energy storage performance. The electrochemical properties of metal–ADC samples were tested in symmetric supercapacitors using aqueous (6 M KOH, Fig. S15) and organic electrolytes (1 M TEABF4 in ACN) (Fig. 5 and S16). The supercapacitors all exhibit nearly rectangular cyclic voltammetry (CV) curves and symmetric galvanostatic charge–discharge (GCD) curves, demonstrating ideal electric double-layer (EDL) energy storage characteristics (Fig. 5a, S15a, b and S16a).57,58 From the electrochemical impedance spectroscopy (EIS) curves, it can be seen that the Sn–ADC sample with the least mesopore content has a significantly larger Warburg impedance (Zw). In the organic electrolyte, the Zw of Sn–ADC reaches approximately 7 Ω, whereas those of other samples are only 2–3 Ω (Fig. 5b), indicating more pronounced hindrance to the ion transport within the electrode.57,59,60 This sample also exhibits a slower ion response speed: as shown in Bode curves, its relaxation time constant τ0 is 6.5 s, which is far greater than those of other samples (Fig. 5c). Considering that the ion response speed is mainly related to the transport channels, this disparity can be ascribed to the least mesopore content in Sn–ADC.The effect of mesoporous structure on the samples' kinetic behaviours was further investigated.30,61 We calculated the kinetic parameter b and ion diffusion coefficient D of metal–ADCs in the organic electrolyte (Fig. S17 and Table S3). The results show that the b values of metal–ADCs range from 0.819 to 0.977, indicating capacitive behaviour that is closer to surface-controlled kinetics. The b values exhibit a positive correlation with the content of 5 nm mesopores. The diffusion coefficient of Cu–ADC attains 2.6 × 10−11 m2 s−1, which is 7.2 times higher than that of samples with non-optimized mesopore configurations (e.g., Sn–ADC: 3.6 × 10−12 m2 s−1). The ion diffusion coefficient also demonstrates a strong positive correlation with the content of 5 nm mesopores. Such an enhancement in ion diffusion can be primarily attributed to the well-engineered mesoporous network of metal–ADCs: a higher content of 5 nm mesopores facilitates the formation of continuous ion transport channels and shortens the ion diffusion path length.
To elucidate the unique role of 5 nm mesopores in high-speed ion transport, we conducted a comparative rate performance analysis across different samples (Fig. 5d–h and S15d, e). In 1 M TEABF4, all metal–ADCs, with similar SSAs, exhibited comparable gravimetric capacitances (150–170 F g−1) at low charge–discharge rates (Fig. 5d). Notably, at 500 mV s−1, the gravimetric capacitance positively correlated with the total mesopore content. Among them, Ca–ADC, which had the highest total mesopore content, showed the highest value (Fig. 5g).
Regarding volumetric performance, Sn–ADC demonstrated the highest capacitance at low scan rates due to its high material density (Fig. 5f). However, its volumetric capacitance sharply declined with increasing scan rates, primarily due to its sluggish ion transport kinetics (Fig. 5e). At 500 mV s−1, both Ca–ADC and Sr–ADC exhibited reduced volumetric capacitances (Fig. 5h). This decrease was attributed to the presence of additional 10–50 nm mesopores, which compromised material density (Fig. 5f). Significantly, the volumetric capacitances of metal–ADCs at 500 mV s−1 were strongly correlated with the 5 nm mesopore content, following the order: Cu > Zn > Ba > Sr > Ca > Sn. Ca–ADC, although containing 9.4% 5 nm mesopores, still showed poor volumetric performance, indicating that the density loss induced by larger mesopores overshadowed the benefits of enhanced ion transport. In contrast, Cu–ADC, featuring 25% 5 nm mesopores, achieved an optimal balance between high gravimetric capacitance (105 F g−1) and favorable volumetric performance (33 F cm−3) by minimizing density loss via the utilization of smaller mesopores. Compared with representative carbons with high volumetric performance reported in the literature, Cu–ADC still retained an impressive 90% capacitance under high-rate charge–discharge conditions (10 A g−1), demonstrating remarkable advantages (Fig. S18). These results confirm that 5 nm mesopores not only facilitate rapid ion transport but also maintain high material density, thereby optimizing the overall electrochemical performance.
Compared with state-of-the-art porous carbons, both Cu–ADC (highest 5 nm content)- and Ca–ADC (highest mesopore content)-based supercapacitors exhibit comparable gravimetric energies and power densities (Fig. S19 and Table S4). Notably, they maintain high energy densities at elevated power densities, underscoring the inherent advantages of hierarchical pore structures in energy storage systems. However, the Cu–ADC achieves 2–2.7 times higher volumetric energy density than Ca–ADC (Fig. 5i), a disparity that can be directly attributed to their different 5 nm mesopore contents: the Cu–ADC's 25% 5 nm mesopores enable optimal density retention (0.32 g cm−3) and ion accessibility, whereas the Ca–ADC's larger mesopores (10–20 nm) compromise the density (0.19 g cm−3) despite its higher total mesopore content. This stark performance contrast confirms 5 nm as the optimal mesopore size for balancing the volumetric performance and ion transport kinetics. The unique advantage of 5 nm mesopores lies in their ability to act as efficient “ion highways” while minimizing density loss, a design paradigm that outperforms both purely high-surface-area carbons and dense materials with inadequate transport pathways.
Stability is also of great importance for the practical applications of electrode materials. The cycling performances of Cu–ADC- and Ca–ADC-based supercapacitors at a current density of 10 A g−1 in 6 M KOH (aqueous electrolyte) and 1 M TEABF4 (organic electrolyte) are depicted in Fig. S20. Cu–ADC retains 95.6% of its initial capacitance after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 consecutive charge–discharge cycles in 6 M KOH, while Ca–ADC maintains 94.0% of its initial capacitance. Even in the organic electrolyte, Cu–ADC and Ca–ADC still retain 94.9% and 94.0% of their initial capacitances, respectively, alongside the excellent coulombic efficiency. These results demonstrate the exceptional cycling stability of metal–ADC-based supercapacitors, thus validating the potential for practical application of hierarchical porous carbons as high-performance electrode materials in supercapacitor devices.
000 consecutive charge–discharge cycles in 6 M KOH, while Ca–ADC maintains 94.0% of its initial capacitance. Even in the organic electrolyte, Cu–ADC and Ca–ADC still retain 94.9% and 94.0% of their initial capacitances, respectively, alongside the excellent coulombic efficiency. These results demonstrate the exceptional cycling stability of metal–ADC-based supercapacitors, thus validating the potential for practical application of hierarchical porous carbons as high-performance electrode materials in supercapacitor devices.
4. Conclusions
In summary, we have developed a scalable mesopore engineering strategy by leveraging metal–alginate crosslinking and the mesopore “structural inheritance” mechanism, effectively addressing the long-standing trade-off between material density and ion transport efficiency in HPC design. Unlike conventional template-assisted synthesis or direct biomass carbonization, our approach utilizes the inherent mesopore structures dictated by coordination between metal ions and biopolymer alginate. This strategy enables both structural controllability and scalability through renewable precursors while eliminating the need for expensive templates and avoiding random pore formation. The results demonstrate the superior efficacy of 5 nm mesopores in balancing material density and ion transport efficiency. This size enables low-resistance ion transport paths while avoiding excessive voids that compromise the material density, ultimately boosting the high-rate volumetric energy/power densities of metal–ADC-based supercapacitors.Beyond this specific system, our findings offer two broader contributions: (1) we identify the “structural inheritance” mechanism for mesopores in biopolymer-derived carbons—crosslinked gel frameworks serve as “mesopore templates” retained during carbonization/activation—providing new insights into regulating pore formation in the direct synthesis of HPCs. (2) The metal ion coordination-driven pre-engineering framework is generalizable: it can be extended to other polymers with abundant carboxyl groups for metal-ion coordination like alginate, such as biopolymers (e.g., pectin, carboxymethyl cellulose, etc.) and even synthetic polymers with metal-coordinating groups. This provides a universal route for mesopore tailoring in diverse materials, laying a foundation for developing next-generation energy storage materials.
Author contributions
Jie Du: writing – review & editing, writing – original draft, methodology, investigation, data curation, conceptualization. Xinkun Zhao: writing – review & editing, visualization, methodology, data curation. Xin Chen: writing – review & editing, methodology, investigation, data curation. Tianxiang Sun: writing – review & editing, methodology, investigation, data curation. Bona Dai: writing – review & editing, methodology, investigation, data curation. Jiaxin Li: methodology. Tangming Mo: writing – review & editing, resources. Bo Cui: writing – review & editing, investigation. Qinglei Liu: writing – review & editing, resources. Di Zhang: resources, supervision.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: mesopore formation in seaweed derived carbon (SDC), preparation and characterization of metal–ADCs, structural evolution of metal–ADCs during synthesis and electrochemical capacitive performance. See DOI: https://doi.org/10.1039/d5ta07090b.Acknowledgements
This work was supported by The National Natural Science Foundation of China (Nos. 52572245 and 52571250), the Fundamental Research Funds for the Central Universities, and Shanghai Jiao Tong University 2030 Initiative.Notes and references
- H. Shao, Y. C. Wu, Z. Lin, P. L. Taberna and P. Simon, Chem. Soc. Rev., 2020, 49, 3005–3039 RSC.
- X. Liu, D. Lyu, C. Merlet, M. J. Leesmith, X. Hua, Z. Xu, C. P. Grey and A. C. J. S. Forse, Science, 2024, 384, 321–325 CrossRef CAS PubMed.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760–1763 CrossRef CAS.
- L. Wu, Y. Li, Z. Fu and B. L. Su, Natl. Sci. Rev., 2020, 7, 1667–1701 CrossRef CAS PubMed.
- J. Du, T. Mo, Y. Li, Y. Fang, X. Chen, J. Li, C. Liang, H. He, L. Zeng, B. Cui, M. Yu, G. Feng, X. Feng, D. Zhang and Q. Liu, ACS Nano, 2025, 19, 22217–22227 CrossRef CAS PubMed.
- H. Sun, J. Zhu, D. Baumann, L. Peng, Y. Xu, I. Shakir, Y. Huang and X. Duan, Nat. Rev. Mater., 2018, 4, 45–60 CrossRef.
- M. R. Benzigar, S. N. Talapaneni, S. Joseph, K. Ramadass, G. Singh, J. Scaranto, U. Ravon, K. Al-Bahily and A. Vinu, Chem. Soc. Rev., 2018, 47, 2680–2721 RSC.
- J. Liu, T. Yang, D.-W. Wang, G. Q. Lu, D. Zhao and S. Z. Qiao, Nat. Commun., 2013, 4, 3798 Search PubMed.
- Y. Zhu, L. Chen, J. Pan, S. Jiang, J. Wang, G. Zhang and K. Zhang, Prog. Mater. Sci., 2025, 148, 101373 CrossRef CAS.
- A. Hayat, M. Sohail, A. Y. A. Alzahrani, H. Ali, A. M. Abu-Dief, M. S. Amin, A. M. Alenad, S. R. Al-Mhyawi, Y. Al-Hadeethi, Z. Ajmal, S.-R. Guo and Y. Orooji, Prog. Mater. Sci., 2025, 150, 101408 CrossRef CAS.
- L. Sun, Y. Gong, D. Li and C. Pan, Green Chem., 2022, 24, 3864–3894 RSC.
- N. S. George, G. Singh, R. Bahadur, P. Kumar, K. Ramadass, C. I. Sathish, M. Benzigar, D. Sajan, A. Aravind and A. Vinu, Adv. Sci., 2024, 11, 2406235 CrossRef CAS.
- J. Li, J. Kossmann, K. Zeng, K. Zhang, B. Wang, C. Weinberger, M. Antonietti, M. Odziomek and N. Lopez-Salas, Angew Chem. Int. Ed. Engl., 2023, 62, e202217808 CrossRef CAS.
- L. Guan, H. Hu, L. Q. Li, Y. Y. Pan, Y. F. Zhu, L. Li, H. L. Guo, K. Wang, Y. C. Huang, M. D. Zhang, Y. C. Yan, Z. T. Li, X. L. Teng, J. W. Yang, J. Z. Xiao, Y. L. Zhang, X. S. Wang and M. B. Wu, ACS Nano, 2020, 14, 6222–6231 CrossRef CAS.
- W. Y. Zhang, S. Wei, Y. N. Wu, Y. L. Wang, M. Zhang, D. Roy, H. Wang, J. Y. Yuan and Q. Zhao, ACS Nano, 2019, 13, 10261–10271 CrossRef CAS PubMed.
- Y. P. Cui, W. Liu, X. Wang, J. J. Li, Y. Zhang, Y. X. Du, S. Liu, H. L. Wang, W. T. Feng and M. Chen, ACS Nano, 2019, 13, 11582–11592 CrossRef CAS.
- Y. Sun, X. L. Shi, Y. L. Yang, G. Suo, L. Zhang, S. Lu and Z. G. Chen, Adv. Funct. Mater., 2022, 32, 2201584 CrossRef CAS.
- J. Yu, C. Yu, W. Guo, Z. Wang, S. Li, J. Chang, X. Tan, Y. Ding, M. Zhang, L. Yang, Y. Xie, R. Fu and J. Qiu, Nano Energy, 2019, 64, 103921 CrossRef CAS.
- D. Halaswamy, S. Borehalli Mayegowda, H. Brijesh and M. Bheemappa, in Marine Biopolymers, 2025, pp. 989–1007, DOI:10.1016/b978-0-443-15606-9.00033-4.
- Alginate Market Size, Share & Trends Analysis Report By Type (High M, High G), By Product (Sodium, Propylene Glycol), By Application (Pharmaceutical, Industrial), By Region, And Segment Forecasts, 2021–2028, 2021, p. 154.
- M. M. Rahman, M. A. Shahid, M. T. Hossain, M. S. Sheikh, M. S. Rahman, N. Uddin, A. Rahim, R. A. Khan and I. Hossain, Discover Appl. Sci., 2024, 6, 443 CrossRef CAS.
- P. Tordi, F. Ridi, P. Samorì and M. Bonini, Adv. Funct. Mater., 2024, 35, 2416390 CrossRef.
- X. Guo, Y. Wang, Y. Qin, P. Shen and Q. Peng, Int. J. Biol. Macromol., 2020, 162, 618–628 CrossRef CAS PubMed.
- D. Kang, Q. Liu, M. Chen, J. Gu and D. Zhang, ACS Nano, 2016, 10, 889–898 CrossRef CAS PubMed.
- B. Liu, R. Feng, M. Busch, S. Wang, H. Wu, P. Liu, J. Gu, A. Bahadoran, D. Matsumura, T. Tsuji, D. Zhang, F. Song and Q. Liu, ACS Nano, 2022, 16, 14121–14133 CrossRef CAS PubMed.
- D. Kang, Q. Liu, J. Gu, Y. Su, W. Zhang and D. Zhang, ACS Nano, 2015, 9, 11225–11233 CrossRef CAS.
- B. E. Conway, E. Gileadi and H. Angerstein-Kozlowska, J. Electrochem. Soc., 1965, 112, 341–349 CrossRef CAS.
- J. Wang, J. Polleux, J. Lim and B. Dunn, J. Phys. Chem. C, 2007, 111, 14925–14931 CrossRef CAS.
- D. Chao, C. Zhu, P. Yang, X. Xia, J. Liu, J. Wang, X. Fan, S. V. Savilov, J. Lin, H. J. Fan and Z. X. Shen, Nat. Commun., 2016, 7, 12122 CrossRef CAS.
- X. Wu, C. Zhong, L. Y. Zhang, J. Lu, Q. He, Q. Zhang, W. Yuan and C. M. Li, J. Mater. Chem. A, 2025, 13, 25082–25092 RSC.
- X. L. Wu, Y. G. Guo, J. Su, J. W. Xiong, Y. L. Zhang and L. J. Wan, Adv. Energy Mater., 2013, 3, 1155–1160 CrossRef CAS.
- Y. Song, T. Liu, M. Li, B. Yao, T. Kou, D. Feng, F. Wang, Y. Tong, X. X. Liu and Y. Li, Adv. Energy Mater., 2018, 8, 1801784 CrossRef.
- J. Romanos, M. Beckner, T. Rash, L. Firlej, B. Kuchta, P. Yu, G. Suppes, C. Wexler and P. Pfeifer, Nanotechnology, 2012, 23, 015401 CrossRef CAS PubMed.
- C. Zhijiang, Z. Cong, X. Ping, G. Jie and Z. Kongyin, J. Mater. Sci., 2018, 53, 14801–14820 CrossRef CAS.
- A. C. K. Bierhalz, M. A. da Silva, M. E. M. Braga, H. J. C. Sousa and T. G. Kieckbusch, LWT--Food Sci. Technol., 2014, 57, 494–501 CrossRef CAS.
- J. Brus, M. Urbanova, J. Czernek, M. Pavelkova, K. Kubova, J. Vyslouzil, S. Abbrent, R. Konefal, J. Horsky, D. Vetchy, J. Vyslouzil and P. Kulich, Biomacromolecules, 2017, 18, 2478–2488 CrossRef CAS.
- M. El Hariri El Nokab, A. Lasorsa, K. O. Sebakhy, F. Picchioni and P. C. A. van der Wel, Food Hydrocolloids, 2022, 127, 107500 CrossRef CAS.
- A. A. Forysenkova, V. A. Ivanova, I. V. Fadeeva, G. V. Mamin and J. V. Rau, Materials, 2023, 16, 2832 CrossRef CAS PubMed.
- G. Seely and R. J. M. Hart, Macromolecules, 1974, 7, 706–710 CrossRef CAS.
- L. W. Chan, Y. Jin and P. W. S. Heng, Int. J. Pharm., 2002, 242, 255–258 CrossRef CAS PubMed.
- Ý. A. Mørch, I. Donati, B. L. Strand and G. J. B. Skjåk-Bræk, Biomacromolecules, 2006, 7, 1471–1480 CrossRef.
- S.-L. Huang and Y.-S. Lin, Adv. Mater. Sci. Eng., 2017, 2017, 1–7 Search PubMed.
- P. W. Ayers, J. Chem. Phys., 2005, 122, 141102 CrossRef PubMed.
- P. W. Ayers, Faraday Discuss., 2007, 135, 161–190 RSC.
- W. K. H. Ho, Z. Y. Bao, X. Gan, K. Wong, J. Dai and D. Lei, J. Phys. Chem. Lett., 2019, 10, 4692–4698 CrossRef CAS PubMed.
- G. Mollica, F. Ziarelli, S. Lack, F. Brunel and S. Viel, Carbohydr. Polym., 2012, 87, 383–391 CrossRef CAS PubMed.
- B. Fortier-McGill, V. Toader and L. Reven, Macromolecules, 2012, 45, 6015–6026 CrossRef CAS.
- K. Saalwachter, F. Lange, K. Matyjaszewski, C. F. Huang and R. Graf, J. Magn. Reson., 2011, 212, 204–215 CrossRef PubMed.
- J. Gao, N. Li, B. Dai, W. Yu, X. Zhou, C. Chen, K. Fujisawa, Z. Yang, S. Dai and Y. Sun, Adv. Funct. Mater., 2025, 2502325 CrossRef CAS.
- S. P. Brown, Solid State Nucl. Magn. Reson., 2012, 41, 1–27 CrossRef CAS PubMed.
- J. R. Yates, T. N. Pham, C. J. Pickard, F. Mauri, A. M. Amado, A. M. Gil and S. P. Brown, J. Am. Chem. Soc., 2005, 127, 10216–10220 CrossRef CAS PubMed.
- B. T. Stokke, K. I. Draget, O. Smidsrod, Y. Yuguchi, H. Urakawa and K. Kajiwara, Macromolecules, 2000, 33, 1853–1863 CrossRef CAS.
- B. K. Ostafiychuk, V. I. Mandzyuk, Y. O. Kulyk and N. I. Nagirna, Nanoscale Res. Lett., 2014, 9, 160 CrossRef.
- D. Saurel, J. Segalini, M. Jauregui, A. Pendashteh, B. Daffos, P. Simon and M. Casas-Cabanas, Energy Storage Mater., 2019, 21, 162–173 CrossRef.
- Y. Li, Y. Lu, Q. Meng, A. C. S. Jensen, Q. Zhang, Q. Zhang, Y. Tong, Y. Qi, L. Gu, M. M. Titirici and Y. S. Hu, Adv. Energy Mater., 2019, 9, 1902852 CrossRef CAS.
- K. Lu, H. Jing, H. Jia, H. Qiang, F. Wang, M. Shi and M. Xia, J. Colloid Interface Sci., 2025, 679, 262–272 CrossRef CAS PubMed.
- D. Boonpakdee, C. F. Guajardo Yévenes, W. Surareungchai and C. La-o-vorakiat, J. Mater. Chem. A, 2018, 6, 7162–7167 RSC.
- J. Wu, Chem. Rev., 2022, 122, 10821–10859 CrossRef CAS.
- S. Wang, J. Zhang, O. Gharbi, V. Vivier, M. Gao and M. E. Orazem, Nat. Rev. Methods Primers, 2021, 1, 41 CrossRef CAS.
- P. L. Taberna, P. Simon and J. F. Fauvarque, J. Electrochem. Soc., 2003, 150, A292–A300 CrossRef CAS.
- R. J. Li, Z. P. Shen, H. Y. Zheng, L. Jin, Y. G. Zhang, W. Y. Yuan and X. F. Wang, J. Energy Storage, 2023, 73, 109521 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |