Open Access Article
Open Access ArticleLipid bilayer-mediated spatiotemporal correlation between near-wall confined motion of micro-carriers
Wei
Liu
a,
Jinwei
Zhong
a,
Pui Wo Felix
Yeung
 b,
Xiahui
Xiao
a,
Yuwei
Zhu
b,
Xiahui
Xiao
a,
Yuwei
Zhu
 *a and
To
Ngai
*a and
To
Ngai
 *b
*b
aThe Key Laboratory of Synthetic and Biological Colloids, Ministry of Education & School of Chemical and Material Engineering, Jiangnan University, Wuxi 214122, P.R. China. E-mail: uvyzhu@gmail.com
bDepartment of Chemistry, The Chinese University of Hong Kong, Shatin, N.T., Hong Kong 999077, P.R. China. E-mail: tongai@cuhk.edu.hk
First published on 18th December 2025
Abstract
We employed intensity fluctuations of evanescent light scattering to probe spatiotemporal correlations in the near-wall confined motion of microspheres on supported lipid bilayers (SLBs). Normalized cross-correlation analysis revealed long-range, time-resolved correlations in particle–wall separation distances, demonstrating that interfacial stress propagation can transmit mechanical signals across membrane interfaces. The motion exhibited broadly corralled diffusion, with both the corral size and diffusion constant confined to the nanoscale. This confinement could be further classified into fast and slow modes, with most diffusion constants residing in the slow regime, indicating that SLBs predominantly retard and localize microsphere dynamics at the interface. Furthermore, a transition in the interbilayer interaction profile—from bimodal to single-peak behavior—introduced a characteristic length scale and a kT-scale energy barrier, underscoring the cooperative interplay between interfacial stress propagation and membrane shape remodeling.
Introduction
Cellular membranes are fundamental to a wide range of biological processes.1–3 For instance, they serve as the outermost barrier, protecting the intracellular cytoplasm and organizing essential components such as genetic material. Within cells, biomembranes enable compartmentalization into subcellular organelles, supporting complex yet highly organized biochemical activities. Notably, membranes also function as two-dimensional (2D) platforms for critical cellular processes such as signal transduction, by facilitating the lateral diffusion and clustering of lipids, proteins, and other macromolecules.4 This diffusive behavior plays a key role in modulating reaction kinetics and mediating intermolecular interactions, including ligand–receptor recognition.5–7Among membrane properties, the viscosity of lipid bilayers critically governs the length and time scales of diffusion-driven processes.8,9 For 2D systems/interfaces, the effective viscosity η can be quantitatively related to the diffusion constant D via the Stokes–Einstein relation
| D = μkBT ∝ η−1kBT | (1) |
| 〈δ2(Δ)〉 = 4DαΔα with 0 < α < 1 | (2) |
While lateral diffusivity on lipid membranes—including planar and colloidal-supported lipid bilayers (SLBs and CSLBs, respectively)—has been extensively characterized using single-molecule and single-particle tracking techniques,12–17 far less is known about how micro- and nanoscale carriers diffuse near membrane surfaces and subsequently interact with or fuse into the membranes, particularly in the normal direction when two lipid bilayers approach one another. A microscopic understanding of SLB approach, adhesion, spreading, and the formation of negative curvature and hemifusion intermediates is essential for elucidating the physical basis of cell–cell communication, endocytosis, and exosome transport, as well as for advancing the development of liposome-based antitumor therapies. Probing membrane interactions requires measurements on well-controlled systems that closely mimic natural conditions, where fluctuations play a critical role. Neutron and X-ray scattering have been employed to investigate the interaction potential between two lipid bilayers, where one adsorbed on a solid surface and the other floating close by.18,19 Total internal reflection microscopy (TIRM) has also been used to directly quantify the kT-scale interactions between lipid bilayers by monitoring the lateral diffusion and z-directional fluctuations of SLB-modified colloids near membrane surfaces.20,21 In addition, simulations provide powerful tools for probing biomolecular diffusivity, phase separation, membrane fusion, and vesicle–membrane interactions.22–26 Collectively, these approaches underscore the central importance of membrane shape remodeling during membrane–membrane interactions.
Importantly, lipid membranes are inherently non-planar, exhibiting three-dimensional (3D) architectures such as cap-like protrusions and bulged domains.27 These micro- and nanostructures, shaped by intrinsic curvature, offer unique opportunities for membrane-mediated interactions. The presence of such protrusions has been confirmed by 3D single-particle tracking and confocal imaging.16,20,28 In parallel, lipid membranes are quasi-2D materials with intrinsic heterogeneity and phase separation. Cholesterol-enriched lipid raft domains are randomly embedded across the membrane surface. Previous studies have shown that cholesterol modulates the bending modulus of lipid bilayers, and membrane bending is widely recognized as a critical early step in fusion processes.29–31 Therefore, elucidating z-directional diffusivity and transient local deformations during bilayer approach is essential for understanding membrane shape remodeling and the principles underlying interbilayer interactions.
In this study, we aim to elucidate—at least in part—the z-directional diffusive behavior and interbilayer interactions that arise when two lipid bilayers approach one another. To this end, we employed a classical ternary lipid system composed of saturated 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), unsaturated 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), and cholesterol at a fixed molar ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, supported on 3 µm polymeric microspheres and planar glass substrates. Using TIRM, a scattering-based technique,32–34 we imaged fluctuations in the z-directional displacement of microspheres near the interface, enabling quantitative extraction of diffusion parameters and interbilayer interaction potentials (see Fig. 1). Remarkably, we observed long-range correlations in the confined motion of microspheres separated by distances exceeding 100 µm. Furthermore, we characterized the temporal evolution, or aging, of both the correlated diffusivity and the interbilayer potential energy over the course of the observation period. Our results suggest that interfacial stress, membrane elasticity, and dynamic remodeling play critical roles in facilitating the long-range transmission of mechanical signals across cellular membranes.
1, supported on 3 µm polymeric microspheres and planar glass substrates. Using TIRM, a scattering-based technique,32–34 we imaged fluctuations in the z-directional displacement of microspheres near the interface, enabling quantitative extraction of diffusion parameters and interbilayer interaction potentials (see Fig. 1). Remarkably, we observed long-range correlations in the confined motion of microspheres separated by distances exceeding 100 µm. Furthermore, we characterized the temporal evolution, or aging, of both the correlated diffusivity and the interbilayer potential energy over the course of the observation period. Our results suggest that interfacial stress, membrane elasticity, and dynamic remodeling play critical roles in facilitating the long-range transmission of mechanical signals across cellular membranes.
Experimental
Preparation of liposomes
We employed a ternary lipid mixture—1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC, 99%, Macklin), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC, >99%, Aladdin), and cholesterol (≥99%, Macklin)—as a model membrane system. Specifically, 0.0100 g DPPC and 0.0035 g DOPC were weighed into a reagent vial. Separately, 0.3867 g powdered cholesterol was dissolved in 1 mL of a mixed organic solvent (cyclohexane/ethanol = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) to prepare a stock solution at 1 mmol mL−1. A volume of 4.45 µL of this cholesterol stock was added to the lipid mixture, followed by 11.813 mL of the same mixed solvent. The solution was sonicated to facilitate dissolution, yielding a liposome sample with a final concentration of 2 × 10−3 mmol mL−1 and a molar ratio of 20%. To remove impurities, the solution was filtered three times using a 0.22 µm Nylon membrane.
1, v/v) to prepare a stock solution at 1 mmol mL−1. A volume of 4.45 µL of this cholesterol stock was added to the lipid mixture, followed by 11.813 mL of the same mixed solvent. The solution was sonicated to facilitate dissolution, yielding a liposome sample with a final concentration of 2 × 10−3 mmol mL−1 and a molar ratio of 20%. To remove impurities, the solution was filtered three times using a 0.22 µm Nylon membrane.
Preparation of colloidal supported lipid bilayers
A volume of 12 µL of lipid solution was added to a sample vial and dried under nitrogen to remove the organic solvent, forming a lipid film with a transparent center and white edges. Then, 100 mM NaCl was added, and the sample was sonicated (5 min) to disperse the lipids in water. The mixture was incubated in a 60 °C water bath for 1 h to form liposomes. Subsequently, 1 µL of PS microspheres (3.1 µm diameter, 8% solids, Thermo Fisher Scientific) was added. After 30 min of incubation, the sample was shaken for another 30 min to yield lipid-coated PS particles (i.e., CSLBs). Upon heating above the lipid phase transition temperature, lipid molecules became more fluid and loosely packed, forming a liquid phase with enhanced mobility.Hydrophilic treatment of glass substrates
Glass slides (25 × 75 × 1 mm, Fisher Scientific) were immersed in piranha solution (H2SO4/H2O2 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) and treated for 2 h. Afterward, they were rinsed with deionized water to remove residual piranha solution. The slides were then cleaned three times with deionized water and absolute ethanol, each followed by 15 min of sonication. Finally, the slides were dried under nitrogen and treated with plasma for 5 min (PDC-002, Harrick Plasma, USA).
1, v/v) and treated for 2 h. Afterward, they were rinsed with deionized water to remove residual piranha solution. The slides were then cleaned three times with deionized water and absolute ethanol, each followed by 15 min of sonication. Finally, the slides were dried under nitrogen and treated with plasma for 5 min (PDC-002, Harrick Plasma, USA).
Formation of supported lipid bilayers on glass substrates
Supported lipid bilayers were fabricated using the Langmuir–Blodgett (LB) technique.35 After instrument calibration, the prepared lipid solution was deposited onto the air–water interface. Upon solvent evaporation and stabilization at ∼1 mN m−1 surface pressure for 30 min, the monolayer was compressed at 10 mm min−1 until the surface pressure reached 40 mN m−1. The first monolayer was transferred onto the glass substrate via vertical lifting at 2 mm min−1. The second monolayer was prepared similarly and deposited by vertical immersion at 2 mm min−1 using a PTFE trough, maintaining the bilayer in an aqueous environment.Principle of total internal reflection microscopy
The central of the technique of TIRM is the application of evanescent wave, which allows it to measure kT-scale interaction between a colloidal microsphere and a flat transparent surface with outstanding distance resolution in direction normal to the wall.32,34,36–39 In principle, the evanescent wave or field is generated by total reflection of a laser beam at an interface of glass slide and solution. The intensity of scattering light I exponentially decays with a separation distance h from the interface, expressed as34| I(h) = I0e−h/dp | (3) |
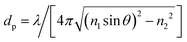 | (4) |
Therefore, in a typical TIRM measurement, the separation distance between the interface and the particle can be given by eqn (3) as
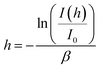 | (5) |
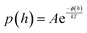 | (6) |
 | (7) |
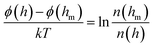 | (8) |
TIRM-based measurement of inter-bilayer interactions
To measure inter-bilayer interactions using TIRM, a flow cell was assembled with a 20% cholesterol-containing lipid-coated slide. The air-exposed surface was cleaned with mixed solvent, rinsed with ethanol and water, and dried under nitrogen. Immersion oil was applied to the cleaned surface, and the slide was tightly coupled to a 70° prism to avoid air bubbles. The flow cell was placed on the microscope stage and connected to a syringe pump. A 20 mL volume of 100 mM NaCl was injected to replace ultrapure water in the cell. Cholesterol content on both the slide and PS particles was varied to modulate system conditions.Lipid-coated PS particles (CSLBs) were loaded into a syringe and introduced into the inverted flow cell. The sample was washed with 20 mL of 100 mM NaCl at 1 mL min−1. After washing, the flow cell was returned to its upright position to begin imaging. Images were recorded in dynamic range mode with gain set to 16-bit, ROI at 512 × 512 pixels and exposure time of 10 ms (Kinetix22, Teledyne Photometrics Inc., US). Seven spatially distinct particles were tracked, with a total of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames captured. Imaging was repeated every 20 min, with the final time point at 80 min. The images were processed based on the radial symmetry method under particle-tracking framework using previously reported MATLAB program.40
000 frames captured. Imaging was repeated every 20 min, with the final time point at 80 min. The images were processed based on the radial symmetry method under particle-tracking framework using previously reported MATLAB program.40
Results and discussion
Spatiotemporal correlation of confined motion
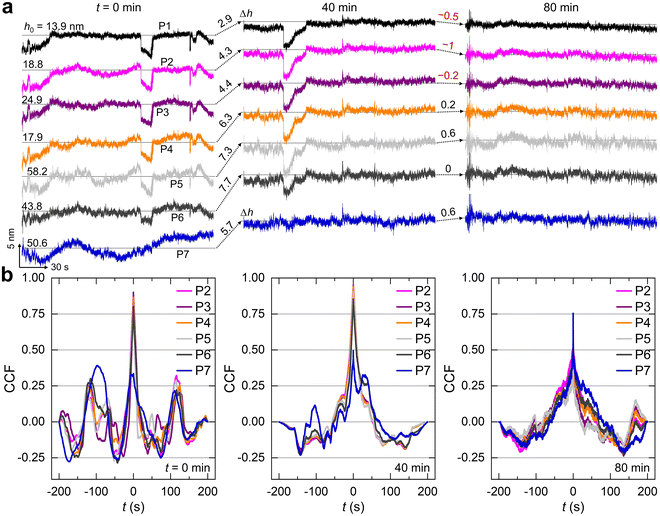
We first examined the spatiotemporal correlations in the scattered intensity and height profiles of microspheres (particles 1–7, P1–7 in Fig. 2). A total of N = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 images (512 × 512 pixels) were acquired at a sampling rate of 100 frames per second, corresponding to an exposure time of 10 ms. To mimic physiological conditions and screen electrostatic repulsion between lipid bilayers (zeta potential ∼−50 mV), an aqueous solution containing 100 mM NaCl was used—potentially facilitating membrane fusion or remodeling.
000 images (512 × 512 pixels) were acquired at a sampling rate of 100 frames per second, corresponding to an exposure time of 10 ms. To mimic physiological conditions and screen electrostatic repulsion between lipid bilayers (zeta potential ∼−50 mV), an aqueous solution containing 100 mM NaCl was used—potentially facilitating membrane fusion or remodeling.
Fig. 2a present representative z-directional trajectories over time (see Fig. S1 for more trajectories). Upon injection, microspheres rapidly settled onto the surface of the SLBs, where interbilayer separations h0 ranged from ∼10 to 50 nm. Short-timescale stochastic fluctuations (∼200–400 ms) were confined within a narrow range of ∼2–3 nm (background noise ≤1 nm, data not shown), consistent with lipid bilayer-mediated confinement. This strictly limited motion echoes findings from our previous study involving SLBs under basic pH conditions.41 Interestingly, beyond these small-scale fluctuations, we observed transient displacements from the equilibrium position. These events manifested as sudden, step-like “jumps” of several nanometers, with dwell times ranging from 10 to 15 seconds or longer. Such behavior may arise from non-specific interactions, potentially driven by microdomain-induced affinity between the two bilayers.42,43
Notably, we observed a striking correlation in the z-directional displacements—particularly the step-like “jumps”— among the seven microspheres of interest. These correlated motions were not attributable to background vibrations, which were carefully ruled out: no such correlation was detected on bare microsphere surfaces or substrates lacking lipid membranes (Fig. S2). As previously discussed, cholesterol increases the bending modulus of cellular membranes and may also enhance the elasticity and interfacial tension of the SLBs. This increased elasticity likely facilitates interfacial stress propagation, enabling pulse-like mechanical signals to be transmitted across the membrane interface.44–47
To quantitatively assess the degree of correlation between the z-directional displacements of CSLBs, we employed a normalized cross-correlation function (CCF) applied to pairs of time-resolved intensity signals (e.g., Ii and Ij)48,49
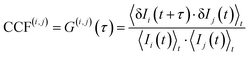 | (9) |
To further visualize this effect, we plotted the 2D distribution of G(0) for all microspheres across different observation times (Fig. 3). Notably, G(0) values among particles P1 to P6 were much larger than G(i=1–6,j=7)(0), where the former increased over time, peaked around 40 minutes, and gradually declined thereafter. Specifically, for P7, we observed relatively stronger correlation after a longer period, with G(0) > 0.75 at 80 min (Fig. S3, right-bottom panel). This temporal evolution of cross-correlation suggests that z-directional displacement and diffusivity between the two approaching bilayers are both long-range (>100 µm) and time-resolved, dynamically evolving over tens of minutes. Such behavior may arise from lipid exchange or the transient formation of bridging structures between bilayers. These events could propagate rapidly across the membrane surface via interfacial tension, potentially giving rise to the observed spatiotemporal correlations.44,50 The relatively weaker and unstable correlation observed for P7 likely reflects the finite range of propagation and concomitant energy dissipation, compounded by a non-uniform local environment.
Anomalous diffusion
We next evaluate the z-directional diffusive behavior between the two approaching lipid bilayers. To quantify the diffusivity, we calculated the time-averaged MSD for individual particle trajectories at various time intervals13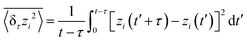 | (10) |
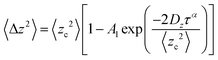 | (11) |
 | ||
| Fig. 4 Anomalous diffusion in the z-direction. (a) Representative mean squared displacements of the seven microspheres of interest. Solid lines represent the non-linear fitting by eqn (11) for corralled diffusion with a relaxed power-law exponent. (b) Time-evolution of the diffusion constants Dz. Lines are drawn for guides of eye. (c) Diffusivity in the fast (dashed dotted line) and slow mode (solid line). Inset: Semi-log plot of Dzversus α. Right-bottom: Stochastic collision between two approaching lipid bilayers. | ||
It is noteworthy that the Dz values are nearly six to seven orders of magnitude lower than those of lipids or proteins diffusing within membranes.12,13,17 Considering the inverse relationship between diffusion coefficient D and particle size a (Stokes–Einstein relation, D ∼ kBT/a), the diffusivity of a microscale particle is expected to be approximately three orders of magnitude lower than that of nanoscale biomolecules. In addition, for near-wall confined diffusion, Bevan and Prieve38 provided a drag correction factor, β⊥, as a close approximation to Brenner's infinite series solution,52 reported that
 | (12) |
Furthermore, the diffusive behavior of confined motion can be classified into two distinct regimes—a fast mode and a slow mode—based on the relationship of Dz-versus-α (Fig. 4c). The corralled diffusion follows a power-law dependence, expressed as
α ∼ 2.302ς![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dz Dz | (13) |
Potential energy
To further quantify membrane shape remodeling, we analysed the interaction potential energy between the two bilayers—namely, the immobilized planar SLBs on solid substrates and the diffusing CSLBs with intrinsic curvature. Fig. 5 shows the time evolution of the potential energy profiles U(h − h0) for individual CSLBs, where h0 denotes the equilibrium height corresponding to the minimum potential. Typically, the profiles transitioned from a bimodal distribution to a single-peak form, suggesting the existence of at least two equilibrium or pseudo-steady states during bilayer approach and deformation. A similar phenomenon was previously reported by Everett and Bevan,20 who employed TIRM to monitor the spreading of supported lipid bilayers from a wall onto bare 1.5 µm silica particles.The bimodal-to-single peak transition also revealed a characteristic length scale, defined as the height difference between the two equilibrium positions. Over time, this length scale decreased from approximately 4–6 nm (0–40 min) to ∼2 nm (∼60 min), suggesting a dynamic process evolving from the transient emergence of SLB bulges to eventual bilayer fusion. Notably, this length scale is much narrower than the ∼18 nm separation between potential energy minima as previously reported.20 Such differences in length scales highlight distinct SLB configurations associated with interbilayer fusion versus single bilayer spreading. When considered together with the ∼1 nm corral size (Fig. S5b and c), our findings provide new insight into the fusion mechanism of apposing SLBs at even smaller nanoscales, thereby deepening the microscopic understanding of lipid vesicle–membrane interactions.
Additionally, a kT-scale energy barrier ΔΦ between transitional membrane fusion configurations—defined as the energy difference between the two potential energy minima—was quantified (Fig. 6). The value of ΔΦ initially increased, reaching a maximum of approximately 3kT around 40 min, before gradually declining to zero. This temporal evolution suggests that transient structural rearrangements initially stabilize intermediate fusion states, but are eventually relaxed as the bilayers proceed toward complete fusion. Notably, a similar time-dependent trend was observed in the zero-lag cross-correlations G(0), underscoring the coupling between diffusivity correlations and energetic barriers. The coincidence of these behaviors highlights the cooperative interplay between interfacial stress propagation and membrane shape remodeling, indicating that mechanical stresses and elastic deformations act in concert to regulate the kinetics and energetics of bilayer fusion.
Conclusions and discussion
Using total internal reflection microscopy, we uncovered a long-overlooked spatiotemporal correlation in the near-wall confined motion of micro-carriers, where both the particle and wall surfaces were modified with lipid bilayers containing cholesterol (20 mol% in this study). Instead of the typical sublinear diffusion behavior, a corralled diffusion pattern was observed and quantitatively analyzed, offering new insights into diffusive mechanisms in bio-membrane systems. Further analysis of the interbilayer interactions revealed a transition in the potential energy profile from a double-well to a single harmonic-like well, reflecting the time-dependent evolution of fusion configurations.Overall, this study advances our understanding of membrane shape remodeling. We demonstrate that non-specific interactions can induce transient deformations, such as bulges or cap-like structures,43,57 thereby providing new experimental evidence for the dynamic mechanisms underlying membrane fusion.20,21 The observed remodeling of membrane morphology and transitions between multiple equilibrium states highlight the critical roles of elasticity and interfacial tension in regulating local deformations, offering insight into how membranes mechanically respond to external forces or interactions.58,59 In addition, the discovery of long-range correlated motion of colloidal-supported lipid bilayers suggests that interfacial fluctuations can transmit mechanical signals across large spatial scales, thereby deepening our understanding of mechanical coupling and signal propagation in cellular membranes.44,50,60 Finally, the identification of fast and slow anomalous diffusivities associated with structural heterogeneity indicates that local membrane inhomogeneity, such as lipid raft domains, may play an essential role in governing membrane–membrane interactions.26,61
Beyond membrane remodeling, a quantitative understanding of interbilayer interactions provides valuable guidance for the development of biomimetic membranes, enabling designs that more closely replicate the stability and functionality of natural cell membranes.62,63 Insights into adhesion and deformation mechanisms can inform the optimization of liposomal drug-delivery carriers, improving their fusion efficiency with cellular membranes and enhancing targeting and release control. Measurements of interaction potentials and diffusion behaviors also contribute to a more comprehensive explanation of cell–cell contact, adhesion, and signal transmission, supporting progresses in cell biology and immunology.64–66 Moreover, the observed particle motion patterns offer a model for lipid vesicle–membrane interactions, helping to predict the behavior of liposomes in vivo and their binding and penetration into cellular membranes.67–69
In summary, our observations collectively suggest that when two lipid bilayers with high internal fluidity approach one another, non-specific interactions can induce the transient formation of bulged structures, most likely protruding from the planar supported lipid bilayers. These dynamic shape changes lead to shifts between distinct equilibrium states in the interbilayer interaction potential. Structural heterogeneity further contributes to the emergence of fast and slow anomalous diffusion behaviors in lipid-bilayer-enveloped micro-carriers. Moreover, membrane elasticity and interfacial tension appear to facilitate spatiotemporal correlations in confined motion. Future investigations employing fast, super-resolution imaging techniques to track the in situ correlated diffusion of interacting cellular membranes are expected to yield direct evidence of membrane shape remodeling.
Author contributions
Wei Liu: conceptualization, methodology, formal analysis, visualization, supervision, project administration, funding acquisition, writing – original draft. Jinwei Zhong: software, validation, formal analysis, investigation, data curation. Pui Wo Felix Yeung: software, validation, formal analysis. Xiahui Xiao: validation, investigation. Yuwei Zhu: funding acquisition, writing – review & editing. To Ngai: conceptualization, project administration, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sm01211b.Acknowledgements
This work was supported by the National Natural Science Foundation of China (22303033) and the Fundamental Research Funds for the Central Universities, China (JUSRP202501136).Notes and references
- S. A. Shelby, I. Castello-Serrano, K. C. Wisser, I. Levental and S. L. Veatch, Nat. Chem. Biol., 2023, 19, 750–758 CrossRef CAS PubMed.
- X. Cheng and J. C. Smith, Chem. Rev., 2019, 119, 5849–5880 CrossRef CAS PubMed.
- D. Krapf, Curr. Opin. Cell Biol., 2018, 53, 15–21 CrossRef CAS.
- S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731 CrossRef CAS PubMed.
- M. Schmick and P. I. Bastiaens, Cell, 2014, 156, 1132–1138 CrossRef CAS.
- Y. K. Lee, H. Lee and J.-M. Nam, NPG Asia Mater., 2013, 5, e48 CrossRef CAS.
- N.-K. Lee, A. Johner, F. Thalmann, L. Cohen-Tannoudji, E. Bertrand, J. Baudry, J. Bibette and C. M. Marques, Langmuir, 2008, 24, 1296–1307 CrossRef CAS.
- T. T. Hormel, M. A. Reyer and R. Parthasarathy, Biophys. J., 2015, 109, 732–736 CrossRef CAS.
- S. Pronk, E. Lindahl and P. M. Kasson, Nat. Commun., 2014, 5, 3034 CrossRef.
- Y. Liu, X. Zheng, D. Guan, X. Jiang and G. Hu, ACS Nano, 2022, 16, 16054–16066 Search PubMed.
- J.-H. Jeon, H. M.-S. Monne, M. Javanainen and R. Metzler, Phys. Rev. Lett., 2012, 109, 188103 CrossRef PubMed.
- X. Xu, C. Xu, W. Zhang, Z. Liu, Y. Wei, K. Yang and B. Yuan, J. Phys. Chem. B, 2025, 129, 5464–5476 Search PubMed.
- L. Gascoigne, R. P. Tas, P. G. Moerman and I. K. Voets, Soft Matter, 2025, 21, 3058–3066 RSC.
- P. Liu and P. J. Beltramo, Soft Matter, 2023, 19, 7708–7716 Search PubMed.
- Y.-J. Chai, C.-Y. Cheng, Y.-H. Liao, C.-H. Lin and C.-L. Hsieh, Biophys. J., 2022, 121, 3146–3161 CrossRef CAS PubMed.
- Y. Zhong and G. Wang, Langmuir, 2018, 34, 11857–11865 CrossRef CAS PubMed.
- J.-H. Jeon, M. Javanainen, H. Martinez-Seara, R. Metzler and I. Vattulainen, Phys. Rev. X, 2016, 6, 021006 Search PubMed.
- T. Mukhina, A. Hemmerle, V. Rondelli, Y. Gerelli, G. Fragneto, J. Daillant and T. Charitat, J. Phys. Chem. Lett., 2019, 10, 7195–7199 Search PubMed.
- A. Hemmerle, L. Malaquin, T. Charitat, S. Lecuyer, G. Fragneto and J. Daillant, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19938–19942 CrossRef CAS.
- W. N. Everett and M. A. Bevan, Soft Matter, 2014, 10, 332–342 RSC.
- W. N. Everett, D. J. Beltran-Villegas and M. A. Bevan, Langmuir, 2010, 26, 18976–18984 Search PubMed.
- S. Pronk, E. Lindahl and P. M. Kasson, J. Am. Chem. Soc., 2015, 137, 708–714 Search PubMed.
- Y. Zhuo, Z. Luo, Z. Zhu, J. Wang, X. Li, Z. Zhang, C. Guo, B. Wang, D. Nie and Y. Gan, Nat. Nanotechnol., 2024, 19, 1858–1868 CrossRef CAS PubMed.
- E. Yamamoto, T. Akimoto, A. C. Kalli, K. Yasuoka and M. S. Sansom, Sci. Adv., 2017, 3, e1601871 Search PubMed.
- M. D. Elola and J. Rodriguez, J. Phys. Chem. B, 2018, 122, 5897–5907 Search PubMed.
- C.-P. Chng, K. J. Hsia and C. Huang, Soft Matter, 2022, 18, 7752–7761 Search PubMed.
- S. Semrau and T. Schmidt, Soft Matter, 2009, 5, 3174–3186 RSC.
- J. C. Stachowiak, C. C. Hayden and D. Y. Sasaki, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7781–7786 CrossRef CAS PubMed.
- F. T. Doole, T. Kumarage, R. Ashkar and M. F. Brown, J. Membr. Biol., 2022, 255, 385–405 CrossRef CAS PubMed.
- J. F. Nagle, Phys. Rev. E, 2021, 104, 044405 Search PubMed.
- S. Chakraborty, M. Doktorova, T. R. Molugu, F. A. Heberle, H. L. Scott, B. Dzikovski, M. Nagao, L.-R. Stingaciu, R. F. Standaert and F. N. Barrera, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21896–21905 Search PubMed.
- J. Wu, W. Liu and T. Ngai, Soft Matter, 2023, 19, 4611–4627 RSC.
- M. A. Bevan and S. L. Eichmann, Curr. Opin. Colloid Interface Sci., 2011, 16, 149–157 CrossRef CAS.
- D. C. Prieve and N. A. Frej, Langmuir, 1990, 6, 396–403 CrossRef CAS.
- J. Yuan, C. Hao, M. Chen, P. Berini and S. Zou, Langmuir, 2013, 29, 221–227 CrossRef CAS PubMed.
- X. Gong, Z. Wang and T. Ngai, Chem. Commun., 2014, 50, 6556–6570 Search PubMed.
- L. Liu, A. Woolf, A. W. Rodriguez and F. Capasso, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E5609–E5615 Search PubMed.
- M. A. Bevan and D. C. Prieve, J. Chem. Phys., 2000, 113, 1228–1236 CrossRef CAS.
- H.-J. Wu and M. A. Bevan, Langmuir, 2005, 21, 1244–1254 CrossRef CAS.
- F. Cao, J. Wu, Y. Li and T. Ngai, Langmuir, 2019, 35, 8910–8920 Search PubMed.
- W. Liu, Z. Zhao, J. Zhong, P. W. F. Yeung, J. Wu, Y. Li, H. Jiang, Y. Zhu and T. Ngai, Chem. Sci., 2025, 16, 16625–16637 Search PubMed.
- A. Sardar, N. Dewangan, B. Panda, D. Bhowmick and P. K. Tarafdar, J. Membr. Biol., 2022, 255, 691–703 Search PubMed.
- H. R. Marsden, I. Tomatsu and A. Kros, Chem. Soc. Rev., 2011, 40, 1572–1585 RSC.
- R. Dharan, A. Barnoy, A. K. Tsaturyan, A. Grossman, S. Goren, I. Yosibash, D. Nachmias, N. Elia, R. Sorkin and M. M. Kozlov, Nat. Commun., 2025, 16, 91 Search PubMed.
- C. Aponte-Santamaría, J. Brunken and F. Gräter, J. Am. Chem. Soc., 2017, 139, 13588–13591 CrossRef.
- L. U. Brinkmann and J. S. Hub, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10565–10570 Search PubMed.
- A. Botan, L. Joly, N. Fillot and C. Loison, Langmuir, 2015, 31, 12197–12202 CrossRef CAS PubMed.
- C. V. Kelly, D. L. Wakefield, D. A. Holowka, H. G. Craighead and B. A. Baird, ACS Nano, 2014, 8, 7392–7404 CrossRef CAS PubMed.
- S. Wennmalm and J. Widengren, Anal. Chem., 2010, 82, 5646–5651 CrossRef CAS PubMed.
- Z. Shi, S. Innes-Gold and A. E. Cohen, Sci. Adv., 2022, 8, eabo1297 Search PubMed.
- M. J. Saxton and K. Jacobson, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 373–399 CrossRef CAS.
- H. Brenner, Chem. Eng. Sci., 1961, 16, 242–251 CrossRef CAS.
- J. Wu, F. Cao, P. W. F. Yeung, M. Li, K. Ohno and T. Ngai, ACS Macro Lett., 2024, 13, 1376–1382 Search PubMed.
- M. M. Kozlov and J. W. Taraska, Nat. Rev. Mol. Cell Biol., 2023, 24, 63–78 Search PubMed.
- K. Sengupta and A. S. Smith, in Physics of Biological Membranes, ed. P. Bassereau and P. Sens, Springer, Cham., 2018 Search PubMed.
- R. Lipowsky, Nature, 1991, 349, 475–481 CrossRef CAS.
- E. Loiseau, J. A. Schneider, F. C. Keber, C. Pelzl, G. Massiera, G. Salbreux and A. R. Bausch, Sci. Adv., 2016, 2, e1500465 CrossRef PubMed.
- K. V. Pinigin, Phys. Rev. E, 2025, 112, 055405 CrossRef CAS.
- Z. Chen, P. Chen, J. Li, E. Landao-Bassonga, J. Papadimitriou, J. Gao, D. Liu, A. Tai, J. Ma and D. Lloyd, Sci. Adv., 2025, 11, eads6132 Search PubMed.
- H. De Belly, S. Yan, H. B. da Rocha, S. Ichbiah, J. P. Town, P. J. Zager, D. C. Estrada, K. Meyer, H. Turlier, C. Bustamante and O. D. Weiner, Cell, 2023, 186, 3049–3061 CrossRef.
- G. P. Pattnaik and H. Chakraborty, Vitamins and hormones, Elsevier, 2021 Search PubMed.
- T. Rasheed, F. Nabeel, A. Raza, M. Bilal and H. Iqbal, Mater. Today Chem., 2019, 13, 147–157 Search PubMed.
- M. Sheikhpour, L. Barani and A. Kasaeian, J. Controlled Release, 2017, 253, 97–109 CrossRef CAS.
- K. Hennig, I. Wang, P. Moreau, L. Valon, S. DeBeco, M. Coppey, Y. Miroshnikova, C. Albiges-Rizo, C. Favard and R. Voituriez, Sci. Adv., 2020, 6, eaau5670 Search PubMed.
- E. E. Hui and S. N. Bhatia, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 5722–5726 CrossRef CAS.
- C. S. Chen, J. Tan and J. Tien, Annu. Rev. Biomed. Eng., 2004, 6, 275–302 CrossRef CAS.
- C. Peetla, A. Stine and V. Labhasetwar, Mol. Pharm., 2009, 6, 1264–1276 Search PubMed.
- S. Paramshetti, M. Angolkar, S. Talath, R. A. M. Osmani, A. Spandana, A. Al Fatease, U. Hani, K. Ramesh and E. Singh, Life Sci., 2024, 346, 122616 CrossRef CAS.
- Y. Chen, N. Douanne, T. Wu, I. Kaur, T. Tsering, A. Erzingatzian, A. Nadeau, D. Juncker, V. Nerguizian and J. V. Burnier, Sci. Adv., 2025, 11, eads5249 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |