Spontaneous rotation of an inclusion in a chiral active bath
Abhra
Puitandy
 * and
Shradha
Mishra
*
* and
Shradha
Mishra
*
Department of Physics, Indian Institute of Technology(BHU), Varanasi-221005, India. E-mail: smishra.phy@iitbhu.ac.in; abhrapuitandy.rs.phy22@itbhu.ac.in
First published on 8th December 2025
Abstract
Active matter systems are known to drive directed transport and rotation when coupled to passive inclusions. We study the dynamics of a geometrically symmetric inclusion, termed a torquer, in a bath of chiral active Brownian particles. Despite being geometrically symmetric and non-motile, the torquer exhibits persistent rotation due to spatially inhomogeneous torques arising from angularly biased collisions with active particles. This interaction-driven symmetry breaking does not rely on shape anisotropy or external forcing. Through simulations, we identify two distinct regimes of rotation: one dominated by density gradients at low chirality and another by increased impact frequency at high chirality. Our results demonstrate that persistent rotational dynamics can be realised in a symmetric inclusion, from anisotropic interaction with the active bath.
I. Introduction
Active matter systems refer to systems composed of self-driven constituents that convert internal or environmental energy into persistent motion, thereby violating the principle of detailed balance at the microscopic scale. These systems span a wide range of scales, from cytoskeletal filaments1 and bacterial colonies2 to animal herds3 and human crowds,4 and exhibit rich emergent collective phenomena5–11 such as swarming,12–14 phase separation,15 dynamic clustering,16 and pattern formation.14 A particularly rich class of active systems are composed of chiral active particles, which, in addition to self-propulsion, exhibit a persistent angular drift due to either internal asymmetry or external torques. These chiral particles have been observed in natural systems such as sperm cells and bacteria,17 as well as in synthetic colloidal systems and are known to exhibit diverse phase behaviours18,19 and nonequilibrium phenomena including hyperuniform phases,20–23 self-reverting vortices,24,25 caging in active glasses,26 and demixing in binary mixtures.27–29An important question regarding chiral active systems is how they interact with foreign inclusions such as walls, obstacles, or passive particles. Several studies have shown that chiral active particles can exert net forces and torques on asymmetric inclusions, leading to effects such as persistent rotation of microgears30–32 in bacterial suspensions33 or mobile inclusions in active nematics34 and ratchet effects.35 These interactions can result in non-reciprocal momentum exchange and symmetry breaking at the level of the embedded object, even in the absence of external drive.
Prior studies typically relied on geometric asymmetry or mobile defects to break symmetry and induce motion.36 However, the role of geometrically symmetric foreign objects in chiral active systems remains less explored. Specifically, it is not yet well understood whether a circular object—one that is spherically symmetric—can exhibit persistent rotation solely due to the structure of its interaction with the active bath.
In this work, we study a circular inclusion immersed in a bath of chiral active Brownian particles (ABPs).37 This object, which we refer to as a torquer, is not self-propelled, but dynamically reorients in response to spatially inhomogeneous torques arising from ABP collision. The net orientation of the torquer at any time is tracked by an angle β, which evolves dynamically under the influence of accumulated torques resulting from the chiral active particles' impact. The name reflects its key role as a torque-responding body, distinct from both passive inclusions and active agents. Examples of such objects can be realised in artificial systems like the response of colloidal systems to external fields, which can be optothermal,38,39 magnetic,40 and chemical41 in nature. In biological systems also, dynamics of leucocytes to locate inflammatory sites in the human body42 provide motivating modelling parallels to our inclusion.
Crucially, while the torquer is geometrically isotropic, the torque imparted by an active particle depends on the angular location of the impact of active particles. This leads to a non-uniform torque distribution around the object's boundary, effectively breaking angular symmetry without invoking any shape anisotropy. Thus, although the inclusion is geometrically isotropic, the interaction is anisotropic due to the angular dependence of force transfer, making the symmetry breaking interaction-induced rather than geometric. In contrast to previous models that rely on geometric or motile asymmetry, here the symmetry-breaking mechanism is encoded in the local interaction and chirality of the bath.
Our comprehensive numerical study reveals that this angular inhomogeneity is sufficient to induce robust and persistent rotation of the torquer. We identify two distinct rotational regimes: (i) at low chirality, the rotation is driven by density inhomogeneities of active particles at the surface of the torquer, which exerts uneven torque around its perimeter; (ii) at high chirality, it is dominated by a more frequent impact of ABPs at its perimeter.
Recent works on surface,43,44 mass,45 or shape asymmetries46 have demonstrated diverse mechanisms of induced motion in colloids, including optothermal propulsion38 and emergent edge flows47 in spinner assemblies.48 These studies underscore how asymmetry—whether structural or interaction-driven—can serve as a powerful design principle in active matter systems. Our work complements these efforts by showing that persistent rotation can emerge even in geometrically symmetric inclusions via interaction-induced symmetry breaking.
The rest of the paper is organized as follows: Section II describes the model details. Section III discusses the detailed results of the system described in Section II. Finally, in Section IV, we summarize our main findings and discuss their broader implications for understanding symmetry breaking and induced motion in chiral active systems.
II. Model
We consider a two-dimensional system consisting of a large, immobile inclusion of radius ap placed at the center of a square box of side length L, surrounded by a bath of chiral active Brownian particles (ABPs) which will be referred to as active particles in the rest of the manuscript. Each active particle is modeled as a disk of radius aac, and the system evolves under overdamped dynamics in the absence of thermal translational noise. Each active particle has a position ri and an orientation angle θi, which defines its self-propulsion direction ni = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi, sin
θi, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi). The dynamics of the ith active particle are governed by the following equations of motion:
θi). The dynamics of the ith active particle are governed by the following equations of motion: | (1) |
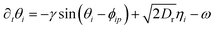 | (2) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij where
ij wherewhere rij = |ri − rj|, ai and aj are the radii of the ith and jth particles respectively and k is the repulsion stiffness. The second type of interaction an active particle experiences is due to the torque at the surface of the inclusion. This interaction tries to effectively reorient the active particles away from the inclusion's surface. Here γ determines the rate of reorientation in the direction of ϕip = arg(ri − rp). The cartoon of this interaction term is shown in Fig. 1(a), depicting the two cases (i) and (ii) of the direction of orientation of active particle θi approaching towards the inclusion. The solid and dashed circles represent the inclusion and active particles respectively. The solid and dashed arrows in the body of the active particle represent the directions of orientation of an active particle, approaching towards and moving away from the inclusion respectively. Dr is the rotational diffusion constant, ηi(t) is Gaussian white noise with zero mean and unit variance, and ω is the intrinsic chirality of the active particle and is the same for all the active particles in the system for a given set of parameter values in a simulation. Later we have also introduced a binary mixture of active particles with two opposite chiralities. Most of the analysis of the results is for active particles with the same chirality.
Now we turn to the dynamics of the inclusion, which is also addressed as a torquer at some places. The inclusion's position is fixed but it is allowed to rotate about its center. We assign with the inclusion an internal asymmetry in the plane of the inclusion, which leads to the inhomogeneous response of the active particle at its perimeter. We introduce β(t) as an orientation variable that tracks the direction of the torque imbalance generated by active particle collisions, marked with a magenta solid arrow in the cartoon shown in Fig. 1(b). The dynamics of β(t) can be given by
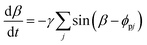 | (3) |
A schematic representation of the variation of torque over the inclusion circumference is shown in Fig. 1(c) for the two cases (i) β < ϕpj and (ii) β > ϕpj. In both the cases the result of the torque term in eqn (3) tries to reorient β(t) in the direction of ϕpj.
It is important to note that the torque interaction between the torquer and an active particle is inherently directional. Specifically, the ith active particle experiences a torque that tends to align its orientation vector along the direction from the torquer to itself (ri − rp), while the torquer feels a torque trying to align its orientation angle β along the direction from the jth active particle to itself (rp − rj). As a result, the preferred torque directions for the two bodies in the pair are opposite, generating a sort of effective anti-alignment geometry. This angular asymmetry underlies the net torque transfer and explains why in symmetric configurations such as shown in Fig. 3(b), the individual contributions can cancel out, leading to no net rotation of the inclusion.
Furthermore, the torque interactions between the inclusion and each active particle are inherently non-reciprocal in nature. The torque experienced by the inclusion depends on its instantaneous orientation β and the angle(ϕpj) defined by the vector pointing from the jth active particle to the inclusion center. In contrast, the active particle experiences torque based on its own orientation, θi and the angle (ϕip) defined by the vector from the inclusion to the particle. Since these orientations and angles are generally not equal and point in opposite directions, the torques are not equal and opposite. This mismatch leads to a breakdown of action–reaction symmetry, a hallmark of non-reciprocal interaction. Importantly, such nonreciprocity constitutes an internal symmetry-breaking mechanism, even though both objects are geometrically symmetric. This seems to obey Curie's principle52 implying that a directed motion such as persistent rotation cannot arise from symmetric causes alone.
In our model, it is the non-reciprocal structure of the interaction that breaks this symmetry. While persistent rotation can arise even in the absence of such non-reciprocity, incorporating it provides a minimal and physically grounded route to capture the kinds of asymmetric interactions observed in many experimental active systems.
For instance, in bacterial baths, collisions with symmetric rotors can transfer a net torque.53 Similarly, in chiral colloidal or Janus swimmer assemblies, asymmetries in propulsion or interaction zones feature directionally biased interactions.54 A compelling biological parallel arises in the rolling adhesion of leukocytes,42 where spatially heterogeneous adhesion footprints on the cell surface cause biased rotational dynamics during contact with the vessel wall. These contact-mediated asymmetries demonstrate how contact receptive interactions can drive directed rotation.
Additionally, the sinusoidal torque profile used in our model mirrors the first squirming mode in classical microorganism models,49,50 where the surface velocity varies sinusoidally around a symmetric body. This mode, responsible for opposite flows across the hemispheres, has been experimentally observed in spherical algae such as Volvox and Chlamydomonas,51 providing a biological analogue for the angularly varying torque distribution employed here. Altogether, these examples provide a strong physical and biological motivation for our minimal torque rule.
Numerical details
The above three equations (eqn (1)–(3)) are numerically integrated with the Euler integration scheme for time. We started with the initial condition of random homogeneous non-overlapping initial positions and orientations of active particles on the two-dimensional substrate of size L = 80aac. Periodic boundary conditions are applied in both directions of the square box. We define the smallest length, the size of the active particle aac and the time scale in our system as τ = DR−1. All other lengths and times are measured in units of aac and τ respectively.The area fraction of active particles, defined as ϕa = Naπaac2/L2, is fixed at 0.5. The strength of chirality ω and size ratio 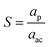 are the two control parameters in our simulations. We vary ω from 0 to 1.5 and S is tuned from 6 to 16. The self-propulsion speed of active particles v0 = 1 and hence the typical persistent length of active particles l = v0/Dr = 10 = 100aac; hence, we considered the size of inclusion either of the order or larger than l. The rotational diffusion constant Dr is fixed to 0.1 or τ = 10. The small time step of integration dt = 10−4τ. The above three equations are simulation for the total number of time steps T = 3 × 105 = 30τ. A single simulation step is counted once all the active particles' positions and orientations are updated once. The observations are performed after 10τ, when the steady state is reached. The steady state is characterized when we do not see any statistical pattern in the dynamics of the particles. The averaging is performed over total 20τ times in the steady state and 80 to 150 independent initial realizations. The number of active particles is 1000 across all parameter sets. For the binary mixture, we have varied the fraction of active particles from positive to negative chirality from 10% to 90% with the fixed size ratio S = 8 magnitude of chirality |ω| = 0.7.
are the two control parameters in our simulations. We vary ω from 0 to 1.5 and S is tuned from 6 to 16. The self-propulsion speed of active particles v0 = 1 and hence the typical persistent length of active particles l = v0/Dr = 10 = 100aac; hence, we considered the size of inclusion either of the order or larger than l. The rotational diffusion constant Dr is fixed to 0.1 or τ = 10. The small time step of integration dt = 10−4τ. The above three equations are simulation for the total number of time steps T = 3 × 105 = 30τ. A single simulation step is counted once all the active particles' positions and orientations are updated once. The observations are performed after 10τ, when the steady state is reached. The steady state is characterized when we do not see any statistical pattern in the dynamics of the particles. The averaging is performed over total 20τ times in the steady state and 80 to 150 independent initial realizations. The number of active particles is 1000 across all parameter sets. For the binary mixture, we have varied the fraction of active particles from positive to negative chirality from 10% to 90% with the fixed size ratio S = 8 magnitude of chirality |ω| = 0.7.
III. Results
We now present the rotational dynamics of inclusion, by varying two key parameters—the chirality ω of the active Brownian particles and the size ratio S = ap/aac.Fig. 2 illustrates the time evolution of the inclusion's orientation β(t) for different chirality values for a particular size ratio (S = 8). The columns from left to right are at different times. With time the direction of inclusion reorients in an anticlockwise manner. In each row, the total time is chosen such that the inclusion completes one full 2 × π rotation. The time to complete one full rotation increases with decreasing chirality. The animations corresponding to these snapshots for three different chiralities are shown in Appendix A.
The magnitude of chirality introduces a natural length scale: the radius of curvature of the active particle's trajectory, given by Rc = v/ω. When the size ratio S is larger than Rc, the inclusion acts as an obstacle with respect to the curved paths of the active particles. Conversely, when Rc > S, the active particles follow nearly straight paths, making them more sensitive to the inclusion. Hence the relative ratio of Rcvs. S differentiates the low and high chirality regimes for the system.
At low chirality, the angular trajectory grows slowly and exhibits stronger fluctuations, whereas at high chirality, the rotation proceeds more quickly and smoothly. This indicates that the net torque experienced by the inclusion is present throughout, but becomes more directionally consistent at higher ω, leading to an increase in angular velocity.
To understand the details of the dynamics of the inclusion, it is useful to examine the structure of the torque acting on the inclusion and how it is influenced by the spatial arrangement and motion of the surrounding active particles. The torque is governed by the angular difference between β and the angle ϕpj. As such, the torque term in the angular dynamic works as a collision avoidance55,56 mechanism, deflecting particles away from potential overlap.
Previous studies show that even spherical ABPs with isotropic repulsion accumulate and reorient at boundaries.44,57 Experiments likewise report boundary-induced angular drift.37,58 In our microscopic model, inter-particle forces are isotropic, while the inclusion–particle interaction includes an angular dependence designed as the simplest possible rule to encode this boundary-induced reorientation. This opens up two possible scenarios (illustrated in Fig. 3) for the inclusion's orientation β to remain unaffected. For a single inclusion-active particle interaction, the torque term is ineffective if the inclusion's orientation and rpj are either parallel or antiparallel to each other. But, when many active particles surround the inclusion, any diametrically opposite arrangement of active particle pairs does not account for any net angular displacement to the inclusion as the individual torque contribution from their contacts would nullify each other. The two such possible scenarios are shown in a schematic diagram in Fig. 3(a) and (b). In the next paragraph we will discuss how the inhomogeneous distribution of active particles at the perimeter of the inclusion affects its rotation.
To test this torque-sector-based mechanism, we compute n+ (yellow) and n− (blue), the number of active particles located in the regions of the inclusion boundary contributing positive and negative torque, respectively. The plot is shown with respect to time t, measured from the reference time t0, which is marked as zero on the x-axis. As seen in Fig. 2(a)–(c), persistent rotation is accompanied by a clear asymmetry in these counts, with n+ typically exceeding n−, thus confirming that sustained motion is correlated with a particle density imbalance across the torque-generating sectors.
The snapshots in Fig. 2 as well as the animations in Appendix A show that the distribution of active particles at the surface of the inclusion is visibly inhomogeneous. In this section we study how the orientation of the inclusion depends on the distribution of the active particles at its surface. We compute a time-averaged cross-correlation between the inclusion's orientation β and the ψgap, where ψgap is the angular location with least population of active particles at the surface of the inclusion. We calculate ψgap in the following manner: the region around the inclusion is divided into angular sectors (Δθ) where  and the number of sectors is 2π/Δθ.
and the number of sectors is 2π/Δθ.
The number of such sectors increases with the inclusion size ratio S, providing finer angular resolution. At each time step, a circular shell of radius rshell = ap + 8aac is considered as shown in Fig. 4(a), and the number of particles within each sector is recorded and averaged over 100 independent realisations. The sector with the lowest occupancy is identified, and its central angle is defined as ψgap. The directional correlation between the inclusion and this depleted sector is measured via the cross-correlation function:
| Cβψgap = 〈cos(β − ψgap)〉t. | (4) |
Fig. 4(b)–(g) shows how Cβψgap varies with chirality ω for different inclusion's sizes. Cβψgap is maximum for an achiral system and a pronounced decrease is observed as chirality increases from zero to small finite values.
The physical mechanism underlying this correlation can be described as follows; the inclusion tends to reorient toward the angular sector of its boundary that is least populated by active particles. This is because the torque term always causes the β to turn away from the point of contact. From eqn (3), each active particle in contact with the inclusion contributes a torque. When particles accumulate unevenly, the torque imbalance is such that β tries to evolve toward the angular position where particle density is lower. In this sense, the dynamics of β may be understood as a continuous “chasing” of the depleted sector ψgap. While our measure Cβψgap is a time-averaged quantity and does not show the instantaneous next-step reorientation, it captures the persistence of this alignment over long times and across ensembles.
At ω = 0, active particles move without intrinsic curvature, and the angular dynamics of the inclusion are slow. In this regime, both the inclusion's orientation and the ψgap evolve slowly with time. As a result, the relative angle between them remains more stable across time steps, leading to a higher time-averaged correlation. When chirality is introduced, even weak curvature in particle trajectories causes them to approach the inclusion from a wider range of directions, shifting the position of the depleted sector more frequently. This change breaks the previous alignment and results in a drop in the measured correlation as ω increases from zero.
As chirality increases further, which is shown in marked circles in Fig. 4(b)–(e), the correlation rises and reaches a peak at intermediate ω. In this range, particle motion becomes sufficiently curved and persistent to induce more consistent patterns where particles accumulate and where gaps tend to form. The least-occupied region appears more regularly at specific angular locations relative to the inclusion, improving the average alignment and increasing the correlation.
At higher chirality, the correlation gradually decreases again. Particles now follow tight curved paths and interact with the inclusion more frequently, but with shorter contact durations. This leads to more uniform exploration of the inclusion boundary and suppresses persistent low-density regions. Consequently, the angular position of the gap becomes more evenly distributed around the inclusion's surface, and the average alignment with the inclusion orientation weakens.
This trend also depends on the inclusion size ratio. For smaller inclusions (Fig. 4(b)–(e)), the features become prominent: the initial drop, the peak, and the high-ω decay are more pronounced. As S increases, the number of angular sectors grows, and the contribution of any single depleted sector to the overall correlation is reduced. The larger perimeter also supports a greater number of particle interactions, which smooths out density variations. As a result, the correlation curve becomes flatter, and for the larger inclusions (Fig. 4(f) and (g)), the peak becomes less distinct. Interestingly, the correlation Cβψgap shows a maximum near ω ≈ 0.15 for intermediate sizes S = 8–12. A simple estimate based on the balance Rc = v0/ω ∼ S would suggest that this peak should shift to lower ω as S increases. Instead, we observe that beyond S ≈ 8 the peak position saturates. This is because the persistence length of active particles (lp = v0/DR = 10 = 100aac) sets a natural length scale for collision geometry. Once the inclusion radius becomes comparable to or larger than l, further growth of S does not change how particles distribute around the boundary, so the peak value of ω stabilizes over the size ratios.
To quantify the rotational dynamics of inclusion we calculate the angle auto-correlation of β(t) defined by
| C(τ) = 〈cos[β(t + τ) − β(t)]〉t | (5) |
At low ω, the autocorrelation decays slowly, indicating that the torquer undergoes weak and slower reorientation over time and retains angular memory over a large time. With increasing chirality, the autocorrelation decays more rapidly. For ω > 0.3, distinct oscillations emerge in C(τ), signaling that the inclusion is rotating frequently and periodically. Each cycle of the oscillation corresponds approximately to a full angular revolution, with maxima and minima denoting recurrent alignment and anti-alignment with the initial orientation, respectively. In Fig. 5(a)–(c), the left panel shows the semi-log-y plot of C(τ) vs. time τ, which shows that for all chiralities and size ratios the early time decay of C(τ) is exponential and becomes periodic at larger times. The periodicity is clear in the right panel plot of C(τ) vs. time on a linear scale. The periodic oscillations are clear for larger chiralities. In bottom two rows (Fig. 5(d) and (e)) we show the plot of C(τ) vs. time for two ω values, 0.1 and 1.0, respectively, and for different size ratios. For a smaller ω of 0.1, the C(τ) remains invariant by increasing S, whereas decay sharpens for larger S at high ω = 1.0, although the dependence on S is much weaker than that on ω.
The overall behavior of C(τ) thus reveals a transition from slow angular dynamics at low chirality to coherent, persistent rotation at higher chirality. In the higher chiral regime, active particles follow more curved trajectories due to stronger rotational drive, leading to more frequent re-encounters with the inclusion boundary. These interactions are shaped by the curvature of their paths and the constraint of volume exclusion, resulting in angularly biased contact patterns around the inclusion. While individual contacts may be brief, the consistent directional tendency of these interactions gives rise to a net torque, conducive to persistent rotation.
Now we characterize the magnitude of rotation of the inclusion by measuring its mean angular velocity.
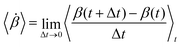 | (6) |
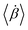 as a function of chirality ω for different size ratios S. 〈⋯〉 has the same meaning as defined before. At low ω, the mean angular velocity is small, indicating weak or incoherent rotation. As chirality increases, the angular velocity rises sharply and reaches a peak at an intermediate value of ω. This trend implies that increased chirality initially enhances rotation, likely due to the collective effect of more directionally consistent particle interactions. However, beyond the peak, the angular velocity does not continue to grow despite increased directional bias in the particle motion. Rather, it leads to a decline in
as a function of chirality ω for different size ratios S. 〈⋯〉 has the same meaning as defined before. At low ω, the mean angular velocity is small, indicating weak or incoherent rotation. As chirality increases, the angular velocity rises sharply and reaches a peak at an intermediate value of ω. This trend implies that increased chirality initially enhances rotation, likely due to the collective effect of more directionally consistent particle interactions. However, beyond the peak, the angular velocity does not continue to grow despite increased directional bias in the particle motion. Rather, it leads to a decline in  . This decline is more pronounced for smaller size ratios (Fig. 6(a) and (b)). In such cases, the inclusion's small surface cannot sustain the persistent rotation of active particles once chirality becomes too high. The rapidly turning active particles fail to establish or maintain persistent directional forces necessary for sustained rotation, resulting in a gradual drop in
. This decline is more pronounced for smaller size ratios (Fig. 6(a) and (b)). In such cases, the inclusion's small surface cannot sustain the persistent rotation of active particles once chirality becomes too high. The rapidly turning active particles fail to establish or maintain persistent directional forces necessary for sustained rotation, resulting in a gradual drop in  . On the other hand, the large inclusion (Fig. 6(c)–(f)), with extended perimeters, continues to interact with a broader distribution of active particles, enabling a more sustained torque input even at higher chirality. This results in a slower, more gradual decline in
. On the other hand, the large inclusion (Fig. 6(c)–(f)), with extended perimeters, continues to interact with a broader distribution of active particles, enabling a more sustained torque input even at higher chirality. This results in a slower, more gradual decline in  for larger size ratios. This indicates that larger torquers are able to sustain faster rotation over a broader range of chirality values, likely due to a greater opportunity for interaction with more active particles along their extended boundary.
for larger size ratios. This indicates that larger torquers are able to sustain faster rotation over a broader range of chirality values, likely due to a greater opportunity for interaction with more active particles along their extended boundary.
 | ||
Fig. 6 (a)–(f) show mean angular velocity 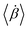 of the torquer as a function of chirality ω for size ratios S = 6, 8, 10, 12, 14, and 16. of the torquer as a function of chirality ω for size ratios S = 6, 8, 10, 12, 14, and 16. | ||
We further estimate how much the interaction time of active particles with the inclusion is influenced by their chirality. We then measure the mean residence time of a single active particle at the surface of the inclusion, where the mean is calculated over all the active particles coming in contact with the inclusion's surface, all of which stayed longer than or equal to 10−2τ. Also the mean is calculated over different independent realisations. In Fig. 7(a)–(e) we show the variation of residence time tr (shown in units of τ) vs. ω for different S. For all size ratios the tr decreases with increasing ω, which is just due to the faster reorientation events of active particles upon increasing ω. For small ω, ≤0.1, decay is slower and then shows a sharp decay for intermediate 0.1 < ω < 0.2 and for larger ω it flattens. Further in Fig. 7(f) we show the scaled residence time trvs. ω and find that data for all S values collapse to a single curve with scaled  .
.
Binary mixture of chiral active particles
We next consider how the rotational dynamics change when the active bath consists of a mixture of clockwise and counterclockwise chiral particles. We fixed the size ratio to 8 and the magnitude of chirality to |ω| = 0.7 and varied the fraction of clockwise active particles in the binary mixture of clock-wise and anti-clockwise active particles keeping the total packing fraction of the active particles fixed at ϕa = 0.5. The fraction ϕa,clock is varied from 0.1 to 0.9. In Fig. 8(a), we plot the mean angular velocity of the inclusion as a function of ϕa,clock. As expected, the rotation reverses sign across the 50–50 mixture point.
of the inclusion as a function of ϕa,clock. As expected, the rotation reverses sign across the 50–50 mixture point.
This confirms that the direction of inclusion rotation is considerably controlled by the net chirality in the system and provides a consistency check on our interaction rules. For our present study we do not observe any phase separation between two types of chiral particles. However, the binary mixture of chiral active particles shows the phase separation when the persistent length of the particle is much larger than the other relevant length scales in the system. In chiral active systems, a comparison can be made for two competitive lengths,  and persistent length
and persistent length  . Rc decides the radius of the contour made by the particles. The phase separation can develop when lp ≫ Rc. In a recent study, ref. 27, it is found that a binary mixture of chiral active particles can phase separate when lp ∼ 100Rc. The relative ratio of lp/Rc varies from 1 to 10 by tuning the magnitude of chirality. Larger lp is not very relevant for the current study, because the system will reach a limit where lp is much larger than the space available for the particles and for such high lp, active particles may not experience any inclusion in their path. The mutual alignment interaction among the particles can promote the phase separation at much smaller lp as found in ref. 19 and 29.
. Rc decides the radius of the contour made by the particles. The phase separation can develop when lp ≫ Rc. In a recent study, ref. 27, it is found that a binary mixture of chiral active particles can phase separate when lp ∼ 100Rc. The relative ratio of lp/Rc varies from 1 to 10 by tuning the magnitude of chirality. Larger lp is not very relevant for the current study, because the system will reach a limit where lp is much larger than the space available for the particles and for such high lp, active particles may not experience any inclusion in their path. The mutual alignment interaction among the particles can promote the phase separation at much smaller lp as found in ref. 19 and 29.
Effect of varying the packing fraction of active particles
Subsequently we also studied how the rotational behavior depends on the overall density of active particles. In Fig. 8(b), we plot as a function of packing fraction (ϕa), for a fixed chirality and size ratio. We observe that below ϕa ≈ 0.2, the angular velocity of the inclusion remains small, indicating insufficient interactions for torque buildup. Above this threshold, the angular velocity rises sharply and saturates at higher densities. This behavior suggests a density-driven onset of rotational activity, possibly linked to collective boundary accumulation and the emergence of edge currents.28
as a function of packing fraction (ϕa), for a fixed chirality and size ratio. We observe that below ϕa ≈ 0.2, the angular velocity of the inclusion remains small, indicating insufficient interactions for torque buildup. Above this threshold, the angular velocity rises sharply and saturates at higher densities. This behavior suggests a density-driven onset of rotational activity, possibly linked to collective boundary accumulation and the emergence of edge currents.28
IV. Discussion
Our study demonstrates that persistent rotational dynamics can emerge in a geometrically symmetric inclusion solely due to the inhomogeneous interaction with a bath of chiral active Brownian particles (ABPs). This result contrasts with earlier works that primarily attribute rotation due to shape asymmetry in the inclusion. By carefully tuning the chirality of the active particles and the size ratio between active particles and the torquer, we uncover two distinct mechanisms that contribute to the angular motion of the torquer: torque imbalance due to spatial inhomogeneities and residence-time–driven torque generation. At low chirality, rotational diffusion of active particles leads to persistent local clustering and density imbalance around the torquer, generating a net torque through uneven force contributions. These density inhomogeneities drive a slower but irregular rotation. The resulting angular dynamics is slow and lacks persistence, as evidenced by the gradual decay in orientation autocorrelation and the high correlation between the torquer orientation and the gap angle. This mechanism is stochastic and indirect, relying on spontaneous clustering and local jamming in the sense that provides a transient crowding at the periphery causing a torque imbalance rather than a permanent arrested state near the inclusion's perimeter.In contrast, in the high-chirality regime, active particles exhibit persistent circular motion, with a strong bias in orientation dynamics. While this chirality enhances the coherence of the torque direction, it simultaneously reduces the residence time of active particles on the inclusion surface. The decreased contact duration limits the efficacy of torque transmission, causing a saturation or even decline in the angular velocity of the inclusion.
Our measurements of residence time directly support this interpretation: the peak in angular velocity corresponds to the crossover point where the directional coherence of particle motion outweighs the loss of contact time, beyond which the torque efficiency diminishes. The non-monotonic dependence of inclusion's rotation on chirality thus emerges from a competition between directional order and interaction duration. Rotation arises from bath particle trajectories: some leave quickly after contact, while others linger near the torquer, especially when rotational diffusion and chirality are small. This asymmetry in long-lived contacts transfers torque to the inclusion. We quantify this mechanism, showing a crossover from density-imbalance–driven torque at low ω to impact-frequency-dominated torque at high ω, along with a universal  scaling of residence time. These provide clear criteria for when rotational motion occurs, even for symmetric inclusions.
scaling of residence time. These provide clear criteria for when rotational motion occurs, even for symmetric inclusions.
Interestingly, increasing the size ratio S enhances both mechanisms: it promotes stronger density fluctuations at low chirality and sustains longer contact arcs at high chirality. As a result, a larger inclusion sustains higher angular velocities over broader chiralities, suggesting a potential control knob for optimizing rotational behavior. We have also verified that including angular inertia in the evolution of the inclusion does not significantly alter the observed rotation dynamics, confirming that the overdamped approximation remains valid within our parameter regime. Besides chirality-induced rotation, we occasionally observed reversed cycles. These are controlled by two ratios: lp/S, which sets the role of density inhomogeneities, and Rc/S, which quantifies curvature effects. Reversed events appear when lp/S ≳ 1 or when Rc/S ≲ 1. Considering rods or other anisotropic shapes may add competing torques and help stabilize such reversed dynamics which will be explored in the future work.
These findings have broader implications for the design of synthetic micromachines and activity driven transport mechanisms. In particular, they demonstrate that shape asymmetry is not a necessary condition for generating persistent motion in active environments. Here we demonstrate that even a perfectly smooth circular disk, with no geometric features such as teeth, undergoes persistent rotation purely from angularly biased collisions with chiral active particles. Instead, chirality-induced alignment interactions alone can suffice. In this study the inclusion was fixed and only rotated, but allowing translation would open new effects. Odd viscosity in the chiral bath means a drifting inclusion could acquire a transverse velocity, similar to a Magnus effect.59,60 With multiple inclusions, such flows may drive interactions that lead to alignment, clustering, or collective rotating structures. These extensions are part of our ongoing work on many passive particles in chiral active baths. For broader context, see the recent works, ref. 61 and 62.
Author contributions
Abhra Puitandy: writing – review and editing, writing – original draft, validation, investigation, funding acquisition, formal analysis, data curation, conceptualization; Shradha Mishra: writing – review and editing, validation, supervision, project administration, funding acquisition, conceptualization, the final version of the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Data availability
All data that support the findings of this study are included within the article.Appendix
A Description of animations
Mov1: The animation shows a single rotation for the size ratio S = 8 and ω = 0.5.Link: https://drive.google.com/file/d/1ROBoccGbVhQMLaie8Osl5yQnr9kVChBV/view?usp=sharing.
Mov2: The animation shows a single rotation for the size ratio S = 8 and ω = 0.7.
Link: https://drive.google.com/file/d/1pwSqLrsNhYYLPngd0kf4kwWpXCWO8zY8/view?usp=sharing.
Mov3: The animation shows a single rotation for the size ratio S = 8 and ω = 1.0.
Link: https://drive.google.com/file/d/1wIKW9SeMHUVcodDGQ-s1QrusjljvMdV0/view?usp=sharing.
Acknowledgements
AP thanks the support and the resources provided by the PARAM Shivay Facility under the National Supercomputing Mision, Government of India at the Indian Institute of Technology, Varanasi. SM thanks DSTSERB India, ECR/2017/000659, CRG/2021/006945 and MTR/2021/000438 for financial support.References
- G. Mahmud, C. J. Campbell, K. J. Bishop, Y. A. Komarova, O. Chaga, S. Soh, S. Huda, K. Kandere-Grzybowska and B. A. Grzybowski, Directing cell motions on micropatterned ratchets, Nat. Phys., 2009, 5(8), 606–612 Search PubMed.
- É. Fodor and M. C. Marchetti, The statistical physics of active matter: From self-catalytic colloids to living cells, Phys. A, 2018, 504, 106–120 CrossRef.
- C. L. Hueschen, A. R. Dunn and R. Phillips, Wildebeest herds on rolling hills: Flocking on arbitrary curved surfaces, Phys. Rev. E, 2023, 108(2), 024610 CrossRef CAS PubMed.
- A. Bottinelli, D. T. Sumpter and J. L. Silverberg, Emergent structural mechanisms for high-density collective motion inspired by human crowds, Phys. Rev. Lett., 2016, 117(22), 228301 CrossRef PubMed.
- M. E. Cates, D. Marenduzzo, I. Pagonabarraga and J. Tailleur, Arrested phase separation in reproducing bacteria creates a generic route to pattern formation, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(26), 11715–11720 CrossRef CAS PubMed.
- S. Dikshit and S. Mishra, Ordering kinetics in active polar fluid, Europhys. Lett., 2023, 143(1), 17001 CrossRef CAS.
- Y. Fily and M. C. Marchetti, Athermal phase separation of self-propelled particles with no alignment, Phys. Rev. Lett., 2012, 108(23), 235702 CrossRef PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Structure and dynamics of a phase-separating active colloidal fluid, Biophys. J., 2013, 104(2), 640a CrossRef.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Continuum theory of phase separation kinetics for active brownian particles, Phys. Rev. Lett., 2013, 111(14), 145702 CrossRef PubMed.
- A. G. Thompson, J. Tailleur, M. E. Cates and R. A. Blythe, Lattice models of nonequilibrium bacterial dynamics, J. Stat. Mech.: Theory Exp., 2011, 2011(02), P02029 CrossRef.
- A. Wysocki, R. G. Winkler and G. Gompper, Cooperative motion of active brownian spheres in three-dimensional dense suspensions, Europhys. Lett., 2014, 105(4), 48004 CrossRef.
- H. Chaté, Dry aligning dilute active matter, Ann. Rev. Condens. Matter Phys., 2020, 11(1), 189–212 CrossRef.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Novel type of phase transition in a system of self-driven particles, Phys. Rev. Lett., 1995, 75(6), 1226 CrossRef CAS PubMed.
- B. Liebchen and D. Levis, Collective behavior of chiral active matter: Pattern formation and enhanced flocking, Phys. Rev. Lett., 2017, 119(5), 058002 CrossRef PubMed.
- J. Bialké, T. Speck and H. Löwen, Active colloidal suspensions: Clustering and phase behavior, J. Non-Cryst. Solids, 2015, 407, 367–375 CrossRef.
- S. Gokhale, J. Li, A. Solon, J. Gore and N. Fakhri, Dynamic clustering of passive colloids in dense suspensions of motile bacteria, Phys. Rev. E, 2022, 105(5), 054605 CrossRef CAS PubMed.
- H. S. Jennings, On the significance of the spiral swimming of organisms, Am. Nat., 1901, 35(413), 369–378 CrossRef.
- V. Semwal, J. Joshi, S. Dikshit and S. Mishra, Macro to micro phase separation of chiral active swimmers, Phys. A, 2024, 634, 129435 CrossRef.
- Y. Wang, B. Ventéjou, H. Chaté and X.-Q. Shi, Condensation and synchronization in aligning chiral active matter, Phys. Rev. Lett., 2024, 133(25), 258302 CrossRef CAS PubMed.
- Q.-L. Lei, M. P. Ciamarra and R. Ni, Nonequilibrium strongly hyperuniform fluids of circle active particles with large local density fluctuations, Sci. Adv., 2019, 5(1), eaau7423 CrossRef PubMed.
- M. Huang, W. Hu, S. Yang, Q.-X. Liu and H. Zhang, Circular swimming motility and disordered hyperuniform state in an algae system, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(18), e2100493118 CrossRef CAS PubMed.
- Y. Zhang, T. Zheng, L. Wang, L. Feng, M. Wang, Z. Zhang and H. Feng, From passive to active sorting in microfluidics: a review, Rev. Adv. Mater. Sci., 2021, 60(1), 313–324 Search PubMed.
- Y. Kuroda and K. Miyazaki, Microscopic theory for hyperuniformity in two-dimensional chiral active fluid, J. Stat. Mech.: Theory Exp., 2023, 2023(10), 103203 CrossRef.
- L. Caprini, B. Liebchen and H. Löwen, Self-reverting vortices in chiral active matter, Commun. Phys., 2024, 7(1), 153 CrossRef.
- D. Nishiguchi, S. Shiratani, K. A. Takeuchi and I. S. Aranson, Vortex reversal is a precursor of confined bacterial turbulence, Proc. Natl. Acad. Sci. U. S. A., 2025, 122(11), e2414446122 CrossRef CAS PubMed.
- V. E. Debets, H. Löwen and L. M. Janssen, Glassy dynamics in chiral fluids, Phys. Rev. Lett., 2023, 130(5), 058201 CrossRef CAS PubMed.
- B.-Q. Ai, S. Quan and F.-G. Li, Spontaneous demixing of chiral active mixtures in motility-induced phase separation, New J. Phys., 2023, 25(6), 063025 CrossRef.
- C. Reichhardt and C. Reichhardt, Reversibility, pattern formation, and edge transport in active chiral and passive disk mixtures, J. Chem. Phys., 2019, 150, 064905 CrossRef CAS PubMed.
- D. Kushwaha and S. Mishra, From flocking to condensation: Collective dynamics in binary chiral active matter, Phys. A, 2025, 130897 CrossRef.
- J.-R. Li, W.-j Zhu, J.-J. Li, J.-C. Wu and B.-Q. Ai, Chirality-induced directional rotation of a symmetric gear in a bath of chiral active particles, New J. Phys., 2023, 25(4), 043031 CrossRef.
- X.-l Li and W.-j Zhu, Directed rotation of a symmetric gear driven by visual-perception-dependent particles, Chaos, Solitons Fractals, 2025, 190, 115782 CrossRef.
- H.-z Xie and J.-r Li, Chirality-induced rectification in asymmetric gear systems, Eur. Phys. J. B, 2025, 98(3), 1–7 CrossRef.
- A. Sokolov, M. M. Apodaca, B. A. Grzybowski and I. S. Aranson, Swimming bacteria power microscopic gears, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(3), 969–974 CrossRef CAS PubMed.
- S. Ray, J. Zhang and Z. Dogic, Rectified rotational dynamics of mobile inclusions in two-dimensional active nematics, Phys. Rev. Lett., 2023, 130(23), 238301 CrossRef CAS PubMed.
- C. O. Reichhardt and C. Reichhardt, Ratchet effects in active matter systems, Ann. Rev. Condens. Matter Phys., 2017, 8, 51–75 CrossRef.
- S. Shankar and M. C. Marchetti, Hydrodynamics of active defects: From order to chaos to defect ordering, Phys. Rev. X, 2019, 9(4), 041047 CAS.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Active particles in complex and crowded environments, Rev. Mod. Phys., 2016, 88(4), 045006 CrossRef.
- R. Chand, A. Shukla, S. Boby and G. P. Kumar, Optothermally induced active and chiral motion of colloidal structures, Soft Matter, 2025, 21, 4622 RSC.
- R. Chand, C. E. Rani, D. Paul and G. P. Kumar, Emergence of directional rotation in an optothermally activated colloidal system, ACS Photonics, 2023, 10(11), 4006–4013 CrossRef CAS.
- P. Tierno, R. Golestanian, I. Pagonabarraga and F. Sagués, Controlled swimming in confined fluids of magnetically actuated colloidal rotors, Phys. Rev. Lett., 2008, 101(21), 218304 CrossRef PubMed.
- L. Wang and J. Simmchen, Determination of the swimming mechanism of au@ tio 2 active matter and implications on active-passive interactions, Soft Matter, 2023, 19(3), 540–549 RSC.
- I. T. Li, Y. R. Chemla and T. Ha, Mapping cell surface adhesion by rotation tracking and adhesion footprinting, Biophys. J., 2017, 112(3), 1a CrossRef.
- O. Pohl and H. Stark, Dynamic clustering and chemotactic collapse of self-phoretic active particles, Phys. Rev. Lett., 2014, 112(23), 238303 CrossRef PubMed.
- P. Eswaran and S. Mishra, Synchronized rotations of active particles on chemical substrates, Soft Matter, 2024, 20(11), 2592–2599 RSC.
- J. Olarte-Plata, J. M. Rubi and F. Bresme, Thermophoretic torque in colloidal particles with mass asymmetry, Phys. Rev. E, 2018, 97(5), 052607 CrossRef PubMed.
- A. Aubret, M. Youssef, S. Sacanna and J. Palacci, Targeted assembly and synchronization of self-spinning microgears, Nat. Phys., 2018, 14(11), 1114–1118 Search PubMed.
- S. Das, A. Sane, S. Bhadra, S. Ghosh, O. Granek, Y. Kafri and D. Levine, Lever rule violation and pressure imbalance in a driven granular system, arXiv, 2024, preprint, arXiv:2410.23863 DOI:10.48550/arXiv.2410.23863.
- B. C. Van Zuiden, J. Paulose, W. T. Irvine, D. Bartolo and V. Vitelli, Spatiotemporal order and emergent edge currents in active spinner materials, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(46), 12919–12924 CrossRef CAS PubMed.
- M. J. Lighthill, On the squirming motion of nearly spherical deformable bodies through liquids at very small reynolds numbers, Commun. Pure Appl. Math., 1952, 5(2), 109–118 CrossRef.
- J. R. Blake, A spherical envelope approach to ciliary propulsion, J. Fluid Mech., 1971, 46(1), 199–208 CrossRef.
- R. E. Goldstein, Green algae as model organisms for biological fluid dynamics, Annu. Rev. Fluid Mech., 2015, 47(1), 343–375 CrossRef PubMed.
- P. Curie, On symmetry in physical phenomena, J. Phys. III, 1894, 3, 393–415 Search PubMed.
- R. Di Leonardo, L. Angelani, D. Dell’Arciprete, G. Ruocco, V. Iebba, S. Schippa, M. P. Conte, F. Mecarini, F. De Angelis and E. Di Fabrizio, Bacterial ratchet motors, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(21), 9541–9545 CrossRef CAS PubMed.
- R. Soto and R. Golestanian, Self-assembly of catalytically active colloidal molecules: tailoring activity through surface chemistry, Phys. Rev. Lett., 2014, 112(6), 068301 CrossRef PubMed.
- O. Chepizhko, E. G. Altmann and F. Peruani, Optimal noise maximizes collective motion in heterogeneous media, Phys. Rev. Lett., 2013, 110(23), 238101 CrossRef PubMed.
- G. Grégoire and H. Chaté, Onset of collective and cohesive motion, Phys. Rev. Lett., 2004, 92(2), 025702 CrossRef PubMed.
- J. Elgeti and G. Gompper, Wall accumulation of self-propelled spheres, Europhys. Lett., 2013, 101(4), 48003 CrossRef CAS.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Hydrodynamic attraction of swimming microorganisms by surfaces, Phys. Rev. Lett., 2008, 101(3), 038102 CrossRef PubMed.
- C. Reichhardt and C. Reichhardt, Active rheology in odd-viscosity systems, Europhys. Lett., 2022, 137(6), 66004 CrossRef CAS.
- C. Reichhardt and C. O. Reichhardt, Active microrheology, hall effect, and jamming in chiral fluids, Phys. Rev. E, 2019, 100(1), 012604 CrossRef CAS PubMed.
- O. Granek, Y. Kafri, M. Kardar, S. Ro, J. Tailleur and A. Solon, Colloquium: Inclusions, boundaries, and disorder in scalar active matter, Rev. Mod. Phys., 2024, 96(3), 031003 CrossRef.
- C. Hargus, F. Ghimenti, J. Tailleur and F. van Wijland, Odd dynamics of passive objects in a chiral active bath, arXiv, 2024, preprint, arXiv:2412.20689 DOI:10.48550/arXiv.2412.20689.
| This journal is © The Royal Society of Chemistry 2026 |











