Shape spectra of elastic shells with surface-adsorbed semiflexible polymers
Hadiya Abdul
Hameed
 a,
Jarosław
Paturej
a,
Jarosław
Paturej
 b and
Aykut
Erbaş
b and
Aykut
Erbaş
 *a
*a
aUNAM-National Nanotechnology Research Center and Institute of Materials Science & Nanotechnology, Bilkent University, Ankara 06800, Turkey. E-mail: aykut.erbas@unam.bilkent.edu.tr
bInstitute of Physics, University of Silesia at Katowice, Chorzów 41-500, Poland
First published on 1st December 2025
Abstract
The shape of biological shells, such as cell nuclei, membranes, and lipid vesicles, often deviates from a perfect sphere due to an interplay of complex interactions with a myriad of molecular structures. In particular, semiflexible biopolymers adsorbed to the surfaces of such shells seem to affect their morphological properties. While the effect of a single, long, semiflexible chain is relatively well characterized, the mechanisms by which a high density of such surface-adsorbed polymers can alter the morphology of a spherical, soft confinement, akin to biological shells, remain relatively poorly understood. Here, we use coarse-grained molecular dynamics to explore how surface adsorption of many semiflexible polymers affects the morphology of a pressurized bead-spring network shell, which is spherical in the absence of these polymers. By varying the attraction strength between the semiflexible chains and the shell surface, chain concentration, and the polymerization degree of chains, we demonstrate that strong surface localization of the chains can induce shape distortions and decreased shell size. Conversely, weak localization does not induce significant shape fluctuations, yet nematically ordered phases appear on the surface. Notably, these ordered phases lead to elliptic shell shapes for chains with sizes comparable to or longer than the radius of the confinement when the elastic shell is composed of extensible, harmonic bonds, which may emulate a liquid-like structure. Overall, our findings offer a strategy to control the morphology of synthetic shells by manipulating peripheral localization and length of semiflexible polymers while suggesting a mechanism for non-spherical shapes appearing in some biological systems.
1 Introduction
The shape regulation of biological shells plays a fundamental role in the stability and functionality of various biological systems. For instance, the force interplay between the viscoelastic actin network making up the cytoplasm and the deformable cell membrane dictates cell shape and size.1,2 Similarly, cellular compartments such as the nucleus experience shape alterations due to chromatin pressure at the interior,3 the mechanics of the cytoskeleton, and nuclear lamina, a layer of filamentous proteins lining the inner nuclear membrane.4–8 Aberrant nuclear shapes are considered hallmarks of several diseases, such as progeria, muscular dystrophy, and even certain types of cancer,9–13 suggesting the importance of shape regulation mechanisms in those systems.Many biopolymers that could intervene in the shape of the above-mentioned shells, such as double-stranded DNA, actin, or lamin supramolecular structures, appear to be of a semiflexible nature. Semiflexibility arises if the persistence length, lp, of the polymer is comparable to its contour length, l.14 The persistence length, lp, defines the characteristic length scale below which thermal fluctuations cannot bend the polymer chain.14–17 On length scales shorter than or comparable to lp (i.e., lp ≥ l), the polymer can behave as a rod-like or semiflexible polymer, respectively.14–17 The persistence length scales with the thickness of a polymer, a, as lp ∼ a4, which renders many biological fibers as highly stiff, semiflexible chains at short length scales. For instance, double-stranded DNA with a thickness of a = 2 nm has a uniform persistence length of lp ≈ 50 nm, which constitutes ≫150 base pairs, elucidating its semiflexible nature.16,18–20 Moreover, lamin protofilaments with a ≈ 4 nm could exhibit persistent length values at around lp ≈ 500 nm.7
If such semiflexible biopolymers are confined inside a deformable shell, such as a lipid vesicle or a hollow-hydrogel shell, they can compete with the bending rigidity of the confinement and lead to various shape fluctuations of the shell. More specifically, if a single semiflexible polymer (e.g., an actin filament) has a contour length, l, larger than the vesicle radius, R, the buckling of the chain is accompanied by increasingly aspherical vesicle shapes.21–23 Notably, increasing confinement by increasing the persistence length (or decreasing the confinement size) localizes the chains towards the periphery in order to minimize chain bending. In turn, this local concentration increase enhances nematic ordering,16,24–26 further contributing to the shape distortion of the shell.21–23,27,28
When “many” such semiflexible chains or their supramolecular structures are confined inside a soft shell, the shape distortion often requires chain adsorption to the confining walls.29 In fact, if the confinement is weak, which can be controlled by decreasing chain concentration or the chain contour length, l, relative to the vesicle radius, R,29,30 the adsorbed chains can form nematic-phase domains or “tennis ball”-like patterns on the surface of the confinement.8,31–33 Nonetheless, adsorbed chains do not change the spherical form of the vesicle at weak confinement.4,29,34,35 Under strong confinement (i.e., increasing chain concentration or contour length, l), the chains can form global phases where most chains align in a parallel fashion on the vesicle surface,32,36–38 which, in turn, can also generate elongated or non-spherical vesicle shapes.29 Similarly, the orientational arrangement of confined anisotropic liquid crystals, such as tactoids, can also overcome the elastic energy of soft shells, leading to non-spherical vesicle forms.39–41 Consistently, implicit modeling of pressurized elastic shells showed that the shape can transition from spherical to an ellipsoid if the shell is composed of anisotropic structural elements.42 Monte Carlo simulations further show that such shells can undergo symmetric shape transitions, such as ellipsoids or buckled configurations, when osmotic pressure is controlled externally.43
In the context of biology, structures such as the nuclear-lamina meshwork are adsorbed to the confinement walls (i.e., nuclear envelope) and can govern the shape of the cell nucleus.3,7,44–46 Notably, in several disease types, lamin structures reminiscent of nematic-phase domains appear on the nuclear surface.8,13,47–49 Similarly, dsDNA scaffolds or DNA origami structures mechanically strengthen lipid vesicles,50–52 but distort the shape at high concentrations.53 Overall, while the effect of chain concentration on the phase behavior of such semiflexible polymers or active filaments has been discussed,8,30,54,55 how this self-assembly on the surface and parameters that can control surface-adsorption could affect the shape of an elastic shell remains to be studied.
In this study, we use an elastic shell model composed of a permanent bead-spring network to study how the adsorption of semiflexible polymers to the internal wall of the shell could change its shape by using coarse-grained molecular dynamics (MD) simulations. The elastic shell was developed in our previous studies and can change its form from a perfect sphere.3,56 Motivated by lamin-protein-driven nuclear shape anomalies in several diseases and actin-confining liposomes, we consider chain densities below and above the chain overlap concentration, alongside chain lengths below and above the dimensions of the confinement, to emulate various confinement scenarios and characterize the structural fluctuations of the shell. Our results show that adsorption of polymers to the shell surface can cause a wide spectrum of shape fluctuations from spherical forms with large undulations to elongated morphologies. “Softer” (liquid-like) shells are more prone to form oval structures by nematically oriented chains on the surface, whereas strong adsorption distorts these phases and leads to shape fluctuation for more elastic shells. Our calculations also demonstrate the effectiveness of combining polymer and vesicle elasticity to design hybrid structures, while qualitatively addressing nuclear shape anomalies observed in several genetic diseases.9–13
2 Methods
2.1 Simulation model
Our MD simulation model emulates a pressurized elastic shell, where semiflexible polymers can adsorb onto the confining interior wall of a soft, deformable shell. The model consists of three components: (i) flexible polymers providing an internal pressure, (ii) semiflexible chains that can adsorb to the surface, and (iii) an elastic shell confining all the polymers defined in (i) and (ii) (see Fig. 1a). All components are represented using a coarse-grained approach, where each constituent is modeled as a collection of spherical beads (monomers) of mass, m. These monomers are connected either into chains (for flexible polymers and semiflexible chains) or into a mesh-like network (for the elastic shell) via springs to capture the mechanical connectivity (see Fig. 1a). All polymer chains consist of monomers linked sequentially, differing in their bending stiffness, while the shell is modeled as a monolayer meshwork of monomers connected to their nearest neighbors.Non-bonded interactions between all monomers are described by a shifted and truncated Lennard-Jones (LJ) potential
 | (1) |
The bonded interactions between monomers are modeled by a finitely extensible non-linear elastic (FENE) potential unless noted otherwise
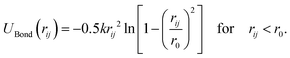 | (2) |
The bending rigidity of semiflexible polymers is governed by a harmonic bending potential
| UBend(θ) = kθ(θijk − θ0)2 | (3) |
As a first step of preparation of simulation systems, we construct the elastic spherical shell as a single-layer meshwork composed of coarse-grained beads (see Fig. 1a).3 All simulations use a shell consisting of Nshell = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 beads, which are initially distributed randomly over a spherical surface with a radius of R0 = 51σ. To prevent bead overlap and ensure a dense but uniform distribution of shell monomers, we introduce a distance parameter, d, which defines the minimum allowed separation between neighboring beads on the shell surface. This parameter is optimized to balance two constraints: avoiding steric clashes and allowing beads to fit into tight regions of the mesh (see Fig. 1a). Specifically, d is chosen within the range
500 beads, which are initially distributed randomly over a spherical surface with a radius of R0 = 51σ. To prevent bead overlap and ensure a dense but uniform distribution of shell monomers, we introduce a distance parameter, d, which defines the minimum allowed separation between neighboring beads on the shell surface. This parameter is optimized to balance two constraints: avoiding steric clashes and allowing beads to fit into tight regions of the mesh (see Fig. 1a). Specifically, d is chosen within the range
| 0.60f < d < 1.0f | (4) |
| 0.66f < r < 0.9f | (5) |
If a minimum of nbond = 5 bonds are not formed under these conditions (eqn (5)), beads are allowed to bond with distant beads by expanding r by 0.30.
In simulations, four long flexible polymers are confined within the elastic shell to generate osmotic pressure that counteracts excessive inward collapse of the shell and avoids any polymer–monomer linkages (see Fig. 1, pink chains). In the absence of semiflexible chains or when semiflexible chains are not adsorbed to the shell surface, the polymer-induced pressure provides a spherical shell. Hence, the interior pressure is not imposed externally, unlike pressurized shells,42,43 but is altered dynamically depending on the localization of the semiflexible chains to the shell interior. These polymers are organized into compact, grid-like blocks, each comprising Npolymer = 6002 monomers, leading to a total polymer volume fraction of approximately ϕ ≈ 10%. Each block is constructed by first placing an initial monomer at a random position within a radius of 34σ from the shell center (see Fig. 1b). A random orientation is then assigned using directional angles constrained to ensure sufficient spacing between the polymer and shell, as enforced by the condition
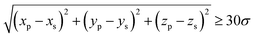 | (6) |
In addition to flexible polymers, we also include semiflexible molecules confined within the elastic shell (see Fig. 1a). Each semiflexible molecule consists of Nsf monomers arranged linearly. To maintain semiflexible behavior, we keep the persistence-to-contour length ratio fixed at lp/l = 2.5 for all semiflexible chains, where l = (Nrod − 1)lb. The number of these chains is varied across simulations to investigate their influence on the shape of the shell.
Initially, semiflexible polymer chains are randomly placed within the elastic shell, as illustrated in Fig. 1b. To close large pores in the shell and prevent polymer or chain escape, the shell is isotropically shrunk by approximately 15% through an energy minimization process. This minimization is carried out for 30τ using an integration time step of Δt = 0.001τ, with a damping coefficient of 0.1mτ−1 (see Fig. 1b, right panel). Following minimization, the system is relaxed for 500τ with a larger time step of Δt = 0.005τ. Only repulsive interactions are active, allowing both the flexible polymers and semiflexible chains to equilibrate and lose memory of their initial configurations (see Fig. 1b, center panel). After this, the main production run is performed for 1.25 × 104τ with Δt = 0.005τ (see Fig. 1b, left panel). During this stage, attractive interactions between the semiflexible chains and the shell are turned on to explore how surface adsorption of these polymers affects shell deformation.
For a subset of simulations, we additionally replace FENE bonds of the shell defined in eqn (2) with harmonic springs to generate a softer shell configuration (see SI, Fig S3). This final equilibration step is run for 106 MD time steps. The harmonic bond potential is defined as
| UBond(rij) = k(rij − r0)2 | (7) |
MD simulations are performed in the canonical ensemble (NVT), using a Langevin thermostat. We confirm that the simulations have reached quasi-equilibrium, where the shell-shape fluctuations are at steady state, by monitoring the elastic shell's radius of gyration, Rg, as a function of simulation time (see SI, Fig. S7).3 Note that the confined chains with Npolymer = 6002 monomers per chain might not reach their statistical equilibrium, as in the case of chromosomes.61 Our extended simulations also confirm that this does not affect the shape fluctuations of the shell (see SI, Fig. S8). All simulations are performed using the LAMMPS molecular dynamics package.62,63 Visualization and data analysis are conducted using OVITO64 and Python, respectively.
We investigate how the collective behavior of surface-adsorbed semiflexible chains influences the shape of an elastic shell. Specifically, we explore the effects of varying three key parameters: (i) the concentration of semiflexible chains inside the shell, denoted by c; (ii) the ratio of the chain contour length to the shell radius, l/R; and (iii) the strength of chain–shell affinity, denoted by URS. The concentration, c, is controlled by adjusting the number of semiflexible polymers within the shell. We discuss concentration as a ratio of the bulk overlap concentration, c*. The overlap concentration, c*, is a polymer physical quantity, where individual chains begin to overlap and interact with one another.14 The overlap concentration for semiflexbile polymers with Nsf = 8 monomers is c* = 0.03σ−3 (see SI, Table S1). We focus on chains of intermediate lengths, particularly in the regime where the contour length is comparable to the shell radius, i.e., l ≈ R, with R ≈ 34σ throughout the study37,55 (see Fig. 1b). The initial size of the shell, prior to minimization, is R0 = 51σ ≈ 1.5R (see Fig. 1b). The chain length, l, is varied from 4σ to 64σ by varying the number of beads per chain, Nsf, corresponding to a range of 0.1 ≤ l/R ≤ 2. The chain–shell interaction strength, URS, is modulated by changing the interaction parameter ε in eqn (1). All beads within a semiflexible polymer are identical and interact uniformly with the shell interior, ensuring that the entire chain participates equally in surface interactions.
2.2 Shape analysis of elastic shell
The equilibrated shapes of the elastic shell are described by the radius of gyration (Rg), asphericity (A), aspect ratio, and shape anisotropy (κ) (see SI, Fig. S9), all derived from the gyration tensor (S),65 as well as by shape fluctuations (see Fig. 1c).3 The gyration tensor, S, of an elastic shell is defined as | (8) |
| S = diag(λ1, λ2, λ3) | (9) |
| Rg2 = Tr(S) = λ1 + λ2 + λ3 | (10) |
The asphericity, A, quantifies the deviation of the shell shape from a perfect sphere and is defined as65
 | (11) |
An asphericity value of A ≈ 0 corresponds to a nearly spherical shape, while higher values (e.g., A ≥ 50) indicate either large elongation or distortions from the primary axis of the gyration tensor of the shell (see Fig. 1c). Asphericity, A, has been widely used to characterize shape fluctuations of polymers under confinement or within vesicles, etc.23,35,39,55 Since A is a dimensional quantity, its magnitude reflects contributions from both the shell size and deviations from a perfect sphere.65 Therefore, to decouple these effects, we also calculate the aspect ratio, a dimensionless measure of elongation (eqn (12)), and the normalized asphericity, Anorm, which excludes size effects, to better support our interpretations of A in the cases discussed below (see Fig. 1c and SI).
Aspect ratio quantifies the degree of elongation of the shell along the principal axis. It is calculated as
 | (12) |
To quantify shell shape fluctuations, 〈uq2〉, we compute Fourier modes from a 1σ-thick shell slice taken through the center along the x-axis at each time step.3,66,67 For each bead in the slice, we calculate its angular deviation from the average radial distance. A fast Fourier transform (FFT)68 is then applied to the lowest q = 230 modes, and the results are time-averaged over the second half of the simulation. This approach captures shape fluctuations independently of the overall shell size (see Fig. 1c).
In the results discussed below, the radius of the elastic shell, R ≈ 34σ, persistence length-to-contour length ratio, lp/l = 2.5, and volume fraction of flexible polymers, ϕ ≈ 10%, are fixed, unless otherwise stated (see Fig. 1a and b). The elastic shell is often transparent in the simulation snapshots shown below for a clear visualization of the semiflexible chain behavior at the shell surface. In most MD simulations, more than 75% of the polymer chains are localized to the interior surface of the elastic shell.
3 Results and discussion
Our study attempts to understand how surface-adsorbed, semiflexible polymer chains can affect the morphology and shape fluctuations of this pressurized elastic shell. Therefore, we vary chain–surface attraction, URS, chain concentrations, c, chain length-to-shell radius ratios, l/R, and shell structure. Our MD trajectories are analyzed to characterize the shape changes by using time-averaged metrics such as fluctuation spectrum, asphericity, aspect ratio, and average dimension of the shell (see Fig. 1c and SI, Fig. S9). For clarity, the terms “chain” and “polymer” will be used to refer to the semiflexible polymers throughout this work. The term “shape fluctuations” refers to the equilibrated, “static” deformations of the elastic shell from a perfect sphere, averaged over the simulation time. Notably, we observe only weak dynamic undulations (i.e., less than 1σ) of the elastic shell over the course of our simulations.3.1 Strong localization of chains to the interior surface leads to shape distortions
We first analyze the effect of the peripheral localization of semiflexible chains on the shape of the elastic shell in our simulations. To do so, we vary the interaction strength between the chains and the inner surface of the elastic shell, URS. We choose a relatively low contour length-to-shell radius ratio (i.e., l/R = 8/34 ≈ 0.25) to avoid the buckling or strong bending of the adsorbed chains due to the surface curvature (see Fig. 2 and SI, Fig. S10). At low to intermediate polymer–shell interaction strengths (i.e., comparable to or higher than thermal energy, URS = 1.5 and 5.0kBT), the shape of the elastic shell appears to be spherical regardless of the chain concentration (see Fig. 2d, first two columns). On the contrary, as the attraction strength between the surface and polymers is increased (i.e., URS > 5.0kBT), the adsorbed chains become largely immobile on the surface, and the elastic shell locally morphs around the chains, leading to stable, non-spherical geometries (see Fig. 2d, last column).Analyses of the shape spectrum (see Methods 2.2, Fig. 1c) also confirm that excess binding of chains to the surface leads to systematically higher fluctuation amplitudes in all wavelengths, suggesting that shape distortions are dominant from the scales of several shell beads up to the scale of the entire shell (see Fig. 2a).
If URS is low enough or repulsive, semiflexible chains unbound to the shell contribute to the osmotic pressure inside the shell, leading to a more isotropically swollen shell (see Fig. 2b). Hence, the radius of gyration of the elastic shell also decreases with increasing chain–shell attraction, URS, due to less or almost no free chains in the interior (see Fig. 2b and SI, Fig. S11a). However, given that chain-free shells are not distorted (see horizontal red line in Fig. 2b and SI, Fig. S12a), shape distortions and decrease in the shell size are due to the strong adsorption of semiflexible chains (i.e., URS > 5.0kBT), rather than the reduction of interior pressure. Note that the overall reduction of the interior pressure by removing the long polymer chains inside can also lead to crumpling of the shell3,43 (see SI, Fig. S12b).
3.2 Shape distortions exhibit concentration dependence under strong localization
Having demonstrated the effect of chain–surface interactions, URS, on the shape of the elastic shell, we next explore whether these trends depend on the concentration of semiflexible chains, c, confined inside the elastic spherical confinement. To explore this, we choose concentrations above, below, and equal to the overlap concentration (i.e., 0.3c* ≤ c ≤ 4.8c*) (see Introduction and SI). Then, we systematically vary URS for each concentration (see Fig. 2d).At low concentrations, c ≤ c*, the shape of the elastic shell appears largely spherical, regardless of polymer–shell attraction strength (see Fig. 2d, first row). On the contrary, at high concentrations (i.e., c > c*), the spherical shell exhibits a more distorted morphology with strong chain localization, URS = 10.0kBT. We also observe significant wrinkles on the shell surface, manifested by increasing fluctuation intensity in the shape spectrum (see Fig. 2d, second and third row, and SI, Fig. S10).
The asphericity, A, is more affected if the chains are bound to the surface strongly. The shape fluctuations also lead to larger error bars in asphericity parameters at high concentrations, pushing the numerical value of asphericity to A ≈ 100 (see Fig. 2c, 2.0c* ≤ c ≤ 4.8c* and SI, Fig. S13). Correspondingly, the normalized asphericity (Anorm) also increases about 30% with increasing concentration (see Methods 2.2 and SI, Fig. S13a, 2.0c* ≤ c ≤ 4.8c*). On the contrary, the aspect ratio shows a slight deviation (i.e., ≈0.2) (see SI, Fig. S13b, 2.0c* ≤ c ≤ 4.8c*), indicating distorted morphologies rather than an elongation along a particular shell axis.
Another immediate effect of concentration under strong-localization conditions observed in simulation is that as the concentration increases, the radius of gyration of the shell, Rg, increases. This occurs for all URS but is more pronounced when chain localization is strong (URS > 5.0kBT) (see Fig. 2b). This is due to crowding of the chains on the surface, further expanding the shell despite there being less translational entropy (and related osmotic pressure) in the shell (see SI, Fig. S14).
Notably, the shape anisotropy parameter, κ, also increases by an order of magnitude as URS increases (see Methods 2.2 and SI, Fig. S11b). This could be due to wrinkles in the shell that emerge at high polymer–shell interactions (i.e., at URS = 7.5 and 10.0kBT) (see Fig. 2d, last column and SI, Fig. S10).
Overall, our calculations show that if the chain concentration is low enough (i.e., c ≤ c*), the adsorption of semiflexible polymers has a weak effect on the shell shape, leading to more spherical geometries (see Fig. 2d, first row). As the concentration increases, c ≥ c*, the chain–surface interaction strength, URS, plays a dominating role in the shell shape since it determines the amount of shell-bound chains. As a result, the shell exhibits stable, distorted shapes under strong localization (see Fig. 2d, last column, and SI, Fig. S14 and S15).
3.3 Strong localization of chains on the shell causes shape distortions irrespective of semiflexible chain length
Next, we examine whether the shape distortions discussed above depend on the chain length, l. In previous Sections 3.1 and 3.2, the chain length to shell radius ratio is fixed at l/R = 8/34 ≈ 0.25. Here, we vary l/R by altering chain length, l, within the range 4σ ≤ l/R ≤ 64σ, while keeping the elastic shell radius unchanged at R ≈ 34σ (see Fig. 1b). The chain–surface interaction strength is adjusted to URS = 10.0kBT to obtain strong surface adsorption. The chain concentration is kept high such that c > c* to observe shape distortions due to strong localization (see Fig. 2). Given that the overlap concentration, c*, varies with the chain length, we keep absolute concentration at c = 0.06σ−3 and 0.1σ−3, corresponding to c > c* for all chain lengths (see SI, Table S2). We choose l/R values at which the chain contour length is comparable to or smaller than the radius of the elastic shell, R (i.e., l/R ≤ 2). Note that as we increase the chain length, we preserve the ratio lp/l = 2.5 for all cases (see Methods 2.1 and Fig. 1a). Thus, the persistence length, lp, also increases and exceeds the radius of the shell, R.For chain concentrations considered here (i.e., c > c* for all chain lengths), the elastic shell exhibits strong shape distortions (see Fig. 2c). That is, fluctuation amplitudes and shape anisotropy parameters are independent of l/R (see SI, Fig. S16 and S17). Nevertheless, visual inspection shows that as l/R increases, the chains distribute non-uniformly on the surface of the elastic shell (see Fig. 3c and see SI, Fig. S18). For instance, while a chain concentration of c ≈ 0.1σ−3 is high enough to densely cover the surface, empty, chain-free sections appear on the surface for longer chain lengths (i.e., l/R = 1.0 and 2.0 in Fig. 3c, second row, and see SI, Fig. S18 for l/R = 1.4).
To further characterize these abnormal shape morphologies, we plot the time-averaged radius of gyration and asphericity of the elastic shell as a function of l/R for a range of ratios, 0.1 ≤ l/R ≤ 2 (see Fig. 3a and b). The elastic shell radius of gyration increases with increasing l/R (see Fig. 3a). Given that longer chains (i.e., l/R ≥ 1.0) buckle inside the shell, the size increase could be due to the swollen, chain-free regions on the surface. Note that in Fig. 3a the radius of gyration does remain below R ≈ 34σ (i.e., the shell does not swell beyond its size at purely repulsive chains–surface interactions) (see Fig. 1b). Given the strong localization of the chains, all cases in Fig. 3b also exhibit high asphericity as well (i.e., 50 ≤ A < 125) (see Fig. 3b). Surprisingly, the asphericity is higher for higher absolute chain concentration (i.e., c ≈ 0.1σ−3) at l/R > 0.5, also leading to large error bars in normalized asphericity (see SI, Fig. S19a). We speculate that these could be due to non-uniform chain distribution on the surface that leads to parallel chain orientation as l/R increases16 (see Fig. 3c, second row). We also observe an increase in aspect ratio up to 1.4 with increasing chain length, l/R (see SI, Fig. S19b), indicating both distortion and slight elongation, also observed visually in Fig. 3c.
Hence, we conclude that strong localization of semiflexible chains can distort the shape of an elastic shell irrespective of chain length (see Fig. 3c). These distortions might not be visible in the fluctuation spectra but can alter asphericity and the size of the shell (see Fig. 2 and 3).
3.4 Weak localization of semiflexible chains results in nematic phases on the shell surface
In the previous sections, we investigate the effect of strong chain localization on the shape of our elastic shell. Under strong localization, the chains distort the shell shape significantly (see Fig. 2 and 3). Nevertheless, strong localization does not allow the formation of distinct nematic phases on the shell surface. Thus, next, we look into the shape alterations that could emerge under weak surface adsorption of semiflexible polymers as a result of nematic phase formation of many chains.Fig. 2 shows that, when the chains are relatively short (i.e., l/R = 0.25), a weak chain–surface interaction strength (i.e., URS ≈ kBT) is enough to localize most of the chains to the shell surface (see Fig. 2d, first column). Nonetheless, this localization does not lead to detectable deviations in the shell shape as indicated by: (i) consistently low fluctuation amplitudes (see Fig. 2a); shell radius of gyration close to the initial shell size (i.e., Rg ≈ R = 34σ) (see Fig. 2b); and low asphericity, A < 25 (see Fig. 2c); for all chain concentrations considered in this work.
Similar to our analyses in Section 3.3, we characterize the effect of increasing l/R for high absolute chain concentration, c ≈ 0.1σ−3, where the surface is completely covered (see Fig. 4 and SI, Fig. S20). The chain–surface interaction is kept constant at a relatively low value of URS = 1.5kBT.
Short chains (i.e., l/R ≈ 0.25, 0.5) coat the surface with no visually uniform orientation (see Fig. 4a, l = 8σ and 16σ). As we increase l/R to 1.0, locally ordered nematic-phase domains emerge on the surface (see Fig. 4a, l = 32σ). This is consistent with previous studies on semiflexible chains in rigid spherical confinements.31,32,36,38,69 Increasing l/R further to higher values (i.e., l/R ≈ 2.0) results in a more unidirectional arrangement of the semiflexible chains on the surface (see Fig. 4a, l = 64σ).
To quantitatively characterize these nematic phase domains, we calculate the average orientational order parameter, P2(z), from the largest eigenvalue of the diagonalized configurational tensor over all chains.8,31,37P2(z) quantifies the orientation of bond vectors, bi, at a distance, z, from the spherical surface, forming an angle, θ(z), with the shell surface normal vector, ni. It is defined as
 | (13) |
Fig. 4b shows that P2(z) decreases as chain length, l/R, increases. For very short chains (i.e., l/R ≤ 0.25), the chains exhibit nearly isotropic arrangement, where 〈P2(z)〉 ≈ 0 (Fig. 4a, l = 8σ and SI, Fig. S20). As chain length increases, P2(z) becomes negative, indicating that chains align parallel to the shell surface. When l/R ≥ 0.5, P2(z) approaches a plateau of ≈−0.15, indicating nematic order on the shell surface (Fig. 4a and b, l ≥ 16σ and SI, Fig. S20).
To summarize, under weak localization, where the shape of the elastic shell is largely spherical, increasing chain length leads to the formation of nematic phases at high concentration (i.e., c > c*).8,36 These domains become more unidirectional as the chain length exceeds the shell radius (see Fig. 4).
3.5 Weak chain localization to the shell leads to elongated shapes for liquid-like shells
So far, to connect the shell beads, we have used a model bond potential referred to as finitely extensible non-linear elastic (FENE) bonds (eqn (1)). We next test whether making the shell more deformable by replacing these non-extensible bonds with an extensible harmonic potential (eqn (7)) would affect the shell shapes (see Methods 2.1, see SI, Fig. S21). Consistent with previous studies,36,69 we chose chain lengths (i.e., l/R values) representing both disordered and ordered (i.e., more nematic) chain orientations on the surface (i.e., l/R ≈ 0.25 and 1.0 in Fig. 4) for high chains concentrations (i.e., c > c* with an absolute concentrations c ≈ 0.06 and 0.1σ−3) (see Fig. 5).Making the shell bonds extensible leads to highly distorted shapes, irrespective of chain length (see Fig. 5d). We visually observe an irregular spherical shape for l/R ≈ 0.25, and an elliptic shape for l/R ≈ 1.0 elongated in the directions. These shapes are reminiscent of lipid vesicles where stiff microtubules were strongly confined29 (see Fig. 5d, first row). The distorted morphologies we observe also manifest themselves as higher fluctuation amplitudes than FENE-bonded spherical shells, when c = 0.06σ−3 (see Fig. 5a).
Surprisingly, when we slightly increase chain concentration to c = 0.1σ−3 from c = 0.06σ−3, where surface-adsorbed chains cover almost the entire surface, shape distortions become l/R dependent (see Fig. 5b). For shorter chains (i.e., l/R ≈ 0.25), the fluctuations for both FENE and harmonic bonded shells are comparable since the chains organize randomly on the elastic-shell surface (see Fig. 4c, second row). On the contrary, with longer chains (i.e., l/R ≈ 1.0), where locally nematically ordered chain domains appear, the harmonic shell undergoes a transition to an elliptic shape (see Fig. 4 and 5c, second row). These shapes exhibit a higher fluctuation amplitude than their FENE-bonded counterparts and also have aspect ratios around 1.5–1.6, indicating elongation along a preferred direction relative to the primary shell axis (see Fig. 6a).
The aspect ratio that the shell can achieve with increasing chain length is determined by an interplay between the chain–shell interaction, URS, the chain persistence length lp, and the elastic modulus of the shell, E, with the units of energy per volume. A simple scaling argument may help rationalize this competition as follows. Assuming that the shell elastic modulus is related to the strength of bonds k composing the shell,70 the elastic free energy for the shell, Fshell, may be expressed as
 | (14) |
 | (15) |
Using the leading order terms and minimizing the total free energy for weak stretching (i.e., R ≫ ΔR) leads to
 | (16) |
Notably, these shape alterations vanish when shell stiffness increases, converging toward FENE-bonded spherical geometries exhibiting nematic order (see Fig. 4 and 6b). This underscores the role of shell deformability in enabling such shape alterations.
Overall, our simulations reveal that weak chain localization to the elastic shell, URS = 1.5kBT, leads to a orientational ordering with increasing chain length, which, in turn, causes strong morphological distortions of the shell in a chain length-dependent manner, provided that bonds of the shell are deformable enough (see Fig. 4 and 5 and SI, Fig. S21 and S22). Interestingly, these elongated shapes with pointy cusps resemble liquid crystal droplets (tactoids), where shape anisotropy arises from a competition between elastic stresses and surface tension.40,41 This analogy is consistent with our observation that the nematic order of confined semiflexible chains correlates with shell elongation (see Fig. 4 and 5).
Such phase behavior and shell elongation are not observed when chains are strongly localized to the shell (i.e., URS = 10.0kBT). Instead, those shells collapse when the shell has extensible harmonic bonds (see SI, Fig. S14). Therefore, using such harmonic bonds is limited to the weak adsorption regime in our parameter space since increasing the chain–shell affinity, URS, leads to a highly crumpled shell where interior contents are squeezed out and the semiflexible chains are wrapped around the shell surface, due to nonphysical stretching of harmonic bonds (see SI, Fig. S5 and S14).
4 Conclusions
In this work, using a shell model composed of a bead-spring network and MD simulations, we study the effects of the surface adsorption of many (i.e., above overlap concentration) semiflexible polymers on the morphology of an elastic shell. We focus on how the morphology of the shell is deviated from a perfect sphere as a result of strong or weak localization of many polymer chains (i.e., binding affinity), depending on the polymer length and concentration. Notably, the shell is pressurized by high-molecular-weight chains; thus, our model system could emulate a vesicle filled by polymers or the cell nucleus3,4,50,55 (see Fig. 1). Our MD calculations show that formation of distinct surface phases (nematic or isotropic) and/or attraction affinity of chains towards the shell surface can lead to a variety of shapes, with shape fluctuations of varying amplitudes, including egg-like shapes and bleb-like protrusions, depending on the structural deformability of the shell.Our results elucidate how surface adsorption of semiflexible polymers may alter the shape of soft shells, such as lipid vesicles or hydrogel shells, via several mechanisms: (i) shell wrinkling and stable morphology due to excess localization of semiflexible chains (see Fig. 2 and 3); and (ii) organized nematic domain formation under weak localization (see Fig. 4), correlated to shell elongation when the shell deformability increases (see Fig. 5 and 6).
Under strong localization (i.e., strong binding affinity to the surface), the shell can undergo significant shape fluctuations with consirable surface roughness see (Fig. 2). These structural fluctuations occur above the bulk overlap concentration, c > c* (see Fig. 2), and are largely independent of chain length (see Fig. 3). As the polymer–surface interaction strength increases, chains become increasingly immobile at the shell surface, further stabilizing the shell—consistent with the idea that polymeric scaffolds can provide mechanical stability35,71,72 (see Fig. 3).
Under weak localization conditions (i.e., binding affinity is on the order of thermal energy), semiflexible chains exhibit nematic ordering on the surface with increasing chain length, l/R, at high concentrations (c > c*) (see Fig. 4). This validates previous studies with rigid confinement, restating that inter-chain interactions are not required to observe local nematic ordering for semiflexible polymers.32,36,69 This ordering alone does not distort shell shape unless shell deformability is increased. As the mechanical “softness” of the shell is increased (i.e., constituting beads of the shell can change their neighbors more easily), the shell is more prone to undergo shape anomalies (i.e., elongated, egg-like shell shapes). This suggests the need for topological changes to undergo shape elongation in addition to a competition between shell mechanics and chain elasticity (see Fig. 5), which also implies that abnormal nuclear forms observed in diseases can result from permanent changes in the molecular structure of the nuclear lamina.7,8,49 Notably, these oval shell shapes become more pronounced with increasing chain length and concentration (see Fig. 5d and 6), consistent with previous studies with actin filaments under strong confinement.29
While our model elucidates various qualitative features of deformable elastic shells, several possible extensions could improve its biological relevance.3,51,56,73 The elastic shell in our simulations is a bead meshwork, unlike membranes and vesicles, which are structurally heterogeneous, with fluid-like behavior that may depend on lipid composition, protein interactions, and external forces. Similarly, our semiflexible polymers, adsorbed at the interior of the shell, interact only via repulsion between them. On the contrary, self-assembled biological networks often consist of sticky ends that could be modeled via intermolecular interactions.8,74 Hence, future models could incorporate inter-chain interactions and/or meshless membrane models for biological accuracy.3,51,56,73
We also limited the scope of this study to intermediate polymer lengths (i.e., 0.1 ≤ l/R ≤ 2), given the unexplored nature of length scales, where l ≈ R, and semidilute concentrations. The ratio of persistence length-to-contour length is also fixed to lp/l = 2.5. Varying bending rigidity and introducing polymer activity (e.g., the time- or confinement-dependent chain length) might lead to more exotic morphologies,4,29 and could be the subjects of future studies.
Overall, our study provides a qualitative perspective on how surface-adsorbed semiflexible polymers distort elastic or liquid-like shells by including the localization of semiflexible filaments to the periphery of the shell as an additional competitive metric, alongside chain shell elasticity and chain concentration.
Conflicts of interest
There are no conflicts to declare.Data availability
All codes, structure files, and input parameters are available online at https://github.com/hadiyaabdulhameed/SoftMatter_Hameedetal_2025.The data supporting this article have been included as part of the Supplementary Information (SI). SI provides additional details on the MD simulations, and details on data analysis metrics. It also includes extended analyses and figures to verify results discussed in the main text. See DOI: https://doi.org/10.1039/d5sm00899a.
Acknowledgements
This research was supported by TUBITAK, the Scientific and Technological Research Council of Turkey under TRANSCAN 3 (SCIE-PANC) [Grant No. 124N935]. The simulations were partially performed at TUBITAK ULAKBIM High Performance and Grid Computing Center (TRUBA).Notes and references
- S. Dmitrieff, A. Alsina, A. Mathur and F. J. Nédélec, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4418–4423 CrossRef CAS PubMed.
- F.-C. Tsai and G. H. Koenderink, Soft Matter, 2015, 11, 8834–8847 RSC.
- A. G. Attar, J. Paturej, E. J. Banigan and A. Erbaş, Nucleus, 2024, 15, 2351957 CrossRef PubMed.
- E. Loiseau, J. A. Schneider, F. C. Keber, C. Pelzl, G. Massiera, G. Salbreux and A. R. Bausch, Sci. Adv., 2016, 2, e1500465 CrossRef PubMed.
- M. Fošnarič, S. Penič, A. Iglič, V. Kralj-Iglič, M. Drab and N. S. Gov, Soft Matter, 2019, 15, 5319–5330 RSC.
- K. Lee, T. Miller, I. Anastassov and D. W. Cohen, Cell Biol. Int., 2004, 28, 299–310 CrossRef CAS PubMed.
- Y. Turgay, M. Eibauer and A. Goldman, et al. , Nature, 2017, 543, 261–264 CrossRef CAS PubMed.
- H. A. Hameed, J. Paturej and A. Erbaş, J. Chem. Phys., 2025, 162, 185101 CrossRef CAS PubMed.
- L. Flores, B. Tader, E. Tolosa, A. Sigafoos, D. Marks and M. Fernandez-Zapico, Cells, 2021, 10, 2624 CrossRef CAS PubMed.
- C. M. Denais, R. M. Gilbert, P. Isermann, A. L. McGregor, M. te Lindert, B. Weigelin, P. M. Davidson, P. Friedl, K. Wolf and J. Lammerding, Science, 2016, 352, 353–358 CrossRef CAS PubMed.
- J. Irianto, C. R. Pfeifer, I. L. Ivanovska, J. Swift and D. E. Discher, Cell. Mol. Bioeng., 2016, 9, 258–267 CrossRef CAS PubMed.
- V. Butin-Israeli, S. A. Adam, A. E. Goldman and R. D. Goldman, Trends Genet., 2012, 28, 464–471 CrossRef CAS PubMed.
- T. Misteli, Cold Spring Harbor Perspect. Biol., 2010, 2, a000794 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- P. Gutjahr, R. Lipowsky and J. Kierfeld, Europhys. Lett., 2006, 76, 994 CrossRef CAS.
- M. Girard, M. O. de la Cruz, J. F. Marko and A. Erbaş, Phys. Rev. E, 2024, 110, 014403 CrossRef CAS PubMed.
- J. Kierfeld, K. Baczynski, P. Gutjahr and R. Lipowsky, AIP Conf. Proc., 2008, 1002, 151–185 CrossRef CAS.
- C. Bustamante, J. F. Marko, E. D. Siggia and S. Smith, Science, 1994, 265, 1599–1600 CrossRef CAS PubMed.
- T. A. Kampmann, H.-H. Boltz and J. Kierfeld, J. Chem. Phys., 2013, 139, 014901 CrossRef PubMed.
- J. Bednar, P. Furrer, V. Katritch, A. Stasiak, J. Dubochet and A. Stasiak, J. Mol. Biol., 1995, 254, 579–594 CrossRef CAS PubMed.
- B. Li and S. M. Abel, Soft Matter, 2018, 14, 185–193 RSC.
- C. Shi, G. Zou, Z. Wu, M. Wang, X. Zhang, H. Gao and X. Yi, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2300380120 CrossRef CAS PubMed.
- M. Fošnarič, A. Iglič, D. M. Kroll and S. May, Soft Matter, 2013, 9, 3976 RSC.
- J. Gao, P. Tang, Y. Yang and J. Z. Y. Chen, Soft Matter, 2014, 10, 4674–4685 RSC.
- D. Marenduzzo and E. Orlandini, Europhys. Lett., 2007, 80, 48004 CrossRef.
- A. J. Spakowitz and Z.-G. Wang, Phys. Rev. Lett., 2003, 91, 166102 CrossRef PubMed.
- K. Guo, J. Wang, F. Qiu, H. Zhang and Y. Yang, Soft Matter, 2009, 5, 1646 RSC.
- B. Li, C.-L. Fu and Z.-Y. Sun, J. Chem. Phys., 2025, 162, 094901 CrossRef CAS PubMed.
- F. C. Keber, E. Loiseau, T. Sanchez, S. J. DeCamp, L. Giomi, M. J. Bowick, M. C. Marchetti, Z. Dogic and A. R. Bausch, Science, 2014, 345, 1135–1139 CrossRef CAS PubMed.
- M. S. Peterson, A. Baskaran and M. F. Hagan, Nat. Commun., 2021, 12, 7247 CrossRef CAS PubMed.
- A. Nikoubashman, D. A. Vega, K. Binder and A. Milchev, Phys. Rev. Lett., 2017, 118, 217803 CrossRef PubMed.
- A. Milchev, S. A. Egorov, D. A. Vega, K. Binder and A. Nikoubashman, Macromolecules, 2018, 51, 2002–2016 CrossRef CAS.
- W.-Y. Zhang and J. Z. Y. Chen, Europhys. Lett., 2011, 94, 43001 CrossRef.
- K. Ostermeir, K. Alim and E. Frey, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 81, 061802 CrossRef PubMed.
- A. Liu, D. Richmond and L. Maibaum, et al. , Nat. Phys., 2008, 4, 789–793 Search PubMed.
- A. Milchev, S. A. Egorov, A. Nikoubashman and K. Binder, J. Chem. Phys., 2017, 146, 194907 CrossRef PubMed.
- M. R. Khadilkar and A. Nikoubashman, Soft Matter, 2018, 14, 6903–6911 RSC.
- A. Nikoubashman, J. Chem. Phys., 2021, 154, 090901 CrossRef CAS PubMed.
- Y.-L. Liu, Y.-L. Zhu, Y.-C. Li and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2024, 26, 6180–6188 RSC.
- P. Wang and M. J. MacLachlan, Philos. Trans. R. Soc., A, 2018, 376, 20170042 CrossRef.
- Y.-K. Kim, S. V. Shiyanovskii and O. D. Lavrentovich, J. Phys.: Condens. Matter, 2013, 25, 404202 CrossRef PubMed.
- A. Maji, K. Dasbiswas and Y. Rabin, Soft Matter, 2023, 19, 7216–7226 RSC.
- V. Agrawal, V. Pandey and D. Mitra, Phys. Rev. E, 2023, 108, L032601 CrossRef CAS PubMed.
- B. Nmezi, J. Xu, R. Fu, T. J. Armiger, G. Rodriguez-Bey, J. S. Powell, H. Ma, M. Sullivan, Y. Tu and N. Y. Chen, et al. , Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4307–4315 CrossRef CAS PubMed.
- N. Wiesel, A. Mattout, S. Melcer, N. Melamed-Book, H. Herrmann, O. Medalia, U. Aebi and Y. Gruenbaum, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 180–185 CrossRef CAS PubMed.
- A. Stephens, E. Banigan, S. Adam, R. Goldman and J. Marko, Mol. Biol. Cell, 2017, 28, 1984–1996 CrossRef CAS PubMed.
- P. Scaffidi and T. Misteli, Science, 2006, 312, 1059–1063 CrossRef CAS.
- R. San Martin, P. Das, J. T. Sanders, A. M. Hill and R. P. McCord, eLife, 2022, 11, e81290 CrossRef CAS PubMed.
- K. N. Dahl, P. Scaffidi, M. F. Islam, A. G. Yodh, K. L. Wilson and T. Misteli, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10271–10276 CrossRef CAS PubMed.
- T. Okano, K. Inoue, K. Koseki and H. Suzuki, ACS Synth. Biol., 2018, 7, 739–747 CrossRef CAS PubMed.
- S.-P. Fu, Z. Peng, H. Yuan, R. Kfoury and Y.-N. Young, Comput. Phys. Commun., 2017, 210, 193–203 CrossRef CAS.
- A. Rajwar, V. Morya, S. Kharbanda and D. Bhatia, J. Membr. Biol., 2020, 253, 577–587 CrossRef CAS PubMed.
- A. Czogalla, D. J. Kauert, H. G. Franquelim, V. Uzunova, Y. Zhang, R. Seidel and P. Schwille, Angew. Chem., Int. Ed., 2015, 54, 6501–6505 CrossRef CAS PubMed.
- H. R. Vutukuri, M. Hoore, C. Abaurrea-Velasco, L. van Buren, A. Dutto, T. Auth, D. A. Fedosov, G. Gompper and J. Vermant, Nature, 2020, 586, 52–56 CrossRef CAS PubMed.
- A. Sciortino, H. Faizi and D. E. A. Fedosov, Nat. Phys., 2025, 21, 799–807 Search PubMed.
- A. Attar, J. Paturej, O. Sariyer, E. Banigan and A. Erbaş, Nucleic Acids Res., 2025, 53, gkaf763 CrossRef CAS PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 4th edn, 2013 Search PubMed.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef CAS.
- J. Smith, Compos. Sci. Technol., 2003, 63, 1599–1605 CrossRef CAS.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- A. Rosa and R. Everaers, PLoS Comput. Biol., 2008, 4, 1–10 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al. , Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- H. Arkin and W. Janke, J. Chem. Phys., 2013, 138, 054904 CrossRef PubMed.
- E. J. Banigan, A. D. Stephens and J. F. Marko, Biophys. J., 2017, 113, 1654–1663 CrossRef CAS PubMed.
- A. E. Patteson, A. Vahabikashi, K. Pogoda, S. A. Adam, K. Mandal, M. Kittisopikul, S. Sivagurunathan, A. Goldman, R. D. Goldman and P. A. Janmey, J. Cell Biol., 2019, 218, 4079–4092 CrossRef CAS PubMed.
- C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg and N. J. Smith, et al. , Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- A. Milchev, S. A. Egorov, A. Nikoubashman and K. Binder, Polymer, 2018, 145, 463–472 CrossRef CAS.
- Y. Kantor, M. Kardar and D. R. Nelson, Phys. Rev. Lett., 1986, 57, 791–794 CrossRef CAS PubMed.
- K. N. Baumann, L. Piantanida, J. García-Nafría, D. Sobota, K. Voïtchovsky, T. P. J. Knowles and S. Hernández-Ainsa, ACS Nano, 2020, 14, 2316–2323 CrossRef CAS PubMed.
- N. Fakhri, A. D. Wessel, C. Willms, M. Pasquali, D. R. Klopfenstein, F. C. MacKintosh and C. F. Schmidt, Science, 2014, 344, 1031–1035 CrossRef CAS PubMed.
- Y. Wang, J. K. Sigurdsson, E. Brandt and P. J. Atzberger, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 88, 023301 CrossRef PubMed.
- X. Yang, J. Leng, C. Sun and S. Keten, Adv. Mater. Technol., 2023, 8, 2202189 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |






