 Open Access Article
Open Access ArticleEngineering active colloidal dynamics at a lipid bilayer interface
Paige
Liu
 a,
Robert K.
Keane
a,
Robert K.
Keane
 b,
Hima Nagamanasa
Kandula
b,
Hima Nagamanasa
Kandula
 b and
Peter J.
Beltramo
b and
Peter J.
Beltramo
 *a
*a
aDepartment of Chemical Engineering, University of Massachusetts Amherst, Amherst, MA 01002, USA. E-mail: pbeltramo@umass.edu
bDepartment of Physics, University of Massachusetts Amherst, Amherst, MA 01002, USA
First published on 2nd January 2026
Abstract
In this work, we discuss the development of an active colloidal system with controllable interactions with an artificial lipid bilayer membrane as a model for investigating the interplay of membrane mechanics and the transport of particles during adhesion and wrapping. We use polystyrene microspheres coated with a hemispherical platinum cap as model swimmers whose active motion is initiated by the addition of hydrogen peroxide (H2O2). Two classes of particle–membrane interactions and particle swimming direction are assessed. For the former, carboxylated particles are used to passively interact with the membrane through electrostatic interactions, while streptavidin coated particles are used to form a strong bond with biotinylated lipid membranes. For the latter, these active Janus particles are designed to be “pushers”, which swim toward their metal face into the bilayer, or “pullers”, which swim away from the membrane, by changing the concentration of CTAB, a cationic surfactant, in the aqueous phase. We find that a negative gravitaxis effect causes the steady movement of unbound pullers up and away from the membrane with increasing H2O2. When the particles are bound, a threshold H2O2 concentration is needed before overcoming the strength of the biotin–neutravidin bond and releasing the particles from the interface. In the case of the pusher system, as the H2O2 concentration increases the particles become increasingly wrapped in the membrane, as evidenced by their altered translational and rotational dynamics. We apply active Brownian models to characterize the nature of the particle–membrane interactions and also particle pair interactions. These results lay the groundwork to combine active colloidal systems with model lipid membranes to understand active transport in cellular contexts.
1 Introduction
Active transport is exploited by a number of biological systems to gain entry into a target cell. The invasion of cells by viruses, for example, occurs through a three-pronged approach: the directed motion of the virus towards a cell, docking via receptors, and finally entry into the cell via endocytosis.1 A similar mechanism is seen in the collective invasion of cancerous cells into surrounding tissue, which occurs during the metastasis of several cancers.2 Although the given examples pose detriments to human health, we postulate that these invasive mechanisms can be re-tooled for beneficial causes, i.e., a drug delivery vehicle which can simultaneously implement both passive and active targeting. Janus particles, which by definition possess two distinct surfaces on each hemisphere, present an ideal platform for such a bi-functional delivery vehicle. In this context, the carrier should exhibit dual functionality that both supports directed swimming of the drug carrier as well as surface functionality to support passive targeting, for example by ligand–receptor interactions.In recent years, there has been a significant amount of work focused on the development of both passive and active Janus particles for directed drug delivery and other biomedical applications. A number of these systems have been reviewed by Tan et al.3 For example, the synthesis of a theranostic Janus particle in which one half of the particle is loaded with a therapeutic agent and the other half is loaded with a diagnostic agent was demonstrated using a solvent emulsion technique.4 By incorporating super-paragmagnetic iron oxide nanoparticles (SPIONs) in the same synthesis step, the same particles could be directed with a magnetic field. Similarly, an applied magnetic field has also been demonstrated as a method to control the swimming direction of Janus particles fabricated with a multi-layered Co/Pt face, allowing for control over particle transport and cargo delivery.5 As an alternative to an applied external field, it may also be possible to leverage biological gradients to direct particle motion. In a study done in simulated body fluids (SBF) and blood plasma, the feasibility of Mg/Pt–PNIPAM (poly(N-isopropylacrylamide)) micromotors for directed transport and release was investigated.6 In another diagnostic application, Mg/Pt Janus micromotors were demonstrated to enhance the chromatic detection of glucose in human serum by increasing the mass transfer rate of the analyte and resulting current signal in solution.7
Once a carrier is transported to the target cell, the next delivery challenge is the successful passage of the drug carrier through the cell membrane. Engineering this uptake process hinges on an understanding of particle–membrane interactions and engulfment mechanisms. For carriers on the nanometer scale and higher, the primary mechanisms that occur are binding and wrapping, leading to endocytosis.8 Binding interactions between a particle and the cell membrane can be mediated by tuning adhesion via electrostatics or receptor–ligand interactions. The factors affecting particle wrapping include particle shape and size,9 the material properties of the bilayer,10 and the aggregation of proteins, such as clathrin, which are involved in the endocytic process.11,12 With these processes in mind, we propose a model system of platinum-capped polystyrene Janus particles (Pt–PS JP), which are propelled by hydrogen peroxide (H2O2) into a free-standing, artificial lipid bilayer with known material properties. An advantage of this model system is that the degree of active motion, and thus the force of the particle interacting with the membrane, can be controlled by the H2O2 concentration. We expect that changes in the dynamics of these particles as they approach and interact with the model membrane will provide insight into particle uptake mechanisms critical to the delivery of nanoparticle-based drug carriers.
To enhance the understanding of the uptake mechanisms of these and other particle-based delivery systems, the interaction between the particle and the membrane needs to be examined in detail. Understanding Janus particle interactions with the cell membrane poses an interfacial transport problem governed by the physicochemical properties of both the membrane and the particle. The active dynamics of Pt–PS JP have been well characterized in bulk aqueous environments.13,14 Their behavior at interfaces, however, is less straightforward. At an air–water interface, particle pinning has been observed to retard the rotational motion of the particles compared to swimming behaviors in a bulk fluid.15 Conversely, the swimming speed of Janus particles at the air–water surface is enhanced.16 Oil–water interfaces have also been used in studies of active Janus particle dynamics. The orientation of Pt–SiO2 Janus particles at an oil–water interface was observed to change in the presence of H2O2 fuel.17 Without H2O2 in the system, the particles were observed to pin metal-cap down to the oil–water interface, but in the presence of H2O2, the particles oriented sideways (so that the axis of the cap is perpendicular to the interface) and hovered above the oil phase, swimming in the aqueous phase. In contrast to bulk environments where orientation generally does not impact particle behavior, the orientation of Janus particles at a 2D interface have been found to directly impact particle velocity.18 Finally, particles pinned between a continuous oil–water interface have been shown to be sensitive to the curvature of the interface.19
The lipid bilayer presents a unique interface, distinct from that created by two bulk fluid phases, characterized by a flexible membrane that is much thinner than the particle it is interacting with. Particle dynamics on a lipid bilayer can be modulated by the deformation of the membrane by the particle, adhesion with the membrane, and local and global curvatures present at the membrane and/or generated by the particle; in short, partial and complete particle wrapping is expected to have an observable effect on particle diffusivity. The extent of particle wrapping is governed by the minimization of the total wrapping energy, E, as described by Dietrich et al.,20
| E = Eel + Ead | (1) |
 | (2) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) is the modulus of Gaussian curvature, and c0 is the spontaneous curvature. The tension contribution can be given by Ete = σA, where σ is the surface tension of the membrane. Finally, the adhesive energy is given by the integral of the particle–membrane interaction potential over A,
is the modulus of Gaussian curvature, and c0 is the spontaneous curvature. The tension contribution can be given by Ete = σA, where σ is the surface tension of the membrane. Finally, the adhesive energy is given by the integral of the particle–membrane interaction potential over A, | (3) |
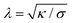 | (4) |
This length scale describes the crossover from bending rigidity dominated to tension dominated interactions; length scales smaller than λ are dominated by bending, while length scales larger than λ are tension dominated. The large area, planar bilayers generated on the experimental set-up used here have reported bending rigidities of around 5kBT23 and tensions of around 1 mN,24 resulting in a characteristic length scale of around 10 nm. Therefore, we expect microparticle interactions with the bilayer to be tension dominated in the absence of other interactions or forces. In our system, we investigate (i) modulating adhesion between the particle and membrane and (ii) an additional force directing Janus swimmers into the membrane, which should increase the bending energy contribution. In comparison, spontaneous wrapping has been observed in low-tension, “floppy” vesicle environments such as GUVs in which the tension is modulated by osmotic pressure,25 or with a depletion agent.26 At higher tensions, higher external forces are needed to drive wrapping. For example, particle wrapping in tense GUVs was induced by centrifugal force,27 where spontaneous wrapping would not have occurred.
In this paper, we discuss the changing dynamics of active Janus particles against increasing fuel (H2O2) concentrations. We investigate the behavior of active particles with different particle adhesion, changes in surface potential from CTAB, and membrane stiffness. The effect of streptavidin–biotin binding between the particle and the bilayer is observed on the onset of particle release from the bilayer surface with increasing H2O2 percentage. By changing the surface potential of the particle using CTAB, a cationic surfactant, we are able to change the direction of particle motion, converting the swimmers from a pulling to pushing motion relative to the bilayer. We note that in this paper we define “pushers” and “pullers” based on the motion relative to the bilayer, which is distinct from syntax used in some active colloidal literature where the same terms are used to describe motion relative to the metal face of the particle. In the case of the pushers, we observe subdiffusive dynamics at low H2O2 concentrations compared to normal Brownian motion when there is no H2O2 in the system. At higher H2O2 concentrations, we observe superdiffusive particle motion as well as the onset of particle aggregation, which results from attractive interparticle forces as the particle becomes increasingly wrapped by the membrane. To describe this behavior, we use active Brownian motion models as well as a force descriptor for tension mediated pair interactions. Finally, we investigate the impact of bilayer material properties by adding LPC to decrease the rigidity of the membrane while keeping all other conditions constant. As expected, the active particle motion becomes slower as the membrane is made less stiff, demonstrating the effect of the extent of deformation on particle wrapping dynamics.
2 Materials and methods
2.1 Materials
The lipids 1,2-dioleoyl-sn-glycero-3-phosphotidylcholine (DOPC), 1-oleoyl-2-hydroxy-sn-glycero-3-phosphocholine (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 LPC), and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl) (DOPE-cB) were obtained in chloroform from Avanti Polar lipids (Alabaster, AL). HPLC-grade chloroform, n-hexadecane, octadecyltrichlorosilane (OTS), D-glucose, 3-aminopropyltriethoxysilane (APTES), methanol, glacial acetic acid, phosphate buffered saline (PBS), and EZ link sulfo-NHS–LC–biotin were purchased from Thermo Fisher Scientific (Waltham, MA). Fluorescent polystyrene beads ranging from 2 µm to 6 µm in diameter with either carboxylate or streptavidin surface functionality were purchased from Polysciences (Warrington, PA). Cetyltrimethylammonium bromide (CTAB) was obtained from Sigma Aldrich (St Louis, MO). All buffers were made using ultrapure deionized water (DI, Millipore Milli-Q) with resistivity >18.2 MΩ-cm. Before use, hexadecane is filtered twice through a 0.2 µm aluminum mesh, and glucose buffer is filtered using an 0.2 µm pore filter.
1 LPC), and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl) (DOPE-cB) were obtained in chloroform from Avanti Polar lipids (Alabaster, AL). HPLC-grade chloroform, n-hexadecane, octadecyltrichlorosilane (OTS), D-glucose, 3-aminopropyltriethoxysilane (APTES), methanol, glacial acetic acid, phosphate buffered saline (PBS), and EZ link sulfo-NHS–LC–biotin were purchased from Thermo Fisher Scientific (Waltham, MA). Fluorescent polystyrene beads ranging from 2 µm to 6 µm in diameter with either carboxylate or streptavidin surface functionality were purchased from Polysciences (Warrington, PA). Cetyltrimethylammonium bromide (CTAB) was obtained from Sigma Aldrich (St Louis, MO). All buffers were made using ultrapure deionized water (DI, Millipore Milli-Q) with resistivity >18.2 MΩ-cm. Before use, hexadecane is filtered twice through a 0.2 µm aluminum mesh, and glucose buffer is filtered using an 0.2 µm pore filter.
2.2 Bilayer fabrication and characterization
A glass microfluidic “bikewheel” chip was fabricated by Micronit (Enschede, Netherlands), and a custom sample holder was 3D printed at the University of Massachusetts ADD/FAB lab using VeroWhite from Stratasys (Eden Prairie, MN). The glass chip contains channels in a bikewheel geometry with 24 spokes leading to an open aperture, which is 0.9 mm in diameter. This chip is installed in an aluminum holder connected to a stainless steel capillary tube. To commission the chip for making lipid bilayers, the chip is first cleaned in a solution of saturated NaOH in ethanol, then functionalized in a solution of OTS in hexadecane to make the surface slightly hydrophobic.Bilayers are formed on the large area model biomembrane (LAMB) platform as previously described.24 Briefly, lipids in their stock solution are further diluted in chloroform and combined in 7 mL scintillation vials according to specified molar ratios, e.g. 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DOPC
1 DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOPE-cB. The excess chloroform is removed under nitrogen, and then any residual chloroform is removed by drying the vial overnight under vacuum (≤30 mbar). After drying, the lipid film is resuspended in hexadecane at a concentration of 2.5 mg mL−1, and the resulting lipid-in-oil suspension is sonicated for at least 2 hours before use.
DOPE-cB. The excess chloroform is removed under nitrogen, and then any residual chloroform is removed by drying the vial overnight under vacuum (≤30 mbar). After drying, the lipid film is resuspended in hexadecane at a concentration of 2.5 mg mL−1, and the resulting lipid-in-oil suspension is sonicated for at least 2 hours before use.
To form a bilayer, the microfluidic chip is first loaded with the well dispersed lipid-in-oil mixture. The chip is then installed into a 3D printed sample holder before aqueous buffer (0.15 M glucose) is added. PTFE tubing is used to connect the stainless steel capillary to a microfluidic pressure control (Elveflow, Paris, France), which is used to control the thickness of the lipid–oil film formed in the center of the aperture and subsequently, the area of the black lipid membrane. The pressure on the chip is rapidly increased at first to form a thick oil film across the aperture, then lowered to allow the film to thin. At sufficient thinning, a lipid bilayer nucleates and populates an area that is kept constant at around 0.5 mm2 using the pressure control system.
The stiffness of binary DOPC/LPC composition bilayers is measured under electrostriction as described in previous work.23,28,29 Briefly, a patch clamp amplifier (HEKA Elektronik, Lambrecht, Germany) is used to apply alternating positive and negative voltages in 1 s “on” pulses at a magnitude ranging from 25 to 200 mV with 2 s “off” pulses at 1 mV in between. A pulse generator file is used to automate the voltage pulse program and manage the recording of the capacitance across the bilayer. Simultaneously, the bilayer is imaged at 10 FPS, allowing for the changing area of the bilayer to be determined after processing using a custom MATLAB script. The capacitance (C) and area (A) data are used to calculate the hydrophobic thickness of the bilayer by the relation d = εε0A/C, where ε0 is the permittivity of free space, and ε is 2.5, the dielectric constant for the bilayer in accordance with prior work.28 The change in thickness relative to applied voltage can be used to determine the membrane Young's modulus, E⊥ by:
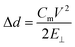 | (5) |
2.3 Janus particle synthesis and characterization
Janus particles were fabricated using metal sputtering on a monolayer of polystyrene particles. Isotropic polystyrene particles are first made into a monolayer by evaporation at ambient conditions on a glass slide. The particles used in for all experiments are coated first with a layer of titanium (5 ± 1 nm) to aid binding, followed by platinum (5 ± 1 nm). Following sputtering, particles are removed from the glass slide by sonication in water and allowed to settle overnight in a 50 mL centrifuge tube. Due to their density, the particles form a pellet if given enough time to sediment so that the resulting suspension can be concentrated and used in experiments. Before use in an experiment, an aliquot of particles is sonicated for 30 minutes to break up any aggregation.To assess the effect of sputtering on the streptavidin functionalization, glass slides were biotinylated using a procedure adapted from Lowndes, et al.30 The glass surface was first silanized using a solution of APTES and acetic acid in methanol and water. Following silanization, the surface was incubated with a solution of sulfo-NHS–LC–biotin in PBS at room temperature for 1 hour in the dark. The functionalized surface was washed 3× with PBS before use with particle tracking experiments.
To test the effect of CTAB on particle surface potential, zeta potential measurements were made on stock COOH functionalized particles in bulk aqueous solutions of varying CTAB concentration using a Malvern Zetasizer ZSP (Malvern Panalytical, Westborough, MA). Measurements were made after allowing for 30 s of temperature equilibration at 25 °C, and each zeta potential value reported is from the average of 10 measurements taken on the same sample.
2.4 Particle tracking and image analysis
After sonication, particles were added to the formed bilayer in 5 µL increments using a micropipette. CTAB, if used, and H2O2 was introduced to the system following particle addition so that the particle dynamics in a controlled environment could be observed first. In between H2O2 additions, the system is allowed to settle for a few minutes so that the bulk drift effects introduced by pipetting are minimized. We note that the trajectories of the particles exhibit random direction and that particles affected by convection in the bulk fluid can be observed to be moving much more quickly than particles at the bilayer interface. Convective effects in the data analysis were further minimized in image processing by calculating a global drift across all particles and subtracting it from the particle trajectories. Particles were imaged at 10–20 FPS for 20–30 s, which allowed for sufficient data collection for trajectories that were relatively uniform and at sufficient particle populations (N > 10).Particle location and tracking was done using a brightness weighted centroid algorithm.31 Videos were taken using two-channel imaging for simultaneous brightfield and fluorescent acquisition on an inverted microscope (Nikon Ti-2). The brightfield images are used to extract particle centers for translational diffusion measurements, and the fluorescent images are used to evaluate the Janus particle orientation relative to the plane of the bilayer.
To evaluate particle dynamics under different conditions, a fit to the time averaged mean square displacement (MSD) for short lag times was used to obtain values for the diffusion coefficient and Brownian diffusion exponent according to the power law fit:
| 〈Δr2〉 = 4DΔtn | (6) |
The out-of-plane zenith angle of the Janus particle, β, is determined by the ratio of the visible area of the fluorescent polymer hemisphere of the particle against the total expected area, as defined by Cui et al.32Fig. 1 shows representations of the zenith particle relative to the plane of the bilayer and as imaged on an inverted microscope. β for a particle oriented metal side down, appearing fully dark, is defined as β = π. In the opposite case, where the particle is oriented polymer face down and appearing fully bright, is defined as β = 0. The angles in between are given by a trigonometric relation B = A/2 × (1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β), where B is the total brightness of the particle area as imaged, and A is the expected brightness of the particle if oriented polymer face down.
β), where B is the total brightness of the particle area as imaged, and A is the expected brightness of the particle if oriented polymer face down.
 | ||
| Fig. 1 Schematic showing the determination of the zenith angle, β, of a fluorescent Janus particle using microscopy. | ||
3 Results and discussion
The results in this paper are organized as follows. We first demonstrate that the Janus particle synthesis process retains particle functionalization and show that CTAB can control the direction of motion before discussing results on the bilayers. Experiments were then designed to interrogate three properties of interest: adhesion between streptavidin functionalized particles and a biotinylated membrane, surface potential modulated by the presence of CTAB, and membrane stiffness tuned by the percentage of LPC in the bilayer. The experiments done to interrogate these properties are summarized in Table 1. We discuss the results of these three properties of interest in sequence before finally discussing the observation of membrane mediated particle–particle pair interactions in specific cases.| Particle diameter | Particle surface chemistry | Aqueous solution conditions | Membrane composition | |||
|---|---|---|---|---|---|---|
| Streptavidin | COOH | No CTAB | 30 µM CTAB | DOPC | + LPC | |
| 3.2 Particle–membrane binding | ||||||
| 6 µm | X | X | X | |||
| 6 µm | X | X | X | |||
| 3.3 Pullers vs. pushers | ||||||
| 6 µm | X | X | X | |||
| 3 µm | X | X | X | |||
| 2 µm | X | X | X | |||
| 2 µm | X | X | X | |||
| 3.4 Membrane stiffness | ||||||
| 2 µm | X | X | X (1%) | |||
| 2 µm | X | X | X (5%) | |||
3.1 Establishment of particle functionalization and swimming direction
We first demonstrate that particle functionalization is retained through Janus particle synthesis and show that CTAB can control the direction of motion before discussing the dynamics of these particles on bilayers. Here, we define particles swimming in the direction of the polymer face as puller particles and particles swimming towards their metal face as pusher particles, as the particles tend to orient metal side down, resulting in pulling away from or pushing into the bilayer.When streptavidin particles were tested on bare glass, the trajectories covered a larger area over the same amount of time compared to biotinylated glass. Following the addition of H2O2, particles on bare glass were observed to swim freely, while particles bound to biotinylated glass largely remained confined, with one or two particles releasing and increasing swimming speed (Fig. 2), demonstrating that the streptavidin functionalization survived sputtering and reduced particle response to fuel in the system.
The activity of Pt–PS Janus particles fueled by H2O2 decomposition has been observed to be sensitive to ions.33 To minimize particle slowdown in response to ions, bilayers are formed in a 0.15 M glucose buffer rather than an electrolyte solution. It was observed that in glucose buffer and at about 0.5% H2O2, particles exhibited a tendency to swim upwards away from the bilayer and did not settle at the bilayer interface for observation. This phenomena, termed “negative gravitaxis”, has been observed in analogous bulk systems34 and relates to the tendency of the particles to orient metal side down due to gravity and swim towards their polymer face. In order to be able to study particles at the interface, the particle addition was done before adding any H2O2 to the environment. The particles are first imaged at the bilayer interface without any fuel before H2O2 is gradually titrated in.
In a 0.15 M glucose buffer, particles were observed to begin swimming upwards at about 0.5% H2O2. To reverse this effect, we introduced the cationic surfactant CTAB into the system, which has been observed to reverse particle swimming direction.33 The result of CTAB on particle swimming direction in a bulk environment with constant 3% H2O2 are shown in Fig. 3A. At 1 µM CTAB, there is no change in particle swimming direction, but at 10 µM CTAB, there is both a slow down and a reversal in particle motion. At 100 µM CTAB, the reversal in swimming direction remains, and the swimming speed of a particle at 1 µM CTAB is recovered. The reversal effect has been discussed extensively33,35 and appears to correlate with changes in the particle surface potential, which we confirmed with zeta potential measurements shown in Fig. 3B.
3.2 Binding restricts active motion of pullers
We compare bound and unbound pullers using 6 µm diameter Janus particles. Active particle dynamics were observed in concentrations of H2O2 ranging from 0 to 0.5% in the unbound case and 0 to 0.4% in the bound case. The change in particle trajectories relative to fuel concentration can be seen in Fig. 4. In the case of the unbound particles (Fig. 4A), the particles gradually gain velocity with even small increments in fuel concentration, and the resulting effect can be seen in trajectories that gradually cover more area over a fixed time period. At 0.5% H2O2, particles begin to pull off of the bilayer as they swim upwards, which results in a reduction of the number of trajectories recorded. In the case of the bound particles, the onset of active dynamics is different (Fig. 4B). From 0.1 to 0.3% H2O2, the initial increases in fuel concentration do not seem to appear to trigger changes in particle dynamics, as the particle trajectories remain relatively confined until there is 0.4% H2O2 in the system. At this point, most of the trajectories seem to stretch out although there are still one or two particles that appear to remain confined. This is because the streptavidin–biotin linkage prevents particle movement at a low H2O2 concentration. At 0.4%, the force induced by the fuel overpowers the chemical bond, and the particles are able to actively diffuse as if they are unbound.These trends are examined quantitatively through the lens of a power law fit to the mean squared displacements (MSDs) of the particle trajectories (Fig. 5). The time averaged MSDs of unbound particles are observed to increase in both slope and magnitude in the unbound particle case (Fig. 5A). However, the MSDs of the bound particles do not change substantially until the concentration of H2O2 reaches 0.4%, the point at which a split in particles that remained bound and particles that “lifted off” occurred (Fig. 5B). The magnitude of the MSDs can be related to a diffusion coefficient and exponent according to eqn (6) and are plotted against H2O2 concentration in Fig. 5C and D. In the unbound case, the magnitude of D and n both steadily become higher with incremental additions of H2O2, demonstrating a step-wise increase in activity with higher fuel concentrations. In the bound case, both D and n remain unchanged until the bond is broken at 0.4% H2O2.
Particle orientation distributions against increasing H2O2% are shown in Fig. 5E and F. Here, a particle sitting with the polymer side facing down is represented by 0, and a particle with the metal side down has the angle π. We expect the particles to settle preferentially with their metal side facing down due to the anisotropic density of the Janus particles. This is shown in the case of 0% H2O2 in both the bound and unbound cases, where the distribution skews towards π, representing a cap down particle. In the case of streptavidin functionalized particles, this preferred orientation may affect binding between the particle and the membrane since the streptavidin coating would be on the polymer face of the particle. However, we observe that the distribution of bound particle orientations appears to be relatively fixed through increasing fuel additions, suggesting that the effect of binding is to keep the particles from freely rotating. In contrast, the distribution of unbound particle orientations can be seen to become more random, resulting in a broadening of the beta distribution, with increasing H2O2.
We can contextualize the effect of binding on particle dynamics by comparing the force expected to separate a bound particle to the force exerted by fueled particle motion. The force exerted by the particle should be equal and opposite to its drag force, which can be estimated by the Stokes drag, F = 6πηaV, which is approximately 0.05 pN using the measured speeds of 6 µm Janus swimmers at 0.5% H2O2 in bulk. This estimate can be refined with models developed for particles moving along a lipid bilayer interface developed by Danov et al.,36,37 which give an increased force estimate of about 0.1 pN for the velocities we measured. This is three orders of magnitude lower than the expected force necessary to break the avidin–biotin bond, which is about 140 pN as measured by AFM38 and two orders of magnitude lower than the force necessary to remove a lipid from the bilayer, reported as 20 pN in the same study.38 Further discrepancies in the forces might be explained by the difference in the direction of force, i.e. a shearing force as the particle pulls laterally against the bilayer as opposed to an orthogonal pulling force, as measured by AFM.
3.3 Pullers vs. pushers
While particle binding effects are apparent on particle dynamics as they pull away from the membrane, we are also interested in particle behaviors as they push into the membrane, as this mimics the wrapping experienced during endocytosis. For this purpose, a system of pushers in which the particles swim in a reverse direction, i.e., towards their metal face as opposed to their polymer face, would allow for the investigation of a different set of interactions. In this case, the particles would be pushing in the same direction as gravity (downwards) instead of against it. A reversal in particle swimming direction was previously observed in an interrogation of ionic effects on the swimming speeds of Pt–PS particles.33 In a bulk aqueous solution, we found that a concentration of 10 µM CTAB was sufficient to reverse swimming direction, as discussed in Section 3.1.CTAB has been previously been observed to modify lipid packing in supported lipid bilayers.39 To minimize the effect of surfactant interactions with the lipid bilayer, pusher particle experiments at the membrane interface were done with 30 µM CTAB, and the bilayer was monitored optically for stability. The particles were added first with a micropipette, then CTAB and H2O2 were titrated in. Between titrations and imaging, the system was allowed to settle for at least a minute to minimize convective disturbances. The particles were imaged after adding CTAB and before H2O2 addition, and no apparent changes in their diffusivity was observed. However, while not directly observed here, we note that CTAB can cause membrane defect formation, alteration of lipid headgroup packing, charge, and membrane tension.40–42 These factors may be negligible or possibly impact particle diffusivity and lipid membrane interactions on longer timescales than the current experiments.
We first compare the dynamics of unbound 6 µm PS–Pt particles against increasing H2O2 concentration with and without CTAB. Here, we first observe much more confined dynamics against higher fuel concentrations in the CTAB case, as shown in Fig. 6. With CTAB, a larger experimental operating window is realized; pusher particles are observed at up to 1.5% H2O2, whereas particles started leaving the bilayer at 0.5% H2O2 in the puller case due to negative gravitaxis. For the larger particles, the bilayer tension may be too high for any wrapping to occur, so the main resistance to motion is the particle pushing against the bilayer as if it were a flat wall. Comparing the distribution of diffusion coefficients as shown in Fig. 6A, the puller particle diffusion coefficients steadily increase in magnitude, while the pusher particle diffusion coefficients decrease slightly. While pullers gain velocity and become superdiffusive at the first addition of H2O2, the pusher exponent distribution only rises slightly above 1 (Fig. 6B), so the particles are gaining activity, but this does not translate into increased diffusivity. When active, the pushers do not appear to be traveling at constant speed as the pullers do but rather are seen “hopping” between areas of slower diffusion. Example tracks can be seen in Fig. 6C. This behavior is consistent with ergodicity breaking observed in anomalous receptor diffusion.43 We can also compare the time averaged (tMSD) to ensemble averaged MSD (eMSD) in our system. Consistent with non-ergodic behavior characterized in other systems,43,44 the slope of the eMSD is much lower than that of the tMSD (Fig. 6D).
To evaluate the effect of particle size on pusher dynamics, Janus particles were made using 2 µm particles with the same composition and functionalization and tested against increasing concentrations of H2O2 with the same concentration of CTAB used to test the 6 µm pushers. We compare the dynamics of these pushers in Fig. 7. The difference in overall diffusivity of the particles is consistent with expected Stokes scaling (Fig. 7A). We compare the scaling of D against the diffusivity in the absence of fuel in Fig. 7B. Interestingly, the overall diffusivity of both particles decreases with increasing % H2O2, which is the opposite of the behavior observed for puller particles and for typical H2O2 fueled Janus swimmers. Here, we observe that the scaling of the smaller particles is slightly steeper than that of the 6 µm pushers, suggesting a size-dependent wrapping effect governs the decrease in diffusivity, as predicted by the particle size dependence of wrapping energy (eqn (4)). These considerations are further discussed in Section 3.5.
In all cases, it was observed that the pusher particles place stress on the bilayer that eventually results in membrane rupture. A collapse inward was observed for smaller particles (the oil annulus was seen to lose its circularity) at about 20–30 minutes after at least 1% H2O2 was added. For the 6 µm pushers, bilayer rupture was observed about 10 minutes after the system was brought up to 1.5% H2O2.
3.4 Effect of membrane stiffness
Previously, we have demonstrated that membrane stiffness increases with increasing concentration of anionic lipids in the bilayer.29 However, the DOPC bilayers used in this work still exhibit much higher membrane tension than other membrane models used to interrogate wrapping. For example, wrapping has been studied on GUVs with tensions ranging from 10−6 to 10−3 mN m−1,26,45 while the tension of the LAMB is around 1 mN m−1.24 To decrease membrane stiffness and tension, we fabricate bicomponent bilayers with a small amount of lysophospholipids (LPCs), which have a single acyl tail, in addition to DOPC. LPCs have previously been shown to decrease the stiffness of model lipid bilayers. For example, in a study of POPC GUVs, a 30% decrease in bending rigidity was measured for a vesicle containing 10 mol% LPC compared to a vesicle made fully with POPC.46To test the effect of LPCs on bilayer stiffness, a membrane compression experiment was run on DOPC and 95/5 DOPC/LPC bilayers, as previously described.24,29 We did not calculate the bending rigidity for these bilayers, but it can be determined from the same measurement, as previously demonstrated,23 and correlates closely to the Young's modulus. The average Young's modulus for each bilayer composition measured over three separate compression cycles is shown in Fig. 8A. With 5% LPC, about a 20% decrease in stiffness is observed relative to DOPC. The modulus of a 99/1 DOPC/LPC bilayer was not measured because no measurable difference in particle diffusivity on 99/1 DOPC/LPC vs. 100 DOPC was observed, as discussed below.
We tested the diffusivity of 2 µm Pt–PS Janus particles on bilayers with the following binary DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC compositions with CTAB present (pusher case): DOPC, 99
LPC compositions with CTAB present (pusher case): DOPC, 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DOPC
1 DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC, and 95
LPC, and 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 DOPC
5 DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC. Since these particles are pushing into the bilayer, we expect that decreasing the stiffness of the bilayers should result in decreased particle diffusivity compared with particles on a stiffer bilayer at the same H2O2 concentration. The response of particle diffusivity vs. increasing H2O2% can be seen in Fig. 8B–D. Comparing the tracks at 1% H2O2 over 20 s (Fig. 8B), it can be seen that the particles cover about the same area in DOPC vs. 99/1 DOPC/LPC, but diffuse over less area overall on 95/5 DOPC/LPC, indicating qualitatively increased membrane wrapping. Fig. 8C compares changes in the diffusion coefficient, D, fitted from the MSD (eqn (6)). There is no noticeable difference in the spread of D between particles on a DOPC bilayer and 99/1 DOPC/LPC bilayer, perhaps because the concentration of LPC is not high enough to make a meaningful difference in bilayer stiffness. On 95/5 DOPC/LPC, however, there is a noticeable decrease in D from around 0.2 to 0.1 µm2 s−1. In all cases, the exponent holds at around 1, indicating normal Brownian diffusion. Interestingly, in the case of all three bilayer compositions, it is seen that D decreases slightly, but n is either steady or increases slightly with increasing H2O2, indicating that an increase in particle activity does not always translate to higher diffusivity on a flexible interface. Despite the decreased stiffness 95/5 DOPC/LPC membrane, there is minimal difference in how the diffusion coefficient varies with increasing H2O2 concentration (Fig. 8D).
LPC. Since these particles are pushing into the bilayer, we expect that decreasing the stiffness of the bilayers should result in decreased particle diffusivity compared with particles on a stiffer bilayer at the same H2O2 concentration. The response of particle diffusivity vs. increasing H2O2% can be seen in Fig. 8B–D. Comparing the tracks at 1% H2O2 over 20 s (Fig. 8B), it can be seen that the particles cover about the same area in DOPC vs. 99/1 DOPC/LPC, but diffuse over less area overall on 95/5 DOPC/LPC, indicating qualitatively increased membrane wrapping. Fig. 8C compares changes in the diffusion coefficient, D, fitted from the MSD (eqn (6)). There is no noticeable difference in the spread of D between particles on a DOPC bilayer and 99/1 DOPC/LPC bilayer, perhaps because the concentration of LPC is not high enough to make a meaningful difference in bilayer stiffness. On 95/5 DOPC/LPC, however, there is a noticeable decrease in D from around 0.2 to 0.1 µm2 s−1. In all cases, the exponent holds at around 1, indicating normal Brownian diffusion. Interestingly, in the case of all three bilayer compositions, it is seen that D decreases slightly, but n is either steady or increases slightly with increasing H2O2, indicating that an increase in particle activity does not always translate to higher diffusivity on a flexible interface. Despite the decreased stiffness 95/5 DOPC/LPC membrane, there is minimal difference in how the diffusion coefficient varies with increasing H2O2 concentration (Fig. 8D).
3.5 Onset of pair interactions
In the case of the pusher particles with CTAB present in the system, the onset of long-rate interparticle attraction and particle aggregation over time was observed when at least 1% H2O2 was present in the system (Fig. 9A). No aggregation was observed in systems held at 0.5% H2O2 for up to 30 minutes, while aggregation was observed after about 5 minutes after the system was titrated up to 1% H2O2. This aggregation was predicated by particle pair interactions, which have not been previously observed in passive particles bound to bilayers using the LAMB platform.47 To elucidate the origins of these pair interactions, we can compare our system to analogous studies done on GUVs. Pair interactions have previously been observed on both floppy and tense GUVs,48–50 which represent membrane tensions of around 10−9–10−8 and 10−6–10−5 Pa s, respectively. On floppy GUVs, the driving force for particle aggregation was observed to be curvature mediated. In this case, the particles would only aggregate if fully wrapped by the membrane, and their interactions were described by an attraction potential of around 3kBT.48 In contrast, particle pair interactions and aggregation in the case of the tense GUV were observed to be tension-mediated, which is analogous to capillary attraction. The potentials determined for these interactions were much higher, at around 100kBT.49 The planar bilayer used for these experiments is even an order of magnitude more tense than the tense GUV, with a surface tension of 10−3 Pa s.24 We thus seek to delineate the driving force for particle migration on a planar bilayer with tension in the mPa s regime.Three examples of pair interaction events are shown in Fig. 9B. These represent systems with different particle radii (2 µm vs. 3 µm), concentrations of H2O2 (1% vs. 2%), and bilayer composition (DOPC vs. 99/1 DOPC:LPC). In all three cases, the change in particle separation (r) scales against (tcontact − t) by a power law relationship with a slope of 0.2, as shown in Fig. 9B. This scaling is in agreement with capillary attraction predicted for spheres at a liquid interface, which are expected to scale with an exponent of 1/5.51 Neglecting inertial and stochastic terms as discussed in ref. 52, the force balance becomes:
| Fdrag = 6πaηdr/dt = −Finter |
Here, we elect to estimate the drag force using the Stokes formula: Fdrag = 6πaη(dr/dt), where a is the particle radius, and η is the bulk viscosity, approximately 1 mPa s. It should be noted that for a particle interacting with a lipid bilayer, especially with adhesive interactions, the actual hydrodyamic drag is more complicated, as discussed in the seminal Saffman–Delbrück derivation53 as well as our prior work.54 The error associated with approximating surface drag by bulk drag is discussed for air–water interfaces by Danov et al.,36 which gives an uncertainty of about 10–20%. We note also that the hydrodynamic drag measured for a lipid bilayer surface was observed to be Cπηa, with C = 5.98.55 While the bulk hydrodynamic drag is not likely to describe particle drag on the bilayer, we can at least rule out a lower constant, so the force here is more likely to be an underestimate than an overestimate. With these limitations in mind, we can still interrogate the effect the effect of experimental conditions on the resulting capillary interactions of the particle pairs.
The pair interaction potential can thus be determined by a spatial integration of the drag force along the particle approach trajectory:
 | (7) |
The interaction potentials determined for the three examples of pair interactions are shown in Fig. 9C. Close to contact, the measured capillary attraction for all three particle pairs are on the scale of 102kBT, ranging from 100–300kBT. This is in good agreement with observations of tension mediated capillary attraction of spherical particles on GUVs,49 which reported a typical binding energy of 100kBT. The marginally higher values in our system are unsurprising considering the higher tension of the planar bilayer system. We can compare the calculated capillary energy to the propulsive energy of the particles generated by the breakdown of H2O2 as well as the bending energy of the bilayer. From measured velocities, we estimate the propulsive energy of the particles to be on the order of 10−5kBT, which is trivial compared to the estimated capillary energy. The bending energy of a DOPC bilayer generated on our platform has been previously calculated to be 5kBT,23 which is also two orders of magnitude smaller than the capillary energy. Wrapping interactions between the particle and bilayer are also dependent on membrane surface tension and particle size, as predicted by eqn (4). For our system, this crossover length scale comes out to about 15 nm, suggesting the system is still in a tension-dominated regime.
We compare the values we measured to the predicted capillary energies for spheres at an air water interface are 103–104kBT. Under the consideration that the drag value used to calculate the drag for our system is likely an underestimate, the capillary energies at the flat lipid membrane interface could be closer to those at air–water and other flat interfaces.
We now consider the differences in interactions determined for the three sets of particles, summarized in Table 2. From these results, we can infer that a higher concentration of H2O2 fuel apparently drives stronger particle interactions, as expected from a higher pushing force into the bilayer, which may increase deformation and drive the onset of contact lines. Furthermore, the smaller, bound particles apparently possess a higher interaction potential than larger, unbound particles under the same H2O2 concentration. The estimation of drag force used here does not actually account for changes in drag as a result of particle adhesion, so the difference measured here is likely due to particle size. In the tension mediated regime, we expect that the smaller particle is more likely to be wrapped by the bilayer, resulting in a higher tension-mediated attraction. Furthermore, in an experiment with 6 µm pushers held at 1.5% H2O2, no particle aggregation was observed, suggesting a threshold for particle radius in which tension-mediated interactions can occur.
| Particle | Bilayer | H2O2 conc. | U(r) |
|---|---|---|---|
| 2 µm unbound | 99/1 DOPC/LPC | 1% | 100kBT |
| 3 µm unbound | DOPC | 2% | 180kBT |
| 2 µm bound | 99/1 DOPC/DOPE-cB | 2% | 270kBT |
4 Conclusions
We observed changes in the dynamics of active Janus particles against adhesion to the membrane, particle swimming direction, and membrane stiffness. Streptavidin functionalized particle, which bind to a biotinylated membrane, exhibited a delayed onset in swimming activity compared to particles that were not bound to the membrane. With only glucose in the buffer solution, the Janus particles half coated with platinum swim up and away from the bilayer in the presence of H2O2, resulting in a loss of particles at the bilayer surface over time. When CTAB is added to the buffer, a reversal in particle swimming direction causes them to push into the bilayer. This results in decreased diffusivity even as the particles become more active, the onset of capillary forces resulting in particle aggregation, and eventual membrane disruption from the pushing force of the particles. We observed that a decrease in membrane stiffness results in a further decrease in pusher diffusivity against the membrane as a result of increased particle wrapping. Finally, we characterized the potential energy of the pusher pair interactions, finding them consistent with capillary attraction. A higher membrane stiffness results in a higher potential energy well for particle aggregation and binding between the particle and bilayer also appears to increase the potential energy well.Future studies could isolate the effect of pushing from changes in buffer composition. Since we postulate that the crossover from puller to pusher behavior is caused by a change in the surface charge of the JP polymer face from negative (−50 mV for COOH functionalized particles) to positive (+50 mV at 100 µM CTAB), it follows that other methods to reverse the swimming direction by charge could be explored. One avenue could be the incorporation of a quaternary amine salt in place of CTAB. The effect of charge could also be isolated to the particle and not the buffer by substituting the COOH functionalized polystyrene particle with an amine-functionalized one. Lastly, changing the swimming direction and magnitude of active motion using aqueous solution conditions is a serial process. Developing active colloidal systems with swimming dynamics that are externally triggered (via light, for example), would enable higher throughput tuning of the particle–membrane interactions. These are among the future directions of interest as increasingly complex artificial experimental platforms mimicking particle–membrane transport are pursued.
Author contributions
PJB and PL conceived the ideas for experiments. PJB and MK acquired funding for the project. RK fabricated the Janus particles used for the experiments. PL ran the experiments, analyzed the results, and drafted the manuscript. All authors discussed the results and edited the final paper.Conflicts of interest
There are no conflicts to declare.Data availability
The data related to this article has been posted to a publicly accessible database, Open Science Framework (OSF), and can be found here: https://doi.org/10.17605/OSF.IO/Q93FU.Acknowledgements
The authors would like to thank the UMass ADD/FAB lab for help fabricating the sample holder used for the thin film balance, the Nanofabrication Cleanroom for metal deposition to create active colloids, and the Biophysical Core Facilities for DLS/zeta potential measurements. This work was supported by funding from the National Science Foundation through award no. CBET-1942581 and through an ADVANCE Collaborative Research Seed Grant. PL also acknowledges a PPG Fellowship for partial support.References
- M. Lakadamyali, M. J. Rust, H. P. Babcock and X. Zhuang, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 9280–9285 CrossRef CAS.
- P. Friedl and D. Gilmour, Nat. Rev. Mol. Cell Biol., 2009, 10, 445–457 Search PubMed.
- K. X. Tan, M. K. Danquah, J. Jeevanandam and A. Barhoum, Pharmaceutics, 2023, 15, 423 CrossRef CAS.
- Y. G. J. Lim, K. Choon Wilson Poh, S. Chye Joachim Loo, Y. G. J. Lim, K. C. W. Poh and S. C. J. Loo, Macromol. Rapid Commun., 2019, 40, 1800801 CrossRef.
- L. Baraban, D. Makarov, R. Streubel, I. Mönch, D. Grimm, S. Sanchez and O. G. Schmidt, ACS Nano, 2012, 6, 3383–3389 CrossRef CAS.
- F. Mou, C. Chen, Q. Zhong, Y. Yin, H. Ma and J. Guan, ACS Appl. Mater. Interfaces, 2014, 6, 9897–9903 CrossRef CAS.
- L. Kong, N. Rohaizad, M. Z. M. Nasir, J. Guan and M. Pumera, Anal. Chem., 2019, 91, 5660–5666 CrossRef CAS PubMed.
- S. Zhang, H. Gao and G. Bao, ACS Nano, 2015, 9, 8655–8671 CrossRef CAS.
- S. Zhang, J. Li, G. Lykotrafitis, G. Bao and S. Suresh, Adv. Mater., 2009, 21, 419–424 CrossRef CAS PubMed.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 Search PubMed.
- T. F. Roth and K. R. Porter, J. Cell Biol., 1964, 20, 313–332 CrossRef CAS.
- E. Blanchard, S. Belouzard, L. Goueslain, T. Wakita, J. Dubuisson, C. Wychowski and Y. Rouillé, J. Virol., 2006, 80, 6964–6972 Search PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- M. R. Bailey, A. R. Sprenger, F. Grillo, H. Löwen and L. Isa, Phys. Rev. E, 2022, 106(5), L052602 CrossRef CAS.
- A. Stocco, B. Chollet, X. Wang, C. Blanc and M. Nobili, J. Colloid Interface Sci., 2019, 542, 363–369 CrossRef CAS PubMed.
- X. Wang, M. In, C. Blanc, M. Nobili and A. Stocco, Soft Matter, 2015, 11, 7376–7384 Search PubMed.
- Z. Jalilvand, H. Haider, J. Cui and I. Kretzschmar, Langmuir, 2020, 36, 6880–6887 CrossRef CAS.
- K. Dietrich, D. Renggli, M. Zanini, G. Volpe, I. Buttinoni and L. Isa, New J. Phys., 2017, 19, 065008 CrossRef.
- S. Villa, G. Boniello, A. Stocco and M. Nobili, Adv. Colloid Interface Sci., 2020, 284, 102262 CrossRef CAS PubMed.
- C. Dietrich, M. Angelova and B. Pouligny, J. Phys. II, 1997, 7, 1651–1682 CrossRef CAS.
- M. Deserno, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031903 CrossRef.
- A. H. Bahrami, M. Raatz, J. Agudo-canalejo, R. Michel, E. M. Curtis, C. K. Hall, M. Gradzielski, R. Lipowsky and T. R. Weikl, Adv. Colloid Interface Sci., 2014, 208, 214–224 CrossRef CAS.
- O. Zabala-Ferrera, P. Liu and P. J. Beltramo, Membranes, 2023, 13(2), 129 CrossRef CAS.
- P. J. Beltramo, R. Van Hooghten and J. Vermant, Soft Matter, 2016, 12, 4324–4331 Search PubMed.
- C. Van Der Wel, D. Heinrich and D. J. Kraft, Biophys. J., 2017, 113, 1037–1046 Search PubMed.
- H. T. Spanke, R. W. Style, C. François-Martin, M. Feofilova, M. Eisentraut, H. Kress, J. Agudo-Canalejo and E. R. Dufresne, Phys. Rev. Lett., 2020, 125, 198102 CrossRef CAS.
- V. Sharma, C. M. Marques and A. Stocco, Nanomaterials, 2022, 12, 1434 CrossRef CAS.
- P. J. Beltramo, L. Scheidegger and J. Vermant, Langmuir, 2018, 34, 5880–5888 CrossRef CAS.
- P. Liu, O. Zabala-Ferrera and P. J. Beltramo, Biophys. J., 2021, 120, 1755–1764 CrossRef CAS PubMed.
- M. Lowndes and W. J. Nelson, Adhesion Protein Protocols, Springer Nature, 2013, pp. 219–230 Search PubMed.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 Search PubMed.
- J. Cui, D. Long, P. Shapturenka, I. Kretzschmar, X. Chen and T. Wang, Colloids Surf., A, 2017, 513, 452–462 Search PubMed.
- A. Brown and W. Poon, Soft Matter, 2014, 10, 4016–4027 Search PubMed.
- A. I. Campbell and S. J. Ebbens, Langmuir, 2013, 29, 14066–14073 CrossRef CAS PubMed.
- A. T. Brown, W. C. K. Poon, C. Holm and J. De Graaf, Soft Matter, 2017, 13, 1200 RSC.
- K. Danov, R. Aust, F. Durst and U. Lange, J. Colloid Interface Sci., 1995, 175, 36–45 CrossRef CAS.
- J. T. Petkov, N. D. Denkov, K. D. Danov, O. D. Velev, R. Aust and F. Durst, J. Colloid Interface Sci., 1995, 172, 147 Search PubMed.
- J. Wong, A. Chilkoti and V. T. Moy, Biomol. Eng., 1999, 16, 45–55 Search PubMed.
- L. M. C. Lima, M. I. Giannotti, L. Redondo-Morata, M. L. C. Vale, E. F. Marques and F. Sanz, Langmuir, 2013, 29, 9152–9361 Search PubMed.
- S. W. Tan, N. Gooran, H. M. Lim, B. K. Yoon and J. A. Jackman, Nanomaterials, 2023, 13, 874 Search PubMed.
- B. Liu, M. I. Hoopes and M. Karttunen, J. Phys. Chem. B, 2014, 118, 11723–11737 Search PubMed.
- K. N. Belosludtsev, N. V. Belosludtseva, A. V. Agafonov, N. V. Penkov, V. N. Samartsev, J. J. Lemasters and G. D. Mironova, Biochim. Biophys. Acta, Biomembr., 2015, 1848, 2200–2205 CrossRef CAS.
- C. Manzo, J. A. Torreno-Pina, P. Massignan, G. J. Lapeyre, M. Lewenstein and M. F. Garcia Parajo, Phys. Rev. X, 2015, 5, 011021 Search PubMed.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438–6443 Search PubMed.
- H. R. Vutukuri, M. Hoore, C. Abaurrea-Velasco, L. van Buren, A. Dutto, T. Auth, D. A. Fedosov, G. Gompper and J. Vermant, Nature, 2020, 586, 52–56 CrossRef CAS PubMed.
- J. R. Henriksen, T. L. Andresen, L. N. Feldborg, L. Duelund and J. H. Ipsen, Biophys. J., 2010, 98, 2199–2205 Search PubMed.
- P. Liu and P. J. Beltramo, Soft Matter, 2023, 19, 7708–7716 RSC.
- C. Van Der Wel, A. Vahid, A. Šarić, T. Idema, D. Heinrich and D. J. Kraft, Sci. Rep., 2016, 6, 32825 Search PubMed.
- R. Sarfati and E. R. Dufresne, Phys. Rev. E, 2016, 94, 12604 CrossRef.
- N. Li, N. Sharifi-Mood, F. Tu, D. Lee, R. Radhakrishnan, T. Baumgart, K. J. Stebe, P. Malgaretti, M. N. Popescu and S. Dietrich, Soft Matter, 2016, 12, 4007–4023 RSC.
- D. Stamou, C. Duschl and D. Johannsmann, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5263 CrossRef CAS.
- J. C. Loudet, A. M. Alsayed, J. Zhang and A. G. Yodh, Phys. Rev. Lett., 2005, 94, 018301 CrossRef CAS PubMed.
- P. Saffman and M. Delbruck, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111–3113 CrossRef CAS PubMed.
- X. Liu, T. Auth, N. I. Hazra, M. Frendø Ebbesen, J. Brewer, G. Gompper, J. J. Crassous and E. Sparr, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(30), e2217534120 Search PubMed.
- P. E. Jahl and R. Parthasarathy, Phys. Rev. Res., 2020, 2, 013132 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |








