Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bridging scales: machine learning for the rational design and modelling of shape memory polymers
Cheng Yan a and
Giulia Scalet
a and
Giulia Scalet *b
*b
aSouthern University and A&M College, Department of Mechanical Engineering, Baton Rouge, LA 70813, USA
bDepartment of Civil Engineering and Architecture, University of Pavia, via Ferrata 3, 27100 Pavia, Italy. E-mail: giulia.scalet@unipv.it
First published on 2nd December 2025
Abstract
Shape memory polymers (SMPs) are a class of stimuli-responsive materials with significant potential across diverse fields including soft robotics, biomedical devices, and mechanical engineering. To realize a scale transition from small molecules to a mechanical structure with excellent SMP behaviour, investigators typically need both material design and constitutive model establishment. Traditionally, the design of SMPs relies on empirical methods, limiting the speed of discovery and property tuning. Moreover, the prediction of their behaviour generally depends on theoretical and numerical tools that, however, require an in-depth understanding of theoretical mechanics. In contrast, machine learning (ML) offers a powerful tool to possibly overcome these limitations and has increasingly drawn attention from investigators in multiple fields. In this perspective, we critically review recent advances in the application of ML techniques to SMPs. We discuss major conventional concepts in the field of SMPs, basic procedures and important approaches to ensure ML-assisted SMP design, how different ML tools have been employed to identify new SMP chemistries and to predict their thermo-mechanical and shape memory properties. Despite these successful advancements, ML-assisted SMP discovery and thermo-mechanical modelling remain at an early stage. We discuss how they are limited, e.g., by incomplete structural representations and challenges in integrating thermal and temporal effects into the neural network. Finally, we outline future directions to explore and implement, including developing tools to capture complex SMP topologies and creating polymer-specific neural networks. The discussion allows us to provide new insights into the use of ML tools for the world of SMPs.
1 Introduction
Shape memory polymers (SMPs) are a versatile class of smart soft materials characterized by their ability to recover an initial permanent shape from a deformed temporary one, upon exposure to an external stimulus, typically a thermal, optical, or electrical trigger.1 Depending on the macromolecular architecture of the polymer and the specific applied protocol (named programming), this ability can manifest itself through different forms of shape memory effects (SMEs), the one-way SME being the most common one.The additional advantages of SMPs, including, for instance, large strains, possible biocompatibility, and processability via 4D printing techniques, make them promising material candidates for various application fields, such as pharmaceutical,2 flame retardancy,3 biomedical devices,4 tissue engineering,5 and soft robotics.6 These applications pose numerous constraints on the physical and functional properties of SMPs and motivate the increasing need for efficient approaches to design novel SMP chemistries that could satisfy application requirements.
Traditional SMP design relies heavily on empirical synthesis and extensive experimental characterization to measure the chemical, physical, thermal, mechanical, and shape memory properties of the developed systems.1,7,8
Alternative solutions supporting the design of SMPs rely on molecular dynamics (MD) simulations which investigate the material at the atomistic level.9–12 While these approaches allow for an in-depth analysis of structure–property relationships, they are time-consuming and can be unpractical for engineering purposes. For example, to estimate the glass transition temperature (Tg), one typically needs about 50–150k atoms to simulate a conventional polymer, such as epoxy or polyurethane. This needs 1–5 days to simulate a dozen to hundreds of physical nanoseconds in the glass transition zone.13 Although direct examples for SMP Tg prediction are limited, other studies provide useful reference values. For instance, Hayashi et al.14 reported that an equilibrium MD simulation for evaluating the physical properties of a conventional amorphous polymer typically requires more than 30–50 hours on a workstation equipped with dual Intel Xeon Gold 6148 CPUs (2.4 GHz, 40 cores). In another study on gas-transport behaviour in polymer membranes, Giro et al.15 simulated systems containing approximately 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. Furthermore, to enable the use of these discovered SMPs in complex mechanical structures, constitutive models are indispensable. Numerical simulations based on constitutive models developed ad hoc represent one of the most used approaches to predict the macroscopic properties of a given SMP-based structure. The literature is very rich in contributions, mostly divided into rheological, phase-transition, and mixed models.16–18 However, this process requires an in-depth understanding of continuum mechanics and polymer physics as well as a time-consuming calibration process of model parameters.
000 atoms. Furthermore, to enable the use of these discovered SMPs in complex mechanical structures, constitutive models are indispensable. Numerical simulations based on constitutive models developed ad hoc represent one of the most used approaches to predict the macroscopic properties of a given SMP-based structure. The literature is very rich in contributions, mostly divided into rheological, phase-transition, and mixed models.16–18 However, this process requires an in-depth understanding of continuum mechanics and polymer physics as well as a time-consuming calibration process of model parameters.
Accordingly, researchers have searched for new methodologies to possibly address limitations of the current approaches.
Recently, machine learning (ML) has rapidly emerged as one possible solution. Essentially, ML aims to learn a mapping function Y = f(X) between input X and output Y. To achieve this, investigators have developed a variety of effective methods, such as artificial neural networks (ANNs), Gaussian process regression (GPR), random forest, and support vector method (SVM).
As shown in Fig. 1, ML can play two key roles for SMPs: bridging the microscopic and macroscopic levels (Fig. 1(a)–(c)) and further linking the macroscopic level to complex mechanical structures with excellent SMP performance (Fig. 1(c)–(e)). These two roles are often referred to as ML-assisted design and ML-based thermo-mechanical behaviour prediction, respectively. The former aims to predict the thermal dynamics of macroscopic molecules from their microscopic molecular structures, while the latter focuses on directly predicting the behaviour of SMP-based structures. Since SMPs often exhibit extremely complex topological structures at the microscopic level, accurately and quantitively describing their macroscopic behaviour is highly challenging. Moreover, the behaviour of SMPs in working or recovery processes not only depends on their intrinsic topology but also on how they are handled in the programming step, making the precise design of their performance even more difficult.
Theoretically, the design includes finding a function from microscopic molecular structures to their ultimate functionalities. As already discussed above, MD simulation is a promising way to design SMPs. However, the realization of the SME often requires hours while MD computation can only be realized during the time scale of nanoseconds, making it impractical with current computational capabilities. In contrast, many ML methods can simulate any function. For example, based on the universal approximation theorem,19 ANNs can approximate any continuous function and form the foundational hypothesis for designing or developing models for SMPs. Therefore, it is not surprising that ML has rapidly emerged as a powerful tool to accelerate materials discovery, optimize structure–property relationships, and guide rational material design.20–23
ML-assisted polymer design started in the 1990s. Back then, Venkatasubramanian and collaborators24,25 employed the genetic algorithm to design some structures for homopolymers. However, the rapid growth of ML-assisted polymer design has primarily emerged in the past decade. As a branch of polymer research, ML-assisted studies on SMPs did not emerge until around 2019. This delay is largely because conventional polymer properties are primarily determined by their topological structures, making them relatively straightforward to model. In contrast, the SME arises from an extremely complex interplay of kinetic relaxation processes,26 including viscoelastic relaxation, phase transitions, and segmental mobility. Unlike conventional polymers, the behaviour of SMPs is not solely structure-dependent but is also strongly influenced by time and external thermo-mechanical loading in both programming and recovery processes.
Basically, current SMP design strategies still follow the framework presented by Yan and Li,27 namely, forward prediction and inverse mining. As shown in Fig. 1, forward prediction is charging of training a ML model from a database based on calculations or data collected from references; reverse mining uses the trained ML model to screen the desired sample from the randomly generated samples through a ML tool or a custom design method.
In addition to replacing the traditional design for material scientists, ML can be also integrated with a solid mechanics framework to obtain some novel models for predicting the thermo-mechanical behaviour of SMPs. Essentially, this process aims to look for a mapping function from temperature, boundary conditions, and initial conditions for stress (strain). To the authors’ understanding, there are three primary reasons to integrate ML into continuum mechanics. Firstly, phase transition behaviour of SMPs, especially for SMPs with multiple phase transitions28,29 or damage-like effects,30 is relatively complex. It is one of the key reasons why current continuum mechanics-based models may involve 15–40 parameters or even more30–32 (an existing model exhibits parameters even up to 10031) to describe SMP behaviour. Secondly, because of the large number of parameters, investigators often struggle to calibrate these parameters. Last but not least, all continuum mechanics-based models exhibit an apparent limitation: material specificity. That is, almost every model can describe one or a few specific types of SMPs, but cannot cover all SMPs, forcing researchers to frequently modify previous models and integrate state-of-the-art branch models to simulate novel SMPs. In other words, none of these simulated functions are able to handle all types of complex functions and are not universal. Fortunately, many ML models can simulate any function. For example, according to the universal approximation theorem,19,33 a feedforward neural network with at least one hidden layer, a sufficient hidden unit, and a suitable activation function can approximate any continuous function on a compact subset of ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n to arbitrary accuracy. Meanwhile, backpropagation enables the training and parameter calibration much easier than manual calibration. Thus, ML is especially suitable to play such a role as the mapping function from thermo-mechanical loading to complex SMP behaviours. Basically, ML approaches can be divided into pure ML technique driven and physics model driven, as discussed in detail in the following sections.
n to arbitrary accuracy. Meanwhile, backpropagation enables the training and parameter calibration much easier than manual calibration. Thus, ML is especially suitable to play such a role as the mapping function from thermo-mechanical loading to complex SMP behaviours. Basically, ML approaches can be divided into pure ML technique driven and physics model driven, as discussed in detail in the following sections.
To the best of the authors’ knowledge, no papers are available that review and discuss current state-of-the-art on ML tools specifically for SMPs.
This perspective aims to provide beginners with the foundational knowledge needed to enter the field, while offering in-depth insights into specific topics for more experienced researchers. Accordingly, we critically review recent advances in the application of ML techniques for the synthesis, design, and property prediction of SMPs. Specifically, we will discuss how different ML tools have been employed to identify new chemistries as well as to predict the thermo-mechanical properties of SMPs and we will summarize their advantages and disadvantages. Furthermore, we will highlight challenges characterizing ML tools, such as data scarcity, model interpretability, and the need for physics-informed ML frameworks. Finally, we will outline future directions, including improvements of current models and the development of open-access databases for SMPs, and so on.
This study is organized as follows. Section 2 will briefly introduce some basic concepts of SMPs. Section 3 will provide an overview of current ML approaches. Section 4 will discuss the approaches used in SMP design and discovery. In Section 5, we will discuss the associate models for the thermo-mechanical prediction of SMPs. Finally, we will present some challenges and limitations in current ML approaches in Section 6 and future opportunities in Section 7. Conclusions will be given in Section 8.
2 Overview of shape memory polymers
This section introduces the reader to the main features of SMPs, which will then be the object of the application of ML approaches discussed in the next sections.2.1 Shape memory effects
SMPs are soft materials able to recover their (initial, processed) permanent shape from one or more (deformed) temporary shapes upon the application of an external stimulus. This feature is known as the SME34,35 (Fig. 2). In general, most polymers exhibit the so-called one-way SME, where the permanent shape is recovered from one single temporary shape. Certain polymers can also display the so-called multiple SME, where the permanent shape is recovered sequentially from two or more temporary shapes. Both the one-way and multiple SMEs are irreversible effects, meaning that, once the recovery is completed, an external mechanical intervention is needed to re-established the temporary shape(s). Finally, some SMPs feature the so-called two-way SME, which instead enables a reversible transition between two temporary shapes under an on–off stimulus.The most common triggering stimulus is the heat, with recovery induced by direct heating. In this kind of case, the recovery in one-way and two-way SMEs are correlated with a transition temperature (Ttrans), whereas in multiple-SME systems, it is associated with different transition temperatures. Typical transition temperatures are the glass transition temperature (Tg) in amorphous polymers and the melting temperature (Tm) in semi-crystalline polymers. Other stimuli, such as light and magnetic field, are also gaining prominence, where recovery occurs through indirect heating.35
All these SMEs result from the appropriate combination of the protocol applied to the material (known as “shape memory cycle”) and the macromolecular architecture of the polymer, as discussed in the following subsections.
2.2 Shape memory cycle
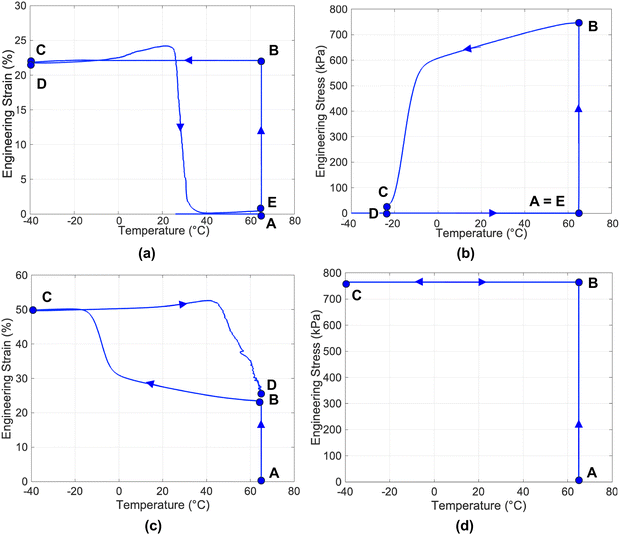
The shape memory cycle for one-way SMPs typically involves two subsequent steps: (i) programming and (ii) recovery. Programming fixes the temporary shape, while recovery restores the permanent shape from the temporary one. In the case of thermal stimuli, the shape memory cycle corresponds to a thermo-mechanical history. An example of a shape memory cycle under uniaxial tensile conditions is shown in Fig. 3(a) and (b) where the cycle is represented in the strain versus temperature and stress versus temperature diagram, respectively. First, the material in its permanent shape is mechanically deformed under isothermal conditions above Ttrans (step A and B); then, the material in its deformed shape is cooled below Ttrans keeping the deformation fixed (step B and C); finally, after load removal (step C and D), the original shape is recovered upon re-heating above Ttrans under load-free conditions (step D and E). It is noted that, upon load removal (step C and D), the deformed shape is generally maintained – only a small elastic strain recovery may take place – and thus corresponds to the fixed temporary shape (i.e., shape in point D).The shape memory cycle can also be setup in order to quantify the recovery stress instead of the recovered strain during the re-heating. In this kind of case, the material in its permanent shape is first mechanically deformed under isothermal conditions above Ttrans; then, the material in its deformed shape is cooled below Ttrans keeping the deformation fixed; finally, the load is removed, and the material is re-heated above Ttrans keeping the deformation fixed. The recovery stress is thus recorded.
For multiple SMPs, more than one programming step (correlated with different Ttrans values) is required to fix different temporary shapes. Heating above all the Ttrans values ensures the recovery of the permanent shape, sequentially passing through all the temporary shapes. A specific type of multiple SME, called temperature-memory effect, ensures the SMP to “memorize” the temperature(s) at which the material was mechanically deformed under isothermal conditions.36 These temperatures are denoted as deformation temperatures. Accordingly, the recovery of the permanent shape takes place by heating above the deformation temperature(s).
For two-way SMPs, an example of a shape memory cycle under uniaxial tensile conditions is shown in Fig. 3(c) and (d), where the cycle is represented in the strain versus temperature and stress versus temperature diagram, respectively. The shape memory cycle involves an initial tensile deformation under isothermal conditions above Ttrans (step A and B), followed by cooling (step B and C), keeping the load fixed, to induce a second temporary shape (i.e., shape in point C). Finally, subsequent heating, keeping the load fixed, leads to recovery (step C and D). A reversible transition between points D and C takes place through cyclic cooling and heating under the applied load (quasi-2W). Under certain conditions, the transition can also occur under stress-free conditions (true-2W).35 Moreover, the transition can even occur under compression (advanced-2W).
Two parameters are generally used to describe one-way SMP performance in a shape memory cycle: (i) the shape fixity ratio, which quantifies the ability of the SMP to maintain its deformation after load removal; and (ii) the shape recovery ratio, which quantifies the ability of the SMP to recover its permanent shape upon heating.
The shape fixity ratio can be calculated as follows:
 | (1) |
The shape recovery ratio can be computed as follows:
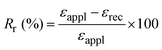 | (2) |
Values of shape fixity and shape recovery ratios close to 100% indicate excellent performance (i.e., C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) D and A
D and A![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) E in Fig. 3(a)), while lower values (down to zero) indicate poor performance. Other parameters, such as the recovery rate or the recovery temperature range, can also be considered. In particular, the recovery stress discussed above is an important parameter quantifying the stress generated when shape recovery is performed under a kinematic constraint.
E in Fig. 3(a)), while lower values (down to zero) indicate poor performance. Other parameters, such as the recovery rate or the recovery temperature range, can also be considered. In particular, the recovery stress discussed above is an important parameter quantifying the stress generated when shape recovery is performed under a kinematic constraint.
For two-way SMPs, the behaviour is quantified by means of: (i) the actuation magnitude (AM); (ii) the recovery magnitude (RM); and (iii) the stress-driven reversible deformation (Δεrev-stress-driven). They are defined, respectively, as follows:
| AM (%) = (εlow − εappl) × 100 | (3) |
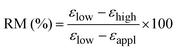 | (4) |
| Δεrev-stress-driven (%) = (εlow − εhigh) × 100 | (5) |
2.3 Macromolecular architecture and classes of SMPs
The macromolecular architecture plays a key role in enabling the SME in SMPs.A common classification is based on describing SMP architecture as being composed of both net-points and switch units7,37–39 (Fig. 2). Net-points determine the permanent shape and can be made of either chemical or physical crosslinks, with an interpenetrated or interlocked supramolecular complex. The switch units are the polymer chain portions responsible for fixing and recovering the temporary shape by undergoing a reversible transition – typically a crystallization/melting or glass transition in thermo-responsive SMPs. In Fig. 2, the switch units correspond to the reversible, thermally-sensitive regions connecting the permanent net-points. Accordingly, depending on the nature of both net-points and switching segments, four classes of thermo-responsive SMPs can be identified. Considering the nature of net-points, SMPs can be divided into physically crosslinked and chemically crosslinked or a combination of chemically and physically crosslinked. Based on the nature of their switch units, SMPs can be further subdivided into either Tg-based SMPs with an amorphous phase or Tm-based SMPs with a crystalline phase. The melting transition can be utilized in chemically crosslinked semi-crystalline rubbers, in liquid crystalline elastomers, in chemically crosslinked semi-crystalline polymers (i.e., semi-crystalline networks) as well as in physically crosslinked (multi)block copolymers. The glass transition can be utilized in chemically crosslinked thermosets as well as in physically crosslinked thermoplastics.
In order to attain the multiple SME, current approaches incorporate two or more well-separated transition temperatures into the system or introduce a broad (either glass or melting) transition temperature range. The latter induces the temperature memory effect.
In order to attain the two-way SME under an applied stress, semi-crystalline networks (i.e., semi-crystalline crosslinked polymers) or liquid crystalline elastomers are needed. The two-way SME under stress-free conditions is a feature shown by semi-crystalline networks with one broad melting temperature or two melting temperatures, semi-crystalline polymer networks prepared via a two-stage cross-linking method, and thermoplastic semi-crystalline polymers with one broad melting temperature or two melting temperatures. For details, the reader can refer to comprehensive reviews such as ref. 7 and 37–39. It is worth highlighting that some approaches use SMP-based composites to increase mechanical performances of SMPs or to introduce additional functionalities,40 or introduce fillers in SMP matrices to induce SME via indirect heating.34
3 Overview of machine learning approaches
This section introduces the reader to the main features of ML, that will then be the object of discussion in the next sections.In order to use computers to explore the mapping from small molecules to specified SMP behaviours, we often require three steps: (i) input the initial information into the computer through fingerprinting; (ii) extracting important features from these information and data; (iii) applying a specified ML approach to look for the relationship between important features and target properties. Notably, the last two procedures are often intertwined. Some important approaches in steps (i) and (ii) are detailed in Sections 3.1 and 3.2, respectively.
3.1 Fingerprinting
In this step, the machine initially converts SMPs’ topological structures into some language that it can recognize. Basically, some important conventional fingerprint methods include:(1) Linear notation. It is able to convert small molecules into a line of language. By defining a dictionary, the linear notation can be converted into a binary matrix for further processing. Specifically, the dictionary entries form the horizontal axis, while the linear notation occupies the vertical axis. If an element appears in both the row and column positions, the corresponding entry in the matrix is set equal to 1; otherwise, it is set equal to 0. For the polymer synthesized by a single monomer, the simplified molecular-input line-entry system (SMILES) notation is often used. For example, a homopolymer poly(3-ethoxyl-carbonyl-phenyl acrylate) can be simply represented by C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC(
CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)Oc1cccc(C(
O)Oc1cccc(C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OCC)c1.41 For copolymers, which are synthesized by two or more monomers or crosslinkers, the investigators often rely on the approach titled “BigSMILES”.42 This approach is essentially a slight modification of the original SMILES. The advantage is that it can reflect the connectivity of structures to some extent through some added symbols. Nevertheless, it cannot reflect complex structures and fail to reflect the molar percentage in its representation. It has been shown that directly using BigSMILEs cannot lead to SMP property prediction with high accuracy.43 A primary reason is that, due to dimension differences between a 3D structure and a 1D notation, some information is inevitably lost in this conversion.
O)OCC)c1.41 For copolymers, which are synthesized by two or more monomers or crosslinkers, the investigators often rely on the approach titled “BigSMILES”.42 This approach is essentially a slight modification of the original SMILES. The advantage is that it can reflect the connectivity of structures to some extent through some added symbols. Nevertheless, it cannot reflect complex structures and fail to reflect the molar percentage in its representation. It has been shown that directly using BigSMILEs cannot lead to SMP property prediction with high accuracy.43 A primary reason is that, due to dimension differences between a 3D structure and a 1D notation, some information is inevitably lost in this conversion.
(2) Morgan fingerprinting or extended connectivity fingerprint (ECFP).44 It is a molecular representation approach that encodes local substructures in a molecule by systematically capturing the topological environment around each atom (treated as the centre), up to a specified radius (Fig. 4). Simply speaking, this approach treats a molecule as atoms connected by bonds. ECFP then examines each atom and its local chemical neighbourhood (the atoms directly surrounding it) and assigns a unique code to each neighbourhood. These codes are combined into a binary vector (a long sequence of 0 s and 1 s) that represents the molecule in a form a computer can process. These operations can be simply conducted by RDKit45 (an open-source cheminformatics software toolkit) in Python. The limitation of this approach is that it is based on elements, and the partial substructure cannot entirely represent the topology. For example, material scientists often treat the benzene ring as a single rigid chain, while the Morgan fingerprint could treat it as a combination of a couple of C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds. Apparently, these combinations cannot reflect the entire rigid structure of the benzene ring. It should also be noted that Morgan fingerprinting can only represent a network composed of two or more monomers (unit cells) with different molar ratios. To resolve this, Yan and collaborators46 introduced a weighted vector combination method (WVCM). To some extent, this approach resolved some problems caused by imperfect chemical reactions, such as a non-uniform network, defeats, and weak interfaces. However, because this approach does not account for connectivity between different monomers, its accuracy is still limited.46
C bonds. Apparently, these combinations cannot reflect the entire rigid structure of the benzene ring. It should also be noted that Morgan fingerprinting can only represent a network composed of two or more monomers (unit cells) with different molar ratios. To resolve this, Yan and collaborators46 introduced a weighted vector combination method (WVCM). To some extent, this approach resolved some problems caused by imperfect chemical reactions, such as a non-uniform network, defeats, and weak interfaces. However, because this approach does not account for connectivity between different monomers, its accuracy is still limited.46
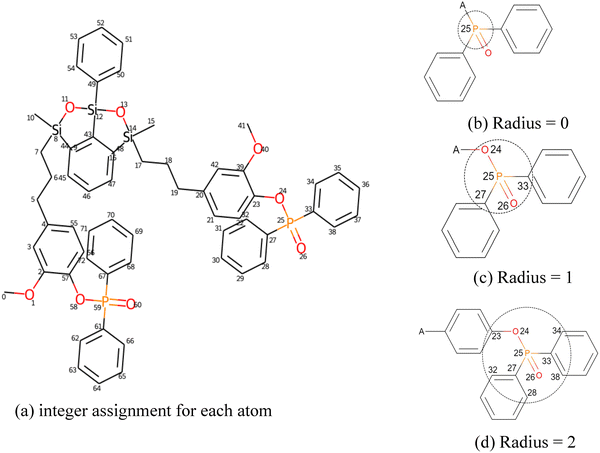 | ||
Fig. 4 Example of substructure decomposition based on Morgan fingerprinting for the molecule of a flame retardant EGN-Si/P. The main idea can be divided into three steps. In the first step (a), distinct integers are assigned to each atom in the chemical structure. Second, every atom is iteratively updated by gradually enlarging the radius of the bond: (b)–(d) involved elements when the Morgan fingerprint radius![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1, and 2, respectively. For example, when radius 0, 1, and 2, respectively. For example, when radius![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, only each element itself is identified. When radius 0, only each element itself is identified. When radius![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, only the single bonds that neighbour the core atom are considered. Finally, all substructures can be found by this method with gradually expanded radius. Reproduced from ref. 47, with permission from AIP Publishing, copyright 2023. 1, only the single bonds that neighbour the core atom are considered. Finally, all substructures can be found by this method with gradually expanded radius. Reproduced from ref. 47, with permission from AIP Publishing, copyright 2023. | ||
(3) Combined tensor represented based on a compositional block. This approach treats the complex polymer network as a combination of different blocks and uses different tensors or matrices to represent these blocks.48–52 The block can be an element or a part including a couple of bonds. The limitation of this approach is that structure splitting is strongly affected by the understanding of investigators and there is no standard splitting approach.
3.2 Feature extraction and mapping function establishment
After inputting initial information, a feature extraction approach is employed to obtain critical information. As stated above, feature extraction often closely accompanies a mapping function and we state them together. Some popular approaches are listed as below.(1) Artificial neural network (ANN). ANN is a type of optimization approach, which was first proposed by Mcculloch and Pitts53 and further developed by Hinton and collaborators.54 It forms one of the central pillars of modern ML techniques. Through adding hidden layers and neurons, ANN is able to construct a composite function with unlimited parameters. Meanwhile, because it can approximate any continuous function (universal approximation theorem), it is extremely popular in the modern scientific community.
(2) Graph method. There are a couple of ways to convert the initial information into a more meaningful interpretation:
• Binary graph method. This is a simple approach which is able to convert linear notation into a graph with a self-defined dictionary. For example, Miccio and Schwartz41 and Yan and collaborators43 converted SMILES or BigSMILES into a binary graph, which can be recognized by a conventional convolution operation. The convolutional layer is often followed by an ANN to map the intermediate features to target properties.
• Graph convolution neural network (GCN). While some early studies explored graph convolution ideas in the spectral domain,55 the canonical and widely adopted GCN formulation was introduced by Kipf and Welling in 2017.56 It defines two matrices to represent the polymer network, i.e., the adjacency matrix (A) and the node feature matrix (X). The first matrix handles the connectivity information and the second handles the element features. The hidden layers at the (l + 1)th iteration can be calculated by
H(l+1) = σ(![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) −1/2Ã −1/2Ã![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) −1/2H(l)W(l)) −1/2H(l)W(l))
| (6) |
![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) is the degree matrix (diagonal matrix) of Ã, H(0) = X, W is a trainable tensor, and σ is an activation function (such the rectified linear unit (ReLU)). It should be mentioned that the updates of the parameters not only extract the features but also obtain the mapping function from these extracted features to target properties. Simply speaking, a GCN updates each atom's representation by aggregating information from its neighbouring atoms and bonds. This transforms the molecular structure into meaningful numerical features, allowing ML models to learn the relationship between polymer topology and material properties.
is the degree matrix (diagonal matrix) of Ã, H(0) = X, W is a trainable tensor, and σ is an activation function (such the rectified linear unit (ReLU)). It should be mentioned that the updates of the parameters not only extract the features but also obtain the mapping function from these extracted features to target properties. Simply speaking, a GCN updates each atom's representation by aggregating information from its neighbouring atoms and bonds. This transforms the molecular structure into meaningful numerical features, allowing ML models to learn the relationship between polymer topology and material properties.
• Weighted directed message passing neural network (wD-MPNN). Early forms of edge-aware message passing were investigated by Dai, Dai and Song in 2016;57 however, the MPNN framework was formalized by Gilmer et al. in 2017,58 and the widely used directed MPNN (D-MPNN) architecture was later introduced by Yang et al. in 2019.55 Unlike GCN, it does not explicitly extract information from the structure and elements. Instead, it repeatedly updates the representation of each element (atom) by implicitly aggregating information from its neighbouring elements (atoms and bonds), enabling hierarchical feature extraction from molecular structures. Since it can be used for copolymers and considers molar percentage, it has drawn much attention in recent years.59,60 Fig. 5 shows the basic algorithm for wD-MPNN. Simply speaking, an MPNN lets each element exchange information from the information of its neighbouring element through chemical bonds. After several rounds of passing, each element obtains an updated representation that reflects its chemical environment. This will help the model to understand the relationship between the overall chemical environment and the properties.
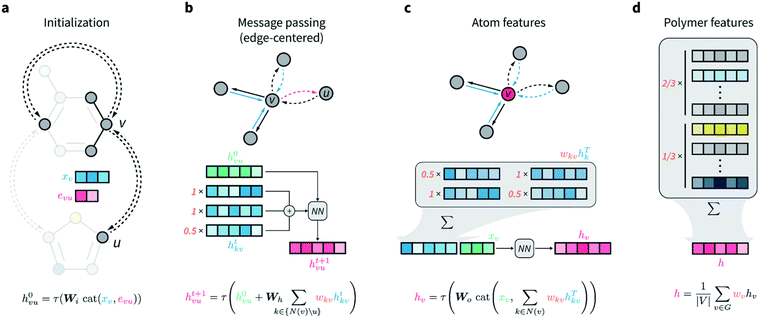 | ||
| Fig. 5 Basic algorithm for wD-MPNN for polymer property prediction. (a) Node and edge features are initialized based on corresponding atomic and bond properties (xv and euv), concatenated and passed through a single neural network layer. (b) Message passing is performed for T steps, in which edge-centered messages of v-outgoing edges are updated based on v-incoming edges. Each message is weighted according to user-specified bond probabilities that reflect the topology of the polymer repeating unit. A D-MPNN with these edge-centered messages learns a hidden representation hvu for each edge in the graph. (c) A hidden representation for each atom hv is obtained by considering all its incoming edges. Specifically, updated atom features are obtained by a weighted sum over the features of all v-incoming edges, followed by concatenation with the initial atom features, and transformation via a single neural network layer. (d) An overall molecular representation h is obtained by averaging or summing over all atom representations hv. Each hv is weighted according to the relative abundance (i.e., stoichiometry) of the monomer they belong to obtain an overall polymer representation. Reproduced from ref. 59, with permission from the Royal Society of Chemistry, copyright 2022. | ||
(3) Generative model. Since the information of polymer networks is often extremely complex, directly exploring the relationship between feature and target properties could be challenging. In this kind of case, the generative model can be used to learn a compact latent representation of the polymer structure. The latent representation will serve as a low dimensional but information-preserving feature, which will be used for a downstream ML model to achieve more accurate property predictions. The popular generative model includes a variational autoencoder (VAE)60–62 and generative adversarial network (GAN).63,64 For example, in a recent paper, Vogel and Weber60 developed a novel VAE model to map the copolymer structures with different monomer stoichiometries and chain architectures into a hidden space. Moreover, by sampling from a Gaussian prior in latent space, the generative model can produce polymer structures with novel architectures, which makes it stand out among many ML models. Although limited by the discontinuity of the mapping function (see Section 6), the new structures designed by the generative model cannot be necessarily synthesized through practical experiments. The very recent development for generative models is to use transformer architecture.65 While VAEs and GANs are currently the most widely used generative models for polymer design, diffusion models66,67 and normalizing flows68,69 have recently emerged as powerful alternatives. Unlike VAEs and GANs, normalizing flows enable exact and reversible probability modelling, while diffusion models offer stable training and high-quality, diverse generation without mode collapse. These advantages make them attractive emerging tools for polymer design. However, to the best of the authors’ knowledge, their application to SMPs has not yet been explored.
(4) Feature descriptor. Some other tools can assist investigators to obtain some features directly from fingerprinting. For example, RDkit45 can provide some physicochemical properties from SMILES, such as molecular weight, LogP (hydrophobicity), number of H-bond donors/acceptors, topological polar surface area, and number of aromatic rings. MD simulation can also be used to compute some feature values to reflect the characteristics of polymer networks, such as epoxy length, hardener length, and the average number of backbone heavy atoms following complete cross-linking.70 This approach transforms the polymer structural/topological information into numerical feature vectors, which greatly facilitates the building mapping function (structure–property) prediction models. The limitations are that RDkit can only provide some simple information and MD simulation-based methods are often time-consuming.
4 Current machine learning studies for shape memory polymer design and discovery
This section presents and critically discusses the main approaches from the literature to design and synthetize new SMPs.The overall aim of these approaches is to find the optimal chemistry that ensures target properties and/or behaviours are achieved. The material design process generally follows the workflow in Fig. 1.
Currently, only a limited number of studies are available for ML guided SMP design (see Table 1).
| Year of publication | Author | Designed polymer | Data source | Target | Fingerprinting method | Feature and mapping function establishment |
|---|---|---|---|---|---|---|
| 2021 | Yan et al.43 | Thermoset SMPs | References | Recovery stress | BigSMILES | Dual-convolutional neural network |
| 2021 | Yan et al.71 | UV curable thermoset SMPs | Drug molecules + SMP references | Glass transition temperature, rubbery modulus | SMILES and mole ratio | Transfer learning-variational autoencoder (TL-VAE) and ANN |
| 2022 | Shafe et al.70 | Thermoset SMPs | Self-defined database (9 epoxies and 22 hardeners) | Glass transition temperature, recovery stress | MD simulation and direct SMILES | Linear regression |
| 2023 | Yan et al.62 | Thermoset shape memory vitrimers | Drug molecules + shape memory vitrimers references | Healing/recycling efficiency, glass transition temperature | SMILES and mole ratio | Transfer learning-variational autoencoder (TL-VAE) and ANN |
| 2024 | Shafe et al.97 | Thermoset SMPs | Self-defined database | Recovery stress | MD based atomistic fingerprints | Multiple linear regression, ridge regression, Bayesian ridge regression, Theil Sen regression, and Poisson regression |
| 2025 | Teimouri and Li73 | Thermoset SMPs | Drug molecules + SMP references | Glass transition temperature | SMILES and mole ratio | Transfer learning-variational autoencoder (TL-VAE) and ANN |
| 2025 | Das et al.72 | Thermoset SMPs | References, same with ref. 73 | Glass transition temperature, rubbery modulus | SMILES | Conditional VAE |
| 2025 | Yan et al.46 | Thermoset SMPs | References | Glass transition temperature | Triple level fingerprinting | Support vector regression (SVR), ANN, and Gaussian process (GP) models |
Most of these studies focus on thermoset SMPs, targeting the Tg, the rubbery modulus, and the recovery stress during shape memory tests.
The earliest studies in this field originated from Yan et al.43,71 in around 2020, who developed two novel approaches: a dual-convolutional-model framework43 and the transfer learning-variational autoencoder (TL-VAE).71 The basic frameworks are shown in Fig. 6(a) and (b). For example, Yan, Feng, and Li71 used a TL-VAE to fingerprint SMP structures and an ANN as a forward model to predict the rubbery modulus of ultraviolet (UV)-curable thermoset SMPs. Then, they generated new candidates by randomly combining different functional groups to produce novel SMP structures. Finally, the ANN was applied to screen approximately 8000 new SMPs and identified five promising candidates. In another example, Shafe et al.70 used MD simulations to extract structural information from polymer networks and employed multiple linear regression as a forward model. They further expanded the chemical space by introducing additional hardeners from PubChem. Using this forward model, inverse design enabled the discovery of an SMP with a 60% increase in recovery stress compared to the best experimentally-validated material.
 | ||
Fig. 6 Three thermoset SMP design approaches. (a) Dual-convolutional-model framework.43 Basic pipeline structures for the network to predict the recovery stress σre. The programming strain εpg, the programming temperature Tpg, and the transition temperature Ttr are different input data types. Convolutional neural networks (CNNs) are used to perform deep learning for the matrices generated by SMILES. (b) TL-VAE framework.71 The VAE model is first trained by 420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 drug molecules, and an intermediate hidden space is obtained in (a1). The VAE model is fine-tuned by 109 monomers, and then, the final hidden space is obtained in (a2). (c) Triple-scale ANN model with two sub-MLP networks.46 The sub-MLP on the top received the features from the microscopic level while the sub-MLP on the bottom received the features from the mesoscopic level and macroscopic level. The outputs are the moduli and temperatures for endset and onset of the glass transition zone. (b) was reprinted with permission from ref. 71. Copyright 2021 American Chemical Society. (c) was reprinted with permission from ref. 46. Copyright 2025 American Chemical Society. 000 drug molecules, and an intermediate hidden space is obtained in (a1). The VAE model is fine-tuned by 109 monomers, and then, the final hidden space is obtained in (a2). (c) Triple-scale ANN model with two sub-MLP networks.46 The sub-MLP on the top received the features from the microscopic level while the sub-MLP on the bottom received the features from the mesoscopic level and macroscopic level. The outputs are the moduli and temperatures for endset and onset of the glass transition zone. (b) was reprinted with permission from ref. 71. Copyright 2021 American Chemical Society. (c) was reprinted with permission from ref. 46. Copyright 2025 American Chemical Society. | ||
These works became the foundation for some other investigators.72,73 For example, in a recent study, Das et al.72 incorporated chemical constraints from four functional groups—epoxy, amine, thiol, and vinyl—into a VAE model, enabling it to produce new monomers consistent with established chemical rules. Teimouri et al.73 expanded the training dataset and modified the VAE architecture to enhance the performance of the TL-VAE framework. In another recent work, Yan et al.46 introduced features across microscopic, mesoscopic, and macroscopic scales and designed an ANN with newly constructed sub-MLP (multilayer perceptron) modules to predict the Tg of SMPs (see Fig. 6(c)).
As shown in Table 1, the approach of database curation employed by the investigators is primarily the manual collection from literature references. Since SMPs have been discovered over 70 years,74 many samples have been studied. In the Web of Science, we can find over 5000 articles through searching the keyword “shape memory polymer”. However, searching for detailed monomers, molar ratios, and target properties from these references requires a strong background in material science. Current large language models (LLMs), such as ChatGPt,75 cannot entirely possess such a capability and are not able to replace investigators to collect this information. For example, when interpreting figures that include multiple storage-modulus curves, such models may fail to correctly identify all corresponding Tg values. An example is provided in the SI to prove our statement. These limitations could potentially be mitigated through model fine-tuning and domain-specific adaptation by researchers.
Another way for dataset establishment is MD simulation. However, unlike conventional data collection, which obtains data from existing data, this way uses a computer to generate new data. For example, Shafe et al.70 revised the monomer structures for bisphenol A diglycidyl ether (DGEBA) and isophorone diamine (IPD) in a certain range, which allowed them to compute the atomic features for further calculation. It should be mentioned that the advantage of an MD-assisted approach is that it allows researchers to explore some novel polymer structures without being limited by current data space. The disadvantage is that current computation power can only perform the computation during nanosecond scale while the Tg transition often requires 30–90 minutes. Therefore, it leads to a gap between the prediction and ground truth for new SMPs.43 Some authors attempted to use a fitting method to make up this scale gap.76 However, the approaches may oversimplify the nature of the complex time scale gap, and the reliability of this approach could need further validation in future studies.
At the same time, another current difficulty lies in that SMPs differ from conventional mechanical properties. That is, SME often relates to both microscopic structure and time effects. For example, with increasing temperature, shape recovery is supposed to occur with the activity of the polymer network. However, simultaneously, if dynamic relaxation happens too fast, shape recovery would still not proceed. Also, the SME is not entirely determined by mechanical stiffness. In practice, both soft polymers and tough polymers can exhibit strong SMEs. That is, SME is a physical feature that is difficult to quantify. To solve this, investigators employed different strategies to design SMPs to achieve better SME performances. For example, Yan et al.43 directly used monomer combinations to predict the recovery stress without considering molar ratios. Later, Yan and collaborators62,71 predicted the rubbery modulus of SMPs to look for SMPs with better SMEs. They found that the latter approach results in a ML model with lower prediction errors.
5 Machine learning assisted thermo-mechanical modelling
This section presents and critically discusses the main approaches from the literature to predict SMP properties. The overall aim of these approaches is to identify the properties of an SMP given some specific inputs. Basically, the prediction for SMP behaviours can be divided into two types: thermo-mechanical constitutive behaviours prediction and other predictions.5.1 Thermo-mechanical constitutive behaviour prediction
We compare all the studies for the thermo-mechanical response of SMPs in Table 2. As can be observed, they are mostly dedicated to the prediction of the behaviours of two-way SMPs. They can be divided into two subclasses, as described below.| Year of publication | Author | SMP type | Predicted polymer behaviour | Database establishment method | ML model |
|---|---|---|---|---|---|
| 2022 | Ibarra et al.79 | Two-way SMP | Strain changes during complex thermo-mechanical loading | Data from previous thermo-mechanical experiments | Fully connected neural network (FCNN), convolutional neural networks (CNN), long short-term memory networks (LSTM), bidirectional LSTM (BiLSTM), CNN-LSTM, convolutional long short-term memory (ConvLSTM), ensemble model |
| 2025 | Yan et al.80 | One-way SMP | Recovery stress, recovery strain | Data from previous thermo-mechanical experiments | Physics-informed ANN (PIANN) |
| 2025 | Mahmud et al.78 | Two-way SMP | Strain changes during complex thermo-mechanical loading | Data from previous thermo-mechanical experiments | Transformer model, FCNN, CNN, LSTM |
| 2025 | Mahmud et al.77 | Two-way SMP | Stress changes during complex thermo-mechanical loading | Data from previous thermo-mechanical experiments | Combination of graph neural networks (GNNs) and time series transformers, feed-forward neural networks (FNN), CNN, LSTM, ConvLSTM, convolutional bidirectional LSTM (ConvBiLSTM) |
Pure data-driven based methods. Chen, Wang and their collaborators77–79 employed different pure data driven methods (see Fig. 7(a) and (b)), including transformers, ML framework by integrating graph neural networks (GNNs) and time series transformers, fully connected neural network (FCNN), the convolutional neural network (CNN), and the long short-term memory (LSTM), to predict the stretch or stress of two-way SMPs under complex thermo-mechanical loading. It should be mentioned that, in a recent study, Mahmud et al.77 developed a novel model, wherein they combined monomer graphs with experimental features, such as time steps, temperature profiles, and sample length, to predict the average stress curves (see Fig. 7(a)). The results demonstrated that the model can predict the stress curve with a root mean squared error (RMSE) as low as 0.1895 and a Pearson correlation coefficient (PCC) of up to 1.000 on unseen datasets (other types of SMPs). We present two primary model architectures in Fig. 7(a) and (b). The advantage of these methods lies in that they can be directly employed based on data without in-depth physical constitutive knowledge. Simultaneously, this approach is scientifically reasonable to some extent. As shown, the studies by Chen, Wang, and their collaborators77–79 primarily treated the thermo-mechanical response of SMPs as a time-series problem. Based on this perspective, the authors employed several state-of-the-art ML architectures to predict the evolution of time-dependent SMP responses. They constructed feature sets containing time steps, temperature profiles, sample length, and moving-averaged stress to represent the time-series behaviour of SMPs. In their framework, LSTM networks served as the primary model, leveraging the assumption that historical deformation states influence future responses. This approach is consistent with the current understanding in SMP modelling, where prior deformation and thermal history are believed to strongly affect the subsequent thermo-mechanical behaviour. However, they also have some limitations. First, these models do not exhibit interpretability. They act as a complete black box and are difficult to understand for human investigators. Next, they have a significantly large number of parameters. For example, in a FCNN model (the best performing model) in Ibarra et al.'s study,79 the model involves 307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060 parameters. In addition, due to lacking physical laws, they could easily be affected by noise. For example, in the prediction of the strain-time curve in Ibarra et al.'s study, there could be some unexpected oscillations (see Fig. 8 in ref. 79).
060 parameters. In addition, due to lacking physical laws, they could easily be affected by noise. For example, in the prediction of the strain-time curve in Ibarra et al.'s study, there could be some unexpected oscillations (see Fig. 8 in ref. 79).
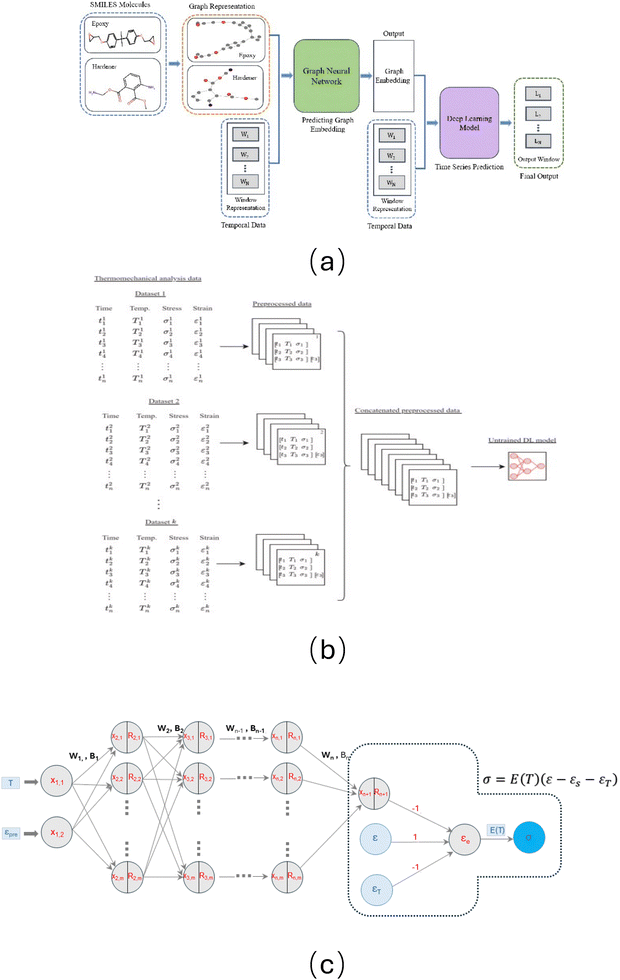 | ||
| Fig. 7 Three primary models used for thermo-mechanical modelling of SMPs. (a) Stress prediction by combining monomer graphs with experimental features based on multiple ML models.77 (b) Strain prediction model based on multiple ML approaches.79 (c) Physics-informed artificial neural network (PIANN), which integrated the storage strain based constitutive model into a neural network.80 (a) and (b) belong to pure data-driven models and they primarily used the time series approach to predict stretch or stress. (a) was reprinted from ref. 77, with permission from Elsevier. (b) was reprinted from ref. 79, with permission from Elsevier. (c) was reprinted with permission from ref. 80. Copyright 2025 The Royal Society (U.K.). | ||
Physics-informed ML modelling. Considering these limitations, researchers attempted to integrate constitutive physical laws into the original ML framework. Basically, physics-informed ML incorporates known physical laws (e.g., conservation laws, constitutive relationships, or first-principles constraints) into the loss functions. Embedding physics into the model reduces the need for large training datasets, improves generalization, and increases the reliability of predictions. In practice, this means that the ML model is not only trained to match data but also penalized when it violates physics. In mechanics, the loss function may include terms that enforce force balance, stress–strain relationships, or energy conservation. During training, the model learns parameters that satisfy both experimental data and physical equations. As a result, the model can make reasonable predictions even with limited data and remains consistent with known physical behaviour. For example, Yan et al.80 integrated a widely recognized storage strain model into an ANN and developed a physics-informed artificial neural network (PIANN). As shown in Fig. 7(c), according to the constitutive equation, they stipulated the weights and bias after three hidden layers and thus guided the architecture design of a novel neural network. The 1D constitutive model reads
| σ = E(T)·εe = E(T)·(ε − Rn+1(Xn+1) − εT) | (7) |
| Rn+1 = Rn+1(Xn+1), Xn+1 = WnRn + Bn | (8) |
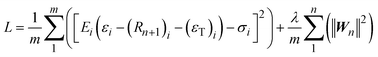 | (9) |
Essentially, physics-informed ML models outperform traditional constitutive models because of multiple reasons. That is, many existing models were developed in a highly phenomenological way—researchers combined known viscoelastic, thermoelastic, plasticity, and phase-transition elements into complex assemblies. This approach is analogous to manually building a machine out of springs, dashpots, and sliders: if enough components are added, the phenomenon can usually be simulated. Similarly, in mathematics, if sufficient parameters are introduced into a function, it can virtually approximate any other function. However, such assemblies quickly become bulky, the frameworks lack conciseness, and the fitting process becomes very time-consuming. In contrast, a physics-informed ML model is like teaching the machine the fundamental physics and allowing it to assemble relationships automatically. Although the number of parameters may not be fewer than in phenomenological models, the process achieves a form of “auto-assembly,” offering greater efficiency. In addition, it should be emphasized that almost all current materials have material specificity and can only describe limited types of SMPs. However, Yan et al.'s PIANN model80 can accurately predict five temperature–stress datasets and four temperature–strain datasets, including experimental data from four different SMP systems and simulation results from a widely accepted constitutive model. Moreover, PIANN successfully predicts four key shape-memory responses: stress evolution during hot programming, stress recovery following both cold and hot programming, and free-strain recovery during the heating process. These results demonstrate the universal approximation capability of this type of model, a feature that conventional fitting functions cannot guarantee.
5.2 Other behaviour prediction
To some specific applications, ML can also be used to predict SMP behaviours. Dutta et al.81 used temperature to predict the angle to pivot and the angle tip for an SMP sample from a video record, separately. Rosales et al.82 employed a simple ANN model to predict the dimensional error on specimens in 3D printing process. The first one is more aligned with graph-based recognition tasks in SMPs, while the second one shows a direct application in SMP manufacturing. These studies do not aim to predict the intrinsic thermo-mechanical behaviours of SMPs but still exhibit some interesting uses in SMP-related fields.6 Challenges and limitations
From an objective perspective, current studies on ML-assisted SMP discovery and thermo-mechanical modelling are still in an early stage, leaving plenty of room for improvement.Firstly, the topological structures of SMPs are relatively complex. Currently, there is no existing method capable of completely capturing all features of a polymer structure, especially of copolymers. So far, all methods can only provide partial descriptions. This partial information makes it difficult to find a mapping function.
Secondly, there is still no existing database including sufficient data points and labels for SMPs. As a comparison, successful protein (a special polymer) databases often include a large amount of datapoints. For example, AlphaFold (structure) includes over 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 protein structures,83 ProBert-BFD includes about 2.1 billion sequences,84 and ProGen2 includes over a billion sequences.85 Although general thermoset SMPs are often chemically more diverse and less standardized than proteins—and therefore, in principle, require more data points—in practice, current studies in ML-assisted SMP design typically rely on hundreds of data points. This severe data limitation significantly constrains model performances.
000 protein structures,83 ProBert-BFD includes about 2.1 billion sequences,84 and ProGen2 includes over a billion sequences.85 Although general thermoset SMPs are often chemically more diverse and less standardized than proteins—and therefore, in principle, require more data points—in practice, current studies in ML-assisted SMP design typically rely on hundreds of data points. This severe data limitation significantly constrains model performances.
Thirdly, although the structure is a hierarchical structure composed of repetitive units, they cannot easily be captured by linear Euclidean geometry. That is, it is challenging to find a minimum unit cell for complex copolymers with different molar ratios.
Fourthly, there is a gap between current research focus and SME's fundamental essence. That is, most existing studies only took the topological structure into consideration. However, SME is a kinetic interaction governed by both topological structures and programming or training protocols. Therefore, the interaction between external loading and topological structure cannot be fully explained by the structure alone, which poses a challenge for predicting the ultimate recovery stress or strain based solely on structural information.
Fifthly, as shown in Fig. 1, current inverse design is only a transformation of forward design or forward mapping function, relying on a method of exhaustion. On the other hand, a true inverse design should aim to obtain the inverse mapping function – from performance parameters back to topological structures – analogous to an inverse function in mathematics.
Sixthly, the data for ML-assisted polymer design is still scarce. It can be seen from Table 1 that most of the data points are still collected from previous references. Thus, most models struggle to generalize beyond their training distributions. Although SMPs were discovered 84 years ago and investigators have conducted numerous studies, researchers have not established a formal database. To date (Nov. 2025), using the Web of Science database and limiting the document types to articles, proceedings papers, editorial materials, early access, and data papers, we have identified about 4800 publications from 2010 to 2025 by searching the keyword “shape memory polymer”. To collect data, researchers need to review articles and extract measurements from the reported graphs. This process is not only time consuming but also highly relies on the chemical knowledge of each researcher, which directly affects data's quality and effectiveness.
Seventh, developing physics-informed ML models for SMPs is more challenging than for conventional polymers. Existing models86–88 already capture the mechanical responses of general polymer materials. The general idea in these studies is to use neural networks to fit simple modulus-like coefficients in the free energy formulation based on available data points. However, SMPs clearly represent a more complex class of polymers. Their constitutive modelling must account not only for mechanical responses but also for thermal effects and kinetic relaxation. In other words, temperature and time must be included as variables in the formulation, and these variables cannot be treated as simple coefficients. Therefore, directly adopting approaches designed for conventional polymers is not feasible.
In a nutshell, overcoming current challenges still requires tremendous efforts and is essential for fully leveraging ML's capabilities in this field.
7 Future directions and opportunities
In the future, investigators will still have plenty of opportunities to explore and implement new ideas.Firstly, as stated above, the topologies of SMPs are often extremely complex – the repetitive unit cell leads to complex systems. It is expected that investigators can develop a tool that can explicitly extract more features directly from monomers and crosslinkers, improving prediction accuracy.
Secondly, most neural network models used for ML-assisted polymer discovery are heavily influenced by developments from graph learning and computer version (image) field. Therefore, they could not entirely deal with specific scenarios. For example, the CNN predictions accuracy for Tg is significantly influenced by incompleteness of the binary graphs (which cannot capture topological structures of polymers) based on BigSMILES.43 In the future, it is expected that more polymer specific neural networks can be developed to improve prediction accuracy.
Thirdly, LLM is expected to expedite information extraction by replacing manually extraction. In the latest GPT-5 model, some simple monomer structures can be directly extracted from references, demonstrating better performance than the GPT-4o model. However, it cannot still guarantee 100% correctness due to the complex chemical reactions (see the example reported in the SI). Thus, it is expected that current LLMs can further extract more useful and accurate information from the published articles.
Fourthly, generative models are expected to be further improved in the future. In current studies, the realization of new polymers often relies on the generation of new samples through adding white noise. It implicitly assumes that mapping being learned is continuous. However, in reality, the target functions that investigators aim to approximate may not be continuous (often constrained by chemistry), which leads to the generation of many impractical polymers (see the bizarre monomers produced by a VAE model73). In other words, chemistry is not a smooth statical space, but it has physical, chemical, and topological rules, which are assumed as a continuous function in ML models. In the future, it is expected that some new constraints can be developed to regulate the mapping of neural networks.
Fifthly, there is a need to use physics-informed ML models to replace pure data-driven models to improve interpretability and physical consistency. From a mathematical perspective,89 the current neural network is a realization of the Kolmogorov-Arnold representation principle:90,91 any multivariate continuous function can be built from simple one-variable nonlinearities and linear combinations (close to Hibert's 13th problem92). However, this process does not involve any boundary constraints and could generate illusion in the lay mappings.93 Because of that, physics must be added to avoid these inconsistencies in mappings.
Sixthly, current ANNs leave a lot of space to improve. Current commonly used ANNs were originally inspired by human being's neural network, but they simply assume all the relationships between any two neurons are purely linear. However, it was shown that the human brain has demonstrated significantly higher efficiency than LLM. That is, the human brain only uses roughly 20 Watts to work, while LLM are consuming power in Gigawatts.94 Thus, the gap suggests that the linear assumption could not be entirely correct. Recently, the Kolmogorov Arnold network (KAN) has modified the linearity into nonlinearity and they have shown similar or even better performance with a traditional ANN model,95 thus exhibited great potential.
Seventhly, the algorithm of neural networks is also expected to be further understood in the future. Essentially, neural networks strongly rely on fitting, and this is a black box operation. This black box nature makes the training process like “alchemy”96 and there is no standard methods available to find the optimal architecture of neural networks. It is expected the algorithm will be fully understood in the future, developing single canonical architectures.
Finally, an open-access database and community benchmarks for SMPs would be extremely helpful to provide data for ML models.
8 Conclusions
In this perspective, we have reviewed recent developments of ML-assisted SMP design and their thermo-mechanical modelling, compared different models, and summarized their advantages and disadvantages. We have also discussed the limitations and challenges of current studies and outlined future directions for this rapidly evolving field. It can be clearly seen that ML is beginning to bridge microscopic scale to macroscopic scale as well as SMP structure to thermo-mechanical behaviour. Looking ahead, the combination of data-efficient learning, physics and chemistry constraints, and more appropriate topological representations should further integrate chemistry, materials science, and mechanical engineering, enabling more direct scale-bridging from molecules to complex SMP architectures and expediting development across engineering domains.Author contributions
Cheng Yan: writing – original draft; writing – review & editing; data curation; conceptualization; project administration; funding acquisition. Giulia Scalet: writing – original draft; writing – review & editing; data curation; conceptualization; project administration; funding acquisition.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sm00980d.The data supporting this perspective are given within this perspective.
Acknowledgements
Giulia Scalet acknowledges that this work was funded by the European Union ERC CoDe4Bio Grant ID 101039467. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. Cheng Yan would like to express sincere gratitude to the National Science Foundation (Grant No. OIA-2418415) and NASA (Grant No. 80NSSC25M0003) for their support.References
- A. Lendlein, Shape-Memory Polymers, Springer, 1st edn, 2010 Search PubMed.
- C. Wischke, A. T. Neffe, S. Steuer and A. Lendlein, J. Controlled Release, 2009, 138, 243–250 CrossRef CAS PubMed.
- K. Deng, X. Feng, H. Yang and C. Yan, Eur. Polym. J., 2023, 112286 CrossRef CAS.
- D. You, L. Lin, M. Dong and Y. Wu, et al., Smart Mater. Med., 2025, 6, 240–269 Search PubMed.
- W. Zhao, C. Yue, L. Liu, Y. Liu and J. Leng, Adv. Healthcare Mater., 2023, 12, 1–32 Search PubMed.
- B. Jin, H. Song, R. Jiang, J. Song, Q. Zhao and T. Xie, Sci. Adv., 2018, 4, eaao3865 CrossRef.
- J. Hu and S. Chen, J. Mater. Chem., 2010, 20, 3346–3355 RSC.
- H. Meng and G. Li, Polymer, 2013, 54, 2199–2221 CrossRef CAS.
- C. D. Wick, A. J. Peters and G. Li, Polymer, 2021, 213, 123319 CrossRef CAS.
- J. Diani and K. Gall, Smart Mater. Struct., 2007, 16, 1575–1583 CrossRef CAS.
- W. Jian, X. Wang, H. Lu and D. Lau, Compos. Sci. Technol., 2021, 211, 108849 CrossRef CAS.
- P. Nourian, C. D. Wick, G. Li and A. J. Peters, Smart Mater. Struct., 2022, 31, 105014 CrossRef CAS.
- H. Gudla and C. Zhang, J. Phys. Chem. B, 2024, 128, 10537–10540 CrossRef CAS PubMed.
- Y. Hayashi, J. Shiomi, J. Morikawa and R. Yoshida, npj Comput. Mater., 2022, 8, 222 CrossRef CAS.
- R. Giro, H. Hsu, A. Kishimoto, T. Hama, R. F. Neumann, L. Hamada and M. B. Steiner, npj Comput. Mater., 2023, 9, 133 CrossRef.
- T. D. Nguyen, Polym. Rev., 2013, 53, 130–152 CrossRef CAS.
- C. Yan and G. Li, J. Appl. Phys., 2022, 131, 111101 CrossRef CAS.
- W. Zhao, L. Liu, X. Lan, J. Leng and Y. Liu, Appl. Mech. Rev., 2023, 75, 020802 CrossRef.
- G. Cybenko, Math. Control Signal Syst., 1989, 2, 303–314 Search PubMed.
- S. Chibani and F. X. Coudert, APL Mater., 2020, 8, 080701 Search PubMed.
- A. Agrawal and A. Choudhary, APL Mater., 2016, 4, 053208 CrossRef.
- L. Himanen, A. Geurts, A. S. Foster and P. Rinke, Adv. Sci., 2019, 6, 1900808 CrossRef.
- Y. Liu, T. Zhao, W. Ju and S. Shi, J. Mater., 2017, 3, 159–177 Search PubMed.
- V. Venkatasubramanian, K. Chan and J. M. Caruthers, Comput. Chem. Eng., 1994, 18, 833–844 CrossRef CAS.
- V. Venkatasubramanian, K. Chan and J. M. Caruthers, J. Chem. Inf. Comput. Sci., 1995, 35, 188–195 Search PubMed.
- H. Lu and S. Du, Sci. Sin., 2023, 50, 123456 Search PubMed.
- C. Yan and G. Li, Adv. Intell. Syst., 2022, 101, 2200243 Search PubMed.
- M. Arricca, N. Inverardi, S. Pandini, M. Toselli, M. Messori and G. Scalet, J. Mech. Phys. Solids, 2025, 195, 105955 CrossRef CAS.
- H. Yuan, Q. Tang, X. Feng, H. Yang and C. Yan, Polymer, 2025, 336, 128921 Search PubMed.
- C. Yan, Q. Yang and G. Li, Int. J. Mech. Sci., 2020, 177, 105552 CrossRef.
- H. Gülaşik, M. Houbben, C. P. Sànchez, J. M. Calleja Vázquez, P. Vanderbemden, C. Jérôme and L. Noels, Int. J. Solids Struct., 2024, 295, 112814 Search PubMed.
- J. Gu, C. Wang, H. Zeng, H. Duan and M. Wan, Smart Mater. Struct., 2024, 33, 065034 Search PubMed.
- K. Hornik, M. Stinchcombe and H. White, Neural Networks, 1989, 2, 359–366 Search PubMed.
- Y. Xia, Y. He, F. Zhang, Y. Liu and J. Leng, Adv. Mater., 2021, 33, 1–33 Search PubMed.
- G. Scalet, Actuators, 2020, 9, 10 CrossRef.
- G. Scalet, S. Pandini, N. Inverardi and F. Auricchio, Smart Materials in Additive Manufacturing: 4D Printing Mechanics, Modeling, and Advanced Engineering Applications, Elsevier, 2022, ch. 10, vol. 2, pp. 279–310 Search PubMed.
- M. D. Hager, S. Bode, C. Weber and U. S. Schubert, Prog. Polym. Sci., 2015, 49–50, 3–33 CrossRef CAS.
- C. Liu, H. Qin and P. T. Mather, J. Mater. Chem., 2007, 17, 1543–1558 Search PubMed.
- J. Hu, Y. Zhu, H. Huang and J. Lu, Prog. Polym. Sci., 2012, 37, 1720–1763 CrossRef CAS.
- Y. Liu, H. Du, L. Liu and J. Leng, Smart Mater. Struct., 2014, 23, 023001 CrossRef CAS.
- L. A. Miccio and G. A. Schwartz, Polymer, 2020, 193, 122341 CrossRef CAS.
- T. S. Lin, C. W. Coley, H. Mochigase, H. K. Beech, W. Wang, Z. Wang, E. Woods, S. L. Craig, J. A. Johnson, J. A. Kalow, K. F. Jensen and B. D. Olsen, ACS Cent. Sci., 2019, 5, 1523–1531 CrossRef CAS.
- C. Yan, X. Feng, C. Wick, A. Peters and G. Li, Polymer, 2021, 214, 123351 Search PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS.
- G. Landrum, RDKit: Open-Source Cheminformatics Software, https://www.rdkit.org/.
- C. Yan, X. Feng, P. Mensah and G. Li, J. Phys. Chem. B, 2025, 129, 2621–2636 CrossRef CAS PubMed.
- C. Yan, X. Lin, X. Feng, H. Yang, P. Mensah and G. Li, Appl. Phys. Lett., 2023, 122, 251902 CrossRef CAS.
- A. Mannodi-Kanakkithodi, G. Pilania, T. D. Huan, T. Lookman and R. Ramprasad, Sci. Rep., 2016, 6, 20952 Search PubMed.
- T. D. Huan, A. Mannodi-Kanakkithodi, C. Kim, V. Sharma, G. Pilania and R. Ramprasad, Sci. Data, 2016, 3, 160012 CrossRef CAS.
- Y. Wu, J. Guo, R. Sun and J. Min, npj Comput. Mater., 2020, 6, 1–8 CrossRef.
- M. A. Webb, N. E. Jackson, P. S. Gil and J. J. de Pablo, Sci. Adv., 2020, 6, eabc6216 Search PubMed.
- K. M. Jablonka, G. M. Jothiappan, S. Wang, B. Smit and B. Yoo, Nat. Commun., 2021, 12, 1–10 CrossRef.
- W. S. Mcculloch and W. Pitts, Bull. Math. Biophys., 1943, 5, 115–143 CrossRef.
- D. E. Rumelhart, G. E. Hinton and R. J. Willams, Nature, 1986, 323, 533–536 Search PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef CAS.
- T. N. Kipf and M. Welling, 5th Int. Conf. Learn. Represent. ICLR 2017 – Conf. Track Proc., 2017, pp. 1–14 Search PubMed.
- H. Dai, B. Dai and L. Song, 33rd Int. Conf. Mach. Learn. ICML 2016, 2016, vol. 6, pp. 3970–3986 Search PubMed.
- J. Gilmer, S. Schoenholz, P. Riley, O. Vinyals and G. Dahl, Proc. 34th Int. Conf. Machine Learning, 2017, vol. 70, pp. 1263–1272 Search PubMed.
- M. Aldeghi and C. W. Coley, Chem. Sci., 2022, 13, 10486–10498 RSC.
- G. Vogel and J. M. Weber, Chem. Sci., 2024, 16, 1161–1178 RSC.
- S. Mohapatra, N. Hartrampf, M. Poskus, A. Loas, R. Gómez-Bombarelli and B. L. Pentelute, ACS Cent. Sci., 2020, 6, 2277–2286 CrossRef CAS PubMed.
- C. Yan, X. Feng, J. Konlan, P. Mensah and G. Li, Phys. Chem. Chem. Phys., 2023, 25, 30049 Search PubMed.
- K. Hiraide, K. Hirayama, K. Endo and M. Muramatsu, Comput. Mater. Sci., 2021, 190, 110278 CrossRef CAS.
- O. Prykhodko, S. V. Johansson, P. C. Kotsias, J. Arús-Pous, E. J. Bjerrum, O. Engkvist and H. Chen, J. Cheminf., 2019, 11, 1–13 Search PubMed.
- D. Hudson and L. Zitnick, Proc. 38th Int. Conf. Machine Learning, 2021, pp. 4487–4499 Search PubMed.
- A. Jain, A. Srivastava and R. Ramprasad, Chem. Mater., 2025, 37, 7337–7346 CrossRef PubMed.
- Z. Yang, W. Ye, X. Lei, D. Schweigert, H. K. Kwon and A. Khajeh, npj Comput. Mater., 2024, 10, 296 Search PubMed.
- Y. Zhu, Z. Ouyang, B. Liao, J. Wu, Y. Wu, C.-Y. Hsieh, T. Hou and J. Wu, Proc. Thirty-Second Int. Joint Conf. Artif. Intell. (IJCAI-23), 2023, pp. 5002–5010 Search PubMed.
- K. Madhawa, K. Ishiguro, K. Nakago and M. Abe, arXiv, 2019, preprint, arXiv:1905.11600 DOI:10.48550/arXiv.1905.11600.
- A. Shafe, C. D. Wick, A. J. Peters, X. Liu and G. Li, Polymer, 2022, 242, 124577 Search PubMed.
- C. Yan, X. Feng and G. Li, ACS Appl. Mater. Interfaces, 2021, 13, 60508–60521 Search PubMed.
- B. Das, A. Peters, G. Li and X. Hei, J. Polym. Sci., 2025, 63, 1334–1344 CrossRef CAS.
- A. Teimouri and G. Li, J. Polym. Sci., 2025, 63, 1095–1107 CrossRef CAS.
- L. B. Vernon and H. M. Vernon, US Pat., 2234993A, 1941 Search PubMed.
- Openai, Improving language understanding with unsupervised learning, https://openai.com/research/language-unsupervised.
- Y. Zheng, P. Thakolkaran, A. K. Biswal, J. A. Smith, Z. Lu, S. Zheng, B. H. Nguyen, S. Kumar and A. Vashisth, Adv. Sci., 2023, 12, 2411385 CrossRef.
- K. R. Mahmud, L. Wang, J. Chen and S. Hassan, Polymer, 2025, 335, 128771 Search PubMed.
- K. R. Mahmud, L. Wang, J. Chen, X. Liu and S. Hassan, Conf. Proc. – IEEE SOUTHEASTCON, 2025, pp. 950–957 Search PubMed.
- D. Ibarra, J. Mathews, F. Li, H. Lu, G. Li and J. Chen, Polymer, 2022, 261, 125395 CrossRef.
- C. Yan, X. Feng, P. Mensah and G. Li, Proc. R. Soc. A, 2025, 481, 20240702 CrossRef.
- R. Dutta, D. Renshaw, C. Chen and D. Liang, Array, 2020, 7, 100036 CrossRef.
- C. A. G. Rosales, M. F. Rahman, H. Xu and T. L. B. Tseng, Proc. Int. Conf. Ind. Eng. Oper. Manag., 2021, pp. 1592–1599 Search PubMed.
- The AlphaFold team, AlphaFold: a solution to a 50-year-old grand challenge in biology, https://deepmind.google/discover/blog/alphafold-a-solution-to-a-50-year-old-grand-challenge-in-biology/.
- A. Elnaggar, M. Heinzinger, C. Dallago, G. Rihawi, Y. Wang, L. Jones, T. Gibbs, T. Feher, C. Angerer, M. Steinegger, D. Bhowmik and B. Rost, arXiv, 2021, preprint, arXiv:2007.06225 DOI:10.48550/arXiv.2007.06225.
- E. Nijkamp, J. A. Ruffolo, E. N. Weinstein, N. Naik and A. Madani, Cell Syst., 2023, 14, 968–978.e3 Search PubMed.
- K. Linka and E. Kuhl, Comput. Methods Appl. Mech. Eng., 2023, 403, 115731 CrossRef.
- A. Ghaderi, V. Morovati and R. Dargazany, Polymers, 2020, 12, 1–20 Search PubMed.
- K. Linka, M. Hillgärtner, K. P. Abdolazizi, R. C. Aydin, M. Itskov and C. J. Cyron, J. Comput. Phys., 2021, 429, 110010 CrossRef.
- V. R. A. Korkov, Neural Networks, 1992, 5, 501–506 CrossRef.
- R. Hecht-Nielsen, Proc. Int. Conf. Neural Networks, New York, 1987, pp. 11–14 Search PubMed.
- A. N. Kolmogorov, Dokl. Akad. Nauk SSSR, 1957, 144, 679–681 Search PubMed.
- D. Hibert, Bull. Am. Math. Soc., 1902, 80, 437–479 Search PubMed.
- M. E. Samadi, Y. Müller and A. Schuppert, arXiv, 2024, preprint, arXiv:2405.11318 DOI:10.48550/arXiv.2405.11318.
- Texas A&M University, ScienceDaily. 27 March 2025. https://www.sciencedaily.com/releases/2025/03/250326123554.htm.
- L. Li, Y. Zhang, G. Wang and K. Xia, Nat. Mach. Intell., 2025, 7, 1346–1354 CrossRef.
- Y. Lecun, My take on Ali Rahimi's’Test of Time’ award talk at NIPS, 2017, https://www2.isye.gatech.edu/~tzhao80/Yann_Response.pdf Search PubMed.
- A. Shafe, P. Nourian, X. Liu, G. Li, C. D. Wick and A. J. Peters, Macromolecules, 2024, 57, 9933–9942 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |