 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Small particle dynamics in glassy polymers: diffusion, relaxation, and machine-learned softness
S. J.
Layding
 and
R. A.
Riggleman
and
R. A.
Riggleman
 *
*
Department of Chemical and Biomolecular Engineering, University of Pennsylvania, Philadelphia, PA 19104, USA. E-mail: rrig@seas.upenn.edu
First published on 23rd December 2025
Abstract
In this work, we explore the simulated transport dynamics of small particles through a polymer melt at temperatures spanning from liquid-like behavior down to near and below the simulated glass transition temperature. Using softness, a machine-learned scalar quantity, we connect the structural neighborhood surrounding a particle with its dynamic behavior to relate the probability of a glassy rearrangement to its local environment. An energetic and entropic scale for the rearrangement process of these small particles emerges and is compared across systems of different particle sizes and interaction strengths. Diffusion coefficients and relaxation times both show strong dependence on our tuning parameters, and the barriers to rearrangement show increasing nonlinearity as the particles become smaller. The trends we observe provide some insight into how local structure plays a role in small molecule transport when the surrounding medium is undergoing a glass transition, leading to large changes in system mobility.
Introduction
Chemical separations processes like distillation and other thermally-driven methods account for nearly fifteen percent of global annual energy consumption.1 The gradual reduction of the world's energy budget and the carbon intensity of the energy economy have been identified as key elements of a strategy to combat climate change.2,3 Increasing concentrations of atmospheric carbon dioxide and other pollutants4 have been shown unequivocally to be direct causes of climate change5 and could be mitigated through either point-source capture upon emission,6–8 or direct air capture of legacy emissions from the atmosphere.9,10 The need for not only a reduction in global energy consumption but also with more advanced and increasingly dilute separations processes points toward polymer membrane, pressure-based separations processes as an attractive alternative. Polymer membranes for gas separations have been in use for decades11,12 and continue to be an area of intense research to push the limits of performance13,14 and drive the development of new hydrocarbon materials that exhibit the potential for fast and energy-efficient separations.15–17Many of these polymer membranes fall under the umbrella of glassy disordered materials,18 which are amorphous and lack long-range structural order like liquids yet possess many of the physical properties of solids.19–21 Dynamical heterogeneities in microscopic behavior of these materials below the glass transition temperature Tg are observed, along with a growing structural relaxation time to around 102 seconds alongside the dynamic viscosity increasing to greater than 1013 centipoise.21 While ubiquitous in glass-forming materials, these behaviors are not entirely explained by any one theoretical approach or understanding.22–28
Building a clearer understanding of structure–function relationships for transport in polymers has important implications in materials design and application for gas separations.29 Glassy polymer membranes used for gas separations processes are characterized by high solubility coefficients for gas species, moderate diffusion selectivity, and nonequilibrium free volume distributions that allow glassy polymers to dominate the limits of performance compared to rubbery polymers.14 The dynamics of small tracer molecules within polymers can be studied experimentally using photobleaching experiments30,31 and tools like quasi-elastic and inelastic neutron scattering.32 Simulations present an important complement to experimental techniques for characterizing materials that have not yet been synthesized or extensively studied at the lab scale.
Computational studies of gas diffusion through polymers have been performed extensively33 over the years in both coarse-grained34–37 and atomistic resolutions,38–41 inspired by classic theoretical frameworks used to describe diffusion in disordered media.42,43 Early atomistic simulation of oxygen transport through linear n-alkane systems demonstrated that diffusion in glassy systems is governed by a hopping mechanism where particles spend much of their time in a single region before moving to another potential energy basin.44 The hopping rearrangement process in glassy systems related to cooperative motion with the nearby polymer chains and does not necessarily correlate with any gradient in local free volume.45,46 The transitions between these localized regions of permeation have been further studied with other traditional methods such as kinetic Monte Carlo in both glassy and rubbery polymers,35,47,48 which have also found utility in other nanoporous materials such as zeolites.49
In the last decade or so, the advent of machine learning and increased capacity for computer simulation of large size and longer timescales has unlocked a wealth of new tools and measures to characterize the dynamics and plasticity of glassy materials.50 One such measure is a scalar quantity called softness, which relates a glassy material's dynamic behavior to its static configuration at a given point in time by using a support vector machine (SVM) to analyze a high-dimensional space of local structural features.51–53 Softness has proven to be useful in gaining understanding around a wide variety of phenomena in glassy materials including the impacts of structural aging,54 spatial variations in thin-film relaxation,55 the behavior of polymer nanocomposites under deformation,53,56–59 and the relationship between static excess entropy and dynamics in the supercooled regime.60 When compared with other methods that relate local structure to free volume, such as Voronoi-based indicators like local density, free volume, or Voronoi anisotropy and its divergence, softness has been shown to outperform them in simulations of both glassy quenched and high-temperature Lennard-Jones systems; indeed, using other metrics to measure local free volume and relate it to dynamics has historically been a challenge.61–63 Softness has been successfully used both in experimental systems51 and in simulations of simple models like the Kob–Andersen glass former52,54,60,64 or coarse-grained bead-spring polymers,55–59,65,66 making it a versatile approach for characterizing glassy dynamics.
The importance of local structure to diffusion and hopping dynamics makes it tempting to use softness or other high-dimensional machine learning tools to investigate the dynamics of small penetrants through a glassy matrix. Softness has been applied extensively to the binary Kob–Andersen system and to bead-spring polymers, but to our knowledge softness has not yet been used to explore the relationship between local structure and dynamics of small particles moving though a glassy medium. Recent work characterizing the diffusion behavior of small penetrants in both rubbery and glassy polymer materials has included the application of self-consistent nonlinear Langevin equation (SCNLE) theory67 and self-consistent cooperative hopping theory (SCCHT),68 which may be used to relate the penetrant–segment size ratio, strength of penetrant attraction to the polymer, and temperature to the diffusion.69–71 These theories are based on the idea that the dynamics in the glassy state are slowed due to a combination of a local barrier for a segment (polymer monomer or a penetrant) to escape its local cage, and the barrier is augmented at low temperatures by the elastic distortion of the matrix required for the cage to dilate and allow the segment to escape. These theories have been corroborated by not only existing experimental measurements of small molecule diffusion, but also molecular dynamics simulations of the purely repulsive penetrant dynamics of small, gas-like molecules in glassy polymers.34,36,37 Building on this work by examining diffusion behavior of particles that have attractive interactions with the surrounding polymer matrix may give some insights into how systems with real chemical interactions can be tuned to promote desirable transport properties.
In this work, we take the framework of softness and use it to investigate the dynamics of small particle transport through a model glass-forming polymer in the spirit of classic the Kremer–Grest model.65,66 We use molecular dynamics (MD) to simulate gas-like, monatomic tracer particles permeating a polymer melt as it nears the glass transition, measuring the self-diffusion and relaxation behavior of the tracers, and compare the tends in mobility from these measures qualitatively with the SCCHT model for activated diffusion in a polymer matrix with cross-interactions. We then calculate softness for these systems and extract the characteristic energetic and entropic scales that describe the structural free energy barriers to tracers’ glassy rearrangement. Finally, we compare these barriers across systems with different tracer particle sizes and interaction strengths with the polymer medium to assess how softness can relate local structure to transport dynamics in glassy systems. We examine the differences between energy barriers computed from softness and from diffusion coefficients or relaxation times and theoretical predictions for activation barriers in penetrating improving the overall understanding of connections between these barriers to activated transport is important in its own right and may be practically helpful in designing new materials that exhibit desirable diffusion behavior for use in separations processes and other important engineering applications.
Methods
System initialization and equilibration
The simulations in this work consider bead-spring polymer chains65,66 consisting of 20 Lennard-Jones (LJ) interaction sites, each representing a monomer of species A. Gas-like tracer particles, which we refer to as species B, are represented as freely moving single LJ interaction sites. We use the standard Lennard-Jones reduced units throughout for time , temperature (T* = T/(ε/kB)), pressure (P* = P/(σ3/ε)), volume (V* = V/σ3), and energy (U* = U/ε), where σ, ε, and m are the length, energy, and mass units of the reduced Lennard-Jones potential and kB is Boltzmann's constant.
, temperature (T* = T/(ε/kB)), pressure (P* = P/(σ3/ε)), volume (V* = V/σ3), and energy (U* = U/ε), where σ, ε, and m are the length, energy, and mass units of the reduced Lennard-Jones potential and kB is Boltzmann's constant.
The reduced Lennard-Jones potential72,73 in its cut-and-shifted form,
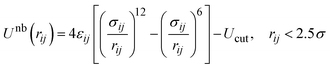 | (1) |
 , while the polymer–tracer interaction energies are chosen to be either εAB = 1.0, 1.2, or 1.5ε. A combining rule is not used for interaction energies to suppress spontaneous phase separation at lower temperatures. A unit Lennard-Jones mass of m = 1 is assigned to both the individual monomer beads and to the tracers.
, while the polymer–tracer interaction energies are chosen to be either εAB = 1.0, 1.2, or 1.5ε. A combining rule is not used for interaction energies to suppress spontaneous phase separation at lower temperatures. A unit Lennard-Jones mass of m = 1 is assigned to both the individual monomer beads and to the tracers.
Adjacent monomer beads along a single polymer chain are bonded together and do not experience the Unb potential with one another. The bonded interactions in our system are defined by the finitely-extensible nonlinear elastic (FENE) bonding potential,65,66 which has the form
 | (2) |
All simulations are performed in the LAMMPS76,77 package with data files initialized by a custom Python script. Each simulation box in our work contains 500 tracer particles and 475 polymer chains, or 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 total particles. Since all particles have a unit mass, the mass fraction of tracers in each simulation box is equal to the number fraction of 5%. The total volume fractions of tracers, taken to be the Lennard-Jones volume of the tracers divided by the total Lennard-Jones volume of all beads in the box, correspond to ϕB = 0.142%, 0.654%, 2.62%, or 5% for tracers of size σBB = 0.3σ, 0.5σ, 0.8σ, and 1.0σ, respectively. For the larger tracer sizes, these are outside of the dilute limit.
000 total particles. Since all particles have a unit mass, the mass fraction of tracers in each simulation box is equal to the number fraction of 5%. The total volume fractions of tracers, taken to be the Lennard-Jones volume of the tracers divided by the total Lennard-Jones volume of all beads in the box, correspond to ϕB = 0.142%, 0.654%, 2.62%, or 5% for tracers of size σBB = 0.3σ, 0.5σ, 0.8σ, and 1.0σ, respectively. For the larger tracer sizes, these are outside of the dilute limit.
To ensure that our starting configuration is not too dense, polymer chains are initialized using a random walk in a large cubic simulation box, after which the tracer particles are inserted randomly. The soft push-off method is then used to relax the overlapping contacts, followed by a final energy minimization.78,79 After the minimization procedure we perform MD using an isothermal–isobaric (NPT) time integrator80,81 with a timestep of dt = 0.002τ and damping coefficients of Tdamp = 100dt and Pdamp = 1000dt for the temperature and pressure, respectively. Velocities are randomly initialized at T* = 1.0 and the system is run at a fixed temperature and pressure of T* = 1.0 and P* = 0.0 for 5 × 106dt or 104τ to equilibrate, at which point the mean-squared displacement of the monomers is several times the mean end-to-end distance of the polymer chains. The equilibrated snapshot is then saved for further use.
Cooling and production runs
An initialized configuration at T* = 1.0 and P* = 0.0 is decreased gradually to zero temperature at a dimensionless cooling rate of Γ = 10−4T*/τ and constant P* = 0.0. Snapshots are saved along the way at incremental temperatures. The density of the system is recorded as a function of time to identify the temperature at which a glass transition occurs, which we estimate using a nonlinear fitting function used previously,82 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V* at the glass transition temperature
V* at the glass transition temperature  .
.
Simulation snapshots from temperatures of interest are then used for production runs at constant temperature and pressure, using the T* corresponding to their ramping time and a constant P* = 0.0 for a total of 5 × 107dt or 105τ. During these quiescent simulations, several trajectories of 101 frames each are recorded with linear spacing Δt between frames corresponding to each decade from 10−2τ to 103τ to calculate relevant dynamic properties, as well as the radial distribution function g(r). For example, a trajectory is recorded during the entire duration of the simulation with frame spacing of Δt = 103τ. Following the production run, a trajectory spaced by Δt = 10−1τ with 104 frames is generated spanning 103τ or 1% of the production time; this is used for evaluating softness in the postprocessing steps, discussed below.
We characterize the structure of our systems using the standard radial distribution function,83 and the dynamic properties are characterized using two metrics. First, we compute the mean-squared displacements84 as
 | (4) |
 | (5) |
Dynamical indicator function and softness
Following the production run and the generation of a 1000τ trajectory with frames spaced by Δt = 0.1τ for each system, we evaluate the softness of each particle in each frame to quantify the structure of the neighborhood around a particle with a single parameter. To describe the local environment around a particle, we employ a set of two-body Gaussian radial structure functions G inspired by Behler and Parrinello85 that have been extensively used for softness,51–60 | (6) |
Using the set of structure functions, a 60-dimensional feature vector Fn is constructed for the particles, the elements of which are used as training data. The training data are divided into an equally sized set of rearranging and non-rearranging particles, which correspond to some binary variable y with values 1 and 0 respectively. We choose an indicator function to assess whether particles in our training set are currently undergoing a rearrangement. The dynamic quantity phop has been extensively studied not only as a way of monitoring glassy rearrangements during simulation86,87 but also as a useful indicator function for evaluating softness.52,54,55,57,60 This function has the form,
 | (7) |
| A = [t − tR/2, t] | (8) |
| B = [t, tR/2] | (9) |
Using the rearranging and non-rearranging training data, a linear support vector machine (SVM) is used to construct a hyperplane that best separates the two classes in the high-dimensional space defined by the Fn feature vectors. The hyperplane, defined by,
| wn·Fn − b = 0 | (10) |
| S = wn·Fn − b | (11) |
 of the hyperplane, we use
of the hyperplane, we use | (12) |
Softness is known to provide a relationship between its conveyance of local structure and the probability of rearrangement through a temperature-independent free energy of rearrangement. The rearrangement barrier ΔF(S) is taken from the Arrhenius definition of the rearrangement probability,
 | (13) |
| ΔF(S) = ΔE(S) − TΣ(S) | (14) |
Results
Glass transition temperature
The glass transition temperature Tg of our neat polymer is computed from the thermal expansion coefficient definition and plotted below in Fig. 1 on the left-hand side. The glass transition temperature is identified to be about in the neat system. The uncertainty and error bars here and elsewhere in this work is defined as the standard deviation of a measured value from three independent configurations. The right-hand side of Fig. 1 shows the calculated values of
in the neat system. The uncertainty and error bars here and elsewhere in this work is defined as the standard deviation of a measured value from three independent configurations. The right-hand side of Fig. 1 shows the calculated values of  for different combinations of σBB and εAB, and compares them with that of the neat system. For all the systems considered,
for different combinations of σBB and εAB, and compares them with that of the neat system. For all the systems considered,  falls within about 4% of the value of the neat system, with the lowest values for a given εAB occurring at the σBB = 0.5σ size. For tracer particles of size σBB = 0.5σ and above, the value of
falls within about 4% of the value of the neat system, with the lowest values for a given εAB occurring at the σBB = 0.5σ size. For tracer particles of size σBB = 0.5σ and above, the value of  increases with the strength of the cross-interaction εAB. The changes in
increases with the strength of the cross-interaction εAB. The changes in  due to the presence of tracers indicate that their concentration in our systems is beyond the dilute limit.
due to the presence of tracers indicate that their concentration in our systems is beyond the dilute limit.
Temperature-dependent diffusion
The ability of tracer particles to diffuse through the polymer system is strongly influenced by temperature, as diffusion of small molecules in porous media is typically an Arrhenius process. Fig. 2(a) shows the MSD of tracers with varying size at two temperatures. At a high temperature of T* = 0.95, over twice , the tracers all transition rapidly from the MSD ∝ τ2 ballistic regime to MSD ∝ τ1 diffusion. For a lower temperature of
, the tracers all transition rapidly from the MSD ∝ τ2 ballistic regime to MSD ∝ τ1 diffusion. For a lower temperature of  , there is a reduction in the mobility related to the polymer glass transition. While the tracers of the smallest size are readily diffusive, the larger particles see a precipitous decrease in their mobility, with the σBB = 1.0σ tracers moving on average about 10 particle diameters over 105 time units. Tracers of the same particle size as a single monomer bead have only a few times greater mobility than the smallest tracers at temperatures near the glass transition temperature. The rigid, glassy structure of the polymer at low temperatures prevents the larger particles from being able to move through the interstices of the glassy matrix without overcoming exceedingly high energy barriers to rearrangement. Changes in the interaction potential εAB between the tracers and the surrounding polymer at a constant size σBB also impact the MSD, as shown in Fig. 2(b). The increase in the depth of the potential well impedes the motion of the tracers, though the impact is minimal for the particles above Tg.
, there is a reduction in the mobility related to the polymer glass transition. While the tracers of the smallest size are readily diffusive, the larger particles see a precipitous decrease in their mobility, with the σBB = 1.0σ tracers moving on average about 10 particle diameters over 105 time units. Tracers of the same particle size as a single monomer bead have only a few times greater mobility than the smallest tracers at temperatures near the glass transition temperature. The rigid, glassy structure of the polymer at low temperatures prevents the larger particles from being able to move through the interstices of the glassy matrix without overcoming exceedingly high energy barriers to rearrangement. Changes in the interaction potential εAB between the tracers and the surrounding polymer at a constant size σBB also impact the MSD, as shown in Fig. 2(b). The increase in the depth of the potential well impedes the motion of the tracers, though the impact is minimal for the particles above Tg.
The self-diffusion coefficient D is measured using the long-time slope of the MSD. The Einstein relation for diffusion88 in three dimensions gives the dependence of D,
 | (15) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MSD = b + log
MSD = b + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ, and transforming its y-intercept b back to a diffusion coefficient, D = eb/6, to get the result in units of σ2/τ. A higher relative value of D indicates that under those conditions one type of particle has on average greater mobility. The values of D are shown in Fig. 3.
τ, and transforming its y-intercept b back to a diffusion coefficient, D = eb/6, to get the result in units of σ2/τ. A higher relative value of D indicates that under those conditions one type of particle has on average greater mobility. The values of D are shown in Fig. 3.
For the smallest of the particles, σBB = 0.3σ, we see that the relationship between D and temperature is Arrhenius, until just above  , when the value of log
, when the value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D no longer decays linearly with inverse temperature and the activation energy increases. The increase in activation energy is further exacerbated by increases in εAB. The larger sizes of particles, σBB ≥ 0.5σ, which are closer in size to a segment of the polymer chain exhibit a more pronounced drop in diffusion that becomes stronger with increasing σBB and εAB. This makes sense intuitively and is analogous to the predicted increase in the relaxation time τα for penetrant molecules with cross-interactions in a polymer matrix by SCCHT, which demonstrated that either increasing tracer size (σBB) or attraction strength (εAB) would lead to an increase in both τα and the activation energy. The diffusion coefficient of small penetrants is generally known to be size-dependent to some extent, and we examine this relationship below.
D no longer decays linearly with inverse temperature and the activation energy increases. The increase in activation energy is further exacerbated by increases in εAB. The larger sizes of particles, σBB ≥ 0.5σ, which are closer in size to a segment of the polymer chain exhibit a more pronounced drop in diffusion that becomes stronger with increasing σBB and εAB. This makes sense intuitively and is analogous to the predicted increase in the relaxation time τα for penetrant molecules with cross-interactions in a polymer matrix by SCCHT, which demonstrated that either increasing tracer size (σBB) or attraction strength (εAB) would lead to an increase in both τα and the activation energy. The diffusion coefficient of small penetrants is generally known to be size-dependent to some extent, and we examine this relationship below.
For each system, the results for D may be fit to the empirical expression of the Vogel–Fulcher–Tammann (VFT) type,
 | (16) |
Experiment and theory has demonstrated that, in polymeric supercooled liquids, the diffusion coefficient obeys a dependence such that log(1/D) ∼ (Tg/T)λ, where the exponent λ is related to system chemistry and is roughly 2 for nonpolar liquids and in the range of 2.2–2.6 for some typical polymers.70 SCCHT predictions for this dependence note that in the low-size-ratio limit, the λ dependence should hold, while in the high-size-ratio limit the exponential scaling should be 3λ, which is due to differences in the local cage vs. elastic barrier being the limiting factor. We can examine our own data in this lens by performing a linear fit to extract the scaling exponent λ and the prefactor K in the expression  , where we de-dimensionalize the diffusion coefficient by the prefactor from (16). To do this we simply plot
, where we de-dimensionalize the diffusion coefficient by the prefactor from (16). To do this we simply plot  , and find K = eb and λ = a. Linearized plots listing the fit parameters when the data above the glass transition region (0.45 ≤ T* ≤ 0.75) can be found in Fig. S2.1. The fit parameters are shown in Fig. 4.
, and find K = eb and λ = a. Linearized plots listing the fit parameters when the data above the glass transition region (0.45 ≤ T* ≤ 0.75) can be found in Fig. S2.1. The fit parameters are shown in Fig. 4.
We identify that, for our smallest particles of size σBB = 0.3σ, the scaling exponent is around λ = 1.2, which increases with tracer size to a value around λ = 2 or just greater. The prefactor K appears to be a logarithmic function of the tracer size, as has been predicted for the large-size-ratio limit in the SCCHT. While generally the value of the scaling exponent increases with tracer size, there is no obvious functional form. It is important to note that in the SCCHT model, the value of the scaling exponent is not a fit parameter – it is taken from experiments or theoretical predictions. While we can draw qualitative and some quantitative comparisons to what one might expect from theory, it is important to note that we are limited by the dynamics in the supercooled and glassy regime that can be reasonably observed in simulations (this is further discussed at the end of the next section). It is important to consider how we might quantify the barrier to the diffusion process based on our calculated values of D, so we might compare them with other energy scales. Recall that for an Arrhenius process, the activation energy Ea is determined from the slope of a line of the logarithm of the measured property versus inverse temperature,
 | (17) |
 | (18) |
Tracer relaxation behavior
Tracer particle relaxation times in the polymer melt are calculated by evaluating the SISF for the wavevector of magnitude k = 7.14σ−1. This value of k approximately corresponds to the first peak of the static structure factor S(k) for the system and serves as a characteristic inverse length scale of the polymer that is constant across all combinations of tracer σBB and εAB values. As previously with the diffusion coefficients, Fig. 5(a) shows the effect of varying particle size at a high and low temperature while Fig. 5(b) shows the impact of changing the interaction strength for a constant particle size.As cooled towards  , we see the emergence of a two-step relaxation behavior in the decay of the SISF, one of the hallmarks of glassy dynamics.89 The shorter β-relaxation takes place on a time scale ∼1τ, while the longer α-relaxation decays on longer time scales as either σBB and εAB increase or with decreasing temperature. In the least mobile of particles, a caging plateau like that observed in the MSD of particles near
, we see the emergence of a two-step relaxation behavior in the decay of the SISF, one of the hallmarks of glassy dynamics.89 The shorter β-relaxation takes place on a time scale ∼1τ, while the longer α-relaxation decays on longer time scales as either σBB and εAB increase or with decreasing temperature. In the least mobile of particles, a caging plateau like that observed in the MSD of particles near  emerges. The relative kinetic arrest of the polymer at
emerges. The relative kinetic arrest of the polymer at  means that the motion of polymer chains restricts particles whose sizes are comparable to one of the segments along the chain. To estimate the relaxation time τα from the decay of Fs, the data are fit to a sum of two Kohlrausch–Wiliams–Watts (KWW) stretched exponential functions,90,91
means that the motion of polymer chains restricts particles whose sizes are comparable to one of the segments along the chain. To estimate the relaxation time τα from the decay of Fs, the data are fit to a sum of two Kohlrausch–Wiliams–Watts (KWW) stretched exponential functions,90,91
 | (19) |
 | (20) |
The calculated values of τeffα are plotted as functions of inverse temperature in an Arrhenius-style manner for each system in Fig. 6, and the stretching exponents bα in Fig. S2.2. As we can see, relaxation times are super-Arrhenius in nature, increasing by several orders of magnitude in the larger particles as the glass transition is approached. Much like the behavior of the diffusion coefficients, this is to be expected for a system with glassy dynamics and the measured values can be fit to a VFT expression. As with the empirical fits to the diffusion coefficients, a temperature-dependent activation barrier may be found by using (16) and (18) with the replacement B → −B to account for the inverse temperature dependence of τα compared to the diffusivity.
The stretching exponents shown in Fig. S2.2 are also below a value of 1.0 at temperatures below the onset of glassy dynamics, indicating clearly that there is dynamical heterogeneity in the motion of the particles. Calculated values of βα larger than unity at high T* are due to the interference of ballistic dynamics with the α relaxation at temperatures where there is not a pronounced caging plateau.
By inspection, the relaxation times increase with particle size and with interaction strength, meaning that smaller particles will be able to overcome the dynamic slowdown at low temperatures, but a decrease in size may not be enough to overcome particularly strong attraction between the chains and the species of interest. For example, in our results, we find some overlap in the relaxation times for the high size ratio particles with σBB = 0.8 and 1.0σ when the value of εAB is increased. Theoretical predictions for activated penetrant dynamics have previously identified such non-monotonic behavior in the relaxation time when size ratio and interaction strength are increased.71 We fit the ratio of the relative effective relaxation time τeffα/τ0, where τ0 is the prefactor in a fit to eqn (16), to an inverse power-law relationship with a scaling exponent λ. Like the fit for the inverse diffusion coefficients in the prior section, we use data above the glass transition region (0.45 ≤ T* ≤ 0.75). Results for the fit parameters are shown on the linearized plots in Fig. S2.3. While the prefactor K was not found to be a logarithmic function of tracer size for the relaxation time data as it was for the diffusion data, the value of λ increases with both σBB and εAB as before.
The dynamic slowdown of the penetrants in the system can be quantified relative to the dynamics of the polymer itself. Following the same method outlined above, we calculate the values of the polymer segmental relaxation time τeffα across different systems and temperatures and compare the polymer relaxation times in the presence of penetrants with results from simulation of a neat polymer. Fig. 7 shows how the polymer segmental relaxation time τeffα,poly evolves with  , parametrized by either σBB or εAB of the penetrant species. It is important to note the collapse in τeffα,poly across different systems when temperature is scaled by
, parametrized by either σBB or εAB of the penetrant species. It is important to note the collapse in τeffα,poly across different systems when temperature is scaled by  , showing that the segmental dynamics are perturbed by the presence of the penetrating species insomuch as the penetrants affect the glass transition temperature.
, showing that the segmental dynamics are perturbed by the presence of the penetrating species insomuch as the penetrants affect the glass transition temperature.
The dynamical decoupling between the mobile penetrants and the polymer matrix can be quantified by plotting the ratio of the relaxation times of the penetrants to the polymer monomers. A ratio of the penetrant-to-segmental relaxation timescales on the order of 1 would imply that the penetrant dynamics track the polymer segmental dynamics, while a smaller value indicates that the tracers are able to resist the slowdown. From the ratios plotted in Fig. 8, we find that tracer dynamics become increasingly decoupled from the matrix as  is approached from above. Increasing the interaction strength εAB indeed increases the ratio, confirming our prior observation that an increase in the interaction strength leads to reduced mobility of penetrants. For the largest penetrants, increasing the interaction strength above that of the polymer–polymer interaction (εAB > 1ε) slows their relaxation times beyond those of the polymer segments. This is consistent with results from a theoretical approach in SCCHT tailored to polymer–penetrant interactions in a homopolymer liquid.71 That work found a decoupling of the relaxation times with increasing effective packing fraction ϕeff of polymer in the system, which approaches a kinetic glass transition in a manner equivalent to our temperature approach to
is approached from above. Increasing the interaction strength εAB indeed increases the ratio, confirming our prior observation that an increase in the interaction strength leads to reduced mobility of penetrants. For the largest penetrants, increasing the interaction strength above that of the polymer–polymer interaction (εAB > 1ε) slows their relaxation times beyond those of the polymer segments. This is consistent with results from a theoretical approach in SCCHT tailored to polymer–penetrant interactions in a homopolymer liquid.71 That work found a decoupling of the relaxation times with increasing effective packing fraction ϕeff of polymer in the system, which approaches a kinetic glass transition in a manner equivalent to our temperature approach to  , and that increasing the strength of the interaction at a given value of ϕeff (or equivalently T*) reduces the rate of decoupling. In the case of theoretical systems where penetrant–polymer interactions were not considered, packing fractions denser than a glass transition of vitrification point ϕglass (or equivalently, temperatures below
, and that increasing the strength of the interaction at a given value of ϕeff (or equivalently T*) reduces the rate of decoupling. In the case of theoretical systems where penetrant–polymer interactions were not considered, packing fractions denser than a glass transition of vitrification point ϕglass (or equivalently, temperatures below  ) are needed to observe this dynamic decoupling.
) are needed to observe this dynamic decoupling.
 | ||
Fig. 8 Ratio of tracer-to-polymer relaxation times fitted from eqn (20) plotted against  . Symbols indicate σBB, while subplots indicate εAB values of (a) 1.0ε, (b) 1.2ε, and (c) 1.5ε. . Symbols indicate σBB, while subplots indicate εAB values of (a) 1.0ε, (b) 1.2ε, and (c) 1.5ε. | ||
The SCCHT approach also predicts that there is a decrease in the decoupling at equivalent packing fractions with increasing size, meaning that the ratio of relaxation times is larger. Interestingly, our work finds that tracers of size σBB = 0.8 and 1.0σ show no dynamic decoupling through their approach to  for the time scales accessible in our simulations. Though the particles with the same size as a Kuhn segment modeled using SCCHT had a slight increase in the calculated valued of τeffα,tracer/τeffα,polymer with increasing ϕeff, they saw a sharp decrease in the region where ϕeff reflects a glass transition or vitrification of the system.71 One possible explanation for this is that the systems modeled in this work feature a high enough concentration of penetrants that the dilute limit predictions from SCCHT begin to break down; we find that for all particle sizes, the glass transition temperature
for the time scales accessible in our simulations. Though the particles with the same size as a Kuhn segment modeled using SCCHT had a slight increase in the calculated valued of τeffα,tracer/τeffα,polymer with increasing ϕeff, they saw a sharp decrease in the region where ϕeff reflects a glass transition or vitrification of the system.71 One possible explanation for this is that the systems modeled in this work feature a high enough concentration of penetrants that the dilute limit predictions from SCCHT begin to break down; we find that for all particle sizes, the glass transition temperature  is perturbed from the neat polymer system, which necessitates being outside the dilute limit. We have, however, identified that the relaxation time of the polymer is roughly constant across systems at the same value of
is perturbed from the neat polymer system, which necessitates being outside the dilute limit. We have, however, identified that the relaxation time of the polymer is roughly constant across systems at the same value of  , meaning that relative mobility should be comparable across systems at the same relative temperature. It is also relevant to note that in the SCHHT theory, the interactions between penetrants and polymer beads have a range of only 0.15 times a segment diameter, meaning that the contacts must be very close for them to interact; in this work, the Lennard-Jones potential has an attractive radius 2.5σ, over 16 times that employed in SCCHT. That work found that increasing the standard range of attractions led to an increase in relaxation time, particularly at high penetrant–polymer interaction strengths.71 Finally, it is known that the accessibility of glassy temperature regimes in equilibrium simulations is subject to greater limitations than in experiments or theory because of the long timescales in real systems and the difficulty in gathering adequate statistics. Simulations on a longer timescale (comparable to that of experiments) that were able to reach an equilibrium closer to or just below the glass transition temperature may demonstrate the beginnings of dynamic decoupling for our largest penetrant particles through the polymer matrix. This would be similar to the predictions in the theoretical approach with the ϕeff ≈ 0.64 reported previously.71 These known limitations in molecular dynamics studies of glassy systems mean that an alternate approach would be warranted in future work.
, meaning that relative mobility should be comparable across systems at the same relative temperature. It is also relevant to note that in the SCHHT theory, the interactions between penetrants and polymer beads have a range of only 0.15 times a segment diameter, meaning that the contacts must be very close for them to interact; in this work, the Lennard-Jones potential has an attractive radius 2.5σ, over 16 times that employed in SCCHT. That work found that increasing the standard range of attractions led to an increase in relaxation time, particularly at high penetrant–polymer interaction strengths.71 Finally, it is known that the accessibility of glassy temperature regimes in equilibrium simulations is subject to greater limitations than in experiments or theory because of the long timescales in real systems and the difficulty in gathering adequate statistics. Simulations on a longer timescale (comparable to that of experiments) that were able to reach an equilibrium closer to or just below the glass transition temperature may demonstrate the beginnings of dynamic decoupling for our largest penetrant particles through the polymer matrix. This would be similar to the predictions in the theoretical approach with the ϕeff ≈ 0.64 reported previously.71 These known limitations in molecular dynamics studies of glassy systems mean that an alternate approach would be warranted in future work.
To directly compare the dynamics in the systems we have studied and to draw analogy to existing experimental and theoretical work on small particle transport, we can also plot the decoupling factor for the tracer molecules, or the product of the diffusion coefficient D and the effective alpha-relaxation time τeffα. For systems where there is dynamic decoupling between penetrant and matrix, as demonstrated in Fig. 8, this can be plotted as the product of the penetrant D and the polymer τeffα. Plots of these quantities similar to Fig. 8 are included in Appendix 2 as Fig. S2.4 and S2.5. The decoupling factor remains less than 1 for all cases studied in the tracer–tracer definition, while for the tracer–polymer definition it demonstrates clear decoupling, Dτ ≫ 1, for large particle sizes as is also seem in Fig. 8.
Softness and barriers to rearrangement
Using the training parameters described in the prior section (pcut,R = 0.25, pcut_NR = 0.02, tR = 10τ, and tNR = 10τ), and a set of M = 60 structure functions surrounding each tracer particle, we trained a hyperplane to describe the softness of our tracers for each of the four values of σBB at a fixed interaction strength of εAB = 1.0ε. We trained our systems at different temperatures to ensure that enough non-rearranging (in the case of smaller particles) or rearranging (in the case of larger particles) could be identified for the set. The training temperatures and the calculated accuracies using eqn (12) are shown in Table 1. A sensitivity analysis of prediction accuracy and the size of the training set versus the choice of pcut,R and pcut,NR for each value of σBB with εAB = 1.0ε was performed and results are shown in Appendix 3. The non-rearrangement threshold of pcut,NR = 0.02 generally corresponds to the value below which there will be less than several thousand examples of both rearranging and non-rearranging particles in all cases. The rearrangement threshold of pcut,R = 0.25 ensures that we are probing displacements that are at least size 0.5σ. Choosing a value below this would increase the size of the training set but not necessarily the accuracy of the classification.Overall, the accuracy of rearrangement prediction from softness with this set of training parameters and structure functions decreases with increasing particle size. Typical accuracies reported in other computational studies vary from 70% to 90%.58,60 While tuning these parameters further may be able to improve the prediction accuracy for a specific set of interactions, since we are interested in trying to directly compare the barriers derived from softness across several systems, it is important that our definition of what a rearrangement is consistent across systems. A constant cutoff value pcut,R ensures that we are probing rearrangements of at least 0.5σ in all cases. The influence of the choice of pcut on our results is discussed further at the end of this section.
Following the training procedure, we take the hyperplane constructed for some σBB and εAB = 1.0 and evaluate S for all our particles, using this particle-size hyperplane for each interaction strength to directly compare the values for similar systems. For each system replica and at each T*, we build two histograms of softness values: one for all particles, and one for rearranging particles, both with a bin size of 0.1 softness units. For a given pair of histograms, the value of the rearrangement probability PR(S) is calculated as the ratio of the two bins with the same softness. As an example, Fig. 9(a) shows the overlaid softness histograms for three independent replicas of the σBB = 0.5σ and εAB = 1.0ε system at its training temperature of T* = 0.375. The dynamical decomposition of the same system from which the softness dependent energy and entropy barriers are extracted is illustrated in Fig. 9(b). Equivalent plots to Fig. 9(b) for other combinations of σBB and εAB may be found in Appendix 4.
From the histograms, we obtain a normalized probability distribution function (PDF) with some mean μ and standard deviation S. The values of μS and μR, with subscripts S and R referring to the distribution of all softness values and those of rearranging particles respectively, are plotted in Fig. 10. It is interesting to note that, for the plots of μ in the cases of σBB = 0.8σ and σBB = 1.0σ, the slope of S(T*) of all particles has a change in value near  . In contrast, the smaller particles for which mobility is less impaired below
. In contrast, the smaller particles for which mobility is less impaired below  , the temperature dependence remains linear with no change in slope. This gives insight into how smaller particles experience the effects of the glass transition occurring in the medium around them, or rather, how they do not.
, the temperature dependence remains linear with no change in slope. This gives insight into how smaller particles experience the effects of the glass transition occurring in the medium around them, or rather, how they do not.
It is important to understand the difference between the softness distributions of the rearranging and of all particles. When local structure plays a greater role in determining the rearranging behavior, the distributions will become less similar than at high temperatures. To quantify this, we define a signal-to-noise-like quantity SNR,
 | (21) |
 .
.
 | ||
| Fig. 11 Signal-to-noise ratios of softness distributions for rearrangement of particles as a function of temperature. Lines are drawn to guide the eye. | ||
Next, to determine the softness-dependent barriers, we perform an Arrhenius decomposition as shown in Fig. 9(b) above to extract the S-dependent functions ΔE(S) and Σ(S). We fit the Arrhenius expression to the PR(S) data in the range  to ensure that the system is in equilibrium with the imposed temperature and that we are below the onset temperature of glassy dynamics. We then directly compare the values of absolute softness across systems with the same σBB and varying εAB because the same hyperplane was used to assess the local structure. This allows us to visualize the relative impact of tuning the interaction strength on ΔE(S) and Σ(S). Results are shown in Fig. 12.
to ensure that the system is in equilibrium with the imposed temperature and that we are below the onset temperature of glassy dynamics. We then directly compare the values of absolute softness across systems with the same σBB and varying εAB because the same hyperplane was used to assess the local structure. This allows us to visualize the relative impact of tuning the interaction strength on ΔE(S) and Σ(S). Results are shown in Fig. 12.
 | ||
| Fig. 12 Energetic and entropic rearrangement barriers as a function of S. Lines indicate a quadratic best fit. | ||
It becomes challenging to compare the energy barriers to rearrangement between systems, because they have been trained on different hyperplanes and therefore have different weights associated with the structure functions of the particle. However, we have shown previously that a rearrangement threshold in phop can translate across systems and corresponds to motion of the about the same absolute distance; definitionally, our “rearranging” particles are all traveling at least some escape distance (in this case, 0.5σ) at the time of observation. By taking advantage of this quality of phop, and with our knowledge of the distribution of softness values for rearranging particles, we can explore how the barriers to this rearrangement change as a function of temperature for the different systems.
We use the fits to our barrier functions and integrate the product of ΔE(S) or Σ(S) with the normalized probability distribution function of softness values for the rearranging particles at some temperature T, P(S|R,T)dS. The three quantities of interest with units of energy are then,
 | (22) |
 | (23) |
| 〈ΔF(T|R)〉 = 〈ΔE(T|R)〉 − T〈Σ(T|R)〉 | (24) |
With the energy barriers evaluated using eqn (22), we can also compare these values with those energy barriers estimated using the diffusion coefficient and relaxation times measured, allowing us to draw a connection between those measures of mobility and the hopping mechanism that gives us softness. These results are shown in Fig. 13. The energy barrier to hopping extracted from softness is of a similar magnitude to the barriers assumed from D and τeffα at temperatures well above  ; however, as we approach the glass transition of the system, the energy barriers from D and τeffα increase rapidly, as opposed to that from softness, which increases much more slowly. The difference in the increase of the activation energy of on cooling as extracted from D and τeffα is expected from the well-known breakdown of the Stokes–Einstein relationship.93 In all cases, for each mode of mobility considered, the extracted energy barrier increases with both σBB and εAB at a constant temperature relative to
; however, as we approach the glass transition of the system, the energy barriers from D and τeffα increase rapidly, as opposed to that from softness, which increases much more slowly. The difference in the increase of the activation energy of on cooling as extracted from D and τeffα is expected from the well-known breakdown of the Stokes–Einstein relationship.93 In all cases, for each mode of mobility considered, the extracted energy barrier increases with both σBB and εAB at a constant temperature relative to  , and the barriers estimated from the alpha-relaxation process are higher than those from diffusion.
, and the barriers estimated from the alpha-relaxation process are higher than those from diffusion.
The increase in the barrier height from softness with increasing εAB is a valuable finding, as it is an extension of the trends observed in the barriers from diffusion and relaxation. Directly comparing the magnitudes of energy barriers derived from softness which were calculated from different hyperplanes (i.e. for the different particle size systems) is tempting but may be an inaccurate choice. Because the weights associated with the individual structure functions in the construction of softness are different, its physical meaning is not the same. Our proposed transformation into temperature units allows some comparison with other temperature-based trends but does not eliminate this factor. It is worthwhile, however, to examine how the barriers within a family of particle sizes change relative to one another.
Notably, the softness-dependent barriers to rearrangement show a temperature dependence that decreases with the penetrant size. For particles with a high size ratio, the barrier predicted based on softness is nearly independent of temperature. This indicates that the local structure and variations in it play less of a role in the transport of these penetrants and may point to other barriers to the hopping process that are not captured by softness. We can again draw an analogue to SCCHT, where it is demonstrated that local caging effects and non-local collective elasticity both govern transport in the high-size-ratio regime, but that the collective effects are negligible for small particles.69,70 For our systems, this may be one potential reason why softness does not fully capture the barrier to rearrangement in larger particles, because the softness analysis does not consider any contributions due to elasticity. One might expect that the effects of elasticity would increase the energy barrier associated with particles of a given softness, as local hopping events lead to the nucleation of cage-expansion effects in the SCCHT framework. Upon cooling the matrix becomes more rigid, and a barrier that takes both the local and nonlocal parts into account should then lead to super-Arrhenius growth of the energy barrier. For the time scales where we can reasonably measure the mobility of the penetrants, we do not observe any growth of energy barriers associated with a particular softness value, and the origins of the differences in the barriers estimated by softness and those from direct mobility measures remain an open question.
Previous work on softness found that the choice of a different rearrangement threshold changed the quantitative measure of the barriers to rearrangement but did not affect the qualitative result.52 It is therefore relevant to explore how a change in the rearrangement definition might impact the results of our analysis. We find that changing the value of pcut affects the results of the analysis in this section quantitatively, but not qualitatively. A lower threshold above which particles are rearranging means that the average barrier to reach that rearrangement threshold is lower, thus the energetic barrier and entropic barrier to rearrangement as a function of softness are shifted down. This is analogous to how relaxation times would be shorter if quantified using a self-intermediate scattering function evaluated over a longer wavevector k (i.e., a shorter length scale of relaxation). To give an example, when the value of the threshold is cut in half to pcut = 0.125, we are now probing rearrangements of at least an escape distance of  . Retraining a hyperplane to seek rearrangements at this value of pcut yields a slightly lower accuracy as there are far greater distinct examples of rearranging particles. When the analysis of this section is repeated, we find the same qualitative result: the average barrier still decreases with increasing softness, and when the transformation to temperature is performed, we see the same trend observed in Fig. 13 for the softness barriers. Results of this comparison for varying σBB and a constant εAB = 1.0ε using pcut = 0.125 are shown in Appendix 5.
. Retraining a hyperplane to seek rearrangements at this value of pcut yields a slightly lower accuracy as there are far greater distinct examples of rearranging particles. When the analysis of this section is repeated, we find the same qualitative result: the average barrier still decreases with increasing softness, and when the transformation to temperature is performed, we see the same trend observed in Fig. 13 for the softness barriers. Results of this comparison for varying σBB and a constant εAB = 1.0ε using pcut = 0.125 are shown in Appendix 5.
Discussion
In this work, we took the well-known model of a bead-spring polymer and used molecular dynamics to simulate the transport of small particles in a manner analogous to gas molecules moving through a glassy polymer. The particles’ relative size to and interaction strength with the surrounding polymer was varied to understand how the dynamics change in response to more favorable interactions and less steric hindrance with the surrounding chains. Super-Arrhenius behavior in the self-diffusion coefficients and effective relaxation time for the particles was observed, and we were able to fit these measured quantities to an inverse-power-law relationship previously described in theory on activated penetrant dynamics. The pre-exponential factors for the inverse-power-law relationship of the diffusion coefficients was found to be a logarithmic function of the penetrant size, in accordance with SCCHT predictions for the large-size-limit ratio of activated penetrant transport. Scaling of the power-law exponent was consistent with the low-size-limit regime prediction, where the inverse diffusion coefficient scales with (Tg/T)λ and the exponent is on the order of λ = 2. While the discrepancy in penetrant size regimes suggests that the systems we have modeled here lie in the intermediate size region, the trends observed in these fits are qualitatively consistent with the predictions from theory and with the kind of scaling observed in experiments.70 We observed a relationship between the penetrant-to-matrix relaxation time ratio and the inverse temperature that is reminiscent of predictions from SSCHT in a homopolymer liquid indicating a dynamical decoupling in regions near the glass transition.71To further compare the limited data we have in the supercooled region with theoretical predictions, it is relevant to consider fitting the logarithm of both the inverse penetrant diffusion coefficients and the penetrant-to-polymer relaxation time ratios to the aforementioned power-law scaling. Shifting the window of temperature data that we fit to the inverse-power-law relationship from the 0.45 < T* < 0.75 previously used in the text to 0.40 < T* < 0.55, closer to and just at the point of glass transition, we can find the relevant values of λ and K and plot them in Fig. S2.6 for the diffusion coefficients and Fig. S2.7 for the relaxation time ratios. The values of the scaling exponent λ increase by about 50% in the case of diffusion of the largest-size penetrants with σBB = 1.0σ, increasing from a range of 2.0 < λ < 2.2 to a range of 2.8 < λ < 3.1. While this is not exactly the 3λ scaling of the theoretical prediction in the high-size-ratio limit, the increase demonstrates that close to the supercooled glassy regime the dynamics we observe in simulations follow trends not unlike the theoretical predictions. In the case of the relaxation time ratios, we see a similar phenomenon where the scaling exponents in the high-size-ratio limit increase from a range of 2.2 < λ < 2.3 to a range of 3.3 < λ < 3.5. Further simulations sampling a broader range of size ratios and at lower particle concentrations to more accurately study a dilute limit, as well as experimental studies in the deeply supercooled and glassy regimes, are warranted to make additional quantitative comparison with established theory.
Using the framework of softness, previously applied to other glassy systems to study dynamics, we investigated the relationship between the local structure around the tracer particles in a glassy matrix and their mobility, extracting softness-dependent energetic and entropic barriers to the rearrangement process. These barriers, known to be approximately linear in systems where all particles are similar in size, become nonlinear as the particle size of the tracer shrinks, and the barriers increase in magnitude with the increasing depth of the Lennard-Jones potential well between tracer and polymer. For systems where we delineate between rearranging and non-rearranging penetrants with the same set of local structure functions and training parameters, the accuracy of the hyperplane training decreases with increasing penetrant size. Typical accuracies reported in other simulations are on the order of 70%–90% for either homopolymers56–59 or Kob–Anderson glass formers52,54,60 where the binary species have similar dynamics. The decrease in the ability of softness, a proxy for the local structure, to accurately predict rearrangements at the larger penetrant-to-matrix size ratios gives rise to an interesting parallel with theory. For high-size limit penetrants it is known that local cage barriers (presumably captured by softness) and collective matrix elasticity (not captured by softness) both play a role in determining mobility, whereas in low-size-limit systems the collective elasticity becomes significantly less important.69,70 The increased role of collective elasticity in determining mobility in the high-size limit may explain why the changes in mobility are not adequately captured by softness, which is a local measure.
Comparison between systems where softness is trained with different hyperplanes has remained a challenge in drawing similarities between the machine-learned quantities and more well-understood, experimentally-accessible properties.94 We propose a simple change-of-variables method to transform the softness-dependent barriers to a temperature dependence by integrating over the distribution of softness values at each temperature, allowing for an examination of the barriers relative to the glass transition. We find that, consistent with other measures examined in this work, the energetic barrier to rearrangement for particles of a given size σBB increases with polymer–penetrant interaction strength εAB. For the different tracer sizes studied, each shows that the barrier height increases as the glass transition temperature is approached, with the rate of increase slowing as opposed to the super-Arrhenius behavior we have seen in the barriers predicted from diffusion coefficients and relaxation times. As we have suggested above, this somewhat unspectacular finding may be indicative of the phenomenon predicted by SCCHT which notes that local caging effects play the dominant role in determining mobility for small penetrants while large penetrants are also affected by collective effects in the matrix. To further explore the phenomena discussed here, future work should explore a greater array of particle sizes and interaction strengths to identify transitions between the low- and high-size-ratio regimes of penetrant behavior to enable a deeper comparison with theory.
Finally, computational methods we have introduced here may be used to extend softness methods to more complex systems which it has not previously been applied to. For purposes of exploring model gas separation systems, limiting use to the low-size-ratio regimes would likely ensure that softness can accurately capture rearrangements in systems with penetrants and a matrix that have decoupled dynamics. One possible study could involve multicomponent diffusion in a polymer matrix with two penetrant species, examining the effects of changing both the penetrant–polymer interactions and the penetrant–penetrant interaction. This could provide some additional insights into the fundamental physics of competitive penetrant transport in glassy systems and create a direct comparison to the real-world application of the membrane-based separation of gas mixtures.
Author contributions
S. J. L.: data curation, formal analysis, investigation, resources, visualization, writing – original draft, writing – review and editing. R. A. R.: conceptualization, funding acquisition, methodology, project administration, resources, supervision, writing – review and editing.Conflicts of interest
The authors have no conflicts of interest to disclose.Data availability
Appendices referenced in this article are available as part of its supplementary information (SI). These include S1 (Quantifying glassy rearrangements), S2 (Tracer diffusion and relaxation behavior), S3 (Sensitivity analysis of hyperplane accuracy to pcut,R and pcut,NR), S4 (Tracer softness training histograms and Arrhenius plots for different systems), and S5 (Impact of changing rearrangement cutoff parameter in softness analysis). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sm00837a.Data for this article, including volume vs. temperature data from cooling simulations, mean-squared displacement, self-intermediate scattering function, and softness histogram data, are available at a GitHub repository hosted at https://github.com/sjlayding/small_particle_transport_SI.git.
Acknowledgements
The authors acknowledge the generous support of both the University of Pennsylvania Ashton Fellowship and NSF Research Traineeship Award #2152205. Simulations were performed using the Stampede2, Stampede3, and Ranch resources at the Texas Advanced Computing Center (TACC) through NSF XSEDE95 allocation TG-DMR150034 and NSF ACCESS96 allocation TG-CHM230003. Additionally, S. J. L. would like to thank Dr. Ian Graham (University of Pennsylvania Department of Physics and Astronomy) for assistance with developing the softness calculation tools and Prof. Zahra Fakhraai (University of Pennsylvania Department of Chemistry) for many useful discussions on glass-forming materials. No generative AI tools were used in the preparation of this manuscript.References
- D. S. Sholl and R. P. Lively, Seven chemical separations to change the world, Nature, 2016, 532, 435–437 CrossRef.
- IEA. Net Zero by 2050. https://www.iea.org/reports/net-zero-by-2050 ( 2021).
- IEA. Net Zero Roadmap: A Global Pathway to Keep the 1.5 °C Goal in Reach. https://www.iea.org/reports/net-zero-roadmap-a-global-pathway-to-keep-the-15-0c-goal-in-reach ( 2023).
- P. Friedlingstein, et al., Global Carbon Budget 2023, Earth Syst. Sci. Data, 2023, 15, 5301–5369 CrossRef.
- K. Calvin et al. IPCC, 2023: Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing Team, H. Lee and J. Romero (Eds.)]. IPCC, Geneva, Switzerland. https://www.ipcc.ch/report/ar6/syr/ ( 2023) DOI:10.59327/IPCC/AR6-9789291691647.
- S. J. Layding and H. S. Caram, Comparing the energy requirements for amine absorption processes for CO2 capture from flue gases calculated using a minimal information simple thermodynamic model with experimental and detailed simulation results, Int. J. Greenhouse Gas Control, 2022, 115, 103595 CrossRef CAS.
- S. J. Layding and H. S. Caram, A thermodynamic approach to energy requirements for CO2 capture and a comparison between the minimum energy for liquid and solid sorbent processes, Int. J. Greenhouse Gas Control, 2024, 137, 104227 CrossRef CAS.
- C. Chao, Y. Deng, R. Dewil, J. Baeyens and X. Fan, Post-combustion carbon capture, Renewable Sustainable Energy Rev., 2021, 138, 110490 CrossRef CAS.
- N. McQueen, et al., A review of direct air capture (DAC): scaling up commercial technologies and innovating for the future, Prog. Energy, 2021, 3, 032001 CrossRef CAS.
- J. Young, et al., The cost of direct air capture and storage can be reduced via strategic deployment but is unlikely to fall below stated cost targets, One Earth, 2023, 6, 899–917 CrossRef.
- L. M. Robeson, Correlation of separation factor versus permeability for polymeric membranes, J. Membr. Sci., 1991, 62, 165–185 CrossRef CAS.
- L. M. Robeson, Polymer membranes for gas separation, Curr. Opin. Solid State Mater. Sci., 1999, 4, 549–552 CrossRef CAS.
- L. M. Robeson, The upper bound revisited, J. Membr. Sci., 2008, 320, 390–400 CrossRef CAS.
- L. M. Robeson, Q. Liu, B. D. Freeman and D. R. Paul, Comparison of transport properties of rubbery and glassy polymers and the relevance to the upper bound relationship, J. Membr. Sci., 2015, 476, 421–431 CrossRef CAS.
- H. W. H. Lai, et al., Hydrocarbon ladder polymers with ultrahigh permselectivity for membrane gas separations, Science, 2022, 375, 1390–1392 CrossRef CAS PubMed.
- T. H. Lee, M. Balcik, W.-N. Wu, I. Pinnau and Z. P. Smith, Dual-phase microporous polymer nanofilms by interfacial polymerization for ultrafast molecular separation, Sci. Adv., 2024, 10, eadp6666 CrossRef CAS.
- Z. Yang, et al., Surpassing Robeson Upper Limit for CO2/N2 Separation with Fluorinated Carbon Molecular Sieve Membranes, Chem, 2020, 6, 631–645 CAS.
- G. M. Iyer, L. Liu and C. Zhang, Hydrocarbon separations by glassy polymer membranes, J. Polym. Sci., 2020, 58, 2482–2517 CrossRef CAS.
- F. H. Stillinger, A Topographic View of Supercooled Liquids and Glass Formation, Science, 1995, 267, 1935–1939 CrossRef CAS.
- P. G. Debenedetti and F. H. Stillinger, Supercooled liquids and the glass transition, Nature, 2001, 410, 259–267 CrossRef CAS.
- C. A. Angell, K. L. Ngai, G. B. McKenna, P. F. McMillan and S. W. Martin, Relaxation in glassforming liquids and amorphous solids, J. Appl. Phys., 2000, 88, 3113–3157 Search PubMed.
- L. Berthier and G. Biroli, Theoretical perspective on the glass transition and amorphous materials, Rev. Mod. Phys., 2011, 83, 587–645 Search PubMed.
- G. Biroli and J. P. Garrahan, Perspective: The glass transition, J. Chem. Phys., 2013, 138, 12A301 CrossRef PubMed.
- L. Berthier and M. D. Ediger, Facets of glass physics, Phys. Today, 2016, 69, 40–46 CrossRef CAS.
- V. Bapst, et al., Unveiling the predictive power of static structure in glassy systems, Nat. Phys., 2020, 16, 448–454 Search PubMed.
- J. Langer, The mysterious glass transition, Phys. Today, 2007, 60, 8–9 CrossRef CAS.
- W. F. Drayer and D. S. Simmons, Is the Molecular Weight Dependence of the Glass Transition Temperature Driven by a Chain End Effect?, Macromolecules, 2024, 57, 5589–5597 CrossRef CAS.
- D. L. Baker, M. Reynolds, R. Masurel, P. D. Olmsted and J. Mattsson, Cooperative Intramolecular Dynamics Control the Chain-Length-Dependent Glass Transition in Polymers, Phys. Rev. X, 2022, 12, 021047 CAS.
- J. Yang, L. Tao, J. He, J. R. McCutcheon and Y. Li, Machine learning enables interpretable discovery of innovative polymers for gas separation membranes, Sci. Adv., 2022, 8, eabn9545 Search PubMed.
- M. D. Ediger, Spatially Heterogeneous Dynamics in Supercooled Liquids, Annu. Rev. Phys. Chem., 2000, 51, 99–128 CrossRef CAS PubMed.
- M. T. Cicerone and M. D. Ediger, Photobleaching technique for measuring ultraslow reorientation near and below the glass transition: tetracene in o-terphenyl, J. Phys. Chem., 1993, 97, 10489–10497 CrossRef CAS.
- L. Liu, et al., Quasielastic and inelastic neutron scattering investigation of fragile-to-strong crossover in deeply supercooled water confined in nanoporous silica matrices, J. Phys.: Condens. Matter, 2006, 18, S2261–S2284 Search PubMed.
- N. Vergadou and D. N. Theodorou, Molecular Modeling Investigations of Sorption and Diffusion of Small Molecules in Glassy Polymers, Membranes, 2019, 9, 98 Search PubMed.
- K. Zhang, D. Meng, F. Müller-Plathe and S. K. Kumar, Coarse-grained molecular dynamics simulation of activated penetrant transport in glassy polymers, Soft Matter, 2018, 14, 440–447 Search PubMed.
- M. L. Greenfield and D. N. Theodorou, Coarse-Grained Molecular Simulation of Penetrant Diffusion in a Glassy Polymer Using Reverse and Kinetic Monte Carlo, Macromolecules, 2001, 34, 8541–8553 CrossRef CAS.
- K. Zhang and S. K. Kumar, Molecular Simulations of Solute Transport in Polymer Melts, ACS Macro Lett., 2017, 6, 864–868 CrossRef CAS.
- D. Meng, K. Zhang and S. K. Kumar, Size-dependent penetrant diffusion in polymer glasses, Soft Matter, 2018, 14, 4226–4230 RSC.
- M. Brownell, A. L. Frischknecht and M. A. Wilson, Subdiffusive High-Pressure Hydrogen Gas Dynamics in Elastomers, Macromolecules, 2022, 55, 3788–3800 CrossRef CAS.
- M. Balçık, S. B. Tantekin-Ersolmaz, I. Pinnau and M. G. Ahunbay, CO2/CH4 mixed-gas separation in PIM-1 at high pressures: Bridging atomistic simulations with process modeling, J. Membr. Sci., 2021, 640, 119838 CrossRef.
- G. S. Larsen, P. Lin, K. E. Hart and C. M. Colina, Molecular Simulations of PIM-1-like Polymers of Intrinsic Microporosity, Macromolecules, 2011, 44, 6944–6951 CrossRef CAS.
- T. R. Cuthbert, N. J. Wagner and M. E. Paulaitis, Molecular Simulation of Glassy Polystyrene: Size Effects on Gas Solubilities, Macromolecules, 1997, 30, 3058–3065 CrossRef CAS.
- J. W. Haus and K. W. Kehr, Diffusion in regular and disordered lattices, Phys. Rep., 1987, 150, 263–406 CrossRef CAS.
- S. Havlin and D. Ben-Avraham, Diffusion in disordered media, Adv. Phys., 1987, 36, 695–798 CrossRef CAS.
- H. Takeuchi, A jump motion of small molecules in glassy polymers: A molecular dynamics simulation, J. Chem. Phys., 1990, 93, 2062–2067 Search PubMed.
- F. Müller-Plathe, L. Laaksonen and W. F. Van Gunsteren, Cooperative effects in the transport of small molecules through an amorphous polymer matrix, J. Mol. Graphics, 1993, 11, 118–120 CrossRef.
- M. L. Greenfield and D. N. Theodorou, Coupling of Penetrant and Polymer Motions During Small-Molecule Diffusion In a Glassy Polymer, Mol. Simul., 1997, 19, 329–361 Search PubMed.
- I. Cozmuta, M. Blanco and W. A. Goddard, Gas Sorption and Barrier Properties of Polymeric Membranes from Molecular Dynamics and Monte Carlo Simulations, J. Phys. Chem. B, 2007, 111, 3151–3166 Search PubMed.
- G. Dorenbos and K. Morohoshi, Modeling gas permeation through membranes by kinetic Monte Carlo: Applications to H2, O2, and N2 in hydrated Nafion®, J. Chem. Phys., 2011, 134, 044133 CrossRef.
- D. Paschek and R. Krishna, Diffusion of Binary Mixtures in Zeolites: Kinetic Monte Carlo versus Molecular Dynamics Simulations, Langmuir, 2001, 17, 247–254 CrossRef CAS.
- D. Richard, et al., Predicting plasticity in disordered solids from structural indicators, Phys. Rev. Mater., 2020, 4, 113609 Search PubMed.
- E. D. Cubuk, et al., Identifying structural flow defects in disordered solids using machine-learning methods, Phys. Rev. Lett., 2015, 114, 108001 CrossRef CAS PubMed.
- S. S. Schoenholz, E. D. Cubuk, D. M. Sussman, E. Kaxiras and A. J. Liu, A structural approach to relaxation in glassy liquids, Nat. Phys., 2016, 12, 469–472 Search PubMed.
- E. D. Cubuk, et al., Structure-property relationships from universal signatures of plasticity in disordered solids, Science, 2017, 358, 1033–1037 Search PubMed.
- S. S. Schoenholz, E. D. Cubuk, E. Kaxiras and A. J. Liu, Relationship between local structure and relaxation in out-of-equilibrium glassy systems, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 263–267 Search PubMed.
- D. M. Sussman, S. S. Schoenholz, E. D. Cubuk and A. J. Liu, Disconnecting structure and dynamics in glassy thin films, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10601–10605 CrossRef CAS PubMed.
- R. J. S. Ivancic and R. A. Riggleman, Identifying structural signatures of shear banding in model polymer nanopillars, Soft Matter, 2019, 15, 4548–4561 Search PubMed.
- E. Yang, R. J. S. Ivancic, E. Y. Lin and R. A. Riggleman, Effect of polymer–nanoparticle interaction on strain localization in polymer nanopillars, Soft Matter, 2020, 16, 8639–8646 RSC.
- E. Yang and R. A. Riggleman, Role of Local Structure in the Enhanced Dynamics of Deformed Glasses, Phys. Rev. Lett., 2022, 128, 097801 CrossRef CAS PubMed.
- E. Yang, et al., Understanding creep suppression mechanisms in polymer nanocomposites through machine learning, Soft Matter, 2023, 19, 7580–7590 RSC.
- I. R. Graham, P. E. Arratia and R. A. Riggleman, Exploring the relationship between softness and excess entropy in glass-forming systems, J. Chem. Phys., 2023, 158, 204504 Search PubMed.
- F. W. Starr, S. Sastry, J. F. Douglas and S. C. Glotzer, What Do We Learn from the Local Geometry of Glass-Forming Liquids?, Phys. Rev. Lett., 2002, 89, 125501 CrossRef.
- A. Widmer-Cooper and P. Harrowell, On the relationship between structure and dynamics in a supercooled liquid, J. Phys.: Condens. Matter, 2005, 17, S4025–S4034 CrossRef CAS.
- R. A. Riggleman, J. F. Douglas and J. J. De Pablo, Tuning polymer melt fragility with antiplasticizer additives, J. Chem. Phys., 2007, 126, 234903 CrossRef.
- W. Kob and H. C. Andersen, Testing mode-coupling theory for a supercooled binary Lennard-Jones mixture I: The van Hove correlation function, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4626–4641 CrossRef CAS.
- G. S. Grest and K. Kremer, Molecular dynamics simulation for polymers in the presence of a heat bath, Phys. Rev. A:At., Mol., Opt. Phys., 1986, 33, 3628–3631 Search PubMed.
- K. Kremer and G. S. Grest, Dynamics of entangled linear polymer melts: A molecular-dynamics simulation, J. Chem. Phys., 1990, 92, 5057–5086 Search PubMed.
- R. Zhang and K. S. Schweizer, Statistical Mechanical Theory of Penetrant Diffusion in Polymer Melts and Glasses, Macromolecules, 2016, 49, 5727–5739 CrossRef CAS.
- R. Zhang and K. S. Schweizer, Correlated matrix-fluctuation-mediated activated transport of dilute penetrants in glass-forming liquids and suspensions, J. Chem. Phys., 2017, 146, 194906 Search PubMed.
- B. Mei and K. S. Schweizer, Activated penetrant dynamics in glass forming liquids: size effects, decoupling, slaving, collective elasticity and correlation with matrix compressibility, Soft Matter, 2021, 17, 2624–2639 Search PubMed.
- B. Mei, G. S. Sheridan, C. M. Evans and K. S. Schweizer, Elucidation of the physical factors that control activated transport of penetrants in chemically complex glass-forming liquids, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2210094119 CrossRef CAS.
- B. Mei and K. S. Schweizer, Theory of the Effects of Specific Attractions and Chain Connectivity on the Activated Dynamics and Selective Transport of Penetrants in Polymer Melts, Macromolecules, 2022, 55, 9134–9151 CrossRef CAS.
- J. E. Jones, On the determination of molecular fields.—I. From the variation of the viscosity of a gas with temperature, Proc. R. Soc. London, Ser. A, 1924, 106, 441–462 CAS.
- J. E. Jones, On the determination of molecular fields. —II. From the equation of state of a gas, Proc. R. Soc. London, Ser. A, 1924, 106, 463–477 CAS.
- H. A. Lorentz, Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase, Ann. Phys., 1881, 248, 127–136 CrossRef.
- J. D. Weeks, D. Chandler and H. C. Andersen, Role of repulsive forces in determining the equilibrium structure of simple liquids, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. P. Thompson, et al., LAMMPS – a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- R. Auhl, R. Everaers, G. S. Grest, K. Kremer and S. J. Plimpton, Equilibration of long chain polymer melts in computer simulations, J. Chem. Phys., 2003, 119, 12718–12728 CrossRef CAS.
- Y. R. Sliozberg and J. W. Andzelm, Fast protocol for equilibration of entangled and branched polymer chains, Chem. Phys. Lett., 2012, 523, 139–143 CrossRef CAS.
- D. J. Evans and B. L. Holian, The Nose-Hoover thermostat, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- G. J. Martyna, D. J. Tobias and M. L. Klein, Constant pressure molecular dynamics algorithms, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- K. Dalnoki-Veress, J. A. Forrest, C. Murray, C. Gigault and J. R. Dutcher, Molecular weight dependence of reductions in the glass transition temperature of thin, freely standing polymer films, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2001, 63, 031801 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University PressOxford, 2017 DOI:10.1093/oso/9780198803195.001.0001.
- E. J. Maginn, R. A. Messerly, D. J. Carlson, D. R. Roe and J. R. Elliot, Best Practices for Computing Transport Properties 1. Self-Diffusivity and Viscosity from Equilibrium Molecular Dynamics [Article v1.0], Living J. Comput. Mol. Sci., 2018, 1(1), 6324 CrossRef.
- J. Behler and M. Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- A. S. Keys, L. O. Hedges, J. P. Garrahan, S. C. Glotzer and D. Chandler, Excitations Are Localized and Relaxation Is Hierarchical in Glass-Forming Liquids, Phys. Rev. X, 2011, 1, 021013 Search PubMed.
- A. Smessaert and J. Rottler, Distribution of local relaxation events in an aging three-dimensional glass: Spatiotemporal correlation and dynamical heterogeneity, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022314 CrossRef PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, 2023 DOI:10.1016/C2009-0-63921-0.
- P. G. Debenedetti, Metastable Liquids: Concepts and Principles, Princeton University Press, 2020 DOI:10.2307/j.ctv10crfs5.
- R. Kohlrausch, Theorie des elektrischen Rückstandes in der Leidener Flasche, Ann. Phys., 1854, 167, 56–82 Search PubMed.
- G. Williams and D. C. Watts, Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function, Trans. Faraday Soc., 1970, 66, 80 Search PubMed.
- J. S. Shaffer, Effects of chain topology on polymer dynamics: Configurational relaxation in polymer melts, J. Chem. Phys., 1995, 103, 761–772 Search PubMed.
- M. T. Cicerone and M. D. Ediger, Enhanced translation of probe molecules in supercooled o-terphenyl: Signature of spatially heterogeneous dynamics?, J. Chem. Phys., 1996, 104, 7210–7218 CrossRef CAS.
- A. R. Moore, Effects of Inter-Molecular and Intra-Molecular Factors on the Properties of Simulated Glasses, ProQuest Dissertations and Theses, University of Pennsylvania, United States, Pennsylvania, 2022 Search PubMed.
- J. Towns, et al., XSEDE: Accelerating Scientific Discovery, Comput. Sci. Eng., 2014, 16, 62–74 Search PubMed.
- T. J. Boerner, S. Deems, T. R. Furlani, S. L. Knuth and J. Towns, ACCESS: Advancing Innovation, Practice and Experience in Advanced Research Computing, ACM, New York, NY, USA, 2023, pp. 173–176 DOI:10.1145/3569951.3597559.
| This journal is © The Royal Society of Chemistry 2026 |


















