 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microbubble-based measurement of shear and loss moduli in polyacrylamide hydrogels at MHz frequencies
Ali
Rezaei
 a,
Kay
Dijs
a,
Kay
Dijs
 a,
David
Fernandez Rivas
a,
David
Fernandez Rivas
 b,
Jacco H.
Snoeijer
b,
Jacco H.
Snoeijer
 a,
Michel
Versluis
a,
Michel
Versluis
 a and
Guillaume
Lajoinie
*a
a and
Guillaume
Lajoinie
*a
aPhysics of Fluids Department, Faculty Science and Technology, University of Twente, P.O. Box 217, Enschede, 7500AE, The Netherlands. E-mail: g.p.r.lajoinie@utwente.nl
bMesoscale Chemical Systems (MCS), Faculty Science and Technology, University of Twente, P.O. Box 217, Enschede, 7500AE, The Netherlands
First published on 5th January 2026
Abstract
The rheology of soft materials is routinely measured at low strain rates to extract constitutive laws necessary for understanding and modeling their behavior. High-frequency rheology, however, remains difficult to access. Consequently, the mechanical properties of soft materials at MHz strain rates are largely unknown. Ultrasound-driven microbubbles, widely used in biomedical imaging, drug delivery, and therapy, act as efficient mechanical actuators at MHz frequencies. Their dynamics depend on nonlinear resonance behavior, the viscoelasticity of their stabilizing shells, and the viscoelastic properties of the surrounding medium. Here, we make use of (nonlinear) bubble dynamics to characterize the rheology of polyacrylamide (PAM) hydrogels at strain rates exceeding 106 s−1. Narrow resonance curves of single coated microbubbles embedded in PAM, obtained through high-speed imaging, were compared to a Rayleigh–Plesset-type model. The results show that the shear modulus is similar in both the Hz and MHz regimes, while the loss modulus behaves very differently, exhibiting an effective shear viscosity at MHz frequencies comparable to that of water. These findings demonstrate a new approach for probing the high-frequency rheology of viscoelastic media.
1 Introduction
Ultrasound contrast agents (UCAs) are widely used in medical imaging to enhance contrast and improve medical diagnosis, e.g., for organ perfusion imaging or to monitor hypervascularization in and around tumors.1,2 Additionally, UCAs are intensively investigated for their ultrasound-mediated therapeutic potential. Microbubbles can indeed increase the permeation of endothelial layers, resulting in the local delivery of drugs or genes.3,4Ultrasound contrast microbubbles have a typical size in the range of 1 to 5 µm in radius. They are filled with a low-solubility high-molecular weight gas, such as sulfur hexafluoride (SF6), or a perfluorocarbon (C3F8, or C4F10), and are stabilized by a shell (most often consisting of a phospholipid mixture) that reduces the interfacial pressure of the microbubbles and hinders the diffusion of gas from the bubble core into the surrounding medium,5–7 which otherwise leads to rapid bubble dissolution.
Upon exposure to ultrasound, microbubbles undergo (nonlinear) volumetric oscillations which are key to their superior scattering cross-section. Furthermore, when the driving frequency is tuned to the resonance frequency of the bubbles, they experience a mechanical resonance with larger bubble oscillations and higher scattering, as well as the generation of nonlinear harmonics, that thus further enhances contrast generation. This unique behavior is routinely exploited in clinical imaging, both in linear and nonlinear contrast imaging modes.
The ultrasound-driven response of UCAs, including the effects of the phospholipid coating, is very well understood in infinitely large media, i.e., where the bubble is free from interactions with boundaries or neighboring bubbles. These dynamics have been measured through both acoustic attenuation and high-speed imaging experiments8–10 and are well described by Rayleigh–Plesset-type models.7 In many biomedical applications such as perfusion imaging, ultrasound localization microscopy, targeted imaging, drug delivery, and blood-brain-barrier opening, bubbles are not oscillating in field. There, the presence of neighboring viscoelastic tissue has a crucial effect on their dynamics. This includes both their linear resonance behavior and their nonlinear dynamics.11 For example, phagocytosed microbubble were shown to have a different behavior than free bubbles.12 Furthermore, the presence of a viscoelastic boundary (e.g., a vessel wall) can increase13–15 or decrease13 the bubbles’ resonance frequency depending on the elasticity of the material, and that confinement decreases the bubbles’ oscillation amplitude.14,16 In the bulk of a viscoelastic medium, it has been shown that elasticity of the medium can increase the resonance frequency of bubbles, while the additional viscous dissipation can lead to overdamped dynamics.17,18
Directly investigating bubble oscillations in tissues in a controlled way is challenging, owing to the opacity, complexity, and variability within and across soft tissues. A first step can therefore comprise a study of the oscillations of ultrasound contrast microbubbles in much simpler materials. While this does not offer a direct translation toward real tissue, it allows to better understand meaningful fundamental aspects. For example, the oscillations of microbubbles in tissues have previously been modeled by adding a linear Kelvin–Voigt (K–V) viscoelastic model or a nonlinear Neo-Hookean elastic model to a Rayleigh–Plesset-type equation.19 Originally, Allen and Roy have developed a framework to compute the oscillations of bubbles in arbitrary linear20 and nonlinear21 viscoelastic media by solving the bubble dynamics equation in conjunction with a stress tensor analysis. This approach was extended by Stride et al. to model the oscillations of bubbles in blood, including both a linear viscoelastic shell and a linear viscoelastic effect of the red blood cells.22 More recently, Oratis et al.23 have developed a unifying framework that allows for a straightforward numerical integration based on the relaxation function of linear viscoelastic media. One major issue that remains is that the use of any of these models requires a priori knowledge of the viscoelastic properties of tissue, which is generally not the case. More specifically, it is well known that the response of a viscoelastic material strongly depends on shear rate.24,25 However, classical rheology measurements can reach a shear rate up to 102 s−1, which is 3 orders of magnitude lower than typical ultrasound driving frequencies.24
Earlier experimental studies have employed a range of methods to investigate the rheology of viscoelastic materials at high strain rates.26,27 Bertin et al.28 utilized atomic force microscopy to study the rheological properties of a medium by observing the displacement of a particle at strain rates of hundreds s−1. Jamburidze et al.17 measured the elastic moduli at a strain rate of 104 s−1 by fitting the linear oscillation amplitude and resonance frequency of 150 µm bubbles to the resonance curves extracted from high-speed recordings. A very similar experiment was performed later by Murakami et al.,29 with bubbles of similar size, but generated using a laser. These studies have offered deeper insights into medium rheology by pushing farther the boundary of measurable elastic moduli in terms of strain rates. Acoustic methods, such has shear wave elastography,30 acoustic radiation force impulse imaging (or ARFI),31 acoustic particle palpation32 have also been used to characterize tissues in the (sub-)kHz range, and some even found their way to the clinics. However, these methods do not reach strain rates of 106 s−1,27,33 which are relevant for biomedical ultrasound. Interestingly, Estrada et al.24 have proposed that a strain rate of 108 s−1 can be achieved by inertial collapse. This, however, is not an oscillatory method and does not directly provide G′ and/or G″. Rheological measurement can be pushed to higher strain rates through the use of smaller microbubbles contained in the medium while being driven by ultrasound. However, such small microbubbles must be stabilized by a shell and the measured response is thus a combination of (known) shell rheology and medium rheology.
In this article, we combine stabilized microbubbles known from the field of ultrasound contrast imaging and optically clear hydrogels with a tunable elasticity to investigate the feasibility of MHz-range rheology using microbubbles. To that end, we use ultra-high-speed imaging of phospholipid-coated microbubbles to extract the shear moduli of a polyacrylamide hydrogel in the 106 s−1 range. Exploiting the narrowband resonance of microbubbles, we can use Rayleigh–Plesset type equation modified by a linear Kelvin–Voigt viscoelastic model to extract the local (in terms of strain rates) storage and loss moduli of the viscoelastic material in the range of 106 to 107 s−1.
2 Bubble dynamics model
The Rayleigh–Plesset (RP) equation of motion for a spherically symmetric gas bubble in an incompressible and uniform medium, in the linear regime of deformation of a viscoelastic medium (traceless stress tensor) can be expressed as follows:20,34 | (1) |
![[R with combining umlaut]](https://www.rsc.org/images/entities/i_char_0052_0308.gif) are the first and second derivatives of R with respect to time, respectively. ρm is the density of the medium and Pg(R) is the pressure inside the bubble, and P∞ is the pressure in the liquid far away from the bubble. σ represents the surface tension at the gas–liquid interface while τrr represents the radial normal stress component, and r is the radial distance from the center of the bubble.11,35,36
are the first and second derivatives of R with respect to time, respectively. ρm is the density of the medium and Pg(R) is the pressure inside the bubble, and P∞ is the pressure in the liquid far away from the bubble. σ represents the surface tension at the gas–liquid interface while τrr represents the radial normal stress component, and r is the radial distance from the center of the bubble.11,35,36
The modeled system is represented in Fig. 1a. The pressure in the bubble, Pg(R), can be expressed using a polytropic law:37
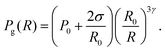 | (2) |
For an incompressible, homogeneous, and isotropic linear viscoelastic medium (in the small deformation regime), the Kelvin–Voigt model gives the relation: τrr = 2(Gεrr + μ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) rr). Here, G represents the shear modulus and εrr = −2(R3 − R03)/3r3 is the shear strain. μ and
rr). Here, G represents the shear modulus and εrr = −2(R3 − R03)/3r3 is the shear strain. μ and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) rr = −2R2Ṙ/r3 are the shear viscosity and strain rates, respectively.40 Substituting τrr in eqn (1) leads to ref. 11:
rr = −2R2Ṙ/r3 are the shear viscosity and strain rates, respectively.40 Substituting τrr in eqn (1) leads to ref. 11:
 | (3) |
The specific choice of a Kelvin–Voigt model may seem arbitrary. However, in the limit of a linearized model i.e. a first-order viscoelastic description, the contribution of the viscoelastic medium will always add two linear damping and elastic contributions, that are both represented in eqn (3). Although the Kelvin–Voigt model may not be valid at all timescales (strain rates), it can be used to describe any arbitrary (linear) medium in an infinitesimal frequency band. This is the strength of the approach, which remains valid as long the storage and loss moduli do not significantly vary over the bandwidth of the bubble resonance used to measure them.
The complex modulus is defined as G*(ω) = G′(ω) + iG″(ω) and describes the entire viscoelastic behavior of the material. G′(ω) is the storage modulus which represents the solid-like (elastic) response of the material, G″(ω) is the loss modulus which represents liquid-like (viscous) properties of the material and ω is the angular frequency (strain rate). In the Kelvin–Voigt model, G = G′ and G″ = μω.41
In the linear bubble oscillation regime eqn (3) can be linearized, which leads to an expression for the eigenfrequency of the bubble:7
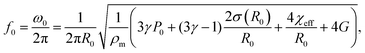 | (4) |
As an illustration of the effect of viscoelasticity, Fig. 1b compares the solution of eqn (3) for a coated bubble in water to that in a hydrogel with a modulus of 150 kPa, which is the upper range that can be expected for soft tissue, at low strain rates.44,45 The bubble with R0 = 1.7 µm is driven at a frequency of 2.2 MHz (its resonance frequency in water) with a 15-cycle, 10-kPa ultrasound pulse tapered with a 2-cycle hyperbolic tangent (tanh) envelope. Increasing the medium's elasticity leads to a decrease in bubble excursion. This is due to the increased medium stiffness, both directly by offering more mechanical resistance to bubble expansion (a lower gain of the system), and indirectly by shifting the bubble's resonance frequency as compared to that in water.19 The resonance curves obtained by numerical integration of eqn (3) are further presented in Fig. 1c and d for a varying shear modulus and viscosity, respectively, at an acoustic driving pressure of 100 kPa. They show the independent effect of the elastic modulus, affecting the resonance frequency, and of the viscosity, affecting the damping of the system, in the context of the Kelvin–Voigt model.
3 Materials and methods
3.1 Experimental procedure
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of DSPC and DPPE–PEG 5000, with a concentration of 12.5 mg mL−1 in Isoton (Beckman Coulter, ISOTON II Diluent). The bubbles were filled with a gas mixture of 15 v% of C4F10 gas in CO2 as detailed by Segers et al.48 Bubble production rate were on the order of one million bubbles per second. Two bubble populations were produced with mean radii of 1.7 and 2.3 µm, and with a polydispersity index on the order of 5%.46
1 molar ratio of DSPC and DPPE–PEG 5000, with a concentration of 12.5 mg mL−1 in Isoton (Beckman Coulter, ISOTON II Diluent). The bubbles were filled with a gas mixture of 15 v% of C4F10 gas in CO2 as detailed by Segers et al.48 Bubble production rate were on the order of one million bubbles per second. Two bubble populations were produced with mean radii of 1.7 and 2.3 µm, and with a polydispersity index on the order of 5%.46
Samples are prepared using the recipe outlined in Table 1.50 When the monomer acrylamide (Acrylamide/bis 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 40 w/v%, SERVA) undergoes polymerization with APS (Ammonium Persulfate, ACS reagent ≥98.0%, Sigma-Aldrich), the polymer forms a cross-linked network, which increases the stiffness of the hydrogel. Microbubbles are added to the acrylamide solution before curing. The rise of the microbubbles to the surface due to buoyancy is prevented by stirring the solution until solidification begins. TEMED (N,N,N′,N′-tetramethylethylenediamine, ReagentPlus, 99%) is added as a catalyst to speed up the reaction. Since the polymerization is exothermic, the concentration of TEMED was reduced as compared to standard recipes. In combination with a cold bath, this allows to keep the temperature below 35 °C so as not to damage the coated microbubbles. The native acrylamide/bis solution was diluted with MilliQ water to create 6.4% and 16% PAM hydrogels, referred to as the soft and stiff hydrogels, respectively.
1, 40 w/v%, SERVA) undergoes polymerization with APS (Ammonium Persulfate, ACS reagent ≥98.0%, Sigma-Aldrich), the polymer forms a cross-linked network, which increases the stiffness of the hydrogel. Microbubbles are added to the acrylamide solution before curing. The rise of the microbubbles to the surface due to buoyancy is prevented by stirring the solution until solidification begins. TEMED (N,N,N′,N′-tetramethylethylenediamine, ReagentPlus, 99%) is added as a catalyst to speed up the reaction. Since the polymerization is exothermic, the concentration of TEMED was reduced as compared to standard recipes. In combination with a cold bath, this allows to keep the temperature below 35 °C so as not to damage the coated microbubbles. The native acrylamide/bis solution was diluted with MilliQ water to create 6.4% and 16% PAM hydrogels, referred to as the soft and stiff hydrogels, respectively.
| Materials | Soft hydrogel (6.4% PAM) | Stiff hydrogel (16% PAM) |
|---|---|---|
| 40% acrylamide (mL) | 1.6 | 4 |
| APS (mg) | 14 | 14 |
| TEMED (µL) | 4 | 4 |
| MilliQ water (mL) | 8.4 | 6 |
The mechanical properties of these hydrogels at low strain rates (<16 s−1) were evaluated using a rotational rheometer (MCR 502e, Anton-Paar) set-up in a parallel plate configuration. To ensure proper contact between the hydrogel and the platform, the samples were cured directly on the rheometer platform. The top parallel plate was lowered to form a gap of 0.5 mm. After curing, a frequency sweep test was performed with 5% strain to measure the storage and loss moduli.
The radius-time curves of oscillating microbubbles in the hydrogel were obtained by analyzing the high-speed recordings with a custom edge detection MATLAB script.51 The frequency content of the microbubble oscillations was determined by performing a fast Fourier transform (FFT) on the radius-time curves in MATLAB. No measurable non-spherical effects or shape modes were observed in our optical recordings. The initial bubble radius found in each movie was determined as the median radius over the first 5 frames prior to ultrasound exposure, and the bubble radius that was retained is the median of these individual radii.
3.2 Numerical methods
Fitting eqn (3) to the experimental data requires a minimum of 3 fitting parameters: G, μ, and Pac. The former two are the sought-after quantities. The latter is a non-negligible experimental uncertainty. The local driving pressure Pac is indeed not known precisely in the hydrogel. This is due, first, to the calibration of the needle hydrophone which are accurate within 20%, and second, due to transmission into the hydrogel (at an incidence angle of ∼45° and refraction).The experimental data was fitted to eqn (3) using the nonlinear optimization routine lsqnonlin in Matlab in 4 steps. The first step allows to find a coarse estimate of the global minimum by smoothing the data with a shape-preserving spline (see Fig. 3c), and fitting the linearized version of eqn (3) for small relative oscillation amplitude x ≪ 1:
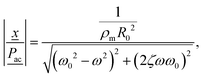 | (5) |
In all cases, the residual was defined as the experimental resonance curve, i.e., bubble oscillation amplitude versus ultrasound transmit frequency, minus the computed resonance curve. Since (i) the method is narrow-band by design and (ii) the transducer output tends to be distorted at the edge of its bandwidth, the residual was weighted by an envelope that was constructed based on the frequency range used in the measurement:
 | (6) |
The 95% confidence intervals of the fitted parameters were determined using the Jacobian returned by lsqnonlin, and the function nlparci. These confidence intervals are given as error bars in Fig. 5.
The effect of the uncertainty caused by an error in determining R0 was assessed by repeating the fitting procedure with radii lower or higher that the measured radius by ±5 and ±10%. Note that the radii extracted from the optical measurements match the size measured using the Coulter Counter and that the size distribution has a polydispersity index (PDI) of 5%.
The other parameters needed to solve eqn (3) and (5) are: P0 = 105 Pa, ρm = 103 kg m−3, γ = 1.07 for C4F10 and σ(R ≫ R0) = 72 mN m−1. The shell parameters for our typical microbubbles are κs = 6 × 10−9 kg s−1, χ = 0.5 N m−1 and σ(R0) = 0 mN m−1.
4 Results
Fig. 3a shows a typical R(t) curve recorded for a frequency of 2.2 MHz and a pressure of 100 kPa in the soft hydrogel. The black dots are the recorded frames and the solid blue line is a spline interpolation for visualization. The corresponding frequency spectrum is shown in Fig. 3b.The resonance curves recorded for transmitted pressures ranging from 70 to 120 kPa in steps of 10 kPa are plotted in Fig. 3c. Each curve is constructed from 41 individual recordings of the very same bubble at different driving frequencies. Fig. 3c shows both the recorded data points, and a shape-preserving spline smoothing for visualization, which shows clearly the main features of the resonance curves, and the pressure dependency. A calculated resonance curve for a 1.7 µm coated bubble in water is also shown by the dashed blue line. As compared to water, the presence of the hydrogel increases the resonance frequency of the bubble by about 26% and decreases the radial excursion amplitude by about 47%. Note that, although an amplitude of oscillation on the order of 0.25 times the resting radius may seem large for the regime of linear elasticity, Gaudron et al.19 have demonstrated that the approximation is still valid.
The fitted values for the shear modulus G, the viscosity μ resulting from the nonlinear root mean square optimization, and the acoustic pressure Pac for both hydrogels are plotted in Fig. 5a–c, respectively, as a function of the driving pressure. The error bars and shaded areas represent the 95% confidence interval for the fitted values. Fig. 5d shows the root mean square error of the best linear and nonlinear fits which are 11.0 ± 1.5 nm (mean and standard deviation) for the soft hydrogel and 10.0 ± 0.3 nm for the stiff hydrogel. Fig. 5a–c show that both linear and nonlinear fits predicts a very reproducible values across driving pressures. More specifically, for the soft hydrogel the nonlinear fit predicts a storage modulus of 61.7 ± 12 kPa while the linear fit predicts a storage modulus of 98.5 ± 14.5 kPa. Thus, while both fits feature a low residual root mean square error, these differences demonstrate the importance of using the full nonlinear equation for fitting the resonance curves. The difference between both fits in terms of viscosity is within the error margins, with μ = 3.3 ± 1.2 mPa s predicted by the nonlinear fit. For the stiff hydrogel, the nonlinear fit predicts G = 433 ± 55 kPa, against G = 484 ± 56 kPa for the linear fit, and μ = 15.7 ± 4.3. Fig. 5c shows that the ratio of the fitted acoustic pressure to the calibration pressure are 1.45 ± 0.08 and 0.72 ± 0.02. Within the confidence intervals, this ratio is constant across all applied pressures.
Since the resting radius of the bubble is extracted from diffraction-limited optical measurements, an unavoidable error in associated with its determination due to a combination of diffraction and unknown optical transfer function of the microscope objective. As we will see, this is the main confounding factor of this measurement and therefore deserves a dedicated discussion. To quantitatively evaluate the importance of R0, we have both increased and decreased it by 5 and 10% before repeating the fitting procedure. Fig. 6 shows the result and displays the same quantities as Fig. 5 but this time as a function of the initial bubble radius. The error bars represent the standard deviation of the values across the applied acoustic pressures. The RMS error (see Fig. 6d) shows no visible influence of the initial bubble radius, suggesting that the fits are of equally good quality in all cases. The storage modulus G and the viscosity μ depend quasi-linearly on the initial radius chosen for the fit. For the soft hydrogel and the nonlinear fit, G and μ feature linear regression coefficients of 303 kPa µm−1 and 7.7 mPa s µm−1, respectively (with adjusted coefficients of determination R2 of 0.996 and 0.999, respectively), see Fig. 6a and b. For the stiff hydrogel, these coefficients become 787 kPa µm−1 and 21.5 mPa s µm−1 for G and μ, respectively (with adjusted coefficients of determination R2 of 0.998 and 0.998, respectively). A ±5% error in the measurement of the initial bubble radius thus represents an error, for G and μ, of ±25 kPa and ±0.65 mPa s in the soft gel, and of ±89 kPa and ±2.4 mPa s in the stiff gel. The uncertainty in R0 is thus larger than both the confidence intervals of the fits in the soft gel, and comparable to it in the stiff gel. The outcome of the linear fit show similar behavior, still with a larger prediction for G.
 | ||
| Fig. 6 (a) Fitted values of G as a function of the resting radius of the bubble used for the fit. R0,fit is the radius used for the fitting procedure, and R0,meas is the radius measured optically. (b) Viscosity extracted from the fit. (c) Ratio of the fitted acoustic pressure to the expected acoustics pressure based on the transducer calibration performed in water. (d) Root mean square error in nanometers corresponding to the best linear and nonlinear fits. The error bars (and shadowed region) the standard deviation of the predictions as a function of the acoustic pressure (see Fig. 5). | ||
For direct comparison, hydrogels produced with the same protocol were also characterized at low shear rates (<16 s−1) using a rotational rheometer. Fig. 7 provides the result for a 5% strain for the soft and stiff hydrogel. The mean values of the storage modulus are G′ = 74 kPa and 144 kPa, respectively. The blue solid lines represent the expected G′ behavior within a Kelvin–Voigt model. Finally, the red dashed lines represent the expected G″ for a viscosity equal to that of water which is the minimum loss modulus that can be expected for these water-based hydrogels.
Fig. 7 shows the values of G′ for a strain rate on the order of 106 s−1 for the soft (Fig. 7a) and the stiff (Fig. 7b) hydrogels. For these specific hydrogels, these values are comparable to those obtained in the low-frequency range. The horizontal error bars of optical measurements correspond to the full width half maximum of the envelop used for the residual in the fit. The vertical error bars are the accumulated error margins, i.e., the sum of the standard deviation across the different transmitted pressures, of the 95% confidence intervals, and of the uncertainty caused by a ±5% uncertainty in R0. Interestingly, the relative uncertainty in the stiff gel is lower than in the soft gel: ±33% and ±43% for G′ and G″, respectively, in the stiff gel versus ±62% and ±58%, respectively, in the soft gel. While G′ shows little frequency dependency, G″ = μω is 3 orders of magnitude larger in the MHz range than at low-strain rates. At high frequencies, G″ exhibits a behavior similar to that of water, but differs significantly from it at low frequencies.
5 Discussion and conclusion
It is important to note that, while soft tissues and associated therapies are a motivation for this proof-of-concept study and that there remains a significant gap between the simple hydrogels we use here, and soft tissues that present inhomogeneities on multiple scales, i.e., from smaller than the bubble size (collagen matrix, organelles, etc.) to that larger than the bubble scale (cells, vessels, etc.). It remains to be seen to what extent tissue may be considered as a continuous medium, and the quality of the information that can be extracted from such a model. The complexity of tissue may ultimately require a statistical description within a 3D model of tissue as an inhomogeneous medium.Underestimating R0 will lead to an underestimation of G, since eqn (4), where 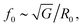 and to an underestimation of μ since the damping (derived from eqn (3)) has the shape
and to an underestimation of μ since the damping (derived from eqn (3)) has the shape  . A similar observation can be made in Fig. 6. This effect is stronger than the uncertainty on the driving pressure. The initial radius R0 is defined as the radius of the bubble measured at the start of the experiments, assuming that the system is perfectly at rest and not pre-constrained. However, the resting radius of the bubble slightly decreases during the measurement. There is thus a build-up of stress around the bubble. This stress can be expressed as an additional pressure term
. A similar observation can be made in Fig. 6. This effect is stronger than the uncertainty on the driving pressure. The initial radius R0 is defined as the radius of the bubble measured at the start of the experiments, assuming that the system is perfectly at rest and not pre-constrained. However, the resting radius of the bubble slightly decreases during the measurement. There is thus a build-up of stress around the bubble. This stress can be expressed as an additional pressure term  . For instance, in the soft hydrogel measurements, the initial radius was approximately 1.69 µm in the first measurement (Pac = 70 kPa), and dropped to approximately 1.66 µm in the last measurement (Pac = 120 kPa). While in principle it is easy to incorporate this factor into the simulations, it requires accurate sizing which in the present case was limited by the optical imaging system.52
. For instance, in the soft hydrogel measurements, the initial radius was approximately 1.69 µm in the first measurement (Pac = 70 kPa), and dropped to approximately 1.66 µm in the last measurement (Pac = 120 kPa). While in principle it is easy to incorporate this factor into the simulations, it requires accurate sizing which in the present case was limited by the optical imaging system.52
Each bubble is exposed to 41 ultrasound pulses for each driving frequency, as shown in Fig. 3c. It is therefore possible that the composition of the bubble gas core changes over time as a result of diffusive processes, e.g., that C4F10 is partly replaced by air, thereby changing the polytropic exponent γ, see eqn (2). A 10% decrease in γ will yield a prediction error of about 7 kPa for G, based on eqn (4), notably from the first term. However, this potential error is less than 10%, even in the soft hydrogel.
The measurement concept proposed here makes use of the resonant response of microbubbles. The resonance is essential to be able to accurately fit the data and extract the viscoelastic parameters of the hydrogel. Thus, this method cannot be applied to viscoelastic media that feature a strongly increasing loss modulus at high strain rates, like e.g. PDMS, since this leads to overdamped bubble dynamics.53 Likewise, it is not a priori clear whether all tissues will allow resonant oscillations in the MHz range.23
The study, while relying on optical methods, also opens possibilities to characterize opaque materials, such as soft tissues, where the resonance curves may be obtained through acoustic attenuation or acoustic scattering instead.10 Our approach assumes that the viscoelastic material is homogenous on the scale of the microbubble. The microstructure of hydrogels comprises pores of the order of 1 nm54–56 which justifies the assumption. Furthermore, our experiments show none of the symmetry breaking in the bubble dynamics that would be expected from the presence of larger pore sizes, i.e. of the order of the bubble size.
Using both experimental and numerical methods, we have successfully used monodisperse, phospholipid-coated microbubbles to measure the storage and loss moduli of hydrogels at MHz strain rates. While these results on simple hydrogels do not translate directly to the complex nature of real tissue, we believe these results may be relevant to the future development of methods for quantifying tissue rheology.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting the findings of this study are available from the corresponding author upon request.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme UCOM Ultrasound Cavitation in Soft Materials under the Skłodowska-Curie grant agreement no. 813766. The authors also acknowledge funding from the 4TU Precision Medicine program supported by High Tech for a Sustainable Future. G. L. also acknowledges funding from the European Union (ERC Starting Grant Super-FALCON, project number 101076844). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. Nathan Blanken's contribution to our paper is deeply appreciated. His thoughtful discussions and readiness to help have greatly benefited our work.References
- E. Stride, T. Segers, G. Lajoinie, S. Cherkaoui, T. Bettinger, M. Versluis and M. Borden, Ultrasound Med. Biol., 2020, 46, 1326–1343 CrossRef.
- S. Roovers, T. Segers, G. Lajoinie, J. Deprez, M. Versluis, S. C. De Smedt and I. Lentacker, Langmuir, 2019, 35, 10173–10191 CrossRef CAS.
- C. S. Lee and K. W. Leong, Curr. Opin. Biotechnol, 2020, 66, 78–87 CrossRef CAS PubMed.
- K. F. Timbie, B. P. Mead and R. J. Price, J. Controlled Release, 2015, 219, 61–75 CrossRef CAS PubMed.
- K. Sarkar, A. Katiyar and P. Jain, Ultrasound Med. Biol., 2009, 35, 1385–1396 CrossRef PubMed.
- J. J. Kwan and M. A. Borden, Soft Matter, 2012, 8, 4756–4766 RSC.
- M. Versluis, E. Stride, G. Lajoinie, B. Dollet and T. Segers, Ultrasound Med. Biol., 2020, 46, 2117–2144 CrossRef.
- S. M. van der Meer, B. Dollet, M. M. Voormolen, C. T. Chin, A. Bouakaz, N. de Jong, M. Versluis and D. Lohse, J. Acoust. Soc. Am., 2007, 121, 648–656 CrossRef CAS PubMed.
- J. Sijl, M. Overvelde, B. Dollet, V. Garbin, N. de Jong, D. Lohse and M. Versluis, J. Acoust. Soc. Am., 2011, 129, 1729–1739 CrossRef PubMed.
- T. Segers, P. Kruizinga, M. P. Kok, G. Lajoinie, N. de Jong and M. Versluis, Ultrasound Med. Biol., 2018, 44, 1482–1492 CrossRef.
- B. Dollet, P. Marmottant and V. Garbin, Annu. Rev. Fluid Mech., 2019, 51, 331–355 CrossRef.
- P. A. Dayton, J. E. Chomas, A. F. Lum, J. S. Allen, J. R. Lindner, S. I. Simon and K. W. Ferrara, Biophys. J., 2001, 80, 1547–1556 Search PubMed.
- S. Qin and K. W. Ferrara, Ultrasound Med. Biol., 2007, 33, 1140–1148 CrossRef PubMed.
- N. Hosseinkhah and K. Hynynen, Phys. Med. Biol., 2012, 57, 785–808 Search PubMed.
- C. Chen, Y. Gu, J. Tu, X. Guo and D. Zhang, Ultrasonics, 2016, 66, 54–64 Search PubMed.
- C. F. Caskey, S. M. Stieger, S. Qin, P. A. Dayton and K. W. Ferrara, J. Acoust. Soc. Am., 2007, 122, 1191–1200 Search PubMed.
- A. Jamburidze, M. De Corato, A. Huerre, A. Pommella and V. Garbin, Soft Matter, 2017, 13, 3946–3953 RSC.
- E. Vlaisavljevich, K.-W. Lin, M. T. Warnez, R. Singh, L. Mancia, A. J. Putnam, E. Johnsen, C. Cain and Z. Xu, Phys. Med. Biol., 2015, 60, 2271 CrossRef PubMed.
- R. Gaudron, M. Warnez and E. Johnsen, J. Fluid Mech., 2015, 766, 54–75 CrossRef CAS.
- J. S. Allen and R. A. Roy, J. Acoust. Soc. Am., 2000, 107, 3167–3178 Search PubMed.
- J. S. Allen and R. A. Roy, J. Acoust. Soc. Am., 2000, 108, 1640–1650 CrossRef CAS.
- E. Stride and N. Saffari, Ultrasound Med. Biol., 2004, 30, 1495–1509 CrossRef.
- A. T. Oratis, K. Dijs, G. Lajoinie, M. Versluis and J. H. Snoeijer, J. Acoust. Soc. Am., 2024, 155, 1593–1605 Search PubMed.
- J. B. Estrada, C. Barajas, D. L. Henann, E. Johnsen and C. Franck, J. Mech. Phys. Solids, 2018, 112, 291–317 CrossRef.
- H. S. Fogler and J. D. Goddard, Phys. Fluids, 1970, 13, 1135–1141 Search PubMed.
- A. Niederquell, A. C. Völker and M. Kuentz, Int. J. Pharm., 2012, 426, 144–152 CrossRef CAS.
- Z. Xing, A. Caciagli, T. Cao, I. Stoev, M. Zupkauskas, T. O’Neill, T. Wenzel, R. Lamboll, D. Liu and E. Eiser, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8137–8142 Search PubMed.
- V. Bertin, Z. Zhang, R. Boisgard, C. Grauby-Heywang, E. Raphaël, T. Salez and A. Maali, Phys. Rev. Res., 2021, 3, L0–32007 Search PubMed.
- K. Murakami, Y. Yamakawa, J. Zhao, E. Johnsen and K. Ando, J. Fluid Mech., 2021, 924, A38 Search PubMed.
- T. Deffieux, G. Montaldo, M. Tanter and M. Fink, IEEE Trans. Med. Imaging, 2008, 28, 313–322 Search PubMed.
- K. Nightingale, Curr. Med. Imaging Rev., 2011, 7, 328–339 CrossRef.
- H. Koruk, A. El Ghamrawy, A. N. Pouliopoulos and J. J. Choi, Appl. Phys. Lett., 2015, 107, 223701 CrossRef.
- S. Catheline, J.-L. Gennisson, G. Delon, M. Fink, R. Sinkus, S. Abouelkaram and J. Culioli, J. Acoust. Soc. Am., 2004, 116, 3734–3741 CrossRef CAS PubMed.
- A. Prosperetti, Phys. Fluids, 1982, 25, 409–410 CrossRef.
- T. Leighton, The Acoustic Bubble, Academic Press, 2012 Search PubMed.
- T. Leighton, Ultrasonics, 2008, 48, 85–90 CrossRef CAS PubMed.
- A. Prosperetti, L. A. Crum and K. W. Commander, J. Acoust. Soc. Am., 1988, 83, 502–514 Search PubMed.
- P. Marmottant, S. van der Meer, M. Emmer, M. Versluis, N. de Jong, S. Hilgenfeldt and D. Lohse, J. Acoust. Soc. Am., 2005, 118, 3499–3505 CrossRef CAS.
- T. Segers, E. Gaud, M. Versluis and P. Frinking, Soft Matter, 2018, 14, 9550–9561 Search PubMed.
- E. Brujan, Cavitation in Non-Newtonian Fluids: With Biomedical and Bioengineering Applications, Springer Berlin Heidelberg, 2011 Search PubMed.
- H. Barnes, I. of Non-Newtonian and F. Mechanics, A Handbook of Elementary Rheology, University of Wales, Institute of Non-Newtonian Fluid Mechanics, 2000 Search PubMed.
- C. Devin Jr, J. Acoust. Soc. Am., 1959, 31, 1654–1667 CrossRef.
- J. Sijl, B. Dollet, M. Overvelde, V. Garbin, T. Rozendal, N. de Jong, D. Lohse and M. Versluis, J. Acoust. Soc. Am., 2010, 128, 3239–3252 Search PubMed.
- J. Liu, H. Zheng, P. S. Poh, H.-G. Machens and A. F. Schilling, Int. J. Mol. Sci., 2015, 16, 15997–16016 Search PubMed.
- P. A. Janmey and R. T. Miller, J. Cell Sci., 2011, 124, 9–18 Search PubMed.
- B. Van Elburg, G. Collado-Lara, G.-W. Bruggert, T. Segers, M. Versluis and G. Lajoinie, Rev. Sci. Instrum., 2021, 92, 035110 CrossRef CAS.
- T. Segers, L. de Rond, N. de Jong, M. Borden and M. Versluis, Langmuir, 2016, 32, 3937–3944 CrossRef CAS PubMed.
- T. Segers, E. Gaud, G. Casqueiro, A. Lassus, M. Versluis and P. Frinking, Appl. Phys. Lett., 2020, 116, 173701 CrossRef CAS.
- A. S. Mikhail, A. H. Negussie, C. Graham, M. Mathew, B. J. Wood and A. Partanen, Med. Phys., 2016, 43, 4304–4311 CrossRef CAS.
- A. H. Negussie, A. Partanen, A. S. Mikhail, S. Xu, N. Abi-Jaoudeh, S. Maruvada and B. J. Wood, Int. J. Hyperthermia, 2016, 32, 239–243 Search PubMed.
- G. Lajoinie, Y. Luan, E. Gelderblom, B. Dollet, F. Mastik, H. Dewitte, I. Lentacker, N. de Jong and M. Versluis, Commun. Phys., 2018, 1, 22 Search PubMed.
- C. A. Sennoga, J. S. Yeh, J. Alter, E. Stride, P. Nihoyannopoulos, J. M. Seddon, D. O. Haskard, J. V. Hajnal, M.-X. Tang and R. J. Eckersley, Ultrasound Med. Biol., 2012, 38, 834–845 CrossRef.
- M. Bruning, M. Costalonga, J. Snoeijer and A. Marin, Phys. Rev. Lett., 2019, 123, 214501 CrossRef CAS PubMed.
- M. Kremer, E. Pothmann, T. Roessler, J. Baker, A. Yee, H. Blanch and J. M. Prausnitz, Macromolecules, 1994, 27, 2965–2973 CrossRef CAS.
- L. M. Lira, K. A. Martins and S. I. Córdoba de Torresi, Eur. Polym. J., 2009, 45, 1232–1238 CrossRef CAS.
- N. L. Cuccia, S. Pothineni, B. Wu, J. Méndez Harper and J. C. Burton, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11247–11256 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |






