π–hole forces enabled programmable supramolecular chirality based on a chiral benzimidazole pincer

Abstract

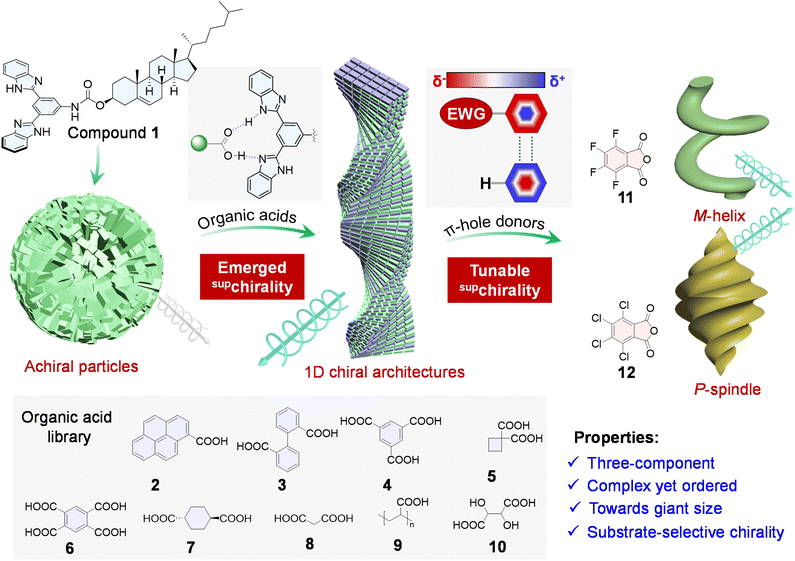
Employing noncovalent forces to fabricate self-assembled nanoarchitectures composed of multiple constituents regulates the expression of chirality across hierarchical levels. Here we report a programmed hierarchical chiral assembly through π–hole interactions synchronized with hydrogen bonding. A chiral molecular pincer composed of benzimidazole and cholesteryl moieties capable of forming complementary hydrogen bonds with carboxylic acids, coassembles with achiral organic acids to generate one-dimensional helical superstructures, enhancing the expression of supramolecular chirality and chiroptical activities. The multicomponent coassembly system accommodates structurally diverse acids-including aliphatic, aromatic, and polymeric acids-exhibiting pronounced substrate-dependent induction of supramolecular chirality. Further incorporating fluorinated or chlorinated components introduced π–hole forces that realize modulation of the macroscopic chirality, affording well-defined chiral microarchitectures with tunable topology and chirality. The resulting materials display complex yet highly ordered chiral nanostructures, with the potential for anisotropic growth toward macroscopic scales. This study establishes a modular platform for the high-throughput fabrication of chiroptical materials with tunable supramolecular chirality, offering insights into the rational design of functional soft materials through π–hole interaction driven hierarchical self-assembly.

---

Introduction

The construction of complex yet ordered chiral organic assemblies offers profound potential for chiral recognition,^1–3 asymmetric catalysis,^4,5 and chiroptical materials.^6–10 With the continuous development of the field of chiral nanomaterials, the application of metal nanoparticles, biopolymers, and synthetic polymers enables more precise control over the size and morphology of nanomaterials.^11–19 By integrating a diverse array of structurally and functionally distinct components, the emergence of intricate chiral behaviors through enhanced molecular cooperativity is facilitated. However, several challenges complicate their synthesis and application. For instance, the underlying mechanisms for chirality transfer and amplification remain poorly understood, making it difficult to reliably transfer molecular chirality into macroscopic helical architectures.^20,21 The competitive nature of non-covalent interactions in these systems exacerbates polymorphism, further impeding structural precision with less phase purity.

Weak non-covalent interactions such as hydrogen bonding, π–π stacking, and van der Waals forces have long been employed in the design of chiral supramolecular assemblies due to their reversibility and adaptability.^22–29 Assemblies based on these interactions offer significant advantages in terms of responsiveness and programmability, making them ideal candidates for designing dynamic, tunable functional materials.^30–37 The directionality and specificity affect the competitive binding between components that further compromises the accuracy and fidelity of the desired structures, presenting a significant barrier to the precise construction of chiral complex architectures. The π–hole interaction, an emerging class of non-covalent forces driven by π–hole donors, offers a promising strategy for overcoming the limitations associated with traditional weak interactions.^38–46 These interactions, characterized by their directional nature and electronic selectivity, allow for the formation of specific and stable non-covalent bonding between electron-rich acceptors (normally polyaromatic hydrocarbons) and electron-deficient donors. Importantly, π–hole interactions maintain the desirable flexibility of weak interactions while providing enhanced stability and fine-tuned control over assembly processes. Consequently, their incorporation into the design of complex chiral systems presents an innovative approach for achieving precise chirality transfer and topological control.

In this study, facilitated by π–hole interaction, we demonstrate a programmable three-component supramolecular co-assembly strategy to construct complex and ordered chiral structures. Compound 1 is a benzimidazole-based pincer molecule functionalized with a cholesteryl group, which self-assembles individually into non-chiral vesicular particles (Scheme 1). Upon the introduction of various achiral organic acids (compounds 2–10), directional and complementary hydrogen bonds between the carboxylic acids and the benzimidazole units induce a transition from achiral aggregates to one-dimensional chiral nanohelices, successfully inducing supramolecular chirality. To better realize a programmable co-assembly strategy, the third components, π–hole interaction donors (compounds 11 and 12), were introduced. These donors engage in π–hole/π interactions, leading to the successful construction of three-component assembly systems that generate cross-scale supramolecular chirality. Specifically, the introduction of π–hole interactions facilitates the formation of micro-chiral structures. Compound 11 favors the formation of M-helices, while compound 12 induces P-spindles, enabling tunable macroscopic chirality. Through electronic effects, complex yet ordered supramolecular three-component assemblies with selective co-assembly are achieved. This cross-scale chirality modulation demonstrates the transition from nano- to micron scales, highlighting the unique role of π–hole interactions in constructing large-scale chiral structures. The study emphasizes the synergistic roles of hydrogen bonding and π–hole interactions in the design of advanced supramolecular materials with programmable/customizable chiroptical properties, particularly in driving the formation of microscale chiral structures.

Scheme 1 Molecular structures of compound 1, achiral acids (2–10), and π–hole donors (11, 12), accompanied by the evolution of chiroptical properties and supramolecular architectures throughout the coassembly process.

Results and discussion

The synthesis of host molecule 1 is detailed in the SI. Compound 1, a benzimidazole-based pincer molecule functionalized with a cholesteryl group, was synthesized via a condensation reaction followed by conjugation. Its structure was confirmed by ¹H and ¹³C NMR spectroscopy and high-resolution mass spectrometry (HRMS) (Fig. S2–S4). The benzimidazole unit adopts a pincer-like conformation, enabling selective recognition of carboxylic acids through complementary hydrogen bonding (Fig. 1a). The formation of the 1·3 complex was confirmed by ¹H NMR spectroscopy. In CDCl₃, the H_a proton within the benzimidazole core exhibited a downfield shift (Δδ = 0.045 ppm), while peripheral protons (e.g., H_e–h) showed upfield shifts, indicating complex formation. This was further validated by HRMS (Fig. 1b), where the isotopic distribution matched the simulated pattern. Two-dimensional nuclear Overhauser effect spectroscopy (NOESY) (Fig. 1c) revealed NOE cross-peaks, such as H_f–H_c, H_e–H_c, H_e–H_b, and H_a–H_e, reflecting spatial proximity between the host and guest molecules. ¹H NMR titration experiments (Fig. 1d and S5) showed gradual downfield shifts of the H_a proton upon adding the guest, with a maximum shift of 0.3 ppm. Binding constants were determined using a 1 : 1 binding model, yielding values of 10² to 10³ M⁻¹, indicating strong affinities that overcome solvation effects in CDCl₃.

Fig. 1 (a) Representation of the hydrogen bonded complexation and ¹H NMR comparison of the 1·3 system measured in CDCl₃ with 5 vol% CD₃OD. (b) HRMS of 1·2 and 1·3 with different binding ratios. (c) 2D NOSEY NMR spectrum of 1·3 (1 : 2 by molar ratio). Red cycles mark the NOE signals of protons from different species measured in CDCl₃ with 5 vol% CD₃OD. (d) ¹H NMR titration of 1·7 in CDCl₃ with 5 vol% CD₃OD. (e) Fitted ¹H NMR curves with the calculated apparent binding constant K for 1·3 and 1·7 respectively. (f) Computational results of supramolecular complexation between 1 and acids. Energy minimalized structures of 1·3 and 1·7 with 1 : 1 and 2 : 1 binding stoichiometry. Green dashed lines represent the observed hydrogen bonds. (g) MD results. Atomic numbering of 1 and 1·3 as well as the RDF profiles. Number of hydrogen bonds as functions of equilibrium time in 1·3.

Density functional theory (DFT) calculations (Fig. 1f) provided further insights into the complexation. The optimized geometries for the 1·3 and 1·7 complexes revealed energetically favorable duplex hydrogen bond formation, with bond angles of approximately 160° and hydrogen bond distances of 1.79 and 1.94 Å. The 2 : 1 complexation mode was also thermodynamically favorable, especially for smaller acids like 7, which promotes internal stacking of benzimidazole units. The binding energies for 1·3 and 1·7 were −18.4 and −20.3 kcal mol⁻¹, respectively, in the 1 : 1 mode, and −37.8 and −41.2 kcal mol⁻¹ in the 2 : 1 mode, indicating synergistic effects (Fig. 1f and S6). Noncovalent interaction (NCI)⁴⁷ analysis (Fig. S7 and S8) showed attractive interactions (blue regions) between complementary hydrogen bonding sites and van der Waals interactions between host and guest molecules, critical for stabilizing the supramolecular complex.

Molecular dynamics (MD) simulations explored the aggregation behavior of compound 1 with various acids. Spontaneous aggregation occurred within a 15 ns equilibrium period, with the system reaching equilibrium within 1 ns (Fig. S9). Radial distribution functions (RDFs) revealed that hydrogen bonds between imidazole and carbamate groups drove aggregation, forming multi-layered vesicles. Upon introducing acid 3, duplex hydrogen bonds were observed, consistent with DFT-optimized structures. The number of hydrogen bonds increased in the 1·3 complex, indicating coassembly rather than self-sorting. Solvent-accessible area (SAA) analysis (Fig. 1g and S10) quantified aggregation. SAA values decreased and plateaued after 10 ns during the self-assembly of compound 1. Introducing acids 3, 7, and 9 showed similar trends, with the rate of decrease following: 7 > 3 > 9. Polyacrylic acid (9) inhibited coassembly, in line with experimental results. These findings highlight the crucial role of hydrogen bonding in driving chiral coassembly.

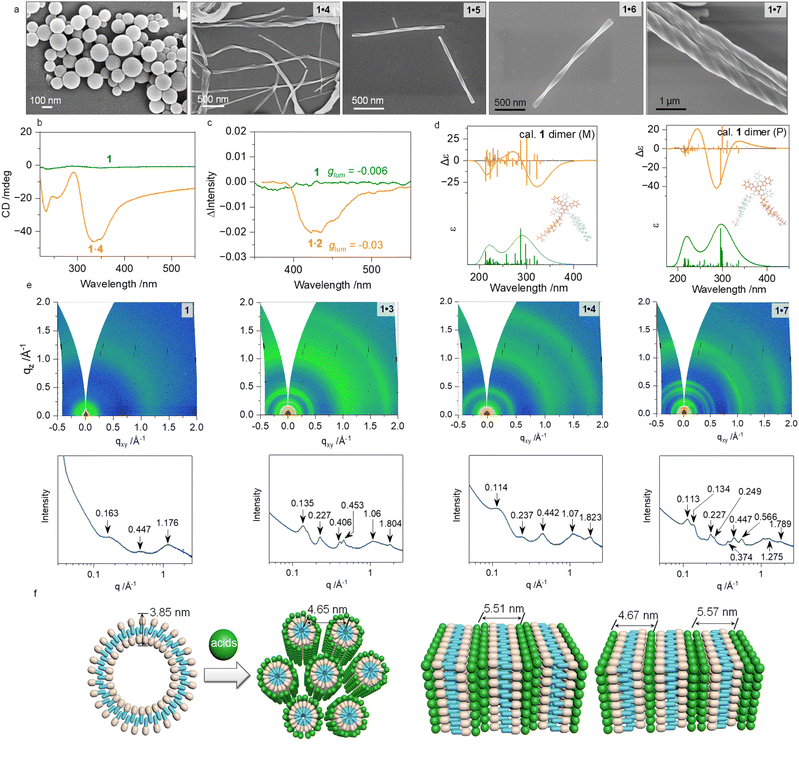
This section focuses on the self-assembly process of 1 in aqueous media. Initially dissolved in tetrahydrofuran (THF), 1 and corresponding acids were mixed with water, with the water fraction (f_w) controlled to be between 70 and 90 vol%. After incubation, water induced the formation of self-assembled dispersions, which were analyzed using TEM and SEM. Across various concentrations and solvent ratios, 1 formed nanoparticles of 100–200 nm (Fig. 2a, S11 and S12). The TEM images revealed hollow vesicles, attributed to the amphiphilic nature of compound 1, facilitated by cholesteryl groups. Upon interaction with carboxylic acids, liposomal nanoparticles transformed into 1D nanostructures, with helices exhibiting supramolecular chirality. These helices, typically P-handed, had diameters of hundreds of nanometers and lengths up to several micrometers, as confirmed by SEM and TEM (Fig. 2a and S13–S37). The cholesteryl domains governed chirality, with acids enhancing amphiphilicity to promote helical growth.

Fig. 2 (a) SEM images of 1 (f_w = 80 vol%), 1·4 (f_w = 70 vol%, 1 : 0.66), 1·5 (f_w = 80 vol%, 1 : 0.5), 1·6 (f_w = 80 vol%, 1 : 1), and 1·7 (f_w = 80 vol%, 1 : 1) respectively. (b) Representative CD spectra of self-assembled compound 1 (1 mM) as well as the coassembly with 4; the molar ratio is 1 : 0.66; the water fraction is 70 vol%. (c) Representative CPL spectra of self-assembled compound 1 (0.1 mM) as well as the coassembly with 2; the molar ratio is 1 : 1; the water fraction is 80 vol%; λ_ex = 310 nm and 340 nm respectively. (d) Geometry optimized P- and M-dimers of 1 as well as their calculated ECD spectra. Basis set: B3LYP/6-311G(d). (e) GIXS patterns and corresponding integral peaks for 1 (f_w = 80 vol%, 1 mM), 1·3 (f_w = 80 vol%, 1 : 1) 1·4 (f_w = 80 vol%, 1 : 1) and 1·7 (f_w = 80 vol%, 1 : 1) coassemblies respectively. (f) Schematic representation of the self-assemblies deduced from GIXS and nanomorphology. [1] = 1 mM.

The circular dichroism (CD) and circularly polarized luminescence (CPL) spectra of the coassemblies (Fig. 2b and S39) reveal that compound 1 itself is CD-silent; however, its coassemblies display pronounced CD activity with a well-defined P-handed chiral morphology. As shown in Fig. S38, both compound 1 and the 1·2 assembly exhibit appreciable fluorescence, and importantly, both systems also display detectable CPL activity. Upon coassembly with compound 2, the luminescence dissymmetry factor (g_lum) of compound 1 increases markedly from −0.006 to −0.03 (Fig. 2c), demonstrating a substantial enhancement in chiral transfer. Taken together, these optical signatures provide clear and consistent evidence that the coassembly process effectively induces and amplifies supramolecular chirality. Time-dependent density functional theory (TDDFT) calculations of P- and M-dimer models (Fig. 2d) showed exciton-type bands for the P-dimer, consistent with the chirality transfer from molecular to supramolecular scales. To probe molecular packing, we conducted grazing incident X-ray scattering (GIXS) measurements on thin-film samples. As shown in Fig. 2e and f, individual compound 1 shows only broad humps at 0.163, 0.447, and 1.176 Å⁻¹, indicating a near-amorphous structure with a bilayer spacing of 3.85 nm, consistent with its CD-silent behavior and TEM results. Coassembly with organic acids induces pronounced structural changes. The intensified and newly appearing peaks on both Q_z and Q_xy axes reveal the formation of well-defined ordered arrangements and fibrous assemblies. For 1·3, peaks at 0.135, 0.227, and 0.406 Å⁻¹ (1 : √3 : 3) indicate hexagonal packing with a 4.65 nm lattice parameter-0.8 nm larger than that of 1 due to acid insertion. Assembly 1·4 exhibits a phase-pure lamellar structure (1 : 2 : 3) with a layer spacing of 5.51 nm, while 1·7 displays mixed lamellar phases (4.67 and 5.57 nm). Additionally, coassemblies show two characteristic Q_xy bands near 1.0 and 1.8 Å⁻¹, corresponding to distorted rectangular packing along the fiber axis. Overall, GIXS confirms that organic acids induce ordered molecular packing, consistent with the observed chiroptical activity and nanohelical morphologies.

We next examined whether polymeric acids could coassemble with compound 1 to generate a preferred screw sense and chiroptical activity. Polymer 9, with an average degree of polymerization of 28, was selected. Although its multiple carboxylic acid units could introduce steric hindrance to ordered packing, clear helical structures were observed under TEM at 90 vol% water (Fig. 3a and b). These helical nanorods-hundreds of nanometers long and about 100 nm in diameter-arise from the cooperative coassembly of 1·9 and differ markedly from assemblies formed with small-molecule acids. Unlike 1·2 to 1·8, the 1·9 coassemblies are highly sensitive to water content. Lowering the water fraction from 90% to 80% or 70% caused the helical structures to disappear, leaving only self-sorted vesicles in TEM. CD spectra further confirm this solvent dependence (Fig. 3c): no cotton effects were detected at f_w = 70% or 80%, whereas strong negative CD bands near 350 nm appeared at higher water content, indicating that polymer 9 binds multiple units of compound 1 to form highly chiral supramolecular helices. Variable-temperature CD measurements were then performed to assess stability (Fig. 3d and e). Heating from 20 to 80 °C led to a gradual decrease in CD intensity, indicating partial disassembly, while cooling restored the signal with slight hysteresis, demonstrating reformation of the helical polymers. As hydrogen bonds between benzimidazole and carboxylic acids weaken at high temperatures, this reversible thermal response highlights the potential of these assemblies as stimuli-responsive supramolecular polymer materials.

Fig. 3 (a and b) TEM images of 1·9 coassemblies (c = 1 mM, ratio = 1 : 5, based on the monomer, f_w = 90 vol%). (c) CD spectra of 1·9 coassemblies (1 : 5, based on the monomer). (d and e) Heating and cooling CD curves of 1·9 coassemblies. (f and g) SEM image of 1·^LTA (f_w = 70 vol%, 1 : 5 by molar ratio) coassemblies. [1] = 1 mM.

We investigated the coassembly of compound 1 with enantiopure acids to clarify whether chirality originates from the chiral acids or the cholesteryl unit. Across broad molar ratios (1 : 0–1 : 10) and various water fractions, no mirror-image CD signals were observed (Fig. S42 and S43), despite overall correlated CD features. This contrasts sharply with the coassembly of enantiopure 10 (TA) and achiral benzimidazoles, which showed perfect mirror CD curves. These findings indicate that the cholesteryl pendant strongly overrides the chiral influence of the acids, diminishing their ability to dictate supramolecular chirality. Consequently, chiral sensing or recognition is unlikely, as homochirality dominates the CD spectra.

Morphological analysis further confirms this: only left-handed (M) helices appear across all conditions, independent of the TA enantiomer. This M-homochirality is intriguing because other achiral acids induce opposite P-homochirality (Fig. S44 and S45), even though both systems remain governed by cholesteryl domains. Acid segments with higher hydrophilicity may therefore contribute to screw-sense selection, though the structural basis remains unclear.

Interestingly, the M-helices tend to curl into chiral toroids (Fig. 3f and g). While spontaneous toroid formation is often attributed to internal-stress release, our curled, disc-like toroids show well-aligned ∼10 nm substructures more clearly than the 1D fibers. This suggests that these substructures arise through primary aggregation and subsequently align into superhelical assemblies.

In addition to investigating the binary assembly properties of compound 1 with carboxylic acids, we successfully constructed a three-component assembly system by incorporating perfluorinated and chlorinated phthalic anhydride (11 and 12). The binding mode and binding strength of compounds 11 and 12 with 1 were examined through ¹H NMR titration (Fig. 4a–c). The strong electron-withdrawing effect introduced by perfluorination in 11 leads to the formation of a markedly deep π–hole region. In this context, the benzimidazole segment of 1 functions as an electron-rich π–hole acceptor, giving rise to a pronounced π–hole interaction between the two components. This interaction induces a deshielding effect, causing the chemical shift of H_a to progressively move downfield with increasing amounts of 11 (Fig. 4a). This observation is consistent with the electrostatic potential analysis: due to the much higher electronegativity of fluorine relative to chlorine, the π–hole at the center of the aromatic ring in 11 reaches an electrostatic potential of 34.09 kcal mol⁻¹ (Fig. 5a), indicating a deep and well-defined π–hole. In contrast, compound 12, bearing chlorine substituents, exhibits a significantly weaker electron-withdrawing capability. As a result, the decrease in electron density on the aromatic ring is much less pronounced and the π–hole formed is substantially shallower, with an electrostatic potential of only 23.74 kcal mol⁻¹ (Fig. 5a). Consequently, the interaction between 12 and 1 is dominated by weaker van der Waals forces rather than electrostatic π–hole contacts. This leads to a mild shielding effect on the protons, reflected by only a subtle upfield shift in the chemical shift of H_a (Fig. 4b and c). These analyses collectively demonstrate that the key distinction between the interactions of 11 and 12 with 1 lies in the dominant driving forces: a strong aromatic-perfluoroaromatic π–hole interaction in the case of 11, versus predominantly van der Waals interactions for 12.

Fig. 4 (a) ¹H NMR comparison of the 1·11 system measured in CDCl₃ with 5 vol% CD₃OD. (b) ¹H NMR comparison of the 1·12 system measured in CDCl₃ with 5 vol% CD₃OD. [1] = 1 mM. (c) The Δδ of H_a varies with different equivalents of 11 and 12. (d) XRD of 2 (f_w = 80 vol%, 0.1 mM), 11 (f_w = 80 vol%, 0.1 mM), 2·11 (f_w = 80 vol%, 1 : 1), 12 (f_w = 80 vol%, 0.1 mM), and 2·12 (f_w = 80 vol%, 1 : 1). (e) GIXS integral peaks for 1 (f_w = 80 vol%, 0.1 mM), 1·11 (f_w = 80 vol%, 1 : 1) 1·2 (f_w = 80 vol%, 1 : 1) and 1·2·11 (f_w = 80 vol%, 1 : 1 : 1) coassemblies respectively. (f) GIXS integral peaks for 1 (f_w = 80 vol%, 0.1 mM), 1·12 (f_w = 80 vol%, 1 : 1) 1·2 (f_w = 80 vol%, 1 : 1) and 1·2·12 (f_w = 80 vol%, 1 : 1 : 1) coassemblies respectively.

Fig. 5 (a) Electrostatic potential maps of 1, 11, and 12, as well as the DFT-optimized structures of the 1·11 and 1·12 complexes. (b) The interaction energies for the formation of the 1·11, 2·11, 1·12, and 2·12 complexes. (c) MD results. Aggregation behaviors within the simulation boxes at 0 ns and 15 ns for comparison. (d) RDF profiles of distances for the intermolecular interaction between 1·11, 2·11, 1·12 and 2·12.

Subsequently, we investigated the interactions between compounds 11, 12, and 2 in the solid state by employing powder X-ray diffraction (XRD). No new diffraction patterns were observed between 11 and 2 under the nanoprecipitation protocol. In this scenario, narcissistic aggregation might occur despite the strong π–hole forces between pyrenes and 11. However, in the system of 2·12, the individual characteristic diffraction peaks disappeared, and new bands appeared at 10.19°, 11.65°, and 26.62°, indicating the coassembly between 2 and 12 (Fig. 4d). To further explore the assembly properties of the ternary system, we conducted GIXS on the samples of 1·11, 1·2, and 1·2·11. Compound 1 exhibited a near-amorphous phase, while the 1·11 assembly displayed a lamellar morphology, with diffraction peaks at 0.189, 0.376, and 0.555 Å⁻¹, corresponding to a 1 : 2 : 3 ratio. Similarly, the 1·2 system showed peaks at 0.180, 0.374, and 0.540 Å⁻¹, also corresponding to a lamellar stacking structure with a D-spacing of 3.49 nm. In the ternary system (1·2·11), scattering peaks at 0.129, 0.182, and 0.375 Å⁻¹ were observed, confirming the presence of a block-like, partially narcissistic co-assembly structure (Fig. 4e). Considering the narcissistic behavior between 2 and 11, in the three-component system, 1 behaves as a molecular glue to combine 2 and 11 to afford a new phase. In Fig. 4f, the diffraction peaks observed for 1·12 at 0.188, 0.375 Å⁻¹, and 0.525 Å⁻¹ further validate the lamellar stacking structure, with an interlayer spacing of 3.34 nm. In 1·2·12, scattering peaks are distributed in a 1 : 2 : 3 ratio at 0.234, 0.467, and 0.706 Å⁻¹. However, the interlayer spacing in this system decreases to 2.68 nm, with a Δ = 0.66 nm, supporting a more compact packing arrangement among the three components.

To gain understanding of the interactions between 1·11 and 1·12, we employed DFT to calculate the electrostatic potential maps and energy-minimized structures of the binary systems.^48,49 As depicted in Fig. 5a, the benzimidazole region of 1 is electron-rich, with an electrostatic potential maximum of −15.94 kcal mol⁻¹. Both 11 and 12 possess π–hole regions at the center of the benzene ring, with slight differences due to the different electron-withdrawing/donating effects. Consequently, the electrostatic potential maxima in the benzene ring regions of 11 and 12 are 34.09 kcal mol⁻¹ and 23.74 kcal mol⁻¹, respectively. Furthermore, it is evident from the electrostatic potential map that the green region in 12 is significantly larger than the blue region, suggesting that 12 has a shallow and weak π–hole region, consistent with the experimental observation in ¹H NMR spectra.

In Fig. 5b, the interaction energies between 1 and 2 with 11 and 12 were calculated. The interaction energies for the pairs 1·11, 2·11, 1·12, and 2·12 were found to be −19.82, −21.42, −21.79, and −22.65 kcal mol⁻¹, respectively. These results indicate that 2 exhibits stronger binding affinities with both 11 and 12 compared to 1. In the ternary system, 1 and 2 engage in competitive interactions, as both can interact with 11 and 12. By comparing the binding energies of the two-component and three-component systems, we found that the binding energies of the 1·2, 1·11, 1·12, 1·2·11, and 1·2·12 complexes are −35.23, −19.82, −21.79, −49.97, and −47.97 kcal mol⁻¹, respectively (Fig. S55). These results clearly indicate that the three-component systems exhibit significantly stronger binding energies than the corresponding two-component systems, demonstrating that the three-component assemblies are thermodynamically more stable. To further investigate the assembly modes of the ternary system, we performed molecular dynamics (MD) simulations. Compounds 1, 2, and 11 were placed in a 10 × 10 × 10 nm³ box at a 1 : 1 : 1 molar ratio, with a total of 300 molecules in a water-filled box. Under the influence of the Amber03 force field, the system reached equilibrium after 15 ns (Fig. 5c). From the final equilibrium state, it is evident that the 1·2·11 system forms a ternary complex through mutual π–hole interactions. Similarly, the 1·2·12 system forms a ternary complex, where the interactions between 1 and 12, as well as between 12 and 2, are essential for the overall stability of the system. Subsequently, we employed radial distribution function (RDF) analysis to gain further insight into the intermolecular interactions within the ternary systems. As illustrated in Fig. 5d, both compounds 1 and 2 exhibit notable interactions with compound 11 in 1·2·11, with intermolecular distances of 3.73 Å and 3.74 Å, respectively. These distances provide direct evidence for the stable coexistence of all three components. The comparison of g(r) values reveals that the interaction between 2 and 11 is stronger than that between 1 and 11, in agreement with the calculated interaction energies presented in Fig. 5b. A similar interaction pattern is observed in the equilibrated 1·2·12, where an interaction distance of 3.80 Å supports the presence of compact molecular packing among 1, 2, and 12. Moreover, the competitive advantage of compound 2 over 1 in binding to 12 is clearly reflected in the relative g(r) intensities. Collectively, these computational findings provide compelling evidence for the specific pairwise interactions within the ternary systems and successfully elucidate the competitive binding dynamics that govern their assembly behavior.

Finally, SEM analysis was performed to elucidate the self-assembled morphologies of the systems (Fig. 6 and S47–S51). Compound 1 predominantly formed vesicular architectures with an average diameter of approximately 150 nm. Upon coassembly with compound 2, twisted rod-like nanostructures emerged, which can be attributed to the presence of intermolecular hydrogen-bonding interactions. In contrast, the combination of 1 with the π–hole donor 11 resulted in the formation of well-defined M-handed helical ribbons with widths of about 500 nm (Fig. S48). Notably, this morphological transformation was accompanied by a reversal in the CPL signal, and the g_lum value significantly increased to 2.0 × 10⁻², indicating a substantial enhancement in CPL performance. Interestingly, the morphology of the 1·2·11 ternary system differed markedly from those of the individual components (1) and binary systems (1·2, 1·11). The block co-assembly approach enabled the ternary system to exhibit bisignate CPL. A negative CPL signal was observed at 400 nm, while a positive signal emerged at 450 nm. It is interesting that, 1·2 and 1·11 both give CPL signals at around 430–450 nm, while a blue-shifted new band at 400 nm clearly indicates the formation of π–hole complexes between pyrene and 11. This blue-shift is reminiscent of the narrowed energy gap brought by arene–perfluoroarene forces (often observed in perfluoronaphthalene complexes).^50–55 These results indicate that the ternary complexes 1·2·11 contain multiple emissive species, including 1·11 and 2·11, each contributing to the overall excited-state chirality as evidenced by their CPL signs and emission maxima. This observation is fully consistent with the partial-narcissistic coassembly behavior inferred from the GIXS and XRD analyses. Moreover, the synergistic interactions among the three components facilitate the formation of a super-helical M-handed structure. Such a phenomenon can be rationalized by the role of the π–hole, which functions as an adhesive element that strengthens directional interactions within the assembly.

Fig. 6 SEM images of 1 (f_w = 80 vol%), 1·2 (f_w = 80 vol%, 1 : 1), 1·11 (f_w = 80 vol%, 1 : 1), 1·12 (f_w = 80 vol%, 1 : 1), 1·2·11 (f_w = 80 vol%, 1 : 1 : 1), and 1·2·12 (f_w = 80 vol%, 1 : 1 : 1) respectively. [1] = 0.1 mM.

In contrast, the 1·12 complex self-assembled into P-handed spindle-like helical structures with a width of up to 800 nm with extended scale (Fig. S50). In addition, the photophysical properties of this assembly underwent notable changes: the emission maximum shifted from 370 nm to 450 nm, significantly broadening the CPL response range and demonstrating the tunability of chiroptical properties via multicomponent co-assembly. Similarly, the 1·2·12 system adopted a P-handed helical morphology, composed of rod-like helices and spindle-like superstructures, reflecting its hierarchical organization (Fig. S51). Unlike the binary system of 1·12, the introduction of 2 into the ternary system created a competition with 1. This competition led the assembly to favor the precursor rod-like structures, forming spindles, and thereby hindered the formation of a uniform P-handed spindle structure. Notably, the CPL activity of 1·2·12 was significantly enhanced compared to the 1·2 or 1·12 systems, with a g_lum value reaching −1.0 × 10⁻². The major band at around 400 nm without a bisignate feature evidenced that the major contribution of excited chirality stems from the strong π–hole/π complexation between 2·12, in agreement with the strong binding affinity probed using XRD (Fig. 4d). By employing chlorinated or fluorinated π–hole donors, the binding affinity towards different components could be adjusted, enabling the construction of distinct macroscopic chiral assemblies with controlled chiroptical activities.

Conclusions

This study presents a substrate-selective supramolecular strategy to construct chiral architectures from achiral components via a three-component co-assembly. Compound 1, bearing a benzimidazole-based hydrogen-bonding pincer, initially forms nonchiral vesicular structures. Upon addition of carboxylic acids, directional hydrogen bonding drives the transformation into chiral 1D assemblies, enabling supramolecular chirality. Further introduction of electron-deficient aromatic compounds (11 and 12), possessing a central π–hole, facilitates π–hole/π interactions with 1 and the acid co-assemblies. These interactions significantly influence the helicity and morphology of the resulting structures. Notably, compound 11 (perfluorinated) induces M-handed helices, while 12 (chlorinated) favors P-handedness, demonstrating tunable chirality via electronic modulation. SEM and CPL measurements confirm the emergence of distinct helical morphologies and enhanced chiroptical responses in the three-component systems. In particular, the 1·2·12 assembly displays strong CPL activity and unique hierarchical “spindle-shaped” structures. Overall, this work offers a modular approach for achieving complex, ordered chiral nanostructures through synergistic hydrogen bonding and π–hole interactions, providing valuable insights for designing advanced supramolecular materials with tailored chiroptical properties.

Experimental

Materials, experimental details, and additional CD and MS spectra can be found in the SI.

Author contributions

W. Ma carried out the main experiments and data analysis. P. Xing and A. Hao proposed the idea and wrote the paper.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: materials, synthesis methods, assembly approaches, theoretical calculation methods, and test details used in this study. See DOI: https://doi.org/10.1039/d5sc09567k.

Acknowledgements

This work was also supported by the National Natural Science Foundation of China (No. 22171165, 22371170, and 22571184) and Natural Science Foundation of Shandong Province (No. ZR2022MB080). The authors are grateful for the technical support of 2D GIWAXS for the Vacuum Interconnected Nanotech Workstation (Nano-X) from the Suzhou Institute of Nano-Tech and Nano-Bionics, Chinese Academy of Sciences.

Notes and references

1. P. Yin, Z.-M. Zhang, H. Lv, T. Li, F. Haso, L. Hu, B. Zhang, J. Bacsa, Y. Wei, Y. Gao, Y. Hou, Y.-G. Li, C. L. Hill, E.-B. Wang and T. Liu, Nat. Commun., 2015, 6, 6475.
2. R. Sethy, J. Kumar, R. Métivier, M. Louis, K. Nakatani, N. M. T. Mecheri, A. Subhakumari, K. G. Thomas, T. Kawai and T. Nakashima, Angew. Chem., Int. Ed., 2017, 56, 15053–15057.
3. T. Noguchi, B. Roy, D. Yoshihara, J. Sakamoto, T. Yamamoto and S. Shinkai, Angew. Chem., Int. Ed., 2017, 56, 12518–12522.
4. C. F. Thompson, T. F. Jamison and E. N. Jacobsen, J. Am. Chem. Soc., 2000, 122, 10482–10483.
5. T. Hong, Z. Zhang, Y. Sun, J.-J. Tao, J.-D. Tang, C. Xie, M. Wang, F. Chen, S.-S. Xie, S. Li and P. J. Stang, J. Am. Chem. Soc., 2020, 142, 10244–10249.
6. G. Liu, M. G. Humphrey, C. Zhang and Y. Zhao, Chem. Soc. Rev., 2023, 52, 4443–4487.
7. L. Zhang, L. Qin, X. Wang, H. Cao and M. Liu, Adv. Mater., 2014, 26, 6959–6964.
8. J. Zhao, Y. Liu, A. Hao and P. Xing, ACS Nano, 2020, 14, 2522–2532.
9. X. Han, P. Cheng, H. Yang, J. Guan, M. Xin, G. Li, X. Li, Y. Zheng, J. Xu and X.-H. Bu, Angew. Chem., Int. Ed., 2025, 64, e202419776.
10. D. Zhai, J. Jiang, C. Yuan, D. Wang, Y. Jiang and M. Liu, Adv. Opt. Mater., 2023, 11, 2300161.
11. K. Dietrich, D. Lehr, C. Helgert, A. Tünnermann and E.-B. Kley, Adv. Mater., 2012, 24, OP321–OP325.
12. L. Branzi, L. Fitzsimmons and Y. K. Gun'ko, Angew. Chem., Int. Ed., 2024, 63, e202409313.
13. I. H. Ha, R. M. Kim, J. H. Han, S. W. Im, J. Jo, Y. H. Lee, J. Lv, U. C. Lee, H.-Y. Ahn, H.-E. Lee, M. Kim and K. T. Nam, J. Am. Chem. Soc., 2024, 146, 30741–30747.
14. Q. Jiang, X. Xu, P.-A. Yin, K. Ma, Y. Zhen, P. Duan, Q. Peng, W.-Q. Chen and B. Ding, J. Am. Chem. Soc., 2019, 141, 9490–9494.
15. C. Fu, D. Li, C. Liu, Y. Zhang, J. Zhang and Y. Cheng, Angew. Chem., Int. Ed., 2025, 64, e202512257.
16. C. Lee, W. Tang, F. Araoka, J. G. Park, R. Zhang and D. K. Yoon, Adv. Mater., 2025, 37, e10782.
17. C. Zhao, Y. Wang, Y. Jiang, N. Wu, H. Wang, T. Li, G. Ouyang and M. Liu, Adv. Mater., 2024, 36, 2403329.
18. A. Nemati, S. Shadpour, L. Querciagrossa, T. Mori, C. Zannoni and T. Hegmann, ACS Nano, 2019, 13, 10312–10326.
19. H. Zhang, S. Li, A. Qu, C. Hao, M. Sun, L. Xu, C. Xu and H. Kuang, Chem. Sci., 2020, 11, 12937–12954.
20. R. Liu, R. Zhang, X. Dong, S. Chen, L. Zhang, T. Shi, J. Yuan, N. Hedin and G. Chen, ACS Nano, 2024, 18, 14367–14376.
21. X. Wang, C. Yi and C. Felser, Adv. Mater., 2024, 36, 2308746.
22. S.-G. Chen, Y. Yu, X. Zhao, Y. Ma, X.-K. Jiang and Z.-T. Li, J. Am. Chem. Soc., 2011, 133, 11124–11127.
23. Z.-M. Shi, C.-F. Wu, T.-Y. Zhou, D.-W. Zhang, X. Zhao and Z.-T. Li, Chem. Commun., 2013, 49, 2673–2675.
24. D. Uraguchi, Y. Ueki and T. Ooi, Science, 2009, 326, 120–123.
25. P. Xing, Y. Li, S. Xue, S. Z. F. Phua, C. Ding, H. Chen and Y. Zhao, J. Am. Chem. Soc., 2019, 141, 9946–9954.
26. W. Zuo, Y. Tao, Z. Luo, A. Li, S. Wang, X. Qiao, F. Ma and C. Jia, Angew. Chem., Int. Ed., 2023, 62, e202300470.
27. K. Wang, D. Qi, H. Wang, W. Cao, W. Li and J. Jiang, Chem. Eur. J., 2012, 18, 15948–15952.
28. M. Vázquez-Nakagawa, L. Rodríguez-Pérez, N. Martín and M. Á. Herranz, Angew. Chem., Int. Ed., 2022, 61, e202211365.
29. K. Sato, Y. Itoh and T. Aida, Chem. Sci., 2014, 5, 136–140.
30. A. Haque, K. M. Alenezi, M. S. Khan, W.-Y. Wong and P. R. Raithby, Chem. Soc. Rev., 2023, 52, 454–472.
31. G. Sinawang, M. Osaki, Y. Takashima, H. Yamaguchi and A. Harada, Chem. Commun., 2020, 56, 4381–4395.
32. G. Morgese, B. F. M. de Waal, S. Varela-Aramburu, A. R. A. Palmans, L. Albertazzi and E. W. Meijer, Angew. Chem., Int. Ed., 2020, 59, 17229–17233.
33. A. J. Savyasachi, O. Kotova, S. Shanmugaraju, S. J. Bradberry, G. M. Ó’Máille and T. Gunnlaugsson, Chem, 2017, 3, 764–811.
34. Q. Xu, B. Zhang, Y. Zeng, A. Zangiabadi, H. Ni, R. Chen, F. Ng, M. L. Steigerwald and C. Nuckolls, Chem. Sci., 2021, 12, 2955–2959.
35. L. Yang, F. Wang, D.-i. Y. Auphedeous and C. Feng, Nanoscale, 2019, 11, 14210–14215.
36. Y. Wang, W. Zhu, W. Du, X. Liu, X. Zhang, H. Dong and W. Hu, Angew. Chem., Int. Ed., 2018, 57, 3963–3967.
37. L. Yang, Y. Li, M. Du, Y. He, Y. Lan, Q. Yin, F. Zhu and G. Chang, Adv. Funct. Mater., 2022, 32, 2111021.
38. R. Siddiqui, S. Burguera, M. de las Nieves Piña, S. Dhamija, H. M. Titi, A. Frontera, A. Bauzá and R. Patra, Angew. Chem., Int. Ed., 2024, 63, e202409963.
39. A. Bauzá, A. Frontera and T. J. Mooibroek, Chem. Eur. J., 2019, 25, 13436–13443.
40. H. Ju, B. Wang, M. Li, J. Hao, W. Si, S. Song, K. Mei, A. C. H. Sue, J. Wang, C. Jia and X. Guo, J. Am. Chem. Soc., 2024, 146, 25290–25298.
41. B. Mallada, M. Ondráček, M. Lamanec, A. Gallardo, A. Jiménez-Martín, B. de la Torre, P. Hobza and P. Jelínek, Nat. Commun., 2023, 14, 4954.
42. P. R. Varadwaj, H. M. Marques, A. Varadwaj and K. Yamashita, Cryst. Growth Des., 2024, 24, 7789–7807.
43. H. Wang, W. Wang and W. J. Jin, Chem. Rev., 2016, 116, 5072–5104.
44. P. Politzer, J. S. Murray and T. Clark, J. Phys. Chem. A, 2019, 123, 10123–10130.
45. J. Lu, N. S. Khetrapal, J. A. Johnson, X. C. Zeng and J. Zhang, J. Am. Chem. Soc., 2016, 138, 15805–15808.
46. L. Li, H. Wang, W. Wang and W. J. Jin, CrystEngComm, 2017, 19, 5058–5067.
47. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
48. T. Lu, J. Chem. Phys., 2024, 161, 082503.
49. S. Manzetti and T. Lu, J. Phys. Org. Chem., 2013, 26, 473–483.
50. B. Liu, J. Gao, A. Hao and P. Xing, Angew. Chem., Int. Ed., 2023, 62, e202305135.
51. E. K. Roesner, D. Asheghali, A. Kirillova, M. J. Strauss, A. M. Evans, M. L. Becker and W. R. Dichtel, Chem. Sci., 2022, 13, 2475–2480.
52. H. Zhang, J. Han, X. Jin and P. Duan, Angew. Chem., Int. Ed., 2021, 60, 4575–4580.
53. W. Ma, X. Li, A. Hao and P. Xing, Sci. China Chem., 2024, 67, 3482–3492.
54. S. S. Babu, V. K. Praveen, S. Prasanthkumar and A. Ajayaghosh, Chem. Eur. J., 2008, 14, 9577–9584.
55. Y. Zhang, H. Wu, Y. Wang, L. Sun, S. Li, Y. Ren, Y. Sun, F. Yang, X. Zhang and W. Hu, J. Mater. Chem. C, 2022, 10, 2562–2568.

---