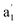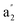Deciphering the molecular origin of the 19.3 eV electronic excitation energy of H₃⁺

Abstract

The trihydrogen cation, H₃⁺, is unique in the Universe. It serves as the primary proton reservoir, driving essential astrochemical reactions, and it functions as a thermostat for giant gas planets. H₃⁺ has also a remarkably low photodissociation rate, explained by its exceptionally high first electronic excitation energy (19.3 eV), which is well above the ionization energy of the much more abundant monohydrogen (13.6 eV). Herein we reveal that the key factors behind the high excitation energy of H₃⁺, and thus, its astrophotochemical inertness, are: (i) aromatic stabilization in its electronic ground state, (ii) antiaromatic destabilization in its first excited state, and (iii) a high nuclear-to-electronic charge ratio (+3 vs. −2). Through comparisons with analogous (isolobal) π-conjugated carbocations, we find that ground state aromatic stabilization plus excited state antiaromatic destabilization raise the excitation energy of H₃⁺ by 4.8–6.0 eV. This means that for H₃⁺, the excited state antiaromatic character (which normally leads to high photoreactivity) contributes to its astrophotochemical inertness. Thus, only with the increase in excitation energy due to ground state aromaticity plus excited antiaromaticity can H₃⁺ act as a thermostat for giant gas planets and as a proton reservoir that drives astrochemical reactions, thereby fulfilling its unique role in space.

---

Introduction

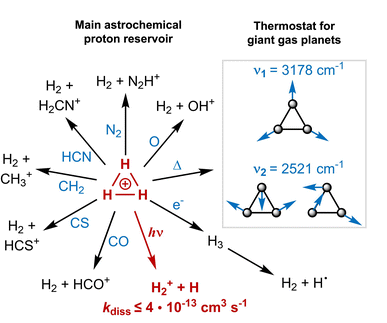
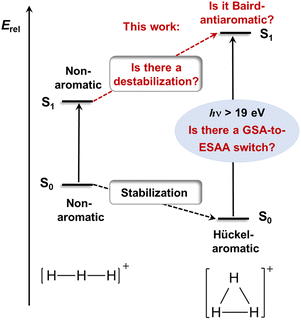
Triangular H₃⁺ is the most abundant polyatomic ion in the interstellar medium, where it functions as the primary interstellar acid, initiating reactions that lead to more complex molecules (Fig. 1).^1–3 It further acts as a thermostat (coolant) in the upper atmospheres of giant gas planets,⁴ and it has been postulated that it even could have functioned as a coolant in the primordial gas (though with a different mechanism than in the giant gas planets).⁵ With three H atoms, it is the smallest molecule that exhibits aromaticity (σ-aromaticity),^6–9 a stabilizing molecular property.¹⁰

Fig. 1 A summary of the functions of H₃⁺ in space, with its role as (i) primary proton reservoir initiating a number of core astrochemical reactions (typical rate constants for these reactions are ∼10⁻⁹ cm³ s⁻¹), and (ii) as a thermostat in the upper atmospheres of giant gas planets ensuring that their temperatures do not exceed a threshold.

The first electronically excited singlet states of H₃⁺, the doubly degenerate 1¹E′ states at the equilateral triangular structure (D_3h symmetric), are of exceptionally high vertical energy (19.3 eV, Fig. 2),¹¹ and they are dipole-allowed and dissociative.^12–14 Despite this, astrochemical databases list a photodissociation rate of 4 × 10⁻¹³ s⁻¹ or lower,^13,15 whereby it is among the astrochemical species with lowest photodissociation rates.^16,17 The reason is that the much more abundant H and H₂, with ionization and excitation energies at 13.1–15.4 eV,^1,18 shield H₃⁺ from high-energy irradiation in the interstellar medium (ISM).^12,13,19,20 In the ISM, H₃⁺ degrades unimolecularly only when exposed to electrons ejected from other molecules or atoms upon cosmic ray ionization.^1,13 Indeed, direct photodissociation only occurs when H₃⁺ is rovibrationally excited, whereby the electronic excitation energy decreases down to 4.9 eV.^12,13 Had it been more prone to photodissociate, this would have impaired its astrochemical and astrophysical functions, and thus, been detrimental to the development of the Universe as we presently know it. However, the molecular origins of its very high vertical excitation energy remain unknown and have never been addressed earlier. With such fundamental knowledge in hand it should also be possible to pinpoint other species of astrochemical relevance that may also exhibit unusually high first electronic excitation energies.

Fig. 2 Tentative changes from the nonaromatic character of linear H₃⁺ in its S₀ and S₁ states to the equilateral triangular H₃⁺ with a stabilizing Hückel-aromaticity in S₀ (GSA = ground state aromaticity) and a destabilizing Baird-antiaromaticity in S₁ (ESAA = excited state antiaromaticity). Factors related to our hypothesis and explored herein written in red, while known factors in black.

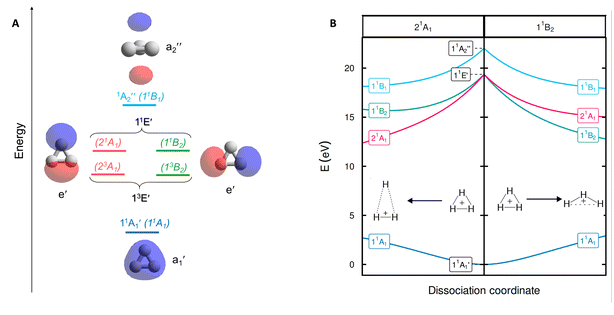
H₃⁺ in its electronic ground state (S₀) has a D_3h symmetric structure^11,21–23 with σ-aromatic character,^6–9 in line with Hückel's 4n + 2 rule (n = 0, 1, 2…) as it has two σ-electrons. We now hypothesize that the counter-concept, antiaromaticity,¹⁰ is relevant for its first excited state of singlet multiplicity (S₁), and thus, its excitation energy (Fig. 2). In this context, the analogous cyclic and fully π-conjugated hydrocarbons (i.e., annulenes) in their lowest excited triplet states (T₁) of ππ* character follow Baird's rule,^24–28 which tells that molecules with 4n + 2 π-electrons are antiaromatic and destabilized in these states while those with 4n are aromatic and stabilized. Although derived for the T₁ state, the rule can often be extended to the lowest ππ* excited state of singlet multiplicity. Thus, the exceptionally high excitation energy of H₃⁺ may stem from σ-antiaromatic destabilization in S₁ (Fig. 2) combined with σ-aromatic stabilization in S₀, i.e., a switch in character from ground state Hückel-aromaticity (GSA) to excited state Baird-antiaromaticity (ESAA), a GSA-to-ESAA switch in character.

Accordingly, we now investigated if the lowest excited states of H₃⁺ are antiaromatic and based this assessment on quantum chemical calculations of various (anti)aromaticity descriptors. Is ESAA the factor that leads to the very high excitation energy or are there other factors? Furthermore, can knowledge gained through this investigation impact on other parts of astrochemistry? The H₃⁺ cation has a 3-center 2-electron bond, a type of bonding it shares with nonclassical carbocations such as the vinyl (C₂H₃⁺) and ethyl (C₂H₅⁺) cations,^29–37 species which are also of astrochemical relevance.^38,39 One can thus argue that the findings herein can be useful to understand the astrophotochemical features of these species as well.

Computations of H₃⁺ were run at the EOM-CCSD level for all species, which for H₃⁺ corresponds to a full configuration interaction (FCI) calculation, i.e., a numerically exact solution of the Schrödinger equation. These computations were performed using the aug-cc-pVTZ basis set of Dunning. For further computational details, see the Computational methods section and the SI.

Results and discussion

Herein, we first present and discuss results of the potential energy surfaces of the S₀ and lowest few singlet excited states, followed by assessments of the (anti)aromatic characters of these states. This allows us to get a first tentative link between the excited state surface profiles and ESAA alleviation, yet, other factors that can impact on the lowest excitation energy of H₃⁺ are also identified and explored. Towards the end we compare with the analogous (isolobal) carbocations, which allows us to estimate the energetic component of a GSA-to-ESAA switch in character on the vertical excitation energy of H₃⁺.

Potential energy surfaces

According to our computations, the H–H distances of equilateral triangular H₃⁺ in S₀ are 0.875 Å which is very close to the earlier computed value of 0.873 Å found with variational Born–Oppenheimer theory using explicitly correlated Gaussian functions.¹¹ The degenerate 1¹E′ states appear vertically 19.28 eV above the S₀ state (Fig. 3A), again very similar to the reference value of 19.33 eV.¹¹ Expansion of the basis set beyond aug-cc-pVTZ has a negligible effect on the vertical excitation energy (19.2883 eV with FCI/aug-cc-pV5Z). The transition is symmetry allowed with an oscillator strength f = 0.562, yet, as it is well above the ionization energy of H (13.6 eV), the excitation has exceptionally low probability.

Fig. 3 (A) The three valence MOs ( and e′), the Rydberg orbital , and the labels of the electronic states within the D_3h (normal print) and C_2v (in parenthesis and italics) point groups. (B) Potential energy surface profiles of H₃⁺ from the D_3h symmetric S₀ equilibrium geometry along the minimum energy path of the 2¹A₁ state keeping C_2v symmetry to an acute isosceles triangle (left), and along the minimum energy path of the 1¹B₂ state to an obtuse isosceles triangle (right).

After excitation, in C_2v symmetry, the 1¹E′ states split into the 2¹A₁ and 1¹B₂ states (Fig. 3B), where 2¹A₁ as S₁ dissociates to H₂⁺ + H while 1¹B₂ as S₁ leads to 2H(1s) + H⁺.¹⁴ These dissociative forces can be understood as a result of the Jahn–Teller theorem.⁴⁰ Along D_3h symmetric geometries, the degenerate ¹E forms a conical intersection seam, which is lifted by symmetry-breaking nuclear distortions along a pair of E type vibrations, leading to electronic stabilization. We recognize that extensive vibronic coupling effects influence the excited state spectrum and that these, as well as different conical intersections, strongly impact on photochemical dissociation dynamics of H₃⁺, as has already been explored in previous studies based on highly accurate potential energy surfaces.^13,41–46 The current work, however, does not attempt to quantitatively model neither spectroscopic data nor photodissociation rates. Instead, the objective of our study is to elucidate the origin of the unusually high electronic excitation energy of H₃⁺, which hitherto is totally unexplored.

The first triplet states (the degenerate 1³E′) have vertical excitation energies of 14.87 eV (Table S1) and exhibit similar dissociative behaviors as 1¹E, in line with earlier findings.⁴⁷ Lastly, the higher energy 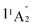state in D_3h symmetry is a dissociative second-order saddle point with H–H distances of 1.620 Å. As this state involves an excitation from an orbital to a nonbonding Rydberg-type orbital (Fig. 3A), only one electron remains in a bonding molecular orbital (MO), which cannot counterbalance the electrostatic repulsion between three protons. For further results and discussions on this state, see Sections S1 and S2 of the SI.

Probing excited state antiaromaticity

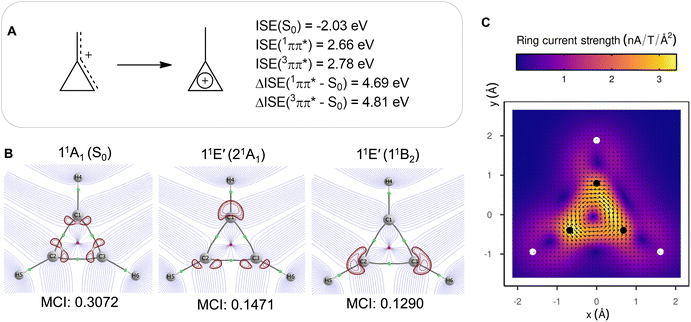
The aromatic or antiaromatic characters of the various electronic states were determined comprehensively through use of energetic, electronic, and magnetic (anti)aromaticity descriptors (for details see Section S3 or ref. 10). Thus, we analyze changes in three of the four aspects of aromaticity, with the geometric aspect being impossible to assess due to the dissociative nature of the excited states. The energetic aspect is determined through the extra cyclic resonance energy (ECRE).^48,49 To measure electron delocalization,⁵⁰ we use the two-center delocalization index (DI)^51,52 and the normalized multicentre index (MCI^1/n)⁵³ that reflect the aromatic character. The magnetic response properties are explored by magnetically induced current densities (MICDs), and also by nucleus independent chemical shifts (NICSs).

Although assessed in earlier reports,^6–9 the values for σ-aromaticity of the S₀ state are discussed briefly in order to contrast the antiaromatic character of the excited states (vide infra). H₃⁺ has two electrons and forms a 3-center 2-electron (3c–2e) bond, both in its linear and triangular structures. Therefore, the energy gain when going from the linear to the triangular structure (1.76 eV) represents the ECRE, reflecting an aromatic stabilization of cyclic H₃⁺ in S₀ (Fig. 2). The topological analysis of the electron density also reveals a species that benefits from extensive 3c–2e bonding, manifested in the formation of a non-nuclear attractor (NNA) in the center (Fig. 4A), in agreement with previous works.^7,8 Large DI values between the hydrogen atoms and the large positive MCI^1/n of 0.62 (Fig. 4A)⁵⁴ are also consistent with σ-aromaticity in S₀ (the MCI^1/n of benzene in S₀ is 0.59 (ref. 55)). Finally, H₃⁺ in its S₀ state displays a diatropic MICD of 4.39 nA T⁻¹, in agreement with the NICS(0)_zz value of −37.1 ppm, confirming the magnetic aromaticity of H₃⁺ in S₀ (see further Section S3 of the SI).

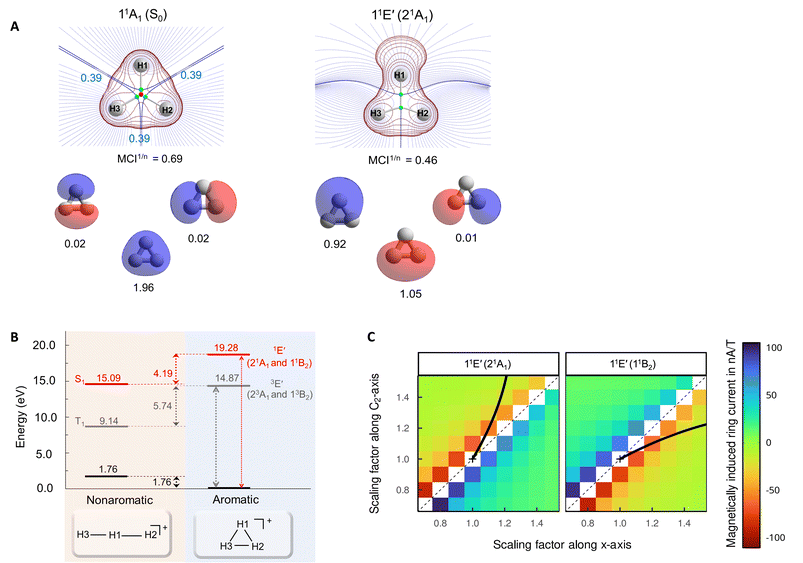Fig. 4 (A) Topological analysis of the electron density, 2D Laplacian of the electron density (in red), and natural orbitals (with populations) for the S₀ and 1¹E′ states, the latter labelled as 2¹A₁ and 1¹B₂ in C_2v symmetry. The rays of the basins drawn in blue and density gradient lines in purple. MCI^1/n values (computed using Becke-rho's partition)⁵⁶ are given below the Laplacian plots of the electron density. (B) Vertical excitation energies and relative energies of H₃⁺ at, respectively, D_∞h and D_3h symmetries. (C) Magnetically induced ring currents for the 2¹A₁ and 1¹B₂ states which stem from the 1¹E′ states upon geometric distortions to C_2v symmetric structures. The scaling factors reflect how large this distortion was (the value 1.0 represents the H–H bond lengths of the S₀ equilibrium geometry). The C₂-axis indicates distortions in the direction of forming an acute isosceles triangle (moving H1 atom) and the x-axis distortions along an obtuse isosceles triangle formation (increasing the separation between H2 and H3).

Evaluation of the potential antiaromaticity in the 1¹E′ states of D_3h symmetric H₃⁺ is more challenging from computational perspectives, requiring separate characterizations of the two states, the 2¹A₁ and 1¹B₂ states in C_2v symmetry. Indeed, our investigation offers a first exploration of whether the concept of excited-state antiaromaticity is applicable to doubly degenerate first excited states. Notably, we find that in the lowest excited state, going from the linear (D_∞h) to the triangular geometry of H₃⁺ (which is the equilibrium geometry in S₀) results in a destabilization in the lowest vertically excited singlet states by 4.19 eV (Fig. 4B). This reveals a negative ECRE indicating antiaromaticity. Thus, the stabilization in S₀ plus destabilization in 1¹E′ (S₁) upon cyclization have implications for the vertical excitation energy as their combined effects amount to 5.95 eV (Fig. 4B). The corresponding sum for the lowest triplet states is 7.50 eV. Both energies are in line with GSA-to-ESAA switches in character upon vertical excitation (Fig. 2).

Yet, the potential excited state antiaromatic character also needs to be probed through electronic and magnetic (anti)-aromaticity descriptors. With regard to the electron densities of these lowest excited states and their Laplacians, they exhibit significant differences from those of S₀, which corroborates the loss of aromaticity upon excitation (Fig. 4A). Despite the D_3h symmetric geometry of H₃⁺ in its vertically excited states, the electron density distribution has lower symmetry as it shifts toward the outer part of the atoms, preceding the dissociations that occur upon excitation to these states. Although the H atoms are still covalently bonded, as indicated by the value of the DIs, the 2¹A₁ and 1¹B₂ states exhibit drastic reductions of the three-center delocalization to 37–39% of the MCI value of S₀ (Fig. 4A). Similar conclusions can be reached on the antiaromaticity of the 1³E′ (1³A₁ and 1³B₂) states based on the analysis of the electron delocalization in Fig. S2.⁵⁴ Thus, the MCI^1/n values for H₃⁺ (0.62 (S₀), 0.46 and 0.45 (1¹E′), and 0.39 and 0.36 (1³E′)), are comparable to those of benzene in its S₀, S₁, and T₁ states (0.59, 0.40, and 0.36, respectively).⁵⁵ This is consistent with an aromatic S₀ state, while the lowest excited singlet and triplet states (1¹E′ and 1³E′) are antiaromatic.

Going to the magnetic aspect of excited state antiaromaticity, the values of the magnetically induced ring currents obtained for the vertically excited 1¹E′ states at the S₀ equilibrium geometry diverge as a result of the two-fold degeneracy at D_3h symmetry. The analysis of ring current strength at the C_2v symmetric structures reveals that the 1¹E′ states exhibit a pole in the ring current at D_3h symmetric geometries (Fig. 4C), i.e., a sudden change from highly diatropic to highly paratropic values, which explains the divergence observed at the vertical excitation. This resembles recent observations on the transient antiaromatic states of the c-C₁₆ molecule where small bond length alterations lead to changes from dia- to paratropicity, or vice versa,⁵⁷ related to the orbital degeneracies at highly symmetric structures.⁵⁸ Now, by following the C_2v symmetric dissociation paths of H₃⁺, and thus, the 2¹A₁ and 1¹B₂ states, we observe gradually diminishing paratropic ring currents (Fig. 4C), in line with antiaromaticity relief. Also the NICS(0)_zz values computed along these paths reveal antiaromaticity, with values of 77.1 and 84.7 ppm at two C_2v symmetric structures distorted by a factor 1.5, leading to, respectively, acute and obtuse isosceles triangular structures as exemplified in Fig. 3B (see further Section S3).

Protons-to-electrons ratios and impacts

Having established the antiaromaticity of the 1¹E′ states of H₃⁺, the question is if the GSA-to-ESAA switch in character (Fig. 2) explains the unusually high vertical excitation energy of this cation. From computations of light atoms, molecules and ions with only two electrons such as He, Li⁺, HHe⁺ and He₂²⁺ (Table S3), we see that high vertical excitation energies are characteristic of these species, which mostly cannot exhibit aromaticity as they are acyclic. Many of these ions are also found in space, e.g., Li⁺ and HHe⁺.⁵⁹ Indeed, it has been argued that HHe⁺ was the first molecule of the Universe,^60,61 and it produces H₂⁺ upon collision with atomic H, which in turn can produce H₃⁺ in a reaction with H₂.⁶²

The excitation energies are higher for more positively charged species, and is highest when the protons are concentrated in one nucleus (He, Li⁺ and Be²⁺). Hence, in the 3p,2e series, Li⁺ and HHe⁺ feature higher vertical E(S₁) than H₃⁺ by, respectively, 41.16 and 6.91 eV, and similar for the vertical E(T₁) (Table S3). For the 2e species He, Li⁺ and Be²⁺, with protons-to-electrons ratios of 1.0, 1.5 and 2.0, respectively, the first excitation energy goes up dramatically from 20.94 eV to 60.44 eV and 121.26 eV as the excitation implies a gradually larger loss in the electrostatic attraction between electrons and nuclei.

Next, to estimate the impact of the protons-to-electrons ratio on the excitation energies, we explored the π-conjugated and S₀ aromatic cyclopropenium cation, c-C₃H₃⁺, which has an equilateral triangular structure and a near-unit ratio of 1.05 between total nuclear and electronic charges (+21 vs. −20) (Sections S4 and S5).^63–65 Indeed, c-C₃H₃⁺ is isolobal with H₃⁺, i.e., its π-orbitals are analogous to the σ-orbitals of H₃⁺.⁶⁶ Thus, this cation helps us decipher the relative contributions of the protons-to-electrons ratio versus the GSA-to-ESAA switch to the 19.28 eV excitation energy of H₃⁺.

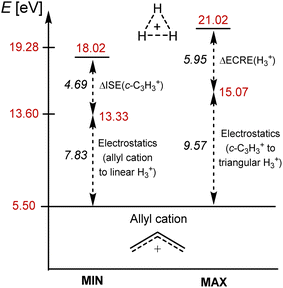
The vertical transition to the lowest ππ* states (1¹E″) of c-C₃H₃⁺ requires 9.71 eV. This is only half that of the transition to the σσ* states of H₃⁺ but significantly higher than the lowest ππ* states of any other π-bonded hydrocarbon, e.g., 7.11 eV for ethylene.⁶⁷ Thus, c-C₃H₃⁺ has its lowest ππ* states at an unusually high excitation energy despite its near-unit protons-to-electrons ratio. Interestingly, there are several σπ* and πσ* states below the first ππ* state. Therefore, the high excitation energy of the lowest ππ* transition of c-C₃H₃⁺ is not caused by a drastically diminished electrostatic attraction upon excitation. Instead, it should arise from the stabilization in the S₀ state due to aromaticity plus destabilization in the ππ* states due to antiaromaticity, and this applies also to the lowest triplet states. From this, one can estimate that the additional energy (9.57 eV) to reach the excitation energy of H₃⁺ is caused by the electrostatic effect.

Also Li₃⁺, valence isoelectronic to H₃⁺, is an equilateral triangle at its global minimum in the S₀ state, but it is nonaromatic and best described as the smallest triatomic molecule with metallic bonding.⁸ We now find its lowest singlet excited states, the degenerate ¹E states, at an energy of merely 2.70 eV. In line with the nonaromatic S₀ state, these states are also nonaromatic (see Table S3 and Section S6 in the SI). Compression to a triangle with half the Li–Li distance leads to no substantial changes in neither the singlet excitation energy nor the electron–nucleus attraction contributions (Table S3). Among the two possible mixed Li and H monocations (H₂Li⁺ and HLi₂⁺), H₂Li⁺ has an acute triangular structure with Li–H and H–H distances of 2.049 and 0.752, respectively (Fig. S7). HLi₂⁺, on the other hand, has a linear structure⁶⁸ and was therefore not further considered here as it is nonaromatic.

Finally, H₂He²⁺ is also interesting in this context as it provides an electronegativity perturbation compared to the isoelectronic H₃⁺,⁵⁹ although our computations reveal that this dication is not a minimum on the S₀ PES. However, when kept at the geometry which is optimal for H₃⁺ but with one H⁺ exchanged to He²⁺, we find that it is nonaromatic in both its S₀ state and lowest singlet excited states (Fig. S10). Accordingly, there is no GSA-to-ESAA switch in character upon the excitation of H₂He²⁺. In line with this, there is no significant increase in excitation energy (+0.24 eV) when going from HHe⁺ to H₂He²⁺, in contrast to what is observed when going from H₂ to H₃⁺ (+6.56 eV, see Table S3 and Section S6 for further discussion).

Comparisons to analogous carbocations

Further analysis of the c-C₃H₃⁺ cation, a molecular ion which also is of astrochemical importance,²⁹ enables us to show that the very high first excitation energy of H₃⁺ is due to both stabilization by GSA plus destabilization by ESAA and the high protons-to-electrons ratio. Among the (anti)aromaticity aspects, we thus first explore the energetic aspect before the electronic and magnetic ones. The isomerization stabilization energy (ISE)⁶⁹ of c-C₃H₃⁺ in S₀, computed as the reaction energy for the 1,3-hydrogen shift from a nonaromatic isomer to the S₀ aromatic methylcyclopropenium cation (Fig. 5A), is −2.03 eV with CCSD. This reveals a stronger aromatic character than that of benzene in S₀ (−1.34 eV with CCSD/aug-cc-pVDZ). In contrast, the lowest vertically excited singlet and triplet ππ* states exhibit large positive ISE values of 2.66 and 2.78 eV with EOM-CCSD, corresponding to strong excited state antiaromatic destabilization. Accordingly, the S₀ stabilization plus excited state antiaromatic destabilizations of c-C₃H₃⁺ are 4.69 and 4.81 eV, respectively, and these should represent lower bounds for the analogous energies in H₃⁺.

Fig. 5 (A) Isomerization stabilization energies (ISEs) of the methylcyclopropenium cation in the S₀ and lowest vertically excited singlet and triplet ππ* states, and the combined ISEs. (B) Topological analysis and Laplacian of the electron density (in red) of S₀ and excited states of c-C₃H₃⁺ at its S₀ geometry (1.0 a.u. above ring plane) and MCI values. (C) MICD of the cyclopropenium cation in its 1¹E″ (1¹B₂) state vertically excited from S₀ showing paratropic (antiaromatic) ring currents (1.0 a.u. above ring plane). Carbon atoms plotted as black balls and hydrogen atoms as white.

A comparison of the various energies of the linear H₃⁺ with the corresponding ones of the allyl cation (H₂CCHCH₂⁺) allows for a second estimate of the impact of the high protons-to-electrons ratio of H₃⁺. The two species are isolobal and nonaromatic in S₀, yet, have different protons-to-electrons counts (3 : 2 vs. 23 : 22). For the allyl cation, with a near-unit protons-to-electrons ratio, the lowest vertical ππ* singlet state is found at 5.50 eV, while the first σσ* excitation energy of linear H₃⁺ is 13.33 eV, i.e., 7.83 eV higher than that of the allyl cation. Both this and the excitation energy difference between c-C₃H₃⁺ and H₃⁺ (9.57 eV) provide estimates of the electrostatic contribution to excitation energies of H₃⁺ (Fig. 6).

Fig. 6 Estimation of the minimum and maximum of the excitation energy of triangular H₃⁺ with the first ππ* excitation energy of the allyl cation as the starting point, to which energy additives representing two types of components are added: (i) the difference in electrostatics upon excitation due to different protons-to-electrons ratio in the carbocations and H₃⁺, and (ii) the GSA-to-ESAA switch in character upon excitation. ΔISE = difference in isomerization stabilization energy between the S₀ and lowest ππ* excited state of c-C₃H₃⁺, and ΔECRE = difference in extra cyclic resonance energy between the S₀ and σσ* states of H₃⁺.

Antiaromaticity assessments of c-C₃H₃⁺ in its first singlet excited ππ* state by usage of electronic and magnetic descriptors reveal a clear resemblance to H₃⁺. The MCI values demonstrate their electronic structural similarities with the values for, respectively, the 1¹E′ and 1¹E″ states being less than half those of the S₀ state (Fig. 4 and 5B), and this is further emphasized by the topological analysis of their excited state electronic structures (Fig. 4A and 5B). Finally, the MICD of the cyclopropenium cation in its lowest ππ* state reveals a paratropic (antiaromatic) ring current in the three-membered ring (Fig. 5C), similar as for the two dissociation pathways of H₃⁺ (Fig. 4C). Furthermore, and as described above, the antiaromatic character of the lowest ππ* states, leading to an extreme destabilization, should be a strongly contributing factor to these states not being the lowest excited states of c-C₃H₃⁺. In contrast, for the allyl cation the lowest ππ* state is the S₁ state. As photochemical reactions normally proceed from the lowest electronically excited state according to Kasha's rule, this will impact on the photochemistry of the c-C₃H₃⁺ and its alkyl substituted derivatives, likely leading to reduced photoreactivities when compared to species where ππ* states are the lowest excited states.

Thus, c-C₃H₃⁺ like H₃⁺, exhibit strong aromaticity in the S₀ state and strong antiaromaticity in, respectively, the lowest ππ* and σσ* excited states, yet the excitation energy of the latter is additionally affected by a high protons-to-electrons ratio. Indeed, by adding energy additives to the lowest excitation energy of the acyclic and nonaromatic allyl cation (5.50 eV) one can estimate the excitation energy of H₃⁺ (Fig. 6). The energy for the GSA-to-ESAA switch in character in c-C₃H₃⁺ (4.69 eV) or the extra cyclic resonance energy of H₃⁺ (5.95 eV), and the excitation energy difference between the allyl cation and linear H₃⁺ or between triangular c-C₃H₃⁺ and H₃⁺ (7.83–9.57 eV), as measures of the electrostatic energy loss between protons and electrons upon excitation, added to 5.50 eV gives 18.0–21.0 eV (Fig. 6). This energy range brackets our computed first excitation energy of H₃⁺ of 19.28 eV. It also becomes clear that it is the GSA-to-ESAA switch in character which places the first singlet excited states well above the ionization energy of monohydrogen, and thus, provides H₃⁺ with its astrophotochemical persistence.

Conclusions

Herein, we decipher the main causes of the very high electronic excitation energy of H₃⁺, which enables its functions in space. This is achieved through a comparison of triangular H₃⁺ and linear H₃⁺ with two analogous π-conjugated hydrocarbon ions, the cyclopropenium cation (c-C₃H₃⁺) and the allyl cation (CH₂CHCH₂⁺). Had the vertical excitation energy been lower (closer to the photoionization of the much more abundant monohydrogen), H₃⁺ would have been more prone to photodissociate in space. We reveal that three factors contribute to the high excitation energy; (i) the change from a stabilizing aromatic character to (ii) a destabilizing antiaromatic character upon excitation from S₀ to the lowest excited states (present also in c-C₃H₃⁺), and (iii) the high ratio between total nuclear and electronic charges (which is present also in small cations). These three factors together provide the origin of the astrophotochemical inertness of H₃⁺. Without this photostability, H₃⁺ could not have had the functions it has in the Universe, which would have led to a Universe different from the one we know. Furthermore, it may also impact on the photostability of species with similar 3-center–2-electron bonding characteristics as the H₃⁺ ion, such as the vinyl and ethyl cations (C₂H₃⁺ and C₂H₅⁺, respectively),^29–31,70 as well as the S₀ state aromatic c-C₃H₃⁺ and derivatives, which are all of astrochemical importance.^29,70 The excited state dynamics of these carbocationic species are not extensively explored but it can be an important direction for future research in astrochemistry.

We show for the first time that excited state antiaromaticity is a molecular electronic structure property with crucial astrochemical influence that also has astrophysical implications. In a broader sense, our findings point to the roles of excited state aromaticity and antiaromaticity as important new concepts for interpretation in astrochemistry. We anticipate that these effects impact on a number of photochemical processes in space.

Computational methods

Geometry and energy calculations

Geometry optimizations and energy calculations were performed with Gaussian 16 revision C.01.⁷¹ The electronic singlet ground state and lowest excited triplet state were calculated using CCSD while singlet excited states were computed with EOM-CCSD. For H₃⁺, this level is equivalent to full configuration interaction (FCI), and we referred to it as FCI in the manuscript. Frequency calculations were performed at the same level of theory to probe if the structures were minima or saddle points on the potential energy surfaces. In all cases, the aug-cc-pVTZ valence triplet-zeta of Dunning and co-workers⁷² was used as the basis set. For wavefunction analysis we employed 6d 10f functions for the latter basis set. To obtain T₂ state the orbital order was altered by usage of the guess = alter keyword in Gaussian. Calculations of electron–nucleus attraction contribution include core electrons for all molecules (see Table S3).

Aromaticity assessment

Results of the multicentre index (MCI)⁵³ were computed by usage of AIMAll,⁷³ APOST-3D, and ESI-3D^56,74 packages. Due to the presence of a non-nuclear attractor (NNA) in some of the species, we consider a different partition of the molecular space to compute the delocalization indices (DI(F))^51,52 and the MCI. Some of us have previously found that Becke-rho's atomic partition provides similar values to partitions based on quantum theory of atoms in molecules (QTAIM),⁷⁵ a theory which uses a topological approach to define an atom in a molecule. Becke's partition employs the position of the bond critical points (BCP) between atoms to define the atomic radii in the original Becke's partition.⁷⁶ This multicentre integration technique assigns weights to atoms in the molecule. The calculation of the DI for correlated wavefunctions employed the so-called Fulton approximation,⁷⁷ which provides very good agreement with the actual DI.

Isomerization stabilization energies (ISE) were computed at (EOM)-CCSD/cc-pVTZ optimized geometries but for the energy values reported we used the aug-cc-pVTZ basis set.

The magnetically induced ring current density (MICD) was calculated by employing complete active space self-consistent field (CASSCF) method (with all electrons, and occupied and virtual orbitals included in the active space, corresponding to an FCI calculation) and aug-cc-pVTZ basis set, using a development version of Dalton Program 2020.^78,79 In order to compute the ring current passing through the bonds of the triangular H₃⁺, the MICD was integrated in a plane perpendicular to the bond, spanning from the centre of mass of the molecule 20 bohr at opposite sides of the plane (along vectors normal to the ring plane and cutting through the bond) using 200 subdivisions in the Gauss–Lobatto quadrature.⁸⁰

Author contributions

Conceptualization: HO; methodology: HO, CFN, EM; investigation: JMT, JKS; visualization: JMT, JKS; funding acquisition: HO; project administration: HO; supervision: HO; analysis: JMT, JKS; writing – original draft: JMT; writing – review & editing: JMT, JKS, EM, CFN, HO.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data underlying this study are openly available in the published article and its supplementary information (SI), and also openly available in zenodo at https://doi.org/10.5281/zenodo.15713452. The data supporting this article have been included as part of the SI. Supplementary information: Section S1: energies and geometries of H₃⁺; Section S2: aromaticity of H₃⁺, electronic properties; Section S3: aromaticity of H₃⁺, magnetic properties; Section S4: protons-to-electrons ratios; Section S5: cyclopropenium cation (C₃H₃⁺); Section S6: Li₃⁺, H₂Li⁺ and H₂He²⁺; Section S7: supplementary references; Section S8: Cartesian coordinates, absolute energies, and imaginary frequencies for all calculated structures. See DOI: https://doi.org/10.1039/d5sc09067a.

Acknowledgements

We thank Dr Radovan Bast for extensive help with the magnetically induced current density calculations, Mr Hannes Gustafsson and Dr Lucia Corti for involvement in preliminary calculations. We also thank Prof. Jochen Autschbach, Prof. Paul Barklem, Prof. Eszter Borbas, Prof. em. Bengt Gustafsson, Prof. Martin Rahm, Prof. Philippe Wernet, and Prof. Judy Wu for discussions on the project at various stages. The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) and the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Center (NSC), Linköping, Sweden, through grant agreements 2022/5-378, 2023/5-335 and 2024/5-422. The Foundation Olle Engkvist Byggmästare is greatly acknowledged for a postdoctoral fellowship to J. M. T. (grant 184-390). H. O. thanks the Swedish Research Council for financial support (grants 2019-05618 and 2023-04179), and J. M. T. thanks the University Claude Bernard Lyon 1 for the funding provided through AAP Accueil EC. E. M. is grateful for the funding and technical support provided by the Donostia FEDER Una manera de hacer Europa International Physics Center (DIPC), and grant PID2022-140666NB-C21 funded by MCIN/AEI/10.13039/501100011033 and “FEDER Una manera de hacer Europa”. C. F.-N. thanks National Science Centre, Poland 2020/39/B/ST4/02022 for funding.

References

1. T. Oka, Chem. Rev., 2013, 113, 8738–8761.
2. T. R. Geballe and T. Oka, Nature, 1996, 384, 334–335.
3. M. Larsson, Int. J. Astrobiol., 2008, 7, 237–241.
4. S. Miller, T. Stallard, H. Melin and J. Tennyson, Faraday Discuss., 2010, 147, 283–291.
5. G. Kannan, J. R. Chien, A. J. Benjamin, N. Bhatia and R. J. Saykally, J. Phys. Chem. A, 2021, 125, 4267–4275.
6. R. W. A. Havenith, F. De Proft, P. W. Fowler and P. Geerlings, Chem. Phys. Lett., 2005, 407, 391–396.
7. S. Sadjadi, Struct. Chem., 2017, 28, 1445–1452.
8. C. Foroutan-Nejad and P. Rashidi-Ranjbar, J. Mol. Struct. THEOCHEM, 2009, 901, 243–248.
9. D. Zhao, X. He, M. Li, C. Guo, C. Rong, P. K. Chattaraj and S. Liu, in Atomic Clusters with Unusual Structure, Bonding and Reactivity, ed. P. K. Chattaraj, S. Pan and G. Merino, Elsevier, 2023, pp. 237–245,  DOI:10.1016/B978-0-12-822943-9.00017-6.
10. M. Solà, A. I. Boldyrev, M. K. Cyrański, T. M. Krygowski and G. Merino, Aromaticity and antiaromaticity: Concepts and applications, John Wiley & Sons, Ltd, 2023.
11. M. Pavanello and L. Adamowicz, J. Chem. Phys., 2009, 130, 034104.
12. A. Petrignani, D. Bing, O. Novotný, M. H. Berg, H. Buhr, M. Grieser, B. Jordon-Thaden, C. Krantz, M. B. Mendes, S. Menk, S. Novotny, D. A. Orlov, R. Repnow, J. Stützel, X. Urbain and A. Wolf, J. Phys. Chem. A, 2010, 114, 4864–4869.
13. X. Urbain, A. Dochain, R. Marion, T. Launoy and J. Loreau, Philos. Trans. R. Soc., A, 2019, 377, 20180399.
14. K. Kawaoka and R. F. Borkman, J. Chem. Phys., 1971, 54, 4234–4238.
15. E. v. Dishoeck and H. R. Hrodmarsson, Leiden photodissociation and photoionization cross section database, https://home.strw.leidenuniv.nl/%7Eewine/photo/display_h3+_f8a0eca1bcc94c898fc68220d4b45be8.html, accessed 10/25, 2024.
16. H. R. Hrodmarsson and E. F. van Dishoeck, Astron. Astrophys., 2023, 675, A25.
17. A. N. Heays, A. D. Bosman and E. F. van Dishoeck, Astron. Astrophys., 2017, 602, A105.
18. S. Lepp, P. C. Stancil and A. Dalgarno, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, R57.
19. E. F. van Dishoeck, Symp. – Int. Astron. Union, 1987, 120, 51–65.
20. D. Galli and F. Palla, Annu. Rev. Astron. Astrophys., 2013, 51, 163–206.
21. L. Adamowicz and M. Pavanello, Philos. Trans. R. Soc., A, 2012, 370, 5001–5013.
22. A. V. Turbiner and J. C. Lopez Vieyra, J. Phys. Chem. A, 2013, 117, 10119–10128.
23. J. Tennyson, O. L. Polyansky, N. F. Zobov, A. Alijah and A. G. Császár, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 232001.
24. N. C. Baird, J. Am. Chem. Soc., 1972, 94, 4941–4948.
25. M. Rosenberg, C. Dahlstrand, K. Kilså and H. Ottosson, Chem. Rev., 2014, 114, 5379–5425.
26. R. Papadakis and H. Ottosson, Chem. Soc. Rev., 2015, 44, 6472–6493.
27. J. Kim, J. Oh, A. Osuka and D. Kim, Chem. Soc. Rev., 2022, 51, 268–292.
28. J. Yan, T. Slanina, J. Bergman and H. Ottosson, Chem.–Eur. J., 2023, 29, e202203748.
29. A. Ali, E. C. Sittler, D. Chornay, B. R. Rowe and C. Puzzarini, Planet. Space Sci., 2013, 87, 96–105.
30. C. M. Gabrys, D. Uy, M. F. Jagod, T. Oka and T. Amano, J. Phys. Chem., 1995, 99, 15611–15623.
31. G. E. Douberly, A. M. Ricks, B. W. Ticknor, W. C. McKee, P. v. R. Schleyer and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 1897–1906.
32. B. Żurawski, R. Ahlrichs and W. Kutzelnigg, Chem. Phys. Lett., 1973, 21, 309–313.
33. R. Beckmann, R. Topolnicki and D. Marx, J. Phys. Chem. A, 2023, 127, 2460–2471.
34. H. S. Andrei, N. Solcà and O. Dopfer, Angew. Chem., 2007, 120, 401–403.
35. P. C. Varras, M. G. Siskos and P. S. Gritzapis, Mol. Phys., 2020, 118, e1706778.
36. B. T. Psciuk, V. A. Benderskii and H. B. Schlegel, Theor. Chem. Acc., 2007, 118, 75–80.
37. R. C. Fortenberry, X. Huang, T. D. Crawford and T. J. Lee, J. Phys. Chem. A, 2014, 118, 7034–7043.
38. A. Ali, E. C. Sittler, D. Chornay, B. R. Rowe and C. Puzzarini, Planet. Space Sci., 2015, 109–110, 46–63.
39. G. A. Olah, T. Mathew, G. K. S. Prakash and G. Rasul, J. Am. Chem. Soc., 2016, 138, 1717–1722.
40. H. A. Jahn and E. Teller, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235.
41. M. Pavanello, W. C. Tung, F. Leonarski and L. Adamowicz, J. Chem. Phys., 2009, 130, 074105.
42. B. Mukherjee, S. Mukherjee and S. Adhikari, J. Phys.: Conf. Ser., 2016, 759, 012050.
43. Z. Peng, S. Kristyan, A. Kuppermann and J. S. Wright, Phys. Rev. A, 1995, 52, 1005–1023.
44. P. Barragán, L. F. Errea, A. Macías, L. Méndez, I. Rabadán and A. Riera, J. Chem. Phys., 2006, 124, 184303.
45. S. Mukherjee, D. Mukhopadhyay and S. Adhikari, J. Chem. Phys., 2014, 141, 204306.
46. A. Znotins, F. Grussie, A. Wolf, X. Urbain and H. Kreckel, J. Mol. Spectrosc., 2021, 378, 111476.
47. L. J. Schaad and W. V. Hicks, J. Chem. Phys., 1974, 61, 1934–1942.
48. Y. Mo and P. v. R. Schleyer, Chem.–Eur. J., 2006, 12, 2009–2020.
49. X. Lin and Y. Mo, Angew Chem. Int. Ed. Engl., 2022, 61, e202209658.
50. F. Feixas, E. Matito, J. Poater and M. Solà, Chem. Soc. Rev., 2015, 44, 6434–6451.
51. R. F. W. Bader and M. E. Stephens, Chem. Phys. Lett., 1974, 26, 445–449.
52. R. F. W. Bader and M. E. Stephens, J. Am. Chem. Soc., 1975, 97, 7391–7399.
53. P. Bultinck, R. Ponec and S. Van Damme, J. Phys. Org. Chem., 2005, 18, 706–718.
54. E. Matito, Phys. Chem. Chem. Phys., 2016, 18, 11839–11846.
55. F. Feixas, J. Vandenbussche, P. Bultinck, E. Matito and M. Solà, Phys. Chem. Chem. Phys., 2011, 13, 20690–20703.
56. E. Matito, M. Solà, P. Salvador and M. Duran, Faraday Discuss., 2007, 135, 325–345.
57. I. Rončević, F. J. Leslie, M. Rossmannek, I. Tavernelli, L. Gross and H. L. Anderson, J. Am. Chem. Soc., 2023, 145, 26962–26972.
58. E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2001, 105, 9553–9562.
59. L. González-Sánchez, N. Sathyamurthy and F. A. Gianturco, Phys. Chem. Chem. Phys., 2023, 25, 23370–23383.
60. R. Güsten, H. Wiesemeyer, D. Neufeld, K. M. Menten, U. U. Graf, K. Jacobs, B. Klein, O. Ricken, C. Risacher and J. Stutzki, Nature, 2019, 568, 357–359.
61. R. C. Fortenberry, Chem, 2019, 5, 1028–1030.
62. Y. Mi, E. Wang, Z. Dube, T. Wang, A. Y. Naumov, D. M. Villeneuve, P. B. Corkum and A. Staudte, Nat. Chem., 2023, 15, 1224–1228.
63. R. Breslow, J. T. Groves and G. Ryan, J. Am. Chem. Soc., 1967, 89, 5048.
64. M. N. Glukhovtsev, S. Laiter and A. Pross, J. Phys. Chem., 1996, 100, 17801–17806.
65. K. B. Wiberg and P. R. Rablen, J. Org. Chem., 2020, 85, 11741–11749.
66. R. Hoffmann, Angew. Chem., Int. Ed., 1982, 21, 711–724.
67. R. S. Mulliken, J. Chem. Phys., 1977, 66, 2448–2451.
68. B. H. Cardelino, W. H. Eberhardt and R. F. Borkman, J. Chem. Phys., 1986, 84, 3230–3242.
69. P. v. R. Schleyer and F. Pühlhofer, Org. Lett., 2002, 4, 2873–2876.
70. G. A. Olah, J. Am. Chem. Soc., 1972, 94, 808–820.
71. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallington CT, 2016.
72. D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358–1371.
73. T. A. Keith, TK Gristmill Software, Overland Park KS, USA, 2019.
74. E. Matito, IQCC (Girona, Catalonia) and DIPC (Donostia, Euskadi), Spain 2015.
75. R. F. W. Bader, Atoms in molecules : a quantum theory, Clarendon press, Oxford, 1990.
76. A. D. Becke, J. Chem. Phys., 1988, 88, 2547–2553.
77. R. L. Fulton, J. Phys. Chem., 1993, 97, 7516–7529.
78. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I. M. Høyvik, M. F. Iozzi, B. Jansík, H. J. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. Samson, A. S. de Merás, T. Saue, S. P. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. Wilson, M. Ziolkowski and H. Agren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284.
79. G. Ganguly, S. Pathak and A. Paul, Phys. Chem. Chem. Phys., 2021, 23, 16005–16012.
80. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.

---

Footnote

† Present Address: Department of Chemistry “Ugo Schiff”, University of Florence, 50019 Sesto Fiorentino, Italy.

---