Probing the weak interaction between silver and boron

Abstract

Understanding the boron-coinage-metal interactions is critical for understanding the nucleation and growth mechanisms of borophene on coinage-metal substrates. Binary metal–boron clusters provide ideal models for obtaining atomic-level information about the metal–boron interactions. Here we report an investigation of the structure and bonding of the AgB₈⁻ cluster as a model system to gain insight into the interaction of boron with silver, the most inert substrate to grow borophene. Photoelectron spectroscopy reveals that the spectra of AgB₈⁻ resemble those of bare B₈⁻, suggesting extremely weak chemical interactions between Ag and boron. Quantum calculations show that AgB₈⁻ (C_s, ¹A′) consists of a B₈ borozene weakly interacting with a Ag atom on its edge. Chemical bonding analyses find that the Ag atom interacts with the B₈ motif primarily through its 5s orbital with little perturbation to the structure and bonding of the B₈ borozene. Compared to CuB₈⁻ and AuB₈⁻, Ag is found to have the weakest interaction with B₈, consistent with the fact that silver substrates are the most inert for borophene syntheses.

---

1. Introduction

The electron deficiency of boron leads to unique bonding patterns and structural motifs that distinguish it from other main-group elements.¹ In the bulk, boron adopts a wide variety of allotropes consisting of the ubiquitous B₁₂ icosahedral cages.^2,3 Over the past two decades, experimental and theoretical investigations have revealed that size-selected boron clusters prefer planar structures, in contrast to the B₁₂-based bulk 3D structures.^4–9 Planar boron clusters consist of fused B₃ triangles, decorated with tetragonal, pentagonal, or hexagonal vacancies as the cluster size increases. Several landmark discoveries have highlighted the structural richness of size-selected boron clusters. The planar B₃₆ cluster with a central hexagonal vacancy provided the first indirect experimental evidence for monolayer 2D boron, i.e. borophene,^10,11 which has been synthesized and forms a new class of synthetic 2D materials.^12–14 Another breakthrough came with the discovery of the B₄₀ cage, the first all-boron fullerene (borospherene).¹⁵

Since boron does not have a bulk layered allotrope, suitable substrates are required to synthesize borophene to prevent nonplanar aggregation. The coinage metals are inert toward boron and were predicted to be ideal substrates for the synthesis of borophene.^16–18 Indeed, borophenes have been grown on the surfaces of all three coinage metals. In particular, silver has been found to be the most inert substrate and is the first substrate used for borophene syntheses.^12,13 Copper substrates display strong tendency for charge transfer to boron and have been shown to be critical for the formation of bilayer borophene,¹⁹ whereas strong boron–gold interactions lead to sub-surface formation of borophene on gold substrates.^20,21 In addition to the coinage metals, borophene has been synthesized on iridium and aluminum substrates,^22,23 although the strong charge transfer from Al to B results in a graphene-like hexagonal lattice on the Al substrate. Clearly, the boron-substrate interaction is critical to control the growth of borophene and to understand their formation mechanisms.

Metal–boron bimetallic clusters provide a valuable platform to unravel atomic-level interactions between boron and the metal substrates. Toward this end, we have investigated a series of Cu-doped boron clusters^24–28 and Au-doped boron clusters.^29–35 We have found that both ionic and covalent interactions exist in Cu–B clusters, whereas gold exhibits strong covalent interactions with boron.³⁶ However, Ag-doped boron clusters have proven to be challenging to produce experimentally. Although a few computational studies have been carried out,^37,38 no experimental characterizations of Ag-doped boron clusters have been reported. The difficulty to produce Ag-doped boron clusters is a direct manifestation of the weak interaction between silver and boron. Clearly, the absence of experimental information on Ag–B clusters represents a critical gap in our current understanding of boron-coinage metal interactions.

In the current work, we present the first experimental and theoretical investigation of a Ag-doped boron cluster. We have produced the AgB₈⁻ cluster and probed its electronic structure and chemical bonding using photoelectron spectroscopy (PES) and quantum chemical calculations. The photoelectron spectra of AgB₈⁻ are found to be surprisingly similar to those of B₈⁻. Theoretical calculations reveal that AgB₈⁻ can be viewed as a Ag-borozene complex, in which the Ag atom is weakly bonded to the periphery of the B₈ molecular wheel framework. The structure and bonding of AgB₈⁻ are compared with those of CuB₈⁻ and AuB₈⁻, revealing that Ag has the weakest interaction with the planar B₈ molecular wheel. It is further shown that the Ag atom can roam around the B₈ surface with a very small potential barrier, establishing AgB₈⁻ as a good model to understand the interaction of boron with the silver substrate for the synthesis of borophene.

2. Experimental and theoretical methods

2.1. Photoelectron spectroscopy

The experiment was conducted using a magnetic-bottle PES apparatus coupled to a laser vaporization supersonic cluster source.⁷ The AgB₈⁻ clusters were generated by laser vaporization of a cold-pressed disk target composed of Ag and ¹⁰B-enriched boron powders. The laser-induced plasma was quenched by a high-pressure He carrier gas seeded with 5% Ar. Clusters formed inside the nozzle were entrained by the carrier gas and cooled by supersonic expansion. After passing through a skimmer, negatively charged clusters in the collimated molecular beam were extracted perpendicularly into a time-of-flight mass analyzer. The AgB₈⁻ cluster was selected by a mass gate and decelerated prior to photodetachment by a laser beam, including 355 nm (3.496 eV) and 266 nm (4.661 eV) from an Nd:YAG laser, and 193 nm (6.424 eV) from an ArF excimer laser. Photoelectrons were collected by the magnetic bottle and analyzed in a 3.5 m long electron flight tube. Photoelectron kinetic energies were calibrated with the known transitions of the Ag⁻ atomic anion. The electron kinetic energy (E_k) resolution (ΔE_k/E_k) of the magnetic-bottle electron analyzer was approximately 2.5%, i.e., ∼25 meV for 1 eV electrons.

2.2. Theoretical calculations

Theoretical calculations were performed to explore the structures and bonding of the AgB₈^−/0 clusters. Global minimum (GM) searches were carried out using the ABCluster^39,40 and Gaussian 16 programs⁴¹ at the PBE0/def2-SVP level. Additional motif-guided searches were performed by placing a single Ag atom around the known planar B₈⁻ borozene framework.^42,43 Low-lying isomers obtained from both searches were subsequently reoptimized at the PBE0 level using the aug-cc-pVTZ basis set for boron atoms and the aug-cc-pVTZ-pp basis set with relativistic pseudopotentials (ECP60MDF) for the silver atom.^44–46 To ensure the reliability of the relative energetics, we performed additional optimizations and energy evaluations at the TPSSh and ωB97X-D levels with the same basis sets. For the GM structure, high-level single-point energy calculations were carried out at the domain-based local pair natural orbital [DLPNO-CCSD(T)] approximation using the PBE0-optimized geometries. We also tested dispersion-corrected functionals [PBE0-D3(BJ) and ωB97X-D] for the GM and several low-lying isomers, and all optimized structures were essentially identical to those obtained with PBE0.

The adiabatic detachment energy (ADE) was calculated as the energy difference between the optimized anion and neutral structures. The first vertical detachment energy (VDE₁) was calculated as the energy difference between the anion and the neutral at the anion geometry. Higher VDEs were computed using time-dependent density functional theory (TD-DFT)^47,48 at the PBE0/aug-cc-pVTZ-pp level and also with the equation-of-motion coupled-cluster approach (EOM-CCSD/aug-cc-pVTZ-pp). All DFT calculations were performed with the Gaussian 16 program, while the DLPNO-CCSD(T) and EOM-CCSD calculations were conducted using the ORCA 6.1.0 program with TightPNO and TightSCF options.^49,50

Chemical bonding was analyzed with the adaptive natural density partitioning (AdNDP) approach developed by the Boldyrev group,⁵¹ as implemented in the Multiwfn program.⁵² As an extension of the natural bond orbital (NBO) analysis, AdNDP describes the chemical bonding in terms of localized and delocalized n-center two-electron (nc–2e) bonds. Molecular orbital (MO) and natural population analyses were also carried out to understand the chemical bonding in the GM of AgB₈⁻.

3. Results

3.1. Experimental results

The mass intensities of the Ag-doped clusters are weaker in comparison to previous studies on the Cu- or Au-doped clusters.^25,35 The photoelectron spectra of AgB₈⁻ are shown in Fig. 1 at three photon energies. Detachment features are denoted by letters, where X indicates the detachment transition from the ground state of the anion to that of the neutral. The bands labeled from A to D represent detachment transitions from the ground state of the anion to the excited states of the neutral final states.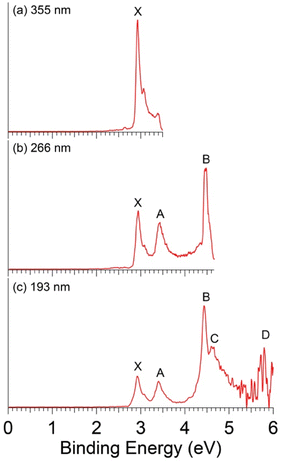

Fig. 1 Photoelectron spectra of AgB₈⁻ at (a) 355 nm (3.496 eV), (b) 266 nm (4.661 eV), and (c) 193 nm (6.424 eV).

The 193 nm spectrum appears relatively simple with five well-defined detachment transitions (Fig. 1c). The signal-to-noise ratios on the high binding energy side are poor, and band D at ∼5.8 eV is tentatively identified. At 266 nm (Fig. 1b), both bands D and C (VDE: 4.60 eV) are cut off, but bands X, A, B are better resolved with VDEs at 2.93 eV, 3.42 eV, and 4.44 eV, respectively. The 355 nm spectrum (Fig. 1a) displays only band X with a partially resolved vibrational feature with a spacing of ∼1100 cm⁻¹. The ADE or the electron affinity (EA) of AgB₈, is estimated from the 355 nm spectrum to be 2.88 eV by drawing a straight line at the leading edge of band X and then adding the instrumental resolution. It should be noted that the spectral features observed for AgB₈⁻ are strikingly similar to those of the bare B₈⁻ cluster,⁴² as compared in Fig. S1. All the observed VDEs for AgB₈⁻ are summarized in Table 1, where they are compared with the theoretical results.

Table 1 The experimental VDEs of AgB₈⁻ in comparison with the calculated values at the DLPNO-CCSD(T) and EOM-CCSD levels for the GM C_s (¹A′) structure. All energies are in eV

Band	VDEs^a (exp.)	Final state and electron configuration	VDEs (theo.)
a The experimental uncertainties are ±0.02 eV.b The experimental ADE is 2.88 ± 0.05 eV. The calculated ADE at the DLPNO-CCSD(T) level is 2.86 eV.
X^b	2.93	^2A″ {…16a′^2 9a″^2 17a′^2 18a′^2 10a″^2 19a′^2 11a″^1}	2.94
A	3.42	^2A′ {…16a′^2 9a″^2 17a′^2 18a′^2 10a″^2 19a′^1 11a″^2}	3.53
B	4.44	^2A′ {…16a′^2 9a″^2 17a′^2 18a′^1 10a″^2 19a′^2 11a″^2}	4.52
C	4.60	^2A″ {…16a′^2 9a″^2 17a′^2 18a′^2 10a″^1 19a′^2 11a″^2}	4.73
D	∼5.8	^2A′ {…16a′^2 9a″^2 17a′^1 18a′^2 10a″^2 19a′^2 11a″^2}	5.57
		^2A′ {…16a′^1 9a″^2 17a′^2 18a′^2 10a″^2 19a′^2 11a″^2}	5.89
		^2A″ {…16a′^2 9a″^1 17a′^2 18a′^2 10a″^2 19a′^2 11a″^2}	5.94

---

3.2. Theoretical results

The GM and four low-lying isomers of AgB₈⁻ and AgB₈ are shown in Fig. 2 at four levels of theory. While there are variations in the relative energies of the low-lying isomers, all four levels of theory give the same GM for AgB₈⁻ with C_s symmetry and a ¹A′ closed-shell electronic state. Triplet states were also examined, and all optimized triplet structures lie significantly higher in energy in comparison to the closed-shell singlet GM, as shown in Fig. S2. The GM of AgB₈⁻ features a quasi-planar B₈ wheel with the Ag atom bridging two peripheral B atoms almost perpendicular to the B₈ plane, with a dihedral angle of ∼95° between the Ag–B₂ coordination plane and the basal plane of the B₈ wheel (Fig. 2a). At the highest level of theory [DLPNO-CCSD(T)], the GM of AgB₈⁻ is more stable than Iso1 by 3.49 kcal mol⁻¹. In all the low-lying isomers of AgB₈⁻, the B₈ framework no longer retains the wheel topology. Iso1 (C_6v, ¹A₁) and Iso3 (C_s, ¹A′) both adopt a compact bipyramidal B₈ framework. In Iso1, the Ag atom is bonded axially to an apex B atom, reminiscent of the umbrella structure of B₈(BO)⁻,⁵³ whereas in Iso3 the Ag atom bridges two equatorial B atoms on the B₈ bipyramid. Iso2 and Iso4 are both planar: Iso2 adopts a double-chain B₈ motif, whereas Iso4 corresponds to a tennis-racket topology. Iso2 to Iso4 are all significantly higher in energy at all levels of theory (Fig. 2a).

Fig. 2 The structures and relative energies of the GM and four low-lying isomers for (a) AgB₈⁻ and (b) AgB₈. The numbers without brackets are the DLPNO-CCSD(T)/aug-cc-pVTZ-pp results calculated on the optimized structures at PBE0/aug-cc-pVTZ-pp. The relative energies (in kcal mol⁻¹) calculated at the PBE0, TPSSh, and ωB97X-D/aug-cc-pVTZ-pp levels are given in the square brackets, curly braces, and regular parentheses, respectively. The coordinates of these structures are given in the SI as Table S6 (anions) and Table S7 (neutrals).

The GM of neutral AgB₈ (C_s, ²A′) is open-shell (Fig. 2b) and its structure is similar to the anion GM, preserving the B₈ wheel with edge capping by Ag. The only significant structure change is the increase of the dihedral angle, between the Ag–B₂ coordination plane and the basal plane of the B₈ wheel, to ∼108°. The Iso1 of neutral AgB₈ is similar to Iso3 of the anion, whereas the Iso4 of the neutral is similar to Iso1 of the anion. All the low-lying isomers are significantly higher in energy than the GM structure at the DLPNO-CCSD(T) level.

The calculated VDEs for the GM structure of AgB₈⁻ at the DLPNO-CCSD(T) and EOM-CCSD levels are compared with the experimental data in Table 1 and the 193 nm spectrum in Fig. 3. The calculated VDEs using TD-DFT at the PBE0/aug-cc-pVTZ-pp level are similar to those at the EOM-CCSD level, as shown in Table S1 and Fig. S3.

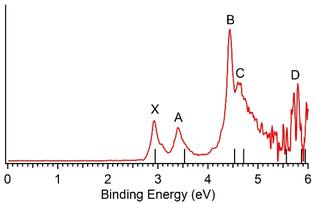Fig. 3 Comparison between the 193 nm PE spectra and the computed VDEs (vertical bars) for the GM of AgB₈⁻ at DLPNO-CCSD(T) and EOM-CCSD levels of theory.

4. Discussion

4.1. Comparison between experiment and theory

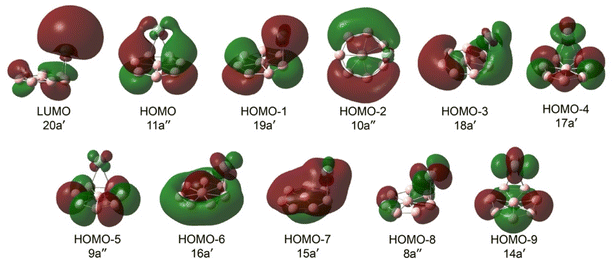
The computed ADE and VDE₁ values at the PBE0 level of theory for the GM structure of AgB₈⁻ and the four low-lying isomers of AgB₈⁻ are compared with the experimental data in Table S2. The GM structure of AgB₈⁻ (C_s, ¹A′) is considerably more stable than the other isomers (Fig. 2): Iso1, Iso2, Iso3, and Iso4 lie 3.49, 25.72, 28.03, and 27.53 kcal mol⁻¹ above the GM, respectively, at the highest level theory [DLPNO-CCSD(T)] carried out in this study. The computed ADE/VDE₁ for Iso1, the lowest-lying isomer above the GM, are significantly higher than the experimental data (Table S2). The computed ADE/VDE₁ for Iso2 are lower and they seem to agree with the weak signals discernible in the 355 nm and 266 nm spectra (Fig. 1). However, Iso2 is 25.72 kcal mol⁻¹ higher in energy than the GM structure. While we cannot completely rule it out, it is highly unlikely that such a high energy isomer would be present under our experimental conditions. The weak features are very likely due to minor impurities. Iso3 and Iso4 can also be ruled out on the basis of their high energies relative to the GM structure. Furthermore, the similarity of the observed spectra for AgB₈⁻ and those for bare B₈⁻ is consistent with the fact that only the GM cluster is present in the experiment.

The valence MOs for the GM of AgB₈⁻ are displayed in Fig. 4. For comparison, we also present the valence MOs of B₈⁻ in Fig. S4b. It can be seen that the Ag binding induces very little change to the MOs of the B₈ motif and that there is very little mixing of the Ag 5s/4d atomic orbitals, consistent with the similarity of their photoelectron spectra. The bare B₈⁻ is open-shell, missing one electron from the closed-shell B₈²⁻ borozene configuration (Fig. 4a).⁴³ The LUMO (20a′, Fig. 4) of AgB₈⁻ is mainly the 5s atomic orbital of Ag, which has transferred the single electron to the B₈ motif to give rise to the borozene complex, Ag⁺[B₈²⁻]. The HOMO (11a″) of AgB₈⁻ is a delocalized π orbital on the B₈ motif, which is similar to the SOMO of B₈⁻ and HOMO of B₈²⁻, as compared in Fig. S4 for the three species. The computed ADE/VDE₁ from electron detachment from the HOMO are 2.86/2.94 eV, in good agreement with the experimental values of 2.88/2.93 eV at the DLPNO-CCSD(T) level (Table 1). It should be noted that there is a large change of the Ag position in the neutral GM of AgB₈ (Fig. 2b), probably due to the reduced electrostatic interaction between Ag and B₈, because the neutral can be viewed as Ag⁺[B₈⁻]. In addition, there is a very small change in the B₈ framework (Fig. S5), consistent with the short vibrational progression of ∼1100 cm⁻¹, which should be due to a B–B stretching mode on the B₈ motif. Our vibrational analysis (Fig. S6) shows that the computed frequency for the ν₂ mode is close to the experimental observation. The line width of the X band should contain contributions from the low-frequency Ag rocking mode (ν₁₂), with a computed frequency of 58 cm⁻¹ (Fig. S6).

Fig. 4 The valence MOs for the GM of AgB₈⁻ (C_s, ¹A′).

The HOMO-1 (19a′, Fig. 4) of AgB₈⁻ is also a delocalized π orbital, which has some mixing with the 5s orbital of the Ag atom. The computed VDE of 3.53 eV is in excellent agreement with the observed VDE of 3.42 eV for band A (Table 1). The HOMO and HOMO-1 correspond to the degenerate π HOMO in the D_7h configuration of B₈²⁻ (Fig. S4).⁴² The splitting due to symmetry breaking in both AgB₈⁻ and the bare B₈⁻ are small. The next two detachment channels are from HOMO-3 (18a′) and HOMO-2 (10a″). The computed VDEs from these two MOs of 4.52 eV and 4.73 eV are very close to each other and agree well with the observed VDEs for bands B and C (Table 1), respectively. The small splitting between the two MOs is consistent with the weak perturbation of the B₈ motif by the Ag atom. The higher binding energy side of the 193 nm spectrum beyond band D is noisy and not well resolved, even though several more detachment channels are expected. Overall, the excellent agreement between the experimental and theorical results confirms unequivocally the GM structure of AgB₈⁻.

4.2. Chemical bonding analyses

To understand the chemical bonding in AgB₈⁻, we carried out a natural population analysis (NPA), as shown in Table S3. The natural electron configuration of Ag is found to be 4d^9.91 5s^0.52, corroborating the predominantly ionic interaction between Ag and the B₈ motif. The Ag 4d shell is essentially filled and the partial charge transfer occurs from the Ag 5s orbital to B₈. Consistent with the NPA result, comparison of the valence MOs of AgB₈⁻ with those of bare B₈⁻ (Fig. S4) shows that they retain essentially the same nodal topologies and spatial distributions with only minor mixing with the Ag 4d/5s atomic orbitals. The one-to-one correspondence of their frontier MOs explains why their PE spectra are similar, as shown in Fig. S1. The structural parameters of B₈ in AgB₈⁻ and AgB₈ are compared with those of bare B₈⁻ (Fig. S5): only very small changes are seen. By overlaying the B₈⁻ structure on AgB₈⁻, it can be seen that the B₈ motif is essentially preserved in AgB₈⁻ with only the two rim boron atoms near the Ag atom displaying a slight out-of-plane displacement (Fig. S5a).

To further appreciate the weak interactions between Ag and B₈, the structures of AgB₈⁻ is compared with those of the CuB₈⁻ and AuB₈⁻ in Fig. S7a. As shown in Table S4, the Ag–B distance (2.28 Å) in AgB₈⁻ is longer than the Au–B distance in AuB₈⁻. In particular, the Ag–B distance is substantially longer than that of a Ag–B single bond (2.13 Å) based on their atomic covalent radii.⁵⁴ We should point out that the Cu–B bond length of 1.94 Å in CuB₈⁻ is very close to the Cu–B single bond distance (1.97 Å) and the Au–B bond length of 2.20 Å in AuB₈⁻ is only modestly longer than the Au–B single-bond distance (2.09 Å), as shown in Table S4. The Wiberg bond index analysis further supports this picture, giving a Ag–B bond order of only ∼0.3 (Table S5), consistent with a weak, largely non-covalent interaction. To provide a more quantitative comparison, we further evaluated the metal–boron bond dissociation energies (BDEs) for CuB₈⁻, AgB₈⁻, and AuB₈⁻ (Table S8). Because the three clusters exhibit different structural motifs, both adiabatic dissociation and dissociation with the frozen B₈ framework were considered. In both cases, AgB₈⁻ shows the smallest BDEs, significantly weaker than CuB₈⁻ and AuB₈⁻. All the comparisons and analyses indicate that the interaction between Ag and B₈ in AgB₈⁻ is the weakest among the coinage metals.

The different positions of the coinage metals on the borozene surfaces (Fig. S7a) are interesting and they directly reflect the nature of their chemical bonding. The Cu atom displays the strongest charge transfer and forms a perfect Cu⁺-borozene complex, Cu⁺[B₈²⁻] with unit charge transfer. We note that the C_7v structure of CuB₈⁻ is identical to that of LiB₈⁻,⁵⁵ indicating that the central position of the metal ion on the C₇ axis is favored for ionic interactions. Gold is known to engage in strong covalent bonding with boron due to the strong relativistic effects.^36,56 The bridging edge-bonding of Au on the B₈ framework is conducive to d–π interaction between Au and B₈, as reported previously.³⁵ Thus, it is understandable that the situation of Ag is exactly in between those of Cu and Au: it cannot engage in covalent bonding with B₈ like Au on one hand, but it also cannot have a full charge transfer like Cu on the other.²⁵ We tested putting the Ag atom on the C₇ axis and found that the C_7v AgB₈⁻ has two imaginary frequencies with 0.94|e| charge transfer (Fig. S7b). When the Ag atom is put on the edge in the same plane as B₈, it is also not stable with one imaginary frequency. In the C_7v case, the charge transfer is not complete as in CuB₈⁻, whereas in the latter case there is little d–π covalent interaction as in AuB₈⁻. The only stable position is when Ag is almost vertical above the edge of the B₈ plane by bridging two peripheral B atoms resulting in the weakest interaction with B₈ among the three coinage MB₈⁻ borozene complexes or among the known MB₈ clusters.⁵⁷

The AdNDP bonding analyses (Fig. S8) also confirm the weak interactions between Ag and B₈, recovering five 1c–2e 4d lone pairs for Ag⁺ and the doubly aromatic B₈²⁻ borozene bonding elements with three totally delocalized σ bonds and three delocalized π bonds, as well as the seven 2c–2e B–B σ bonds on the periphery of the borozene.⁴³ We also present the AdNDP bonding analyses of B₈⁻ (Fig. S9), CuB₈⁻ (Fig. S10), and AuB₈⁻ (Fig. S11) for comparison. It can be seen that the Ag atom has very little perturbation to the bonding of the B₈ motif. On the other hand, the strong covalent interaction of Au with B₈ has imposed significant changes to the π bonds on B₈ in AuB₈⁻ (Fig. S11).

4.3. Fluxionality of AgB₈⁻: roaming of Ag on the surface of the B₈ borozene

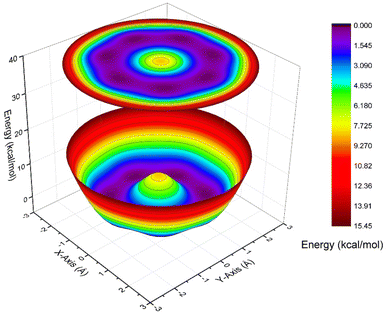
The lowest frequency vibrational mode in AgB₈⁻ is only 58 cm⁻¹ (ν₁₂, Fig. S6), involving the rocking of the B₈ motif around Ag or the rocking of the Ag atom on the B₈ surface. The next lowest frequency mode is ν₂₁, involving a rotating motion of the B₈ frame relative to the Ag atom (Fig. S6). Along the edge of the B₈ motif, there should be seven equivalent bridging positions or minima for the Ag atom. Following the ν₂₁ mode, we should be able to reach these minima with the transition state being on top of one B atom, as shown in Fig. S12. The energy barrier computed at the PBE0/aug-cc-pVTZ-pp level is merely 0.33 kcal mol⁻¹ including zero-point energy (ZPE) correction, consistent with the weak Ag and B₈ interaction. The presence of only one imaginary frequency, whose displacement connects two minima, suggests that this geometry corresponds to a transition state. Indeed, subsequent transition-state optimizations confirmed its identity. This finding implies that the Ag atom can migrate rather freely across the B₈ surface due to the weak interaction between Ag and B, thus, the Ag atom is highly fluxional and it can roam around the edge of the B₈ surface.

Further evidence arises from potential energy curve scans along two coordinates, which reveal very flat profiles and small barriers, as shown in Fig. 5, again consistent with the facile motion of Ag. This dynamic behavior provides further evidence that the Ag–B bonding interaction is weak, manifesting primarily as a shallow, non-directional perturbation of the B₈ electronic framework. Since boron does not have any layered allotropes, the formation of borophene requires an inert substrate. During the borophene formation, boron atoms must be mobile on the surface of the substrate for nucleation. Silver surfaces have been found to be the best and most inert substrate to grow borophenes.^12–14 The fluxionality of Ag on the B₈ surfaces should mirror the fluxionality of B on the silver surfaces, making AgB₈⁻ an ideal molecular model for understanding the interactions between B and silver. The weak Ag–B interaction is completely captured in the fluxional behavior of Ag on the B₈ surface, as revealed in Fig. 5 and S12.

Fig. 5 Three-dimensional potential energy curve of AgB₈⁻, generated by scanning the Ag atom in the XY-plane (−3.0 to 3.0 Å) with 360° degree at a constant Z-distance of 2.2 Å above the D_7h B₈ structure. The projection on the top plane illustrates the energy contour map corresponding to lateral displacements of Ag. Single-point calculations for the potential energy curve are done in Gaussian 16 program set at PBE0 level of theory.

5. Conclusions

In conclusion, we report a study on the structure and bonding of the AgB₈⁻ cluster using photoelectron spectroscopy and quantum chemical calculations. Photoelectron spectra of AgB₈⁻ are observed to be similar to those of the bare B₈⁻. It is found to be a Ag-borozene complex with the Ag atom bridging two peripheral B atoms of the B₈ wheel in a near vertical position relative to the B₈ plane. Chemical bonding analyses reveal that there is partial charge transfer from Ag to the B₈ motif to yield the closed shell B₈²⁻ configuration, but without any covalent interactions. The structure and bonding of AgB₈⁻ is compared with those of CuB₈⁻ and AuB₈⁻ and the Ag–B interaction is found to be the weakest. The weak Ag–B interaction leads to fluxional behavior of Ag on the B₈ surface. This study provides molecular level information about the weak Ag–B interaction, which makes silver the favorite substrate for borophene growth.

Author contributions

H. W. C. led the experiment, did the calculations, analyzed the data, and led the writing of the manuscript. D. K. and W. J. C. helped with the experiment. L. S. W. guided and advised the project, helped analyze the data, revised and finalized the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon request.

Supplementary information (SI): comparison of the photoelectron spectra of AgB₈⁻ with that of B₈⁻; comparison of the computed VDEs at PBE0 with the experimental spectrum; the valence MOs for B₈⁻, comparison of the B₈⁻ structural parameters with those of AgB₈⁻ and AgB₈; vibrational normal mode analysis for AgB₈; comparison of the structure of AgB₈⁻ with those of CuB₈⁻ and AuB₈⁻; AdNDP analyses for AgB₈⁻, B₈⁻ and B₈²⁻; potential energy curve for the roaming of Ag on the edge of B₈; natural population analyses and Wiberg bond index analyses for AgB₈⁻ (PDF). See DOI: https://doi.org/10.1039/d5sc08598e.

Acknowledgements

This work was supported by the National Science Foundation under Grant No. CHE-2403841. The calculation was performed using computational resources and services provided by the Center for Computation and Visualization (CCV) of Brown University. We gratefully acknowledge Dr Edward Brewer for his help with equipment maintenance.

References

1. W. N. Lipscomb, Science, 1977, 196, 1047–1055.
2. B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668.
3. A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863–867.
4. A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811–2866.
5. E. Oger, N. R. M. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503–8506.
6. A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358.
7. L. S. Wang, Int. Rev. Phys. Chem., 2016, 35, 69–142.
8. S. Pan, J. Barroso, S. Jalife, T. Heine, K. R. Asmis and G. Merino, Acc. Chem. Res., 2019, 52, 2732–2744.
9. T. Jian, X. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591.
10. Z. A. Piazza, H. S. Hu, W. L. Li, Y. F. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 3113.
11. W. L. Li, Q. Chen, W. J. Tian, H. Bai, Y. F. Zhao, H. S. Hu, J. Li, H. J. Zhai, S. D. Li and L. S. Wang, J. Am. Chem. Soc., 2014, 136, 12257–12260.
12. A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516.
13. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568.
14. Y. V. Kaneti, D. P. Benu, X. Xu, B. Yuliarto, Y. Yamauchi and D. Golberg, Chem. Rev., 2022, 122, 1000–1051.
15. H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731.
16. Y. Liu, E. S. Penev and B. I. Yakobson, Angew. Chem., Int. Ed., 2013, 52, 3156–3159.
17. H. Liu, J. Gao and J. Zhao, Sci. Rep., 2013, 3, 3238.
18. Z. Zhang, Y. Yang, G. Gao and B. I. Yakobson, Angew. Chem., Int. Ed., 2015, 54, 13022–13026.
19. C. Chen, H. Lv, P. Zhang, Z. Zhuo, Y. Wang, C. Ma, W. Li, X. Wang, B. Feng, P. Cheng, X. Wu, K. Wu and L. Chen, Nat. Chem., 2022, 14, 25.
20. B. Kiraly, X. Liu, L. Wang, Z. Zhang, A. J. Mannix, B. L. Fisher, B. I. Yakobson, M. C. Hersam and N. P. Guisinger, ACS Nano, 2019, 13, 3816–3822.
21. H. E. Wang, P. C. Ding, G. J. Xia, X. Y. Zhao, W. L. E, M. Yu, Z. B. Ma, Y. G. Wang, L. S. Wang, J. Li and X. M. Yang, Angew. Chem., Int. Ed., 2014, 63, e202406535.
22. N. A. Vinogradov, A. Lyalin, T. Taketsugu, A. S. Vinogradov and A. Preobrajenski, ACS Nano, 2019, 13, 14511–14518.
23. W. Li, L. Kong, C. Chen, J. Gou, S. Sheng, W. Zhang, H. Li, L. Chen, P. Cheng and K. Wu, Sci. Bull., 2018, 63, 282–286.
24. A. S. Pozdeev, H. W. Choi, W. J. Chen, L. S. Wang and I. A. Popov, J. Phys. Chem. A, 2025, 129, 6024–6033.
25. W. J. Chen, A. S. Pozdeev, H. W. Choi, A. I. Boldyrev, D. F. Yuan, I. A. Popov and L. S. Wang, Phys. Chem. Chem. Phys., 2024, 26, 12928–12938.
26. A. S. Pozdeev, W. J. Chen, H. W. Choi, M. Kulichenko, D. F. Yuan, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2023, 127, 4888–4896.
27. A. S. Pozdeev, W. J. Chen, M. Kulichenko, H. W. Choi, A. I. Boldyrev and L. S. Wang, Solid State Sci., 2023, 142, 107248.
28. M. Kulichenko, W. J. Chen, H. W. Choi, D. F. Yuan, A. I. Boldyrev and L. S. Wang, J. Vac. Sci. Technol., A, 2022, 40, 042201.
29. Q. Chen, H. J. Zhai, S. D. Li and L. S. Wang, J. Chem. Phys., 2013, 138, 084306.
30. D. Yu. Zubarev, J. Li, L. S. Wang and A. I. Boldyrev, Inorg. Chem., 2006, 45, 5269–5271.
31. H. J. Zhai, L. S. Wang, D. Yu. Zubarev and A. I. Boldyrev, J. Phys. Chem. A, 2006, 110, 1689–1693.
32. Q. Chen, H. Bai, H. J. Zhai, S. D. Li and L. S. Wang, J. Chem. Phys., 2013, 139, 044308.
33. H. J. Zhai, C. Q. Miao, S. D. Li and L. S. Wang, J. Phys. Chem. A, 2010, 114, 12155–12161.
34. H. Bai, H. J. Zhai, S. D. Li and L. S. Wang, Phys. Chem. Chem. Phys., 2013, 15, 9646.
35. W. J. Chen, Y. Y. Zhang, W. L. Li, H. W. Choi, J. Li and L. S. Wang, Chem. Commun., 2022, 58, 3134–3137.
36. L. S. Wang, Phys. Chem. Chem. Phys., 2010, 12, 8694–8705.
37. Y. Jin, Y. Tian, X. Kuang, C. Zhang, C. Lu, J. Wang, J. Lv, L. Ding and M. Ju, J. Phys. Chem. A, 2015, 119, 6738–6745.
38. P. Fu, B. Chen, W. Sun and C. Lu, Phys. Lett. A, 2025, 548, 130553.
39. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181.
40. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016.
42. H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008.
43. L. S. Wang, Acc. Chem. Res., 2024, 57, 2428–2436.
44. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
45. K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112.
46. R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
47. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
48. C. Bannwarth and S. Grimme, Comput. Theor. Chem., 2014, 1040–1041, 45–53.
49. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
50. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2025, 15, e70019.
51. D. Yu. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
52. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
53. W. J. Tian, W. J. Chen, M. Yan, R. Li, Z. H. Wei, T. T. Chen, Q. Chen, H. J. Zhai, S. D. Li and L. S. Wang, Chem. Sci., 2021, 12, 8157–8164.
54. P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337.
55. A. N. Alexandrova, H. J. Zhai, L. S. Wang and A. I. Boldyrev, Inorg. Chem., 2004, 43, 3552–3554.
56. P. Pyykkö, Chem. Rev., 1988, 88, 563–594.
57. J. Barroso, S. Pan and G. Merino, Chem. Soc. Rev., 2022, 51, 1098–1123.

---