Open Access Article
Open Access ArticleIsoenergetic symmetry breaking charge separation in far-red absorbing orthogonal BODIPY dimer – a classic case of no energy loss during the process of light capture and conversion
Ram R.
Kaswan
,
Aida
Yahagh
and
Francis
D'Souza
 *
*
Department of Chemistry, University of North Texas, 1155 Union Circle, #305070, Denton, TX 76203-5017, USA. E-mail: Francis.dsouza@unt.edu
First published on 15th December 2025
Abstract
Symmetry-breaking charge separation (SB-CS) in a far-red capturing, orthogonally linked BODIPY dimer, 2, revealing minimal electronic coupling, is demonstrated under isoenergetic conditions (with little or no energy loss), thus helping to maximize the process of solar light capture and conversion. The orthogonal design of the dimer and proximity resulted in poor orbital overlaps between the chromophores, promoting a long-lived SB-CS state without the need for a thermodynamic driving force—a crucial factor for increasing solar device efficiency. Multiple techniques were employed to establish and prove this phenomenon. Steady-state and time-resolved emission studies revealed substantial quenching of the dimer in both nonpolar and polar solvents compared to the BODIPY monomer, 1, providing initial evidence of SB-CS. The redox gap, measured to assess thermodynamic feasibility through electrochemical studies, confirmed the event as a barrierless process (ΔGET ∼0.0 eV). TD-DFT calculations supported this realization by illustrating the generation of excited-state electron density and hole–electron distribution, revealing an unsymmetrical dipolar distribution. Short-range and long-range electronic coupling calculations yielded negligible values, confirming weak excitonic coupling, reducing the coulombic interactions between the hole and electron, thereby facilitating the formation of radical ion pairs with minimal energy loss. Transient absorption spectroscopy further provided conclusive evidence of SB-CS and allowed the extraction of kinetic parameters. Finally, Marcus's theory of electron transfer was applied, yielding a low electronic coupling (V) value of as little as 7.6 meV. These findings indicate that electron transfer can occur even under weak-coupling (null-exciton) conditions without an energy barrier—a step forward in maximizing solar energy harvesting.
Introduction
Photo-induced SB-CS is a phenomenon that occurs when two identical chromophores (a dimer) capture a photon and use its energy to transfer an electron from one chromophore to the other, disrupting the symmetry in the dimer.1–20 The SB-CS mechanism appears in various systems, ranging from a special pair of chlorophyll found in the natural photosynthetic reaction center to organic photovoltaic devices for light-to-energy conversion. The importance of this phenomenon can be understood from the natural photosynthesis process, where a special pair of identical chromophores triggers a sequential electron transfer event, finally producing a long-lived radical ion pair. Eventually, the energy of this pair is used in the synthesis of adenosine triphosphate (ATP).21 This process of generating radical ion pairs differs significantly from the asymmetric conventional donor–acceptor (D–A) systems, where hole (or electron) transfer requires a difference in redox potential to generate D+–A− having much lower energy than that used for excitation (typically over 500 mV energy loss). Conversely, in symmetrical molecules, weakly coupled chromophores generate an instantaneous localized excited state (LE) upon photoexcitation, and subsequent variations in the solvent environment (driven by solvent polarity), leading to the formation of charge carrier ion pairs. Recent research has shown that SB-CS has various applications in designing artificial models to mimic natural photosynthesis and developing highly efficient light-harvesting devices.17–21 This is in contrast to D–A molecules, where the energy loss between the LE (excitons) and CS state can substantially reduce the power conversion efficiency of light-harvesting devices.22–26 Therefore, understanding the mechanistic details of SB-CS under various conditions in synthetic models of different geometry and orientation is crucial. To address the above issue, the scientific community worldwide is focusing on SB-CS in synthetic chromophore dimers, where the energy loss in SB-CS is as small as 100 mV. Various chromophores, viz., perylenediimide (PDI),26–29 phthalocyanine,30 subphthalocyanine,31 perylene,32,33 BODIPY,24,34 bianthyryl,35 and metallopyrrins34,36,37 have been successfully used to explore this mechanism. Among these, BODIPY (4,4-difluoro-4-bora-3a,4-diaza-s-indacene) has become one of the most promising candidates because of its robustness, high molar extinction coefficient, and ease of tuning its optoelectronic properties by modifying the substituents on its periphery.It is known that in the photosynthetic reaction center, the chlorophyll dimer undergoes efficient SB-CS in a nonpolar environment (with a dielectric constant ranging between 3 and 9). This natural event presents a significant challenge in constructing chromophore dimers that can undergo SB-CS in nonpolar media, thereby mimicking the natural process. In the present work, we address this challenge and report the synthesis of a BODIPY dimer with perfect orthogonal geometry (Fig. 1), revealing little to no communication between the entities of the dimer. Here, instead of simple BODIPYs that absorb and emit light in the 510 nm range, we aimed for far-red capturing π-extended BODIPYs to enhance absorption in the far-red region of the solar spectrum. Two phenyl-styryl entities were attached to each BODIPY to shift the optical spectra to the 650 nm range.38–41 A series of techniques, including absorption spectroscopy, steady-state and time-resolved emission spectroscopy, electrochemical and spectroelectrochemical methods, DFT and TD-DFT calculations, and transient spectroscopy, was employed to observe SB-CS and determine the coupling constant, a crucial parameter for evaluating the communication strength between the two entities. As summarized below, we successfully demonstrate the occurrence of SB-CS under null-exciton conditions not only in polar solvents but also in nonpolar solvents.
Results and discussion
Synthetic
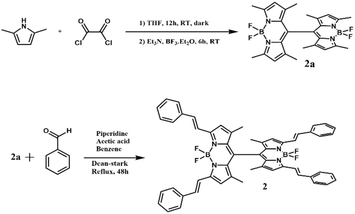
Scheme 1 outlines the synthetic route to produce dimer 2. This involves the initial synthesis of directly linked dimer BODIPY (2a), followed by appending the bis-styryl tails. Preparation of monomer 1 involved the synthesis of meso-phenyl BODIPY, 1a, and its transformation into 1 (see SI for synthetic details). The structures' integrity was confirmed using various techniques, including 1H and 13C NMR, as well as MALDI-TOF mass analysis. Additional information is available in the SI (see Fig. S1–S10).Spectroscopic studies
As depicted in Fig. 2, the ground-state electronic behavior of the dimer 2 and monomer 1 was explored using steady-state absorption and emission spectroscopy in three different polarity solvents: toluene (dielectric constant, E = 2.38), o-dichlorobenzene (o-DCB, E = 9.93), and dimethyl sulfoxide (DMSO, E = 46.7). Fig. 2a shows the absorption spectrum of monomer 1 in toluene, displaying characteristic spectral features of BODIPY,42–44 with its absorption maximum (A0−0, λabsmax) observed at 627 nm, attributed to an allowed π → π* transition between the ground and first excited states (S0 → S1). Conversely, dimer 2 showed similar spectral properties to the monomer, with a bathochromic shift of 20 nm. Notably, the intensity of the second vibronic band (A0−1) increased, possibly due to weak communication between the two chromophores. To gain further insight into the excited state processes, steady-state emission studies were conducted in the same solvents, as shown in Fig. 2c. Two well-resolved vibronic bands emerged at 642 nm (λemmax) and 700 nm, with a Stokes shift of 9 nm (225.7 cm−1), observed for monomer 1 upon photoirradiation. The emission quantum yield (ϕFl) was quantified as 76%, consistent with known BODIPY values.45 Interestingly, dimer 2 exhibited a significant quenching of emission (ϕFl = 18%) along with markedly different spectral features, suggesting that excitons may undergo non-radiative SB-CS processes in a nonpolar medium with minimal driving force. To further examine the effect of solvent polarity, studies were performed using the highly polar solvent DMSO. Fig. 2b presents the absorption spectra of the compounds, showing similar features to those in toluene, with slight red shifts. However, the monomer's fluorescence emission remained unaffected by the change in solvent, whereas nearly complete quenching was observed for dimer 2, providing strong evidence of excited state SB-CS (Fig. 2d). Using a moderate polar solvent, o-DCB, the results are shown in Fig. S11.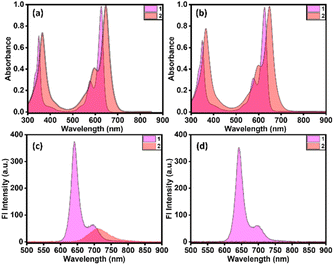 | ||
| Fig. 2 Ground state absorption (a and b) and emission (c and d) spectra of 1 and 2 in toluene (a and c) and DMSO (b and d). | ||
To support these steady-state observations, time-correlated single photon counting (TCSPC) was employed to measure singlet lifetimes, with nano-LED serving as the excitation source at 624 nm, and emission monitored at the respective wavelengths. The singlet lifetimes of 1 and 2 were recorded as approximately 6.0 and 5.59 ns, respectively.
Increasing solvent polarity had a negligible effect on the lifetime of 1, but the lifetime of 2 could not be measured due to the instrument's detection limit (see Fig. S12). Overall, both steady-state and time-resolved fluorescence studies confirmed the presence of excited-state photophysical processes in 2, regardless of solvent polarity. Next, the optical bandgap (E0,0) of the locally excited (LE) state was estimated by averaging the 0, 0 vibronic transition of the absorption and emission peaks. The E0,0 values for compounds 1 and 2 were evaluated as 1.96 eV and 1.83 eV, respectively. Furthermore, the radiative (kr) and non-radiative (knr) rate constants were evaluated, as they provide key insights into the decay pathways from the excited state. A higher knr relative to kr in the dimer indicates that non-radiative CS state formation is more favorable than photon emission, as summarized in Table 1.
| Compound | Solvent | λ absmax (nm) | λ emmax (nm) | E 0,0 (eV) | ΔṽStokes (cm−1) | ϕ Fl (%) | τ Fl (ns) | k r 107 s−1 | k nr 107 s−1 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Toluene | 627 | 636 | 1.96 | 225.7 | 76 | 6 | 12.6 | 4 |
| DCB | 630 | 644 | 1.95 | 345.1 | 74 | 5.48 | 13.5 | 4.75 | |
| DMSO | 627 | 643 | 1.95 | 397 | 69 | 5.48 | 12.6 | 5.65 | |
| 2 | Toluene | 647 | 710 | 1.83 | 1371.5 | 18 | 5.59 | 3.2 | 14.7 |
| DCB | 651 | — | — | — | — | — | — | — | |
| DMSO | 649 | — | — | — | — | — | — | — |
Electrochemical and spectroelectrochemical studies
To confirm the thermodynamic feasibility of the photoinduced charge-separated states, electrochemical experiments were conducted in o-DCB using tetrabutylammonium perchlorate (TBAClO4) as the supporting electrolyte. These experiments were performed at room temperature under a nitrogen atmosphere. The results from these electrochemical studies are essential to evaluate the redox gap (ΔE1/2) and the change in Gibbs free energy for the SB-CS process. Fig. 3a shows the differential pulse voltammograms of monomer 1 and dimer 2. Monomer 1 displayed a reversible reduction wave at −0.81 V and a quasi-reversible oxidation wave at 1.05 V, while dimer 2 exhibited two distinct reduction wave potentials at −0.59 and −0.81 V. An anodic shift of 220 mV for the first redox wave confirmed electronic interaction between the orthogonally arranged BODIPY moieties. Additionally, three quasi-reversible oxidation peaks at 1.13, 1.26, and 1.49 V were observed for dimer 2 (the reversibility of the redox waves was confirmed by cyclic voltammetry, as shown in Fig. S13). The estimated redox gaps were 1.86 V for monomer 1 and 1.72 V for dimer 2. A smaller electrochemical bandgap than the previously determined E0,0 supported the thermodynamic feasibility of SB-CS in dimer 2. | ||
| Fig. 3 (a) DPVs of the indicated compounds and (b) charge-separated spectrum deducted from spectroelectrochemical experiments for dimer 2. | ||
After determining redox potential through electrochemical experiments, spectroelectrochemical studies were conducted to identify the charge-separated features. An optically transparent thin-layer cell with three electrodes—a platinum (Pt) button, a Pt wire serving as the working and counter electrodes, respectively, and an Ag/AgCl reference electrode was utilized to conduct this experiment. As shown in Fig. S14a, during the oxidation process, the peaks of the neutral compound at 368 and 651 nm decreased in intensity, accompanied by the appearance of new peaks at 449 and 590 nm, as well as a broad peak from 720 to 850 nm. Additionally, clear isosbestic points appeared at 415 and 717 nm. Conversely, when the first reduction potential was applied, the original peaks disappeared, and two new intense bands emerged at 450 nm and a broad peak spanning 710 to 900 nm (Fig. S14b). These peaks are expected to appear in the same region during the event of charge separation. Next, a charge-separated spectrum was obtained by averaging the spectra of the radical cation and anion, then subtracting the spectrum of the neutral compound, as shown in Fig. 3b. Such a spectrum, closely resembling spectral features, can be expected when a CS spectrum is generated from transient studies.
Theoretical investigation
Having rationalized the existence of SB-CS in dimer 2, we conducted DFT calculations to understand the molecules' structural and electronic properties. The dimer was fully optimized on the Born–Oppenheimer potential energy surface in the most polar medium using B3LYP/6-311G (df,pd) SCRF (IEFPCM, Solvent = Dimethylsulfoxide) theory.46 Ground-state optimization confirmed that both chromophores are perpendicular to each other, with a dihedral angle of 89° and a B–B distance of 7.14 Å. As expected for symmetric dimers, the first two HOMO and the first two LUMO pairs were degenerate. Subsequently, the ground state-optimized structure was subjected to excited-state optimization, revealing a slight twist in the dihedral angle, which decreased to 79°. This twist may enhance communication and orbital overlap between the two moieties, potentially facilitating SB-CS. The molecular electrostatic potential (ESP) map was generated in the same solvent to visualize the distribution of electron density. As expected, a symmetrical distribution was observed, confirming the presence of a quadrupolar state in the ground state. Additionally, the ground state potential energy surface (PES) was generated by scanning the coordinates of the optimized geometry to determine the energy barrier for rotation of the chromophores as a function of the dihedral angle between the two moieties. The energy required to rotate the molecule from its most stable (orthogonal, global minimum) orientation to the planar and most unstable (global maximum) orientation was calculated as 51 kcal mol−1 (2.2 eV) and 160 kJ mol−1 (7 eV), respectively. The relatively high energy barriers suggest that the compound is rigid, making the orthogonal conformation the most favorable. The optimized structures and ESP maps are shown in Fig. S15.Furthermore, to investigate the nature of electronic transitions and excitonic interactions, TD-DFT calculations were performed on the ground-state-optimized structure. Here, the initial five excited states were considered to understand the hole–electron transfer mechanism. The two nearly degenerate states, S1 and S2, with the same low oscillator strength (f) of 0.12, possess a significant CT character (% CT = 78), where the hole is positioned on one fragment and the electron is confined to the second chromophore.47
Additionally, two nearly degenerate Frenkel states, S3 and S4, with the same f (1.12), were identified, where the electron density is localized on the same chromophore. Similarly, the S5 state can be attributed to a Frenkel state, as it also has electron density on the same fragment. Fig. 4 shows the hole–electron transfer results, where natural transition orbitals (NTO) calculations were used to analyze the distribution of the hole (column b) and electron (column c). NTO results revealed a dominant orbital pair, along with other complex pairs involved in a specific electronic transition, as shown in Fig. 4 and S16, along with the corresponding percent contributions.47,50 These results clearly indicate that states S1 and S2 are responsible for CT transitions, while the other three are associated with Frenkel states, based on the distribution of electron density cubes. After performing TD-DFT calculations, the output files were loaded into the MultiWFN codes for a more concise and physically intuitive visualization of the electronic transition.48 These tools helped generate the combined hole–electron distribution, shown in column d, along with the percentage of CT and LE character for each transition (Table S1). To validate these findings, charge density difference maps were also created by subtracting the electron density of the ground state from that of the excited state. An asymmetric distribution of electron density was observed for the first two excited states, where red indicates the electron-donating region and blue marks the electron-accepting area, which differs from the following three states. Based on these results, it can be ascertained that the symmetrical electron density distribution in the ground state is effectively transformed into an unsymmetrical dipolar state, leading to SB-CS and the formation of the BODIPY+-BODIPY− species (additional information is provided in Table S1).
Following the realization of SB-CS from experiments and computational studies, the excitonic coupling constant (J) was calculated to predict the interaction between excited states localized on different chromophores. This constant includes inputs from both short-range (JCT) and long-range (Jcoul) interactions. The point-dipole approximation method can be used to determine the interaction between the transition charge distributions of two chromophores, which accounts for Jcoul. In this work, the transition charge from the electrostatic potential (TrESP) method was employed to calculate the coulombic energy between the two moieties. This method yields satisfactory results when the interchromophoric distance is smaller than the chromophore size, as the dipole–dipole assumption tends to overestimate the exciton coupling energy. In the TrESP approach, partial point charges are assigned to individual atoms to generate an electrostatic field that represents the movement of electrons. This field is then used to determine how one chromophore's field interacts with the other. The Jcoul can be efficiently calculated using eqn (1):49–51
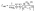 | (1) |
The effective excitonic interaction, mainly defined as charge-mediated short-range coupling (JCT), arises from the overlap of wavefunctions between adjacent chromophores. When the Frenkel and CT states are energetically distinct, an approximate value of JCT can be calculated as:29,50
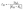 | (2) |
 | (3) |
 | (4) |
The calculated values of th and te based on these equations are 363 and 40 cm−1. Next, eqn (2) was used to determine the final value of JCT after incorporating all variables into the equation, resulting in −12.1 cm−1. Ultimately, the overall excitonic coupling (J) was obtained by adding the short-range coupling constant (JCT) and the long-range coupling (Jcoul), given as29,50
| J = Jcoul + JCT | (5) |
The net excitonic coupling between two neighboring BODIPY chromophores was found to be 3.9 cm−1, indicating very weak or negligible excitonic coupling due to the orthogonal orientation.
SB-CS dynamics
A Jablonski-type energy diagram (Fig. 5) was created for 2 using optical and electrochemical data to analyze photophysical processes. The change in Gibbs free energy (ΔGCS) for these events was estimated based on solvent polarity using Rehm–Weller equations.53 This method yielded ΔGCS ≈ values of approximately 0.11, −0.30, and −0.40 eV for the dimer in toluene, DCB, and DMSO, respectively. The Born dielectric continuum model tends to overestimate the polarity of nonpolar solvents, which may explain why ΔGCS in toluene appears slightly higher than expected.54 Nonetheless, emission studies were supportive of SB-CS, confirming that this event could occur with zero driving force (ΔGCS = 0 or iso-energetic process) in toluene. As mentioned earlier, this realization of generating radical ion pairs without energy loss from the excited state is a key factor when designing devices aimed at achieving extremely high light conversion efficiency.55 The thermodynamic driving force for charge separation (ΔGCS) and charge recombination (ΔGCR) is summarized in Table 2. | ||
| Fig. 5 As a function of solvent polarity, the Jablonski-type energy map illustrates SB-CS in dimer 2. | ||
| Compound | Solvent | ΔGsol (eV) | ΔGCS (eV) | τ A→SB-CS (ps) | k A→SB-CS × 1010 (s−1) | ΔGCR (eV) | τ B←SB-CS (ps) | k B←SB-CS × 109 (s−1) |
|---|---|---|---|---|---|---|---|---|
| 2 | Toluene | 0.213 | 0.11 | 87 | 1.2 | −1.93 | 3200 | 0.31 |
| DCB | −0.196 | −0.30 | 40 | 2.5 | −1.52 | 367 | 2.72 | |
| DMSO | −0.297 | −0.40 | 6 | 16.7 | −1.42 | 153 | 6.54 |
Next, solvent-dependent pump-probe studies were performed to explore the excitation-state phenomenon using femtosecond transient absorption (fs-TA) spectroscopy. The fs-TA measurements of monomer 1 in all three solvents are shown in Fig. S17. These measurements were taken at room temperature in an argon-purged environment using a 100 fs pulse laser. As shown in Fig. S17a, upon photoexcitation of monomer 1 at 625 nm, defining characteristics of the singlet excited state absorption (ESA) of BODIPY were observed. Instantaneous ESA signals appeared at 458, 594, and 661 nm, along with three negative signals at 575, 625, and 700 nm. Comparing these spectral features and peak positions with steady-state absorbance and emission spectra, signals at 575 and 625 nm were attributed to ground-state bleaching (GSB). In comparison, the peak at 700 nm was assigned to stimulated emission (SE). Similar spectral behavior was observed across solvents of different polarities. Additionally, the fs-TA data were analyzed using GloTarAn56 analysis, which involved singular value decomposition (SVD) of the three-dimensional time-wavelength map, followed by target analysis (using A → GS) to extract key components and their kinetic details from the spectra. The species-associated spectra (SAS) primarily displayed a single component (A) representing the LE state absorption (S1 → Sn electronic transitions). The lowest singlet excited state of BODIPY did not fully decay to the ground state GS within our instrument's time window, so it was labeled as >3 ns, consistent with the TCSPC decay lifetime for monomer 1. These findings are illustrated in Fig. S17 in three different solvents. Further, fs-TA experiments were conducted on dimer 2 to observe the SB-CS (Fig. 6). In this case, the same spectral features appeared, along with the formation of a new transient species, identified by positive features around 700 nm. At the same location, new peaks emerged during spectroelectrochemistry, which confirms the formation of the CS state. This signal was not visible in the case of 1, which directly confirms the occurrence of SB-CS in dimer 2. In toluene (Fig. 5a), the intensity of this peak remains nearly constant during SB-CS, likely due to an equilibrium between the LE and SB-CS states. A target model (A ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) SB-CS → B → GS) was used to fit the fs-TA of the dimer, considering an equilibrium mechanism between the two states, where B represents the triplet state. The charge separation and recombination rate constants (kA→SB-CS and kB←SB-CS) were determined as (84 ps)−1 and (3.2 ns)−1, respectively. In polar media, such as o-DCB, the energy of the SB-CS state was lowered through solvation, making it more energetically favorable with ΔGCS ≈ −0.30 eV. A three-component target model, representing A → SB-CS → B → GS, was employed to extract the transient components and their decay kinetics, yielding kA→SB-CS of (39 ps)−1 and kB←SB-CS of (367 ps)−1 (Fig. 6b).
SB-CS → B → GS) was used to fit the fs-TA of the dimer, considering an equilibrium mechanism between the two states, where B represents the triplet state. The charge separation and recombination rate constants (kA→SB-CS and kB←SB-CS) were determined as (84 ps)−1 and (3.2 ns)−1, respectively. In polar media, such as o-DCB, the energy of the SB-CS state was lowered through solvation, making it more energetically favorable with ΔGCS ≈ −0.30 eV. A three-component target model, representing A → SB-CS → B → GS, was employed to extract the transient components and their decay kinetics, yielding kA→SB-CS of (39 ps)−1 and kB←SB-CS of (367 ps)−1 (Fig. 6b).
In the most polar solvent tested, DMSO, signals decayed rapidly due to enhanced solvation stabilization or larger changes in Gibbs free energy, which drive faster ultrafast photodynamics such as CS and CR. The SB-CS state formed in 6 ps from LE states and recombined back to the triplet state in 153 ps (Fig. 6c). The component extracted from the target analysis, representing SB-CS, closely resembles the earlier spectrum deduced from spectroelectrochemistry, validating the excited-state symmetry-breaking charge separation in dimer 2 across all three solvents used. The time and rate constants for SB-CS and CR, along with their Gibbs free energy changes, are summarized in Table 2.
Theoretical assessment
After describing the nature of exciton coupling using a theoretical approach, the classical Marcus theory was applied to the newly synthesized dimer 2 to assess the experimental coupling strength between the two chromophores.57 Electron transfer theory can also be used to explain the dynamics of SB-CS and CR, as they are broader parts of the electron transfer process. The following expression of Marcus' theory allows for a quantitative understanding of the electron transfer mechanism.58,59 | (6) |
The rate constants kA→SB-CS and kB←SB-CS were determined as 16.6 × 1010 and 65.3 × 108 s−1. For consistency, the same solvent used in the computational calculations was chosen. Applying these values to eqn (6) produced V and λ values of 0.0076 and 0.77 eV. Due to the orthogonal orientation, V was significantly reduced, confirming a nonadiabatic regime and very weak interaction between the BODIPY chromophores. Overall, this indicates that SB-CS occurs between states with minimal orbital overlap. Additionally, the activation barrier for SB-CS was estimated using the following expression,60–62
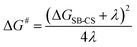
| (7) |
resulting in a value of 0.045 eV. The low barrier value may be attributed to the strong solvation effect of the polar DMSO medium. Ultimately, these results facilitated plotting the Marcus parabola, where λ > −ΔGSB-CS and λ < −ΔGCR, confirming that SB-CS operates within the Marcus normal region, while CR falls into the Marcus inverted region, respectively, as shown in Fig. 7.63,64
Conclusion
In summary, the occurrence of SB-CS in dimer 2via far-red photo-irradiation, independent of solvent polarity, has been successfully demonstrated. The presence of styryl moieties extended the π-conjugation, which led to strong absorption in the far-red region. A significant quenching of emission was observed in all three solvents used, an early indication of SB-CS in the dimer 2, which was not detected in Monomer 1. The redox gap, determined from electrochemical experiments, was found to be lower than the energy of the locally excited state (E0,0), confirming the thermodynamic feasibility of SB-CS. To support these experimental observations, extensive theoretical studies were performed, revealing an orthogonal spatial orientation. TD-DFT calculations revealed an unsymmetrical distribution (dipolar state) of electron density, indicating the presence of hole–electron pairs on different chromophores in excited states. Additionally, the short-range coupling (JCT) and long-range coupling (Jcoul) were determined; their negligible values suggested a very weak interaction with null-excitonic coupling, responsible for SB-CS at minimal energy loss. Femtosecond transient absorption experiments were conducted to observe signals related to SB-CS transient species. Analysis of fs-TA data by GloTarAn revealed the lifetime of SB-CS, which ranged from 0.153 to 3.2 ns depending on the solvent polarity. Finally, the degree of communication between the two BODIPY chromophores was evaluated using Marcus's electron transfer theory, with results aligning well with theoretical coupling constants. This work demonstrates how the proper modeling of distance and orientation in symmetrical dimers can generate a long-lasting charge-separated state without a driving force (zero energy loss), which is useful for designing optoelectronic and energy-harvesting devices with significantly improved photoconversion efficiency.Author contributions
Methodology: synthesis, A. Y.; R. R. K carried out the measurements; R. R. K and F. D. analysed the results and wrote the manuscript; F. D. conceived the project, supervised the work, and secured funding.Conflicts of interest
The authors declare no conflicts of interest.Data availability
All the data supporting this article have been included in supplementary information (SI). Supplementary information: synthesis and experimental details, additional CV and fs-TA spectral data. See DOI: https://doi.org/10.1039/d5sc07818k.Acknowledgements
This work was supported by the National Science Foundation (grant # 2514911 to FD).References
- L. Estergreen, A. R. Mencke, D. E. Cotton, N. V. Korovina, J. Michl, S. T. Roberts, M. E. Thompson and S. E. Bradforth, Acc. Chem. Res., 2022, 55, 1561–1572 CrossRef CAS PubMed.
- (a) T. Kumpulainen, B. Lang, A. Rosspeintner and E. Vauthey, Chem. Rev., 2017, 117, 10826–10939 CrossRef CAS; (b) B. Dereka and E. Vauthey, J. Phys. Chem. Lett., 2017, 8, 3927–3932 CrossRef CAS PubMed.
- A. H. Proppe, Y. C. Li, A. Aspuru-Guzik, C. P. Berlinguette, C. J. Chang, R. Cogdell, A. G. Doyle, J. Flick, N. M. Gabor and R. van Grondelle, Nat. Rev. Mater., 2020, 5, 828–846 CrossRef CAS.
- Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899–4032 CrossRef.
- A. N. Bartynski, M. Gruber, S. Das, S. Rangan, S. Mollinger, C. Trinh, S. E. Bradforth, K. Vandewal, A. Salleo and R. A. Bartynski, J. Am. Chem. Soc., 2015, 137, 5397–5405 CrossRef CAS.
- B. Dereka, M. Koch and E. Vauthey, Acc. Chem. Res., 2017, 50, 426–434 Search PubMed.
- J. M. Giaimo, A. V. Gusev and M. R. Wasielewski, J. Am. Chem. Soc., 2002, 124, 8530–8531 CrossRef CAS.
- M. E. El-Khouly, E. El-Mohsnawy and S. Fukuzumi, J. Photochem. Photobiol., C, 2017, 31, 36–83 CrossRef CAS.
- M. W. Holman, P. Yan, D. M. Adams, S. Westenhoff and C. Silva, J. Phys. Chem., 2005, 109, 8548–8552 Search PubMed.
- (a) W. Kim, A. Nowak-Król, Y. Hong, F. Schlosser, F. Würthner and D. Kim, J. Phys. Chem. Lett., 2019, 10, 1919–1927 CrossRef CAS; (b) Y. Hong, J. Kim, W. Kim, C. Kaufmann, H. Kim, F. Würthner and D. Kim, J. Am. Chem. Soc., 2020, 142, 7845–7857 CrossRef CAS PubMed; (c) Y. Hong, F. Schlosser, W. Kim, F. Würthner and D. Kim, J. Am. Chem. Soc., 2022, 144, 15539–15548 CrossRef CAS PubMed; (d) S. Medina Rivero, M. J. Alonso-Navarro, C. Tonnelé, J. M. Marín-Beloqui, F. Suárez-Blas, T. M. Clarke, S. Kang, J. Oh, M. M. Ramos, D. Kim, D. Casanova, J. L. Segura and J. Casado, J. Am. Chem. Soc., 2023, 145, 27295–27306 CrossRef CAS.
- S. Bhosale, A. L. Sisson, P. Talukdar, A. Fürstenberg, N. Banerji, E. Vauthey, G. Bollot, J. Mareda, C. Röger and F. Würthner, Science, 2006, 313, 84–86 Search PubMed.
- A. L. Sisson, N. Sakai, N. Banerji, A. Fürstenberg, E. Vauthey and S. Matile, Angew. Chem., Int. Ed., 2008, 47, 3727–3729 CrossRef CAS.
- Y. Wu, R. M. Young, M. Frasconi, S. T. Schneebeli, P. Spenst, D. M. Gardner, K. E. Brown, F. Würthner, J. F. Stoddart and M. R. Wasielewski, J. Am. Chem. Soc., 2015, 137, 13236–13239 CrossRef CAS PubMed.
- Z. Szakacs and E. Vauthey, J. Phys. Chem. Lett., 2021, 12, 4067–4071 CrossRef CAS PubMed.
- M. T. Whited, N. M. Patel, S. T. Roberts, K. Allen, P. I. Djurovich, S. E. Bradforth and M. E. Thompson, Chem. Commun., 2012, 48, 284–286 RSC.
- E. A. Margulies, J. L. Logsdon, C. E. Miller, L. Ma, E. Simonoff, R. M. Young, G. C. Schatz and M. R. Wasielewski, J. Am. Chem. Soc., 2017, 139, 663–671 CrossRef CAS PubMed.
- M. H. Vos, F. Rappaport, J.-C. Lambry, J. Breton and J.-L. Martin, Nature, 1993, 363, 320–325 CrossRef CAS.
- A. L. Sisson, N. Sakai, N. Banerji, A. Fürstenberg, E. Vauthey and S. Matile, Angew. Chem., Int. Ed., 2008, 47, 3727–3730 Search PubMed.
- A. N. Bartynski, M. Gruber, S. Das, S. Rangan, S. Mollinger, C. Trinh, S. E. Bradforth, K. Vandewal, A. Salleo, R. A. Bartynski, W. Brütting and M. E. Thompson, J. Am. Chem. Soc., 2015, 137, 5397–5405 CrossRef CAS.
- E. Romero, V. I. Novoderezhkin and R. Van Grondelle, Nature, 2017, 543, 355–365 CrossRef CAS.
- X. Sheng, Z. Li, M. Zhang, X. Chen, L. Xue, W. Han, Y. Li, F. Wang and L. Jiang, Energy Environ. Sci., 2025, 18, 1722–1731 Search PubMed.
- E. Vauthey, ChemPhysChem, 2012, 13, 2001–2011 Search PubMed.
- W. Rettig, Angew Chem. Int. Ed. Engl., 1986, 25, 971–988 CrossRef.
- M. Kellogg, A. Akil, D. S. M. Ravinson, L. Estergreen, S. E. Bradforth and M. E. Thompson, Faraday Discuss., 2019, 216, 379–394 Search PubMed.
- Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Structural Changes Accompanying Intramolecular Electron Transfer: Focus on Twisted Intramolecular Charge-Transfer States and Structures, Chem. Rev., 2003, 103(10), 3899–4032 CrossRef.
- A. F. Coleman, M. Chen, J. Zhou, J. Y. Shin, Y. Wu, R. M. Young and M. R. Wasielewski, J. Phys. Chem. C, 2020, 124, 10408–10419 CrossRef CAS.
- Y. Wu, R. M. Young, M. Frasconi, S. T. Schneebeli, P. Spenst, D. M. Gardner, K. E. Brown, F. Würthner, J. F. Stoddart and M. R. Wasielewski, J. Am. Chem. Soc., 2015, 137, 13236–13239 CrossRef CAS PubMed.
- Y. Guo, Z. Ma, X. Niu, W. Zhang, M. Tao, Q. Guo, Z. Wang and A. Xia, J. Am. Chem. Soc., 2019, 141, 12789–12796 CrossRef CAS PubMed.
- E. Sebastian and M. Hariharan, J. Am. Chem. Soc., 2021, 143, 13769–13781 Search PubMed.
- R. R. Kaswan, D. Molina, L. Ferrer-López, J. Ortiz, P. A. Karr, Á. Sastre-Santos and F. D'Souza, Angew. Chem., Int. Ed., 2025, 64, e202502516 CrossRef CAS.
- P. Roy, G. Bressan, J. Gretton, A. N. Cammidge and S. R. Meech, Angew. Chem., Int. Ed., 2021, 60, 10568–10572 CrossRef CAS PubMed.
- A. Aster, G. Licari, F. Zinna, E. Brun, T. Kumpulainen, E. Tajkhorshid, J. Lacour and E. Vauthey, Chem. Sci., 2019, 10, 10629–10639 RSC.
- V. Markovic, D. Villamaina, I. Barabanov, L. M. Lawson Daku and E. Vauthey, Angew. Chem., Int. Ed., 2011, 50, 7596–7598 CrossRef CAS.
- J. H. Golden, L. Estergreen, T. Porter, A. C. Tadle, M. R. D. Sylvinson, J. W. Facendola, C. P. Kubiak, S. E. Bradforth and M. E. Thompson, ACS Appl. Energy Mater., 2018, 1, 1083–1095 CrossRef CAS.
- J. J. Piet, W. Schuddeboom, B. R. Wegewijs, F. C. Grozema and J. M. Warman, J. Am. Chem. Soc., 2001, 123, 5337–5347 CrossRef CAS PubMed.
- C. Trinh, K. Kirlikovali, S. Das, M. E. Ener, H. B. Gray, P. Djurovich, S. E. Bradforth and M. E. Thompson, J. Phys. Chem. C, 2014, 118, 21834–21845 Search PubMed.
- T. Kim, J. Kim, H. Mori, S. Park, M. Lim, A. Osuka and D. Kim, Phys. Chem. Chem. Phys., 2017, 19, 13970–13977 RSC.
- A. Yahagh, R. R. Kaswan, S. Kazemi, P. A. Karr and F. D'Souza, Chem. Sci., 2024, 15, 906–913 RSC.
- S. Kazemi, A. Z. Alsaleh, P. A. Karr and F. D'Souza, J. Am. Chem. Soc., 2024, 146, 13509–13518 Search PubMed.
- R. R. Kaswan, D. R. Subedi, R. Reid and F. D’Souza, Chem.–Asian J., 2025, e70222 Search PubMed.
- S. Ghosh, S. Mula, P. Biswas and A. Patra, J. Phys. Chem. C, 2024, 128, 12762–12774 Search PubMed.
- I. S. Yadav, R. R. Kaswan, A. Liyanage, R. Misra and F. D'Souza, J. Phys. Chem. C, 2024, 128, 4934–4945 CrossRef CAS.
- A. Loudet and K. Burgess, Chem. Rev., 2007, 107, 4891–4932 Search PubMed.
- M. E. El-Khouly, S. Fukuzumi and F. D'Souza, ChemPhysChem, 2014, 15, 30–47 Search PubMed.
- T. Yogo, Y. Urano, Y. Ishitsuka, F. Maniwa and T. Nagano, J. Am. Chem. Soc., 2005, 127, 12162–12163 Search PubMed.
- M. E. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- (a) M. Wazid, Y. Rout, A. Z. Alsaleh, R. R. Kaswan, R. Misra and F. D'Souza, Chem. Commun., 2025, 61, 6803–6806 RSC; (b) C. Risko, M. D. McGehee and J.-L. Brédas, Chem. Sci., 2011, 2, 1200–1218 RSC; (c) R. R. Kaswan, S. Washburn, U. Oji, H. Wang and F. D'Souza, Chem.–Eur. J., 2025, 31, e202404165 Search PubMed; (d) R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS.
- K. Wang, X. Chen, S. Peng, G. L. J. Xu, L. Zhang, D. Wu and J. Xia, J. Chem. Phys., 2024, 160, 164719 Search PubMed.
- G. D. Scholes and K. P. Ghiggino, J. Phys. Chem., 1994, 98, 4580–4590 Search PubMed.
- A. Mazumder, K. Vinod, P. D. Maret, P. P. Das and M. Hariharan, J. Phys. Chem. Lett., 2024, 15, 5896–5904 CrossRef CAS.
- M. D. Newton, Chem. Rev., 1991, 91, 767–792 CrossRef CAS.
- D. Rehm and A. Weller, Isr. J. Chem., 1970, 8, 259–271 CrossRef CAS.
- H. Imahori, K. Hagiwara, M. Aoki, T. Akiyama, S. Taniguchi, T. Okada, M. Shirakawa and Y. Sakata, J. Am. Chem. Soc., 1996, 118, 11771–11782 Search PubMed.
- T. M. Clarke, Nat. Energy, 2020, 5, 644–645 CrossRef CAS.
- J. J. Snellenburg, S. Laptenok, R. Seger, K. M. Mullen and I. H. Van Stokkum, J. Stat. Software, 2012, 49, 1–22 Search PubMed.
- Glotaran, http://glotaran.org/.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 Search PubMed.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 Search PubMed.
- T. Umeyama and H. Imahori, Nanoscale Horiz., 2018, 3, 352–366 Search PubMed.
- M. Smitha, E. Prasad and K. Gopidas, J. Am. Chem. Soc., 2001, 123, 1159–1165 Search PubMed.
- G. A. Parada, Z. K. Goldsmith, S. Kolmar, B. Pettersson Rimgard, B. Q. Mercado, L. Hammarström, S. Hammes-Schiffer and J. M. Mayer, Science, 2019, 364, 471–475 CrossRef CAS PubMed.
- I. R. Gould, J. E. Moser, B. Armitage, S. Farid, J. L. Goodman and M. S. Herman, J. Am. Chem. Soc., 1989, 111, 1917–1919 CrossRef CAS.
- D. M. D'Alessandro and F. R. Keene, Chem. Soc. Rev., 2006, 35, 424–440 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |