Open Access Article
Open Access ArticleRegulation of heteroatom positioning in multiple resonance thermally activated delayed fluorescence materials: performance optimization for blue/red emission
Lifang
Yin
a,
Yi
Zhao
a,
Qiang
Gao
a,
Yajun
Yin
a,
Tengfei
He
a,
Yufei
Yang
a,
Aimin
Ren
 a,
Tongshun
Wu
b,
Hui
Li
a and
Luyi
Zou
a,
Tongshun
Wu
b,
Hui
Li
a and
Luyi
Zou
 *a
*a
aInstitute of Theoretical Chemistry, College of Chemistry, Jilin University, Changchun 130023, P. R. China. E-mail: zouly@jlu.edu.cn
bKey Laboratory of Functional Materials Physics and Chemistry of Ministry of Education, Jilin Normal University, Changchun 130103, China
First published on 2nd December 2025
Abstract
Strategically incorporating Se into B/N-heteropolycyclic frameworks is key to modulating multiple resonance (MR) systems and developing high-performance TADF materials. Combining density functional theory and spin-component scaled coupled cluster calculations, this study reveals the TADF mechanism regulated by the heavy-atom effect in model molecule BNSSe, and designs two types of high-performance MR-TADF materials based on BNSSe. (1) The blue-emission molecule 1 (469 nm) achieves complementary short-range charge transfer/long-range charge transfer advantages via three para-B–π–N units. Its reverse intersystem crossing rate (kRISC) reaches 108 s−1 (three orders of magnitude higher than BNSSe), benefiting from the synergy of a reduced singlet–triplet energy gap, moderately enhanced spin–orbit coupling (SOC), and suppressed structural relaxation. (2) The red-emission molecules 2–7 (≈630 nm) were further developed via a delicately designed π-bonding/non-bonding molecular orbital hybridization strategy. This series of molecules not only maintain a high radiative decay rate but also effectively inhibit the non-radiative decay process, and their design concept is expected to break through the constraints of the traditional energy gap law. Theoretical studies reveal that the spatial position of heteroatoms can modulate molecular geometry and induce axial redistribution of frontier molecular orbital electron density, thereby selectively enhancing the contribution of Se atoms to the excited-state transition orbitals and enabling precise regulation of SOC strength. This work not only deepens the theoretical understanding of the heavy-atom effect mechanism but also provides a new strategy for developing high-performance MR-TADF materials through the targeted regulation of SOC and kRISCvia atomic site engineering.
1 Introduction
Organic light-emitting diodes (OLEDs), as the core of next-generation display technologies, have achieved a leapfrog upgrade from traditional display devices to intelligent interface platforms integrating three features: functional integration, diverse forms, and scenario adaptation.1 Their breakthroughs in high contrast, flexible integration, and low latency will continue to redefine future human–computer interaction modes. The key to the breakthrough of this technology lies in the iterative innovation of materials. Thermally activated delayed fluorescence (TADF) materials, with the dual advantages of 100% exciton utilization and no noble metal dependence, are widely recognized in the industry as the most promising next-generation luminescent materials after phosphorescent materials.2–5In recent years, multiple resonance (MR)-TADF materials have shown narrow emission bands (full width at half maximum, FWHM < 70 nm). This is attributed to their rigid structural skeletons and localized distribution of frontier molecular orbitals (FMOs), which result in weak electron-vibration coupling and small structural relaxation. They have thus become a key material system for achieving the BT.2020 ultra-high-definition display color gamut standard.6–13 However, such materials still face severe challenges in practical device applications. Limited by relatively low reverse intersystem crossing rates (kRISC, usually <105 s−1), triplet excitons accumulate excessively at high current densities. This is because they cannot be rapidly converted to singlet excitons through the RISC channel. Such accumulation leads to significant efficiency roll-off via non-radiative pathways like triplet–triplet annihilation.14,15 This phenomenon is particularly prominent in blue-emitting MR-TADF materials. Their high triplet energy levels (T1 > 2.8 eV) not only exacerbate exciton annihilation effects but also easily trigger radical cation degradation (e.g., intramolecular cyclization reactions). As a result, the device lifetime (LT50) is generally less than 100 hours.16
For molecular design aiming to enhance kRISC, there are currently two main strategies. One is to reduce the singlet–triplet energy gap (ΔEST) by expanding the B/N skeleton. For example, Huang et al. developed DABNA-3B and BCzBN-3B blue-emitting materials based on the π-extension strategy of B–N covalent bonds, with their kRISC reaching 105 s−1.17 Although this performance is outstanding among pure organic MR-TADF materials, it still lags behind that of typical metal complex systems (>106 s−1). The other is to enhance the spin–orbit coupling (SOC) effect by introducing heavy atoms. For instance, the BNSSe and BNSeSe green-emitting materials designed by Hu et al. achieved a kRISC of 105–106 s−1 through embedding Se atoms into the B/N skeleton.18 In particular, the Yasuda group from Kyushu University achieved a kRISC of 108 s−1 in the CzBSe molecule by introducing Se atoms.19 These findings provide important insights for the molecular design in this study. By synergistically regulating B/N skeleton expansion and heavy atom effects, it is expected that the existing kRISC limit will be broken.
Inspired by the above strategies, two key scientific questions are proposed from the perspective of synergizing excited-state regulation and molecular engineering. First, how can precise π-extension of the B/N skeleton be achieved through structural design while maintaining the MR effect? This process requires establishing a dynamic balance mechanism of “orbital localization–delocalization”. Excessive delocalization weakens the atomic localization of frontier molecular orbitals, leading to intensified vibrational relaxation. Insufficient extension, however, fails to effectively reduce ΔEST to enhance kRISC. Second, although introducing Se atoms can significantly improve kRISC, the synthesis of organic Se compounds often faces great challenges. In practical applications, it is necessary to balance the amount of Se atoms introduced and performance gains. Then, how can the two be balanced to maximize kRISC while keeping the number of Se atoms unchanged? By cleverly designing the molecular geometry and electronic distribution, it may be possible to effectively regulate the excited-state properties. This can give full play to the advantages of the heavy atom effect while minimizing the amount of Se atoms introduced. The potential of Se atom introduction in improving kRISC performance is further explored, providing new ideas for the design and development of related materials.
Current systematic investigations of MR-TADF materials in our group reveal a pronounced imbalance in development among the three primary colors (red, green, blue).20 Compared to the significant advancements in blue and green systems, research progress on pure red MR-TADF emitters substantially lags behind, as evidenced by both the scarcity of reported molecular structures and their inferior photophysical performances. The reasons include, in addition to solving common issues such as kRISC enhancement, that red emitters face special challenges from the energy gap law. That is, as the emission wavelength redshifts, the reduced energy gap leads to a significant increase in non-radiative transition rates, resulting in a sharp decline in luminous efficiency. This creates a dilemma where high luminous efficiency and red emission are difficult to reconcile, severely restricting the commercial development of OLED display technology.21,22 Although Liu et al. achieved a redshift of the emission spectrum by introducing strong electron-withdrawing cyano groups to lower the lowest unoccupied molecular orbital (LUMO) energy level, and developed CNCz–BNCz as the first orange-red MR-TADF material, its emission peak at 581 nm still has a significant gap from the 630 nm red emitter required by the BT.2020 standard.23,24 This performance gap severely hinders the commercialization of OLED full-color display technology, highlighting the urgency of theoretical innovation and molecular design breakthroughs in the development of red material systems.
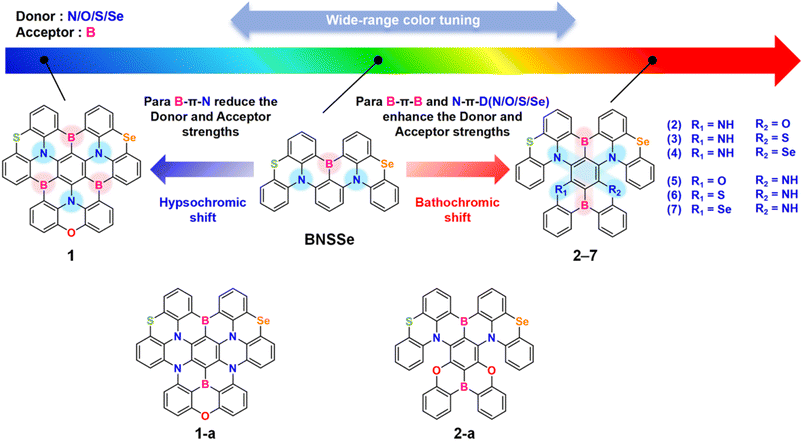
Based on the BNSSe molecular skeleton containing a single Se atom, we introduced a B/N fused-ring rigid structure for π-extension and synergistically utilized the heavy atom effect, designing molecule 1 with fast RISC characteristics (Fig. 1). Compared with the molecule BNSSe with short-range charge transfer (SRCT) properties, molecule 1 exhibits hybrid SRCT/long-range CT (LRCT) characteristics due to the expanded B/N skeleton. It has both a smaller ΔEST and a larger SOC, increasing the kRISC to 108 s−1 (a 3-orders-of-magnitude enhancement), which is comparable to that of typical metal complex systems. Meanwhile, molecule 1 adopts a modification strategy using three sets of para-B–π–N units, which synergistically weakens the electron-withdrawing/donating abilities of B/N atoms. This raises the LUMO energy level and lowers the HOMO energy level, significantly widening the HOMO–LUMO energy gap (ΔEH–L) and achieving a blue-shifted emission wavelength of 469 nm. This result provides a new design idea for developing blue TADF materials with both high kRISC and narrowband emission.
To meet the BT.2020 standard requirements for pure red emitters, we modified the skeleton of molecule 1. By exchanging N and B atoms at specific sites, we constructed molecule 1-a containing two sets of para-N–π–N and one set of para-B–π–B structures. This design significantly enhanced the electron-withdrawing/donating abilities of B/N atoms, increasing the HOMO energy level and lowering the LUMO energy level. The ΔEH–L was notably reduced. Combined with the π-conjugation extension effect of the rigid fused ring, its emission spectrum redshifted to 703 nm. However, this wavelength deviates from the target value. Further studies revealed that although molecule 1-a exhibits certain SRCT characteristics, the two lower N atoms are directly bonded to the benzene rings at both ends. While this structure enhances molecular rigidity, excessive conjugation causes electron clouds to be overly localized in the π bonding orbitals of the three central benzene rings. As a result, the reorganization energy is only slightly lower than that of the BNSSe molecule. Combined with the ultra-narrow energy gap effect, the non-radiative transition rate (kSnr = 4.18 × 107 s−1) significantly exceeds the radiative transition rate (kSr = 1.81 × 107 s−1), leading to luminescence quenching. Drawing on these results, we adjusted the design strategy. While keeping the main skeleton unchanged, we innovatively fused the DOBNA25 molecule (with significant MR-TADF characteristics) with the BNSSe skeleton to construct molecule 2-a. This design introduced an O-bridged unit to break the direct connection between the two lower N atoms and the benzene rings at both ends, forming a unique B–N–O structural arrangement. This structure not only enhances SRCT characteristics but also, through the hybrid π-bonding/non-bonding molecular orbitals formed by the central benzene ring with B, N, and O units, effectively reduces the reorganization energy while maintaining the same order of magnitude of radiative transition rate as molecule 1-a. Thus, the non-radiative transition rate is significantly reduced (kSnr = 2.48 × 105 s−1). However, the emission wavelength of molecule 2-a is 595 nm, still deviating from the target of 630 nm (Fig. S8–S10 and Table S8). To further optimize performance, we attempted fine regulation. By replacing one O atom with an N atom (with stronger electron-donating ability), we designed molecules 2 and 5, whose emission wavelengths were successfully adjusted to around 630 nm. Subsequently, based on molecules 2 and 5, we introduced S and Se atoms (with heavy atom effects) to replace O atoms, constructing molecules 3/6 and 4/7, respectively. All these molecules achieved pure red emission around 630 nm. Meanwhile, their kSnr is much smaller than kSr, creating conditions to break through the limitations of the energy gap law.
Notably, given the asymmetric structural characteristics of the parent molecule BNSSe, in our designed red emitters 2–7, with the main skeleton unchanged, only adjusting the relative positions of the lower heteroatoms (O/S/Se) and Se in the main skeleton for the two structures of B–π–B/Se–N–π–N (R1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) = NH, R2
= NH, R2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) = O/S/Se) and B–π–B/S–N–π–N (R1
= O/S/Se) and B–π–B/S–N–π–N (R1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) = O/S/Se, R2
= O/S/Se, R2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) = NH) can cause a certain degree of change in geometric structure. This further drives the rearrangement of FMO axial distribution. With the rearrangement of FMO axial distribution, the contribution of Se atoms in the main skeleton to excited-state transition orbitals is directionally regulated, ultimately leading to significant differences in SOC and RISC rates. This core finding challenges the cognitive framework of traditional heavy atom effects: the enhancement of SOC not only depends on the number of Se heavy atoms. When the number of Se atoms is the same, differences in the spatial sites of heteroatoms can indirectly regulate the contribution of Se atoms to excited-state transition orbitals, thus giving fuller play to the advantages of Se's heavy atom effect. This provides important theoretical guidance for in-depth understanding of the intrinsic mechanisms underlying SOC enhancement and RISC rate improvement.
= NH) can cause a certain degree of change in geometric structure. This further drives the rearrangement of FMO axial distribution. With the rearrangement of FMO axial distribution, the contribution of Se atoms in the main skeleton to excited-state transition orbitals is directionally regulated, ultimately leading to significant differences in SOC and RISC rates. This core finding challenges the cognitive framework of traditional heavy atom effects: the enhancement of SOC not only depends on the number of Se heavy atoms. When the number of Se atoms is the same, differences in the spatial sites of heteroatoms can indirectly regulate the contribution of Se atoms to excited-state transition orbitals, thus giving fuller play to the advantages of Se's heavy atom effect. This provides important theoretical guidance for in-depth understanding of the intrinsic mechanisms underlying SOC enhancement and RISC rate improvement.
2 Computational methods
2.1 Computational details
Choosing appropriate theoretical methods is the cornerstone for accurately simulating molecular structures and predicting properties. In this study, for the geometric structures of the ground state (S0), first excited singlet state (S1), and first excited triplet state (T1) of the studied molecules, we optimized them using density functional theory (DFT) and time-dependent DFT (TD-DFT) methods26–29via the Gaussian 16 program.30 Meanwhile, the vibrational frequencies of the corresponding structures were calculated to ensure the optimized structures are stable without imaginary frequencies. In both DFT and TD-DFT calculations, the hybrid B3LYP-D3(BJ) functional31–33 was adopted. For Se atoms, the SDD pseudopotential basis set34 was used, while for other atoms, the 6-31G(d) basis set35 was employed.Due to the problem that the TD-DFT method severely underestimates the T1 state energy, the singlet–triplet energy gap (ΔEST) obtained at the B3LYP-D3(BJ)/6-31G(d) level shows a large deviation from the experimental value (Table S1). Additionally, theoretical studies on MR-TADF molecules have indicated that the TD-DFT method tends to overestimate ΔEST when simulating MR-TADF molecules, with a mean average deviation (MAD) generally exceeding 0.2 eV. In contrast, the wavefunction-based high-precision spin-component scaling second-order approximate coupled-cluster (SCS-CC2) method36,37 exhibits higher accuracy, with a MAD of only 0.04 eV.38 To balance the accuracy of ΔEST and affordable computational cost, this study combined the TD-B3LYP method and SCS-CC2 method to simulate ΔEST of all studied MR-TADF molecules. Specifically, based on the S1 structure optimized at the B3LYP-D3(BJ)/6-31G(d) level, the vertical excitation energies of S1 → S0 and T1 → S0 transitions were calculated using the SCS-CC2 method with the cc-PVTZ basis set via the MRCC program.39,40
The spin–orbit coupling (SOC) between singlet and triplet states was calculated using the ORCA 5.0 program41 based on the S1 and T1 state structures optimized by the Gaussian 16 program. The calculations were performed under the one-component zeroth-order regular approximation (ZORA)42,43 with all atoms uniformly using the B3LYP-D3(BJ)/ZORA-def2-SVP44 level. The reorganization energy was obtained from calculations using the MOMAP program.45
2.2 Radiative and non-radiative decay rate constants
The luminescence mechanism of the studied MR-TADF molecules involves several key processes. These specifically include the prompt fluorescence radiative and non-radiative transition processes of S1 → S0, the phosphorescence radiative and non-radiative processes of T1 → S0, and the intersystem crossing (ISC) and reverse intersystem crossing (RISC) processes between the S1 and T1 states.46The prompt fluorescence and phosphorescence transitions can be calculated from Einstein's spontaneous radiation equation.47
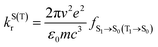 | (1) |
The ISC and RISC rates were calculated according to the formulae proposed by Katsuyuki Shizu and Hironori Kaji.48 Previously, this method was successfully applied to BNSSe series molecules (BNOO, BNSS, and BNSeSe), verifying its accuracy.
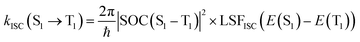 | (2) |
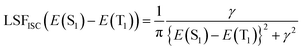 | (3) |
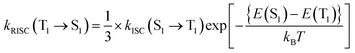 | (4) |
To maintain theoretical consistency with the calculation of ISC/RISC rates, the non-radiative transition rate of T1 → S0 was also calculated using the formula proposed by Katsuyuki Shizu and Hironori Kaji.48
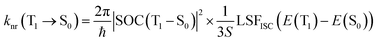 | (5) |
The non-radiative transition rate of S1 → S0 was calculated using the MOMAP program.50 We have also simulated the non-radiative transition rate of the experimental molecule BNSSe in the solid-state environment, with specific details provided in the SI (see SI pages 12 and 13).
It should be noted that in the rate calculations, the energies of all singlet and triplet states adopted the values corrected by the SCS-CC2 method.
In addition, we also calculated the quantum efficiency of delayed fluorescence at room temperature.51
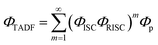 | (6) |
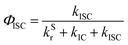 | (7) |
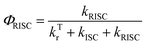 | (8) |
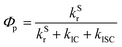 | (9) |
3 Results and discussion
3.1 Geometry and electronic structure
Geometric differences between the ground and excited states are a key factor determining the photophysical properties of TADF molecules. Superposition analysis of the optimized configurations of the S0, S1, and T1 states of molecules was performed using PyMOL software. The degree of structural change was quantitatively evaluated using root-mean-square deviation (RMSD,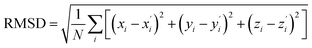 ). RMSD analysis (Fig. 2) shows that compared with the parent molecule BNSSe (0.098), the structural distortion between the S0/S1 states of molecules 1, 2, and 5 is reduced. In particular, the RMSD value of molecule 1 is significantly reduced (0.033), indicating that introducing a B/N-containing fused-ring rigid structure (including O atoms with a radius close to that of N atoms) can effectively suppress structural relaxation between the S0/S1 states. This enhanced structural rigidity not only facilitates the realization of narrowband emission but also improves the photoluminescence quantum yield (PLQY) by significantly suppressing vibrational coupling losses in non-radiative channels. Although the larger atomic radii of S and Se atoms slightly increase the structural differences between the S0/S1 states of molecules 3/6 and 4/7 compared with BNSSe, the RMSD values between isomers are highly similar. Does this imply that their photophysical processes are also similar?
). RMSD analysis (Fig. 2) shows that compared with the parent molecule BNSSe (0.098), the structural distortion between the S0/S1 states of molecules 1, 2, and 5 is reduced. In particular, the RMSD value of molecule 1 is significantly reduced (0.033), indicating that introducing a B/N-containing fused-ring rigid structure (including O atoms with a radius close to that of N atoms) can effectively suppress structural relaxation between the S0/S1 states. This enhanced structural rigidity not only facilitates the realization of narrowband emission but also improves the photoluminescence quantum yield (PLQY) by significantly suppressing vibrational coupling losses in non-radiative channels. Although the larger atomic radii of S and Se atoms slightly increase the structural differences between the S0/S1 states of molecules 3/6 and 4/7 compared with BNSSe, the RMSD values between isomers are highly similar. Does this imply that their photophysical processes are also similar?
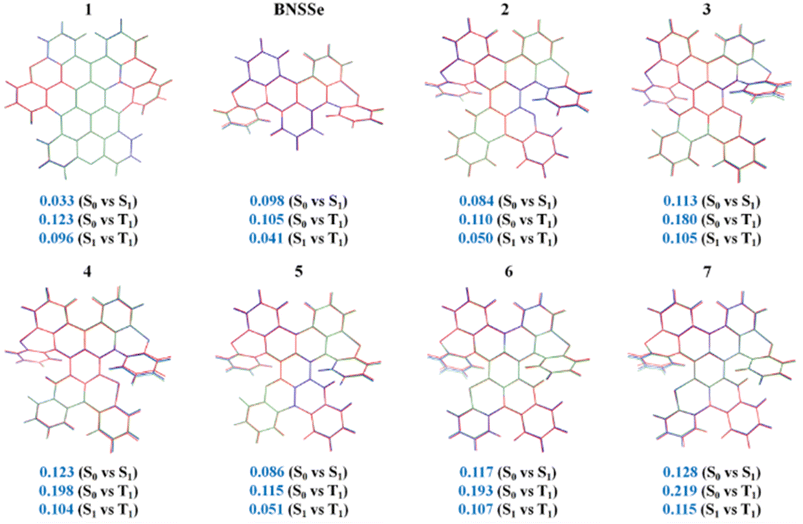 | ||
| Fig. 2 Superimposed geometric structures of the investigated molecules in S0 (red), S1 (blue), and T1 (green) states with corresponding RMSD (Å) values. | ||
In the designed series of red emitters 2–7, all molecules exhibit small structural differences between the S1/T1 states. This structural similarity between excited states is significantly better than the corresponding configurational changes between the S0/S1 or S0/T1 states, providing a favorable structural basis for efficient ISC and RISC processes. However, bis-Se-containing molecules 4 and 7 exhibit large configurational differences between the S0/T1 states (RMSD = 0.198 and 0.219, respectively). This geometric change may significantly increase the non-radiative transition rate of T1 → S0 by enhancing the nonadiabatic coupling effect. In this case, to maintain efficient TADF properties, a faster kRISC is necessary to enable molecules to smoothly upconvert from the T1 state to the S1 state, thereby competitively suppressing triplet quenching channels. We will discuss how to optimize the RISC process through heavy atom effects and molecular orbital regulation in the subsequent rate calculation section.
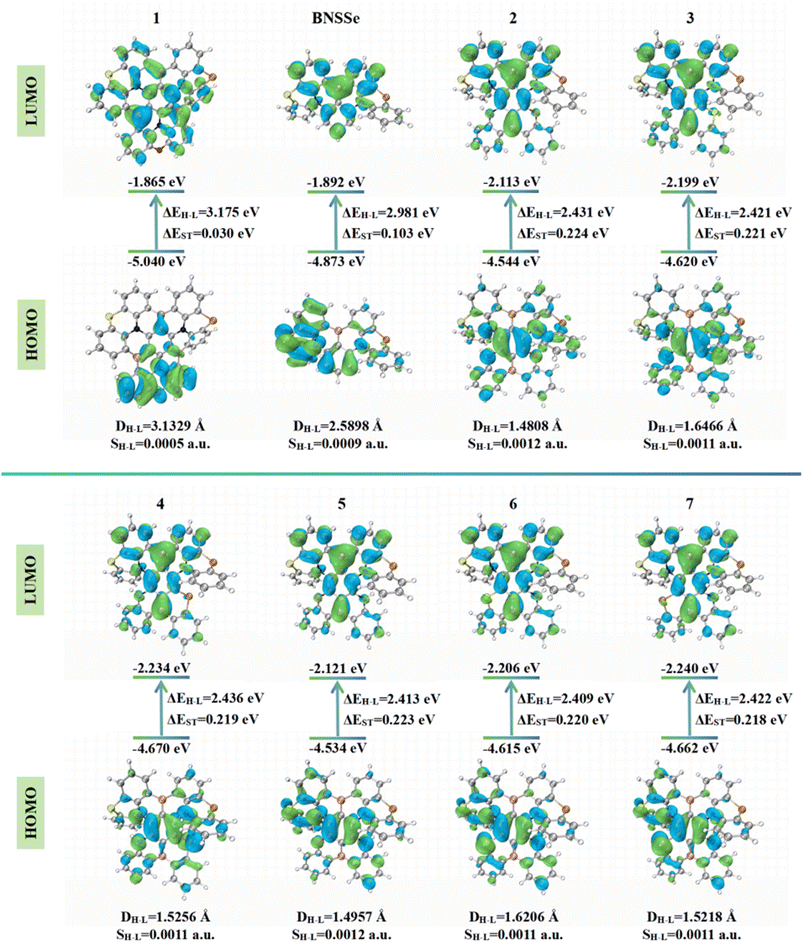
Frontier molecular orbital (FMO) analysis is a key means to reveal the structure–activity relationship between molecular electronic structures and photophysical properties. The HOMO–LUMO energy gap (ΔEH–L) directly affects the emission color of materials, while its spatial distribution characteristics influence charge transfer properties and emission efficiency. In molecular design, N atoms can significantly raise the HOMO energy level due to the electron-donating nature of their lone pairs. In contrast, B atoms, with the strong electron-withdrawing ability of their empty p orbitals, obviously lower the LUMO energy level. Molecule 1 introduces an additional B–N pair below the parent structure, forming three sets of para-B–π–N structures. This design subtly weakens the electron-withdrawing/donating effects of B/N atoms, leading to a lower HOMO energy level and a higher LUMO energy level. Consequently, ΔEH–L increases (ΔEH–L in the S0 state rises from 3.328 eV to 3.351 eV; ΔEH–L in the S1 state increases from 2.981 eV to 3.175 eV), successfully achieving a significant blue shift in absorption/emission spectra. In comparison, molecules 2–7 adopt the para structure of B–π–B and N–π–D (donor D = N/O/S/Se). This arrangement synergistically enhances the electron-withdrawing/donating effects of B/D atoms, increasing the HOMO energy level and lowering the LUMO energy level (ΔEH–L in the S0 state decreases to 2.633–2.656 eV; ΔEH–L in the S1 state reduces to 2.409–2.436 eV), corresponding to a redshift in absorption/emission wavelengths.
Systematic studies on the FMO distribution of molecules in the S0 and S1 states (Fig. 3 and S1) reveal the following. For the parent molecule BNSSe, the HOMO is mainly localized on electron-donating N/S/Se atoms and adjacent benzene ring C atoms, while the LUMO is primarily concentrated on electron-withdrawing B atoms and surrounding benzene ring C atoms. This distinct SRCT characteristic can effectively suppress electron-vibration coupling, serving as a key structural feature for achieving narrowband emission. For the designed red emitters 2–7, their HOMO/LUMO distributions are also localized on electron-donating/electron-withdrawing atoms and surrounding benzene rings, maintaining the SRCT characteristic. This allows regulation of spectral redshift while avoiding increased electron-vibration coupling and structural relaxation. As for the designed blue emitter 1, although the LUMO is mainly localized on atoms, the HOMO is partially localized on the main skeleton atoms and partially delocalized in the lower π-extended region, forming a hybrid SRCT/LRCT characteristic. This dynamic balance mechanism of “orbital localization–delocalization” not only helps reduce ΔEST but also further improves emission efficiency.
We first conducted a preliminary evaluation of ΔEST, which is jointly determined by the spatial distance between the HOMO and LUMO (DH–L) and the orbital overlap degree (SH–L). The energies of S1 and T1 are determined by the orbital energy (E) of two unpaired electrons, coulomb repulsion energy (K), and electron exchange energy (J), with specific expressions as follows:
| ES1 = E + K + J | (10) |
| ET1 = E + K − J | (11) |
| ΔEST = 2J | (12) |
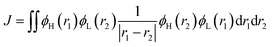 | (13) |
Compared with BNSSe, the designed blue emitter 1 shows enhanced intramolecular charge transfer characteristics. This significantly increases DH–L to 3.1329 Å and reduces SH–L to 0.0005 a.u., leading to a notable decrease in the ΔEST to 0.03 eV, which indicates a significant improvement in RISC rate. Notably, the introduction of the B/N fused-ring structure exhibits multiple synergistic effects. RMSD analysis confirms that this structure can significantly enhance the rigidity of the molecular skeleton, thereby effectively suppressing structural relaxation between S0/S1 states. In addition, while imparting LRCT characteristics, this design achieves a synergy between SRCT and LRCT, successfully avoiding non-radiative energy loss pathways caused by electron-vibration coupling and structural relaxation. This strategy of balancing SRCT and LRCT provides a new idea for developing efficient narrow-spectrum luminescent materials.
For the designed red emitters 2–7, RMSD analysis has shown that replacing O atoms with S/Se (with larger atomic radii) increases the structural differences between S0/S1 states. However, by regulating the increase in SH–L and the decrease in DH–L, the molecules exhibit stronger SRCT characteristics, still enabling effective suppression of electron-vibration coupling. Although this design moderately increases ΔEST to approximately 0.2 eV, it is still lower than the energy gap threshold of typical TADF materials (usually <0.3 eV). This ensures that the T1 state can be upconverted to the S1 state through thermal activation, achieving TADF emission characteristics. This will provide a reference for the design of red-emitting TADF materials. It is worth noting that although molecules 2–4 and 5–7 all adopt the structural arrangement of para-B–π–B and N–π–D (donor D = N/O/S/Se), differences in the positions of heteroatoms O/S/Se lead to significant differences in geometric and electronic structures, which may further result in variations in their photophysical properties.
To address this issue, we conducted an in-depth analysis of the geometric and electronic structures of the S1 state of molecules 2–7. According to the Valence Shell Electron Pair Repulsion (VSEPR) theory,54 electron pairs (including bonding pairs and lone pairs) around the central atom repel each other. They tend to stay as far apart as possible in space, thus determining the molecular geometry. Within this theoretical framework, the observed structural differences can be described more accurately: the N atoms, as central atoms, contain only one pair of lone electrons, while O/S/Se atoms have two pairs of lone electrons. Since lone pairs occupy more space than bonding pairs, and the repulsion between lone pairs is the strongest (repulsion order: lone pair–lone pair > lone pair–bonding pair > bonding pair–bonding pair), and this enhanced repulsion forces the bonding pairs around O/S/Se atoms to be closer. As a result, the bond angle C2–X–C3 (X = O/S/Se) is significantly smaller than the bond angle C4–N–C5 at the N atom position (Fig. 4), similar to how H2O (104.5°) exhibits a smaller bond angle compared to NH3 (107°). This bond angle compression effect exacerbates the structural distortion of the fragment containing O/S/Se, reducing molecular planarity. Further comparison of two key dihedral angles—the dihedral angle C1–C2–X–C3 (θ) on the side with O/S/Se and the dihedral angle C1–C4–N–C5 (α) on the side with N—reveals that θ is consistently larger than α. This also confirms that the planarity of the fragment containing O/S/Se is poorer (Fig. S2). Therefore, the conjugation degree between the six-membered ring containing O/S/Se, adjacent benzene rings, and the central benzene ring is lower than that of the fragment containing N. This hinders the delocalization of the HOMO electron cloud along the axial direction from the O/S/Se-containing fragment to the obliquely upper part, making the HOMO delocalization more inclined to the axial direction from the N-containing fragment to the obliquely upper part. As a result, in molecules 2–4, the HOMO electron cloud is more distributed on the Se atom of the main skeleton. In contrast, in molecules 5–7, the HOMO is barely distributed on the Se atom of the main skeleton (Fig. 5). It is generally accepted that the magnitude of SOC is proportional to the fourth power of the nuclear charge number (Z4).14 As a fourth-period element, the contribution of Se to the excited-state transition orbitals will greatly affect the SOC and RISC rate of the molecule. We further calculated the percentage contribution of Se to the hole orbital in the S1 state of molecules 2–7 using Multiwfn.55 Since molecules 4 and 7 have an additional Se atom introduced into the original main skeleton, the Se atom on the main skeleton is named Se(1), and the additionally introduced Se atom in our design is named Se(2). According to Table 1, the contribution of Se to the hole in molecules 2–4 ranges from 1.289–15.807%, which is significantly higher than the 0.335–12.661% in molecules 5–7. Therefore, the higher contribution of Se atoms to the excited-state transition orbitals in molecules 2–4 endows them with a stronger heavy atom effect, indicating that they will have larger SOC constants and faster RISC rates.
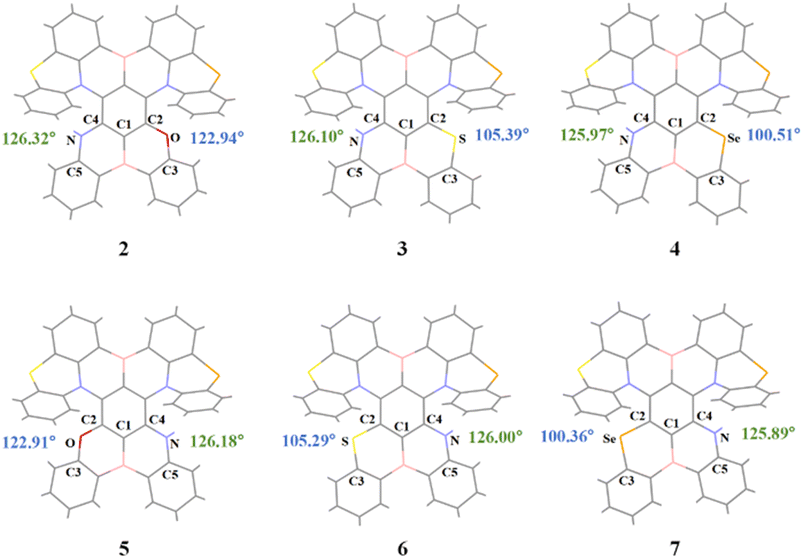 | ||
| Fig. 4 Geometric structures of the S1 state and key bond angle C2–X–C3 and C4–N–C5 parameters of the investigated red emitters. | ||
| 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|
| Se(1) | 2.198 | 1.289 | 1.389 | 0.402 | 0.335 | 0.333 |
| Se(2) | — | — | 14.418 | — | — | 12.328 |
| Se(sum) | 2.198 | 1.289 | 15.807 | 0.402 | 0.335 | 12.661 |
3.2 Absorption and emission spectra
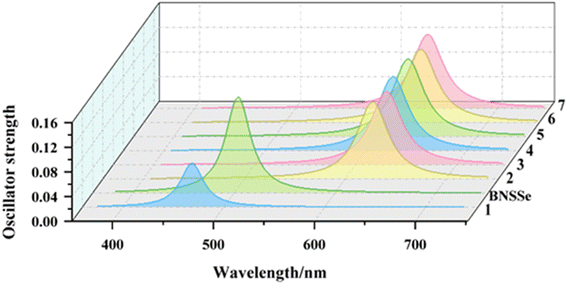
Based on the optimized geometric structures of the ground and excited states, we conducted a systematic theoretical calculation study on the electronic transition properties of each molecule. Table 2 details the key parameters of absorption and emission spectra, including wavelength, vertical excitation energy, oscillator strength (f), and transition configuration, which are compared and verified with experimental value. The results show that the emission wavelength of the parent molecule BNSSe calculated by the TDDFT/B3LYP-D3(BJ) method is 504 nm, which is highly consistent with the experimental value of 520 nm, verifying the reliability of the calculation method. The lowest absorption and emission transitions of the studied molecules are mainly derived from the HOMO → LUMO electronic transition, which further confirms the effectiveness of our previous strategy for predicting spectral redshift and blueshift by regulating FMOs.| Electronic transition | Vertical excitation energy (eV) | λ (nm) | f | Configuration | ||
|---|---|---|---|---|---|---|
| a Experimental value from ref. 18. | ||||||
| Absorption | ||||||
| 1 | S0 → S1 | 2.787 | 445 | 0.0477 | HOMO → LUMO | 71% |
| HOMO−1 → LUMO+1 | 17% | |||||
| HOMO → LUMO+1 | 4% | |||||
| HOMO−2 → LUMO+1 | 3% | |||||
| BNSSe | S0 → S1 | 2.799 | 443 | 0.2145 | HOMO → LUMO | 98% |
| 2 | S0 → S1 | 2.212 | 561 | 0.1590 | HOMO → LUMO | 99% |
| 3 | S0 → S1 | 2.191 | 566 | 0.1466 | HOMO → LUMO | 99% |
| 4 | S0 → S1 | 2.194 | 565 | 0.1430 | HOMO → LUMO | 99% |
| 5 | S0 → S1 | 2.200 | 564 | 0.1571 | HOMO → LUMO | 99% |
| 6 | S0 → S1 | 2.183 | 568 | 0.1444 | HOMO → LUMO | 99% |
| 7 | S0 → S1 | 2.188 | 567 | 0.1412 | HOMO → LUMO | 99% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Fluorescence | ||||||
| 1 | S1 → S0 | 2.646 | 469 | 0.0716 | HOMO → LUMO | 82% |
| HOMO → LUMO+1 | 7% | |||||
| HOMO−1 → LUMO+1 | 5% | |||||
| BNSSe | S1 → S0 | 2.459 | 504/520a | 0.1567 | HOMO → LUMO | 99% |
| 2 | S1 → S0 | 1.976 | 627 | 0.1263 | HOMO → LUMO | 99% |
| 3 | S1 → S0 | 1.965 | 631 | 0.1195 | HOMO → LUMO | 99% |
| 4 | S1 → S0 | 1.977 | 627 | 0.1209 | HOMO → LUMO | 99% |
| 5 | S1 → S0 | 1.962 | 632 | 0.1264 | HOMO → LUMO | 99% |
| 6 | S1 → S0 | 1.954 | 634 | 0.1194 | HOMO → LUMO | 99% |
| 7 | S1 → S0 | 1.964 | 631 | 0.1201 | HOMO → LUMO | 99% |
More importantly, the calculation results clearly reveal the regulation law of molecular structure on emission color: molecule 1 successfully achieves blue emission (469 nm) by introducing the para-B–π–N structure, while molecules 2–7 adopt the para-B–π–B and N–π–D (donor D = N/O/S/Se) structures, with emission wavelengths redshifted to the range of 627–634 nm, showing pure red fluorescence characteristics (Fig. 6). These results not only verify the prediction of FMO analysis but also confirm the feasibility of designing blue and red MR-TADF materials by precisely regulating molecular structures. Most importantly, the blue emission (469 nm) of molecule 1 and red emission (627–634 nm) of molecules 2–7 designed by us are highly consistent with the blue (467 nm) and red (630 nm) standards defined by BT.2020 announced by the International Telecommunication Union (ITU).24 This finding provides theoretical guidance for developing high-performance narrowband luminescent materials that meet the standards of the display industry, and also opens up new research ideas for designing high-performance MR-TADF materials with a wide color gamut through precise regulation of electronic structures.
3.3 Excited state radiative and non-radiative transition rates
We know that the luminescence mechanism of TADF materials is very complex, involving radiative and non-radiative transitions of fluorescence and phosphorescence, as well as ISC and RISC processes between S1 and T1 states. To achieve high-performance TADF materials, several key conditions must be met simultaneously: fast fluorescence radiative decay, efficient RISC process, slow phosphorescence radiation, and significantly suppressed non-radiative decay. Based on this understanding, our research is not only committed to regulating the emission color of MR-TADF molecules. More importantly, through quantitative calculation of the mutual conversion rates between various electronic states and their competitive relationships, we systematically optimize these key luminescence processes to achieve higher luminescence efficiency. This research idea of multi-parameter synergistic optimization provides a comprehensive theoretical basis for the development of high-performance TADF materials.| fij = ⅔(Ej − Ei)|µij|2 | (14) |
The magnitude of the transition dipole moment depends on the overlap integral of the wavefunctions of the S1 and S0 states. If the transition mainly corresponds to the electronic excitation from the HOMO to LUMO, it can be approximately equivalent to the spatial overlap degree of the HOMO and LUMO orbitals.57,58
µS1–S0 = |〈ψS1|![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) |ψS0〉| ≈ |〈L| |ψS0〉| ≈ |〈L|![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) |H〉| ∝ S[H/L] |H〉| ∝ S[H/L] | (15) |
To design blue emission MR-TADF molecules with fast RISC rates and thereby suppress the efficiency roll-off of blue emission devices, molecule 1 achieves π-extension by introducing a rigid B/N-fused ring structure, forming hybrid SRCT/LRCT characteristics. Its CT character is significantly enhanced compared to the parent molecule BNSSe (which exhibits SRCT characteristics). This design strategy reduces the overlap degree between the HOMO and LUMO of molecule 1 (molecule 1: 0.0005 a.u.; BNSSe: 0.0009 a.u.), leading to a remarkable decrease in its ΔEST (molecule 1: 0.030 eV; BNSSe: 0.103 eV), which is conducive to improving the RISC rate. However, the reduced HOMO–LUMO overlap inevitably results in decreases in the transition dipole moment and oscillator strength (Table S2), ultimately leading to a lower prompt fluorescence radiative transition rate of blue emission molecule 1 compared to BNSSe (Table 3). On the other hand, by introducing the para-B–π–N structure, molecule 1 successfully achieves blue emission, with a vertical excitation energy (2.885 eV) significantly higher than that of the green emission molecule BNSSe (2.710 eV). This ensures that its kSr remains on the same order of magnitude as BNSSe (molecule 1: 2.58 × 107 s−1; BNSSe: 4.99 × 107 s−1), indicating favorable fluorescence performance.
| Vertical excitation energy/eV | f | k Sr/s−1 | τ/µs | |
|---|---|---|---|---|
| 1 | 2.885 | 0.0716 | 2.58 × 107 | 0.039 |
| BNSSe | 2.710 | 0.1567 | 4.99 × 107 | 0.020 |
| 2 | 2.121 | 0.1263 | 2.46 × 107 | 0.041 |
| 3 | 2.114 | 0.1195 | 2.32 × 107 | 0.043 |
| 4 | 2.126 | 0.1209 | 2.37 × 107 | 0.042 |
| 5 | 2.112 | 0.1264 | 2.44 × 107 | 0.041 |
| 6 | 2.105 | 0.1194 | 2.29 × 107 | 0.044 |
| 7 | 2.116 | 0.1201 | 2.33 × 107 | 0.043 |
In addition, to achieve the design goal of pure red emission MR-TADF molecules, we successfully tuned the emission spectrum to around 630 nm by introducing para-B–π–B and N–π–D (donor D = N/O/S/Se) structures into the main skeleton of the parent molecule BNSSe. However, the significant red-shift of the emission spectrum inevitably leads to a substantial reduction in the vertical excitation energy of molecules 2–7 compared to BNSSe, ultimately resulting in a decrease in their kSr. Notably, despite the lower kSr relative to BNSSe, it still maintains the order of magnitude of 107 s−1, which is comparable to representative high-efficiency red emission materials reported in the literature (Table S3). This fast fluorescence radiative characteristic makes it promising to break through the limitations of the traditional energy gap law.
According to the energy gap law, the non-radiative transition rate of S1 → S0 (kSnr) depends exponentially on the energy gap between the S0 and S1 states. A large energy gap between S0/S1 states and a small electron-vibration coupling parameter can both suppress kSnr. Here, we express this using a simple approximate relationship.21,59,60
| kSnr ∼ exp(−βΔE) | (16) |
In the development of OLED materials, the energy gap law has long been a key bottleneck restricting the performance improvement of red emitters. This forces material designers to make trade-offs between luminous efficiency and red emission characteristics. To break this limitation, this study successfully achieved effective suppression of non-radiative transition processes through an innovative molecular design strategy. The results show that compared with the parent molecule BNSSe (the reorganization energies of the S1 and S0 potential energy surfaces are defined as λ1 and λ2, respectively, with λ1 = 1632 cm−1 and λ2 = 1303 cm−1), in the designed red emitters 2–7, although the ΔE values are smaller, the λ values between S1 and S0 states (Fig. 7 and Table 4, with λ1 = 939–1022 cm−1 and λ2 = 858–922 cm−1) are significantly reduced through careful regulation of molecular structure. To our surprise, despite the significant decrease in ΔE (approximately 0.653 eV/5267–0.674 eV/5436 cm−1), which should have led to an exponential increase in kSnr according to the energy gap law, the actually measured kSnr did not increase but instead decreased. This phenomenon indicates that although the reduction in λ is limited (for example, λ1 and λ2 of molecule 2 decreased by 612 cm−1 and 397 cm−1, respectively), its inhibitory effect on kSnr almost completely offsets the promoting effect caused by the decrease in ΔE. This striking contrast demonstrates that within this energy level range, kSnr is extremely sensitive to changes in λ, and λ becomes the key factor dominating the non-radiative transition process. This breakthrough improvement stems from the unique molecular structure design: fusing another MR molecular skeleton (DOBNA derivative) with the central benzene ring in the BNSSe main skeleton, forming a hybrid π-bonding/non-bonding molecular orbital co-constructed by the central benzene ring and B, N, and X (X = O/S/Se) units. This effectively suppresses structural relaxation between S1 and S0 states. A significant effect of this structural regulation is reflected in the remarkable reduction of kSnr. Calculation data show that although the ΔE values of red emitters 2–7 are relatively small, their kSnr values are much smaller than the corresponding kSr (Tables 3 and 4). This means these materials are expected to achieve high luminous efficiency and break through the limitations of the energy gap law.
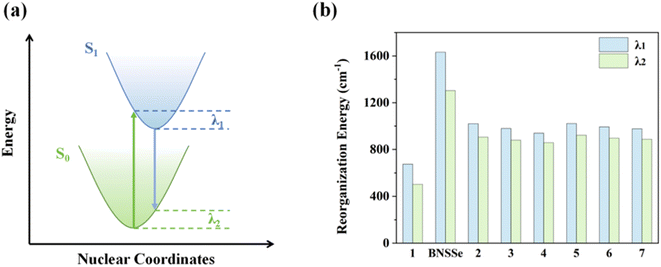 | ||
| Fig. 7 (a) Schematic diagram of the reorganization energy between the S1 and S0 states. (b) Bar charts of λ1 and λ2 for the investigated molecules. | ||
| ΔE/eV | λ 1/cm−1 | λ 2/cm−1 | k Snr/s−1 | |
|---|---|---|---|---|
| 1 | 3.037 | 675 | 503 | 1.06 × 103 |
| BNSSe | 2.974 | 1632 | 1303 | 8.65 × 106 |
| 2 | 2.321 | 1020 | 906 | 3.50 × 106 |
| 3 | 2.310 | 979 | 879 | 4.87 × 106 |
| 4 | 2.303 | 939 | 858 | 6.40 × 106 |
| 5 | 2.317 | 1022 | 922 | 2.68 × 106 |
| 6 | 2.305 | 993 | 897 | 6.42 × 106 |
| 7 | 2.300 | 977 | 888 | 1.15 × 107 |
It is worth noting that a similar molecular design strategy also has significant effects in blue-emitting materials. Molecule 1 reduces λ1 and λ2 to 675 cm−1 and 503 cm−1, respectively, through the extended B/N fused-ring structure. Combined with its large ΔE, the kSnr of S1 → S0 is as low as 1.06 × 103 s−1, which will greatly improve its luminous efficiency and provide a new design idea for developing high-efficiency blue-emitting materials. These findings not only provide new insights into understanding the relationship between molecular structure and luminous performance but also offer new perspectives for developing high-performance OLED luminescent materials.
Studies have shown that in addition to the non-radiative transition rate, the FWHM of the emission spectrum is also affected by the reorganization energy of the S0 state potential energy surface (λ2).61 To further investigate the kSnr of the studied molecules and determine whether the molecules designed herein possess narrowband emission characteristics, we decomposed λ2 into contributions from each normal mode. The displacement vectors corresponding to the normal modes with the largest contributions in the low-frequency and high-frequency regions are also marked in Fig. S3 and S4. It can be seen that the reorganization energies in both the low-frequency and high-frequency regions of the parent molecule BNSSe mainly originate from the bending vibrations of the entire molecular skeleton. Compared with BNSSe, the reorganization energy vibration modes of molecules 1–7 are significantly reduced, indicating that their geometric structural relaxation is well suppressed, suggesting that all designed molecules can maintain good narrowband emission characteristics. The reorganization energies in the low-frequency and high-frequency regions of molecule 1 mainly come from the stretching vibrations of the molecular skeleton and the bending vibrations of C–H bonds. For molecules 2–7, the low-frequency reorganization energy arises from the bending vibrations of C–H bonds in the peripheral benzene rings, while the high-frequency reorganization energy mainly comes from the bending vibrations of C–H bonds in the peripheral benzene rings and the stretching vibrations of the central benzene ring and surrounding six-membered rings.
In addition, the sources of reorganization energy λ2 were decomposed into contributions from bond lengths, bond angles, and dihedral angles. The reorganization energy of BNSSe mainly comes from dihedral angles, while that of molecules 1–6 is mainly from bond lengths, with their kSnr significantly lower than that of the parent molecule. Notably, when observing the two groups of molecules 2–4 and 5–7, as the atomic radii of O, S, and Se increase, the contribution of bond lengths to reorganization energy gradually decreases, while that of dihedral angles gradually increases. Correspondingly, their kSnr also increases. Therefore, we speculate that in the total reorganization energy, contributions from dihedral angles can more significantly enhance electron-vibration coupling and structural relaxation. In particular, consistent with BNSSe, the reorganization energy of molecule 7 also mainly comes from dihedral angles, and its kSnr is even larger than that of the parent molecule. On the one hand, this is because molecule 7 has the smallest ΔE, which significantly increases kSnr. On the other hand, it may be due to the vibrations from dihedral angles that enhance structural relaxation. Thus, for this system, reducing the reorganization energy contributed by dihedral angles may be an effective method to suppress structural relaxation and non-radiative decay.
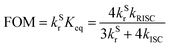 | (17) |
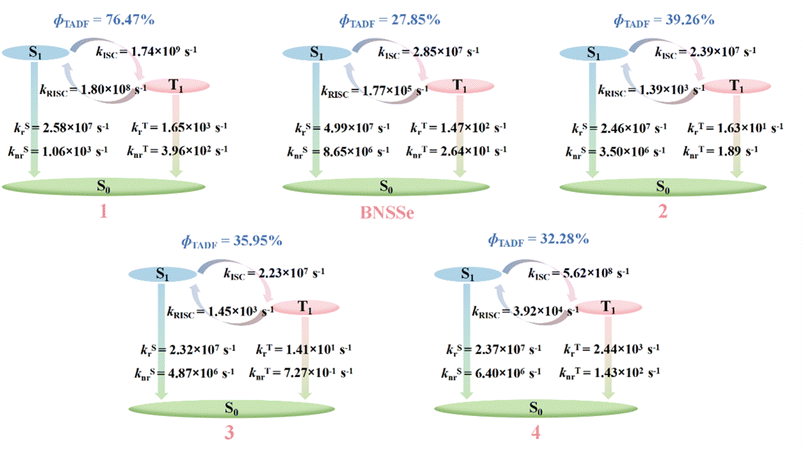
| ΔEST/eV | SOC(S1–T1)/cm−1 | k ISC/s−1 | k RISC/s−1 | |
|---|---|---|---|---|
| a Experimental values from ref. 18. | ||||
| 1 | 0.030 | 1.69 | 1.74 × 109 | 1.80 × 108 |
| BNSSe | 0.103/0.120a | 0.38 | 2.85 × 107/2.90 × 108a | 1.77 × 105/6.00 × 105a |
| 2 | 0.224 | 0.67 | 2.39 × 107 | 1.39 × 103 |
| 3 | 0.221 | 0.64 | 2.23 × 107 | 1.45 × 103 |
| 4 | 0.219 | 3.17 | 5.62 × 108 | 3.92 × 104 |
| 5 | 0.223 | 0.25 | 3.37 × 106 | 2.00 × 102 |
| 6 | 0.220 | 0.22 | 2.74 × 106 | 1.84 × 102 |
| 7 | 0.218 | 2.68 | 4.05 × 108 | 2.93 × 104 |
According to the data in Table S4, the figure of merit (FOM) of molecule 1 is significantly enhanced compared to that of BNSSe. This demonstrates that the efficiency roll-off of the designed blue emission MR-TADF molecule is remarkably suppressed, providing an effective strategy for addressing the efficiency roll-off issue of such materials. These results confirm that introducing SRCT/LRCT hybrid characteristics via the rigid B/N-fused ring structure can effectively reduce the molecular ΔEST and enhance kRISC, providing an important design strategy for the development of high-efficiency MR-TADF materials.
For the designed red emitters 2–7, enhanced SRCT characteristics lead to decreased DH–L and increased SH–L, resulting in the ΔEST increasing to approximately 0.2 eV and the kRISC being lower than that of BNSSe. Fortunately, molecules 4 and 7 exhibit significantly enhanced SOC through the heavy-atom effect of dual Se incorporation, achieving kRISC on the order of 104 s−1 and establishing them as high-performance red-emitting MR-TADF materials (Table S3). Further comparison of the structure–performance relationships between molecules 2/5, 3/6, and 4/7 reveals that differences in the spatial positions of O/S/Se heteroatoms cause significant changes in SOC, thereby affecting the magnitude of kRISC. This calculation result confirms the previous theoretical prediction: changing only the spatial positions of heteroatoms (O/S/Se) causes changes in molecular geometric structure, which drives the axial distribution rearrangement of frontier molecular orbitals, thereby directionally altering the contribution of main skeleton Se atoms to excited-state transition orbitals, ultimately leading to obvious differences in SOC and RISC rates.
Notably, for molecules containing only one Se atom (2/5, 3/6), changing the spatial position of the heteroatom can increase kRISC by an order of magnitude. For molecules 4 and 7 with two Se atoms, however, the increase in kRISC is relatively limited. This indicates that the strategy of enhancing kRISC by regulating heteroatom spatial positions is more effective for molecules with a single Se atom introduced. Although bis-Se molecules (4/7) exhibit better kRISC (104 s−1), considering that Se-containing reagents generally have high toxicity and poor stability, the synthesis of organic Se compounds often faces great challenges.67 In practical applications, a balance must be struck between the number of Se atoms and performance gains. In recent years, researchers have developed various new selenium reagents with better stability, low toxicity, and easy availability, making the synthesis of various organic Se compounds more feasible. However, in the development of MR-TADF materials, it remains important to maximize the heavy atom effect while minimizing Se atom usage. The heteroatom site regulation strategy proposed in this study provides an effective solution to this key issue.
The non-radiative transition rate of T1 → S0 was calculated using formula (5). The kTnr values of BNSSe and designed molecules 1–7 are 2.64 × 101 s−1, 3.96 × 102 s−1, 1.89 s−1, 7.27 × 10−1 s−1, 1.43 × 102 s−1, 1.12 s−1, 2.47 s−1 and 2.01 × 102 s−1, respectively. Data in Table S6 show that molecules 1, 4, and 7 exhibit a significant SOC enhancement effect between T1 and S0 states, with coupling constants of 28.74 cm−1, 12.17 cm−1, and 14.41 cm−1, respectively. These are significantly higher than that of the parent molecule BNSSe (7.04 cm−1), a characteristic that leads to a corresponding increase in their non-radiative transition rates. In addition, the large structural distortion between the T1 and S0 states of molecules 4 and 7 also indicates that they will dissipate part of the energy (Fig. 2). Fortunately, excited-state dynamics analysis reveals that the kRISC of these molecules is significantly higher than the corresponding kTnr (Tables 5 and S6). This rate advantage ensures that T1 state excitons can effectively upconvert to the S1 state, thereby maintaining an efficient TADF process.
3.4 Theoretical prediction of the emission spectrum FWHM
In terms of theoretical prediction of the spectral FWHM, this study adopted a dual verification strategy combining theoretical calculations and deep learning for systematic evaluation. First, vibrationally resolved emission spectra of each molecule were calculated using MOMAP software, and FWHM values were extracted from them (Fig. S6 and S7). The calculated FWHM for the parent molecule BNSSe is 59 nm, closely matching the experimental value of 50 nm. Notably, the designed molecules 1–7 also exhibit narrowband emission, with calculated FWHM values of 32, 57, 60, 62, 59, 65 and 65 nm, all falling within the narrowband regime below 70 nm. This demonstrates successful modulation of emission color and decay rates without compromising the narrowband linewidth.To further verify this result, we also used the SOGCN model based on a graph convolutional neural network independently developed by our research group to predict the FWHM of these molecules (Table S7).20 The model predicts the FWHM of BNSSe to be 56 nm, which is highly consistent with the experimental value, fully verifying the reliability of the model. Strikingly, the SOGCN model predicts that the FWHM values of molecules 1–7 are stable around 40 nm, showing a systematic difference from the MOMAP calculation results but with a consistent trend. This difference may stem from the different handling of molecular vibration modes by the two methods: MOMAP is based on precise vibrationally resolved calculations, while SOGCN captures the correlation between the molecular structure and spectrum through a data-driven approach.
The conclusions drawn by the two methods mutually confirm each other, jointly revealing the success of the molecular design: by introducing rigid fused-ring structures and enhancing SRCT characteristics, excited-state structural relaxation is effectively suppressed, leading to reduced reorganization energy. This dual-track verification mode of “computational simulation + AI prediction” confirms the excellent performance of the designed molecules in maintaining narrowband emission from different perspectives.
3.5 Red emitter design strategy
Based on the structure of the parent molecule BNSSe, the blue emitter 1 synergistically weakens the electron-withdrawing/donating abilities of B/N atoms through a modification strategy involving three sets of para-B–π–N. This causes the LUMO energy level to rise and the HOMO energy level to drop, significantly widening ΔEH–L, with the emission wavelength blue-shifted to 469 nm. To prepare pure red emitters meeting the BT.2020 standard, it is necessary to synergistically enhance the electron-withdrawing/donating abilities of B/N atoms to reduce ΔEH–L. Therefore, we attempted to replace the lower N and B atoms with each other based on the structure of molecule 1, designing molecule 1-a (Fig. S8). Molecule 1-a exhibits SRCT characteristics, which are beneficial for suppressing electron-vibration coupling and structural relaxation. Thus, the reorganization energy between the S0 and S1 states is slightly lower than that of the molecule BNSSe (Fig. S9 and Table S8). However, due to the structural arrangement of two sets of N–π–N and one set of B–π–B significantly enhancing the electron-withdrawing/donating abilities of B/N atoms, and the π-expanded structure of rigid fused rings increasing conjugation, the emission spectrum of molecule 1-a is redshifted to 703 nm. The extremely small emission energy gap leads to a significant increase in the non-radiative transition rate, exceeding the fluorescence radiative rate and causing severe luminescence quenching (Fig. S10).Based on the above results, we adjusted the design strategy. Studies have shown that in traditional polycyclic aromatic hydrocarbons without B/N heteroatoms, the HOMO and LUMO are mainly concentrated in the π-bond regions formed between atoms. In this case, the bonding/antibonding characteristics enhance electron-vibration coupling between S0 and S1 states, making excited states prone to deactivation through non-radiative pathways. In MR-TADF materials containing B/N heteroatoms, the HOMO and LUMO are localized on different atoms, minimizing their bonding/antibonding characteristics. The resulting non-bonding molecular orbitals reduce electron-vibration coupling and structural relaxation in the materials. Therefore, we attempted to fuse another MR-TADF molecule (DOBNA) onto the BNSSe main skeleton, designing molecule 2-a (Fig. S8). The DH–L of molecule 2-a decreases to 0.7941 Å, and SH–L increases to 0.0012 a.u., indicating enhanced SRCT characteristics. Moreover, it forms unique hybrid π-bonding/non-bonding molecular orbitals using the central benzene ring and B, N, and O units, effectively reducing the reorganization energy between S0 and S1 states. This significantly lowers the non-radiative transition rate to 2.48 × 105 s−1 (Fig. S9 and Table S8), showing potential to break through the limitations of the energy gap law. However, due to the weak electron-donating ability of O atoms, the introduction of a para-N–π–O structural distribution results in a limited redshift of the emission wavelength of molecule 2-a, reaching only 595 nm, which is far from the 630 nm specified in the BT.2020 standard. To address this, we further attempted to replace the O atom on one side with an N atom with a stronger electron-donating ability, designing molecules 2 and 5, whose emission wavelengths are successfully regulated to around 630 nm. Additionally, based on molecules 2 and 5, we replaced the O atom with S and Se atoms (which exhibit heavy atom effects) to design molecules 3 and 6, and 4 and 7, all with emission wavelengths of around 630 nm.
Although the designed molecules 1-a and 2-a did not meet the expected goals, they provided valuable insights for research on preparing pure red emitters meeting the BT.2020 standard. Furthermore, due to enhanced SRCT characteristics and hybrid π-bonding/non-bonding molecular orbitals, electron-vibration coupling and structural relaxation during the transition process of molecule 2-a are well suppressed. This is reflected not only in the significant decrease in its non-radiative transition rate but also in the narrowing of the FWHM of its emission spectrum to 48 nm (Fig. S11), providing theoretical guidance for the preparation of high-performance narrowband orange-red-emitting MR-TADF materials.
4 Conclusions
In this study, we conducted an in-depth investigation into the luminescence mechanism of BNSSe by employing DFT, TD-DFT, and SCS-CC2 methods. Based on the structure characteristics of BNSSe, we successfully designed high-performance blue-emitting and red-emitting MR-TADF materials through precise regulation of molecular structures, and revealed the regulatory mechanism of heteroatom spatial site specificity on excited-state dynamics. The primary conclusions are outlined as follows:(1) By incorporating a rigid B/N fused-ring structure into the BNSSe molecular framework and leveraging hybrid SRCT/LRCT characteristics, molecule 1 was designed to exhibit accelerated RISC. Compared with BNSSe, molecule 1 features a smaller ΔEST, enhanced SOC, and suppressed structural relaxation, collectively contributing to a remarkable increase in kRISC to 108 s−1 (3 orders of magnitude higher than that of the BNSSe). The introduction of three para-configured B–π–N units effectively moderates the electron-withdrawing/donating strengths of the B/N atoms, enlarges the ΔEH–L, and regulates spectral blue-shift. This molecular design offers a new strategy for developing efficient and stable blue-emitting MR-TADF materials.
(2) A series of red emitters 2–7 were designed by incorporating para-B–π–B and N–π–D (donor D = N/O/S/Se) to synergistically enhance the electron-withdrawing/donating abilities of B/N atoms. Their emission wavelengths are concentrated around 630 nm, basically meeting the red standard defined by BT.2020. Theoretical calculations confirm that fusing another MR molecular skeleton (DOBNA derivative) with the central benzene ring in the BNSSe main skeleton, and forming hybrid π-bonding/non-bonding molecular orbitals using the central benzene ring and B, N, and X (X = O/S/Se) units, can effectively reduce the λ between the S1 and S0 states, thereby suppressing structural relaxation. Although the ΔE of red emitters decreases significantly, the inhibitory effect of λ on kSnr almost completely offsets the promoting effect induced by the decrease in ΔE. Benefiting from this molecular design, their kSnr is much smaller than kSr, creating favorable conditions for breaking through the limitations of the energy gap law. This provides key insights for the precise design of high-performance MR-TADF materials: while regulating the energy gap, efforts should be made to pursue molecular rigidification to minimize λ, thereby synergistically achieving efficient suppression of non-radiative transition channels.
(3) The directional regulation mechanism of heteroatom spatial sites on SOC was revealed: without increasing the number of Se atoms, the axial distribution rearrangement of frontier molecular orbitals is driven by the differences in O/S/Se sites, optimizing the contribution of Se atoms to excited-state transitions, thereby significantly increasing SOC and improving the kRISC of single-Se molecules by an order of magnitude. This finding goes beyond the cognitive framework of traditional heavy atom effects, providing important theoretical guidance for in-depth understanding of the intrinsic mechanism between SOC enhancement and RISC rate improvement.
Author contributions
Lifang Yin: conceptualization, methodology, validation, formal analysis, investigation, data curation, writing – original draft, visualization. Yi Zhao and Qiang Gao: validation, formal analysis, data curation. Yajun Yin, Tengfei He, and Yufei Yang: methodology. Aimin Ren, Tongshun Wu, and Hui Li: validation, methodology. Luyi Zou: conceptualization, methodology, formal analysis, resources, supervision, project administration, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
Data are available in the supplementary information (SI) and from the authors on request. Supplementary information is available. See DOI: https://doi.org/10.1039/d5sc06741c.Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 22573039) and the International Science and Technology Cooperation Project of Jilin Provincial Department of Science and Technology (No. 20240402047GH).References
- G. Hong, X. Gan, C. Leonhardt, Z. Zhang, J. Seibert, J. M. Busch and S. Bräse, Adv. Mater., 2021, 33, 2005630 CrossRef CAS.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- Y. Olivier, M. Moral, L. Muccioli and J.-C. Sancho-García, J. Mater. Chem. C, 2017, 5, 5718–5729 RSC.
- Y. Olivier, B. Yurash, L. Muccioli, G. D'Avino, O. Mikhnenko, J. C. Sancho-García, C. Adachi, T. Q. Nguyen and D. Beljonne, Phys. Rev. Mater., 2017, 1, 075602 CrossRef.
- A. Pershin, D. Hall, V. Lemaur, J.-C. Sancho-Garcia, L. Muccioli, E. Zysman-Colman, D. Beljonne and Y. Olivier, Nat. Commun., 2019, 10, 597 CrossRef CAS.
- T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Adv. Mater., 2016, 28, 2777–2781 CrossRef CAS PubMed.
- X.-C. Fan, K. Wang, Y.-Z. Shi, Y.-C. Cheng, Y.-T. Lee, J. Yu, X.-K. Chen, C. Adachi and X.-H. Zhang, Nat. Photonics, 2023, 17, 280–285 CrossRef CAS.
- H. J. Kim and T. Yasuda, Adv. Opt. Mater., 2022, 10, 2201714 CrossRef CAS.
- Z. Xue, Y. Hu, S. Xiao, J. Liu, J. Miao and C. Yang, Angew. Chem., Int. Ed., 2025, 64, e202500108 CrossRef CAS.
- J.-J. Hu, X. Liang, Z.-P. Yan, J.-Q. Liang, H.-X. Ni, L. Yuan, J.-L. Zuo and Y.-X. Zheng, Angew. Chem., Int. Ed., 2025, 64, e202421102 CrossRef CAS PubMed.
- Y. Kondo, K. Yoshiura, S. Kitera, H. Nishi, S. Oda, H. Gotoh, Y. Sasada, M. Yanai and T. Hatakeyama, Nat. Photonics, 2019, 13, 678–682 CrossRef CAS.
- J. Liu, Y. Zhu, T. Tsuboi, C. Deng, W. Lou, D. Wang, T. Liu and Q. Zhang, Nat. Commun., 2022, 13, 4876 CrossRef CAS.
- X. Wu, S. Ni, C.-H. Wang, W. Zhu and P.-T. Chou, Chem. Rev., 2025, 125, 6685–6752 CrossRef CAS.
- H. Jiang, J. Jin and W.-Y. Wong, Adv. Funct. Mater., 2023, 33, 2306880 CrossRef CAS.
- Q.-Y. Meng, R. Wang, Y.-L. Wang, X.-W. Guo, Y.-Q. Liu, X.-L. Wen, C.-Y. Yao and J. Qiao, Nat. Commun., 2023, 14, 3927 CrossRef CAS.
- B. H. Jhun, Y. Park, H. S. Kim, J. H. Baek, J. Kim, E. Lee, H. Moon, C. Oh, Y. Jung, S. Choi, M.-H. Baik and Y. You, Nat. Commun., 2025, 16, 392 CrossRef CAS.
- X. Huang, J. Liu, Y. Xu, G. Chen, M. Huang, M. Yu, X. Lv, X. Yin, Y. Zou, J. Miao, X. Cao and C. Yang, Natl. Sci. Rev., 2024, 11, nwae115 CrossRef CAS PubMed.
- Y. X. Hu, J. Miao, T. Hua, Z. Huang, Y. Qi, Y. Zou, Y. Qiu, H. Xia, H. Liu, X. Cao and C. Yang, Nat. Photonics, 2022, 16, 803–810 CrossRef CAS.
- I. S. Park, H. Min and T. Yasuda, Angew. Chem., Int. Ed., 2022, 61, e202205684 CrossRef CAS.
- Y. Li, B. Zhang, A. Ren, D. Wang, J. Zhang, C. Nie, Z. Su and L. Zou, Chem. Eng. J., 2024, 501, 157676 CrossRef CAS.
- C. Erker and T. Basché, J. Am. Chem. Soc., 2022, 144, 14053–14056 CrossRef CAS.
- Y. Zhang, D. Zhang, T. Huang, A. J. Gillett, Y. Liu, D. Hu, L. Cui, Z. Bin, G. Li, J. Wei and L. Duan, Angew. Chem., Int. Ed., 2021, 60, 20498–20503 CrossRef CAS PubMed.
- Y. Liu, X. Xiao, Y. Ran, Z. Bin and J. You, Chem. Sci., 2021, 12, 9408–9412 RSC.
- X. Fan, X. Hao, F. Huang, J. Yu, K. Wang and X. Zhang, Adv. Sci., 2023, 10, 2303504 CrossRef CAS.
- H. Hirai, K. Nakajima, S. Nakatsuka, K. Shiren, J. Ni, S. Nomura, T. Ikuta and T. Hatakeyama, Angew. Chem., Int. Ed., 2015, 54, 13581–13585 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- L. Y. Zou, Z. L. Zhang, A. M. Ren, X. Q. Ran and J. K. Feng, Theor. Chem. Acc., 2010, 126, 361–369 Search PubMed.
- T.-F. He, A.-M. Ren, Y.-N. Chen, X.-L. Hao, L. Shen, B.-H. Zhang, T.-S. Wu, H.-X. Zhang and L.-Y. Zou, Inorg. Chem., 2020, 59, 12039–12053 CrossRef CAS.
- Y.-L. Zhang, T.-F. He, Z.-K. Zhao, A. Shen, Q. Gao, A.-M. Ren, Z.-M. Su, H. Li, H.-Y. Chu and L.-Y. Zou, Inorg. Chem., 2023, 62, 7753–7763 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Mol. Phys., 1974, 27, 209–214 CrossRef CAS.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- A. Hellweg, S. A. Grün and C. Hättig, Phys. Chem. Chem. Phys., 2008, 10, 4119–4127 RSC.
- D. Hall, J. C. Sancho-García, A. Pershin, G. Ricci, D. Beljonne, E. Zysman-Colman and Y. Olivier, J. Chem. Theory Comput., 2022, 18, 4903–4918 CrossRef CAS.
- D. Mester, P. R. Nagy, J. Csóka, L. Gyevi-Nagy, P. B. Szabó, R. A. Horváth, K. Petrov, B. Hégely, B. Ladóczki, G. Samu, B. D. Lőrincz and M. Kállay, J. Phys. Chem. A, 2025, 129, 2086–2107 CrossRef CAS PubMed.
- Mrcc, a quantum chemical program suite written by M. Kállay, P. R. Nagy, D. Mester, L. Gyevi-Nagy, J. Csóka, P. B. Szabó, Z. Rolik, G. Samu, B. Hégely, B. Ladóczki, K. Petrov, J. Csontos, Á. Ganyecz, I. Ladjánszki, L. Szegedy, M. Farkas, P. D. Mezei, R. A. Horváth, and B. D. Lőrincz, See https://www.mrcc.hu/.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- Y. Niu, L. Wenqiang, P. Qian, G. Hua, Y. Yuanping, W. Linjun, N. Guangjun, W. Dong and Z. Shuai, Mol. Phys., 2018, 116, 1078–1090 CrossRef CAS.
- Z.-K. Zhao, T.-F. He, Q. Gao, A.-M. Ren, T.-S. Wu, J.-F. Guo, H.-Y. Chu, Z.-M. Su, H. Li and L.-Y. Zou, Inorg. Chem., 2024, 63, 17435–17448 CrossRef CAS.
- B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2018, 148, 034104 CrossRef.
- K. Shizu and H. Kaji, Nat. Commun., 2024, 15, 4723 CrossRef CAS.
- K. Shizu and H. Kaji, J. Phys. Chem. A, 2021, 125, 9000–9010 CrossRef CAS PubMed.
- Q. Peng, Y. Yi, Z. Shuai and J. Shao, J. Am. Chem. Soc., 2007, 129, 9333–9339 CrossRef CAS.
- Q. Peng, D. Fan, R. Duan, Y. Yi, Y. Niu, D. Wang and Z. Shuai, J. Phys. Chem. C, 2017, 121, 13448–13456 CrossRef CAS.
- X. Zou, N. Gan, Z. Lin, H. Ma, Y. Wu, A. Lv, Z. An, L. Gu and W. Huang, Nat. Commun., 2025, 16, 6412 CrossRef CAS.
- L. Ge, W. Zhang, Y.-H. Hao, M. Li, Y. Liu, M. Zhou and L.-S. Cui, J. Am. Chem. Soc., 2024, 146, 32826–32836 CrossRef CAS PubMed.
- R. J. Gillespie, J. Chem. Educ., 1963, 40, 295 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- R. C. Hilborn, Am. J. Phys., 1982, 50, 982–986 CrossRef CAS.
- X.-K. Chen, Y. Tsuchiya, Y. Ishikawa, C. Zhong, C. Adachi and J.-L. Brédas, Adv. Mater., 2017, 29, 1702767 CrossRef.
- X.-K. Chen, D. Kim and J.-L. Brédas, Acc. Chem. Res., 2018, 51, 2215–2224 CrossRef CAS.
- T. He, W. Zhao, M. Lin, B. Sun, Y. Chen, H.-L. Zhang and G. Long, J. Phys. Chem. Lett., 2024, 15, 9844–9851 CrossRef CAS.
- P. O. Andersson, S. M. Bachilo, R.-L. Chen and T. Gillbro, J. Phys. Chem., 1995, 99, 16199–16209 CrossRef CAS.
- J. Zhao, H. Liu, J. Fan and Q. Mu, Phys. Chem. Chem. Phys., 2024, 26, 5156–5168 RSC.
- Y. Pu, X. Cai, Y. Qu, W. Cui, L. Li, C. Li, Y. Zhang and Y. Wang, Angew. Chem., Int. Ed., 2025, 64, e202420253 CrossRef CAS PubMed.
- X. Cai, Y. Pan, C. Li, L. Li, Y. Pu, Y. Wu and Y. Wang, Angew. Chem., Int. Ed., 2024, 63, e202408522 CrossRef CAS PubMed.
- A. Ying, N. Li, X. Chen, J. Xia, C. Yang and S. Gong, Chem. Sci., 2025, 16, 784–792 RSC.
- A. Ying, L. Zhan, Y. Tan, X. Cao, C. Yang and S. Gong, Sci. China: Chem., 2023, 66, 2274–2282 CrossRef CAS.
- S. Diesing, L. Zhang, E. Zysman-Colman and I. D. W. Samuel, Nature, 2024, 627, 747–753 CrossRef CAS.
- M. Elsherbini, W. S. Hamama and H. H. Zoorob, Coord. Chem. Rev., 2017, 330, 110–126 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |