Local entropy in proteins

Abstract

Proteins populate dynamic ensembles, yet how temperature and mutations reshape these ensembles remains poorly understood. We introduce a local entropy metric that assigns each residue a Shannon entropy based on a graph-derived map of accessible substates, providing a continuous measure of structural complexity across folded, unfolded, and intrinsically disordered states. In molecular dynamics simulations of the fast-folding gpW protein, the average local entropy exhibits a sharp transition near the melting point. Residue-specific entropy curves cluster into distinct unfolding categories and reveal that the apparent unfolding transition depends on the spatial scale used to describe amino-acid environments. We further show that local entropy captures features that differ markedly from other residue-level measures of structural fluctuations, such as the accessible volume (and the associated packing entropy), which is correlated with B-factors and primarily reflects the hydrophobic effect. In simulations of α-synuclein, an intrinsically disordered protein, local entropy varies strongly along the sequence at physiological temperature and resembles that of gpW near its melting point. Parkinson's-disease mutations in α-synuclein locally reduce entropy while also perturbing distant regions including P1, P2 and NAC segments implicated in fibril formations. These results highlight how temperature and subtle perturbations—such as single-residue changes—remodel conformational ensembles. Local entropy correlates with NMR observables and provides a generalizable framework for quantifying disorder, with broad potential applications beyond protein science.

---

Introduction

At physiological temperatures, folded proteins adopt a relatively narrow distribution of accessible conformations, dominated by those contributing most significantly to their free-energy minimum.^1–3 Typically, a single structural model—determined experimentally by X-ray diffraction or Nuclear Magnetic Resonance (NMR), or predicted computationally using deep learning methods^4,5—is used to represent this conformational ensemble. The classification of folded proteins is facilitated by the identification and characterization of recurrent local motifs or patterns in these structural models.^6–17

In contrast, unfolded proteins, intrinsically disordered proteins (IDPs), or intrinsically disordered regions (IDRs)^18–21 cannot be accurately represented by a single structure, as a large ensemble of accessible states contribute significantly to their free-energy. The classification of IDRs and IDPs primarily relies on functional features related to recurring local sequence properties – such as linear motifs or molecular recognition elements associated with intermolecular interactions.²² Computational analyses of large conformational ensembles of IDRs and IDPs focus on clustering full-length conformations based on structural parameters.^23,24 Because amino-acid composition strongly influences both protein disorder^25,26 and dynamics,²⁷ global structural features of IDRs are often correlated with their sequence.²⁸ At the local scale, however, unfolded proteins and IDPs display dynamic structural organization, as shown by NMR and single-molecule spectroscopy.²⁹

In reality, the distinction between the structural representations of folded and disordered proteins is not as clear-cut as often assumed. Even folded proteins exist as ensembles of conformations fluctuating around a well-defined structural state, whereas disordered proteins populate a much broader and more heterogeneous ensemble. A single representation of a folded protein structure does not adequately reflect the dynamic landscape of its local conformational substates.³⁰ A unifying characteristic of protein conformations is the presence of short-range structural order around each amino acid, which varies continuously with thermodynamic parameters such as temperature and pH. This continuum is evident during thermal denaturation, where the local structural changes occur progressively with temperature. Below 240 K,³¹ local structural fluctuations are harmonic and can be represented by stationary motifs at short and long distances, enabling the identification and definition of recurrent patterns^6–17 such as secondary structural elements.^6–8 At physiological temperatures, proteins behave as surface-molten solids: surface-exposed (hydrophilic) residues undergo thermal fluctuations, while core (hydrophobic) regions retain relatively stable structures.³² Above the melting temperature—or in intrinsically disordered states—all residues fluctuate within dynamic micro-environments resembling molecular liquids, as demonstrated by NMR and single-molecule studies.³⁰

In this work, we show that analyzing ensembles of short-range structures around each amino acid under varying conditions enables the quantification of local disorder along the protein sequence. This is achieved by computing a local entropy derived from a protein graph (PG). Replacing molecular geometries with graph representations—where amino acids are nodes and edges denote geometric relationships—have long been employed in protein science^33–35 to facilitate the detection of recurrent local patterns in databases of single-structure folded proteins. Since then, graph-based models have become powerful tools for analyzing protein structure, dynamics and function.^36–52

Accurately computing the entropic contribution to the free energy of protein conformations remains a long-standing challenge.^53–67 Since the early days of protein science,^53–56 various methods have been developed to approximate this contribution by decomposing entropy into local components,^65,68–70 based on local structural properties—for example, the NMR order parameter S²,^71–73 atomic coordinate fluctuations within the (quasi)-harmonic approximation,^53,55,56 backbone and side-chain torsion angles,⁷⁰ or the amino acid packing fraction.⁶⁵ In the present work, we do not aim to calculate this thermodynamic quantity directly. Instead, we employ Shannon entropy to quantify the degree of intrinsic disorder in the protein backbone, beyond local conformational descriptors such as Ramachandran angles or residue accessible volume. In this framework, local entropy serves as a measure of structural diversity within the interaction network surrounding each residue. Our approach differs from previous site-resolved entropy estimations by explicitly incorporating residue–environment interactions, thereby providing a more integrative and context-sensitive description of local conformational variability during protein folding and unfolding. Finally, by comparing our definition of local entropy with the packing entropy⁶⁵—which is known to correlate strongly with site-resolved entropies derived from quasi-harmonic approximations and B factors⁶⁵—we demonstrate both the differences and the complementarity between these two measures of structural entropy.

The present approach is applicable to both folded and unfolded proteins, including intrinsically disordered proteins and intrinsically disordered regions. Entropy plays a central role in IDP function, binding and aggregation.^63,66 We first examined how local entropy evolves during thermal unfolding using all-atom molecular dynamics (MD) simulations of the W protein of bacteriophage lambda (gpW, PDB ID: 2L6Q).⁷⁴ This 62-residue polypeptide adopts a folded structure comprising two α-helices (residues 4–19 and 40–54) stacked above a β-hairpin (residues 23–28 and 31–36),⁷⁴ and folds via a downhill mechanism.^74,75 Experimental local unfolding curves for gpW were inferred from temperature-dependent chemical shifts of atomic probes.⁷⁶ These NMR measurements revealed abrupt chemical shift changes near the melting temperature, supporting their interpretation as local heat-induced denaturation curves.⁷⁶ This behavior, along with the weak cooperativity of gpW's folding/unfolding transition, was successfully reproduced by all-atom MD simulations.⁷⁶ In earlier work, we showed that these local denaturation curves could be captured using a coarse-grained two-state (folded/unfolded) model based on C^α–C^α pseudobond angles.^77,78 Here, we demonstrate that local entropy varies along the sequence in the folded state, including within secondary structural elements, and acts as an order parameter for the unfolding phase transition, correlating well with experimental C^α chemical shifts.

Second, using coarse-grained MD simulations,⁷⁹ we show that local entropy is heterogeneously distributed along the sequence of α-synuclein, a prototypical IDP. To enable comparison between the simulation results for local entropy and experimental data for wild-type α-synuclein, we selected two residue-level disorder descriptors derived from chemical shifts: the ¹³C^α secondary chemical shift^80,81 and the Chemical Shift Z-score used to assess order/disorder.⁸² A detailed analysis of the three descriptors reveals both common features—when averaged over the three regions of the protein—and key differences in their local behavior. Finally, we show that local entropy is sensitive enough to detect subtle changes in the conformational ensemble induced by single-point mutations (A30P, E46K, and A53T) in α-synuclein, including long-range effects potentially linked to aggregation.^83–85

Methods

Definition of the local entropy

Local entropy is a combinatorial property derived from protein graphs. In a PG, each vertex represents a C^α atom of an amino acid within the protein, while an edge connects two vertices if their corresponding atoms are separated by a distance smaller than a predefined cutoff value, R. This cutoff is carefully selected to include at least the second-nearest neighbor C^α atoms, consistent with coarse-grained elastic network models of proteins.³⁷ Typically, R ranges from 6 to 10 Å to ensure that the relevant dynamic interactions are adequately captured. For the results presented in the main text, we adopt R = 8 Å. Similar conclusions hold for other values of R, as illustrated in the SI using α-synuclein as an example (Fig. S1). Increasing the cutoff distance R primarily shifts the S profile toward higher values.

For each conformation in the protein ensemble, we construct a corresponding PG. In each PG, we define a protein subgraph (sPG) centered on a selected node by including all nodes within a graph distance D from it. For D = 1, the sPG comprises the immediate neighbors of the central node, along with all edges connecting them. For D = 2, second-nearest neighbors in the PG are also included, thereby extending the structural context. In this study, we analyze sPGs with D = 1 and D = 2, which represent the local micro-environment of a residue, encompassing its first and second neighbors on the graph, respectively. Throughout the text, each graph node is identified by its sequence position and the corresponding amino acid name.

The local entropy S_k is then calculated for each residue at position k along the sequence, based on the ensemble of its sPGs, using the Shannon entropy definition:

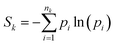where n_k is the number of different sPG for residue k in the structural ensemble and p_i is the probability to observe the ith sPG with i = 1 to n_k.

As predicted by the Boltzmann formula, the maximum value of S_k is constrained by the number of its accessible micro-environments in the ensemble, and equals:

S_k,max = ln(n_k) (2)

The maximum value of n_k is the number N of protein conformations in the ensemble. In the main text, we report normalized entropy values of S_k/S_max where S_max = ln(N). The local entropy S_k defined by eqn (1), is dimensionless. In information theory, entropy is typically expressed in natural units (nats). When interpreted as a thermodynamical quantity with k_B = 1, a value of S = 1 corresponds to an entropy of 1.987 cal mol⁻¹ K⁻¹, equivalent to a free-energy contribution of −0.616 kcal mol⁻¹ at T = 310 K, for example.

In a sPG, permuting the node labels alters the amino acid sequence of the protein; thus, graph homomorphisms are not treated as equivalences. The probabilities p_i used in the entropy calculation are obtained by identifying automorphic sPGs—that is, structurally identical subgraphs across conformations. The local entropy values of S_k are computed using the NetworkX Python library.⁸⁶ For simplicity, we denote local entropy as S instead of S_k in the remainder of the text.

Conformational ensembles

The protein graph ensembles analyzed in this study were derived from structural configurations obtained from previous all-atom MD simulations of gpW^77,78 and from coarse-grained MD simulations of α-synuclein,⁷⁹ as well as from reference ensembles of random conformations generated solely from steric constraints, i.e., self-avoiding random walks (SAWs) in three-dimensional space, as described in the SI.

In the main text, local entropy values were computed from 100 000 randomly selected snapshots from each MD trajectory and from SAW ensembles of the same size. As illustrated in the SI using wild-type α-synuclein as an example (Fig. S2), this sampling strategy provides sufficient statistical accuracy while substantially reducing computational cost compared to full-ensemble analyses.

Results and discussion

The local entropy is a local order parameter of protein unfolding

How does local entropy vary during protein unfolding ? We address this question by analyzing the heat-induced denaturation of the 62-residue polypeptide gpW. Fig. 1 presents the local entropy computed along the amino acid sequence of gpW at different temperatures, based on all-atom MD simulations in explicit solvent.^77,78

Fig. 1 Local entropy S at a graph distance D = 1 (upper panel) and D = 2 (lower panel) is shown as a function of the amino acid sequence of gpW at various temperatures, calculated from all-atom MD simulations for R = 8 Å. Normalized values of the local entropy S/S_max are presented with S_max = ln(100 000) = 11.513 (eqn (2)). Lines are provided as guide for the eye. The thick black solid line corresponds to results at T = 280 K (native, folded state). Symbols indicate residue properties: red for positively charged amino acid, blue for negatively charged ones, black for glycine, triangles for residues in β-sheets, and empty black circles for all other cases. Gray shading highlights regions corresponding to α-helices. Results at the experimental melting temperature T_m = 330 K are shown as a thick red line. Thin red dotted lines represent results at T = 325 K and 335 K. Gray dotted lines show results at increasing temperatures, from bottom to top: T = 280, 285, 290, 295, 305, 310, 315, 320, 325, 335, 340, 355, 380 K. The black dashed line represents the local entropy computed from a SAW ensemble representing for a chain of 62 atoms.

We begin by examining the variation of local entropy S as a function of amino acid position at graph depth D = 1. In the native state (280 K), S is highly heterogeneous along the sequence, including within well-defined secondary structures represented in Fig. S3. The lowest entropy values are observed in the central region of the sequence, corresponding to residues involved in β-sheets. A clear trend emerges: S increases from the center toward the termini of the chain. The highest local entropy is observed for residue T54, located at the interface between the two helices within the three-dimensional structure of gpW, as shown in Fig. S3. Notably, if the folded protein was represented by a single static structure, S would be exactly zero for all residues. The results in Fig. 1 underscore the necessity of representing even folded proteins as conformational ensembles, rather than single snapshots.³⁰

The spatial variations of S in the folded state provide complementary insight into protein dynamics, focusing on the network of intramolecular interactions rather than on local positional fluctuations (as captured by B-factors), bond vector order parameters (such as the NMR-derived S²)^71–73 or local accessible volume (such as the packing fraction⁶⁵). For comparison, we computed the packing entropy S_P, which has been demonstrated to correlate strongly with entropies derived from the quasi-harmonic approximation or from B factors,⁶⁵ at all temperatures along the amino acid sequence of gpW using structures extracted every nanosecond from all trajectories. The packing entropy of each amino acid, S_P(k), is computed for every protein structure from its packing fraction (see ref. 65 and the SI). The results shown in Fig. S4 reveal that S_P represents a distinct quantity. As expected for its small size, glycine residues contribute the most, and the packing entropy values of G20, G30, G55, and G62 are of the same order of magnitude. Importantly, in contrast, the local entropy S depends more strongly on the position of the residue within the sequence than on the chemical nature of the amino acid itself. For instance, residues G30 and G55 display markedly different entropy values in the folded state at T = 280 K (0.11 and 6.27, respectively as shown in Fig. 1). Local entropy is a property of the interaction network and depends on the identity of the interacting residues, whereas packing entropy measures the locally accessible volume around a residue and is less sensitive to the chemical nature of the amino acids forming the surface of this volume. Both quantities contribute to the overall entropy of the protein.

For the majority of residues, local entropy S increases progressively with temperature up to 320 K, i.e. below T_m as shown in Fig. 1. Beyond this point, a notable shift occurs: the curves of S at 325 K, the melting temperature T_m = 330 K, and 335 K form a clearly distinct cluster, separated from those at 320 K and 340 K. This abrupt change is hallmark of the unfolding phase transition. By contrast, the packing entropy S_P does not vary much with the temperature and no global unfolding phase transition is observed in Fig. S4. This can be understood as according to the Gaussian model of an ideal polymer and molecular dynamics simulations, the unfolded state is a compact structure and for most of the residues the accessible volume will not be very different in folded and unfolded states.

At T_m and above (i.e., in the unfolded state), local entropy becomes approximately uniform along the sequence, except at the N-terminus (residues 1–3) and C-terminus (residues 60–62), where S remains lower (Fig. 1 and S3). Interestingly, this pattern closely resembles the entropy profile derived from ensembles of self-avoiding random walks of the same chain length. In particular, the SAW ensemble also exhibits reduced entropy at the chain ends, suggesting a common geometrical origin linked to reduced connectivity or spatial constraint near termini.

The low values of local entropy S observed at the N- and C-termini can be interpreted through combinatorial considerations. In the absence of specific interactions—such as in SAW models where only steric constraints are present—or at high temperatures in MD simulations where the potential energy landscape exerts minimal influence, the conformational ensemble is governed primarily by geometrical and entropic factors. In such regimes, the local entropy reflects the combinatorial diversity of local environments. According to the Gaussian polymer model, the probability of forming a contact between two residues i and j decreases sharply with their sequence separation d_seq = |i − j|.⁸⁷ As a result, residues located at the chain termini have fewer opportunities to establish contacts, since they can interact with residues only on one side of the sequence. This asymmetry limits the number of distinct subgraph configurations that can form around terminal residues, reducing the diversity of micro-environments and therefore leading to lower local entropy values compared to residues in the interior of the chain.

Second, we examined the variation of local entropy at D = 2 in Fig. 1. The profile of S along the sequence exhibits features similar to those observed at D = 1, with the main difference being a marked increase in entropy values across all residues and a more uniform local entropy in the C-terminal region beyond residue L50. This increase arises from the fact that, by construction, the subgraphs at D = 2 contain more nodes and edges, and are thus more sensitive to conformational fluctuations over time.

At the melting temperature T_m, the local entropy reaches values close to the maximum possible entropy S_max for nearly all residues, except at positions 19 and 30, where the entropy remains low—consistent with their strong structural constraints in the native state at D = 1. At 380 K, the local entropy remains uniform across the central region of the sequence, similarly to the behavior observed at D = 1. Notably, the gap between the curve at T_m and those at 5 K above or below is smaller at D = 2, indicating that the temperature dependence of S is smoother at this scale.

Each sPG can be interpreted as a microstate of the local environment of a residue, defined by its network of connections. At equilibrium and sufficiently high temperatures, the local entropy for each residue is expected to approach a maximum given by the Boltzmann formula (eqn (2)). In this regime, the variations of S_k and of the number n_k of accessible microenvironments (i.e., distinct sPGs) along the sequence should be highly correlated.

To quantify this, we computed the Pearson correlation coefficient r between the vectors S_k and n_k as functions of the residue index k, at various temperatures, for gpW at D = 1 (Fig. S5). The correlation remains high across all temperatures, with a modest discontinuity at T_m. Specifically, at D = 1, the average value of r is 0.915 for T < T_m and 0.954 for T > T_m. At D = 2 (Fig. S6), the correlation is even stronger, increasing from 0.970 at 280 K to 0.992 at 380 K. These results show that, to a very good approximation, local entropy reflects the number of accessible structural states around each residue in the graph representation.

In addition, the Pearson correlation between the average size of each sPG (measured by the number of peptide bonds it includes) and S at D = 1 displays an abrupt shift at the melting temperature and converges at high temperatures to values comparable to the correlation between S_k and n_k (see Fig. S5). In the unfolded state, the number of accessible sPGs n_k becomes nearly uniform across the sequence, except at the terminal residues. As also observed for the global entropy curve S, the transition is less pronounced at D = 2, as illustrated in Fig. S6.

The curves S(T) extracted from Fig. 1 at D = 1 are shown for selected residues in Fig. 2 a, and for all residues in the SI (Fig. S7). For most residues, S(T) exhibits a sharp change near the melting temperature (T_m = 330 K), which supports the interpretation of local entropy as a local order parameter of the unfolding phase transition.

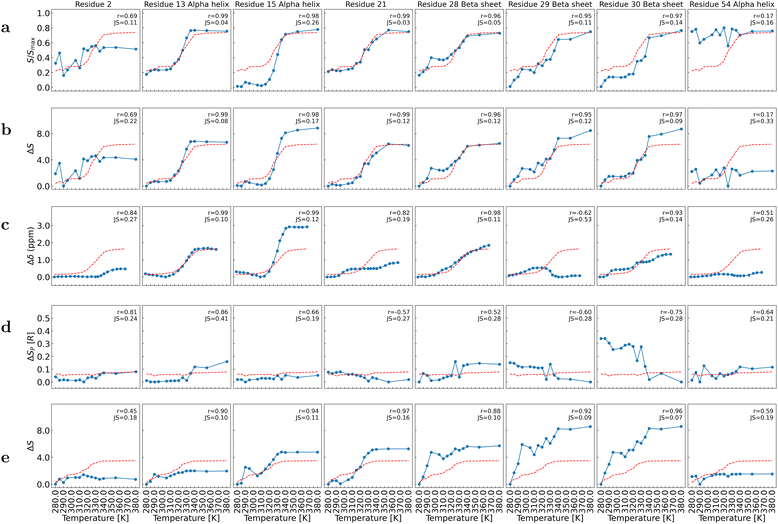Fig. 2 Local heat denaturation curves from MD of gpW and those extracted from NMR chemical shifts data δ (in ppm) from ref. 76 for selected residues of gpW. The curves S(T)/S_max extracted from Fig. 1 at D = 1 are showed (panel (a)). The local entropy differences, represented at D = 1 (panel (b)) and D = 2 (panel (e)), are ΔS = S(T) − S_min where S_min is the minimum value of S between 280 K and 380 K. The chemical shifts data are shown Δδ = δ(T) − δ_min if δ increases with T, and Δδ = δ_max − δ(T) if δ decreases with T (panel (c)). The local packing entropy differences, represented (panel (d)), are ΔS_P = S_P(T) − S_P,min where S_P,min is the minimum value of S_P between 280 K and 380 K. Solid lines are provided as guide for the eye. A red dashed curve represents the average of the curves over all residues for each quantity. The values of the Pearson correlation coefficient r and the Jensen–Shannon distance JS computed between each local entropy curve and the average curve are shown.

For each residue, the curve S(T) is compared to the average over all residues, denoted 〈S(T)〉. Although the local entropies are not strictly independent—since residues are connected—the average serves as a useful global entropic descriptor. The S(T) curves can be qualitatively classified into four categories based on their deviation from 〈S(T)〉, as illustrated in Fig. 2a. The similarity between the local entropy curve and the average curve is quantified using both the Pearson correlation coefficient (r) and the Jensen–Shannon distance (JS) computed using SciPy library.⁸⁸ The correlation coefficient measures the linear relationship between two curves and reaches its maximum value, i.e., 1, when the two curves are identical up to a multiplicative constant, whereas the JS distance quantifies the dissimilarity between the distributions of values along the two curves and reaches its minimum value, i.e., 0, for identical distributions.

The first category includes 41 out of 62 residues whose local entropy curves S(T) are highly correlated with the average entropy 〈S(T)〉 (r ≥ 0.96). For this category, the unfolding transition is clearly cooperative. The local entropy curves can be further divided into two classes. In the first class (JS ≤ 0.06), 20 residues display local entropy profiles that closely follow the average curve, such as A13, K21, and K28 (Fig. 2a). This class also includes E5, L7, A9, A10, L14, M18, R22, A24, T25, V26, Q27, F35–A37, S39, V40, and L43 (Fig. S7). The second class (0.09 ≤ JS ≤ 0.28) comprises 21 residues whose S(T) curves undergo sharper transitions than the global curve due to their very low entropy in the folded state. Examples include H15 and G30 (Fig. 2a), as well as R11, A12, D16, T19, G20, V23, R31, R32–E34, T38, S41, D42, and K44–E49 (Fig. S7). Notably, G30 exhibits a multistep transition with three distinct plateaus, indicating complex unfolding behavior. Except for K21, R22, A37, and T38, residues in the first category are located within secondary structure elements.

The second category includes residues located in secondary structure elements whose S(T) curves are highly correlated with the average entropy curve (r ≥ 0.9), but that increase approximately linearly with temperature up to the unfolded state (0.07 ≤ JS ≤ 0.11), as illustrated by D29 in Fig. 2a. Additional examples include E6, L50, E51, M56, and T57 (Fig. S7).

The third category includes residues exhibiting more complex S(T) profiles that remain significantly correlated with the average entropy curve (0.83 ≤ r ≤ 0.96 and 0.07 ≤ JS ≤ 0.16). Examples include A8, R11, V52, Q53, and G55, which are located within secondary structure elements, and Q58–G62 in the C-terminal region (Fig. S7). These patterns may reflect the presence of intermediate states during unfolding.

Finally, the fourth category consists of five residues showing little to no variation in S(T) across the temperature range (0.11 ≤ JS ≤ 0.16), with low correlation (r ≤ 0.83) between the local and average entropy curves. Representative examples are V2 and T54 (Fig. 2a), the latter located at the interface between the two helices (Fig. S3). Other members include M1, R3, and Q4 (Fig. S7). These residues, mostly located at the termini, appear structurally disordered or only weakly affected by unfolding.

For all residues, the number of links in their sPGs decreases significantly above the melting temperature, and the probability distribution of the sPGs becomes flatter at T > T_m, as shown at 280 K (folded), 330 K (T_m), and 380 K (unfolded) in Fig. S8 for selected residues.

The first category of S(T), which accounts for more than two-thirds of the amino acids, corresponds to distinct behaviors of the sPG probability distribution p_i in the folded state. In the first class of this category, where S(T) agrees closely with the average S(T) (JS ≤ 0.06), the most probable sPG has a probability of about 0.3–0.4, and only around ten sPGs have significant probabilities. In the second class of this category (0.09 ≤ JS ≤ 0.28), the most probable sPG has a probability close to 1, and only about three sPGs occur with non-negligible probabilities. This indicates that the links of these residues—such as H15 and G30—are very stable, even at the melting temperature.

The local entropy clearly reveals distinct behaviors among residues, depending on the stability of their local environments. This indicates that the unfolding transition is not a strict all-or-none, two-state process. In particular, extremely low values of S in the native state—such as those observed for residues H15 and G30—highlight key residues that contribute significantly to the stability of the folded structure. Both of these residues with low local entropy are located within secondary structural elements.

The S(T) curves extracted from Fig. 1 at D = 2 are shown in the SI (Fig. S9). As previously observed in Fig. 1, the unfolding transition is much less pronounced at D = 2, except for a few residues—mainly those located in secondary structure elements, notably residues M18–V23, T36–T38, and S41. As a result, the average curve of S does not exhibit a clear phase transition at D = 2 but instead shows a gradual increase with temperature up to T_m, beyond which S becomes nearly constant.

Previous NMR studies have revealed a variety of denaturation behaviors in the chemical shifts of gpW during unfolding, as measured by ¹³C^α nuclei.⁷⁶ Given that the local entropy is a combinatorial property derived from the short-range environment of each C^α atom, we investigate here the relationship between this theoretical local order parameter and the variations in ¹³C^α chemical shifts observed during protein unfolding.

It is well established that ¹³C^α chemical shifts are sensitive indicators of secondary structure.⁸⁹ More specifically, their values are known to vary with the Ramachandran angles⁸⁹ or with the local backbone curvature θ and torsion γ.⁷⁸ More generally, chemical shifts are highly sensitive to local structural segments or motifs.⁹⁰ As temperature increases, the conformational space explored by atoms in the (θ, γ) map expands.⁷⁸ However, the connection between a theoretical local order parameter and an experimental observable depends on both the nature of the probe and its resolution.⁹¹ As previously shown, changes in the shape and size of the (θ, γ) region explored by an atom during unfolding may lead to chemical shift variations too subtle to be detected experimentally.⁷⁸ Nevertheless, since the number of microstates visited by an atom correlates with the accessible surface in this map, a link between local entropy and chemical shifts is expected.

To compare δ(T) and S(T)—two fundamentally different physical observables—we define normalized variations based on their temperature-dependent changes. For the local entropy computed from MD, we define ΔS(T) ≡ S(T) − S_min, where S_min is the minimum value observed between 280 and 380 K. For the chemical shift, we define Δδ(T) as either δ(T) − δ_min or δ(T) − δ_max, depending on the monotonicity of δ(T) across the temperature range. Specifically, we use the first expression if δ(T) increases with T, and the second if it decreases.

The ΔS(T) curves computed at D = 1 (Fig. 2b) and D = 2 (Fig. 2e) are compared to the Δδ(T) profiles (Fig. 2c) for the selected residues shown in Fig. 2. Results for all residues are provided in the SI (Fig. S10 and S11 for ΔS(T) at D = 1 and Δδ(T), respectively).

In Fig. 2, we observe a remarkable similarity between ΔS(T) and Δδ(T) at D = 1, with the exception of residues K21 and D29. Notably, the multi-step transition observed in S(T) for residue G30 is also reflected in the δ(T) data. Similar correlations are found across the full set of residues, as shown in the SI. These observations confirm that, at D = 1, the different classes of S(T) curves closely reproduce the δ(T) behaviors previously reported by Sborgi et al.⁷⁶

In contrast, ΔS(T) computed at D = 2 does not exhibit a clear phase transition (see Fig. S12), and diverges significantly from the corresponding Δδ(T) measurements. This discrepancy is evident when comparing panels c and e in Fig. 2, as well as Fig. S11 and S12 in the SI. This result is expected, as the chemical shift of a nucleus is primarily influenced by its immediate local environment. The comparison of experimental δ(T) data with entropy calculations at two different graph distances suggests that the cooperative features of protein unfolding resemble a phase transition only within a limited interaction range. This conclusion holds for the complete set of residues, as illustrated in Fig. S10–S12.

It is relevant to compare the local packing entropy ΔS_P(T) curves extracted from the Fig. S4 with the local packing entropy curves ΔS(T) at D = 1 (Fig. 2b and S12) and NMR chemical shifts variations (Fig. 2c and S11). The curves ΔS_P(T) are shown in Fig. 2d for selected residues and in Fig. S13 for all residues. As it can be anticipated from Fig. S4, most of the local curves ΔS_P(T) do not show a significant variation and consequently the average entropy curve 〈ΔS_P(T)〉 does not show clearly a phase transition, in contrast with the local entropy ΔS(T) (Fig. 2b and S10) and NMR chemical shifts Δδ (Fig. 2c and S11).

Nevertherless, a zoom on the average curve is shown in Fig. S14 where we observed a small increase of the 〈ΔS_P(T)〉 with T between 280 K and 380 K and a small jump between 325 K and 335 K which can be interpreted as due to the unfolding process. This small jump is due to only a few residues for which the local entropy does indeed show a transition as observed for residue A13 in Fig. 2d. Other residues in this category are L7, A9, A10, L14, L17, A24, V26, L43, Y46, L50. Their local packing entropy curve is correlated to average one with Pearson correlation coefficient r > 0.7 but also deviates significantly as the Jensen–Shannon distance is high 0.16 ≤ JS ≤ 0.46. All these residues are hydrophobic.

Two residues show a transition anti-correlated with 〈ΔS_P(T)〉, i.e., the entropy of these residues decreases with T, as shown in Fig. 2d for G30 and in Fig. S13 for G20. Glycine residues tend to cluster with polar amino acids regarding change in contacts related to entropy variations.⁶⁴ The decrease in S_P for G20 and G30 with increasing T may be related to the hydrophobic effect, similarly to the increase in entropy observed for the hydrophobic residues mentioned above.⁶⁵ Packing entropy is indeed correlated with the accessible surface area of residues.⁶⁵ In the early days of protein science, Janin proposed a hydrophobicity scale by computing a free energy ΔG_t = RT ln f, which can be interpreted as the free energy of transferring a residue from the protein interior to the surface, where f is the ratio of the buried to accessible molar fractions of that residue across a set of proteins.⁹³ The values of ΔG_t, computed using the ProtScale server,⁹² are compared with the variation of ΔS_P = S_P(380 K) − S_P(280 K) in Fig. S15. Residue G30 is predicted to be more stable at the protein surface, and one can see that the change in packing entropy contributes to this stability. In contrast, residue L43—which exhibits a marked increase in entropy at high temperature (Fig. S13)—has a positive value of ΔS_P ≡ S_P(380 K) − S_P(280 K) in Fig. S15. Representative snapshots of gpW at 280 K and 380 K, shown in Fig. S16, confirm the relocation of G30 toward the protein interior and the movement of L43 toward the surface at high temperature. Packing entropy is therefore a powerful tool for quantifying the hydrophobic effect from static structures.

Clearly, packing entropy quantifies a contribution to the total entropy that is distinct from local entropy, as it is directly related to accessible surface area and thus to the hydrophobic effect. This explains why it does not correlate with local entropy or with NMR chemical-shift variations, as shown by comparing panels b, c, and d of Fig. 2 and S9, S13, and S12. The two entropies do not probe the same microstates. For packing entropy (which correlates with B-factors⁶⁵), the microstates correspond to local configurations of the accessible volume around a residue, without distinguishing the chemical nature of the surrounding amino acids. Local entropy, in contrast, accounts for the interaction network, which varies even for the same accessible volume depending on the identity and arrangement of neighboring residues. The number of microstates—and its variation with temperature—is therefore larger for local entropy, which also correlates with NMR chemical shifts that depend on nuclear interactions and structural organization. Both entropies contribute to the total entropy of the protein.

Local entropy in a disordered protein ensemble

Large entropy changes are expected during IDP binding and aggregation.^63,66 Quantifying entropy in IDPs is clearly needed, but it is even more challenging than for globular proteins because of the broad conformational ensembles sampled by these macromolecules. In this context, local entropy S may serve as a computational ruler, as illustrated here for α-synuclein. As shown in our previous work, the conformational ensembles of wild-type and mutant α-synuclein monomers⁷⁹ and dimers⁸⁵ studied here are in good agreement with available experimental data.

The monomeric form of α-synuclein is well known to be intrinsically disordered in solution. Fig. 3 displays the local entropy S at T = 310 K computed at distances D = 1 and D = 2 from coarse-grained MD simulations for the wild-type α-synuclein monomer, along with values obtained for a SAW ensemble of the same chain length. On average, the local entropy of α-synuclein is close to that of the SAW ensemble: the ratios 〈S〉/〈S_saw〉 are 0.856 and 0.979 at D = 1 and D = 2, respectively.

Fig. 3 Local entropy S at a graph distance D = 1 (lower curves) and D = 2 (upper curves) is shown as a function of the amino acid sequence of α-synuclein at physiological temperatures, calculated from coarse-grained MD trajectories at R = 8 Å. Normalized values of the local entropy, S/S_max, are presented with S_max = ln(100 000) = 11.513 (eqn (2)). Lines are provided as guide for the eye. Solid and dashed lines represent local entropies computed from MD and SAW structural ensembles, respectively. Solid red symbols indicate positively charged amino acids, while blue symbols indicate negatively charged ones. Diamond symbols mark the positions of missense mutations at A30, E46 and A53. Light gray shading indicates the P1 (residues 36–42) and P2 (residues 45–57) segments, while dark gray shading indicates the NAC region (residues 61–95).

It is informative to compare these values to the ones calculated between the local entropy of the unfolded state of gpW and those of SAW of the same chain length. We found: 〈S〉/〈S_saw〉 = 1.139 at D = 1 and 1.046 at D = 2. These ratios greater than one reflect the presence of enhanced fluctuations in the unfolded globular protein, due to transient interactions between amino acids, which are less frequent in more extended structures like SAWs or intrinsically disordered proteins. As shown by comparing Fig. 1 and 3, the variation of S in gpW at T_m relative to its SAW reference closely resembles the entropy profile of α-synuclein at T = 310 K, for both D = 1 and D = 2. At T_m, gpW exhibits 〈S〉/〈S_saw〉 = 0.730 at D = 1 and 0.996 at D = 2. This suggests that the conformational disorder of a folded protein at the transition state can closely match that of a fully disordered protein under physiological conditions. Further investigation is required to determine whether this observation reflects a general principle applicable to other protein systems. Indeed, these observations may also arise from the different models employed (all-atom versus coarse-grained force fields) and from the different time scales involved (microsecond versus millisecond effective time scales).

Among the different regions, the NAC domain appears as the most disordered, while the C-terminal domain is comparatively more structured, particularly at D = 1. Specifically, the entropy ratios 〈S〉/〈S_saw〉 at D = 1 are 0.893, 0.907, and 0.762 for the N-terminal, NAC, and C-terminal regions, respectively. The same trend holds at D = 2 with values of 0.982, 0.992, and 0.965.

At D = 2, the local entropy is nearly uniform along the sequence, except at the termini and for a few specific residues. Distinct local minima of S are observed at residues E13, G25, G31, K45, T59, E110, and D119, with shallower minima in the NAC region around residues G68, V74, and E83. Many of these residues also exhibit low entropy at D = 1, particularly E13, K45, T59, E83, E110, and D119.

As evident from both D = 1 and D = 2, the minima at K45 and T59 lie at the centers of the low-entropy segments K43–E46 and K58–E61, respectively, which separate the P1 and P2 regions. These regions were recently shown to play a crucial role in α-synuclein aggregation, in addition to the well-known NAC region.⁸³ Maxima of local entropy at D = 1 are observed in these regions at hydrophobic residues L38 (P1), V52–A53 (P2), and I88–A89 (NAC). Interestingly, the residues forming native contacts in α-synuclein fibril-like dimers with probability greater than 0.9 in our previous simulations on a millisecond time scale are located near this flexible segment in the NAC (residues G86–F94).⁸⁵ Further work will be required to establish whether a clear relationship exists between the local entropy of the monomeric state and aggregation propensity.

Interestingly, residues with the lowest entropy values tend to be charged. As for gpW, the Pearson correlation coefficient between the local entropy S_k and the number of distinct micro-environments n_k visited by each residue is high (P = 0.954). Low S values can therefore be interpreted as reflecting a reduced number of accessible microstates, due to strong electrostatic interactions or hydrogen bonding. For example, deep entropy minima at K45, K60, and E110 correspond to the sampling of only 7217, 6349, and 3282 distinct sPGs, respectively, out of a maximum of 100 000, compared to the average 〈n_k〉_k = 17 800 and the maximum, 40 633, observed for L38.

Local order in α-synuclein from theory and experiment

In gpW, we observed strong correlations between the temperature-dependent chemical shifts δ(T) and the local entropy S(T), particularly for residues located within secondary structural elements. These correlations reflect larger excursions of the main chain in dihedral space, originating from local minima in the folded state. For α-synuclein, however, no experimental chemical shift data are currently available at multiple temperatures. Furthermore, this protein only exhibits transient secondary structures,⁷⁹ making the interpretation of ¹³C^α chemical shift variations along the sequence in terms of local order/disorder more challenging.

In the absence of experimental measurements of the temperature-dependent chemical shift variation Δδ(T) for α-synuclein—which would provide direct evidence for a link between Δδ and S in IDPs—we instead compare variations in S to two residue-level disorder descriptors based on chemical shifts at a single temperature and compared them to the function 1 − S/S_saw. This function is designed to reflect the relative degree of local order, with a maximum value of 1 corresponding to S = 0 (i.e., a single stable micro-environment), and values approaching zero when S = S_saw, which corresponds to maximal steric disorder as represented by self-avoiding walks.

Notably, values of S exceeding S_saw may occur when multiple minima in the interaction potential generate a greater diversity of sPGs. In such cases, the probability of the contact-free sPG—typically dominant in SAWs—drops significantly, resulting in negative values of the function 1 − S/S_saw.

The first experimental descriptor used for comparison is the ¹³C^α secondary chemical shift,^80,81 which reflects local backbone conformational preferences. The second is the Chemical Shift Z-score for assessing Order/Disorder (CheZOD score), which integrates the secondary chemical shifts of all backbone atoms into a quantitative measure of local order.⁸²

It is important to note that the chemical shifts of α-synuclein are sensitive to solvent conditions and pH.⁸¹ For consistency with the simulation conditions, we used NMR data collected under near-physiological conditions, corresponding to the α-synuclein monomer entry in the Biological Magnetic Resonance Bank (bmrb ID: 6968).^80,81

We first compare the ¹³C^α secondary chemical shifts,^80,81 δC^α, to the function 1 − S/S_saw in Fig. 4. As discussed above, MD simulations indicate that the NAC region is the most disordered, while the C-terminal is the most ordered. This is reflected in the averaged values of the entropy-based order parameter: 〈1−S/S_saw〉_N-term/〈1−S/S_saw〉_NAC = 1.19, and 〈1−S/S_saw〉_C-term/〈1−S/S_saw〉_NAC = 2.63. These estimates can be compared to the experimental secondary chemical shifts: 〈|δC^α|〉_N-term/〈|δC^α|〉_NAC = 1.75, and 〈|δC^α|〉_C-term/〈|δC^α|〉_NAC = 2.13, supporting the conclusion that the NAC region is the most flexible and the C-terminal the most structured—consistent with MD results.

Fig. 4 Representation of 1/(S − S_saw) of α-synuclein at a graph distance D = 1 and R = 8 Å as a function of the amino acid sequence, computed from coarse-grained MD simulations (solid line, open symbols) at physiological temperature, and of the absolute values of C^α secondary chemical shifts δC^α extracted from Fig. 1 of ref. 81 (dashed line, solid symbols). The dot-dashed lines correspond to the condition S = S_saw (right Y axis) and to random coils values of the chemical shifts (left Y axis). All lines are provided as guide for the eye. Light gray shading indicates the P1 (residues 36–42) and P2 (residues 45–57) segments, while dark gray shading indicates the NAC region (residues 61–95).

A similar conclusion arises from the CheZOD descriptor⁸² (see SI, Fig. S15), which also shows increased order in the N-terminal and C-terminal regions. When averaged (after shifting to positive values), the CheZOD values yield: 〈CheZOD〉_N-term/〈CheZOD〉_NAC = 1.19, and 〈CheZOD〉_C-term/〈CheZOD〉_NAC = 2.63. This is also in agreement with NMR measurements of the ¹⁵N transverse relaxation rate R₂, which indicate enhanced backbone flexibility in the NAC region under physiological pH and temperature conditions.^94,95

Fig. 4 and S14 highlight noticeable differences between the two NMR-derived disorder descriptors and the entropy-based data at the residue level. A quantitative residue-by-residue comparison is thus difficult, given the inherent uncertainties in both NMR chemical shift measurements and MD simulations, but shared patterns do emerge. Along the N-terminal region, peaks indicative of increased local order appear at residues K6, V16–A29, K34, K45, V52, and T59 in |δC^α|, and at comparable positions in 1 − S/S_saw (notably K6, E13, K21–E35, K45, K60). The CheZOD score also shows elevated values at K6, V15–T33, and A53, but differs by presenting a distinct peak at V40 and lower order at K60.

In the NAC region, |δC^α| shows peaks at V70, T75, A85, and I88. The entropy-based descriptor 1 − S/S_saw displays corresponding peaks at G67, G73, K80, and G84. The CheZOD score shows similar variations with peaks at V66, K80, and A85.

The C-terminal region displays significant variability in all three descriptors. In |δC^α|, prominent peaks are observed at A124, E126, and E137. The CheZOD score presents additional maxima at K96, A107, M116, G132, E126, and E137. The entropy-derived profile also reveals numerous peaks within residues K96–E139, including E110, D119, M127, G132, and P138.

While a perfect residue-by-residue correspondence is not observed, even between the two experimental descriptors based on the same δ data, overall trends and relative variations in local order along the α-synuclein sequence are consistent across all three descriptors, albeit with some positional shifts. Interestingly, the similarity between |δC^α| and the entropy-based descriptor is stronger than with the CheZOD score. This is expected, as both |δC^α| and S are sensitive to the local environment of C^α atoms, whereas CheZOD is derived from chemical shifts of all backbone atoms and therefore captures a broader range of structural features. The present discussion highlights the need for further experimental studies on IDPs across different temperatures to clarify the role of local entropy in protein dynamics and aggregation.

Effects induced by single amino-acid subsitutions in disordered protein ensembles as measured by the local entropy

The conformational ensemble of an IDP is vast, characterized by a rugged free-energy landscape with numerous minima of comparable energy. As a result, deciphering the impact of a single amino acid substitution on its structural diversity remains a significant challenge. This issue is particularly relevant for studying missense mutations in α-synuclein. The familial Parkinson's disease-associated variants A30P, E46K, and A53T exhibit distinct amyloid aggregation kinetics, leading to different pathological outcomes. Notably, the E46K mutation is associated with more severe clinical symptoms.

In this context, we propose using local entropy as a quantitative descriptor to assess the impact of single-point mutations on the structural ensemble of α-synuclein. This analysis is based on coarse-grained MD simulations reported in a previous study.⁷⁹

The variations of the local entropy S at D = 1 and D = 2 for the mutants A30P, E46K, and A53T are presented in the SI (Fig. S1 panels c to h). The average values of S across the N-terminal, NAC, and C-terminal regions follow the same trend observed for the wild-type protein, as discussed in the previous section, namely: 〈S〉 _C-term < 〈S〉_N-term < 〈S〉_NAC. As in the wild-type, local inhomogeneities of S are observed along the sequence, with values tending to converge toward those of the SAW ensemble at D = 2. In general, residues near the mutation sites exhibit a decrease in local entropy, while distant residues can experience either an increase or a decrease. These effects are examined in more detail at D = 1 in Fig. 5, and are discussed below for each mutant.

Fig. 5 Local entropy S at graph distance D = 1 as a function of the amino acid sequence of α-synuclein mutants at physiological temperature, calculated from a coarse-grained MD trajectory with R = 8 Å. Normalized values of the local entropy, S/S_wt, are shown, where S_wt corresponds to the local entropy of the wild-type protein. Lines are provided as guides for the eye. Full red symbols indicate positively charged amino acids, and blue symbols indicate negatively charged amino acids. Diamond symbols mark the positions of mutated residues: P30, K46, and T53. Light gray shading indicates the P1 (residues 36–42) and P2 (residues 45–57) segments, while dark gray shading indicates the NAC region (residues 61–95).

In the A30P mutant, the substitution of alanine by proline induces a marked local effect, with a sharp reduction of S in the A27–K34 segment. The lowest entropy values are found at P30 and G31. Notably, P30 explores only 2521 microstates (sPGs), compared to 23 736 for A30 in the wild-type. Additional significant changes in S are observed at or near K21, as well as in key regions associated with aggregation: at K43, between the P1 and P2 regions; at E57, between the P2 and NAC regions; and at G73 within the NAC region. In contrast, the highly negatively charged C-terminus remains largely unaffected.

For the E46K mutant, the replacement of glutamate by lysine leads to substantial changes in local entropy across the sequence, including long-range effects in the C-terminal region far from the mutation site. The most prominent variations are observed at K46 and E110: the number of explored sPGs decreases from 9482 for E46 in wild-type to 6527 for K46 in mutant and increases from 3282 in wild-type to 4803 for E110 in mutant. Additional fluctuations are noted at S9, K32, and K60 in the N-terminal, and at E110 and E119 in the C-terminal. The key-related regions for aggregation are significantly affected by the mutation: the entire region P2 and the residues between P1 and P2 and P2 and the NAC regions. In the NAC region, aside from G73, S decreases significantly at T81 and increases at G86 and G93.

The A53T mutation also causes significant changes in local entropy, particularly in the N-terminal region. The largest reduction is observed at E57, where the number of substates decreases from 16 050 in the wild-type to 8343 in the mutant. For comparison, the number of sPGs varies from 36 556 in the wild-type to 28 276 in the mutant for residue 53. Substantial entropy variations are also seen for G25, G31, K43, and T53. In the C-terminal region, S generally decreases, except at P120 and D121. In the NAC region, N65 shows a notable reduction in entropy.

Interestingly, the residues that form native contacts in α-synuclein fibril-like dimers with a probability greater than 0.9 in our previous millisecond-timescale simulations (nucleation phase) are located in regions spanning both the P1 and P2 segments (L38–V55 in E46K and L38–E57 in A53T). These regions display substantial alterations in local entropy compared with the wild-type protein, for which residues with native-contact probabilities above 0.9 lie in the NAC region (G86–F94).⁸⁵

The localization of these mutation-induced changes in local order/disorder correlates with the physicochemical properties of the substituted amino acids. Alanine is small and flexible, whereas proline introduces a rigid constraint due to its side chain being covalently linked to the backbone, explaining the strong local reduction in S for A30P. The E46K mutation replaces a negatively charged glutamate with a positively charged lysine, which significantly alters the network of long-range electrostatic interactions. Similarly, the A53T mutation introduces a polar side chain (threonine), which explain the extended perturbation along the sequence.

Although a detailed analysis of the impact of a single mutation on the full network of interactions is complex, the local entropy can quantify these effects by comparing the values of S for the wild-type and mutant proteins, as shown in Fig. 5. These variations can be further interpreted by examining the individual sPGs.

As an example, we describe how the A30P mutation induces long-range effects on residues K21, K43, E57, and G73. Since describing each individual sPG would be overly detailed and cumbersome, we summarize the mechanisms underlying these distant mutational effects in Tables S1 and S2.

Table S1 lists the nodes of the most probable sPGs (i.e., with p_i > 0.01) for residues A30, E43, V52, A53, T54, and V55 in the wild-type protein. Table S2 contains the corresponding nodes for residues P30 and E43 in the A30P mutant.

In the wild-type protein, three regions—namely A19–K23, E28–E35, and V52–V55—are involved in the sPGs of A30, showing high diversity with 15 graphs having p_i > 0.01 (Table S1). In the mutant, two of these regions, A19–K21 and E28–K32, are still present in the sPGs of residue 30 (Table S2). The first has a slightly lower probability, explaining the increase of S around K21 in the mutant. The second exhibits much greater stability, with a probability an order of magnitude higher, accounting for the substantial decrease of S around P30.

Additionally, two new regions, M1–V3 and T64–V66, interact with residue 30 in the mutant, while one region, V52–V55, is no longer part of its micro-environment (Table S2). This loss explains the long-range effects on residues E57 and G73, since in the wild-type, residues A53–V55 interact with E57 and G73 (Table S1). Moreover, A30 was indirectly connected to region T64–V66, which is involved in the sPGs of the now-missing residues V52–V55 in the mutant. The substitution of A30 with P30 shifts the segment V62–V66 from being connected to residue 30 at a graph distance D = 2 in the wild-type protein to a distance D = 1 in the mutant. This reorganization impacts the local entropy.

The effect of the mutation on the entropy of E43 can be understood by comparing the node ensembles in Tables S1 and S2. In the A30P mutant, the absence of the region A53–A56 and the reduced probability of the A19–T22 segment compared to the wild-type result in a redistribution of the sPG probabilities for E43. Specifically, the probability associated with the Y39–K45 segment is significantly reduced in the mutant.

In conclusion, the substitution of a single amino acid in the N-terminal region of α-synuclein alters the local order/disorder not only near the mutation site but also at distant positions in key regions associated with aggregation, i.e., the P1, P2, and NAC segments, and, in the case of E46K, even in the C-terminal region. These modifications are expected to influence the dimerization behavior of α-synuclein. Indeed, we previously found that the nucleation centers for the formation of amyloid precursors in dimers are located in the NAC region for the wild-type and A30P proteins, whereas they shift predominantly to the N-terminal region (V40–K60 segment) for the A53T and E46K mutants.⁸⁵

Conclusions

The present results demonstrate that local entropy is a valuable theoretical order parameter for characterizing residue-level protein disorder, and it can be directly compared with NMR observables. It complements established descriptors such as the NMR S² order parameter—which quantifies bond-vector orientational fluctuations—X-ray crystallographic B-factors—which measure atomic positional variability— and the packing entropy, which quantifies residue packing fractions.⁶⁵ Unlike packing entropy⁶⁵—which is tightly correlated with B-factors and strongly influenced by the hydrophobic effect—local entropy does not probe the accessible volume around a residue but instead captures the diversity of its interactions with its microenvironment. By quantifying the variability of the structural pattern groups (sPGs) in the neighborhood of each amino acid, local entropy provides residue-specific insight into local conformational heterogeneity.

In structured proteins, local entropy varies significantly along the sequence, as the B factors and packing entropy, including within secondary structure elements. This makes it a powerful tool for identifying inhomogeneities in unfolding transitions at the residue level, in good agreement with experimental observations, as illustrated here for the gpW protein.

In intrinsically disordered proteins such as α-synuclein, local entropy shows substantial sequence dependence and is, on average, lower than that of a self-avoiding walk (SAW) ensemble of the same chain length or the unfolded state modeled for gpW. The descriptor S is particularly sensitive to amino-acid substitutions and can capture their effects through a single quantitative metric. Significant differences in local entropy are observed between mutants and the wild-type protein, particularly in regions implicated in aggregation such as P1, P2, and the NAC segment. Further work will be required to determine whether the local entropy of the monomeric state is predictive of fibril formation.

Beyond quantifying disorder, the concept of local entropy has broad potential applications. For instance, it could be employed to study protein–protein interactions by characterizing the sPGs stabilized at binding interfaces, or to investigate allosteric mechanisms by quantifying entropy changes upon ligand binding or post-translational modifications. More generally, local entropy could be used outside protein science—for example, to characterize heterogeneity and temperature dependence in polymer hydration, or to quantify molecular-level or atom-level entropies at liquid–solid or disordered solid–solid interfaces.

Author contributions

Visualization, validation, investigation, programing, software development, figures, writing – original draft. P. S.; writing – review and editing. All authors; project administration, funding acquisition, conceptualization. P. S.

Conflicts of interest

The authors declare no conflict of interest.

Data availability

The codes for the calculation of local entropy⁹⁶ and for the simulations of SAW ensembles⁹⁷ used in this study are licensed and can be accessed in the Zenodo repository at https://doi.org/10.5281/zenodo.16911661 and https://doi.org/10.5281/zenodo.16914457, respectively. The input data required to reproduce the results of this article with these codes are available in Zenodo repository at https://doi.org/10.5281/zenodo.16912838.

Additional data supporting the findings of this work are included in the supporting information (SI). Supplementary information: details of the methods, supporting figures and tables . See DOI: https://doi.org/10.1039/d5sc06411b.

Acknowledgements

The simulations were performed using HPC resources from DSI-CCuB (Université Bourgogne Europe). The work is part of the project SEPIA supported by the EIPHI Graduate School (contract ANR-17-EURE-0002), the Conseil Régional de Bourgogne-Franche-Comté, and the European Union through the PO FEDER-FSE Bourgogne 2021/2027 program. The authors gratefully acknowledge the reviewers for their constructive and careful review of the original manuscript.

References

1. C. B. Anfinsen, Principles that Govern the Folding of Protein Chains, Science, 1973, 181, 223–230,  DOI:10.1126/science.181.4096.223.
2. C. B. Anfinsen and H. A. Scheraga, in Advances in Protein Chemistry, Anfinsen, C. B., Edsall, J. T. and Richards, F. M., Academic Press, 1975; vol. 29, pp. 205–300,  DOI:10.1016/S0065-3233(08)60413-1.
3. K. A. Dill, S. B. Ozkan, M. S. Shell and T. R. Weikl, The Protein Folding Problem, Annu. Rev. Biophys., 2008, 37, 289–316,  DOI:10.1146/annurev.biophys.37.092707.153558.
4. J. Jumper, et al., Highly accurate protein structure prediction with AlphaFold, Nature, 2021, 596, 583–589,  DOI:10.1038/s41586-021-03819-2.
5. M. Baek, et al., Accurate prediction of protein structures and interactions using a three-track neural network, Science, 2021, 373, 871–876,  DOI:10.1126/science.abj8754.
6. G. N. Ramachandran, C. Ramakrishnan and V. Sasisekharan, Stereochemistry of polypeptide chain configurations, J. Mol. Biol., 1963, 7, 95–99,  DOI:10.1016/S0022-2836(63)80023-6.
7. C. Ramakrishnan and G. N. Ramachandran, Stereochemical Criteria for Polypeptide and Protein Chain Conformations: II. Allowed Conformations for a Pair of Peptide Units, Biophys. J., 1965, 5, 909–933,  DOI:10.1016/S0006-3495(65)86759-5.
8. P. Y. Chou and G. D. Fasman, Conformational parameters for amino acids in helical, beta-sheet, and random coil regions calculated from proteins, Biochemistry, 1974, 13, 211–222,  DOI:10.1021/bi00699a001.
9. C. K. Smith, J. M. Withka and L. Regan, A Thermodynamic Scale for the .beta.-Sheet Forming Tendencies of the Amino Acids, Biochemistry, 1994, 33, 5510–5517,  DOI:10.1021/bi00184a020.
10. C. N. Pace and J. M. Scholtz, A helix propensity scale based on experimental studies of peptides and proteins, Biophys. J., 1998, 75, 422–427.
11. N. Bhattacharjee and P. Biswas, Position-specific propensities of amino acids in the beta-strand, BMC Struct. Biol., 2010, 10, 29,  DOI:10.1186/1472-6807-10-29.
12. A. G. Murzin, S. E. Brenner, T. Hubbard and C. Chothia, SCOP: a structural classification of proteins database for the investigation of sequences and structures, J. Mol. Biol., 1995, 247, 536–540,  DOI:10.1006/jmbi.1995.0159.
13. K. Karplus, R. Karchin, J. Draper, J. Casper, Y. Mandel-Gutfreund, M. Diekhans and R. Hughey, Combining local-structure, fold-recognition, and new fold methods for protein structure prediction, Proteins: Struct., Funct., Bioinf., 2003, 53, 491–496,  DOI:10.1002/prot.10540.
14. C. Etchebest, C. Benros, S. Hazout and A. G. de Brevern, A structural alphabet for local protein structures: Improved prediction methods, Proteins: Struct., Funct., Bioinf., 2005, 59, 810–827,  DOI:10.1002/prot.20458.
15. B. Offmann, M. Tyagi and A. G. de Brevern, Local Protein Structures, Curr. Bioinf., 2007, 2, 165–202,  DOI:10.2174/157489307781662105.
16. C. J. A. Sigrist, L. Cerutti, N. Hulo, A. Gattiker, L. Falquet, M. Pagni, A. Bairoch and P. Bucher, PROSITE: A documented database using patterns and profiles as motif descriptors, Briefings Bioinf., 2002, 3, 265–274,  DOI:10.1093/bib/3.3.265.
17. C. J. A. Sigrist, E. de Castro, L. Cerutti, B. A. Cuche, N. Hulo, A. Bridge, L. Bougueleret and I. Xenarios, New and continuing developments at PROSITE, Nucleic Acids Res., 2013, 41, D344–D347,  DOI:10.1093/nar/gks1067.
18. P. E. Wright and H. J. Dyson, Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm, J. Mol. Biol., 1999, 293, 321–331,  DOI:10.1006/jmbi.1999.3110.
19. V. N. Uversky, J. R. Gillespie and A. L. Fink, Why are “natively unfolded” proteins unstructured under physiologic conditions?, Proteins: Struct., Funct., Bioinf., 2000, 41, 415–427,  DOI:10.1002/1097-0134(20001115)41:3¡415::AID-PROT130¿3.0.CO;2-7.
20. V. N. Uversky, Intrinsically Disordered Proteins and Their “Mysterious” (Meta)Physics, Front. Phys., 2019, 7(10), 1–18,  DOI:10.3389/fphy.2019.00010.
21. A. Deiana, S. Forcelloni, A. Porrello and A. Giansanti, Intrinsically disordered proteins and structured proteins with intrinsically disordered regions have different functional roles in the cell, PLoS One, 2019, 14, e0217889,  DOI:10.1371/journal.pone.0217889.
22. R. van der Lee, et al., Classification of Intrinsically Disordered Regions and Proteins, Chem. Rev., 2014, 114, 6589–6631,  DOI:10.1021/cr400525m.
23. C. K. Fisher and C. M. Stultz, Protein Structure along the Order–Disorder Continuum, J. Am. Chem. Soc., 2011, 133, 10022–10025,  DOI:10.1021/ja203075p.
24. H. Ali, S. Urolagin, O. Gurarslan and M. Vihinen, Performance of Protein Disorder Prediction Programs on Amino Acid Substitutions, Hum. Mutat., 2014, 35, 794–804,  DOI:10.1002/humu.22564.
25. A. H. Mao, S. L. Crick, A. Vitalis, C. L. Chicoine and R. V. Pappu, Net charge per residue modulates conformational ensembles of intrinsically disordered proteins, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 8183–8188,  DOI:10.1073/pnas.0911107107.
26. R. K. Das and R. V. Pappu, Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13392–13397,  DOI:10.1073/pnas.1304749110.
27. H. Hofmann, A. Soranno, A. Borgia, K. Gast, D. Nettels and B. Schuler, Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16155–16160,  DOI:10.1073/pnas.1207719109.
28. A. Holla, E. W. Martin, T. Dannenhoffer-Lafage, K. M. Ruff, S. L. B. König, M. F. Nüesch, A. Chowdhury, J. M. Louis, A. Soranno, D. Nettels, R. V. Pappu, R. B. Best, T. Mittag and B. Schuler, Identifying Sequence Effects on Chain Dimensions of Disordered Proteins by Integrating Experiments and Simulations, JACS Au, 2024, 4(12), 4729–4743,  DOI:10.1021/jacsau.4c00673.
29. H. J. Dyson and P. E. Wright, Unfolded Proteins and Protein Folding Studied by NMR, Chem. Rev., 2004, 104, 3607–3622,  DOI:10.1021/cr030403s.
30. T. A. Ramelot, R. Tejero and G. T. Montelione, Representing structures of the multiple conformational states of proteins, Curr. Opin. Struct. Biol., 2023, 83, 102703,  DOI:10.1016/j.sbi.2023.102703.
31. W. Doster, The dynamical transition of proteins, concepts and misconceptions, Eur. Biophys. J., 2008, 37, 591–602,  DOI:10.1007/s00249-008-0274-3.
32. Y. Zhou, D. Vitkup and M. Karplus, Native proteins are surface-molten solids: application of the lindemann criterion for the solid versus liquid state1, J. Mol. Biol., 1999, 285, 1371–1375,  DOI:10.1006/jmbi.1998.2374.
33. E. M. Mitchell, P. J. Artymiuk, D. W. Rice and P. Willett, Use of techniques derived from graph theory to compare secondary structure motifs in proteins, J. Mol. Biol., 1990, 212, 151–166,  DOI:10.1016/0022-2836(90)90312-A.
34. H. M. Grindley, P. J. Artymiuk, D. W. Rice and P. Willett, Identification of Tertiary Structure Resemblance in Proteins Using a Maximal Common Subgraph Isomorphism Algorithm, J. Mol. Biol., 1993, 229, 707–721,  DOI:10.1006/jmbi.1993.1074.
35. P. J. Artymiuk, A. R. Poirrette, H. M. Grindley, D. W. Rice and P. Willett, A Graph-theoretic Approach to the Identification of Three-dimensional Patterns of Amino Acid Side-chains in Protein Structures, J. Mol. Biol., 1994, 243, 327–344,  DOI:10.1006/jmbi.1994.1657.
36. D. J. Jacobs, A. Rader, L. A. Kuhn and M. Thorpe, Protein flexibility predictions using graph theory, Proteins: Struct., Funct., Bioinf., 2001, 44, 150–165,  DOI:10.1002/prot.1081.
37. A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin and I. Bahar, Anisotropy of Fluctuation Dynamics of Proteins with an Elastic Network Model, Biophys. J., 2001, 80, 505–515,  DOI:10.1016/S0006-3495(01)76033-X.
38. A. Scala, L. A. N. Amaral and M. Barthélémy, Small-world networks and the conformation space of a short lattice polymer chain, Europhys. Lett., 2001, 55, 594–600,  DOI:10.1209/epl/i2001-00457-7.
39. M. Vendruscolo, N. V. Dokholyan, E. Paci and M. Karplus, Small-world view of the amino acids that play a key role in protein folding, Phys. Rev. E, 2002, 65, 061910,  DOI:10.1103/PhysRevE.65.061910.
40. A. J. Rader, B. M. Hespenheide, L. A. Kuhn and M. F. Thorpe, Protein unfolding: Rigidity lost, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 3540–3545,  DOI:10.1073/pnas.062492699.
41. S. Vishveshwara, K. V. Brinda and N. Kannan, Protein structure: insights from graph theory, J. Theor. Comput. Chem., 2002, 01, 187–211,  DOI:10.1142/S0219633602000117.
42. A. R. Atilgan, P. Akan and C. Baysal, Small-World Communication of Residues and Significance for Protein Dynamics, Biophys. J., 2004, 86, 85–91,  DOI:10.1016/S0006-3495(04)74086-2.
43. F. Rao and A. Caflisch, The Protein Folding Network, J. Mol. Biol., 2004, 342, 299–306,  DOI:10.1016/j.jmb.2004.06.063.
44. G. Bagler and S. Sinha, Network properties of protein structures, Phys. A, 2005, 346, 27–33,  DOI:10.1016/j.physa.2004.08.046.
45. V. A. Higman and L. H. Greene, Elucidation of conserved long-range interaction networks in proteins and their significance in determining protein topology, Phys. A, 2006, 368, 595–606,  DOI:10.1016/j.physa.2006.01.062.
46. A. Giuliani, A. Krishnan, J. P. Zbilut and M. Tomita, Proteins As Networks: Usefulness of Graph Theory in Protein Science, Curr. Protein Pept. Sci., 2008, 9, 28–38,  DOI:10.2174/138920308783565705.
47. C. Atilgan, O. B. Okan and A. R. Atilgan, Network-Based Models as Tools Hinting at Nonevident Protein Functionality, Annu. Rev. Biophys., 2012, 41, 205–225,  DOI:10.1146/annurev-biophys-050511-102305.
48. Y. Yin, G. G. Maisuradze, A. Liwo and H. A. Scheraga, Hidden Protein Folding Pathways in Free-Energy Landscapes Uncovered by Network Analysis, J. Chem. Theory Comput., 2012, 8, 1176–1189,  DOI:10.1021/ct200806n.
49. K. F. Kantelis, V. Asteriou, A. Papadimitriou-Tsantarliotou, A. Petrou, L. Angelis, P. Nicopolitidis, G. Papadimitriou and I. S. Vizirianakis, Graph theory-based simulation tools for protein structure networks, Simulat. Model. Pract. Theor., 2022, 121, 102640,  DOI:10.1016/j.simpat.2022.102640.
50. D. Srivastava, G. Bagler and V. Kumar, Graph Signal Processing on protein residue networks helps in studying its biophysical properties, Phys. A, 2023, 615, 128603,  DOI:10.1016/j.physa.2023.128603.
51. S. Tyler, C. Laforge, A. Guzzo, A. Nicolaï, G. G. Maisuradze and P. Senet, Einstein Model of a Graph to Characterize Protein Folded/Unfolded States, Molecules, 2023, 28, 6659,  DOI:10.3390/molecules28186659.
52. L. K. Madan, C. L. Welsh, A. P. Kornev and S. S. Taylor, The “violin model”: Looking at community networks for dynamic allostery, J. Chem. Phys., 2023, 158, 081001,  DOI:10.1063/5.0138175.
53. N. Go and H. A. Scheraga, Analysis of the Contribution of Internal Vibrations to the Statistical Weights of Equilibrium Conformations of Macromolecules, J. Chem. Phys., 1969, 51, 4751–4767,  DOI:10.1063/1.1671863.
54. R. M. Levy, M. Karplus, J. Kushick and D. Perahia, Evaluation of the configurational entropy for proteins: application to molecular dynamics simulations of an alpha-helix, Macromolecules, 1984, 17, 1370–1374,  DOI:10.1021/ma00137a013.
55. M. Karplus, T. Ichiye and B. M. Pettitt, Configurational entropy of native proteins, Biophys. J., 1987, 52, 1083–1085,  DOI:10.1016/S0006-3495(87)83303-9.
56. J. Schlitter, Estimation of absolute and relative entropies of macromolecules using the covariance matrix, Chem. Phys. Lett., 1993, 215, 617–621,  DOI:10.1016/0009-2614(93)89366-P.
57. G. P. Brady and K. A. Sharp, Entropy in protein folding and in protein—protein interactions, Curr. Opin. Struct. Biol., 1997, 7, 215–221,  DOI:10.1016/S0959-440X(97)80028-0.
58. I. Andricioaei and M. Karplus, On the calculation of entropy from covariance matrices of the atomic fluctuations, J. Chem. Phys., 2001, 115, 6289–6292,  DOI:10.1063/1.1401821.
59. K. K. Frederick, M. S. Marlow, K. G. Valentine and A. J. Wand, Conformational entropy in molecular recognition by proteins, Nature, 2007, 448, 325–329,  DOI:10.1038/nature05959.
60. H. Meirovitch, Recent developments in methodologies for calculating the entropy and free energy of biological systems by computer simulation, Curr. Opin. Struct. Biol., 2007, 17, 181–186,  DOI:10.1016/j.sbi.2007.03.016.
61. A. J. Wand, The dark energy of proteins comes to light: conformational entropy and its role in protein function revealed by NMR relaxation, Curr. Opin. Struct. Biol., 2013, 23, 75–81,  DOI:10.1016/j.sbi.2012.11.005.
62. M. C. Baxa, E. J. Haddadian, J. M. Jumper, K. F. Freed and T. R. Sosnick, Loss of conformational entropy in protein folding calculated using realistic ensembles and its implications for NMR-based calculations, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15396–15401,  DOI:10.1073/pnas.1407768111.
63. T. Flock, R. J. Weatheritt, N. S. Latysheva and M. M. Babu, Controlling entropy to tune the functions of intrinsically disordered regions, Curr. Opin. Struct. Biol., 2014, 26, 62–72,  DOI:10.1016/j.sbi.2014.05.007.
64. K. Sankar, K. Jia and R. L. Jernigan, Knowledge-based entropies improve the identification of native protein structures, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2928–2933,  DOI:10.1073/pnas.1613331114.
65. P. M. Khade and R. L. Jernigan, Entropies Derived from the Packing Geometries within a Single Protein Structure, ACS Omega, 2022, 7, 20719–20730,  DOI:10.1021/acsomega.2c00999.
66. K. Skriver, F. F. Theisen and B. B. Kragelund, Conformational entropy in molecular recognition of intrinsically disordered proteins, Curr. Opin. Struct. Biol., 2023, 83, 102697,  DOI:10.1016/j.sbi.2023.102697.
67. R. Georgelin and C. J. Jackson, Entropy, enthalpy, and evolution: Adaptive trade-offs in protein binding thermodynamics, Curr. Opin. Struct. Biol., 2025, 94, 103080,  DOI:10.1016/j.sbi.2025.103080.
68. D. Yang and L. E. Kay, Contributions to Conformational Entropy Arising from Bond Vector Fluctuations Measured from NMR-Derived Order Parameters: Application to Protein Folding, J. Mol. Biol., 1996, 263, 369–382,  DOI:10.1006/jmbi.1996.0581.
69. Z. Li, S. Raychaudhuri and A. J. Wand, Insights into the local residual entropy of proteins provided by NMR relaxation, Protein Sci., 1996, 5, 2647–2650,  DOI:10.1002/pro.5560051228.
70. C.-L. Towse, M. Akke and V. Daggett, The Dynameomics Entropy Dictionary: A Large-Scale Assessment of Conformational Entropy across Protein Fold Space, J. Phys. Chem. B, 2017, 121, 3933–3945,  DOI:10.1021/acs.jpcb.7b00577.
71. G. Lipari and A. Szabo, Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity, J. Am. Chem. Soc., 1982, 104, 4546–4559,  DOI:10.1021/ja00381a009.
72. G. Lipari and A. Szabo, Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 2. Analysis of experimental results, J. Am. Chem. Soc., 1982, 104, 4559–4570,  DOI:10.1021/ja00381a010.
73. Y. Cote, P. Senet, P. Delarue, G. G. Maisuradze and H. A. Scheraga, Nonexponential decay of internal rotational correlation functions of native proteins and self-similar structural fluctuations, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19844–19849,  DOI:10.1073/pnas.1013674107.
74. L. Sborgi, A. Verma, V. Muñoz and E. d. Alba, Revisiting the NMR Structure of the Ultrafast Downhill Folding Protein gpW from Bacteriophage lambda, PLoS One, 2011, 6, e26409,  DOI:10.1371/journal.pone.0026409.
75. A. Fung, P. Li, R. Godoy-Ruiz, J. M. Sanchez-Ruiz and V. Muñoz, Expanding the Realm of Ultrafast Protein Folding: gpW, a Midsize Natural Single-Domain with alpha+beta Topology that Folds Downhill, J. Am. Chem. Soc., 2008, 130, 7489–7495,  DOI:10.1021/ja801401a.
76. L. Sborgi, A. Verma, S. Piana, K. Lindorff-Larsen, M. Cerminara, C. M. Santiveri, D. E. Shaw, E. de Alba and V. Muñoz, Interaction Networks in Protein Folding via Atomic-Resolution Experiments and Long-Time-Scale Molecular Dynamics Simulations, J. Am. Chem. Soc., 2015, 137, 6506–6516,  DOI:10.1021/jacs.5b02324.
77. P. Grassein, P. Delarue, H. A. Scheraga, G. G. Maisuradze and P. Senet, Statistical Model To Decipher Protein Folding/Unfolding at a Local Scale, J. Phys. Chem. B, 2018, 122, 3540–3549,  DOI:10.1021/acs.jpcb.7b10733.
78. P. Grassein, P. Delarue, A. Nicolaï, F. Neiers, H. A. Scheraga, G. G. Maisuradze and P. Senet, Curvature and Torsion of Protein Main Chain as Local Order Parameters of Protein Unfolding, J. Phys. Chem. B, 2020, 124, 4391–4398,  DOI:10.1021/acs.jpcb.0c01230.
79. A. Guzzo, P. Delarue, A. Rojas, A. Nicolaï, G. G. Maisuradze and P. Senet, Missense Mutations Modify the Conformational Ensemble of the alpha-Synuclein Monomer Which Exhibits a Two-Phase Characteristic, Front. Mol. Biosci., 2021, 8, 1104,  DOI:10.3389/fmolb.2021.786123.
80. W. Bermel, I. Bertini, I. C. Felli, Y.-M. Lee, C. Luchinat and R. Pierattelli, Protonless NMR Experiments for Sequence-Specific Assignment of Backbone Nuclei in Unfolded Proteins, J. Am. Chem. Soc., 2006, 128, 3918–3919,  DOI:10.1021/ja0582206.
81. D.-H. Kim, J. Lee, K. H. Mok, J. H. Lee and K.-H. Han, Salient Features of Monomeric Alpha-Synuclein Revealed by NMR Spectroscopy, Biomolecules, 2020, 10, 428,  DOI:10.3390/biom10030428.
82. J. Nielsen and F. Mulder, There is Diversity in Disorder—“In all Chaos there is a Cosmos, in all Disorder a Secret Order”, Front. Mol. Biosci., 2016, 3(4), 1–12,  DOI:10.3389/fmolb.2016.00004.
83. C. P. A. Doherty, S. M. Ulamec, R. Maya-Martinez, S. C. Good, J. Makepeace, G. N. Khan, P. van Oosten-Hawle, S. E. Radford and D. J. Brockwell, A short motif in the N-terminal region of alpha-synuclein is critical for both aggregation and function, Nat. Struct. Mol. Biol., 2020, 27, 249–259,  DOI:10.1038/s41594-020-0384-x.
84. T. A. Tripathi, Master Regulator of alpha-Synuclein Aggregation, ACS Chem. Neurosci., 2020, 11, 1376–1378,  DOI:10.1021/acschemneuro.0c00216.
85. A. Guzzo, P. Delarue, A. Rojas, A. Nicolaï, G. G. Maisuradze and P. Senet, Wild-Type alpha-Synuclein and Variants Occur in Different Disordered Dimers and Pre-Fibrillar Conformations in Early Stage of Aggregation, Front. Mol. Biosci., 2022, 9, 9101104,  DOI:10.3389/fmolb.2022.910104.
86. A. A. Hagberg, D. A. Schult and P. J. Swart, Exploring Network Structure, Dynamics, and Function using NetworkX, Proceedings of the 7th Python in Science Conference, Pasadena, CA USA, 2008, pp 11–15.
87. M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, Oxford, 1986.
88. P. Virtanen, et al., SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261–272,  DOI:10.1038/s41592-019-0686-2.
89. S. Spera and A. Bax, Empirical correlation between protein backbone conformation and C.alpha. and C.beta. 13C nuclear magnetic resonance chemical shifts, J. Am. Chem. Soc., 1991, 113, 5490–5492,  DOI:10.1021/ja00014a071.
90. Y. Shen, et al., Consistent blind protein structure generation from NMR chemical shift data, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 4685–4690,  DOI:10.1073/pnas.0800256105.
91. S. Sukenik, T. V. Pogorelov and M. Gruebele, Can Local Probes Go Global? A Joint Experiment–Simulation Analysis of lambda6–85 Folding, J. Phys. Chem. Lett., 2016, 7, 1960–1965,  DOI:10.1021/acs.jpclett.6b00582.
92. E. Gasteiger, C. Hoogland, A. Gattiker, S. Duvaud, M. R. Wilkins, R. D. Appel and A. Bairoch, in The Proteomics Protocols Handbook, Walker, J. M., Humana Press, Totowa, NJ, 2005, pp 571–607.
93. J. Janin, Surface and inside volumes in globular proteins, Nature, 1979, 277, 491–492,  DOI:10.1038/277491a0.
94. P. Rotkiewicz and J. Skolnick, Fast procedure for reconstruction of full-atom protein models from reduced representations, J. Comput. Chem., 2008, 29, 1460–1465,  DOI:10.1002/jcc.20906 , preprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/jcc.20906.
95. N. Rezaei-Ghaleh, G. Parigi, A. Soranno, A. Holla, S. Becker, B. Schuler, C. Luchinat and M. Zweckstetter, Local and Global Dynamics in Intrinsically Disordered Synuclein, Angew. Chem., Int. Ed., 2018, 57, 15262–15266,  DOI:10.1002/anie.201808172.
96. P. Senet, Zenodo repository: patricksenet/Local-entropy-V4.0.0, Zenodo repository, 2025, https://zenodo.org/records/16911661.
97. P. Senet, Zenodo repository: patricksenet/SAW-3D-v2.0.1, Zenodo repository, 2025, https://zenodo.org/records/16914457.

---