Organic cation conformational flexibility governs mechanical response in organic–inorganic hybrid materials

Abstract

Organic–inorganic hybrids, that couple the structural design flexibility of organics and the rigidity of inorganic lattices, are gaining attention as next-generation stimuli-responsive materials for adaptive actuation applications. Understanding and controlling mechanical responses in organic–inorganic hybrids is vital for the development of smart materials. Herein, we designed and introduced five- and six-membered ring cations with distinct conformational rigidities to obtain two hybrid metal-halide crystals, (Hmpy)PbI₃ (1, Hmpy = 2-hydroxymethyl-pyrrolidinium) and (Hmpi)PbI₃ (2, Hmpi = 2-hydroxymethyl-piperidinium). Compound 1 exhibits a moderate reversible deformation of 5% with pronounced shape-locking. In contrast, compound 2 shows a large reversible deformation up to 17%. Structural and variable-temperature Raman analyses establish the adaptability of organic cations as the governing factor for ferroelastic strain modulation, operating through controlled ring dynamics and lattice slippage mechanisms. These results establish a clear structure-mechanics relationship: conformational rigidity promotes shape-locking, while enhanced conformational flexibility enables greater actuation freedom. Decoding the structural code behind mechanical response offers a rational basis for designing adaptive crystals with shape memory function.

---

Introduction

Stimuli-responsive materials, capable of undergoing structural or functional transformations, are attracting increasing attention for applications in actuators, sensors, energy conversion and soft robotics.^1–7 Shape memory alloys (SMAs) exemplify a well-developed class of intelligent materials within this field. Their unique shape memory effect (SME) arises from a reversible phase transition between high-temperature austenite and low-temperature martensite.^8–11 A distinctive feature of conventional SMAs is their ability to undergo large reversible deformations (typically 5–10%) via a thermoelastic martensitic transformation.^12–14 NiTi-based SMAs have been widely utilized in aerospace, biomedical, and defense applications due to their excellent mechanical properties, biocompatibility, and corrosion resistance.^15–17 However, the significant work hardening, limited chemical tunability, and environmental concerns associated with these alloys restrict their integration into miniaturized or temperature-sensitive devices.^18–23 Organic dynamic crystals offer a complementary approach that integrates structural diversity with low density characteristics.^3,24–26 These materials exhibit diverse mechanical responses such as bending, jumping or twisting, in response to thermal, photonic, or humidity stimuli.^27–32 Such responses are frequently driven by rapid structural transitions and anisotropic thermal expansion. Despite notable advantages, brittleness and limited durability, especially under repeated cycling or harsh conditions, remain major challenges.³³

To overcome these limitations, organic–inorganic hybrid (OIH) crystals offer a promising platform by combining the conformational programmability of organic cations with the rigidity and anisotropic functionality of inorganic frameworks. Hybrid metal-halide one-dimensional (1D) chain materials are particularly attractive. The chain-like structural units impart pronounced anisotropy and flexibility, enabling cooperative motions between chains that accommodate external stress and facilitate reversible lattice strain, ferroelastic switching, or shape-memory-like behavior. In OIHs, lattice reorganization in the phase transition is accompanied by internal stress, primarily induced by order–disorder transformations of the organic moieties.^34,35 The incorporation of flexible organic cations imparts dynamic adaptability, allowing the release of strain energy and mitigating structural fatigue under repeated stimuli. Rapid stress dissipation enables substantial deformation and may convert stored elastic energy into kinetic output that drives crystal motion. The interaction between flexible organic cations and rigid inorganic frameworks enables the design of materials with cooperative and tunable mechanical responses.^36–39 Realizing controllable mechanical motion in these systems shows meaningful progress toward the development of practical adaptive materials. Although interest in this area is growing, reports on hybrid mechanical responsive materials remain limited. In particular, the influence of organic cations on dynamic lattice behavior requires further exploration to clarify the underlying molecular mechanisms, providing critical scientific insight and guiding principles for the rational design of mechanically responsive materials.

In this work, we designed and systematically investigated two hybrid metal-halide one-dimensional crystals, (Hmpy)PbI₃ (1, Hmpy = 2-hydroxymethylpyrrolidine) and (Hmpi)PbI₃ (2, Hmpi = 2-hydroxymethylpiperidine), incorporating five- and six-membered organic cations that differ in conformational flexibility, to elucidate the molecular basis of shape-locking behavior. Compound 1 exhibits a moderate deformation of about 5%, along with pronounced shape-locking behavior, reminiscent of shape-memory behavior. In contrast, compound 2 undergoes a much larger reversible deformation of up to 17% without shape-locking capability. Detailed mechanistic analysis reveal that the conformational flexibility of the organic cations governs the magnitude, anisotropy, reversibility, and retention of macroscopic deformation, as the distinct mechanical responses arise from differences in the adaptability of the cations during the ferroelastic transition. The rigid five-membered ring in 1 enforces cooperative distortion and supports mechanical memory, while the flexible six-membered ring in 2 allows strain accommodation. These findings clarify the microscopic origin of shape-locking versus reversible actuation in OIH crystals and establish a direct correlation between conformational rigidity and mechanical function in molecular crystals, offering foundational design principles for next-generation adaptive hybrid materials.

Results and discussion

The yellow block crystals (Hmpy)PbI₃ (1) and (Hmpi)PbI₃ (2) were obtained by slowly cooling the clear solution to room temperature (Fig. S1). Thermogravimetric analysis (TGA) curves showed that the compounds start to lose weight at 570 K (1) and 560 K (2) with superior thermal stability (Fig. S2), and the homogeneous phase of samples was verified by the powder X-ray diffraction test (PXRD) and could be used for the next studies (Fig. S3).

Further thermal characterization was performed using Differential Scanning Calorimetry (DSC). As depicted in Fig. 1a, there is an endothermic peak with near 375 K and an exothermic peak near 370 K. The pair thermal peaks suggest that a reversible phase transition has occurred in the compound 1. Similarly, 2 displays endothermic and exothermic peaks at approximately 405/420 K, suggesting a reversible phase transition at higher temperatures (Fig. 1c). The dielectric response as one of the fundamental properties of thermos-responsive materials, usually shows obvious anomalies during the structural phase transition.⁴⁰ The dielectric constant curve of compound 1 at 1 MHz becomes steeper and has an inflection point near 375 K (Fig. 1b), which is consistent with the DSC results. With increasing temperature, the value of dielectric (ε′) constant increases from 4.5 at 310 K to 10.5 at 420 K. During cooling, the ε′ of 1 decreases from 10.5 at 420 K to 4.0 at 310 K, reflecting the same dielectric anomaly observed during heating. Compound 2 also exhibits a distinct step-like dielectric transition around 405/420 K (Fig. 1d).

Fig. 1 DSC curve of 1 (a) and 2 (c). The real part (ε′) of the dielectric constant of compound 1 (b) and 2 (d) measured during heating and cooling at 1 MHz.

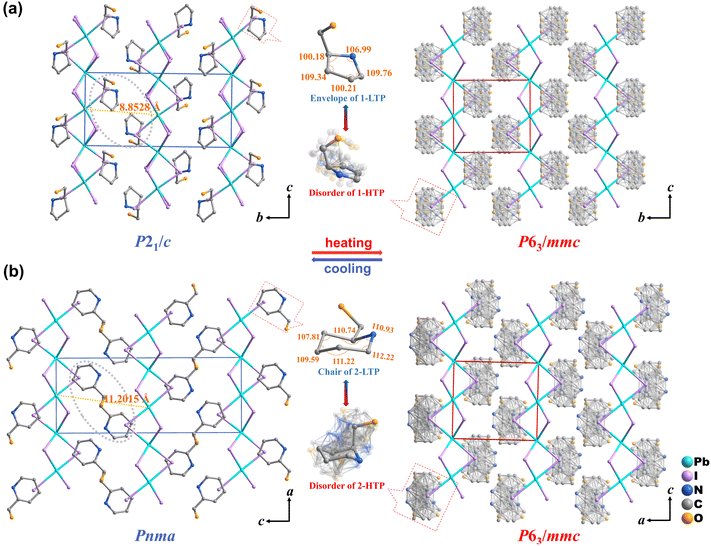
The structural phase transition was analyzed using single-crystal X-ray diffraction (SCXRD). Variable temperature SCXRD determinations were performed at 293 K (low-temperature phase, LTP) and 393 K (high-temperature phase, HTP) for 1 (Table S1). At 293 K, it turns out that 1 adopts the monoclinic space group P2₁/c. The asymmetric unit of 1 is composed of a 2-(hydroxymethyl)pyrrolidinium cation, three I atoms, and a Pb atom (Fig. S4a). The face-sharing octahedral chains of 1 propagate along the c-axis, creating a linear framework (Fig. 2a). The Pb–I distances vary in the range of 3.124–3.388 Å and the Pb–I–Pb angles range from 76.72 to 77.94° (Table S3). In comparison to the LTP, the space group of the HTP changes to the hexagonal P6₃/mmc. The Pb–I bond lengths converge uniformly to 3.194 Å, while the Pb–I–Pb angles slightly increase to approximately 78.22° (Table S4). These adjustments exhibit a reduction in the distortion of inorganic PbI₆ octahedra, leading to a highly symmetric configuration in the HTP (Fig. 2a).

Fig. 2 Packing structure for 1 (a) and 2 (b) in LTP and HTP.

Compound 2 crystallizes in orthorhombic Pnma in the LTP, with the asymmetric unit comprising half a 2-hydroxymethyl-piperidine cation, one and a half iodide ions, and half a lead atom (Fig. S4b). The Pb–I bond lengths range from 3.1538 to 3.4114 Å and the Pb–I–Pb bond angles vary between 77.71° and 78.50° (Table S5). Upon heating to 440 K, 2 transitions to the same space group P6₃/mmc as 1 (Table S2). The Pb–I bond lengths are stabilized at 3.170 Å, and the Pb–I–Pb bond angles shift to approximately 79.80°, indicating a transition toward a more symmetric octahedral coordination compared to the low-temperature phase (Fig. 2b and Table S6). In the HTP, the Hmpy and Hmpi cations become significantly disordered with near-free rotation, driving the phase transitions. In 1-LTP, the organic cation forms strong directional hydrogen bonds with the Pb–I framework, which stabilizes its ordered orientation. As the temperature increases to the high-temperature phase (1-HTP), this ordered state is gradually disrupted. The C, N, and O atoms of the organic cation can be clearly located, but the electron density becomes significantly smeared, indicating a molecular rotation. The orientation becomes dynamically disordered and can be approximated as a spherical distribution on a macroscopic scale. This continuous dynamic motion allows the cation to switch rapidly between different orientations, resulting in partially occupied orientational disorder in the crystal structure (Fig. 2a). In compound 2, the high-temperature phase also shows multiple coexisting conformations and smeared electron density, confirming the orientational disorder and conformational flexibility of the organic cations (Fig. 2b).

To gain a more intuitive understanding of the intermolecular interactions in the crystal structures, Hirshfeld surface analyses were performed by using CrystalExplorer, complemented by two-dimensional fingerprint plots. In a typical Hirshfeld surface, red spots correspond to short contacts with negative d_norm values, indicating strong hydrogen-bonding interactions. White regions are associated with van der Waals interactions (d_norm ≈ 0), and blue regions represent weak longrange interactions with positive d_norm values.⁴¹ In 1-LTP, the hydroxyl groups of the cations interact most strongly with iodine atoms, as evidenced by the most intense red regions on the surface. The organic cations interact with surrounding cations and the inorganic framework through both hydrogen bonding and van der Waals contacts (H⋯ALL = 92.6%). H⋯I contributes 48.4%, showing that H⋯I dominates the organic–inorganic interactions (Fig. S5a). For 2-LTP, partial disorder of the organic cations at room temperature was resolved using Materials Studio. The total hydrogen-involving contacts increase to H⋯ALL = 93.2%, with H⋯I at 56.8% (Fig. S5b). The stronger H⋯I interactions in compound 2 raise the dynamic barrier of the cations and require larger intermolecular forces to overcome during the phase transition, resulting in a higher transition temperature.^42,43 These results demonstrate that hydrogen bonding is critical for both structural organization and phase-transition behavior in these materials.

Thermally induced phase transitions in 1 (6/mmmF2/m) and 2 (6/mmmFmmm) conform to Aizu's ferroelastic species classification.⁴⁴ This suggests that 1 and 2 may exhibit ferroelastic properties. To test this, we examined their domain structures, a key feature of ferroelasticity. Polarizing microscopy at variable temperatures revealed characteristic ferroelastic stripe domains below the phase transition temperature (Fig. 3a and b). These domains disappeared above the curie temperature (T_C), confirming a transition to the paraelastic phase. The calculated spontaneous strain values are X_S (1) = 0.06119 and X_S (2) = 0.01982 in SI.³⁷

Fig. 3 Temperature-dependent evolution of ferroelastic domains of 1 (a) and 2 (b).

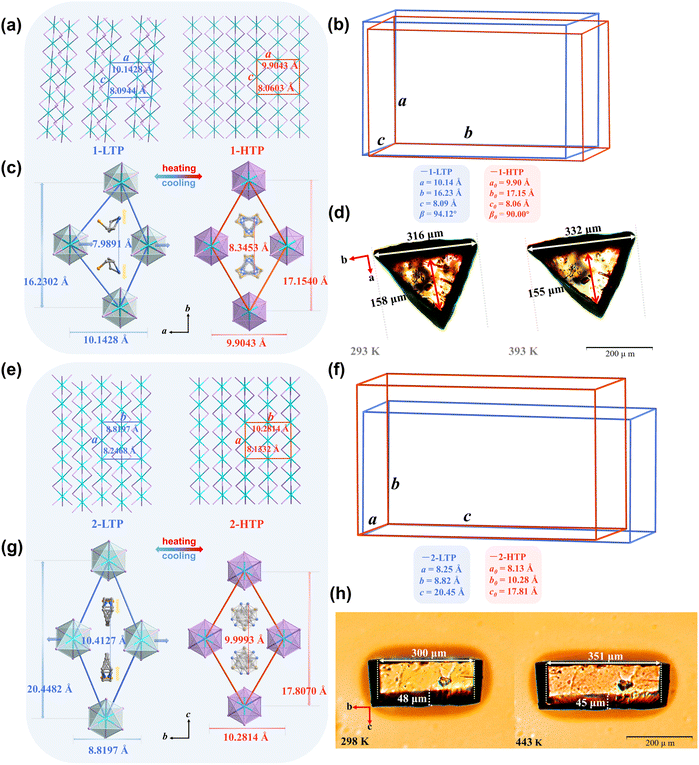
The LTP–HTP transition in 1 revealed significant cellular shear perpendicular to the b-axis from the 1D inorganic chain. To provide a more intuitive comparison of unit cells, the normalized unit cell parameters of different phases were plotted as unit cell diagrams for detailed analysis (Fig. 4a–c). When heating the crystal from 293 K to 393 K, the a-axis shows negligible change (Δa = −2.35%), c-axis remains almost unchanged (Δc = −0.42%) and an elongation of along the b-axis (Δb = +5.69%) occurs. According to the normalisation results, the β angle changed from 94.12° to 90° (from 1-LTP to 1-HTP). For compound 2, although the a-axis contracts slightly from 8.2468 to 8.1332 Å (Δc = −1.38%), this change is negligible relative to the pronounced shear distortion perpendicular to the c-axis, which results in significant b-axis elongation (Δb = +16.55%) and c-axis contraction (Δc = −12.92%) during the LTP–HTP transition (Fig. 4e–g). Then, we placed regular crystals on a microscope equipped with a precision-controlled heating stage. Single-crystal 1 showed a macroscopic deformation of approximately 5%, increasing from 316 µm to 332 µm (Fig. 4d), while 2 markedly enhanced deformation capacity to 17% from 300 µm to 351 µm (Fig. 4h), surpassing the conventional SMAs (10%).¹²

Fig. 4 Normalized unit cell parameters of compounds 1 (a) and 2 (e) from the LTP (blue) to the HTP (red). Comparison of the unit cells of 1 (b) and 2 (f) in the LTP and HTP. Cooperative interaction between organic caions and inorganic chains in 1 (c) and 2 (g). Shape evolution of 1 (d) and 2 (h) under thermal stimuli.

The difference in deformation is closely related to the synergistic interaction between the organic and inorganic components. In the 1-LTP, the distance between adjacent organic cations is 7.9891 Å. The hydroxyl group extending along the a-axis interacts with the inorganic chain, inducing significant distortion in the framework. Upon heating, increased disorder of the organic cations results in an expansion of the inter-cation distance along the b-axis to 8.3453 Å. The structure simultaneously undergoes slippage of the inorganic chains, leading to an increase in the b-axis length from 16.2302 Å to 17.1540 Å and a slight contraction of the a-axis from 10.1428 to 9.9043 Å in 1-HTP, reflecting a moderate anisotropic lattice response (Fig. 4c). In contrast, compound 2 exhibits much larger structural deformation during the LTP–HTP phase transition. The organic cations in compound 2 contain a bulkier six-membered ring, which undergoes a more pronounced order-to-disorder transition. Rotation and flipping of the ring change the orientation of the organic cations and significantly alter their spatial occupation along the b- and c-axes. The resulting steric rearrangement induces more extensive lattice distortion. Specifically, during the transition from 2-LTP to 2-HTP, the distance between adjacent organic cations along the c-axis decreases by 0.4134 Å (from 10.4127 Å to 9.9993 Å), accompanied by a 2.6412 Å contraction of the inorganic chain in the same direction (from 20.4482 Å to 17.8070 Å). Along the b-axis, lattice expansion of 1.4617 Å (from 8.8197 Å to 10.2814 Å) is observed, likely due to changes in organic cation packing and steric effects (Fig. 4g). These results indicate that the distinct size, geometry, and conformational flexibility of the organic cations dictate not only the magnitude but also the principal directions of lattice deformation. In compound 1, the smaller and less flexible five-membered ring cation drives moderate anisotropic distortion mainly along the a- and b-axes. In compound 2, the bulkier six-membered ring exerts stronger steric and conformational effects that redistribute geometric stress toward the b- and c-axes, enhancing bidirectional deformation and anisotropic lattice response. Such highly cooperative organic–inorganic coupling accounts for the pronounced structural response of compound 2 and highlights a strategy to tune anisotropic deformation through cation design.

Furthermore, their responses under thermal cycling differed sharply. Compound 1 retained its deformed state under thermal cycles, consistent with shape-locking behavior, whereas 2 maintained reversibility across multiple cycle (Fig. S6 and Movies 1 and 5). Detailed investigation reveals that 1 undergoes shape release below 298 K, indicating a temperature-dependent unlocking mechanism (Movie 2). The PXRD results confirm the hysteretic behavior (Fig. S7). The experimental patterns at 293 K and 393 K align with the simulated low- and high-temperature phases, confirming the transition from the 1-LTP to the 1-HTP. However, upon cooling, although thermodynamically the low-temperature phase is expected to recover around 345 K, the experimental patterns reveal that the original diffraction peaks fully reappear only when cooled to 293 K or below. This discrepancy likely stems from an intermediate phase that stabilizes the high-temperature structure, causing the crystal to retain its high-temperature shape until cooled to 293 K. To further elucidate the structural origin of the observed behavior, we examined the role of organic components in modulating structural flexibility and thermal response. The five-membered ring, with bond angles near 109°, imposes geometric rigidity (Fig. 2a). In contrast, the six-membered ring adopts low-strain chair conformations, promoting greater conformational freedom. This conformational adaptability enables diverse molecular interactions and structural accommodation (Fig. 2b and S8).^45–47 Supporting this, torsion angle analysis further reveals the conformational flexibility differences between compounds 1 and 2 (Table S8). In 1-HTP, most of the ring torsion angles are within single-digit values (e.g., C3–C4–N1–C1: 1°, N1–C4–C3–C2: 2°), while a few torsion angles (e.g., C5–C1–N1–C4: −123°, C3–C2–C1–C5: 124°) reflect limited ring flexibility. Overall, the five-membered ring of Hmpy remains relatively rigid at 393 K, with only minor flexibility. In contrast, in 2-HTP, torsion angles are generally in the 55–65° range, involving the six-membered ring and adjacent bonds (e.g., C6–N1–C2–C1 and C2–N1–C6–C5), resulting in pronounced nonplanar distortions. This indicates increased intramolecular flexibility and enhanced conformational adaptability, enabling the organic cations to more effectively accommodate lattice strain.

Structural analysis also demonstrates that organic cations inserted between inorganic chains directly modulate Pb–Pb distances. Compound 1 restricts Pb–Pb distances to 8.85 Å (<9 Å), indicating a relatively compact inorganic framework. Although compound 1 exhibits reversible deformation, Pb–Pb spacing suggests a degree of shape locking, which may limit the extent of lattice reorganization during phase transitions. In contrast, enlargement of the ring structure and greater conformational flexibility in the organic cations of compound 2 allow this distance to extend to 11.20 Å (Fig. 2), facilitating more pronounced structural adaptability. The Pb–Pb distances exceeding 9 Å are frequently observed in other reversibly deformable hybrid systems, further underscoring the critical role of organic cation-mediated modulation in enabling large, reversible lattice deformations (Table S9).

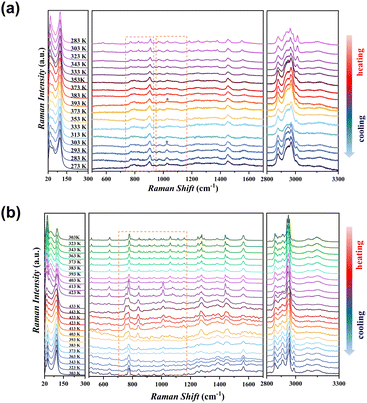
In order to gain deeper insight into the molecular mechanisms underlying the distinct thermodynamic behaviors of compounds 1 and 2, variable-temperature Raman spectroscopy was carried out. Fig. 5a presents the spectra of compound 1 during heating and cooling cycles. According to the literature,^48–51 the region from 740 to 1055 cm⁻¹ primarily corresponds to ring vibrational modes. The strong bands at 740–900 cm⁻¹ arise from ring breathing vibrations, while others are associated with C–C and C–N stretching and bending. Fundamental vibrations between 800 and 1500 cm⁻¹ are mainly attributed to CH₂ modes. Upon heating, several vibrational modes involving C–H and N–H motions (300–1200 cm⁻¹) broaden and shift slightly. In the high-frequency region (2800–3300 cm⁻¹), corresponding to N–H and C–H stretching, a pronounced intensity redistribution is observed. These changes point to a coupled process of structural reorganization and hydrogen bond modulation. Notably, several ring vibration peaks in the 740–1200 cm⁻¹ range significantly weaken with increasing temperature. The peak at 1025 cm⁻¹ (marked with a star) even disappears, suggesting reduced ring ordering triggered by thermal activation. Upon cooling to around 303 K, the vanished peak gradually returns and the vibrational mode becomes more distinct, consistent with structural reordering. However, the Raman peaks associated with the organic moieties show minimal change throughout the cycle, indicating a stable conformation and limited flexibility. The delayed reappearance of some vibrational peaks upon cooling from 393 K to 303 K indicates sluggish structural recovery. The high-temperature-induced conformational “locking” likely accounts for the inability of compound 1 to recover its shape until cooled below room temperature. However, compound 2 exhibits clearer and sharper vibrational features across the entire temperature range (Fig. 5b). Both low- and high-frequency vibrational modes display continuous and reversible intensity variations during heating and subsequent cooling, reflecting enhanced dynamic adaptability of the flexible six-membered ring. In 2-LTP (ordered chair conformation), multiple well-resolved peaks are observed in the 650–1200 cm⁻¹ range, corresponding to characteristic ring stretching and deformation modes (C–C and C–N stretching coupled with bending vibrations). Upon heating to 2-HTP, these peaks gradually broaden and weaken significantly, indicating that the single ordered chair conformation is disrupted and the system enters an orientationally disordered state, likely involving a mixture of boat and intermediate conformations.^52–54 Upon cooling, these peaks reappear and sharpen, confirming that the six-membered ring undergoes a reversible chair-boat-chair conformational transition during the phase change. Notably, certain peaks, especially in the 1000–1100 cm⁻¹ region, exhibit distinct frequency shifts during the phase transition. This may arise from the substantial morphological deformation (∼17%) and the formation of dense, stripe-like ferroelastic domains, which perturb the local spectroscopic environment and measurement conditions. In addition, a broad band around 3150 cm⁻¹ corresponds to the O–H stretching vibration, with its redshift and broadening reflecting strong hydrogen-bonding interactions between the hydroxyl groups and halide ions. The disappearance of this band upon heating indicates disordering of the hydrogen-bond network, consistent with Hirshfeld surface analysis, which highlights the key role of hydrogen bonding in the phase transition and in stabilizing the low-temperature ordered phase of 2.^55,56 Collectively, these spectral variations provide direct molecular-level evidence for the divergent thermally induced behaviors of compounds 1 and 2. In addition, Wang et al. proposed an ‘entropy amplification’ strategy that overcomes energy barriers through thermodynamically driven entropy gain.⁵⁷ Consistent with this approach, thermal analysis shows that compound 2 exhibits 16-fold enhanced entropy change (ΔS = 34.16 J mol⁻¹ K⁻¹) over compound 1 (ΔS = 2.18 J mol⁻¹ K⁻¹), as evidenced by the evolution of distinct endothermic peaks (Fig. 1a and c). These coupled structural-thermodynamic signatures establish that the organic cation conformational flexibility synergizes with its 16-fold entropy enhancement to collectively drive the macroscopic reversible actuation.

Fig. 5 Temperature-dependent Raman spectra of 1 (a) and 2 (b) in wavenumber range 20–3300 cm⁻¹.

The pronounced thermally induced elongation in 1 and 2 enables their microactuation for driving external loads (Movies 3 and 4). To evaluate their driving performance, the crystals were fixed to a heating stage with silver paste (Fig. 6a). Thermal actuation at 393 K drives 1 (3 mg) to deform and eject a 60 mg silica gel sphere in Fig. 6b, resulting in a net elongation of approximately 1 mm (Fig. 6b and S9a). Compound 2, on the other hand, demonstrated a more efficient stress transfer and achieved a larger actuation amplitude, with an elongation of approximately 3 mm and sustained extension after ejecting the load (Fig. 6c and S9b). These results highlight the critical role that structural differences and physical properties between compounds play in macroscopic response behavior, providing robust experimental support for the design of miniature drive systems and adaptive structures. Existing studies have shown that certain crystals undergo significant phase transitions upon heating, giving rise to diverse dynamic responses.^58–62 Motivated by this, crystals with varying sizes and morphologies were systematically examined. The experimental results reveal that micron-sized crystals primarily exhibit relatively simple and controllable deformations, such as localized expansion or contraction. However, millimeter-sized crystals display more complex mechanical behaviors, including jumping in 1 (Fig. 6d) and swinging in 2 (Fig. 6e), driven by the buildup and release of internal stress, which were further corroborated by additional experiments exploring their mechanical response (Fig. S9c–e). The observed size-dependent behavior highlights the critical role of crystal structure and geometry in governing dynamic responses, thereby expanding the functional scope of these materials for advanced mechanical applications.

Fig. 6 (a) Crystal-driven actuation for silicone ball propulsion. Thermal-induced ball displacement in compound 1 (b) and 2 (c) under microscopic view. Thermally triggered mechanical motions: jumping in 1 (d) and swaying in 2 (e).

Conclusions

In summary, we synthesized two hybrid metal-halides (Hmpy)PbI₃ (1) and (Hmpi)PbI₃ (2), and demonstrated a direct correlation between the adaptive flexibility of organic cations and the thermal mechanical behavior of hybrid metal-halide crystals. Thermal stimulation induces an order–disorder transition of the organic cations that drives a ferroelastic phase transition. We found that the conformational flexibility of the organic cations not only governs the magnitude and direction of the deformation but also strongly influences the strength of the shape-locking effect. Compound 1, with a rigid five-membered ring, shows moderate reversible deformation and shape-locking due to thermally induced conformational locking. In contrast, compound 2 features a flexible six-membered ring that enables enhanced, reversible actuation by accommodating lattice distortion through dynamic hydrogen-bond rearrangement. Variable-temperature PXRD and Raman spectroscopy collectively reveal hysteretic phase recovery and restricted vibrational reversibility in 1, contrasting with the fully reversible structural and vibrational responses of 2. These findings provide clear design principles for engineering adaptive hybrid materials with programmable ferroelastic and shape-memory properties.

Author contributions

Ya-Wen Yang and Ke Xu conceived and designed the project, and wrote the manuscript. Zi-Ning Zhou and Ming-Liang Jin provided technical support and data analysis. Ryo Tsunashima and Takayoshi Nakamura contributed suggestions and improvements to the project. Chao-Yang Chai reviewed and edited the manuscript. Qiong Ye managed the project, acquired funding, reviewed and edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

Additional datasets are available from the corresponding author upon reasonable request.

CCDC 2476437–2476440 contain the supplementary crystallographic data for this paper.^63a–d

All data supporting this article are included in the main text and the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sc06333g.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (22275033, U24A20504 and W2521008). This research work was also supported by the Big Data Computing Center of Southeast University.

Notes and references

1. F. Tong, W. Xu, M. Al-Haidar, D. Kitagawa, R. O. Al-Kaysi and C. J. Bardeen, Angew. Chem., Int. Ed., 2018, 57, 7080–7084.
2. W. Zou, B. Jin, Y. Wu, H. Song, Y. Luo, F. Huang, J. Qian, Q. Zhao and T. Xie, Sci. Adv., 2020, 6, eaaz2362.
3. P. Naumov, D. P. Karothu, E. Ahmed, L. Catalano, P. Commins, J. M. Halabi, M. B. Al-Handawi and L. Li, J. Am. Chem. Soc., 2020, 142, 13256–13272.
4. Z. Zhang, N. Xu, Z. Huang, J. Lai, J. Liu, G. Deng, X. Wang and W. Zhao, Adv. Devices Instrum., 2023, 4, 0019.
5. A. Khalil, D. P. Karothu and P. Naumov, J. Am. Chem. Soc., 2019, 141, 3371–3375.
6. Y. Yang, X. Ji, Z. H. Lu, J. Yang, C. Gao, H. Zhang, B. Z. Tang, J. L. Sessler and H. Y. Gong, Nat. Commun., 2020, 11, 77.
7. Y. Yang, X. Ji, Z. H. Lu, J. Yang, C. Gao, H. Zhang, B. Z. Tang, J. L. Sessler and H. Y. Gong, Nat. Commun., 2023, 14, 2287.
8. S. Miyazaki and K. Otsuka, ISIJ Int., 1989, 29, 353–377.
9. K. Otsuka and T. Kakeshita, MRS Bull., 2002, 27, 91–100.
10. K. Otsuka and X. Ren, Prog. Mater. Sci., 2005, 50, 511–678.
11. J. M. Jani, M. Leary, A. Subic and M. A. Gibson, Mater. Des., 2014, 56, 1078–1113.
12. P. Sedmák, J. Pilch, L. Heller, J. Kopeček, J. Wright, P. Sedlák, M. Frost and P. Šittner, Science, 2016, 353, 559–562.
13. J. M. Vallejos, M. F. Giordana, C. E. Sobrero and J. A. Malarria, Scr. Mater., 2020, 179, 25–29.
14. P. La Roca, L. Isola, Ph. Vermaut and J. Malarría, Scr. Mater., 2017, 135, 5–9.
15. C. Bil, K. Massey and E. J. Abdullah, J. Intell. Mater. Syst. Struct., 2013, 24, 879–898.
16. A. Emiliavaca, C. J. de Araújo, C. R. Souto and A. Ries, Smart Mater. Struct., 2019, 28, 015010.
17. M. Ho, A. B. McMillan, J. M. Simard, R. Gullapalli and J. P. Desai, IEEE Trans. Robot., 2012, 28, 213–222.
18. N. Gangil, A. N. Siddiquee and S. Maheshwari, J. Manuf. Process., 2020, 59, 205–222.
19. Y. Wu, Y. Xiao, G. Chen, C. T. Liu and Z. Lu, Adv. Mater., 2010, 22, 2770–2773.
20. L. Zhang, H. Zhang, W. Li, T. Gemming, P. Wang, M. Bonisch, D. Sopu, J. Eckert and S. Pauly, J. Alloys Compd., 2017, 708, 972–981.
21. L. Zhang, Z. W. Zhu, H. M. Fu, H. Li and H. F. Zhang, Mater. Sci. Eng. A, 2017, 689, 404–410.
22. J. M. Jani, M. Leary, A. Subic and M. A. Gibson, Mater. Des., 2014, 56, 1078–1113.
23. N. Gangil, A. N. Siddiquee and S. Maheshwari, J. Manuf. Process., 2020, 59, 205–222.
24. Y. Duan, S. Semin, P. Tinnemans, H. Cuppen and J. Xu, Nat. Commun., 2019, 10, 4573.
25. D. Yan, Z. Wang and Z. Zhang, Acc. Chem. Res., 2022, 55, 1047–1058.
26. B. B. Rath and J. J. Vittal, Acc. Chem. Res., 2022, 55, 1445–1455.
27. R. Chandrasekar, Small, 2021, 17, 2100277.
28. J. B. Zhong, J. B. Sun, C. Chen, X. Q. Yang, K. Q. Ye, L. Li, P. Naumov and R. Lu, Angew. Chem., Int. Ed., 2025, 64, e202502107.
29. R. Chandrasekar, Chem. Commun., 2022, 58, 3415–3428.
30. D. P. Karothu, J. Weston, I. T. Desta and P. Naumov, J. Am. Chem. Soc., 2016, 138, 13298–13306.
31. D. P. Karothu, J. M. Halabi, E. Ahmed, R. Ferreira, P. R. Spackman, M. A. Spackman and P. Naumov, Angew. Chem., Int. Ed., 2022, 61, e202113988.
32. Y. Sun, Y. Lei, H. Dong, Y. Zhen and W. Hu, J. Am. Chem. Soc., 2018, 140, 6186–6189.
33. A. K. Nangia and G. R. Desiraju, Angew. Chem., Int. Ed., 2019, 58, 4100–4107.
34. X. B. Han, C. Y. Chai, B. D. Liang, C. C. Fan and W. Zhang, CrystEngComm, 2022, 24, 1507–1517.
35. S. Liu, R. Guo and F. Xie, Mater. Des., 2022, 221, 110951.
36. K. Xu, Z. Z, X. Han, Y. Yang, W. Zhang and Q. Ye, Angew. Chem., Int. Ed., 2024, 63, e202408247.
37. B. D. Liang, C. C. Fan, C. D. Liu, C. Y. Chai, X. B. Han and W. Zhang, Nat. Commun., 2022, 13, 6599.
38. M. L. Jin, X. B. Han, C. D. Liu, B. D. Liang, C. Q. Jing, W. Wang, C. C. Fan, T. Y. Ju, J. M. Zhang and W. Zhang, Adv. Funct. Mater., 2024, 34, 2408120.
39. M. L. Jin, X. B. Han, C. D. Liu, C. Y. Chai, C. Q. Jing, W. Wang, C. C. Fan, J. M. Zhang and W. Zhang, J. Am. Chem. Soc., 2024, 146, 6336–6344.
40. M. Liberka, M. Zychowicz, J. Hooper, K. Nakabayashi, S. Ohkoshi and S. Chorazy, Angew. Chem., Int. Ed., 2023, 62, e202308284.
41. P. Liu, J.-W. Cao, J. Li, H. Li, J.-B. Wang, J. Cai, L. Li and K.-J. Chen, Adv. Funct. Mater., 2025, e18494.
42. Y. Y. Tang, Y. Ai, W. Q. Liao, P. F. Li, Z. X. Wang and R. G. Xiong, Adv. Mater., 2019, 31, 1902163.
43. X. T. Sun, Y. Y. Zhang, Y. Han, X. P. Wang, J. Li, J. Y. Li, H. F. Ni, D. W. Fu and Z. X. Zhang, Dalton Trans., 2023, 52, 16406–16412.
44. K. Aizu, J. Phys. Soc. Jpn., 1969, 27, 387–396.
45. K. B. Wiberg, Angew. Chem., Int. Ed., 1986, 25, 312–322.
46. J. I. Wu and P. R. Schleyer, Pure Appl. Chem., 2013, 85, 921–940.
47. K. Omoto, T. Nakae, M. Nishio, Y. Yamanoi, H. Kasai, E. Nishibori, T. Mashimo, T. Seki, H. Ito, K. Nakamura, N. Kobayashi, N. Nakayama, H. Goto and H. Nishihara, J. Am. Chem. Soc., 2020, 142, 12651–12657.
48. O. Fandino, S. Sasidharanpillai, D. V. Soldatov and P. R. Tremaine, J. Phys. Chem. B, 2018, 122, 10880–10893.
49. Q. Y. Yang, Q. Yang, Y. F. Song, A. W. Liu, J. Wang, Y. Tan, Y. R. Sun and S. M. Hu, J. Phys. Chem. A, 2025, 129, 3183–3193.
50. Y. Qiu, H. Liu, N. Ma, J. Chen, H. Ding, Z. Hu and D. Zhong, Energy Fuels, 2023, 37, 10296–10309.
51. Z. G. Lada, K. S. Andrikopoulos, A. Chrissanthopoulos, S. P. Perlepes and G. A. Voyiatzis, Inorg. Chem., 2019, 58, 5183–5195.
52. X. G. Chen, Y. R. Weng, Y. Zhang, X. J. Song, H. P. Lv, Y. Qin, W. Q. Liao, R. G. Xiong and Y. Ai, J. Am. Chem. Soc., 2025, 147, 36539–36546.
53. H. P. Lv, S. Q. Hu, Y. J. Bai, J. S. Zhou, L. Y. Ji, Z. X. Wang, Y. Ai, Y. Qin and X. G. Chen, Chem. Sci., 2025, 16, 9109–9116.
54. M. Mączka, J. K. Zaręba, A. Gągor, K. Fedoruk-Piskorska, D. Stefańska, D. Drozdowski, M. Ptak and A. Sieradzki, ACS Appl. Mater. Interfaces, 2024, 16, 60564–60575.
55. B. A. Kolesov, Int. J. Mol. Sci., 2021, 22, 5380.
56. S. Katemala, A. Molee, K. Thumanu and J. Yongsawatdigul, Poult. Sci., 2022, 101, 101829.
57. Z. Wang, R. Shi, I. Tahir, D. P. Karothu, P. Cheng, W. Han, L. Li, Y. Zheng, P. Naumov, J. Xu and X. H. Bu, J. Am. Chem. Soc., 2025, 147, 7749–7756.
58. L. Catalano and P. Naumov, CrystEngComm, 2018, 20, 5872–5883.
59. Z. S. Yao, H. Guan, Y. Shiota, C. T. He, X. L. Wang, S. Q. Wu, X. Zheng, S. Q. Su, K. Yoshizawa, X. Kong, O. Sato and J. Tao, Nat. Commun., 2019, 10, 4805.
60. X. D. Qiu, L. Chen, J. W. Hou, H. Y. Lin, T. Y. Xu, F. Tong, H. Tian and D. H. Qu, J. Am. Chem. Soc., 2025, 147, 17772–17783.
61. M. Jin, S. Yamamoto, T. Seki, H. Ito and M. A. Garcia-Garibay, Angew. Chem., Int. Ed., 2019, 58, 18003–18010.
62. B. B. Rath, G. Gallo, R. E. Dinnebier and J. J. Vittal, J. Am. Chem. Soc., 2021, 143, 2088–2096.
63. (a) CCDC 2476437: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2p3y2v; (b) CCDC 2476438: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2p3y3w; (c) CCDC 2476439: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2p3y4x; (d) CCDC 2476440: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2p3y5y.

---

Footnote

† These authors contribute equally to this work.

---