Soft crystalline properties of 2D frameworks constructed from lithium ions and dinitriles

Abstract

We constructed two-dimensional (2D) molecular frameworks composed of lithium ions (Li⁺) and dinitrile aliphatic ligands to explore their mechanical and thermal properties. Calorimetry, X-ray diffraction, density functional theory calculations, alternating current impedance, and solid-state nuclear magnetic resonance evidenced behaviours and properties originating from the weakly linked 2D system. We found low melting temperatures (<100 °C), high mechanical deformability, large positive and negative thermal expansion, and metal ion diffusion. These features were uniquely observed in the integration of Li⁺ and dinitriles into extended molecular structures.

---

Introduction

Coordination polymers (CPs) and metal–organic frameworks (MOFs) are molecular frameworks featuring well-defined, periodic structures. Conventional design and synthesis of CP/MOFs have focused on the robustness and stability of frameworks based on stronger coordination bonds by applying high-valent transition metal ions such as oxophilic Zr⁴⁺ and Cr³⁺ and rigid ligands.^1,2 On the other hand, frameworks based on weaker metal–ligand interactions have been relatively unexplored, despite their potential to exhibit distinct dynamic and thermomechanical behaviours.

In recent studies, synthetic approaches to incorporate weak metal–ligand interactions have been adopted to create CP/MOF crystals with phase changes, including melting behaviours.^3–7 Controlling the bond strength (enthalpic factor) and the mobility of molecular components (entropic factor) reduces the melting temperature (T_m) to a value lower than the decomposition temperature, yielding a stable liquid state.^8,9 In other words, CP/MOFs constructed from metal ions and bridging ligands with weak interactions would represent not only the chance to explore the melting phenomena but also their unique physical (especially, thermal) properties in the crystalline state; however, many of them have been overlooked.

Here, we report molecular frameworks constructed from lithium ions (Li⁺) and dinitriles. We selected Li⁺ as nodes and dinitrile aliphatic linkers to construct crystalline frameworks, utilising their non-directional bonding and the inherent flexibility of the linker molecules.^10–13 A solvent-free melt-cooling reaction was employed instead of a self-assembling process in solutions to incorporate these components into single crystalline phases. The crystalline products are two-dimensional (2D) structures and exhibit low T_m ranging from 59 to 90 °C, below those typically reported for CP/MOFs. They exhibited Young's moduli below 18 GPa, and one compound showed large positive and negative thermal expansion, with the absolute value of the coefficient exceeding 100 × 10⁻⁶ K⁻¹. The weak interactions between the metal and ligands facilitate dissociation of the coordination interactions, resulting in the diffusion of the metal ions in the crystalline phase.

Results and discussion

Crystal structures

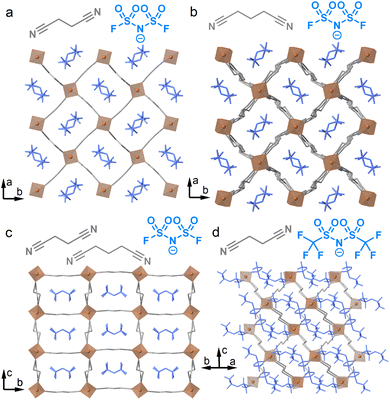
Four Li-based frameworks, Li(FSI)(SN)₂ (1), Li(FSI)(GN)₂ (2), Li(FSI)(SN)(GN) (3), and Li(TFSI)(SN)_1.5 (4) (FSI⁻ = bis(fluorosulfonyl)imide, TFSI⁻ = bis(trifluoromethanesulfonyl)imide, SN = succinonitrile, and GN = glutaronitrile) were synthesised (see the SI for the detailed synthetic methods).^10,14–16 A solvent-free melt-cooling reaction was performed under an Ar atmosphere to effectively trap the metastable, weak interactions in the crystalline states. This reaction is necessary because no crystals were formed using conventional solvothermal reactions with ethanol, acetonitrile, or tetrahydrofuran. In Fig. 1 and S1, we reveal the structures through single crystal X-ray diffraction (SC-XRD) analyses of 2, 3, and 4, along with the previously reported structure of 1. All obtained crystals consist of tetrahedral Li⁺ and dinitrile linkers. 2, 3, and 4 feature 2D sheet structures. Compounds 2 and 3 consist of frameworks with tetracoordinated Li⁺ and SN/GN linkers, containing FSI within them. In contrast, 4 has two inequivalent Li⁺ sites; one site is coordinated with four SN, while the other has two SN and two TFSI⁻. The TFSI⁻ anions cap the sheets to form a 2D extended structure. The 2-nm sheets exhibit a sql topology, as determined by TOPOS Pro,¹⁷ with a two-fold inclined interpenetration. Mixtures of Li(BF₄) and SN, and Li(PF₆) and SN, at the molar ratio of 1/2 formed solids with unclear melting behaviours, suggesting the formation of impurity phases. These results indicate the importance of FSI⁻ and TFSI⁻ for the formation of pure single phases.

Fig. 1 Schematic representations of dinitriles and anions, and crystal structures of (a) Li(FSI)(SN)₂ (1) at −100 °C, (b) Li(FSI)(GN)₂ (2) at 0 °C, (c) Li(FSI)(SN)(GN) (3) at 0 °C, and (d) Li(TFSI)(SN)_1.5 (4) at −175 °C. SN/GN: grey, Li⁺: orange, and FSI⁻/TFSI⁻: blue. H atoms are omitted for clarity.

Thermal behaviours

Thermogravimetric analysis (TGA) determined the decomposition temperatures of 1–4 to be 109, 140, 139, and 139 °C (Fig. S2), forming a stable liquid state over a temperature window of 50 °C. In Fig. 2, differential scanning calorimetry (DSC) revealed melting peaks for 1–4 at 63, 90, 90, and 59 °C (Fig. 2a–d). T_m of 1 aligns with the reported value, suggesting high phase purity.¹⁰ Variable-temperature (VT) powder X-ray diffraction (PXRD) of powder samples, matching the patterns simulated from SC-XRD structures, confirmed the complete transformation during melting (Fig. S3). We synthesised Li(TFSI)(bpe)₂ (bpe = 1,2-bis(4-pyridyl)ethane) to elucidate the role of the ligand in reducing T_m (Fig. S4 and Table S1). It showed a T_m of 219 °C in DSC, without significant weight loss in TGA (Fig. S5), a temperature comparable to reported TFSI⁻- and pyridine-based melting CPs and analogues (168–245 °C).^18–21 This indicates that the origin of the low T_m of 1–4 arises from the weak interaction between Li⁺ and nitrile groups. In the DSC of 4, a glass transition was observed at −48 °C (T_g) in the second heating process. This indicates the low diffusivity of the components due to the bulky TFSI⁻ and a high Li⁺/linker ratio, suppressing crystallisation to form a glassy state.²² We performed DSC at different ramping rates (Fig. S6). While ramping rates of 3 K min⁻¹ or higher observed no crystallisation, the heating process at 2 K min⁻¹ resulted in crystallisation. This indicates that ramping rates above 2 K min⁻¹ are required for the formation of a stable glassy/liquid phase of 4.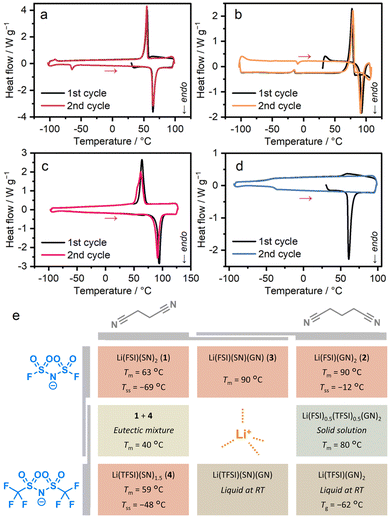

Fig. 2 DSC profiles of (a) 1, (b) 2, (c) 3, and (d) 4. Red arrows indicate heating processes. (e) Summary of thermal and phase behaviours.

To gain an understanding of low-melting behaviours, we studied the thermodynamic parameters. The melting enthalpy (ΔH_fus) and melting entropy (ΔS_fus) for 1, 2, 3, and 4 are presented in Table 1. The lower ΔH_fus for 2 compared to 1 results from the increased cation–anion distances, which reduce the electrostatic stability of 2.^8,23 According to the equation T_m = ΔH_fus/ΔS_fus, a higher ΔH_fus corresponds to a higher T_m. However, 2 exhibits a higher T_m than 1 despite its lower ΔH_fus. This can be attributed to the significantly lower ΔS_fus of 2, highlighting the important role of entropy, which has been discussed in relation to ionic liquids and CPs.^20,24 Among the low-melting MOFs, entropy also plays a significant role in their melting behaviours. The lower ΔS_fus of 2, despite the longer alkyl chain, indicates a higher degree of freedom, or more ‘liquid-like’ dynamics of GN in 2. The high ΔH_fus and ΔS_fus of 3 originate from the more densely packed structure, supported by the density (Table S1). The lower ΔH_fus and ΔS_fus of 4 are explained by the lower symmetry of the crystal and fewer aliphatic components in the composition.

Table 1 Thermodynamic parameters of 1–4 and 1_0.54_0.5

Sample	Tm/°C	ΔHfus/kJ mol^−1	ΔSfus/J K^−1 mol^−1	Tss/°C	ΔHss/kJ mol^−1	ΔSss/J K^−1 mol^−1	Tg/°C
1	63	34	100	−69	3.8	18.5	—
2	90	29	80	−12	1.3	5.0	—
3	90	39	107	—	—	—	—
4	59	27	81	—	—	—	−48
10.540.5	40	30	97	—	—	—	—

---

In addition to melting, small sharp peaks were observed in DSC of 1 and 2 at −69 and −12 °C (T_ss). The solid–solid transition (SST) entropies (ΔS_ss) of 1 and 2 were 18.5 and 5.0 J K⁻¹ mol⁻¹. They are equal to 2.2 R and 0.6 R, where R is the universal gas constant. These results indicate an increase in the number of states (W) by 9.3 and 1.8 times, as derived from Boltzmann's equation, S=R In(W).²⁵ The W of 1.8 for 2 is almost equal to 2, and this is consistent with the disordering of GN into two possible conformations at a higher temperature than T_ss. The W of 9.3 for 1 suggests the disordering of both SN and FSI⁻ in the SST.

Phase behaviours of mixtures and analogues

We investigated the mixture of the crystals and analogues to further understand the phase behaviours of the systems (Fig. 2e). We applied physical mixing for 1 and 2 with equimolar amounts. The PXRD pattern after five-minute hand grinding in a mortar matched that of 3, without diffraction peaks of 1 or 2 (Fig. S7). The pattern was fitted with the space group of Pbcm, supporting the formation of 3 (Fig. S8 and Table S2). This indicates the formation of 3, suggesting high diffusivity of the components and formability of the crystalline state of 3.

For the mixture of 1 and 4, we studied 1_x4_1−x (x = 0.25, 0.5, 0.75), prepared by melt-cooling processes of the mixtures with a molar ratio of x/(1 − x) on a Li⁺ basis. PXRD patterns after the melt-cooling process confirmed the co-presence of 1 and 4 crystal phases in all the mixtures without forming any new phases (Fig. S9). While 1_0.254_0.75 and 1_0.754_0.25 showed two melting peaks in DSC, 1_0.54_0.5 exhibited a single melting peak at 40 °C (Fig. S10). These indicate the formation of a eutectic mixture with a T_m of 40 °C.^26,27 The ΔH_fus and ΔS_fus were analysed to elucidate the thermodynamic origin of the reduction of T_m (Table 1). The ΔH_fus value of 30 kJ mol⁻¹ is comparable to the average of 1 and 4, suggesting the absence of enthalpic stabilisation by mixing the crystals. ΔS_fus was calculated as ΔH_fus/T_m = 97 J K⁻¹ mol⁻¹. This value is larger than the average of 1 and 4 ([101 + 80]/2 = 91) by 6 J K⁻¹ mol⁻¹, indicating the entropic contributions to the reduction of T_m. The value of 6 J K⁻¹ mol⁻¹ is close to R ln(2), and this is interpreted as the term of mixing entropy (ΔS_mix) in the liquid state, which is given by the equation for ideal solutions as ΔS_mix = − R [x ln(x) + (1 − x) ln (1 − x)]. These results highlight the pure and significant effect of mixing entropy on the minimisation of the T_m of the mixture.

The mixture of Li(FSI), Li(TFSI), and GN at the molar ratio of 1 : 1 : 4 formed a colourless crystalline powder. DSC of the product showed a sharp melting peak at 80 °C (Fig. S11), suggesting the formation of a pure crystalline phase. The PXRD pattern showed peaks at positions comparable to those of 2 (Fig. S12), proving the formation of a solid solution state with randomised anion positions with the formula of Li(FSI)_0.5(TFSI)_0.5(GN)₂. We performed fitting of the PXRD pattern at 30 °C (Fig. S13). The extracted lattice constants are 0.1% larger than those of 2 (Tables S3 and S5), suggesting the expansion of the unit cell by including TFSI⁻ inside the frameworks.

We also attempted the synthesis of Li(TFSI)–GN and Li(TFSI)–SN–GN frameworks with the corresponding formula of Li(TFSI)(GN)₂ and Li(TFSI)(SN)(GN). Each mixture of the precursors gave liquid states that remained uncrystallised over three years, forming a stable liquid state at room temperature. The DSC of Li(TFSI)(GN)₂ observed a glass transition at −62 °C (Fig. S14), a temperature lower than the T_g of 4 by 14 °C, suggesting a possible T_m of 38 °C, assuming the T_g T_m ratio based on that of 4 (0.68, for the absolute temperatures). This suggests a T_m close to RT, preventing crystal formation and resulting in the room temperature liquid phase.

Mechanical properties

To investigate the mechanical properties associated with the weak metal–linker interaction, thermal expansivity was calculated from VT-PXRD patterns (Fig. S15–S17 and Tables S4–S6). Fig. 3a–c display the relative lattice constants of 1–3 as functions of temperature. For 1 and 2, temperatures above each T_ss were taken into account. The coefficient of thermal expansion (CTE) was −69 × 10⁻⁶ and +370 × 10⁻⁶ K⁻¹ for the a/b- and c-axes of 1, and +69 × 10⁻⁶, +76 × 10⁻⁶ and +200 × 10⁻⁶ K⁻¹ for the a-, b-, and c-axes of 2. The CTE is substantial compared to reported CP/MOFs and is comparable to that of organic polymers.²⁸ The negative thermal expansion (NTE) in 1 is understood as a result of expansion along the c-axis and flexible deformation of the 3D network. For 3, the CTE was +270, +180, and −110 × 10⁻⁶ K⁻¹ for the a-, b-, and c-axes, across the temperature range of −100–80 °C. Both positive and negative thermal expansions are considered ‘colossal’, reaching the CTE as large as ±100 × 10⁻⁶ K⁻¹, and significant anisotropic expansion was observed.^29,30 The NTE in 3 indicates the contraction of the Li–GN–Li linkage, suggesting that the higher deformability of the longer aliphatic chain contributes to the softer mechanical properties.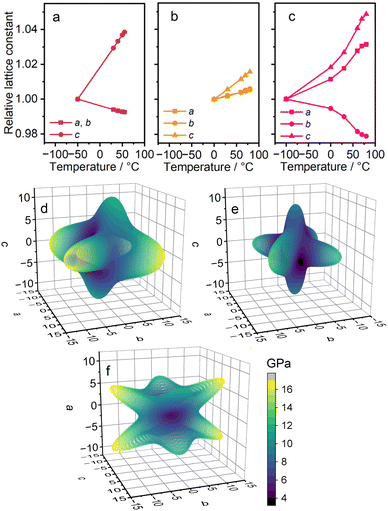

Fig. 3 Mechanical properties of 1–3. Relative lattice constants of (a) 1, (b) 2, and (c) 3. Computed spatial dependence of Young's moduli of (d) 1, (e) 2, and (f) 3.

The mechanical properties of 1–3 were computed. The elastic tensors are calculated using the density functional theory (DFT) method (Fig. S18 and S19).^31,32 Fig. 3d–f show the spatial dependence of Young's moduli. The anisotropies in the ab plane of 1 and 2 are attributed to the low-symmetric initial structures considered in DFT calculations.^33,34 The calculated Young's moduli range 4.3–17.7 (1), 3.3–13.7 (2), and 0.3–16.8 GPa (3). These values are smaller compared with reported CP/MOFs, such as Zr₆(OH)₄O₄(1,4-benzenedicarboxylate)₆ (UiO-66, 37.1–46.3 GPa) or Zn₃O(1,4-benzenedicarboxylate)_2, (MOF-5, 9.5–19.7 GPa), suggesting the effect of the weak metal–linker interaction on stiffness.^35,36 1 and 2 are stiff along the Li–SN/GN–Li linkage. The smaller Young's modulus of 2 compared to 1 suggests the softness of the longer aliphatic chain of GN relative to SN. Despite similarities in the crystal structures, 3 exhibits a different shape of spatial dependence. The low Young's modulus along the a-axis of 3 indicates the deformability of the zig-zag structure in the Li–SN–Li linkage.

Diffusion behaviours

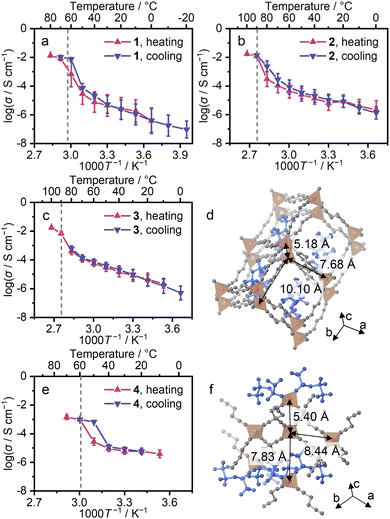
Impedance measurements were conducted for 1–4 (Fig. S20 and S21). A high transference number (0.95) and a hopping conduction mechanism of Li⁺ were reported for 1, suggesting potential opportunities for Li⁺ conductivity in 2–4 as well.^10,37 Temperature-step DSC was conducted for 4 with the same temperature program as the impedance measurements (Fig. S22), observing crystallisation at 50 °C. Ion conductivity was calculated from the semi-circles of the obtained Nyquist plot. Fig. 4 shows Arrhenius plots for the first and after-melting cycles. The conductivity (σ) of 1–4 at 30 °C in the after-melting cycle was 1.3, 1.5, 1.3, and 1.2 × 10⁻⁵ S cm⁻¹, and the activation energies (E_a) were 16, 13, 21, and 8 kJ mol⁻¹ (Fig. S23). The comparable σ and E_a of 1–3 suggest the identical Li⁺ hopping mechanism in the conduction. The E_a of 4 is lower by 0.5 times, suggesting different Li⁺ conduction paths in 4. The crystal of 4 is in a lower symmetry with a higher number of neighbouring Li⁺ sites, and this leads to the formation of several possible Li⁺ ion paths, reducing the E_a in Li⁺ conduction (Fig. 4d and f). The ⁷Li T₁ relaxation time in VT solid-state nuclear magnetic resonance (SS-NMR) corroborates the E_a of conductivity. In Fig. S24, the ⁷Li T₁ relaxation time is plotted as a function of temperature. The E_a values of each ⁷Li T₁ relaxation time followed the same trend as those observed from Li⁺ conductivity (Table S7). This suggests a Li⁺-conduction mechanism based on Li⁺ hopping, and the difference of E_a between 1–3 and 4 supports the identical Li⁺ hopping mechanism in 1–3 and multiple conduction paths in 4.

Fig. 4 Li⁺ conductivity (σ) of 1–4. Arrhenius plots of Li⁺ conductivity for (a) 1, (b) 2, (c) 3, and (e) 4. Red and blue plots represent heating and cooling processes. The dashed lines indicate the T_m. The crystal structures of (d) 3 and (f) 4. The distances between neighbouring Li⁺ are indicated.

Conclusions

Four framework crystals, Li(FSI)(SN)₂, Li(FSI)(GN)₂, Li(FSI)(SN)(GN), and Li(TFSI)(SN)_1.5, were synthesised from Li⁺ and aliphatic dinitrile linkers by a solvent-free melt-cooling process. These are constructed through weak metal–ligand interactions, as explained by HSAB theory, leading to low T_m below 90 °C. DFT-based elasticity analyses revealed high and anisotropic deformability, attributed to the aliphatic softness and framework topology. XRD-based thermal expansion analyses observed a large linear CTE of +370 × 10⁻⁶ K⁻¹ in one framework, as well as a large negative thermal expansion with a CTE of −110 × 10⁻⁶ K⁻¹ in another one, attributed to structural anisotropy. AC impedance and solid-state NMR elucidated an ionic conductivity of 1.5 × 10⁻⁵ S cm⁻¹ at room temperature based on the weak metal–linker interactions. This work provides clear evidence and guidelines for synthesising mechanically soft, thermally active molecular frameworks based on weak metal–linker interactions.

Author contributions

T. N. and K. K. contributed equally to this work. T. N., K.·K., and S. H. conceptualised the project. K. K., T. N., T. K., N.·S., S. To., S. Ts, and N. M. contributed to data collection and formal analyses. T. N. and S. H. summarised the findings in the manuscript, and all the authors approved the final version.

Conflicts of interest

There are no conflicts to declare.

Data availability

CCDC 2463044 Li(FSI)(GN)₂, 2463045 Li(FSI)(SN)(GN) and 2480466 Li(TFSI)(bpe)₂ contain the supplementary crystallographic data for this paper.^38a–c

The data supporting this article have been included in the supplementary information (SI). Supplementary information: the details of experiments, crystallographic data, computational analyses, thermogravimetric analysis, differential scanning calorimetry, variable-temperature powder X-ray diffraction and fitting, impedance and ion conductivity measurements, and solid-state nuclear magnetic resonance. See DOI: https://doi.org/10.1039/d5sc06222e.

Acknowledgements

This work was supported by the Japan Society of the Promotion of Science (JSPS) for Transformative Research Areas (A) “Supraceramics” (JP22H05147), the Fund for the Promotion of Joint International Research (International Collaborative Research, JP24K0112), the Japan Science and Technology Agency (JST) for NEXUS (JPMJNX25B4), and the Asahi Glass Foundation. T. N. acknowledges SPRING (JPMJSP2110) from JST and the Ginpu Fund from the Graduate School of Science, Kyoto University. We acknowledge SPring-8 beamtime at BL02B2 and BL04B2 for PXRD (proposal No. 2023A1748, 2023B1639, 2023B1721, and 2025B1683) with the approval of the Japan Synchrotron Radiation Research Institute (JASRI). We acknowledge Drs Takuji Hatakeyama and Masahiro Hayakawa for the opportunities for SC-XRD measurements. K. K. and T. N. thank Drs Kazuyoshi Kanamori and Kei Morisato for the insightful discussion.

Notes and references

1. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444.
2. S. Horike, S. S. Nagarkar, T. Ogawa and S. Kitagawa, Angew. Chem., Int. Ed., 2020, 59, 6652–6664.
3. T. D. Bennett, A. K. Cheetham, A. H. Fuchs and F.-X. Coudert, Nat. Chem., 2016, 9, 11–16.
4. T. D. Bennett and S. Horike, Nat. Rev. Mater., 2018, 3, 431–440.
5. N. Ma and S. Horike, Chem. Rev., 2022, 122, 4163–4203.
6. L. León-Alcaide, R. S. Christensen, D. A. Keen, J. L. Jordá, I. Brotons-Alcázar, A. Forment-Aliaga and G. Mínguez Espallargas, J. Am. Chem. Soc., 2023, 145, 11258–11264.
7. N. Ma, S. Kosasang, E. K. Berdichevsky, T. Nishiguchi and S. Horike, Chem. Sci., 2024, 15, 7474–7501.
8. M. Liu, R. D. McGillicuddy, H. Vuong, S. Tao, A. H. Slavney, M. I. Gonzalez, S. J. L. Billinge and J. A. Mason, J. Am. Chem. Soc., 2021, 143, 2801–2811.
9. Y. Ohara, T. Nishiguchi, S. Horike and D. M. Packwood, Inorg. Chem., 2025, 64, 5682–5687.
10. K. Tanaka, Y. Tago, M. Kondo, Y. Watanabe, K. Nishio, T. Hitosugi and M. Moriya, Nano Lett., 2020, 20, 8200–8204.
11. P. Prakash, B. Fall, J. Aguirre, L. A. Sonnenberg, P. R. Chinnam, S. Chereddy, D. A. Dikin, A. Venkatnathan, S. L. Wunder and M. J. Zdilla, Nat. Mater., 2023, 22, 627–635.
12. J. Luo, Y. Chang, J.-W. Shi, X. Wang, H. Huang, Y. Zhang, X. Wang, J. Zhang, Y.-X. Huang and R. Zhao, Nano Lett., 2024, 24, 15035–15042.
13. C. Luo, C. Ning, X. Huang, P. Zhang, L. Yang, S. Wang, J. Wang, Y. Wang, K. Wan, Z.-H. Guo, K. Yue and Z. Liang, Angew. Chem., Int. Ed., 2025, e202507051.
14. Y. Ugata, M. L. Thomas, T. Mandai, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2019, 21, 9759–9768.
15. Y. Ugata, R. Tatara, K. Ueno, K. Dokko and M. Watanabe, J. Chem. Phys., 2020, 152, 104502.
16. H. Katsuragawa, S. Mori, Y. Tago, S. Maeda, S. Matsuda, H. Toriu, R. Nakayama, S. Kobayashi, T. Hitosugi and M. Moriya, ACS Appl. Energy Mater., 2025, 8, 3599–3605.
17. V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586.
18. X. Zheng, K. Fukuhara, Y. Hijikata, J. Pirillo, H. Sato, K. Takahashi, S.-I. Noro and T. Nakamura, Commun. Chem., 2020, 3, 1–7.
19. X. Zheng, M. Kato, Y. Uemura, D. Matsumura, I. Yagi, K. Takahashi, S.-I. Noro and T. Nakamura, Inorg. Chem., 2023, 62, 1257–1263.
20. Y. Ohara, T. Nishiguchi, X. Zheng, S.-I. Noro, D. M. Packwood and S. Horike, Chem. Commun., 2024, 60, 9833–9836.
21. T. Nishiguchi, Y. Ohara, K. Kadota, X. Zheng, S.-I. Noro and S. Horike, Chem. Sci., 2025, 16, 621–626.
22. A. Nazet, S. Sokolov, T. Sonnleitner, T. Makino, M. Kanakubo and R. Buchner, J. Chem. Eng. Data, 2015, 60, 2400–2411.
23. L. Schkeryantz, P. Nguyen, W. D. McCulloch, C. E. Moore, K. C. Lau and Y. Wu, Inorg. Chem., 2021, 60, 14679–14686.
24. T. Endo, K. Sunada, H. Sumida and Y. Kimura, Chem. Sci., 2022, 13, 7560–7565.
25. A. Wehrl, Rev. Mod. Phys., 1978, 50, 221–260.
26. A. Lang, C. Chen, C. Ye, L. N. McHugh, X. W. Chua, S. D. Stranks, S. E. Dutton and T. D. Bennett, J. Am. Chem. Soc., 2024, 146, 33945–33955.
27. K. Atthawilai, H. Tabe, K. Ohara, K. Kongpatpanich and S. Horike, J. Am. Chem. Soc., 2025, 147, 5140–5148.
28. S. Li, S. Yu, S. M. Collins, D. N. Johnstone, C. W. Ashling, A. F. Sapnik, P. A. Chater, D. S. Keeble, L. N. McHugh, P. A. Midgley, D. A. Keen and T. D. Bennett, Chem. Sci., 2020, 11, 9910–9918.
29. A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. O. Evans, D. A. Keen, L. Peters and M. G. Tucker, Science, 2008, 319, 794–797.
30. W. Cai and A. Katrusiak, Nat. Commun., 2014, 5, 1–8.
31. R. Golesorkhtabar, P. Pavone, J. Spitaler, P. Puschnig and C. Draxl, Comput. Phys. Commun., 2013, 184, 1861–1873.
32. R. Gaillac, P. Pullumbi and F.-X. Coudert, J. Phys. Condens. Matter, 2016, 28, 275201.
33. A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, Phys. Rev. Lett., 2012, 109, 195502.
34. E. Kiely, R. Zwane, R. Fox, A. Reilly and S. Guerin, CrystEngComm, 2021, 23, 5697–5710.
35. D. F. Bahr and J. A. Reid, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 184106.
36. H. Wu, T. Yildirim and W. Zhou, J. Phys. Chem. Lett., 2013, 4, 925–930.
37. R. Sasaki, M. Moriya, Y. Watanabe, K. Nishio, T. Hitosugi and Y. Tateyama, J. Mater. Chem. A, 2021, 9, 14897–14903.
38. (a) CCDC 2463044: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2np01f; (b) CCDC 2463045: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2np02g; (c) CCDC 2480466: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2p8415.

---

Footnote

† These authors contributed equally.

---