Challenges in data-driven catalysis modelling: case study on palladium-NHC catalyzed Suzuki–Miyaura reactions

Abstract

In this study, we synthesized a set of 21 N-heterocyclic carbene (NHC)Pd complexes and evaluated them in a benchmark reaction for Suzuki–Miyaura coupling under 12 different conditions, resulting in a high-quality dataset tailored for machine learning applications. We present a detailed analysis of the data, enabling a thorough assessement of the various parameters (ligand structure and reaction parameters) influencing the reaction yield. We used a new workflow to select descriptors for building linear regression models. The models achieved satisfactory performance in interpolation across all reaction conditions. To ensure these results were not artifacts, we critically examined our models, assessing features explainability, featurization strategies, the impact of train-test splits, and the influence of conformer sets. This work highlights key practical considerations for modeling catalytic activity using machine learning.

---

Introduction

Machine learning (ML) has recently emerged as a transformative tool in chemical research, enabling data-driven approaches to predict molecular properties, optimize reaction conditions, and design catalysts with improved performance.^1–6 Its application in transition metal catalysis, in particular, has provided valuable insights into ligand design, reaction optimization, and mechanistic understanding.^7–9 Recent studies have demonstrated the utility of ML in analyzing extensive chemical datasets, uncovering structure–reactivity relationships, and accelerating the development of effective catalytic systems.^10–13 For example, ML has been applied to optimize ligand properties and reaction conditions in nickel- and palladium-catalyzed cross-couplings, resulting in enhanced reactivity and selectivity.^6,14–16 These advances underscore the potential of data-driven methods to streamline catalyst design and expand the scope of catalytic transformations, making it a powerful tool for modern chemistry.

One of the most promising applications of ML in chemistry is the development of predictive models capable of forecasting the outcome of reactions based on input parameters. Such models could significantly enhance the efficiency of reaction optimization and, more importantly, guide the design of more effective (pre-)catalysts and ligands for key transformations. Among these, the Suzuki–Miyaura cross-coupling stands out as one of the most widely utilized and versatile reactions in modern synthetic chemistry.^17–19 This transformation is particularly crucial for constructing biaryl motifs, which serve as fundamental building blocks in pharmaceuticals, natural products, and materials science.^20–23

While several transition metals can mediate this transformation, palladium remains the preferred metal due to its unparalleled efficiency and reliability.^17,22,24,25 Two primary families of ligands, phosphines^26,27 and N-heterocyclic carbenes,^28,29 are commonly employed as ligands in palladium-catalyzed cross-coupling reactions. Although phosphines were historically the first to be adopted,^30–32 NHC ligands now occupy a prominent role in the area, owing to their superior thermal and oxidative stability, strong σ-donating properties, and excellent catalytic performance.^33–35

Despite the increasing integration of machine learning in catalyst design and optimization, ML studies in cross-coupling catalysis remain relatively underdeveloped and notably have been focused on phosphine ligands.^14,15,36 NHC ligands, in particular, have received minimal attention in data-driven analyses,^37,38 not only in the context of Suzuki–Miyaura coupling but also in homogeneous catalysis in general. Moreover, the existing literature often lacks a comprehensive and critical assessment of modelling approaches, such as for example the evaluation of descriptor types (for example, density functional theory (DFT)-derived vs. more computationally efficient extended connectivity fingerprints (ECFPs)), the influence of catalysts/ligands conformer selection, and the impact of test-train splits. This gap is especially notable in the context of small datasets, where the relevance of descriptors and model performance can be significantly affected by sample and conformer choices. In our opinion, the absence of systematic theoretical investigations prevents a deeper understanding of the advantages and limitations of data-driven approaches for homogeneous catalyst development.

In the present study, we investigated linear regression models for predicting the catalytic activity of NHC-palladium catalysts in Suzuki–Miyaura coupling reactions under various conditions. To achieve this, we prepared 21 distinct Pd-NHC precatalysts and tested them across 12 different reaction conditions. The resulting dataset was utilized as input for predicting reaction yields. Our primary objective was to determine whether catalyst features broadly applicable across diverse reaction conditions could be identified, or whether changes in reaction parameters necessitate the selection of entirely distinct features. In parallel, we systematically compared different molecular representations (including DFT-derived descriptors, extended connectivity fingerprints, and structural motifs) and evaluated the impact of training/test splits and conformer selection on model performance.

Results and discussion

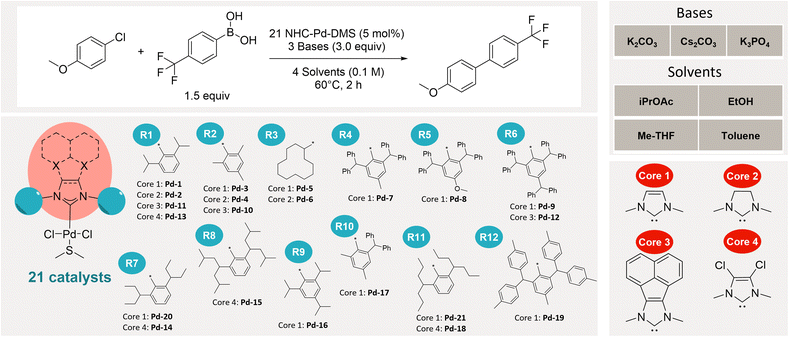
For our investigation, we selected 4-chloroanisole and 4-trifluoromethylphenyl boronic acid as the model substrates for Suzuki–Miyaura coupling. To systematically evaluate reaction conditions, we explored all 12 possible combinations of four different solvents—ethanol, isopropyl acetate, 2-methyltetrahydrofuran, and toluene—and three different bases—K₂CO₃, Cs₂CO₃, and K₃PO₄.

As precatalysts, we employed the recently reported NHC-Pd-DMS complexes developed by the Nolan group.³⁹ These precatalysts feature N-heterocyclic carbene as an actor ligand and dimethyl sulfide (DMS) as weakly-coordinating ancillary (throw-away) ligand. This design facilitates efficient precatalyst activation and enables straightforward removal of the volatile DMS at the end of the reaction. These complexes have demonstrated comparable performance to PEPPSI analogues in both Suzuki–Miyaura and Buchwald–Hartwig couplings.

In total, we synthesized and studied 21 distinct NHC-Pd-DMS precatalysts incorporating a diverse range of symmetric NHC ligands featuring 4 cores and 12 different wingtips (Fig. 1). Our set of NHC ligands includes widely used ligands alongside several less frequently reported in the literature. The ligands feature alkyl and aryl substituents on their wingtips, and although they may appear structurally similar, they span a broad range of electronic and steric properties. While electronic effects are largely governed by the core scaffold, variations in steric bulk from different R substituents can also influence the overall electronic character of the ligand.⁴⁰ Notably, 16 out of the 21 NHC-Pd-DMS complexes synthesized in this study were prepared for the first time, further contributing to the novelty of the dataset.

Fig. 1 Overview of the project. Reaction parameters and set of precatalysts explored.

Experimental design

High Throughput Experimentation (HTE) procedures were used to test all 21 precatalysts across the selected reaction conditions (see SI for details). The following parameters were kept constant across all 12 solvent/base combinations: 1.5 equivalents of boronic acid, 3 equivalents of base, 5 mol% of precatalyst, a reaction temperature of 60 °C, and a reaction time of 2 hours.

We first tested two plating methods PM1 and PM2 with a subset of eight catalysts (see SI) to ensure that our HTE protocol is robust in providing reliable and reproducible data. The two methods differ in the order of additions of the various reaction components. PM1 consisted in pre-plating the Pd precatalysts in stock solutions, removing volatiles under reduced pressure, and subsequently adding the bases as solids on top of the dry precatalyst. Afterwards, boronic acid and aryl chloride were added as stock solutions in the anhydrous reaction solvent. For PM2, the bases were first dosed as solids in the reaction vials using a solid handling robot. The precatalysts were then added as stock solutions with subsequent solvent removal. Afterwards, similarly to PM1, reagents are added as stock solutions in the reaction solvent. The slowest step is the solid dispensing of the bases (4–5 hours using our solid handling robot). Therefore, PM2 offers higher productivity by allowing to use plates of bases prepared in advance. However, we were concerned that the addition of the precatalysts in solution onto the solid bases in absence of substrates could lead to some catalyst degradation.

Initial experiments aimed at comparing PM1 and PM2 were run in duplicates for each plating method, resulting in four 96-well plates in total. The results were analyzed using ultra-performance liquid chromatography (UPLC). Replicates within the same plating method demonstrated excellent reproducibility, with Pearson coefficients above 0.95 (see SI). Pearson coefficients between the plating methods remained relatively high (0.84–0.91), indicating that despite differences in absolute values, the overall reactivity trends among the precatalysts were preserved forming a solid basis for model development (see SI, Fig. S4). The Wilcoxon Signed-Rank Test^41,42 performed on average yield values for each method failed to reject hypothesis of equal distribution between two plating methods (p-value 0.05), indicating that the two plating methods do not differ significantly from statistical point of view. However, the delta values, i.e., the difference in yield between two runs within each plating method, were not equally distributed. This latter outcome revealed that PM2 exhibits higher consistency than PM1 (see SI, Fig. S2). Based on this observation, we proceeded with the more time-efficient PM2 as the main plating method for the project.

Upon further examination of yield distributions, we noticed that in most of the reactions with K₃PO₄, the yields were higher for PM2 than for PM1. Interestingly, an opposite trend, albeit less pronounced, was observed for K₂CO₃. A possible explanation might be a change in morphology of the base caused by addition of solvent/vacuum removal prior to the reaction in the case of PM2. We assume that in the case of K₃PO_4, such a treatment would make the base more soluble while it would be the opposite for K₂CO₃. It is worth to mention that solid morphology is an important factor which is often overlooked in cross-coupling reactions with insoluble inorganic bases.^43,44 This observation reinforces the necessity of standardizing experimental workflows to ensure robust and reproducible datasets, especially for data-driven approaches.

After selecting PM2 as the plating method, the remaining NHC-Pd-DMS precatalysts were tested with the model substrates in 12 selected reaction conditions. For reaction analysis, we transitioned from UPLC to GC, as it provided comparable reliability (see SI, Fig. S5) while also offering additional information (discussed vide infra). Each reaction was conducted in duplicate to ensure reproducibility, from two identical 96-well plates containing the same set of precatalysts prepared in parallel. The result for each reaction was considered consistent if yield and conversion both were within 20%, leading us to identify 46 reactions that were investigated with further repetitions. For reactions with four replicates, outliers were removed based on normalized deviation, and the median value was subsequently used for analysis (see SI, Fig. S7 and S8). In most cases, the new experimental results were in accordance with one of the previously acquired data point. At this stage, we considered our data to be highly reliable for the subsequent ML modeling.

In addition to the desired biaryl product, we also identified the two usual by-products of the Suzuki–Miyaura coupling reaction—namely, the homocoupling product of the boronic acid, 4,4′-trifluoromethyl-biphenyl and the dehalogenation product, anisole. Across all reactions, the homocoupling product was observed in amounts ranging from 2–7%, which aligns with proposed mechanisms of precatalyst activation in the presence of a weak base.⁴⁵ The dehalogenation occurred exclusively in ethanol with sterically bulky ligands (see SI, Fig. S29 and S30).

Experimental data analysis

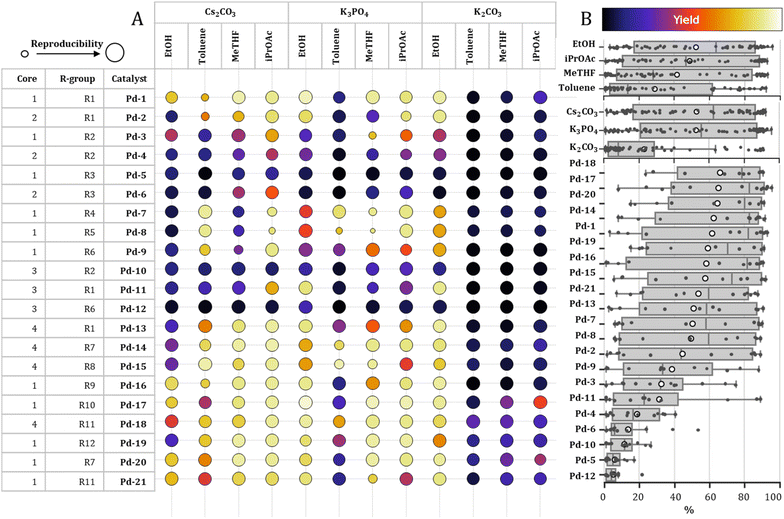
The performance of all 21 catalysts under 12 reaction conditions was analyzed to uncover general trends in reactivity. For most of the reaction conditions, a wide distribution of yields was obtained across the various catalysts, suggesting that solvent or the base effects alone were not the only key determinants of catalytic performance (Fig. 2).

Fig. 2 (A) Overview of generated experimental values. Lighter color represents higher yield, the circle size is proportional to the observed reproducibility. (B) Yield distribution in the final dataset grouped by the base, solvent and catalyst. Empty circles and the vertical line within the box indicate mean and median values, respectively.

Notably, Pd-18, Pd-17, Pd-20, Pd-14, and Pd-1—bearing the IHept^Cl, IPaul, IPent, IPent^Cl, and IPr ligands, respectively—demonstrated superior performance across the full range of conditions, each with average yield exceeding 60% and median yield around 80% (Fig. 2B). While IPr, IPent, and IHept ligands are well-established as high-performing NHCs in palladium-catalyzed cross-couplings, this study marks the first evaluation of the IPaul-based complex Pd-14 in Suzuki–Miyaura coupling. Remarkably, its performance was on par with these “privileged” ligands. Additionally, Pd-16, featuring the IPr^iPr ligand—an IPr analogue with an extra isopropyl group in the para position of the phenyl ring—also exhibited a high median yield, although its average yield was slightly below 60%.

Similarly, yield distributions varied widely depending on the solvent and base used. Among the solvents tested, ethanol consistently afforded higher average yield (52%), while among the bases, cesium carbonate and potassium phosphate showed same average yields (53%), with Cs₂CO₃ displaying a slightly higher median. Toluene, by contrast, consistently resulted in lower yields (29% on average) than any other solvent. Interestingly, K₂CO₃ exhibited a distinct bimodal distribution: high yields were observed only in ethanol, while its use in other solvents led to poor performance, with most yields falling below 20%. This phenomenon may partially account for the higher overall efficiency observed with ethanol as a solvent.

Further analysis was conducted by grouping the results based on catalyst structure using core and R groups of the NHC ligands. Some catalysts were found to be inefficient under all tested conditions, exhibiting uniformly low conversions and yields (Fig. 2). Two of them, Pd-5 and Pd-6 precatalysts, are the only tested complexes with alkyl-substituted R-groups, namely cyclododecyl rings (R3). Such ligands are rarely utilized in Pd-catalyzed cross-couplings, as they are usually less efficient than aryl-substituted congeners.⁴⁶ Pd-12 catalyst, bearing BIAN-IPr# ligand, exhibited the lowest average yield in all studied conditions. Interestingly, it is the first palladium complex with this NHC reported and it represents the bulkiest NHC in our study.⁴⁷

We also explored potential trends in catalytic performance based on the NHC ligand core structure and wingtip substituents. Among the core types analyzed, Core 4 (4,5-dichloroimidazolium) and Core 1 (unsubstituted imidazolium) demonstrated the highest average and median product yields, with Core 4 topping the list at a median yield of approximately 70%. In contrast, Core 3, representing BIAN-type ligands, and Core 2, corresponding to imidazolinium-based scaffolds, were consistently associated with lower yields across the dataset (see SI).

We further examined the influence of wingtip substituents. Ligands featuring R2 (mesityl), R3 (cyclododecyl), and R6 (1,3,5-tribenzhydryl) groups afforded significantly lower yields compared to other substituents. Catalysts with other R groups displayed a broad range of reactivity, suggesting that their performance is highly dependent on specific combinations of solvents and bases. It is important to note, however, that this analysis is limited by the unequal representation of cores and substituents in our catalyst library.

In Fig. 2A, the variance of the yields obtained for replicates for a given catalyst/condition is represented by the size of the circle with larger circles corresponding to a lower variance and a higher reproducibility. Overall, most of the replicates in the final dataset are within 10–20% variance of yield. Smaller circles are more prominent for K₃PO₄ in toluene or Me-THF suggesting that these combinations of base and solvent could lead to less robust processes. Pd-7 and Pd-8 also feature less reproducible results. Although these two catalysts (both featuring Core 1 and bulky benzhydryl substituents) are related, another member of their family Pd-9 does not confirm this trend.

While most of the solvent-base pairs showed wide distribution of the yields, i-PrOAc-Cs₂CO₃ combination exhibited highest average and median yields across all catalysts tested, as well as narrower interquartile range (i.e. range where middle 50% of the datapoints reside). Five specific solvent-base pairs (toluene-K₂CO₃, Me-THF-K₂CO₃, i-PrOAc-K₂CO₃, toluene-K₃PO₄, and EtOH-Cs₂CO₃) led to a highly skewed distribution of yield with a median value below 25% (i.e. 50% of the obtained yields were below 25%).

Modelling strategy

Our experimental dataset included twelve reaction conditions, allowing for two possible modeling strategies: (1) condition-wise modeling, in which a separate model is trained for each set of base and solvent – treating catalysts as samples, or (2) a unified model trained on combined samples of catalyst, solvent, and base, with the latter two encoded using one-hot encoding. We opted to employ the first strategy—the condition-wise—since our primary objective was to explore catalyst features. In a unified model, these catalyst features could be overshadowed by the features of the solvent and the base. Additionally, we aimed to assess whether it would be possible to identify catalyst features that consistently perform well across all condition-specific models. Therefore, we decided to exclude from modelling the five solvent-base pairs (toluene-K₂CO₃, Me-THF-K₂CO₃, i-PrOAc-K₂CO₃, toluene-K₃PO₄, and EtOH-Cs₂CO₃) for which all catalysts performed poorly (median value below 25%). The narrow range of yields obtained for these conditions was expected to introduce more noise than information. Furthermore, catalysts Pd-5 and Pd-6 were excluded from further analysis to concentrate the modeling effort on systems featuring aromatic R-groups within our condition-wise framework.

Three catalysts—with ligands IPr (Pd-1), BIAN-IMes (Pd-10), and IPent^Cl (Pd-14)—were excluded from all preprocessing steps described below and designated for use solely as an external test set, ensuring representation of Core 1, Core 3 and Core 4 with R1, R2 and R7 in distinct combinations. This selection was a strategic compromise to balance representativeness within the core/R group table and yield. IPr (Pd-1) generally exhibited high yield, BIAN-IMes (Pd-10) consistently performs poorly, while IPent^Cl (Pd-14) displayed an intermediate yield behavior.

Feature generation

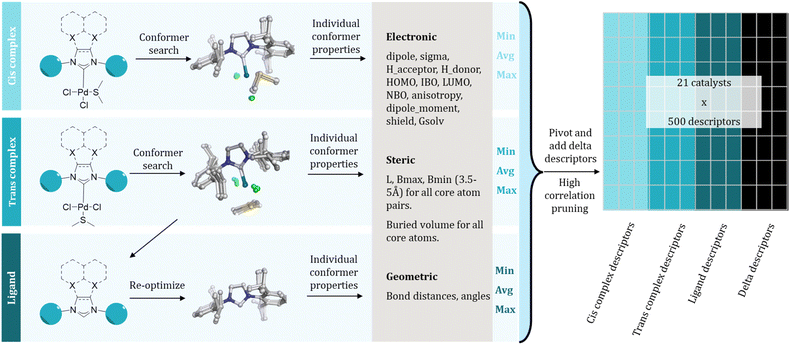
All precatalysts were parametrized using three distinct approaches. The simplest approaches relied on one-hot encoding (OHE) of each ligand based on their distinct core (Cores 1–4) and R-group (R1–R12) and on Extended Connectivity Fingerprints (ECFPs, radius = 2, number of bits = 1024).⁴⁸ In addition, 3D-based electronic, steric, and geometric descriptors were generated from structures optimized at DFT level. These features exhibit an increasing level of information complexity but are concomitantly more expensive than OHE and ECFPs in terms of computation resources.

For generating the catalyst descriptors at DFT level, we selected as initial structure two different square planar [Pd(NHC)(DMS)Cl₂] complexes with the two chlorides in cis- or trans-positions using AaronTools.^49,50 Conformer ensembles were generated via metadynamics runs for both configurations at the GFN-FF level⁵¹ as implemented in CREST 2.11 (ref. 52) and xTB 6.4 (ref. 53 and 54) programs keeping the [Pd(DMS)Cl₂] fragment constrained during the simulation. These ensembles were used to identify a maximum of 10 representative conformers with Principal Component Analysis and Clustering using the MEANS cluster algorithm as implemented in CREST. The conformer ensembles of the trans-[Pd(NHC)Cl₂] and the ligand structures were generated from these ensembles by removing the corresponding atoms (Fig. 3), which were then optimized at DFT level as detailed below.

Fig. 3 Overview of generated conformers and descriptors.

The DFT level structures were optimized using the TPSS-D3 (ref. 55 and 56) functional with def2-SVP^57,58 basis sets in gas phase, followed by energy and property evaluation at higher level, using TPSS-D3 and BP86 (ref. 59) functionals with def2-TZVP basis sets in gas phase and with COSMO^60,61 (with dielectric constant of 4.81) to analyze the method dependence of the chosen descriptors and calculating the solvation free energies using the COSMO-RS^62–64 theory as implemented in COSMOTherm version 2020.⁶⁵ All DFT calculations were performed using TURBOMOLE 7.6.1 (ref. 66) with standard settings except finer integration grid of m4 was used throughout.

The final geometric, electronic and solvent-dependent descriptors were extracted from the obtained structures. Additionally, steric descriptors, i.e., sterimol parameters and buried volumes, were calculated on each atom and pair of atoms of the core structure and [Pd(DMS)Cl₂] substructure using the DBSTEP package.⁶⁷ The extracted electronic descriptors included both (1) atom centric properties, such as NBO and IBO charges and absolute NMR shielding for the NHC core and the [Pd(DMS)Cl₂] fragment, and (2) global properties, such as HOMO/LUMO energies and dipole/quadrupole moment. The geometric descriptors focused on bond lengths and bond and torsion angles around the NHC core and the Pd center. Solvent-dependent features analyzed the interactions between solvent and solute interactions using COSMOTherm. Finally, we also generated energy based and “delta descriptors” to capture changes in energy or descriptor values with respect to structural changes, e.g., [Pd(NHC)(DMS)Cl₂] → [Pd(NHC)Cl₂] + DMS. For more in-depth explanation of the feature generation, see SI.

Machine learning enabled feature selection

Identifying or designing chemically relevant features for small datasets is often a challenging task that requires a solid understanding of the underlying molecular mechanisms.^68,69 To enable a more general and consistent approach, we focused on a broad parametrization of multiple complexes to capture catalyst descriptors that are linked to the catalyst activity across multiple conditions. However, having generated over 500 DFT-based descriptors for only 19 catalysts in our data set, feature pruning and selection became critical to mitigate the risk of overfitting.

Since all our NHC ligands were symmetrical, our first pruning step consisted in aggregating the descriptors of most of the symmetrical atoms, retaining only their average, minimum and maximum values for local electronic and geometric descriptors. Then, we included only conformers within 4 kcal mol⁻¹ from the lowest energy conformer, based on TPSS-D3/def2-TZVP//def2-SVP level, and aggregated the conformer properties into complex-wide properties by keeping their average, minimum and maximum values. Finally, for highly correlated descriptors with Pearson correlation coefficients exceeding 0.9, we included only one representative descriptor. We reduced the descriptor space further by only considering electronic descriptors at TPSS-D3/def2-TZVP level with COSMO. Further details on the pruning procedure are provided in the SI.

Next, we applied a brute-force feature selection approach whereby we evaluated the performance of approximately 3.2 million linear regression models predicting yield individually for each condition based on all possible combinations up to two descriptors. Each model's efficacy was assessed through both fitting (i.e., performance on the training set) and in Leave One Out Cross Validation (LOOCV).⁷⁰ To account for potential nonlinear relationships, we expanded the search space to include squared terms of each descriptor. The best-performing descriptor set for each condition was selected based on the lowest mean absolute errors (MAE) in LOOCV and referred later as “condition-specific” descriptors. Pursuing our goal to identify descriptors with general applicability across all reaction conditions, we ranked all descriptor sets by the median of the MAEs for the seven conditions obtained in leave-one-out cross-validation. The set of descriptors exhibiting the lowest median MAE is referred below as “condition-agnostic” descriptors (see SI Tables S2–S5). As mentioned earlier, we did not train a unified model. The models below are based on data from specific conditions. To simplify terminology, ‘conditions-agnostic models’ will refer to those using the same catalyst features across conditions, while ‘condition-specific models’ will denote models where features vary with reaction conditions.

Model development and performance

The modeling phase followed a standardized procedure in which linear regression models using Ridge regularization were trained on subsets of up to 16 catalysts. Yield values were normalized to approximate a Gaussian distribution prior to training (see SI for details). The alpha parameter was optimized through LOOCV. Once the alpha value was established, another LOOCV round was performed to compute performance metrics during cross-validation, including R² score and MAE. The final model was then retrained on the 16 catalysts of the training set and used to predict the yield for the three catalysts in the external test set. Only the descriptors that were chosen during feature selection were included as input.

An additional goal of our investigation was to understand the impact of catalyst featurization and selection on the final model performance. For this purpose, we performed a systematic comparison of training and test set performance when catalysts were represented using OHE, ECFP, condition-specific and condition-agnostic DFT descriptors. As control, we also added “random-selection” as descriptors obtained from brute-force selection of random numbers.

For every model, we calculated the mean absolute error in fitting (TrainMAE), in LOOCV (LOOMAE), and in predicting the yield for three catalysts not included in training (TestMAE).

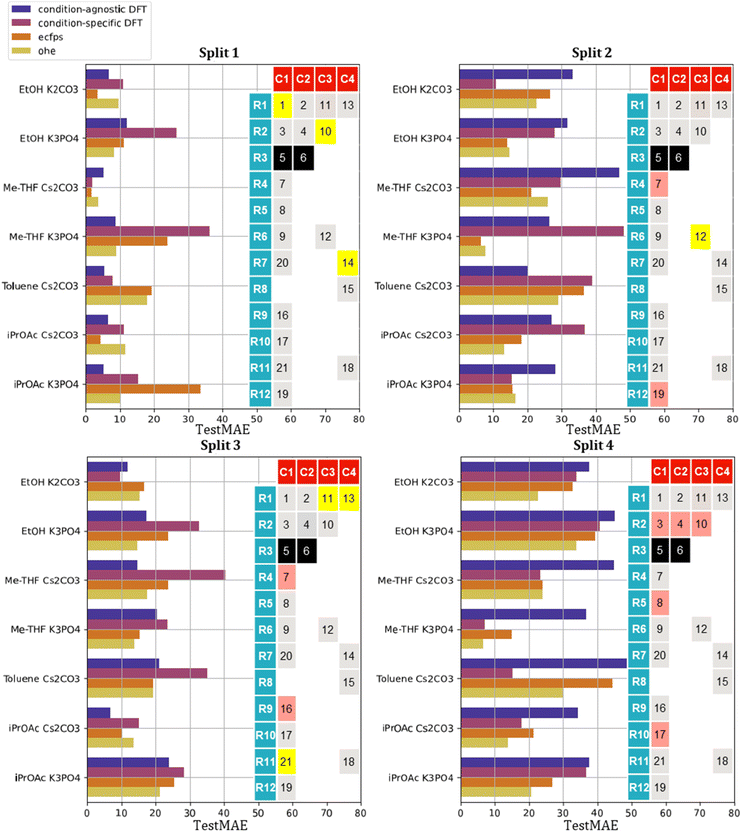
The TestMAE results across all conditions are summarized in Fig. 4. Remarkably, condition-agnostic models (average TestMAE of 7%) outperform condition-specific models (average TestMAE of 16%) and those built with ECFP (average TestMAE of 14%) and OHE (average TestMAE of 10%). Clearly, the chemical information incorporated in all models significantly improves the accuracy compared to models built on “random” descriptors (average TestMAE of 38%). Notably, the best models achieved TestMAEs close to 6%, which aligns well with the expected experimental error of 5%, representing the modeling goal. This estimation was based on replicates conducted after the removal of outliers (see SI for further details).

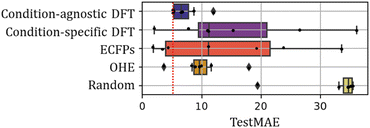Fig. 4 Comparison of test set outcomes using different set of features. Vertical dotted red line represents the expected experimental error calculated as mean absolute difference between replicates.

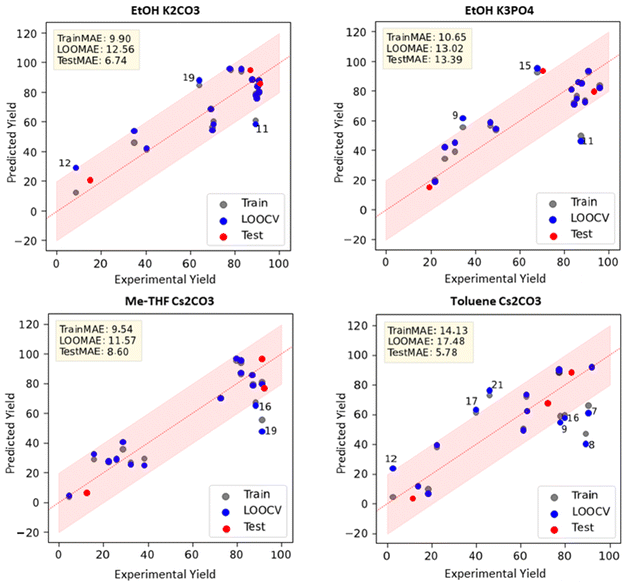
While one of our study's objectives was to explore the existence of condition-agnostic descriptors, we did not anticipate that these descriptors would outperform those specifically chosen for individual reaction conditions. A common approach to visualize the performance of ML models is to plot predicted yields against experimental yields (parity plot). In Fig. 5, we present the results from four condition-agnostic models for the solvent-base combinations of EtOH/K₂CO₃, EtOH/K₃PO₄, MeTHF/Cs₂CO₃, and toluene/Cs₂CO₃ (for results across all conditions, see SI, Fig. S22). Although we were satisfied with the visual representation of our models, we felt it necessary to further test our model's robustness.

Fig. 5 Selected examples of linear regression models based on condition-agnostic descriptors.

We investigated whether the nature of the two chosen condition-agnostic descriptors could provide insight into their exceptional performance. The first descriptor is the percentage of buried volume (% V_bur) of the carbene carbon in the free NHC ligand with a radius of 4 Å. Its coefficient in our regressions is consistently positive, indicating that bulkier ligands are associated with higher yields. Notably, while % V_bur is well-documented in the literature,^71,72 it is typically calculated for metal-NHC complexes with the metal at the center of the sphere rather than the carbene carbon. Although the latter descriptor was present in our feature library, % V_bur calculated on C2 atom of the free ligand was chosen by the brute-force approach.

The second descriptor is the anisotropy derived from the electronic quadrupole moment of the trans-[Pd(NHC)(DMS)Cl₂] complexes, calculated at the TPSS-D3/def2-TZVP//def2-SVP level with COSMO, later referred to simply as anisotropy. Its coefficient is consistently negative, suggesting that higher values lead to lower yields. Although anisotropy is a challenging descriptor to interpret in catalysis due to its global nature, it has been referenced to explain some aspects of catalytic activity.⁷³ Interestingly, it does not show strong correlations with any other descriptors, which may indicate its potential as a unique descriptor for representing electrostatic interactions of relevance for catalysis.⁷⁴ In any case, the examination of these descriptors did not provide significant insights into the performance of the models built upon them.

We discovered that these two condition-agnostic descriptors allow for a clear separation between the cores and R-groups (see SI Fig. S28). Notably, higher anisotropy values are observed for Core 3 (median equal to 60) and R6 (median equal to 57), consistent with the poor catalytic activity of Pd-12.

Lower percentages of buried volume are associated with R2 (median equal to 52%), R3 (median equal to 51%), and Core 2 (median equal to 52%), correlating well with the lower yields obtained with Pd-4 and Pd-6. Conversely, catalysts containing Core 4 such as Pd-18 and Pd-14 – typically exhibiting higher yields on average – are distinguished by a notably low anisotropy value (median equal to 21). The high correlation between cores and R-groups and the two condition-agnostic descriptors explains very well the strong performance of models based on simple OHE (Fig. 4). It is important to note that OHE-based representations of core and R structures inherently are unable to be generalized to new structures, unlike DFT-based descriptors that could guide the design of more effective catalysts.

The performance of the models within the training set proved informative. The condition-agnostic models do not outperform the condition-specific ones in LOOCV (LOOMAE of 11% for condition-specific vs. 17% for condition-agnostic). Condition-agnostic models show superior performance only in the external test set. This could stem from a reduced susceptibility to overfitting (consistent with the higher LOOMAE) and spurious correlations, especially with limited data. Since the condition-agnostic models are built from data obtained in different reaction conditions, the selected descriptor pair can explain most of the scenarios reasonably well. In contrast, the condition-specific models may be more prone to chance correlations, overfitting and noise in the experimental data. Another possible explanation for the superior performance of the condition-agnostic descriptors could also be related to the train-test split. As explained earlier, our external test set was composed of three catalysts, chosen to encompass a diverse range of core/R groups and yields. However, within our limited data set, we could not exclude that the choice of test catalysts significantly influences the TestMAE, potentially failing to accurately represent the model's predictive power and therefore we undertook to study the influence of train-test split on our model's performance.

Test set dependance

The entire workflow—from brute-force descriptor selection to model training—was repeated for three additional training-test set splits, which were chosen randomly (Fig. 6). In the second split, we kept the training-test ratio of 16 : 3 as in the original split, while in the third and fourth split we increase the number of catalysts in the test set with a training-test ratio of 14 : 5. Split 2 excluded catalysts Pd-7, Pd-12 and Pd-19, split 3 catalysts Pd-7, Pd-11, Pd-13, Pd-16 and Pd-21, and split 4 catalysts Pd-3, Pd-4, Pd-8, Pd-10 and Pd-17, from the descriptor selection and training set. As shown in Fig. 6, the out-of-domain nature of the test set (i.e. number of unseen R groups in the training set) is increasing from split 1 to split 4.

Fig. 6 Representation of the four different training-test splits with corresponding results in terms of MAE on the test set for each condition and set of features. Color code: gray – catalysts in the training set, yellow – catalysts in the test set in-domain (i.e. R wingtips present in the training set), red – catalysts in the test set out of domain (R wingtips not present in the training set) and black – excluded catalysts.

Although the optimal pair of descriptors identified by the brute-force approach is split-specific, the two condition-agnostic descriptors identified for split 1 (namely, percent buried volume at C2 and anisotropy) are frequently leading to good models in both condition-agnostic and condition-specific contexts, (see SI, Tables S2–S5). Remarkably, in the third split, they were again selected in the condition-agnostic scenario.

Changing the train-test split provides a more nuanced perspective on the performance of condition-agnostic descriptors compared to condition-specific ones. In two out of four cases (split 1 and 3), condition-agnostic models outperform condition-specific ones. We were surprised to observe that OHE models occasionally outperformed other models, particularly on the most out-of-domain test set (split 4). In split 4, some R groups were entirely excluded from the training set and therefore, OHE only encoded the cores. For this split, the OHE model predicted that the yield for a catalyst with a given core would be nothing else than the median yield of catalysts from the training set sharing the same core. Remarkably, it leads to very low MAE such as in the case of K₃PO₄/Me-THF since the core information in the training data sufficiently explains the catalyst performance. More granular descriptors, such as those based on DFT, may be less effective due to the noise introduced by descriptors that are strongly influenced by the R group and end up being selected based on chance correlations. Conversely, in the case of toluene with Cs₂CO₃, the core information is less impactful, leading to a decline in the performance of the OHE-based model and an improvement when more granular DFT-based features are considered.

Overall, we observed that the greater the out-of-domain nature of the test set, the lower the predictive performance tends to be. Higher TestMAE was observed in splits where the selected test catalysts contained R-groups were not present in the training set. Specifically, considering condition-agnostic descriptors, split 4, which included only new R-groups, had an average TestMAE of 29%; split 2, with 2 out of 3 new R-groups, had an average TestMAE of 25%; split 3, with 2 out of 5 new R-groups, had an average TestMAE of 20%; and split 1, with no new R-groups, had an average TestMAE of 12% (Fig. 6). The splits with the lowest proportions of new R-groups (split 1 and split 3), despite consisting of different catalysts in the test set, led to the condition-agnostic selection of the same two descriptors suggesting that these two descriptors carry significant information related to catalytic activity.

As a final control, we analyzed the performance of our models against a baseline model predicting the median yield of the training set as the predicted yield for all test set catalysts. The TestMAE from this dummy model was 28%, 36%, 20%, and 38% for the four splits, respectively. This comparison indicates that even with partial out-of-domain test sets, the TestMAE averages are lower when utilizing chemical information rather than just the median of training set yields.

Influence of the conformers set on the catalyst descriptors

As stated earlier, all our features were generated from a set of conformers for the Pd complexes and free ligand used in our study. We were interested in assessing how the performance of the models would be affected when using descriptors generated from one single conformer per complex. For this purpose, we predicted the yields using the two condition-agnostic descriptors (anisotropy and buried volume) from different conformers while keeping the coefficients of the regressions derived from our trained models with the train-test split 1 (Fig. 7).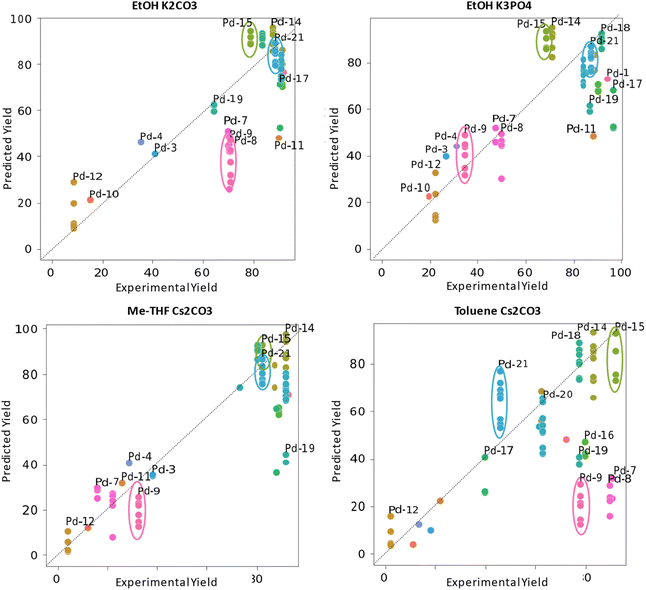

Fig. 7 Representation of the selected models in Fig. 5 with predictions of the yield for each conformer separately.

As can be seen in Fig. 7, the predicted yields can vary significantly across different conformers for a given catalyst. Notably, three complexes—Pd-9, Pd-15, and Pd-21—exhibited the most pronounced fluctuations across conditions. Pd-9 is the most sterically bulky ligand among those studied, as noted earlier. Although structurally similar to Pd-7 and Pd-8, it contains large benzhydryl groups at the para-position of the aryl rings on the wingtips. These bulky substituents experience less steric hindrance to rotation, resulting in a greater number of accessible conformers. The complexes Pd-15 and Pd-21 feature highly flexible wingtip substituents, which are predictably resulting in a larger ensemble of conformers within the chosen energy threshold (17 conformers for Pd-15, 36 conformers for Pd-21 across all structures including free ligand vs. as little as 4 for SIMes based Pd-4). Both INon and IHept are known representatives of the “bulky-yet-flexible” family of NHC ligands,⁷⁵ widely utilized in palladium-catalyzed cross-coupling reactions for their ability to adapt conformationally to facilitate various stages of the catalytic cycle. Overall, this study shows that utilizing a different selection of conformers or relying solely on a single conformer for each catalyst, would likely alter performance outcomes of our models and could lead to a distinct set of selected condition-agnostic descriptors.

Conclusions

Our study presents the first attempt to model the catalytic activity of NHC-based palladium catalysts in Suzuki–Miyaura coupling. A high-quality dataset was generated from 21 [Pd(NHC)(DMS)Cl₂] precatalysts tested under 12 different conditions using our HTE platform. We employed a brute-force approach to build linear regression models from these experimental data. An original selection strategy helped us identify two descriptors that perform best across all reaction conditions. Models based on these descriptors—the percent buried volume of the carbene carbon and catalyst anisotropy—consistently outperformed those using condition-specific descriptor pairs.

Intrigued by this finding, we conducted a systematic analysis of the models to assess their robustness, a practice that is relatively uncommon in literature and, in our view, crucial for advancing machine learning-driven catalyst development. This analysis suggested that the high performance of the condition-agnostic descriptors was due to a lower tendency to overfitting, compared to models based on the optimal set of descriptors for each individual condition. However, this finding was only partially confirmed when evaluating other training-test splits, particularly when the test set was out-of-domain.

We also explained that the good performance achieved by the models solely based on OHE could be traced back to a correlation between the DFT descriptors and OHE categorization of core and R groups. Finally, we demonstrated that the models are dependent on the ensemble of conformers underlying the descriptors for the catalysts. Restarting the descriptor selection with a different train-test split or a different conformer ensemble could yield markedly different outcomes.

In conclusion, we explored the potential of machine learning models for developing homogeneous NHC-based Pd catalysts. The study produced an intriguing model that we plan to validate with additional data. It also highlights the importance of rigorous experimental protocols for reproducible results and the need for critical assessment of model performance, even when the first obtained metrics are high. We believe that such practices are essential for advancing data-driven catalysis research.

Author contributions

All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

Supplementary information (SI): methods description, characterization data for catalysts, spectroscopic and computational data. See DOI: https://doi.org/10.1039/d5sc06138e.

Acknowledgements

Support of this work through the VLAIO grant (HBC.2022.0991) is gratefully acknowledged. The FWO is acknowledged for financial support (G0A6823N to SPN). Umicore AG are thanked for their generous gifts of materials. The authors thank L. Cavallo for helpful discussions and critical insights.

Notes and references

1. K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555.
2. A. C. Mater and M. L. Coote, J. Chem. Inf. Model., 2019, 59, 2545–2559.
3. J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872.
4. M. Meuwly, Chem. Rev., 2021, 121, 10218–10239.
5. J. P. Liles, C. Rouget-Virbel, J. L. H. Wahlman, R. Rahimoff, J. M. Crawford, A. Medlin, V. S. O'Connor, J. Li, V. A. Roytman, F. D. Toste and M. S. Sigman, Chem, 2023, 9, 1518–1537.
6. M. E. Akana, S. Tcyrulnikov, B. D. Akana-Schneider, G. P. Reyes, S. Monfette, M. S. Sigman, E. C. Hansen and D. J. Weix, J. Am. Chem. Soc., 2024, 146, 3043–3051.
7. A. M. Żurański, S. S. Gandhi and A. G. Doyle, J. Am. Chem. Soc., 2023, 145, 7898–7909.
8. J. Y. Wang, J. M. Stevens, S. K. Kariofillis, M.-J. Tom, D. L. Golden, J. Li, J. E. Tabora, M. Parasram, B. J. Shields, D. N. Primer, B. Hao, D. Del Valle, S. DiSomma, A. Furman, G. G. Zipp, S. Melnikov, J. Paulson and A. G. Doyle, Nature, 2024, 626, 1025–1033.
9. L. W. Souza, B. R. Miller, R. C. Cammarota, A. Lo, I. Lopez, Y.-S. Shiue, B. D. Bergstrom, S. N. Dishman, J. C. Fettinger, M. S. Sigman and J. T. Shaw, ACS Catal., 2024, 14, 104–115.
10. W. Beker, R. Roszak, A. Wołos, N. H. Angello, V. Rathore, M. D. Burke and B. A. Grzybowski, J. Am. Chem. Soc., 2022, 144, 4819–4827.
11. P. Raghavan, A. J. Rago, P. Verma, M. M. Hassan, G. M. Goshu, A. W. Dombrowski, A. Pandey, C. W. Coley and Y. Wang, J. Am. Chem. Soc., 2024, 146, 15070–15084.
12. K. Atz, D. F. Nippa, A. T. Müller, V. Jost, A. Anelli, M. Reutlinger, C. Kramer, R. E. Martin, U. Grether, G. Schneider and G. Wuitschik, RSC Med. Chem., 2024, 15, 2310–2321.
13. S. K. Ha, D. Kalyani, M. S. West, J. Xu, Y. Lam, T. Struble, S. Dreher, S. W. Krska, S. L. Buchwald and K. F. Jensen, J. Am. Chem. Soc., 2025, 147, 19602–19613.
14. L. van Dijk, B. C. Haas, N.-K. Lim, K. Clagg, J. J. Dotson, S. M. Treacy, K. A. Piechowicz, V. A. Roytman, H. Zhang, F. D. Toste, S. J. Miller, F. Gosselin and M. S. Sigman, J. Am. Chem. Soc., 2023, 145, 20959–20967.
15. N. P. Romer, D. S. Min, J. Y. Wang, R. C. Walroth, K. A. Mack, L. E. Sirois, F. Gosselin, D. Zell, A. G. Doyle and M. S. Sigman, ACS Catal., 2024, 14, 4699–4708.
16. Z. Fu, X. Li, Z. Wang, Z. Li, X. Liu, X. Wu, J. Zhao, X. Ding, X. Wan, F. Zhong, D. Wang, X. Luo, K. Chen, H. Liu, J. Wang, H. Jiang and M. Zheng, Org. Chem. Front., 2020, 7, 2269–2277.
17. N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457–2483.
18. A. Suzuki, Angew. Chem., Int. Ed., 2011, 50, 6722–6737.
19. I. P. Beletskaya, F. Alonso and V. Tyurin, Coord. Chem. Rev., 2019, 385, 137–173.
20. S. Kotha, K. Lahiri and D. Kashinath, Tetrahedron, 2002, 58, 9633–9695.
21. J. Magano and J. R. Dunetz, Chem. Rev., 2011, 111, 2177–2250.
22. B. S. Kadu, Catal. Sci. Technol., 2021, 11, 1186–1221.
23. J. Boström, D. G. Brown, R. J. Young and G. M. Keserü, Nat. Rev. Drug Discovery, 2018, 17, 709–727.
24. C. C. C. Johansson Seechurn, M. O. Kitching, T. J. Colacot and V. Snieckus, Angew. Chem., Int. Ed., 2012, 51, 5062–5085.
25. A. Biffis, P. Centomo, A. Del Zotto and M. Zecca, Chem. Rev., 2018, 118, 2249–2295.
26. R. Martin and S. L. Buchwald, Acc. Chem. Res., 2008, 41, 1461–1473.
27. C. C. C. Johansson Seechurn, H. Li and T. J. Colacot, in Catalysis Series, ed. T. Colacot, Royal Society of Chemistry, Cambridge, 2014, pp. 91–138.
28. G. C. Fortman and S. P. Nolan, Chem. Soc. Rev., 2011, 40, 5151.
29. N-heterocyclic Carbenes in Transition Metal Catalysis and Organocatalysis, ed. C. S. J. Cazin, Springer, Dordrecht, New York, 2011.
30. Homogeneous Catalysis with Metal Phosphine Complexes, ed. L. H. Pignolet, Springer US, Boston, MA, 1983.
31. J. F. Hartwig, Organotransition Metal Chemistry: from Bonding to Catalysis, University Science Books, Sausalito, Calif, 2010.
32. V. Iaroshenko, Organophosphorus Chemistry: from Molecules to Applications, Wiley-VCH, Weinheim, 2019.
33. N-Heterocyclic Carbenes in Synthesis, ed. S. P. Nolan, Wiley-VCH; John Wiley [distributor], Weinheim, Chichester, 2006.
34. N-heterocyclic Carbenes: Effective Tools for Organometallic Synthesis, ed. S. P. Nolan, WILEY-VCH, Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014.
35. Science of Synthesis: N-Heterocyclic Carbenes in Catalytic Organic Synthesis, ed. S. Nolan and C. Cazin, Thieme, Stuttgart, 1. Auflage., 2017, vol. 1.
36. S. H. Newman-Stonebraker, S. R. Smith, J. E. Borowski, E. Peters, T. Gensch, H. C. Johnson, M. S. Sigman and A. G. Doyle, Science, 2021, 374, 301–308.
37. N. Fey, M. F. Haddow, J. N. Harvey, C. L. McMullin and A. G. Orpen, Dalton Trans., 2009, 8183.
38. G. Takasao, B. Maity, S. Dutta, R. Kancherla, M. Rueping and L. Cavallo, ACS Catal., 2025, 15, 5915–5927.
39. Y. Liu, V. A. Voloshkin, T. Scattolin, M. Peng, K. Van Hecke, S. P. Nolan and C. S. J. Cazin, Eur. J. Org Chem., 2022, 2022, e202200309.
40. D. G. Gusev, Organometallics, 2009, 28, 6458–6461.
41. F. Wilcoxon, Biom. Bull., 1945, 1, 80.
42. R. F. Woolson, in Wiley Encyclopedia of Clinical Trials, ed. R. B. D'Agostino, L. Sullivan and J. Massaro, Wiley, 1st edn, 2008, pp. 1–3.
43. N. Qafisheh, S. Mukhopadhyay, A. V. Joshi, Y. Sasson, G.-K. Chuah and S. Jaenicke, Ind. Eng. Chem. Res., 2007, 46, 3016–3023.
44. D. M. Barnes, S. Shekhar, T. B. Dunn, J. H. Barkalow, V. S. Chan, T. S. Franczyk, A. R. Haight, J. E. Hengeveld, L. Kolaczkowski, B. J. Kotecki, G. Liang, J. C. Marek, M. A. McLaughlin, D. K. Montavon and J. J. Napier, J. Org. Chem., 2019, 84, 4873–4892.
45. T. Zhou, S. Ma, F. Nahra, A. M. C. Obled, A. Poater, L. Cavallo, C. S. J. Cazin, S. P. Nolan and M. Szostak, iScience, 2020, 23, 101377.
46. E. A. B. Kantchev, C. J. O'Brien and M. G. Organ, Angew. Chem., Int. Ed., 2007, 46, 2768–2813.
47. G. Utecht-Jarzyńska, S. Jarzyński, M. M. Rahman, G. Meng, R. Lalancette, R. Szostak and M. Szostak, Organometallics, 2024, 43, 2305–2313.
48. D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754.
49. Y. Guan, V. M. Ingman, B. J. Rooks and S. E. Wheeler, J. Chem. Theory Comput., 2018, 14, 5249–5261.
50. V. M. Ingman, A. J. Schaefer, L. R. Andreola and S. E. Wheeler, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1510.
51. S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673.
52. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
53. S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862.
54. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493.
55. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
56. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
57. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762.
58. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
59. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
60. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
61. A. Schäfer, A. Klamt, D. Sattel, J. C. W. Lohrenz and F. Eckert, Phys. Chem. Chem. Phys., 2000, 2, 2187–2193.
62. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
63. A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085.
64. F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385.
65. BIOVIA COSMOtherm, Release, Dassault Systèmes, 2020, http://www.3ds.com.
66. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. Van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
67. G. Luchini, T. Patterson and R. Paton, patonlab/DBSTEP (version 1.1.0), Zenodo, 2023.
68. S. Yu, J. C. McWilliams, O. Dirat, K. L. Dobo, A. S. Kalgutkar, M. O. Kenyon, M. T. Martin, E. D. Watt and M. Schuler, Chem. Res. Toxicol., 2024, 37, 1382–1393.
69. L. Morán-González and F. Maseras, Artif. Intell. Chem., 2024, 2, 100061.
70. T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning, Springer New York, New York, NY, 2009.
71. A. C. Hillier, W. J. Sommer, B. S. Yong, J. L. Petersen, L. Cavallo and S. P. Nolan, Organometallics, 2003, 22, 4322–4326.
72. H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861.
73. P. Krzesiński, C. Dinoi, I. Del Rosal, L. Vendier, P. Kumandin, S. Bastin, V. César, A. Kajetanowicz and K. Grela, ChemRxiv, 2024, preprint,  DOI:10.26434/chemrxiv-2023-b4btj-v2.
74. M. C. Holland, J. B. Metternich, C. Mück-Lichtenfeld and R. Gilmour, Chem. Commun., 2015, 51, 5322–5325.
75. S. Meiries, G. Le Duc, A. Chartoire, A. Collado, K. Speck, K. S. A. Arachchige, A. M. Z. Slawin and S. P. Nolan, Chem. Eur. J., 2013, 19, 17358–17368.

---

Footnote

† Contributed equally.

---