Open Access Article
Open Access ArticleReactor and kinetic study advances for highly acidic solvolysis-mediated Friedel–Crafts reaction
Colin
Bailey
 a,
Connor
Donlan
a,
Connor
Donlan
 b,
Matthew
Glace
b,
Matthew
Glace
 a,
Gabrielle
Broussard
a,
Someshwar
Nagamalla
a,
Gabrielle
Broussard
a,
Someshwar
Nagamalla
 a,
Lane B.
Carasik
a,
Lane B.
Carasik
 b and
Thomas D.
Roper
b and
Thomas D.
Roper
 *a
*a
aDepartment of Chemical and Life Science Engineering, Virginia Commonwealth University, Richmond, VA, USA. E-mail: tdroper@vcu.edu
bDepartment of Mechanical and Nuclear Engineering, Virginia Commonwealth University, Richmond, VA, USA
First published on 5th December 2025
Abstract
This study presents a kinetic model that simulates the consumption of 4-hydroxybenzoic acid (4-HBA), the formation of di-isopropyl benzoic acid (DIPBA) via a Friedel–Crafts alkylation reaction, and the generation of key impurities. The model provides valuable insights into reaction dynamics by capturing the intricate interplay between reaction kinetics and competing pathways. In addition, we introduce a cost-effective, scalable reactor design that overcomes the limitations of traditional laboratory-based reactor systems. The reactor system enhances safety, efficiency, and adaptability, making it ideal for large-scale, highly acidic reactions in laboratory settings. Together, this work underscores the insights and limitations of conventional kinetic modeling for solvolysis-mediated Friedel–Crafts reactions and lays the foundation for more efficient and innovative approaches to chemical process development.
Introduction
Within the broad field of reaction kinetics, solvolysis reactions hold a significant place due to their unique characteristics and practical importance.1–3 For example, the hydrolysis of tert-butyl chloride in water is a prototypical SN1 solvolysis reaction used to investigate carbocation stability and solvent effects on reaction rates.4–6 In industrial settings, methanolysis of triglycerides plays a central role in biodiesel production, where methanol acts as both solvent and nucleophile.7,8 Similarly, acid-catalyzed solvolysis of alkyl sulfonates or halides in isopropanol or acetic acid is crucial for generating esters or alkylated intermediates in pharmaceutical synthesis.9–11 These reactions not only serve as foundational models in mechanistic organic chemistry but also have practical value in energy, pharmaceutical, and materials applications.In the solvolysis reaction, the solvent serves as both the reaction medium and a reactant, participating directly in the chemical transformation. This dual role introduces complexities in accurately determining reaction kinetics, as traditional models often assume a constant solvent concentration.12–19 Understanding the kinetics of solvolysis-mediated reactions is particularly important when the reaction involves complex networks with multiple competing pathways and intermediates. These systems often exhibit challenges such as overlapping reaction timescales, solvent-reactant interactions, and the formation of numerous side products, making them difficult to model accurately. Such complexities are exemplified in the synthesis of a propofol precursor, where the dual role of the solvent, isopropyl alcohol (IPA), and the presence of sulfuric acid as a catalyst create a reaction environment rich in side reactions and intermediate species during the subsequent Friedel–Crafts alkylation.20–22 Investigating this system's kinetic behavior provides valuable insights into optimizing yield and selectivity while addressing the broader challenges associated with solvolysis reaction kinetics.
Fig. 1 highlights the six major reaction components selected for our kinetic model, chosen for their pivotal roles in the reaction network: the product, DIPBA (1), residual remaining 4-HBA (2), a sulfonated impurity (3), the mono-alkylated (4), constitute the core species of interest; 4-HBA ester (5) participates in a major competing pathway that influences DIPBA formation; and the DIPBA ester (6) is the predominant byproduct formed after DIPBA production. The mono-alkylated ester (7) originates from the 4-HBA ester (5) or mono-alkylated (4) before subsequently converting into the DIPBA ester (6). Because DIPBA (1) itself can undergo esterification under the reaction conditions, inclusion of the mono-alkylated ester (7) as a precursor was essential for accurate model fitting.
 | ||
| Fig. 1 Reaction scheme of compounds used for kinetic modeling in the solvent-mediated Friedel–Crafts reaction. | ||
Moreover, conducting experiments with highly corrosive Friedel–Crafts reactions necessitates specialized equipment capable of withstanding harsh chemical environments. Flow chemistry was selected for this study due to its inherent advantages in handling such demanding reaction conditions.23,24 Unlike traditional batch processes, flow systems provide precise control over reaction parameters such as temperature, pressure, and residence time, enabling safer and more consistent operation.25 The enhanced heat and mass transfer in flow reactors also improves reaction efficiency and selectivity, making it an ideal choice for optimizing complex solvolysis reactions such as the alkylation of 4-HBA (2).26 This study utilizes flow chemistry to ensure a safer, more controlled, and scalable approach to studying and modeling the reaction system.
We began by collecting kinetic data in small-scale flow reactors, systematically varying residence times, temperatures, and reactant concentrations to explore the reaction under solubility-limited conditions. Insights from these experiments informed the design and construction of a larger-scale continuous reactor system, engineered to replicate pilot-scale conditions while maintaining safety and consistent mass flow. In parallel, we developed an integrated computational framework featuring stiff-ODE solvers for identifying reaction kinetics and plug-flow reactor models that account for advection, axial dispersion, and transient intermediates. Together, these efforts established a unified platform for fitting, simulating, and validating reaction kinetics, ultimately enabling a direct comparison between model predictions and experimental outcomes in a scalable reactor environment.
Materials
The chemicals used for this project were 4-hydroxybenzoic acid (99%) from Sigma-Aldrich. Concentrated sulfuric acid (ACS reagent grade) from Sigma-Aldrich. Acetonitrile (HPLC grade) from Sigma-Aldrich. IPA (reagent grade) from Fischer Scientific. Water was from an in-house Milli-Q system.Methods
Small-scale reactor development
To develop a kinetic model capable of predicting our complex solvolysis reaction in a large-scale continuous reactor, we first collected datasets from two small-scale flow systems engineered to probe solubility-limited conditions at various substrate loadings. In reactor system 1, we held 4-HBA (2) at 0.9 M. We introduced an in-line dilution stream to prevent precipitation during short, 3 and 5 minute residence times, allowing us to capture rapid reaction kinetics without clogging. In reactor system 2, we increased the feed concentration to 1.8 M and extended the minimum residence time to 10 minutes to maintain solubility, thereby characterizing reaction progress under higher concentration conditions. Together, these experiments provided the concentration and time-resolved data needed to fit our kinetic equations, and ultimately enable scale-up predictions for a new large-scale reactor.Perfluoroalkoxy (PFA) tubing was used in both of the flow reactor systems, each consisting of a 10 mL main reaction coil and two to three separate 5 mL preheating loops dedicated to individual feed streams: 4-HBA (2), sulfuric acid, and an optional dilution stream. The starting material stock bottles (1, 2 and 3 in Fig. 2 above) were preheated to 45 °C to maintain solubility throughout experiments. Eldex pumps were used for the precise delivery of the organic substrate and diluent streams, while a PTFE Smoothflow pump (Tacmina) accurately pumped concentrated sulfuric acid. Reaction conditions included temperatures maintained between 70 °C and 90 °C to avoid precipitation and clogging, with experiments typically lasting up to 20 minutes and aliquots sampled at intervals ranging from 3 to 20 minute residence times. Concentrations of 4-HBA (2) were systematically varied between 0.45 M and 1.8 M, with a focus around 0.9 M to optimize kinetic data collection. These experiments produced comprehensive, high-quality datasets, providing the essential inputs for accurate parameterization, and scaling of the kinetic model.
 | ||
| Fig. 2 Process flow diagram of reactors 1 (blue) and 2 (red) for the solvolysis-mediated Friedel–Crafts reactions. | ||
Reactor 1, which was equipped with a dilution stream to manage solubility issues, was also operated without the dilution stream under otherwise identical conditions to assess the dilution impact. Both sets of experiments were conducted within the same reactor setup, and the comparative results are provided in the SI in Fig. S3. The results demonstrated less than ∼4% change in the impurity patterns, indicating that the inclusion of the dilution stream did not significantly impact the reaction outcomes.
To ensure accurate and reproducible kinetic data, each experiment was conducted under continuous flow conditions, sampling only after at least three full reactor residence times had elapsed. This procedure allowed the reaction system to reach a steady state, effectively minimizing transient fluctuations and ensuring that the collected samples represented stable reaction conditions. The sample dilution procedure is outlined in the SI section; adherence to this rigorous sampling practice reinforced confidence in the reproducibility and reliability of the generated datasets, ultimately enhancing the robustness of the kinetic modeling process.
After each experiment, collected samples were diluted to approximately 1 mg mL−1 to align analyte concentrations with the optimal detection range of our high-performance liquid chromatography (HPLC) system. This careful dilution step ensured precise and accurate quantification of the desired reaction products as well as associated impurities. Detailed experimental data and comprehensive HPLC method parameters are provided in the SI section.
Large-scale reactor development
The reactor is based on a shell and tube heat exchanger. The shell side of the reactor was connected to a Huber Unistat 405 to maintain a constant temperature and circulate heated mineral oil up to 100 °C. The shell side consisted of an outer stainless-steel shell with a threaded rod welded in the center, a gasket, and a cap that held the tube support structure. The tube support structure was designed to accommodate different tube sizes and materials based on the desired reactor volumes and reagents. The tubing used in this reaction included 30 mL of 1/8 inch outer diameter PFA tubing wound into a helical coil around the support structure in the cap. The reagent inlet side was connected to a Tacmina and Eldex pump that converged at the T-junction before entering the reactor. The final design and manufactured reactor are shown in Fig. 3.This reactor was designed to be cost-effective while maintaining adaptability for a range of reaction conditions. Its modular design allows for rapid adjustments to tubing configurations, making it suitable for diverse experimental needs. Additionally, the use of PFA tubing and stainless-steel components ensures chemical compatibility and resistance to corrosion, particularly under highly acidic conditions. This adaptability is crucial for scaling up reactions, as it enables efficient testing of different parameters without the need for costly redesigns. The combination of simplicity, safety, and versatility makes this reactor an ideal tool for advancing chemical process development in academic settings (Fig. 4).
 | ||
| Fig. 4 PFD of reactor 3 utilizing shell-in-tube heat exchanger with PFA tubing at approximately 30 mL volume, heated by Huber Unistat 405. | ||
To evaluate the influence of temperature-dependent physical properties on flow characteristics, the Reynolds and Dean numbers were calculated using literature-based viscosity and density values for the 50 wt% sulfuric-acid/isopropanol mixture at 70–90 °C (Table 1).27 As temperature increases, the viscosity decreases from 1.5 mPa s to 0.9 mPa s, leading to a modest rise in Reynolds number from approximately 26 to 43 and in Dean number28 from 6 to 9. These values remain well within the laminar regime and indicate only weak secondary circulation.
 | (1) |
| Temperature (°C) | Viscosity (mPa s) | Density (g cm−1) | Reynolds number | Dean number |
|---|---|---|---|---|
| 70 | 1.5 | 1.35 | 25.9 | 5.7 |
| 80 | 1.2 | 1.35 | 32.2 | 7.0 |
| 90 | 0.9 | 1.33 | 42.6 | 9.7 |
The reactor system described above was utilized to compare the outcomes of large-scale DIPBA (1) production with the simulations obtained from the kinetic simulation model. This comparison allowed for the validation of the simulation's accuracy in capturing the reaction dynamics under experimental conditions. By integrating the simulated kinetic results with the observed large-scale production data, key insights were gained into the reactor's performance, including product yield, impurity formation, and overall reaction efficiency.
Code development: kinetic parameter evaluation
Python was selected as the programming language for its ease of use, extensive scientific libraries, and adaptability to complex and evolving reaction networks.29–35 While multiple candidate reaction schemes were initially explored, iterative refinement of the model ultimately identified a reaction network that provided the closest alignment with the experimental data. This model included the 7 compounds depicted in Fig. 1. The experimental data obtained from small-scale reactor systems 1 and 2 were used in conjunction with the kinetic parameter evaluation code to determine the Arrhenius parameters presented in the Results and discussion section.The kinetic modeling code estimates Arrhenius parameters (pre-exponential factors and activation energies) by fitting experimental concentration-time data to a set of coupled ordinary differential equations (ODEs). The ODEs explicitly include the carbocation intermediate ([C3H7]+), whose formation rate constant (k_form), dependent on IPA concentration, serves as an adjustable parameter to optimize the model fit. Numerical integration (solve_ivp) calculates predicted concentrations, and parameter estimation (least_squares) minimizes residuals between predictions and experimental data. The final output provides optimized kinetic parameters, along with R2 and normalized root mean square error (NRMSE) metrics to evaluate the overall quality and accuracy of the kinetic model.
All compounds found in Fig. 1 above were included in the system of ODEs and fit using the parameter estimation methods described above. In addition, compound 7 was introduced as a theoretical intermediate, representing the presumed mono-alkylated ester (7) formed between the 4-HBA ester (5) and the DIPBA ester (6). Since no corresponding peak was identified by HPLC analysis, its retention time and chromatographic behavior remain unknown. Thus, mono-alkylated ester (7) functions solely as a modeling placeholder, enabling the kinetic model to include this plausible intermediate and maintain mass balance within the proposed reaction pathway, despite the lack of direct experimental confirmation. In later sections, the DIPBA ester (6) will be used as a ‘mass sink’ in the simulation, serving as a catch-all for impurities not explicitly modeled.
The kinetic model implemented in this paper was selected through iterative trial and error, during which several alternative reaction networks were evaluated for predictive performance. The final model was chosen based on its ability to most accurately reproduce experimental trends while maintaining reasonable fidelity. Two representative alternative models that were considered, but ultimately not selected, are provided in the SI for comparison.
The reaction network implemented in the simulation code consists of eight reactions that represent the key transformation pathways leading to DIPBA (1) and its associated impurities. The system assumes a pseudo-steady-state concentration for the carbocation intermediate ([C3H7]+), modeled as a function of isopropyl alcohol concentration and a formation rate constant (k_form). The network includes two parallel initial reactions of 4-HBA (2) with the carbocation to form either the 4-HBA ester (5) or the mono-alkylated (4). The 4-HBA ester (5) can undergo further alkylation to form the mono-alkylated ester (7), which then reacts again to form the DIPBA ester (6). In the main product-forming pathway, the mono-alkylated (4) reacts with the carbocation to form DIPBA (1), while a competing side reaction leads to sulfonated impurity (3) formation. Finally, DIPBA (1) itself can undergo reversible esterification to form DIPBA ester (6). This network allows the model to account for both the desired product pathway and multiple impurity-forming routes. The modeled species collectively represent over 95% of the total measured mass across all experiments, confirming adequate mass closure within the system.
| [C3H7]+ss = kform × IPAc | (2) |
| 4HBA (2) + [C3H7]+ → 4HBA Ester (5) | (3) |
| 4HBA (2) + [C3H7]+ → Mono Alkylated (4) | (4) |
| 4HBA Ester (5) + [C3H7]+ → Mono Ester (7) | (5) |
| Mono Alkylated Ester (7) + [C3H7]+ → DIPBA Ester (6) | (6) |
| Mono Alkylated (4) + [C3H7]+ → DIPBA (1) | (7) |
| Mono Alkylated (4) → Sulfonated Impurity (3) | (8) |
| DIPBA (1) + [C3H7]+ ⇄ DIPBA Ester (6) | (9) |
 | (10) |
 | (11) |
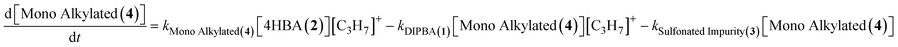 | (12) |
 | (13) |
 | (14) |
 | (15) |
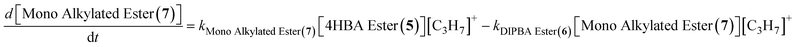 | (16) |
| Compound | R 2 | Normalized root mean square error (NRMSE) |
|---|---|---|
| 4-HBA (2) | 0.752 | 0.085 |
| DIPBA (1) | 0.714 | 0.121 |
| Sulfonated impurity (3) | 0.273 | 0.187 |
| 4-HBA ester (5) | −0.111 | 0.205 |
| DIPBA ester (6) | −0.719 | 0.311 |
| Mono-alkylated (4) | −1.007 | 0.299 |
Code development: reactor simulation
The reactor simulation code was developed in Python, capitalizing again on its robust scientific libraries (NumPy, SciPy, and Pandas) for efficient numerical integration, matrix operations, and data handling. Python has also proven valuable in conducting computational fluid dynamics (CFD) simulations of chemical reactors, offering flexibility for integrating numerical solvers with custom reactor geometries and flow conditions.36–41 Python's readability, modular design, and visualization capabilities enabled streamlined development and thorough validation of our reactor simulation framework. The reactor simulation code was developed to represent the large-scale reactor described in the preceding sections, capturing its key design features and operating conditions to enable direct comparison between simulated and experimental performance.Within this framework, each species was modeled by a dedicated mass-balance equation, parameterized using the Arrhenius constants determined from the kinetic fitting procedure. As an illustrative example, the equations describing concentration profiles of 4-HBA (2) and mono-alkylated (4) within the discretized plug-flow reactor incorporate advective transport (due to flow velocity, u), axial diffusion (1 × 10−5 m s−1) between spatial points (Δx), reaction kinetics, and associated source terms. Specifically, the mono-alkylated (4) equation accounts for the formation from 4-HBA (2) and its subsequent consumption via two competing reactions. The equation for 4-HBA (2) similarly captures its depletion through the formation of the 4-HBA ester (5) and mono-alkylated (4). Together, these equations form a comprehensive numerical approach for predicting dynamic concentration distributions, seamlessly integrating physical transport phenomena with chemical reaction kinetics.
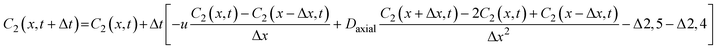 | (17) |
 | (18) |
| Δ2, 5 = k4HBA Ester (5)[4HBA (2)][C3H7]+, Δ2, 4 = kMono Alkylated (4)[4HBA (2)][C3H7]+ | (19) |
| Δ4, 1 = kDIPBA (1)[Mono Alkylated (4)][C3H7]+, Δ4, 3 = kSulfonated Impurity (3)[Mono Alkylated (4)] | (20) |
The resulting coupled ODE system presented numerical stiffness due to a wide range of reaction timescales, combining rapid carbocation-driven reactions with comparatively slower bimolecular steps. To manage this stiffness, we employed an implicit solver specifically designed for such challenging problems. Solver accuracy and stability depend heavily on the appropriate selection of time-step size (dt = 0.01 s): excessively large steps result in numerical instability, whereas excessively small ones cause computational inefficiency. Through careful optimization, we established a stable and computationally efficient time-step range, enabling accurate modeling of both rapid intermediate dynamics and slower product formation across reactor segments. Although this step required substantial tuning, it produced a reliable simulation framework for assessing reactor performance and steady-state behavior under realistic reaction conditions.
Results and discussion
In the results section below, we demonstrate how our simulation framework integrates kinetic data from small-scale reactor experiments to predict concentration profiles, which we subsequently validate against data from reactor 3.Applying the kinetic parameter evaluation code to the reactor 1 and 2 data allowed us to extract Arrhenius parameters for each reaction step. Fitting performance was strong for key compounds, including 4-HBA (2), the sulfonated impurity (3), and DIPBA (1), as reflected in favorable R2 values. However, transient intermediates, mono-alkylated (4) and 4-HBA ester (5), exhibited weaker fits due to their rapid formation and subsequent consumption, making their concentrations more difficult to model accurately. Similarly, the DIPBA ester (6) presented challenges due to its lower abundance and indirect formation pathway. Despite these limitations, the derived Arrhenius constants provided a sufficient basis for reactor simulation.
Negative R2 values arise from applying a linear statistical metric to a non-linear kinetic model governed by time-coupled ODEs. In our approach, residuals, defined as the difference between experimental and predicted concentrations, are squared and minimized using a least squares optimizer, which can yield negative R2 even when the model captures key reaction trends.
Despite limitations in fitting certain intermediates due to their transient nature and rapid consumption under strongly acidic conditions, the Arrhenius parameters obtained from the fitting process remain valuable. These discrepancies primarily arise because mono-alkylated (4) and 4-HBA ester (5) exist only briefly within the residence-time window, making them difficult to capture experimentally and challenging to resolve numerically. Additionally, these intermediates may participate in minor reversible or parallel reactions that are represented implicitly in the present network to preserve model stability. The parameter estimation procedure nevertheless considers the entire reaction network simultaneously, adjusting each rate constant to best reproduce the observed concentration profiles of all species.
Even when individual intermediates are poorly represented, their rate constants are indirectly constrained by the need to accurately model more stable, well-measured compounds such as 4-HBA (2) and DIPBA (1). The solver enforces mass balance and reaction connectivity, allowing it to back-calculate the intermediate behavior while maintaining the system's overall dynamics. As a result, the final parameters provide a consistent description of the dominant pathways.
The normalized root mean square error (NRMSE) values presented in the table provide a scale-independent measure of the model's predictive accuracy for each compound. Lower NRMSE values indicate closer agreement between the model and experimental data. For instance, 4-HBA (2) and DIPBA (1) exhibit low NRMSE values of 0.085 and 0.121, respectively, suggesting strong model performance for these key species. The sulfonated impurity (3) shows moderate predictive accuracy with an NRMSE of 0.187. In contrast, higher NRMSE values for the mono-alkylated (4), 4-HBA ester (5), and DIPBA ester (6) – 0.299, 0.205, and 0.311, respectively, highlight greater discrepancies, which may stem from the transient or low-concentration nature of these intermediates and by-products. These elevated errors underscore the challenges in modeling less stable or indirectly measured species and suggest areas where additional experimental data or refinement of the reaction network could improve predictive fidelity.
In Table 3 above, a few of the estimated Arrhenius parameters (A, Ea) exhibit wide or even non-physical confidence intervals, particularly for the mono-alkylated pathway. This results from strong collinearity between A and Ea, which occurs when both are simultaneously regressed from temperature data. In essence, different combinations of A and Ea can produce nearly identical rate constants at the experimental temperatures, leading to structural non-identifiability. Despite this, the corresponding rate constants k(T) at the studied temperatures are well constrained, and the model reproduces the observed concentration–time profiles of 4-HBA (2), DIPBA (1), and sulfonated impurity (3) with reasonable accuracy. We therefore report the full A and Ea confidence intervals for transparency.
| Reaction parameter | Arrhenius constant(A: L mol−1 s−1) | Activation energy(Ea: J mol−1) |
|---|---|---|
| k 4HBA ester [4HBA][C3H7]+ | 2.11 × 107 (95% CI: 1.88 × 107–2.34 × 107) | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 574.77 (95% CI: 35 574.77 (95% CI: 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 595.28–69 595.28–69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 554.26) 554.26) |
| k Mono alkylated [4HBA][C3H7]+ | 6.54 × 104 (95% CI: −1.83 × 107–1.84 × 107) | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818.67 (95% CI: −7.67 × 105–8.41 × 105) 818.67 (95% CI: −7.67 × 105–8.41 × 105) |
| k Mono alkylated ester [4HBA ester][C3H7]+ | 2.05 × 107 (95% CI: 1.82× 107–2.28 × 107) | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486.44 (95% CI: 29712–63 486.44 (95% CI: 29712–63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261) 261) |
| k DIPBA [mono alkylated][C3H7]+ | 3.59 × 107 (95% CI: 3.59 × 107–3.60 × 107) | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 463.55 (95% CI: −2.18 × 106–2.27 × 106) 463.55 (95% CI: −2.18 × 106–2.27 × 106) |
| k Sulfonated impurity [mono alkylated] | 1.35 × 106 (95% CI: 1.12 × 106–1.58 × 106) | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 754.73 (95% CI: 20 754.73 (95% CI: 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845–52 845–52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664) 664) |
| k DIPBA ester [DIPBA][C3H7]+ | 2.99 × 106 (95% CI: 2.64 × 106–3.34 × 106) | 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925.99 (95% CI: 33 925.99 (95% CI: 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012–66 012–66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839) 839) |
| k DIPBA ester [mono alkylated ester][C3H7]+ | 6.01 × 106 (95% CI: 5.45 × 106–6.57 × 106) | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042.22 (95% CI: 40 042.22 (95% CI: 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 125–75 125–75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960) 960) |
| k DIPBA ester, rev [DIPBA ester] | 2.35 × 107 (95% CI: 2.12 × 107–2.58 × 107) | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 716.43 (95% CI: 32 716.43 (95% CI: 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745–68 745–68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688) 688) |
Fig. 5 shows the parameter correlation matrix (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A/Ea space) quantifies interdependence among the fitted kinetic parameters. Strong correlations between ln
A/Ea space) quantifies interdependence among the fitted kinetic parameters. Strong correlations between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A and Ea within individual reactions (dark red or blue cells) reflect the well-known kinetic compensation effect arising from the limited temperature range used for parameter estimation. In contrast, correlations between different reactions remain weak, indicating that the model is numerically stable and parameters are largely independent across the reaction network. This analysis confirms that while individual Arrhenius pairs exhibit inherent coupling, the overall parameter set remains well conditioned for predictive simulation.
A and Ea within individual reactions (dark red or blue cells) reflect the well-known kinetic compensation effect arising from the limited temperature range used for parameter estimation. In contrast, correlations between different reactions remain weak, indicating that the model is numerically stable and parameters are largely independent across the reaction network. This analysis confirms that while individual Arrhenius pairs exhibit inherent coupling, the overall parameter set remains well conditioned for predictive simulation.
In Fig. 6, the correlation heatmap provides a visual summary of the linear relationships between simulated and experimental concentrations across all monitored species. Strong positive correlations, shown as darker red regions, indicate species where the model captures experimental behavior closely. For example, DIPBA (1) exhibits a high correlation, reflecting the model's ability to reproduce its concentration profile throughout the reactor. In contrast, species such as the ester byproducts display lower correlations, shown in lighter shades, suggesting that the model does not fully account for all mechanistic pathways contributing to their formation. This distinction highlights both the strengths of the current kinetic model in capturing major product trends and the limitations in describing impurity formation in detail.
The covariance heatmap was also generated to examine the degree of variability shared between simulated and experimental data. However, unlike the correlation matrix, the covariance values are highly dependent on the scale of each species and therefore provide limited interpretive value for comparing trends across compounds. As a result, the covariance heatmap did not reveal any additional mechanistic insight beyond what was observed in the correlation analysis. For completeness, it is included in the SI rather than the main text.
Chart 1 shows that overall, when comparing the model to experimental results from the 30 mL reactor developed for this project, we see several notable outcomes. The model seems to suggest that DIPBA ester (6) is formed rapidly, as is DIPBA (1), and then, towards the end of the reaction, DIPBA ester (6) begins to degrade to form DIPBA (1). The substantial overestimation observed for the DIPBA ester (6) is likely due to the structure of the simulation code, which is based on mass conservation principles. Although other impurities are not explicitly defined within the simulation, their formation is inherently accounted for through mass balance. Consequently, DIPBA ester (6) inadvertently acts as a mass sink within the simulation, absorbing discrepancies caused by these unmodeled impurities. Thus, while labeled here specifically as the DIPBA ester (6), it effectively represents a collective placeholder for all other possible impurities generated during the reaction.
 | ||
| Chart 1 Example of simulation code along reactor at T = 80 °C, τ = 15 minutes, V = 30 mL, IPA = 4.10 mol L−1, and 4-HBA (2) = 0.305 mol L−1. The final yield of DIPBA (1): 63.80%. | ||
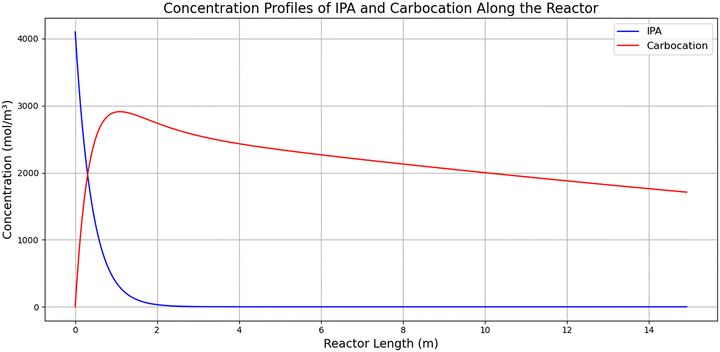
Chart 2 illustrates the generation and consumption of carbocation (C3H7+), which drives the reaction. Due to a lack of direct experimental data, a formation rate constant (k_form) was estimated to approximate the rate of carbocation formation. The carbocation formation is found by fitting k_from as a steady-state formation constant based on the downstream reactions that require the carbocation to proceed.
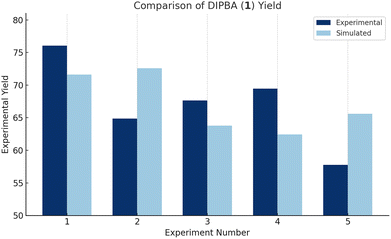
Chart 3 shows all simulated results compared to the experimental data for DIPBA (1). The comparison was carried out using five blinded experimental data points obtained from reactor 3. Across all runs, the majority of simulated yields for DIPBA (1) were within approximately 10% of the corresponding experimental values, indicating good overall agreement between the model and the experimental system. Among these, simulation 3 exhibited the closest alignment with experimental results. For this reason, simulation 3 was selected for a more detailed breakdown and discussion in the following section, as it provides the most representative case for assessing model performance.
In Table 4, the results compare experimental and simulated yields for the condition set showing the best agreement: 0.9 M 4-HBA (2), 80 °C, 15 minute residence time, and 40 equivalents of sulfuric acid. The simulation closely predicts the yield of DIPBA (1), the target product, differing by less than 4%, which reflects strong model performance. The sulfonated impurity (3) also shows good agreement, with only a 1.6% absolute difference between experimental and simulated values. The starting material, 4-HBA (2), and the 4-HBA Ester (5) were both undetectable at the end of the reaction and are accurately reflected as 0% in both datasets. For the mono-alkylated (4), the simulation underpredicts its presence slightly, likely due to its transient role in the reaction network. The DIPBA ester (6) shows a larger deviation, with the simulation predicting 30.08% compared to the experimental 5.63%. Overall, the simulation performs well for the major species of interest and highlights areas for refinement in representing secondary impurity pathways.
| Compounds | Experiment 3 | Simulation 3 |
|---|---|---|
| 4 HBA (2) | 0.00% | 0.00% |
| Sulfonated impurity (3) | 4.53% | 6.12% |
| Mono-alkylated (4) | 1.42% | 0.00% |
| 4-HBA ester (5) | 0.00% | 0.00% |
| DIPBA (1) | 67.62% | 63.80% |
| DIPBA ester (6) | 5.63% | 30.08% |
The results summarized in Table 5 illustrate varying levels of agreement between simulated predictions and experimental yields across different reaction components. The starting material, 4-HBA (2), shows close agreement with experimental data, with only a minor average deviation (0.42%) and a confidence interval that includes zero, indicating no statistically significant bias. The sulfonated impurity (3) is consistently overpredicted, as evidenced by a negative average difference and a confidence interval fully below zero, suggesting systematic model overestimation. In contrast, the mono-alkylated (4) is significantly underpredicted, with the model yielding higher values across all experiments and a confidence interval fully above zero. For the primary product, DIPBA (1), the model demonstrates strong predictive reliability, with an average error of just −0.05% and a wide confidence interval that includes zero. Given that average experimental yields are above 60%, with some runs reaching into the 70% range, a deviation within ±10% represents a relatively small margin of error. This supports the model's utility as a reliable tool for yield estimation within practical experimental variability. The DIPBA ester (6) is substantially overpredicted, with an average error of −20.26% and a confidence interval entirely below zero, likely due to the model lumping several untracked impurities into this category. Finally, the apparent perfect agreement for 4-HBA ester (5) reflects its consistent absence at the end of the reaction, rather than a mechanistic prediction. Collectively, these results highlight both the strengths of the model, particularly for DIPBA (1), and opportunities for improvement.
| Compounds | Average difference in yield | 95% confidence interval (CI) | Interpretation |
|---|---|---|---|
| a The experimental conditions chosen always showed no 4-HBA ester (5) present at the end of the reaction. Not a sign of goodness of fit from the simulation. | |||
| 4-HBA (2) | 0.42% | (−0.52%, 1.37%) | Simulation slightly underestimates but is close to experimental data |
| Sulfonated impurity (3) | −2.19% | (−2.84%, −1.53%) | Simulation consistently overestimates |
| Mono-alkylated (4) | 2.02% | (0.46%, 3.59%) | The simulation always underestimates |
| 4-HBA ester (5) | 0.00% | (0.00%, 0.00%) | Simulation and experimental data are in exact agreementa |
| DIPBA (1) | −0.05% | (−9.98%, 9.88%) | The model is generally accurate for DIPBA (1), with a <10% yield error |
| DIPBA ester (6) | −20.26% | (−25.82%, −14.71%) | Simulation significantly overestimates |
To evaluate the predictive capability of the kinetic model beyond the fitted temperature range (70–90 °C), an additional experiment was performed at 95 °C,1.8 M HBA, and 10 minute residence time. Table 6 below compares the experimental and simulated concentrations for the principal and impurity species. The model continues to capture the overall thermal acceleration of conversion, with DIPBA (1) remaining the dominant product; however, quantitative deviations become more pronounced under these extrapolated conditions. The sulfonated impurity (3) was underpredicted by nearly an order of magnitude, while the DIPBA ester (6) was overpredicted, consistent with the model's tendency to lump untracked mass into this term. These discrepancies stem from applying the model beyond its trained temperature range, resulting in reduced accuracy for impurity predictions. Despite these deviations, the model correctly reproduces the qualitative selectivity trend, favoring DIPBA (1) formation at elevated temperature, while identifying clear directions for refinement of secondary impurity pathways.
| Compounds | Experimental | Simulation |
|---|---|---|
| 4 HBA (2) | 0.00% | 0.00% |
| Sulfonated impurity (3) | 13.28% | 3.64% |
| Mono-alkylated (4) | 0.56% | 0.00% |
| 4-HBA ester (5) | 0.00% | 0.00% |
| DIPBA (1) | 79.21% | 75.97% |
| DIPBA ester (6) | 2.22% | 20.39% |
Overall, this high-temperature validation confirms that the kinetic framework remains predictive for the primary product formation but highlights its limitations in describing secondary impurity pathways under extrapolated conditions. These findings emphasize the importance of incorporating refined temperature-dependent and medium-sensitive terms in future model iterations, providing a direct bridge to the broader implications and next steps discussed in the following section.
Conclusion
In this work, we developed a kinetic model for the alkylation of 4-HBA (2) and paired it with a large-scale PFA-tubing reactor system optimized for DIPBA (1) production. The model achieved strong fits for both 4-HBA (2) and the desired product, DIPBA (1), capturing their concentration profiles with good accuracy. While the stiff-ODE solver and Arrhenius parameter fitting successfully represented the main reaction pathways, the model showed only moderate overall accuracy, particularly struggling with transient intermediates and low-level by-products.The custom reactor design offers a low-cost, modular alternative to specialized commercial reactor systems, while still delivering high-quality, reproducible data for model calibration and validation. By tightly integrating this experimental platform with our simulation framework, we established a practical workflow for bridging small-scale kinetic studies with scalable continuous manufacturing.
Future efforts will focus on improving the accuracy of the kinetic model by collecting more targeted data on transient intermediates and low-level by-products, expanding the reaction network to include additional mechanistic possibilities, impurity-forming pathways, and exploring solvent polarity and viscosity effects that may further refine the solvolysis mechanism. These efforts aim to enhance parameter identifiability and capture medium-dependent kinetic behavior more explicitly in future model iterations. Enhancing detection sensitivity and broadening sampling windows will help capture these species more effectively, further strengthening model performance. In parallel, continued development of the custom reactor, such as incorporating automated flow and temperature control, will enable more precise, scalable experiments. Ultimately, this work demonstrates the value of integrating kinetic modeling with experimental reactor design, showing that predictive models can be meaningfully compared against large-scale system performance. This workflow provides a broadly applicable framework for studying other solvolysis-mediated and Friedel–Crafts systems, offering a transferable approach to linking kinetics with scalable reactor optimization across diverse carbocation-driven chemistries.
Conflicts of interest
The authors claim no conflicts of interest for this article.Data availability
Data for this article, including all chemical data and Python codes are available at Zenodo at https://doi.org/10.5281/zenodo.16994064.Supplementary information (SI): the SI includes the Python-based kinetic fitting and reactor simulation codes, evaluation of alternative kinetic models, and detailed fitting metrics and simulation results supporting model selection. It also provides full experimental and analytical methods, reactor schematics, reproducibility studies, and comparisons between experimental and simulated yields across all reaction conditions. See DOI: https://doi.org/10.1039/d5re00379b.
Acknowledgements
This work was supported by Virginia Commonwealth University as well as the VCU/VSU - Joint Degree and Research Program supported by the Department of Commerce grant 01-79-15308.References
- T. Turányi and A. S. Tomlin, Analysis of Kinetic Reaction Mechanisms, Springer Berlin Heidelberg, Berlin, Heidelberg, 2014, DOI:10.1007/978-3-662-44562-4.
- K. A. Connors, Chemical Kinetics: The Study of Reaction Rates in Solution, Wiley-VCH, New York, 1990 Search PubMed.
- B. K. Carpenter, Determination of Organic Reaction Mechanisms, Wiley, New York, 1984 Search PubMed.
- E. D. Hughes, 56. Mechanism of Substitution at a Saturated Carbon Atom. Part V. Hydrolysis of Tert.-Butyl Chloride, J. Chem. Soc., 1935,(0), 255–258, 10.1039/jr9350000255.
- T. H. Lowry and K. S. Richardson, Mechanism and Theory in Organic Chemistry, Harper & Row, New York, 3rd edn, 1990 Search PubMed.
- T. Otomo, H. Suzuki, R. Iida and T. Takayanagi, SN1 Reaction Mechanisms of Tert-Butyl Chloride in Aqueous Solution: What Can Be Learned from Reaction Path Search Calculations and Trajectory Calculations for Small Hydrated Clusters?, Comput. Theor. Chem., 2021, 1201, 113278, DOI:10.1016/j.comptc.2021.113278.
- F. Ma and M. A. Hanna, Biodiesel Production: A review1Journal Series #12109, Agricultural Research Division, Institute of Agriculture and Natural Resources, University of Nebraska–Lincoln.1, Bioresour. Technol., 1999, 70(1), 1–15, DOI:10.1016/S0960-8524(99)00025-5.
- A. V. Tomasevic and S. S. Siler-Marinkovic, Methanolysis of Used Frying Oil, Fuel Process. Technol., 2003, 81(1), 1–6, DOI:10.1016/S0378-3820(02)00096-6.
- A. Teasdale, E. J. Delaney, S. C. Eyley, K. Jacq, K. Taylor-Worth, A. Lipczynski, W. Hoffmann, V. Reif, D. P. Elder, K. L. Facchine, S. Golec, R. Schulte Oestrich, P. Sandra and F. David, A Detailed Study of Sulfonate Ester Formation and Solvolysis Reaction Rates and Application toward Establishing Sulfonate Ester Control in Pharmaceutical Manufacturing Processes, Org. Process Res. Dev., 2010, 14(4), 999–1007, DOI:10.1021/op900301n.
- A. Teasdale, S. C. Eyley, E. Delaney, K. Jacq, K. Taylor-Worth, A. Lipczynski, V. Reif, D. P. Elder, K. L. Facchine, S. Golec, R. Schulte Oestrich, P. Sandra and F. David, Mechanism and Processing Parameters Affecting the Formation of Methyl Methanesulfonate from Methanol and Methanesulfonic Acid: An Illustrative Example for Sulfonate Ester Impurity Formation, Org. Process Res. Dev., 2009, 13(3), 429–433, DOI:10.1021/op800192a.
- A. Martinelli, R. Volpicelli, M. Verzini, L. Cotarca, L. Maini, P. Pengo and L. Pasquato, Stereoselective Solvolysis in the Synthesis of Dorzolamide Intermediates, ACS Omega, 2023, 8(31), 28851–28858, DOI:10.1021/acsomega.3c03959.
- V. K. Prasad, R. A. Ricci and A. P. Granatek, Kinetics of Solvolysis of Intrazole, J. Pharm. Sci., 1972, 61(10), 1579–1585, DOI:10.1002/jps.2600611007.
- P. K. Verma, A. Makhal, R. K. Mitra and S. K. Pal, Role of Solvation Dynamics in the Kinetics of Solvolysis Reactions in Microreactors, Phys. Chem. Chem. Phys., 2009, 11(38), 8467, 10.1039/b905573h.
- S. Winstein, E. Grunwald and H. W. Jones, The Correlation of Solvolysis Rates and the Classification of Solvolysis Reactions into Mechanistic Categories, J. Am. Chem. Soc., 1951, 73(6), 2700–2707, DOI:10.1021/ja01150a078.
- N. Streidl, B. Denegri, O. Kronja and H. Mayr, A Practical Guide for Estimating Rates of Heterolysis Reactions, Acc. Chem. Res., 2010, 43(12), 1537–1549, DOI:10.1021/ar100091m.
- E. M. Anderson, M. L. Stone, M. J. Hülsey, G. T. Beckham and Y. Román-Leshkov, Kinetic Studies of Lignin Solvolysis and Reduction by Reductive Catalytic Fractionation Decoupled in Flow-Through Reactors, ACS Sustainable Chem. Eng., 2018, 6(6), 7951–7959, DOI:10.1021/acssuschemeng.8b01256.
- C. M. Hemens and K. Vaughan, Kinetic Study of the Solvolysis Reactions of 1-Aryl-3-Acetoxymethyl-3-Alkyltriazenes: Evidence for Iminium Ion Intermediates and the S N1 Mechanism, J. Chem. Soc., Perkin Trans. 2, 1986, 1, 11–15, 10.1039/p29860000011.
- M. J. Blandamer, R. E. Robertson, E. Ralph and J. M. W. Scott, Kinetics of Solvolytic Reactions. Dependence of Composition on Time and of Rate Parameters on Temperature, J. Chem. Soc., Faraday Trans. 1, 1983, 79(5), 1289, 10.1039/f19837901289.
- Y. Shi, X. Xia, J. Li, J. Wang, T. Zhao, H. Yang, J. Jiang and X. Jiang, Solvolysis Kinetics of Three Components of Biomass Using Polyhydric Alcohols as Solvents, Bioresour. Technol., 2016, 221, 102–110, DOI:10.1016/j.biortech.2016.09.008.
- R. Mougeot, P. Jubault, J. Legros and T. Poisson, Continuous Flow Synthesis of Propofol, Molecules, 2021, 26(23), 7183, DOI:10.3390/molecules26237183.
- L. Vinet, L. Di Marco, V. Kairouz and A. B. Charette, Process Intensive Synthesis of Propofol Enabled by Continuous Flow Chemistry, Org. Process Res. Dev., 2022, 26(8), 2330–2336, DOI:10.1021/acs.oprd.1c00416.
- G. M. Martins, M. F. A. Magalhães, T. J. Brocksom, V. S. Bagnato and K. T. De Oliveira, Scaled up and Telescoped Synthesis of Propofol under Continuous-Flow Conditions, J. Flow Chem., 2022, 12(3), 371–379, DOI:10.1007/s41981-022-00234-0.
- M. T. Rahman and T. Wirth, Safe Use of Hazardous Chemicals in Flow, in Flow Chemistry for the Synthesis of Heterocycles, ed. U. Sharma and E. Van der Eycken, Topics in Heterocyclic Chemistry, Springer, Cham, 2018, vol. 56, DOI:10.1007/7081_2018_17.
- M. Movsisyan, E. I. P. Delbeke, J. K. E. T. Berton, C. Battilocchio, S. V. Ley and C. V. Stevens, Taming Hazardous Chemistry by Continuous Flow Technology, Chem. Soc. Rev., 2016, 45(18), 4892–4928, 10.1039/C5CS00902B.
- M. Guidi, P. H. Seeberger and K. Gilmore, How to Approach Flow Chemistry, Chem. Soc. Rev., 2020, 49(24), 8910–8932, 10.1039/C9CS00832B.
- L. Capaldo, Z. Wen and T. Noël, A Field Guide to Flow Chemistry for Synthetic Organic Chemists, Chem. Sci., 2023, 14(16), 4230–4247, 10.1039/D3SC00992K.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press, 97th edn, 2016, DOI:10.1201/9781315380476.
- A. Sheeba, C. M. Abhijith and M. Jose Prakash, Experimental and Numerical Investigations on the Heat Transfer and Flow Characteristics of a Helical Coil Heat Exchanger, Int. J. Refrig., 2019, 99, 490–497, DOI:10.1016/j.ijrefrig.2018.12.002.
- A. Milsom, A. Lees, A. M. Squires and C. Pfrang, MultilayerPy (v1.0): A Python-Based Framework for Building, Running and Optimising Kinetic Multi-Layer Models of Aerosols and Films, Geosci. Model Dev., 2022, 15(18), 7139–7151, DOI:10.5194/gmd-15-7139-2022.
- M. T. Tillmann and F. Galvanin, Development of a Holistic Python Package for Optimal Selection of Experimental Design Criteria in Kinetic Model Discrimination, in Computer Aided Chemical Engineering, Elsevier, 2023, vol. 52, pp. 631–636, DOI:10.1016/B978-0-443-15274-0.50100-1.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Reaction Mechanism Generator: Automatic Construction of Chemical Kinetic Mechanisms, Comput. Phys. Commun., 2016, 203, 212–225, DOI:10.1016/j.cpc.2016.02.013.
- C. Müller, T. Pascher, A. Eriksson, P. Chabera and J. Uhlig, KiMoPack: A Python Package for Kinetic Modeling of the Chemical Mechanism, J. Phys. Chem. A, 2022, 126(25), 4087–4099, DOI:10.1021/acs.jpca.2c00907.
- E. D. Hermes, A. N. Janes and J. R. Schmidt, Micki: A Python-Based Object-Oriented Microkinetic Modeling Code, J. Chem. Phys., 2019, 151(1), 014112, DOI:10.1063/1.5109116.
- D. R. Weilandt, P. Salvy, M. Masid, G. Fengos, R. Denhardt-Erikson, Z. Hosseini and V. Hatzimanikatis, Symbolic Kinetic Models in Python (SKiMpy): Intuitive Modeling of Large-Scale Biological Kinetic Models, Bioinformatics, 2023, 39(1), btac787, DOI:10.1093/bioinformatics/btac787.
- J. Lym, G. R. Wittreich and D. G. Vlachos, A Python Multiscale Thermochemistry Toolbox (pMuTT) for Thermochemical and Kinetic Parameter Estimation, Comput. Phys. Commun., 2020, 247, 106864, DOI:10.1016/j.cpc.2019.106864.
- A. Mounaam, Y. Chhiti, A. Souissi, M. Salouhi, Y. Harmen and M. E. Khouakhi, Simulation and Optimization of an Industrial Sulfuric Acid Plant with Contact Process Using Python-Unisim Design, in Simulation and Modeling Methodologies, Technologies and Applications. SIMULTECH 2020, ed. M. S. Obaidat, T. Oren and F. D. Rango, Lecture Notes in Networks and Systems, Springer, Cham, 2022, vol. 306, DOI:10.1007/978-3-030-84811-8_4.
- J. Sutton, G. Wiggins and C. Daw, Chemics-Reactors: A Preliminary Python Program for Implementing Network Models of Multiphase Reactors, ORNL/TM-2017/748, 2018, p. 1465051, DOI:10.2172/1465051.
- A. Okullo, N. Tibasiima and J. Barasa, Modeling and Simulation of an Isothermal Suspension Polymerization Reactor for PMMA Production Using Python, Adv. Chem. Eng. Sci., 2017, 7(4), 408–419, DOI:10.4236/aces.2017.74029.
- J. L. Ansoni and P. Seleghim, Optimal Industrial Reactor Design: Development of a Multiobjective Optimization Method Based on a Posteriori Performance Parameters Calculated from CFD Flow Solutions, Adv. Eng. Softw., 2016, 91, 23–35, DOI:10.1016/j.advengsoft.2015.08.008.
- J. Bousquet, A. Seubert and R. Henry, New Finite Element Neutron Kinetics Coupled Code System FENNECS/ATHLET for Safety Assessment of (Very) Small and Micro Reactors, J. Phys.:Conf. Ser., 2020, 1689(1), 012008, DOI:10.1088/1742-6596/1689/1/012008.
- R. V. Sawaki, K. Tannous and J. B. F. Filho, Development of an Educational Tool Aimed at Designing Ideal Chemical Reactors, Comput. Appl. Eng. Educ., 2020, 28(3), 459–476, DOI:10.1002/cae.22208.
| This journal is © The Royal Society of Chemistry 2026 |