Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
ANN-based prediction of equilibrium gas composition and carbon yield in methane pyrolysis and reforming methods
Robert Cherbański *,
Tomasz Kotkowski,
Stanisław Murgrabia,
Eugeniusz Molga and
Andrzej Stankiewicz
*,
Tomasz Kotkowski,
Stanisław Murgrabia,
Eugeniusz Molga and
Andrzej Stankiewicz
Warsaw University of Technology, Faculty of Chemical and Process Engineering, ul. Waryńskiego 1, Warsaw, Poland. E-mail: robert.cherbanski@pw.edu.pl
First published on 27th November 2025
Abstract
We investigate the potential of artificial neural networks (ANNs) to approximate the equilibrium gas-phase composition and carbon yield in methane pyrolysis (MP), dry reforming of methane (DRM), steam methane reforming (SMR), and partial oxidation of methane (POM). Unlike the conventional thermodynamic approach, which relies on the Gibbs free energy minimization, the ANN-based method provides a data-driven alternative. Using supervised learning, the model captures the complex, nonlinear relationships between process parameters, such as temperature, pressure, and reactant ratios, and the resulting equilibrium product compositions. This approach not only circumvents the computationally intensive nature of Gibbs energy minimization but also enables rapid predictions across a broad range of operating conditions. The study evaluates the performance of a representative ANN architecture and compares its predictions with conventional thermodynamic calculations to assess the method's accuracy and generalization capability. The results demonstrate that the trained ANN predicts the gas-phase compositions and carbon yields very well, even when all input variables are interpolated. Moreover, the ANN performs the same task several thousand times faster than the conventional method. Overall, the results demonstrate the potential of ANNs as efficient tools for accelerating equilibrium calculations in methane conversion processes. The developed and validated approach can be considered a useful tool for predicting the equilibrium gas composition and carbon yield in methane pyrolysis and reforming processes. The SI provides the synaptic weights necessary for the practical application of ANNs to calculate the equilibrium gas composition and carbon yield in MP, DRM, SMR, and POM over a wide range of temperatures, pressures, and initial reactant compositions.
1. Introduction
Methane, the primary component of natural gas, plays a critical role in the global energy and chemical industries due to its high hydrogen-to-carbon ratio, the highest of any hydrocarbon. As the demand for low-carbon and hydrogen-based energy carriers continues to rise, the development of efficient and cleaner methods of methane utilization has attracted significant attention.Table 1 summarizes the reactions occurring in various process alternatives for hydrogen generation from methane. To date, steam methane reforming (SMR) has been established as the leading industrial process for hydrogen generation, accounting for approx. 62% of global H2 production.1 Given that the SMR reaction (eqn (1) in Table 1) is usually carried out along with the water–gas shift reaction (WGS reaction, eqn (5)), the SMR process yields 4 moles of H2 per mole of CH4. Basic calculations based on this stoichiometry indicate that CO2 emissions amount to 5.5 kg CO2 per kg H2. When life cycle emissions are considered, about 9 kilograms CO2-equivalent per kilogram of H2 is reported for a non-CCS process.1 When additional methane emissions (e.g., venting, leakages) and associated CO2 emissions (e.g. methane flaring) are considered, total emissions can reach 11 kg CO2-eq/kg H2 for SMR-based hydrogen production from natural gas without CCS.2
| Reaction | Occurrence in a process/processes | ΔH0 [kJ mol−1] | Type of reaction | Equation |
|---|---|---|---|---|
| CH4 + H2O ⇌ CO + 3H2 | DRM, SMR, POM | 205.9 | Main (SMR) | (1) |
| CH4 + CO2 ⇌ 2H2 + 2CO | DRM, SMR, POM | 247.0 | Main (DRM) | (2) |
| CH4 ⇌ C(s) + 2H2 | MP, DRM, SMR, POM | 75.0 | Main (MP) | (3) |
| CH4 + 0.5O2 ⇌ CO + 2H2 | POM | −36.0 | Main (POM) | (4) |
| CO + H2O ⇌ CO2 + H2 | DRM, SMR, POM | −41.0 | Side | (5) |
| 2CO ⇌ C(s) + CO2 | DRM, SMR, POM | −172.5 | Side | (6) |
| CO2 + 4H2 ⇌ CH4 + 2H2O | DRM, SMR, POM | −164.7 | Side | (7) |
| H2 + CO ⇌ C(s) + H2O | DRM, SMR, POM | −175.3 | Side | (8) |
| CO2 + 2H2 ⇌ C(s) + 2H2O | DRM, SMR, POM | −134.4 | Side | (9) |
| CO + 0.5O2 ⇌ CO2 | POM | −283.0 | Side | (10) |
| C(s) + O2 ⇌ CO2 | POM | −393.5 | Side | (11) |
| 2C(s) + O2 ⇌ 2CO | POM | −221.0 | Side | (12) |
| CH4 + 2O2 ⇌ CO2 + 2H2O | POM | −890.3 | Side | (13) |
In response to the need for decarbonized H2 production, several promising alternative methods have emerged, including dry reforming of methane (DRM, eqn (2)), methane pyrolysis (MP, eqn (3)) and partial oxidation of methane (POM, eqn (4)). Please note that similar to the SMR process (eqn (1) and (5)), both DRM and POM can also be coupled with the WGS reaction (eqn (5)) to improve the H2/CH4 molar ratio.
DRM (eqn (2)) is considered an environmentally friendly alternative to SMR, as it converts CH4 and CO2, two primary greenhouse gases, into syngas (a mixture of H2 and CO). Under appropriate process conditions, an equimolar mixture of H2 and CO can be obtained, which is ideal for Fischer–Tropsch synthesis3 and the production of long-chain hydrocarbons and oxo-alcohols.4 This equimolar ratio is also favourable for the synthesis of dimethyl ether, a compound regarded as a promising green fuel of the future.
The most significant benefit of MP (eqn (3)) is that it produces H2 without emitting CO2. Instead, solid carbon is generated in large quantities (3 kg of C per 1 kg of H2), which can be utilized as a raw material in the production of rubber, tires, printers, and plastics, or safely sequestrated. As a result, MP is frequently considered a bridge technology in transitioning from fossil to renewable fuels.5
Unlike the methods above, POM is exothermic, which makes it energy-efficient; however, it is more prone to hot-spot formation and catalyst sintering. Additionally, pure oxygen is required instead of air, which increases CAPEX due to the need for an oxygen production facility.
The performance of above methane conversion methods strongly depends on operational parameters such as temperature, pressure and feed composition. Accurate prediction of equilibrium gas composition and solid carbon yield under different conditions is central for process optimization, scale-up and environmental impact assessment. Conventional modelling approach using the Gibbs minimization method requires knowledge of thermodynamics. On the other hand, replacing this classical modelling approach with artificial neural networks (ANNs) shifts the problem from a physics-oriented to a data-driven one. While the Gibbs minimization method relies on detailed thermodynamics and minimizes the system's Gibbs free energy to determine equilibrium compositions, an ANN builds input–output relationships using only data, without prior knowledge of the underlying thermodynamic laws. This makes ANNs particularly attractive in scenarios where quick predictions are needed. Significantly, unlike the Gibbs minimization method, ANNs may suffer from extrapolation beyond the training data. Therefore, while ANNs can complement or even replace traditional methods in certain contexts, careful validation and consideration of their limitations are essential.
A few studies have investigated thermodynamic equilibrium using the Gibbs free energy minimization method for SMR,6–10 DRM,6–8,10,11 POM,6,7,12 MP.6,7,13 Additionally, several articles have addressed steam reforming of various liquid fuels such as methanol,9,14 ethanol,9,15,16 glycerol,9,15,17,18 as well as coal gasification.6,19
To the best of our knowledge, there are very limited literature on an application of ANNs to predict thermodynamic equilibrium in such systems. However, some successful attempts at modeling liquid–liquid and vapor–liquid equilibria using ANNs can be found in the relevant literature.20–24
Da Silva Pimentel et al.25 developed an ANN to predict syngas composition. They considered various types of biomass, gasification agents and gasifiers using data collected from the literature. A total number of 33 ANN topologies with different activation functions were tested, each comprising 10 input neurons and 4 output neurons. The best topology showed R2 values ranging from 0.88 to 0.98 for training, and from about 0.70 to 0.91 for testing. The authors recommended an ANN architecture with a maximum of two hidden layers and the use of either the Bayesian regularization backpropagation algorithm or the Levenberg–Marquardt backpropagation algorithm. A comparison between the ANN model within a reliable prediction range and the results from the minimization of Gibbs free energy was also performed confirming the consistency of the ANN model.
Igwegbe et al.26 used ANNs to model the steam reforming of naphthalene. The training dataset was generated using the Gibbs free energy minimisation method. They investigated the effect of temperature and steam-to-oil ratio on the selectivity of H2, CO2, CO and CH4 in the product stream. The R2 coefficient and the root mean square error (RMSE) for the training, validation and testing datasets and all gases was higher than 0.99 and lower than 1 mol%, respectively.
Hossain et al.27 reported on an application of ANNs for modelling DRM over Ni/CaFe2O4 catalysts. The ANN training was performed using experimental data. Two types of ANNs, multi-layer perceptron (MLP) and radial basis function (RBF), were employed for the modelling. Both ANNs were fed with input signals consisting of the CH4/CO2 feed ratio, reaction temperature and catalyst metal loading, while the output signals included the CO2 and CH4 conversions and the H2 and CO yields. The MLP-based ANN model demonstrated superior performance compared to the RBF-based model.
Zamaniyan et al.28 investigated the application of an ANN to model an industrial hydrogen plant. They employed a three-layer ANN, and the training dataset was generated using conventional modelling by varying parameters such as feed temperature, reformer pressure, the steam-to-carbon ratio and carbon dioxide-to-methane ratio in the feed stream. A tangent sigmoid activation function was used in both the hidden and output layers, and the ANN was trained with a gradient descent algorithm. The optimum number of neurons in the hidden layer was determined by minimizing the MSE. The ANN model predicted temperature, pressure and mole fraction of hydrogen and carbon monoxide in the product of the hydrogen plant.
In the work of Ayodele and Cheng29 the process of synthesis gas production from DRM over ceria supported cobalt catalyst in a fixed bed stainless steel reactor was investigated. ANN and Box Behnken design (BBD) were employed to investigate the effects of reactant partial pressures, reactant feed ratios, reaction temperature on the reactor performance. Good agreement was shown between the predicted outputs from the ANN model and the experimental data. Optimum reactant feed ratio of 0.60 and CH4 partial pressure of 46.85 kPa were obtained at 728 °C with corresponding conversions of 74.84% and 76.49% for CH4 and CO2, respectively.
This paper investigates the potential of using an ANN as a modelling tool for describing the gas-phase composition and carbon yield in MP and three widely studied reforming processes: DRM, SMR and POM. The nonlinear approximation capabilities of ANNs provide a robust computational framework for capturing the complex relationships governed by thermodynamics. Moreover, the high computational efficiency of a trained ANN makes it a promising alternative to conventional thermodynamic models, especially in scenarios which require rapid predictions or the incorporation of equilibrium data into CFD simulations. To highlight this advantage, it is useful to compare the two methods. While the classical thermodynamic approach takes approximately 15 seconds to compute DRM equilibrium data for 31 temperatures and 3 pressures, the ANN performs the same task in just 0.00233 seconds, making it 6438 times faster.
2. Methods
2.1. The Gibbs free energy minimization method
The method of minimizing the Gibbs free energy was used to calculate equilibrium gas compositions and carbon yields in methane pyrolysis (MP), dry reforming of methane (DRM), steam methane reforming (SMR) and partial oxidation of methane (POM).Thermodynamic equilibrium in a system is achieved when the total Gibbs free energy, Gt, reaches its minimum value, i.e., when its change is zero at a given temperature, pressure, and chemical species composition (eqn (14)).
| min GtT,P = f(n1, n2, …, ni, …, nN, nC) | (14) |
This minimization considers CH4, CO2, H2, CO, H2O, O2, N2 and C(s), as the side reactions associated with MP, DRM, SMR, and POM, as outlined in the Introduction, involve only these species. Since these compounds represent the gas and solid phases, the total Gibbs free energy to be minimized can be expressed as follows
 | (15) |
Then, introducing the definition of chemical potential and utilizing the fact that the fugacity of a solid (carbon) is unity, eqn (15) can be rewritten as:
 | (16) |
 | (17) |
 | (18) |
| Z3 − (1 − B)Z2 + (A − 3B2 − 2B)Z − (AB − B2 − B3) = 0 | (19) |
 | (20) |
 | (21) |
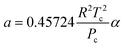 | (22) |
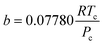 | (23) |
 | (24) |
Solving eqn (19) and using the largest real root, Zg, yields eqn (25), which is used to calculate the fugacity coefficient:30
 | (25) |
| G0(T) = H0(T) − TS0(T) | (26) |
For carbon (graphite), the following relationship for the molar heat capacity was employed:32
| C0p,C = A + BT + CT2 + DT3 + ET4 + FT5 + GT6 | (27) |
| H0C(T) = H0C(298.15) + ∫T298.15C0p,CdT | (28) |
 | (29) |
• Mass balance
 | (30) |
• Nonnegative number of moles
| ni ≥ 0 | (31) |
Modelling results were generated and are presented in this work using the following definitions:
• For gaseous species as mole fractions, 
The thermodynamic calculations were validated using the following expression obtained for MP elsewhere.33
 | (32) |
| Kp = e−ΔG/RT | (33) |
 | (34) |
Then, utilizing the definition of Ky for MP, one obtains:
 | (35) |
 | (36) |
 .
.
Since Δn is the number of converted CH4, the CH4 conversion can be calculated as:
 | (37) |
 | ||
| Fig. 1 Comparison of CH4 conversion profiles calculated using the Gibbs minimization method and those calculated using eqn (32) taken from ref. 33 at pressures of 1, 2, and 5 bar. | ||
2.2. ANNs
To enable an accurate approximation of the equilibrium gas composition and carbon yield for MP, DRM, SMR, and POM using an ANN, the following input and output vectors were defined:
 | (38) |
| outputs = [yCH4, yCO2, yCO, yH2, yH2O, YC] | (39) |
The outputs were chosen to reflect the primary species participating in methane conversion reactions as well as the carbon yield, YC, which quantifies solid carbon formation. This selection ensures that the ANN captures both the gas-phase composition and the extent of carbon deposition, that is key indicators of reactor performance across MP, DRM, SMR and POM (Fig. 2).
The ANN training was carried out in Matlab R2024b (MathWorks, Inc.) using the Neural Net Fitting toolbox.
Following the recommendations of Pimentel et al.,25 the use of the satlin activation function in the output layer and training algorithms other than trainlm or trainbr (specifically traingdx, traingd, traingda, traingdm, trainbfg, traincgb, traincgf, traincgp, or trainrp) was avoided, as the authors suggested these configurations exhibit poor performance. Consequently, the Levenberg–Marquardt (trainlm) algorithm was selected for network optimization.
The outputs were calculated as follows:
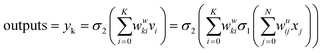 | (40) |
| σ1 = σ1(βS) = σ1(S) = tanh(S) | (41) |
| σ2 = σ2(S) = a·S + b = S | (42) |
 | (43) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,
, ![[z with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_007a_20d1.gif) ), p = 1, …, P indexes the individual samples from the training, validation and testing datasets, M is the number of output neurons, k = 1, …, M indexes the output neurons, yk is the network's output for the k-th output neuron, zk is the target value for the k-th output neuron.
), p = 1, …, P indexes the individual samples from the training, validation and testing datasets, M is the number of output neurons, k = 1, …, M indexes the output neurons, yk is the network's output for the k-th output neuron, zk is the target value for the k-th output neuron.
Despite the recommendation of Pimentel et al.25 to employ two hidden layers in data-driven modelling for predicting biomass gasification and for comparison with thermodynamic equilibrium models, rather than using three or four layers, we adopted a single hidden layer, as also implemented by Igwegbe et al.26 This choice is supported by the universal approximation theorem, which states that continuous feedforward neural networks with a single hidden layer and any continuous sigmoidal nonlinearity can approximate arbitrary decision regions with arbitrary accuracy.34,35
The ANN used in this study has a 5–40–6 architecture, corresponding to 5 input neurons, one hidden layer of 40 neurons, and 6 output neurons. While several architectures were tested during preliminary experiments, the primary aim was to demonstrate the predictive capability of the ANN rather than to perform an exhaustive hyperparameter optimization. The 5–40–6 structure was selected as it provided satisfactory performance while maintaining simplicity and clarity in presentation.
Overfitting risks were mitigated by evaluating ANN predictions on separate testing sets that were not used during training (Fig. 7–9, no. 2.1–5.3). For each tested architecture, predicted values were compared with the corresponding target values across all testing sets using a MATLAB script. The high agreement between predictions and targets, as shown in Fig. 13, 15 and 17–20 indicate that overfitting was minimal.
Table 2 summarizes all training and testing cases considered in this study. For example, the ANN was trained using 2233 input samples (as defined in eqn (38)) in dataset no. 1, which included:
| No | Training/testing | T [C] | P [bar] | |||
|---|---|---|---|---|---|---|
| 1. | Training | 0 (MP) | 0 | 0 | [0, 50, 100, …, 1500] | [1, 3, 5] |
| 0.25 (DRM) | ||||||
| 0.5 (DRM) | ||||||
| 0.75 (DRM) | ||||||
| 1 (DRM) | ||||||
| 1.25 (DRM) | ||||||
| 1.5 (DRM) | ||||||
| 1.75 (DRM) | ||||||
| 2 (DRM) | ||||||
| 0 | 0.25 (SMR) | 0 | ||||
| 0.5 (SMR) | ||||||
| 0.75 (SMR) | ||||||
| 1 (SMR) | ||||||
| 1.25 (SMR) | ||||||
| 1.5 (SMR) | ||||||
| 1.75 (SMR) | ||||||
| 2 (SMR) | ||||||
| 0 | 0.1 (POM) | |||||
| 0.2 (POM) | ||||||
| 0.3 (POM) | ||||||
| 0.4 (POM) | ||||||
| 0.5 (POM) | ||||||
| 0.6 (POM) | ||||||
| 0.7 (POM) | ||||||
| 2.1 | Testing - interpolation | 0 (MP) | 0 | 0 | [25, 75, 125, …, 1500] | [1, 3, 5] |
| 2.2 | 1 (DRM) | 0 | 0 | |||
| 2.3 | 0 | 1 (SMR) | 0 | |||
| 2.4 | 0 | 0 | 0.5 (POM) | |||
| 3.1 | Testing - interpolation | 0 (MP) | 0 | 0 | [0, 50, 100, …, 1500] | [2, 4] |
| 3.2 | 1 (DRM) | 0 | 0 | |||
| 3.3 | 0 | 1 (SMR) | 0 | |||
| 3.4 | 0 | 0 | 0.5 (POM) | |||
| 4.1 | Testing - interpolation | 0.875 (DRM) | 0 | 0 | [0, 50, 100, …, 1500] | [1, 3, 5] |
| 4.2 | 0 | 1.125 (SMR) | 0 | |||
| 4.3 | 0 | 0 | 0.45 (POM) | |||
| 5.1 | Testing - interpolation | 0.875 (DRM) | 0 | 0 | [25, 75, 125 …, 1500] | [2, 4] |
| 5.2 | 0 | 1.125 (SMR) | 0 | |||
| 5.3 | 0 | 0 | 0.45 (POM) |
• 1 data subset for MP,
• 8 data subsets for DRM,
• 8 data subsets for SMR,
• 7 data subsets for POM.
These data subsets cover temperatures from 0 to 1500 °C in 50 °C increments, at pressures of 1, 3, and 5 bar. The number of input samples was selected to ensure adequate coverage of the input space while maintaining computational efficiency. This number was determined after preliminary tests indicated that further increasing the dataset size resulted in negligible improvement in prediction accuracy. Therefore, while the same trends could in principle be represented with a smaller number of data points, this would likely come at the expense of predictive precision and robustness across the full range of operating conditions considered. Overall, this is always a trade-off between data density and ANN generalization capability. A denser dataset can improve the accuracy of the ANN within the training domain, as it allows the network to better capture nonlinear dependencies between variables. However, excessively increasing the number of training points may lead to redundancy, longer training times, and potential overfitting. Conversely, using fewer data points can make the model more efficient but may reduce interpolation (or generalization) accuracy, especially in regions where the underlying thermodynamic relationships change rapidly.
The corresponding targets for the supervised training of ANN were calculated using the thermodynamic approach described in section 2.1.
The ANN training was carried out by monitoring the network performance using a validation set (15% of the data) and a test set (15% of the data).
The interpolation ability of the ANN was evaluated in separate tests with respect to temperature (no. 2.1–2.4), pressure (no. 3.1–3.4), and reactant ratios (no. 4.1–4.3). Additionally, test sets 5.1–5.3 were devoted to the simultaneous evaluation of interpolation performance across temperature, pressure, and reactant ratios. The extrapolation ability of the ANN was not assessed, in recognition of the inherent limitations of data-driven models in such scenarios.
3. Results and discussion
3.1. Thermodynamic calculation results
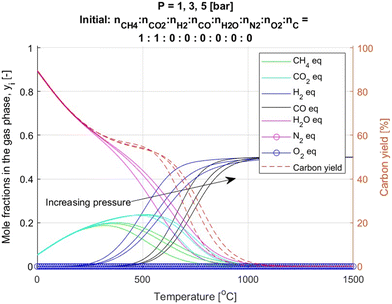
Fig. 3 presents the calculation results for MP at 1, 3, and 5 bar. Only CH4, H2 and solid carbon are observed in the system between 0 and 1500 °C in accordance with eqn (3). Since MP is an endothermic process, higher temperatures favour the conversion of CH4 into H2 and solid carbon. Conversely, increasing the pressure has the opposite effect, decreasing CH4 conversion in line with Le Chatelier's principle.Fig. 4 shows the calculation results for DRM, which is supplied with an equimolar mixture of CH4 and CO2. Similar to MP, DRM is an endothermic process (eqn (2)). The equilibrium at temperatures above 1100 °C is strongly shifted toward the formation of H2 and CO, in accordance with thermodynamic principles. At lower temperatures, the system also contains H2O and solid carbon, along with partially unreacted CH4 and CO2. Increasing the total pressure shifts all equilibrium profiles toward higher temperatures, which aligns with Le Chatelier's principle. It is also notable that within the temperature range of 0–500 °C, the equilibrium mole fractions of CH4 and CO2 initially have relatively low values but gradually increase. This behaviour is due to the high contribution of water vapor in the gas phase at low temperatures. Above 500 °C, the influence of water vapor diminishes, leading to a shift in the equilibrium composition.
Fig. 5 presents the thermodynamic results for the SMR process using an equimolar mixture of H2O and CH4. The analysis was conducted over the same temperature and pressure ranges as those discussed for the previous two cases. At temperatures above 1100 °C, the equilibrium composition aligns with the stoichiometry of the overall reaction (eqn (1)), yielding mole fractions of 0.75 for H2 and 0.25 for CO. At lower temperatures, unreacted CH4 and H2O are also present in the system. Additionally, small amounts of CO2 and solid carbon are observed, indicating the occurrence of side reactions such as the CH4 cracking and the Boudouard reaction (eqn (3) and (6)). As expected, increasing the total pressure reduces the conversion of reactants, as the main reaction (eqn (1)) results in an increase in the total number of moles.
Fig. 6 shows the results for POM with the typical nO2/nCH4 ratio of 0.5. As before, the equilibrium of the main reaction (eqn (4)) shifts toward the products at temperatures above approx. 1100 °C. However, this is due to the Gibbs free energy, which becomes more negative at higher temperatures. As a result, the mole fractions of H2 and CO are 0.66 and 0.33, respectively. At lower temperatures, unreacted CH4 is observed. Additionally, varying amounts of H2O, CO2 and solid carbon are present resulting from side reactions. In this figure, a similar effect to that observed in Fig. 4 is visible. Namely, the equilibrium concentration of CH4 slightly increases within the temperature range of 0–300 °C. This behaviour is due to the significant presence of water vapor in the equilibrium mixture at lower temperatures, whose contribution decreases substantially as the temperature rises.
3.2. ANN results
Fig. 7–9 present the results of the ANN training and the assessment of its generalization abilities. The numbering of the figures, as given in their titles, corresponds to the respective rows in Table 2. | ||
| Fig. 7 Comparison of fitting quality between ANN predictions and thermodynamic calculations for the training set no. 1 and interpolation sets no. 2.1–2.4 (Table 2). | ||
 | ||
| Fig. 8 Comparison of fitting quality between ANN predictions and thermodynamic calculations for the interpolation sets no. 3.1–3.4 (Table 2). | ||
 | ||
| Fig. 9 Comparison of fitting quality between ANN predictions and thermodynamic calculations for the interpolation sets no. 4.1–4.3 and 5.1–5.3 (Table 2). | ||
For comparative purposes, we also developed a Matlab script to perform polynomial fitting of the relevant variables using third- (56 parameters), fourth- (126 parameters), and fifth-order (252 parameters) polynomials. Similar to the ANN approach, this approach offered a straightforward implementation and reduced computational time compared to Gibbs free energy minimization simulations. However, the predictive accuracy depended on the polynomial order and was generally lower than that achieved with the ANN predictions (see a comparison in Fig. 10). This comparison highlights the trade-off between simplicity and predictive performance. While polynomial fitting reduces computational cost, it does not attain the same level of accuracy as the ANN model.
 | ||
| Fig. 10 Comparison of fitting quality between polynomial fitting using third-, fourth- and fifth-order polynomials. | ||
The training set no. 1 (Table 2) shows the training quality for the entire dataset, which includes data for MP, DRM, SMR and POM (a total of 2232 patterns). Overall, the ANN predictions demonstrate excellent agreement across all output signals (Fig. 11). However, the carbon yield exhibits slightly poorer agreement with the training subset.
 | ||
| Fig. 11 Comparison of the ANN predictions and targets for training set no. 1 (see Table 2 and Fig. 7). | ||
For temperature interpolation, all tested methods: MP, DRM, SMR and POM produced very similar results. Fig. 12 and 13 present the parity plots and the ANN prediction quality for DRM, respectively (see also Fig. 7). Please note that parity plots for the remaining methods are provided in the SI.
 | ||
| Fig. 12 Comparison of the ANN predictions and targets for testing set no. 2.2 (see Table 2). | ||
 | ||
| Fig. 13 Comparison of the ANN predictions and targets for testing set no. 2.2 (see Table 2). | ||
The ability of the ANN to predict data for interpolated pressures was demonstrated using the SMR subset (no. 3.3 in Fig. 8). As shown in Fig. 14 and 15, the ANN predicts gas-phase concentrations more accurately than carbon yields. Nonetheless, the agreement between predicted and training patterns remains satisfactory.
 | ||
| Fig. 14 Comparison of the ANN predictions and targets for testing set no. 3.3 (see Table 2). | ||
 | ||
| Fig. 15 Comparison of the ANN predictions and targets for testing set no. 3.3 (see Table 2). | ||
Further similarities are observed when the ANN predicts results for interpolated ratios of nCO2/nCH4, nH2O/nCH4 and nO2/nCH4. To avoid redundancy, Fig. 16 and 17 highlight the ANN performance for POM only (parity plots for the other methods are presented in the SI).
 | ||
| Fig. 16 Comparison of the ANN predictions and targets for testing set no. 4.3 (see Table 2). | ||
 | ||
| Fig. 17 Comparison of the ANN predictions and targets for testing set no. 4.3 (see Table 2). | ||
Finally, the ability of the ANN to interpolate all signals, i.e. the ratios nCO2/nCH4, nH2O/nCH4 and nO2/nCH4, temperature and pressure, was thoroughly examined. Fig. 18 and 19 illustrate the ANN prediction performance for DRM, SMR and POM, showing very good agreement between the predictions and targets.
 | ||
| Fig. 18 Comparison of the ANN predictions and targets for testing set no. 5.1 (see Table 2). | ||
 | ||
| Fig. 19 Comparison of the ANN predictions and targets for testing set no. 5.2 (see Table 2). | ||
 | ||
| Fig. 20 Comparison of the ANN predictions and targets for testing set no. 5.3 (see Table 2). | ||
Overall, the ANN performs slightly less accurately for carbon yield, with the lowest fitting observed for SMR (R2 = 0.8399, Fig. 9). This is likely because the carbon yield in SMR is more sensitive to variations in process parameters compared to MP, DRM, or POM. However, a more detailed investigation would be required to fully clarify this behaviour.
For practical use of the elaborated method, i.e. an application of ANNs for predicting the equilibrium gas composition and carbon yield in each considered process, the set of properly trained networks parameters (synaptic weights) is given in the SI. Using eqn (40) and the appropriate set of weights a prediction of the equilibrium gas composition and carbon yield in MP and methane reforming methods (SMR, DRM and POM) processes can be easily, fast and accurate executed.
Data-driven models, such as black-box ANNs or other reduced-order approaches (e.g., response surfaces, polynomial regressions), can be readily integrated into real-time process control systems by serving as virtual sensors or surrogate models that predict key process variables. Once trained on historical or simulated process data, the ANN can rapidly estimate system behaviour without relying on complex first-principles models.
In a real-time control framework, these predictive outputs can be incorporated into optimization algorithms that continuously adjust reactor parameters (e.g., feed rate, pressure, temperature or catalyst concentration) to maintain optimal operating conditions. Furthermore, such models can be updated online as new process data become available, enabling adaptive learning and sustained accuracy under changing conditions. The short computation time required for parameter estimation makes this approach particularly attractive for dynamic optimization and process monitoring applications.
Recently, Physics-Informed Artificial Neural Networks (PIANNs) have emerged as a promising extension of conventional black-box ANNs, combining data-driven learning with physical laws expressed as differential equations or thermodynamic constraints. By embedding these physical relationships into the training process, PIANNs can improve model interpretability, reduce the need for large datasets, and enhance extrapolation capability beyond the training domain. Such hybrid models are especially valuable in chemical process systems, where they can bridge the gap between purely empirical data-driven approaches and rigorous mechanistic modelling.
Overall, integrating both conventional ANNs and PIANN frameworks into process control architectures enables faster decision-making, enhanced process stability, and improved product quality, while simultaneously minimizing energy consumption and raw material use.
4. Conclusions
This study demonstrates that the proposed ANN-based modelling approach is a powerful and efficient tool for approximating the equilibrium gas-phase composition and carbon yield in key methane conversion processes of MP, DRM, SMR and POM. Unlike the conventional thermodynamic approach, which relies on computationally intensive Gibbs free energy minimization, the ANN model employs a data-driven methodology to learn the complex, nonlinear dependencies between process variables, such as temperature, pressure and reactant ratios, and the resulting equilibrium concentrations and carbon yield.Our findings confirm that the trained ANN not only achieves high predictive accuracy, closely matching the results obtained from classical thermodynamic calculations, but also generalizes effectively to unseen input conditions within the studied domain. This generalization capability highlights the robustness of the ANN framework and its applicability across a wide operating window relevant to industrial methane reforming.
The computational efficiency of the ANN is particularly notable. For instance, in the case of DRM, while the conventional method requires approximately 15 seconds to evaluate equilibrium compositions for 31 temperatures at three different pressures, the ANN accomplishes the same task in just 0.00233 seconds, what gives over six thousand times faster. This makes the ANN-based approach especially appropriate for applications where rapid evaluation of equilibrium states is integrated with CFD simulations that require frequent equilibrium data evaluations.
From the practical perspective, this work facilitates the implementation of the ANN model in other computational applications as the ANN weights are provided in the SI.
In conclusion, the proposed ANN-based approach presents as a promising alternative to conventional thermodynamic modelling for methane conversion processes.
Author contributions
R. C. (conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing - original draft, writing - review & editing), T. K (writing - original draft), S. M. (investigation, writing - original draft, writing - review & editing), E. M. (funding acquisition, writing - original draft), A. S. (funding acquisition, writing - original draft).Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: the SI includes parity plots for all cases listed in Table 2 of the article, as well as the ANN weights, allowing researchers and engineers to directly incorporate the network into their own equilibrium calculations. See DOI: https://doi.org/10.1039/d5re00322a.Acknowledgements
This work is related to the TITAN project (No. 101069474) funded by the European Union (HORIZON EUROPE Climate, Energy and Mobility). Views and opinions expressed are however those of the authors only and do not necessarily reflect those of the European Union or the European Climate, Infrastructure and Environment Executive Agency (CINEA). Neither the European Union nor the granting authority can be held responsible for them.References
- International Energy Agency, Towards Hydrogen Definitions Based on their Emissions Intensity, OECD, 2023, Available from: https://www.oecd.org/en/publications/towards-hydrogen-definitions-based-on-their-emissions-intensity_44618fd1-en.html Search PubMed.
- Global Hydrogen Review 2023, OECD, 2023, Available from: https://www.oecd-ilibrary.org/energy/global-hydrogen-review-2023_cb2635f6-en Search PubMed.
- Z. Taherian, M. Yousefpour, M. Tajally and B. Khoshandam, Catalytic performance of Samaria-promoted Ni and Co/SBA-15 catalysts for dry reforming of methane, Int. J. Hydrogen Energy, 2017, 42(39), 24811–24822, DOI:10.1016/j.ijhydene.2017.08.080.
- A. M. Gadalla and B. Bower, The role of catalyst support on the activity of nickel for reforming methane with CO2, Chem. Eng. Sci., 1988, 43(11), 3049–3062 CrossRef CAS.
- N. Sánchez-Bastardo, R. Schlögl and H. Ruland, Methane Pyrolysis for Zero-Emission Hydrogen Production: A Potential Bridge Technology from Fossil Fuels to a Renewable and Sustainable Hydrogen Economy, Ind. Eng. Chem. Res., 2021, 60(32), 11855–11881, DOI:10.1021/acs.iecr.1c01679.
- K. Ahmad, M. A. Jaoude, A. A. Bankole and K. Polychronopoulou, Hydrogen production towards carbon-free economy: A comprehensive thermodynamic analysis, Energy Convers. Manage., 2025, 326(December 2024), 119492, DOI:10.1016/j.enconman.2025.119492.
- K. Ahmad, K. Polychronopoulou and M. Abi Jaoude, CH4 valorisation reactions: A comparative thermodynamic analysis and their limitations, Fuel, 2022, 320(December 2021), 123877, DOI:10.1016/j.fuel.2022.123877.
- D. V. Demidov, I. V. Mishin and M. N. Mikhailov, Gibbs free energy minimization as a way to optimize the combined steam and carbon dioxide reforming of methane, Int. J. Hydrogen Energy, 2011, 36(10), 5941–5950, DOI:10.1016/j.ijhydene.2011.02.053.
- A. Di Nardo, M. Portarapillo, D. Russo and A. Di Benedetto, Hydrogen production via steam reforming of different fuels: thermodynamic comparison, Int. J. Hydrogen Energy, 2024, 55(July 2023), 1143–1160, DOI:10.1016/j.ijhydene.2023.11.215.
- K. Jabbour, Tuning combined steam and dry reforming of methane for “metgas” production: A thermodynamic approach and state-of-the-art catalysts, J. Energy Chem., 2020, 48, 54–91, DOI:10.1016/j.jechem.2019.12.017.
- C. Jensen and M. S. Duyar, Thermodynamic Analysis of Dry Reforming of Methane for Valorization of Landfill Gas and Natural Gas, Energy Technol., 2021, 9(7), 1–12 Search PubMed.
- J. Zhu, D. Zhang and K. D. King, Reforming of CH4 by partial oxidation: Thermodynamic and kinetic analyses, Fuel, 2001, 80(7), 899–905 CrossRef CAS.
- C. Guéret, M. Daroux and F. Billaud, Methane pyrolysis: Thermodynamics, Chem. Eng. Sci., 1997, 52(5), 815–827 CrossRef.
- K. Faungnawakij, R. Kikuchi and K. Eguchi, Thermodynamic evaluation of methanol steam reforming for hydrogen production, J. Power Sources, 2006, 161(1), 87–94 CrossRef CAS.
- C. C. R. S. Rossi, C. G. Alonso, O. A. C. Antunes, R. Guirardello and L. Cardozo-Filho, Thermodynamic analysis of steam reforming of ethanol and glycerine for hydrogen production, Int. J. Hydrogen Energy, 2009, 34(1), 323–332, DOI:10.1016/j.ijhydene.2008.09.071.
- A. Lima da Silva, C. D. F. Malfatti and I. L. Müller, Thermodynamic analysis of ethanol steam reforming using Gibbs energy minimization method: A detailed study of the conditions of carbon deposition, Int. J. Hydrogen Energy, 2009, 34(10), 4321–4330 CrossRef CAS.
- A. Ismaila, X. Chen, X. Gao and X. Fan, Thermodynamic analysis of steam reforming of glycerol for hydrogen production at atmospheric pressure, Front. Chem. Sci. Eng., 2021, 15(1), 60–71 CrossRef.
- S. Adhikari, S. Fernando, S. R. Gwaltney, S. D. Filip To, R. Mark Bricka and P. H. Steele, et al., A thermodynamic analysis of hydrogen production by steam reforming of glycerol, Int. J. Hydrogen Energy, 2007, 32(14), 2875–2880 CrossRef CAS.
- S. Shabbar and I. Janajreh, Thermodynamic equilibrium analysis of coal gasification using Gibbs energy minimization method, Energy Convers. Manage., 2013, 65, 755–763, DOI:10.1016/j.enconman.2012.02.032.
- A. Carranza-Abaid, H. F. Svendsen and J. P. Jakobsen, Thermodynamically consistent vapor-liquid equilibrium modelling with artificial neural networks, Fluid Phase Equilib., 2023, 564, 113597 CrossRef CAS , Available from: https://www.sciencedirect.com/science/article/pii/S0378381222002175?via%3Dihub.
- O. Del-Mazo-Alvarado and A. Bonilla-Petriciolet, Assessment of the simultaneous regression of liquid-liquid and vapor-liquid equilibria data of binary systems using NRTL and artificial neural networks, Fluid Phase Equilib., 2022, 561, 113537 CrossRef CAS , Available from: https://www.sciencedirect.com/science/article/pii/S0378381222001601?via%3Dihub.
- V. D. Nguyen, R. R. Tan, Y. Brondial and T. Fuchino, Prediction of vapor–liquid equilibrium data for ternary systems using artificial neural networks, Fluid Phase Equilib., 2007, 254(1–2), 188–197 CrossRef CAS , Available from: https://www.sciencedirect.com/science/article/pii/S0378381207001537.
- K. Piotrowski, J. Piotrowski and J. Schlesinger, Modelling of complex liquid–vapour equilibria in the urea synthesis process with the use of artificial neural network, Chem. Eng. Process., 2003, 42(4), 285–289 CrossRef CAS , Available from: https://www.sciencedirect.com/science/article/pii/S0255270102000600.
- H. E. Reynel-Ávila, A. Bonilla-Petriciolet and J. C. Tapia-Picazo, An artificial neural network-based NRTL model for simulating liquid-liquid equilibria of systems present in biofuels production, Fluid Phase Equilib., 2019, 483, 153–164 CrossRef , Available from: https://www.sciencedirect.com/science/article/abs/pii/S037838121830462X?via%3Dihub.
- S. Pimentel, B. Ferreira, F. Pradelle, F. da Silva Pimentel, B. Ferreira dos Santos and F. Pradelle, Investigation of artificial neural network topologies to predict biomass gasification and comparison with a thermodynamic equilibrium model, Energy, 2024, 308(February), 132762, DOI:10.1016/j.energy.2024.132762.
- C. A. Igwegbe, A. G. Adeniyi and J. O. Ighalo, ANN modelling of the steam reforming of naphthalene based on non-stoichiometric thermodynamic analysis, Chem. Pap., 2021, 75(7), 3363–3372, DOI:10.1007/s11696-021-01566-2.
- M. A. Hossain, B. V. Ayodele, C. K. Cheng and M. R. Khan, Artificial neural network modeling of hydrogen-rich syngas production from methane dry reforming over novel Ni/CaFe2O4 catalysts, Int. J. Hydrogen Energy, 2016, 41(26), 11119–11130, DOI:10.1016/j.ijhydene.2016.04.034.
- A. Zamaniyan, F. Joda, A. Behroozsarand and H. Ebrahimi, Application of artificial neural networks (ANN) for modeling of industrial hydrogen plant, Int. J. Hydrogen Energy, 2013, 38(15), 6289–6297, DOI:10.1016/j.ijhydene.2013.02.136.
- B. V. Ayodele and C. K. Cheng, Modelling and optimization of syngas production from methane dry reforming over ceria-supported cobalt catalyst using artificial neural networks and Box–Behnken design, J. Ind. Eng. Chem., 2015, 32, 246–258 CrossRef CAS , Available from: https://www.sciencedirect.com/science/article/abs/pii/S1226086X15004025?via%3Dihub.
- T. Ahmed, Equations of State and Phase Equilibria. In: Equations of State and PVT Analysis, Elsevier, 2016, pp. 467–597, Available from: https://app.knovel.com/hotlink/pdf/id:kt010WOPB3/equations-state-pvt-analysis/simulating-laboratory Search PubMed.
- NIST standard reference database number 69, NIST Chemistry WebBook, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 2005, p. 20899, Available from: https://cir.nii.ac.jp/crid/1573105974095160192%0Ahttp://webbook.nist.gov/chemistry Search PubMed.
- C. L. Yaws, Yaws' Handbook of Properties of the Chemical Elements, Knovel, 2011, Available from: https://app.knovel.com/hotlink/toc/id:kpYHPCE007/yaws-handbook-properties/yaws-handbook-properties Search PubMed.
- J. I. Villacampa, C. Royo, E. Romeo, J. A. Montoya, P. Del Angel and A. Monzón, Catalytic decomposition of methane over Ni-Al2O3 coprecipitated catalysts, Appl. Catal., A, 2003, 252(2), 363–383 CrossRef CAS , Available from: https://linkinghub.elsevier.com/retrieve/pii/S0926860X03004927.
- K. Hornik, M. Stinchcombe and H. White, Multilayer feedforward networks are universal approximators, Neural Networks, 1989, 2(5), 359–366 CrossRef.
- G. Cybenko, Approximation by superpositions of a sigmoidal function, Math. Control Signals Syst., 1989, 2(4), 303–314, DOI:10.1007/BF02836480.
| This journal is © The Royal Society of Chemistry 2026 |