 Open Access Article
Open Access ArticleKinetic modeling of multi-step transformations using sequential dynamic flow experiments
Klara
Silber
ab,
Florian L.
Wagner
ab,
Christopher A.
Hone
*ab and
C. Oliver
Kappe
 *ab
*ab
aCenter for Continuous Flow Synthesis and Processing, Research Center Pharmaceutical Engineering GmbH and University of Graz, Graz, Austria. E-mail: christopher.hone@rcpe.at
bInstitute of Chemistry, University of Graz, Graz, Austria. E-mail: oliver.kappe@uni-graz.at
First published on 12th November 2025
Abstract
In this paper, we present the development of a kinetic model for multi-step transformations, comprising of a Paal–Knorr pyrrole reaction followed by a nucleophilic aromatic substitution within a continuous-flow process, utilizing data obtained from sequential dynamic flow experiments. The reaction networks were fitted to achieve successful parameter estimation (7 parameters in total) with a R2 of 0.974 for the desired Paal–Knorr product and a R2 of 0.998 for the nucleophilic aromatic substitution product. Model validation based on dynamic flow experiments was extended beyond the previously explored experimental space. In silico simulation involving a threefold higher concentration of the nucleophile than previously studied resulted in approximately 7% model predicted difference to the experimental results.
Introduction
The synthesis of active pharmaceutical ingredients (APIs) has been traditionally performed under batch conditions, requiring multiple discrete steps with intermediate workup and purification. This approach, while well-established, generates substantial solvent waste, extends processing times, and necessitates significant operator intervention.1 Recently, there has been a shift in pharmaceutical manufacturing to continuous flow synthesis with reaction telescoping, where multiple reaction steps are conducted sequentially without intermediate purification. This strategy offers considerable advantages, including reduced waste generation, enhanced process efficiency, and improved safety by limiting direct human interaction with potentially hazardous materials.1,2 However, implementing reaction telescoping presents substantial challenges, as complex interactions between intermediates, by-products/side products, and reaction conditions must be considered.3 Unlike discrete optimization of individual steps, telescoped processes require simultaneous global optimization to ensure overall efficiency and product quality (Fig. 1).4,5Process analytical technology (PAT)6 has become an integral part of continuous flow synthesis, facilitating real-time reaction monitoring for process control,7,8 self-optimization,9,10 and reaction kinetic studies.11,12 The combination of multiple PAT tools enhances process understanding and enables the possibility to obtain concentration values for species of complex reaction mixtures. Notable examples include Nambiar et al., who implemented inline FTIR spectroscopy and online liquid chromatography-mass spectrometry LC-MS to monitor and optimize a three-step continuous flow synthesis of sonidegib.3 Clayton et al. successfully applied Bayesian self-optimization for a telescoped Heck cyclization–deprotection reaction sequence, utilizing multipoint sampling for online HPLC for accurate real-time reaction monitoring.10 These examples highlight how real-time analytical methods support the efficient implementation and control of telescoped reactions.
Optimization strategies play a crucial role in refining chemical reactions. A simple approach is the one-factor-at-a-time (OFAT) method, where a single parameter is varied while others are held constant. However, this approach is inefficient and often misleading, as it fails to capture interaction effects between parameters.13 Thus, the global optimal conditions within the design space can be missed. Design of experiments (DoE), which generates statistical models to describe system behavior, can be considered as more robust methodology.14,15 Although, as the model is not based on underlying chemistry, only interpolation within the generally narrow design space is typically valid.13 Fath et al. applied DoE to optimize an imine synthesis in a microreactor.16 Self-optimization does not require a priori knowledge of the reaction system. Instead, reactions are performed iteratively suggested by the algorithm based on results of the previous experiments. Self-optimization can cover a wider design space when compared to DoE. In addition, recently utilized optimization algorithms can focus on both, exploration of a wider space and exploitation around regions where good results have previously been measured.17 Several examples of successful integration for automated flow reactors, operating in closed-loop systems without human intervention are shown in literature.18,19 Amara et al. applied self-optimization to continuous-flow reactors.20 Moore et al. describes the reaction optimization of a Paal–Knorr reaction in a microfluidic system.21 Wagner et al. showed the implementation of Bayesian self-optimization for pharmaceutically relevant amide coupling reactions.22 Cortés-Borda et al. applied autonomous self-optimization for the synthesis of carpanone in flow.23 Kinetic modeling, which provides chemical insights, enables in silico simulations even beyond the explored design space, offering a powerful tool for process optimization.13,24 Moreover, as they are based on the underlying chemical reaction processes they can be easily linked to reactor performance equations to consider different reactor types and configurations. Although, additional information on mass transfer and heat evolution within the process is an important consideration for scale-up, alongside to the kinetics.25
The work described herein focuses on the exploitation of kinetic modeling as an optimization approach for a two-step continuous flow synthesis. Flow reactors can be operated either under steady-state or dynamic conditions. While steady-state operation requires extended equilibration times, dynamic experimentation—where input parameters such as flow rate and temperature are continuously varied—allows for rapid data acquisition and therefore experimental time and material consumption can be reduced.26 Hone et al. and Taylor et al. applied dynamic experimentation for rapid development of a kinetic model.11,27 Fath et al. used non-steady state conditions for kinetic modeling applying FTIR as PAT.28 Moore et al. investigated the Paal–Knorr pyrrole synthesis using 2,5-hexanedione and ethanolamine as substrates, applying flow ramps and online infrared spectroscopy as PAT.21 Silber et al. used dynamic experimentation to build a digital twin based on kinetic modeling.12,29 The implementation of dynamic experiments for data-rich optimization was recently reviewed.30 The challenges of automating the optimization of multistep process were reviewed by Clayton.5 However, to date, no research kinetic model has been derived for a two-step reaction sequence using a dynamic experimentation approach.
This study aimed to consider the gap in the utilization of dynamic experimentation to develop a rate-based understanding of a two-step telescope flow process. A focus was on dealing with complex interactions of intermediates from a previous step to minimize impurity formation and ensuring solubility of all species involved in the concentrations present. Complex chemometric models were required for accurate quantification of involved species and a sophisticated experimental design was implemented to have a broad experimental space accessible.
Results and discussion
Reactions of interest and experimental setup
This project investigated a Paal–Knorr pyrrole synthesis using ethylenediamine (1) and 2,5-hexanedione (2) as reactants, followed by a nucleophilic aromatic substitution (SNAr) reaction between 2-fluoronitrobenzene (5) and the Paal–Knorr product (Scheme 1). Preliminary experiments showed that the Paal–Knorr reaction resulted in two products: a pyrrole on one amino group (product (3)) or on both amino groups (overreacted product (4)). The free amino group in 3 can then react as a nucleophile in the SNAr reaction. Although, 3 is a relatively unreactive nucleophile in the SNAr reaction, requiring temperatures above the boiling point of acetonitrile to achieve desired reaction times of several minutes. Therefore, it would be difficult to study the kinetics of this reaction under moderate conditions in batch.Telescoping these two reactions posed many challenges, in particular the selection of a suitable solvent and base, and in the management of side product formation. The solvent must have good solubility for all species involved in both steps over the concentration range studied to prevent reactor clogging and ensure compatibility with the equipment. Acetonitrile (MeCN) was chosen as it met these criteria, can be considered as green solvent31 and influenced the reaction kinetics. In particular, it limited the formation of 4 in the Paal–Knorr reaction to less than 3% within the experimental space studied. Another solvent considered for the Paal–Knorr reaction is a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of toluene and methanol, which significantly increased the rate for the formation of 4 and complicated UHPLC analysis due to overlaying peaks of toluene and reaction components. DMSO was initially tested in batch reactions for the SNAr reaction, which significantly increased the reaction rate of the SNAr reaction. However, due to issues with equipment compatibility MeCN was chosen as a reaction solvent for the telescoped process. The significantly higher viscosity of DMSO impacted the accuracy of the utilized HPLC pumps and caused pressure-related issues with our UHPLC injection system. In terms of base selection, 1,1,3,3-tetramethylguanidine (TMG, 6) was used, but its nucleophilicity led to unwanted side-product formation in the SNAr reaction, necessitating its inclusion in the kinetic model (see SI). To avoid this side product formation, 2-tert-butyl-1,1,3,3-tetramethylguanidine (tBuTMG) was used as a non-nucleophilic base in a reference experiment. Other bases, such as triethylamine and 1,8-diazabicyclo[5.4.0]undec-7-ene (DBU), were also evaluated. Triethylammonium fluoride from triethylamine led to precipitation, while DBU showed high reactivity,32 increasing 2-fluoronitrobenzene consumption beyond that observed with TMG.
1 mixture of toluene and methanol, which significantly increased the rate for the formation of 4 and complicated UHPLC analysis due to overlaying peaks of toluene and reaction components. DMSO was initially tested in batch reactions for the SNAr reaction, which significantly increased the reaction rate of the SNAr reaction. However, due to issues with equipment compatibility MeCN was chosen as a reaction solvent for the telescoped process. The significantly higher viscosity of DMSO impacted the accuracy of the utilized HPLC pumps and caused pressure-related issues with our UHPLC injection system. In terms of base selection, 1,1,3,3-tetramethylguanidine (TMG, 6) was used, but its nucleophilicity led to unwanted side-product formation in the SNAr reaction, necessitating its inclusion in the kinetic model (see SI). To avoid this side product formation, 2-tert-butyl-1,1,3,3-tetramethylguanidine (tBuTMG) was used as a non-nucleophilic base in a reference experiment. Other bases, such as triethylamine and 1,8-diazabicyclo[5.4.0]undec-7-ene (DBU), were also evaluated. Triethylammonium fluoride from triethylamine led to precipitation, while DBU showed high reactivity,32 increasing 2-fluoronitrobenzene consumption beyond that observed with TMG.
Another complication in the telescoped process was the interaction between species from different reaction steps. Residual ethylenediamine (1) participated in the SNAr reaction with 2-fluoronitrobenzene (5), causing precipitation of products where 1 had reacted as a nucleophile with one or two molecules of 5. In addition, 1 is a stronger nucleophile than 3, further reducing the formation of the desired SNAr product (7).
Initially, we attempted to perform the dynamic experiments for both reactions simultaneously in a telescoped configuration. However, this process led to insoluble impurity formation with leftover ethylenediamine (1), meaning full conversion of the ethylenediamine was required to telescope the reaction. This highlights the challenge associated with processing two steps simultaneously, the presence of multiple species and reactive sites increases the level of complexity significantly. Instead, the kinetics of the Paal–Knorr reaction were studied independently, while the telescoped setup was used to study the kinetics of the SNAr reaction. In order to maintain flexibility for dynamic experiments for the SNAr reaction while ensuring complete conversion of 1 in the first step, a reservoir was introduced to separate the two reactions, as shown in Fig. 2.
The kinetics of the Paal–Knorr pyrrole reaction and the SNAr reaction were studied using a 4.23 mL coil reactor. For the telescoped process another 12.0 mL coil reactor was implemented to the setup to operate the Paal–Knorr reaction under constant conditions. Automated dynamic experimentation was achieved using HPLC pumps for reagent delivery and a thermostat for temperature control, managed by a HiTec Zang Lab Manager, with flow rate ramps and temperature profiles programmed in HiText (HiTec Zang). Real-time process monitoring was implemented using inline Fourier transform infrared spectroscopy (FTIR) (Mettler Toledo, React IR 702L, DS Micro Flow Cell Diamond) and online ultra-high-performance liquid chromatography (UHPLC) (Shimadzu, Nexera X2) as process analytical technologies (PAT). FTIR data were quantified using a partial least squares (PLS) model using the second derivative of the spectrum, allowing quantification of 2, 3 and 4. UHPLC data was quantified by calibration of 3, 4, 5 and 7.
The implementation of inline FTIR for the Paal–Knorr pyrrole reaction posed a chemometric challenge due to the structural similarity between 3 and 4, resulting in similar IR spectra. Simpler examples were previously studied using FTIR as PAT by Moore et al.33 and Schrecker et al.,34 although without the challenge to distinguish between the desired and an overreacted product. To ensure accurate quantification, online UHPLC was used alongside FTIR. FTIR is especially interesting due to its rapid data acquisition, giving a datapoint every 15 s, whereas UHPLC samples were measured approximately every 3.7 min. 2,5-Hexanedione (2) can be quantified only by FTIR while accurate quantification of ethylenediamine was not possible with the selected PAT methods. Mass balance analysis using FTIR-derived concentrations alone resulted in an average mass balance error of about 7%, which was reduced to below 3% by using UHPLC data from 3 and 4. In the telescoped process, concentrations of 2, 3 and 4 were determined by FTIR at the inlet of the second reactor, while the SNAr reaction mixture was quantified using online UHPLC.
Dynamic flow experiments to study kinetics of the Paal–Knorr pyrrole reaction
To efficiently study the kinetics of the Paal–Knorr pyrrole reaction in flow, a dynamic automated experimentation approach was implemented. In this approach, the flow rate was linearly decreased while keeping the temperature and input concentrations of ethylenediamine (1) and 2,5-hexanedione (2) constant throughout each ramp (Fig. 3). The design space was chosen to cover a wide temperature range to accurately fit the activation energy, as the reaction shows only low temperature dependence, and the stoichiometry was chosen to operate in a range enabling full conversion of ethylenediamine while limiting excess of 2 and formation of 4 as much as possible. The concentrations were varied within the range desired to operate in for the telescoped reaction and to evaluate the reaction order for each reactant. A total of 14 dynamic ramps were performed at temperatures ranging from 25 °C to 125 °C. Concentrations of 1 were varied from 0.2 to 0.4 mol L−1, using 1.0 to 1.6 equivalents of 2. In addition, a steady-state experiment was performed at flow rates of 2 mL min−1, 1 mL min−1, 0.5 mL min−1, and 0.33 mL min−1 to validate the dynamic experimentation approach (details in SI).Kinetic fitting was performed in Dynochem35 (Scale-up Systems, Mettler Toledo) using second-order rate equations corresponding to the reaction scheme shown in Scheme 2. Dynochem uses a modified Arrhenius equation which uses a rate constant at a specified reference temperature (kref). This approach resulted in the differential eqn (1) and (2) used in the fitting process. Residence time distribution (RTD) experiments were performed within a flow rate range of 0.5 mL min−1 to 2.0 mL min−1 resulting in Bodenstein (Bo) numbers of >600. Based on this analysis, minimal axial dispersion and minimal deviations from plug flow would be expected (values above 100 indicate plug flow behaviour).36 Therefore, the influence of dispersion on the kinetic parameters could be assumed to be negligible.
Parameter fitting was performed using data from 9 out of the 14 experiments, with the remaining 5 experiments used for model validation. An overall reaction order of 2 gave the best fit with a model selection criterion of 3.35 while models with an order of 1 only for one reactant and 0 for the other resulted in a worse fit (model selection criterion of 2.67 for the model with reaction order of 1 for the amine 1 or 3 and 2.87 for the model with reaction order of 1 for 2,5-hexandione 2). In addition, another model, including intermediate formation was fitted resulting in the same model selection criterion of 3.35 as the simple second order model (details in SI). As inclusion of intermediate formation did not improve the quality of the model, the simpler model was chosen to describe the reaction. This model showed good agreement with the experimental data (Fig. 4). The identified kinetic parameters (kref,1 = 1.95e−2 ± 0.12e−2 L mol−1 s−1, kref,2 = 3.54e−4 ± 0.10e−4 L mol−1 s−1, Ea,1 = 4.67 ± 2.13 kJ mol−1) correspond to a reference temperature of 75 °C. The formation of 4 was observed to have a slow reaction rate and very low temperature dependence. Based on preliminary studies, the formation of 4 appears to primarily be influenced by the reaction solvent. In the reaction solvent (MeCN) experiments were performed in a range from 25 to 125 °C, each resulting in very low formation of 4, nearly independent of the temperature. Consequently, the empirical activation energy for this step (Ea,2) was found to be close to zero and was fixed at 0 kJ mol−1 in the model. However, when this reaction was performed in toluene/methanol 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the formation of 4 was significantly faster than in acetonitrile and significant temperature dependence was found (kref,2 = 4.21e−3 ± 0.05e−3 L mol−1 s−1, Ea,2 = 18.9 ± 0.4 kJ mol−1) demonstrating solvent dependence of this reaction step.
1, the formation of 4 was significantly faster than in acetonitrile and significant temperature dependence was found (kref,2 = 4.21e−3 ± 0.05e−3 L mol−1 s−1, Ea,2 = 18.9 ± 0.4 kJ mol−1) demonstrating solvent dependence of this reaction step.
 | (1) |
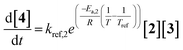 | (2) |
 | ||
| Fig. 4 Model predicted concentration vs. measured concentration for the Paal–Knorr pyrrole reaction (a) 2,5-hexandione 2 and (b) product 3. | ||
Dynamic flow experiments in a telescoped reaction setup
To investigate the kinetics of the SNAr reaction within a telescoped process setup, the Paal–Knorr reaction was conducted at 75 °C with a constant flow rate of 0.3 mL min−1 for each pump, using 1.2 equivalents of 2 to ensure complete conversion of ethylenediamine (1), to avoid side product formation that would result in reactor clogging in the following nucleophilic aromatic substitution. The resulting reaction mixture was continuously collected in a reservoir and directly used in the second step. Inline FTIR was employed to analyze the mixture immediately before mixing with other reagents, ensuring accurate determination of input concentrations resulting in 89 ± 4% of 3 within the experimental time. Within a ramp the concentration of 3 changed less than ±2.5% and therefore a constant average concentration of 3 was used for the fitting process. For the second step, dynamic experimentation was carried out by linearly varying the flow rate from 1 mL min−1 to 0.33 mL min−1. Six dynamic experiments were performed at temperatures ranging from 130 °C to 150 °C using 1.2 to 2.0 equivalents of the first step product (3) and using a fixed concentration of 100 mmol L−1 of 2-fluoronitrobenzene (5) (Fig. 5).1,1,3,3-Tetramethylguanidine (TMG) was used as base for the SNAr reaction; however, it also acted as a nucleophile, leading to the formation of impurity (8). This resulted in a discrepancy in the mass balance between 5 and the desired SNAr product (7), which was attributed to the formation of 8, requiring consideration of this impurity formation in the kinetic model.
Kinetic fitting was performed using Dynochem based on the reaction scheme shown in Scheme 3. Three rate equations were applied in this model. The parameters for the third reaction were set to kref = 100 L mol−1 s−1 and Ea = 0 kJ mol−1. This was based on the assumption that the acid/base reaction is significantly faster than the other reactions involved.
 | (3) |
 | (4) |
 | ||
| Scheme 3 Reaction network of the SNAr reaction used for kinetic modelling. The reaction rate of the fast acid–base reaction was fixed at 100 L mol−1 s−1. | ||
 | ||
| Fig. 6 Model predicted concentration vs. measured concentration for the SNAr reaction of (a) 2-fluoronitrobenzene 5 and (b) SNAr product 7. | ||
Model validation, in silico exploration
The kinetic models could then be applied for in silico exploration beyond the experimentally investigated space to investigate the performance at different experimental conditions. To demonstrate this capability, simulations were conducted using 4.0 to 6.0 equivalents of product (3) – far exceeding the range used for model development (1.2 to 2.0 equivalents), while applying the same experimental design as used for model development, with 100 mmol L−1 of 5 at a temperature of 140 °C. To validate the simulation, the experiments were performed in the laboratory, increasing the yield of 7 from 30% up to 64% at 140 °C. The simulated results are ∼7% higher than experimental results (Fig. 7). This deviation of the experimental result from the model prediction can be attributed to a combination of model limitations and experimental error. Although, these simulations show that kinetic modelling is an excellent tool for in silico optimization beyond the experimentally investigated space.Conclusions
We have successfully addressed the challenges of telescoping, particularly in minimizing the unwanted interaction of species from different steps within the two-step Paal–Knorr pyrrole reaction and nucleophilic aromatic substitution. Utilizing a reservoir between the two steps allowed us to leverage a dynamic experimentation approach, enabling rapid exploration of a wide experimental space. The data collected has been utilized for kinetic modeling, and the model's validity has been demonstrated to extend beyond the explored space through in silico simulation of reaction conditions, resulting in excellent agreement with the experimental data. Our future efforts will be directed towards automating data processing and kinetic fitting, aiming to establish a fully automated workflow with minimal human intervention and to perform the process fully continuously without the need of separation for optimization.Conflicts of interest
There are no conflicts to declare.Data availability
Hereby we confirm that all the data necessary to reproduce our work are available in the supplementary information (SI) of this work. This document contains general methods, analytical methods, experimental design of the flow setup, as well as all the kinetic results of the continuous-flow experiments.Supplementary information is available. See DOI: https://doi.org/10.1039/d5re00306g.
Acknowledgements
The Research Center Pharmaceutical Engineering (RCPE) is funded within the framework of COMET – Competence Centers for Excellent Technologies by BMK, BMAW, Land Steiermark, and SFG. The COMET program is managed by the FFG. This work was funded through the Austrian Research Promotion Agency (FFG) as part of the “Twin4Pharma” project within the COMET Module program. We would like to thank Scale-up Systems/Mettler Toledo for providing the kinetic software and Charles Gordon for his support.Notes and references
- A. Domokos, B. Nagy, B. Szilágyi, G. Marosi and Z. K. Nagy, Org. Process Res. Dev., 2021, 25, 721–739 CrossRef CAS.
- B. Pieber, K. Gilmore and P. H. Seeberger, J. Flow Chem., 2017, 7, 129–136 CrossRef CAS.
- A. M. K. Nambiar, C. P. Breen, T. Hart, T. Kulesza, T. F. Jamison and K. F. Jensen, ACS Cent. Sci., 2022, 8, 825–836 CrossRef CAS PubMed.
- T. Dietz, K. Klamroth, K. Kraus, S. Ruzika, L. E. Schäfer, B. Schulze, M. Stiglmayr and M. M. Wiecek, Eur. J. Oper. Res., 2020, 280, 581–596 CrossRef.
- A. D. Clayton, Chem.: Methods, 2023, 3, e202300021 CAS.
- J. J. Workman, B. Lavine, R. Chrisman and M. Koch, Anal. Chem., 2011, 83, 4557–4578 CrossRef CAS PubMed.
- D. E. Fitzpatrick and S. V. Ley, Tetrahedron, 2018, 74, 3087–3100 CrossRef CAS.
- P. Sagmeister, R. Lebl, I. Castillo, J. Rehrl, J. Kruisz, M. Sipek, M. Horn, S. Sacher, D. Cantillo, J. D. Williams and C. O. Kappe, Angew. Chem., Int. Ed., 2021, 60, 8139–8148 CrossRef CAS PubMed.
- C. Mateos, M. J. Nieves-Remacha and J. A. Rincón, React. Chem. Eng., 2019, 4, 1536–1544 RSC.
- A. D. Clayton, E. O. Pyzer-Knapp, M. Purdie, M. F. Jones, A. Barthelme, J. Pavey, N. Kapur, T. W. Chamberlain, A. J. Blacker and R. A. Bourne, Angew. Chem., 2023, 135, e202214511 CrossRef.
- C. A. Hone, N. Holmes, G. R. Akien, R. A. Bourne and F. L. Muller, React. Chem. Eng., 2017, 2, 103–108 RSC.
- K. Silber, P. Sagmeister, C. Schiller, J. D. Williams, C. A. Hone and C. O. Kappe, React. Chem. Eng., 2023, 8, 2849–2855 RSC.
- C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, R. A. Bourne, C. N. Johnson and A. A. Lapkin, Chem. Rev., 2023, 123, 3089–3126 CrossRef CAS PubMed.
- D. W. Lendrem, B. C. Lendrem, D. Woods, R. Rowland-Jones, M. Burke, M. Chatfield, J. D. Isaacs and M. R. Owen, Drug Discovery Today, 2015, 20, 1365–1371 CrossRef PubMed.
- M. R. Owen, C. Luscombe, L. W. Lai, S. Godbert, D. L. Crookes and D. Emiabata-Smith, Org. Process Res. Dev., 2001, 5, 308–323 CrossRef CAS.
- V. Fath, N. Kockmann, J. Otto and T. Röder, React. Chem. Eng., 2020, 5, 1281–1299 RSC.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104, 148–175 Search PubMed.
- G. Tom, S. P. Schmid, S. G. Baird, Y. Cao, K. Darvish, H. Hao, S. Lo, S. Pablo-García, E. M. Rajaonson, M. Skreta, N. Yoshikawa, S. Corapi, G. D. Akkoc, F. Strieth-Kalthoff, M. Seifrid and A. Aspuru-Guzik, Chem. Rev., 2024, 124, 9633–9732 CrossRef CAS PubMed.
- M. Abolhasani and E. Kumacheva, Nat. Synth., 2023, 2, 483–492 CrossRef CAS.
- Z. Amara, E. S. Streng, R. A. Skilton, J. Jin, M. W. George and M. Poliakoff, Eur. J. Org. Chem., 2015, 2015, 6141–6145 CrossRef CAS.
- J. S. Moore and K. F. Jensen, Org. Process Res. Dev., 2012, 16, 1409–1415 CrossRef CAS.
- F. L. Wagner, P. Sagmeister, T. G. Tampone, V. Manee, D. Yerkozhanov, F. G. Buono, J. D. Williams and C. O. Kappe, ACS Sustainable Chem. Eng., 2024, 12, 10002–10010 CrossRef CAS.
- D. Cortés-Borda, E. Wimmer, B. Gouilleux, E. Barré, N. Oger, L. Goulamaly, L. Peault, B. Charrier, C. Truchet, P. Giraudeau, M. Rodriguez-Zubiri, E. Le Grognec and F.-X. Felpin, J. Org. Chem., 2018, 83, 14286–14299 CrossRef PubMed.
- M. J. Willis and M. von Stosch, Comput. Chem. Eng., 2016, 90, 31–43 CrossRef CAS.
- E. H. Stitt and M. J. H. Simmons, in Process Understanding, 2011, pp. 155–198 Search PubMed.
- S. Mozharov, A. Nordon, D. Littlejohn, C. Wiles, P. Watts, P. Dallin and J. M. Girkin, J. Am. Chem. Soc., 2011, 133, 3601–3608 CrossRef CAS PubMed.
- C. J. Taylor, M. Booth, J. A. Manson, M. J. Willis, G. Clemens, B. A. Taylor, T. W. Chamberlain and R. A. Bourne, Chem. Eng. J., 2021, 413, 127017 CrossRef CAS.
- V. Fath, P. Lau, C. Greve, N. Kockmann and T. Röder, Org. Process Res. Dev., 2020, 24, 1955–1968 CrossRef CAS.
- P. Sagmeister, C. Schiller, P. Weiss, K. Silber, S. Knoll, M. Horn, C. A. Hone, J. D. Williams and C. O. Kappe, React. Chem. Eng., 2023, 8, 2818–2825 RSC.
- J. D. Williams, P. Sagmeister and C. O. Kappe, Curr. Opin. Green Sustainable Chem., 2024, 47, 100921 CrossRef CAS.
- F. P. Byrne, S. Jin, G. Paggiola, T. H. M. Petchey, J. H. Clark, T. J. Farmer, A. J. Hunt, C. Robert McElroy and J. Sherwood, Sustainable Chem. Processes, 2016, 4, 7 CrossRef.
- J. Muzart, ChemistrySelect, 2020, 5, 11608–11620 CrossRef CAS.
- J. S. Moore and K. F. Jensen, Angew. Chem., Int. Ed., 2014, 53, 470–473 CrossRef CAS PubMed.
- L. Schrecker, J. Dickhaut, C. Holtze, P. Staehle, M. Vranceanu, K. Hellgardt and K. K. Hii, React. Chem. Eng., 2023, 8, 41–46 RSC.
- Dynochem, Scale-up Suite 1.0, Mettler Toledo, Dublin, Ireland, 2025 Search PubMed.
- O. Levenspiel, Chemical reaction engineering, 1999, vol. 38 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |







