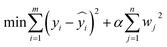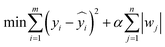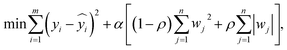Machine learning-driven optimization of extraction process and development of quality standards for traditional Chinese medicine (TCM) formulae in primary liver cancer

Abstract

Traditional Chinese medicine (TCM) formula extraction optimization is vital for clinical efficacy and standardization. This study targeted an anti-hepatocarcinoma formula, combining orthogonal experimental design (OED) with machine learning (ML) to optimize extraction—focused on extraction yield and paeoniflorin content. OED revealed extraction time as the key factor influencing both metrics, while ML modeling identified optimal parameters. Experimental validation achieved a 43.21% extraction yield and 74.2 mg total paeoniflorin, confirming ML's utility in process refinement. The OED–ML integration proves a powerful tool for TCM preparation optimization, accelerating cost-effective, eco-friendly technology development and advancing formula standardization. This work highlights AI's role in modernizing TCM R&D, offering a replicable framework to balance efficacy, affordability, and sustainability.

---

Introduction

Traditional Chinese Medicine (TCM), a time-honored system integrating ancient wisdom with modern scientific validation, has emerged as a global cornerstone for pharmaceutical innovation and a catalyst for its own systematic modernization.¹ The extraction process of Chinese medicinal materials represents a critical step in both pharmaceutical research and the modernization of TCM. Its significance is manifested not only in enhancing the purity and biological activity of pharmacologically active constituents but also in advancing the standardization, internationalization, and multidisciplinary application of TCM.^2,3 In the field of extraction technologies, not only are traditional water extraction methods employed,⁴ but also advanced techniques such as supercritical fluid extraction^5,6 and ultrasound-assisted extraction⁷ are utilized. Nevertheless, conventional water extraction remains the dominant approach. According to the Chinese Pharmacopoeia, the processing of 646 proprietary Chinese medicines involves water extraction technology.⁸ Furthermore, pharmacological studies on traditional classical formula preparations of Chinese herbal compounds primarily focus on “decoction in water” as the main method of administration. Water extraction or decoction not only aligns with the theories of TCM but also contributes to the conservation of Chinese medicinal resources, facilitates the preservation of traditional processing techniques, and reduces costs in industrial production. Traditional water extraction processes are typically evaluated based on conventional characteristic indicators (extraction yield). These features often possess subjectivity and specificity, lacking a comprehensive perspective. Against the backdrop of the global Pharma 4.0 revolution, traditional water extraction processes, characterized by conventional evaluation metrics, are increasingly inadequate to meet the current demands of drug development research.^9,10 There is an urgent need to develop digitalized and intelligent water extraction processes, centered on automation, digitization, and intellectualization, to better leverage the core role of these traditional techniques in pharmaceutical formulation research and development.

In recent years, the concept of Quality by Design (QbD) has been introduced to optimize extraction processes, thereby promoting the standardization, modernization, and comprehensive quality control of pharmaceutical preparations throughout their entire lifecycle.¹¹ By OED or response surface methodology (RSM), the critical extraction process parameters (CPPs) that influence the critical quality attributes (CQAs) of TCM compounds can be identified. This approach enables the establishment of quantitative relationships between CQAs and CPPs.^12,13 Subsequently, a design space for the extraction process can be constructed to ensure product quality and stability within this defined space, thereby achieving comprehensive quality control throughout the entire drug manufacturing process. This QbD-based approach demonstrates high experimental efficiency and strong model robustness, making it suitable for multi-objective optimization of complex processes. However, it remains inadequate for handling high-dimensional nonlinear problems and exhibits limited capability in interpreting interactions involving more than three factors. As a first-generation intelligent optimization strategy for TCM preparations, it falls short in addressing the needs of complex formulation processes—particularly for multi-component TCM compounds with intricate interactions.

With the rapid advancement of artificial intelligence across various fields, ML has been increasingly applied to multiple domains within the pharmaceutical industry.¹⁴ It enables the analysis of historical data to predict and characterize relationships between influencing factors and observed outcomes. It enables the transformation of traditional development models reliant on trial-and-error and empirical experience by adopting data-driven methodologies to accelerate R&D processes, optimize workflows, and enhance product quality. In the context of pharmaceutical extraction process optimization, this approach analyzes historical experimental data to construct complex mapping relationships between extraction parameters and outcomes.¹⁵ It enables the prediction of globally optimal process parameters with minimal data requirements, followed by experimental validation to evaluate model predictive accuracy and robustness.^16,17 This approach not only enables researchers and enterprises to rapidly identify optimal extraction conditions and enhance the extraction efficiency of target compounds, but reduces R&D costs and minimizes resource wastage. It is widely recognized as a second-generation intelligent solution for extraction process optimization research and has been extensively applied in studies focusing on the enhancement of extraction techniques.

Chinese herbal formulas, as a unique form of natural medicine, are widely popular in China and Southeast Asian countries. Maximizing the extraction of active substances from these formulas is a crucial prerequisite for their therapeutic efficacy.¹⁸ In our previous work, we successfully screened effective TCM prescriptions for the treatment of primary liver cancer (PLCTCMP) based on Traditional Chinese Medicine Inheritance Computer System (TCMICS) V3.0. Through integrative pharmacology and molecular simulation approaches, combined with in vitro experiments, we elucidated that the prescription and its primary active component, paeoniflorin, inhibit the proliferation of liver cancer cells by modulating the Ras/Raf/MEK/ERK, AKT/NF-κB, and JAK-STAT signaling pathways.¹⁹ To maximize the characterization of active constituents in the formula, paeoniflorin was utilized as the observation index in an OED for the preliminary screening of the extraction process. This approach served as an initial exploration and factor screening, establishing a foundational dataset for further optimization via ML. Therefore, this study further employed an expanded OED dataset and multiple ML algorithms, focusing on the liver cancer formula, to establish a quantitative analysis method for paeoniflorin as the primary active constituent. Subsequently, using key active constituents (e.g., paeoniflorin) and extract yield as critical observation indices, we characterized key process parameters including water addition volume, extraction time, and extraction frequency. Establishing a more refined non-linear model to achieve global optimization of the extraction process for the liver cancer formula. The optimization outcomes were subsequently subjected to rigorous experimental validation. This methodology aims to provide a theoretical foundation and technical support for the standardization of compound formulations and their clinical translation and application.

Materials and methods

Instruments

High-performance liquid chromatograph (LC-2030C 3D Plus) and C18 column (4.6 × 250 mm, 5 µm) were obtained from Shimadzu Corporation. Desktop low-speed centrifuge (SF-TDL-4A) was purchased from Shanghai Fulgor Analysis Apparatus Co., Ltd, handheld centrifuge (S1010E) was obtained from SCILOGEX, LLC. Ultrasonic cleaner (KQ5200E) was purchased from Kun Shan Ultrasonic Instruments Co., Ltd. Electronic balances (B6002 and BSA224S) were obtained from Shanghai Liangping Instrument Co., Ltd and Sartorius Scientific Instruments (Beijing) Co., Ltd respectively. Analytical balance (MS105DU) was purchased from Mettler-Toledo International Trading (Shanghai) Co., Ltd. Glass instrument airflow dryer (C-30) was obtained from Zhengzhou Asus Instrument Co., Ltd. Electronic thermostat type electric heating sleeve (DZTW) was purchased from Beijing Brightness Medical Equipment Co., Ltd. Electric-heated thermostatic water bath (DK-2000-IIIL) and electric thermostatic drying oven (WGL-125L) were purchased from Tianjing Taisote Medical Equipment Inc. Vacuum drying oven was obtained from Shanghai Huitai Instruments Manufacturing Co., Ltd.

Chemicals and materials

Phosphoric acid (cat. no. 190900), acetonitrile (cat. no. F24O86202), and methanol (cat. no. F24O85202) were obtained from Thermo Fisher Scientific (China) Co., Ltd. Purified water (cat. no. 20240819) were purchased from Hangzhou Wahaha Group Co., Ltd. Ethyl alcohol (cat. no. 20210512) were obtained from Sinopharm Chemical Reagent Co., Ltd. Paeoniflorin (cat. no. 23072811) were purchased from Shanghai Topscience Co., Ltd. Bupleurum chinense DC., Paeonia lactiflora Pall., Atractylodes macrocephala Koidz., Poria cocos (Schw.) Wolf, Glycyrrhiza uralensis Fisch., and Angelica sinensis (Oliv.) Diels were obtained from Bozhou Chongyuan Pharmaceutical Co., Ltd.

Standard solution and sample solution preparation

Precisely weigh 0.1 g of pulverized Paeonia lactiflora Pall. sample powder, transfer to a 50 mL volumetric flask, add 35 mL of dilute ethanol, subject to ultrasonic treatment (power 240 W, frequency 45 kHz) for 30 minutes, allow to cool, then dilute with dilute ethanol to the mark, and mix well to obtain a Paeonia lactiflora Pall. sample (PLPS) containing 2 µg per mL.

According to the Chinese Pharmacopoeia 2025 Edition, Volume I, an appropriate amount of paeoniflorin reference standard was accurately weighed, dissolved and diluted with methanol, and then made up to volume to obtain a paeoniflorin standard solution (PSS) containing 60 µg mL⁻¹.

According to our previous research methodology,¹⁹ the PLCTCMP sample (PLCTCMPS) solution was prepared as follows: precisely weigh 0.050 g of the dried extract powder, transfer to a 10 mL volumetric flask, dissolve with dilute ethanol, and subject to ultrasonic treatment. Subsequently, dilute to the mark with dilute ethanol and mix thoroughly to obtain a homogeneous solution.

Chromatographic conditions

The quantitative analysis of paeoniflorin was performed using high-performance liquid chromatography (HPLC) (Shimadzu 2030 system) equipped with a C18 column (4.6 × 250 mm, 5 µm). The mobile phase consisted of acetonitrile (A) and 0.1% phosphoric acid aqueous solution (B), with the following gradient elution program: 0–15 min: 14–14% A; 15–35 min: 14–19% A; 35–42 min: 19–100% A; 42–50 min: 100–100% A; 50–50.01 min: 100–14% A; 50.01–60 min: 14–14% A. The flow rate was set at 1.0 mL min⁻¹, and the detection wavelength was 230 nm. The injection volumes were 10 µL for the reference standard solution and 20 µL for the test sample solution.

Validation parameters

The HPLC method for determination of paeoniflorin in Paeonia lactiflora Pall. and PLCTCMP was validated for specificity test, linearity, precision, stability, repeatability, accuracy, limit of quantification (LOQ), limit of detection (LOD), and durability.

Specificity. Aliquots (10 µL each) of PSS, test solutions (including PLPS and PLCTCMPS), and blank solvent (dilute ethanol) were precisely withdrawn and injected in duplicate under the chromatographic conditions specified in section “ Chromatographic conditions” for analysis. The average peak areas were calculated. The purpose was to evaluate whether the blank solvent peak interferes with the determination of paeoniflorin content, and to qualitatively and quantitatively analyze the presence and content of paeoniflorin in both the PSS and test solutions. This study provides a basis for calculating the required weighing amount of dried extract powder for preparing the test solution, ensuring that the paeoniflorin content in the PSS and test solutions is essentially consistent in subsequent stages.

Calibration curves, limits of detection and quantification. A series of PSS spanning concentrations from 20% to 200% were prepared, with the concentration specified in the Pharmacopoeia of the People's Republic of China designated as the 100% concentration point. Each concentration level was injected in triplicate under the “Chromatographic conditions”. The mean peak area was calculated for each concentration. A linear regression analysis was performed by plotting the mean peak area (y-axis) against the corresponding nominal concentration (x-axis). The linearity of the method was assessed based on the correlation coefficient (r) and the goodness-of-fit. The limit of detection (LOD) and limit of quantitation (LOQ) were determined based on the signal-to-noise ratio (S/N). The 20% linearity PSS was injected, and the peak height (signal intensity) and the baseline noise in a representative blank region were measured. The LOD was defined as the concentration yielding an S/N ratio of 3 : 1, and the LOQ was defined as the concentration yielding an S/N ratio of 10 : 1.

Precision, stability, repeatability. Precision measurements were conducted by successively injecting PSS (10 µL) six times using the “Chromatographic conditions” to verify precision. The stability was validated by assaying both PSS and test solutions (including PLPS and PLCTCMPS) at various time intervals after preparation according to the “Chromatographic conditions”. Finally, repeatability was evaluated by preparing six PLCTCMPS in parallel and analyzing them via the same “Chromatographic conditions”.

Accuracy. The recovery test was used to evaluate the accuracy of this method. For the percent recovery experiments, selected samples were also spiked with known amount paeoniflorin, and then analyzed as described in “Chromatographic conditions”. The average recoveries were calculated by the formula: recovery (%) = (observed amount original amount)/spiked amount 100%.

Durability. To evaluate the ability of the analytical method to maintain its performance unaffected by deliberate, minor variations in parameters, the content of paeoniflorin in both PSS and test solutions (including PLPS and PLCTCMPS) was determined according to the analytical method by individually altering the column temperature (±5 °C), flow rate (±0.1 mL min⁻¹), and phosphoric acid concentration (±0.01%, v/v).

OED for PLCTCMP

OED, which scientifically arranges trials to obtain comprehensive information with a minimal number of experiments, is widely applied in multi-factor optimization studies. In the context of TCM extraction processes, this approach constructs an orthogonal learning strategy to effectively discover and retain valuable information regarding the extraction procedure. In the present study, the extract yield of PLCTCMPS and the content of paeoniflorin were selected as evaluation indicators for assessing the extraction efficiency. Key parameters, including the volume of water added, decoction time, and number of decoction cycles, were investigated through an OED (Table 1) to optimize the extraction process of PLCTCMPS.

Table 1 Orthogonal factor and level table

Factor	Level 1	Level 2	Level 3
A: solid–liquid ratio	1 : 8	1 : 10	1 : 12
B: extraction time (h)	0.5	1	1.5
C: number of extraction cycles (n)	1	2	3

---

ML-based optimization of extraction processes

Development of regression equation fitting. Based on the principle of small-sample learning compatibility, nine ML models were selected to perform regression analysis on the results of an OED using limited sample data. The implementation was carried out in Python v3.12 with the scikit-learn machine learning library (version 1.4.2) to optimize the extraction process.
Linear regression. A linear relationship between process parameters and target indicators (extraction yield and paeoniflorin content) was constructed by minimizing the squared error between predicted and actual values. This approach, implemented without regularization, is suitable for capturing simple linear associations
Let y_i denote the actual value of the i-th sample (i.e., the experimentally measured yield of the extract or paeoniflorin content); 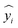represent its predicted value calculated by the model; m be the total sample size.
Ridge regression. Based on ordinary linear regression, L2 regularization (penalizing the sum of squared coefficients) was incorporated to mitigate parameter multicollinearity. For small-sample scenarios, hyperparameter tuning (α = 0.01/0.1/1.0) was employed to balance model fitting and generalization performance.
Let m denote the total sample size; for the i-th sample, y_i represents the actual value (i.e., the experimentally measured yield of the extract or paeoniflorin content); 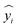is its corresponding predicted value generated by the model; the model incorporates a regularization term controlled by the parameter α (with candidate values of 0.01, 0.1, and 1.0); where a larger α indicates a stronger regularization strength, imposing a greater penalty on the model parameters to promote simplicity; let w_j be the weight coefficient associated with the j-th feature; n be the total number of features (e.g., solid–liquid ratio, extraction time, and number of extraction cycles).
Least absolute shrinkage and selection operator (LASSO). L1 regularization was applied to shrink the coefficients of non-critical parameters to zero, enabling automated feature selection. This approach enhances the interpretability of models trained on small-sample datasets by emphasizing the influence of key process parameters (e.g., water addition volume).
Let m denote the sample size; for the i-th sample, y_i represents the actual value (i.e., the experimentally measured yield of the extract or paeoniflorin content); denotes the corresponding predicted value calculated by the model; the parameter α is the regularization strength coefficient (with candidate values of 0.01, 0.1, and 1.0); a larger α imposes a stronger penalty on the model parameters, leading to a simpler model; the absolute value of the weight coefficient for the j-th feature is given by |w_j|; n represents the number of features (e.g., solid–liquid ratio, extraction time, and number of extraction cycles).
Elastic net regression. By integrating both L1 and L2 regularization, the model simultaneously selects critical parameters (e.g., extraction time) and mitigates multicollinearity, making it particularly suitable for feature selection and fitting in small-sample scenarios with high-dimensional parameters.
Let m represent the sample size; for the i-th sample, y_i denotes the actual value (i.e., the experimentally measured yield of the extract or paeoniflorin content); is the corresponding predicted value generated by the model; the parameter α is the regularization strength coefficient (with values set to 0.01, 0.1, or 1.0); a larger α imposes a stronger penalty on the model parameters, promoting a simpler model structure; the absolute value of the weight coefficient for the j-th feature is given by |w_j|; n indicates the total number of features (e.g., solid–liquid ratio, extraction time, and number of extraction cycles); the parameter ρ denotes the L1 regularization ratio within the elastic net framework, which ranges from 0 to 1.
Bayesian ridge regression. An extension of ridge regression based on the Bayesian framework, which employs probabilistic models to automatically optimize regularization parameters without manual tuning, is particularly suitable for assessing parameter uncertainty in small-sample scenarios.

min[−log p(y|X, w) − log p(w)]; p(y|X, w)

p(w) denotes the prior distribution (the probability distribution of parameter w); X is the feature matrix, i.e., the process parameters of all samples; y is the target vector, i.e., the true values of all samples; w is the weight vector, i.e., the model parameters.
Characteristic polynomial + ridge regression. L2 regularization (L2 norm penalty) is introduced. Second-order polynomial features (including squared terms and interaction terms) are constructed based on the original features to expand nonlinear relationships. Meanwhile, L2 regularization is leveraged to alleviate the multicollinearity problem caused by polynomial feature expansion. This method is suitable for the scenario of nonlinear fitting of multiple parameters with small sample sizes where overfitting needs to be avoided.
Let m denote the total sample size; for the i-th sample, y_i represents the actual value (i.e., the experimentally measured yield of the extract or paeoniflorin content); and denotes its corresponding predicted value generated by the model; the parameter α is the regularization strength coefficient (with candidate values of 0.01, 0.1, and 1.0); a larger α imposes a stronger penalty on the model parameters, promoting a simpler model structure; let w_j be the weight coefficient associated with the j-th feature; n be the total number of features (e.g., solid–liquid ratio, extraction time, and number of extraction cycles).
Random forest. To mitigate overfitting risks, an ensemble of 50 simplified decision trees is constructed by restricting the maximum depth and the minimum sample size required for splitting. This approach leverages averaged predictions from multiple trees to enhance generalization performance, while controlling model complexity under limited sample conditions to ensure robust out-of-sample applicability.

min[MSE(L) + MSE(R)]

MSE(L) is the mean squared error of the left child node; MSE(R) is the mean squared error of the right child node.
Support vector regression. The linear kernel function constructs a direct linear mapping between parameters and targets, offering computational efficiency and suitability for scenarios with linearly distributed features in small-sample settings.
w represents the weight vector defining the separating hyperplane; C is the penalty parameter (or regularization parameter) that controls the trade-off between maximizing the margin and minimizing the classification error, a larger value of C imposes a stricter penalty on training errors; a positive slack variable ξ_i is introduced for each sample to quantify the error where the prediction exceeds the true value; while a negative slack variable ξ_i* quantifies the error where the prediction falls below the true value, particularly in support vector regression.
Partial least squares regression. Extracting principal components strongly correlated with the target variable (n_components = 2) compresses parameter dimensionality while retaining critical information, making it particularly suitable for scenarios involving multicollinearity among multiple parameters

max_w,ccov(X_w, y_c)s.t.‖w‖ = 1, ‖c‖ = 1

w is the weight vector along the X-direction (i.e., the feature projection direction); c is the weight vector along the y-direction (i.e., the target projection direction); X_w denotes the projection of the feature matrix onto the direction w; yielding a score vector; y_c represents the projection of the target vector y onto the direction c.

Evaluation of regression equation. To evaluate model performance and identify the optimal model, we assess the accuracy and reliability of each ML model based on the following six evaluation metrics: the coefficient of determination (R²), adjusted coefficient of determination (Adj_R²), difference in R-squared (R²-Diff), mean absolute error (MAE), root mean square error (RMSE), and Corrected Akaike Information Criterion (AICc).

R² quantifies the proportion of variance in the dependent variable explained by a regression model, reflecting the overall goodness-of-fit between predicted and observed values. Values closer to 1 indicate superior model performance, and it is computationally implemented via sklearn.metrics.r2_score (y, y_pred)

y_i represents the true value obtained from experimental measurement for the i-th sample, which includes key performance indicators such as the extraction yield and the paeoniflorin content; ŷ_i represents the predicted value for the i-th sample, generated by the forward propagation of the input data through the trained model; ȳ represents the mean of all true observed values.

The adjusted coefficient of determination (Adj_R²) is a modified version of R² that incorporates penalties for the number of parameters in the model and the sample size. It is particularly useful for comparing models with different numbers of predictors, as it penalizes excessive model complexity. A higher value indicates a better fit, provided the model maintains simplicity. It is calculated as follows:

R² represents the coefficient of determination; n denotes the sample size; k indicates the number of features in the model (including solid–liquid ratio, extraction time, and number of extraction cycles); and n − k − 1 represents the degrees of freedom after accounting for the intercept term.

The difference in R-squared (R²-Diff), defined as the difference between the coefficient of determination (R²) and the adjusted coefficient of determination (Adj_R²), serves as a rapid assessment metric for evaluating the rationality of model parameters. A smaller R²-Diff value indicates more reasonable model parameterization and a lower.

R²-Diff = R² − Adj_R²

R² denotes the coefficient of determination; Adj_R² represents the adjusted coefficient of determination; n is the sample size; and k signifies the number of features (predictor variables) in the model.

RMSE is defined as the square root of the average of the squared differences between predicted and actual values. It quantifies the magnitude of prediction errors, where a lower value indicates higher predictive accuracy. This metric is computationally implemented as np.sqrt (mean_squared_error (y, y_pred)).

y_i represents the true value obtained from experimental measurement for the i-th sample, which includes key performance indicators such as the extraction yield and the paeoniflorin content; ŷ_i represents the predicted value for the i-th sample, generated by the forward propagation of the input data through the trained model; m be the sample size.

MAE quantifies the average magnitude of absolute differences between predicted and actual values, reflecting the degree of mean prediction error. A lower MAE value indicates reduced average deviation and superior model accuracy. It is computationally implemented via sklearn.metrics.mean_absolute_error (y, y_pred).

y_i represents the true value obtained from experimental measurement for the i-th sample, which includes key performance indicators such as the extraction yield and the paeoniflorin content; ŷ_i represents the predicted value for the i-th sample, generated by the forward propagation of the input data through the trained model; m be the sample size.

The Corrected Akaike Information Criterion (AICc) is a bias-corrected version of the AIC for finite sample sizes. It balances model goodness-of-fit against complexity and provides a more accurate model selection metric than AIC under small-sample conditions (typically when n/k < 40). A lower AICc value indicates better model performance.

AIC = n × ln(MSE) + 2k

n represents the sample size, k represents the number of model parameters (including the intercept), and MSE represents the mean squared error.

Validation of the extraction process from computational calculating and OED. Based on the optimal model established and evaluated through the aforementioned process, the extraction process of the PLCTCMP was validated. The pre-established paeoniflorin quantification method was employed to determine the paeoniflorin content, thereby verifying the model's performance and establishing a standardized extraction workflow.

Results

Method validation for analytical of PLCTCMP

To better optimize the extraction process and ensure the effective detection of the core component paeoniflorin, as well as to provide a reliable experimental method for subsequently constructing orthogonal tests and ML applications, this study established a methodology validation using paeoniflorin as a standard and performed preliminary detection on samples.

The methodology first investigated specificity. The results indicated that the PLPS and PSS exhibited chromatographic peaks at the same retention time, with no significant interference from the solvent in the determination of paeoniflorin content (Fig. 1 and S1). The resolution of paeoniflorin was ideal (all >1.5), demonstrating excellent specificity of the method.

Fig. 1 HPLC chromatogram of PSS and PLPS samples.

A linear regression experiment was conducted by preparing standard solutions covering a concentration range of 20% to 200%. The calibration curves exhibited good linear regression within this range (y = 121 41x − 16 305(r = 0.9993), r = 9993). The limit of detection (LOD) (signal-to-noise ratio S/N = 3) and limit of quantification (LOQ) (S/N = 10) for paeoniflorin were 2.81 µg mL⁻¹ and 9.37 µg mL⁻¹, respectively.

Precision was evaluated based on the relative standard deviation (RSD) of six replicate analyses, yielding an RSD value of 0.96% (Table 2). The stability of the test samples was assessed by injecting them at intervals over 0–24 hours after preparation; the RSD of the peak area was 1.21% (Table 3), indicating good sample stability.

Table 2 Precision experiment

No.	Peak area	Average	RSD%
1	873 125	881 118	0.96
2	885 132
3	874 512
4	873 991
5	886 089
6	893 859

---

Table 3 Stability experiment

No.	Peak area	Average	RSD%
0 h	1 003 814	999 774	1.21
2 h	988 451
4 h	1 021 838
8 h	996 208
12 h	997 275
24 h	991 060

---

Repeatability was demonstrated by analyzing six independently prepared samples in succession. The average paeoniflorin content was 6.63 mg g⁻¹, with an RSD of 0.72% (Table 4). For accuracy, known amounts of paeoniflorin were added to the samples, and analyses were performed before and after spiking. The recovery rates from six determinations ranged from 91.98% to 95.33%, with an RSD of 1.35%, confirming the method's accuracy and reliability (Table 5).

Table 4 Repeatability experiment

No.	Content	Average (mg g^−1)	RSD%
1	6.570	6.63	0.72
2	6.674
3	6.585
4	6.661
5	6.679
6	6.605

---

Table 5 Recovery experiment

No.	Sample weight (mg)	Measured (mg)	Content (mg)	Addition (mg)	Recovery%	Average%	RSD%
1	24.97	0.320126031	0.165528395	0.165	93.69553686	94.30	1.35
2	24.95	0.322294654	0.165395813	0.165	95.09020676
3	24.90	0.321339174	0.165064358	0.165	94.71200957
4	24.96	0.32220932	0.165462104	0.165	94.998313
5	24.95	0.317169455	0.165395813	0.165	91.98402535
6	25.03	0.323219658	0.16592614	0.165	95.32940451

---

Finally, robustness was evaluated by introducing minor variations in column temperature, flow rate, and phosphoric acid concentration. The RSD values under these conditions were 1.77% (n = 3), 7.25% (n = 3), and 0.77% (n = 3), respectively (Table 6). These changes partially met the system suitability test requirements, indicating that the method is relatively robust.

Table 6 Suitability experiment

Condition	Content (mg g^−1)	Average (mg g^−1)	RSD%
Column temperature (25 °C)	7.946875053	7.853234867	1.77
Column temperature (35 °C)	7.693760895
Normal	7.919068653
Flow rate (0.9 mL min^−1)	8.452052768	7.893018366	7.25
Flow rate (1.1 mL min^−1)	7.307933677
Normal	7.919068653
Phosphoric acid (0.09%)	7.90241242	7.945090821	0.76
Phosphoric acid (0.11%)	8.013791391
Normal	7.919068653

---

Data generation factor contribution based on OED

Factor importance analysis serves as a robust methodological tool for evaluating the effectiveness of input factors in predicting target observations, thereby providing an empirical basis for factor screening. To systematically investigate factors influencing extraction performance, an OED was constructed. This design enables the quantification of associations between observed responses (extraction yield and paeoniflorin content) and controlled factors (solid–liquid ratio, extraction time, and number of extraction cycles), while simultaneously characterizing response levels under each factor variation. The resultant dataset provides critical support for subsequent ML-driven optimization processes by establishing reliable input–output relationships for predictive modeling.

When extraction yield was employed as the observation indicator, range analysis (Table 7) revealed the following order of influence among the three factors: number of extraction cycles (R = 12.88) > solid–liquid ratio (R = 2.21) > extraction time (R = 2.13). Consistent with this, variance analysis (Table 8) demonstrated that the effect of the number of extraction cycles substantially exceeded that of both solid–liquid ratio and extraction time, further confirming its extremely significant impact on extraction yield (F = 144.21). With paeoniflorin content as the target observation, both range analysis (Table 9) and variance analysis (Table 10) similarly identified the number of extraction cycles as the most influential factor, exhibiting a range value (R) of 20.72, followed by solid–liquid ratio (R = 4.97) and extraction time (R = 1.65). Variance analysis indicated a highly significant effect of the number of extraction cycles on total paeoniflorin content (F = 33.12), with solid–liquid ratio and extraction time being less influential.

Table 7 OED and range analysis of extract yield

No.	Factor A solid–liquid ratio	Factor B extraction time/h	Factor C extraction cycles/time (s)	Factor D blank column	Extraction yield (%)
1	1	1	1	1	26.79
2	1	2	2	2	36.69
3	1	3	3	3	42.64
4	2	1	2	3	37.97
5	2	2	3	1	42.49
6	2	3	1	2	30.27
7	3	1	3	2	41.68
8	3	2	1	3	31.12
9	3	3	2	1	39.93
K1	106.12	106.44	88.18	109.21
K2	110.73	110.30	114.59	108.64
K3	112.73	112.84	126.81	111.73
k1	35.37	35.48	29.39	36.40
k2	36.91	36.77	38.20	36.21
k3	37.58	37.61	42.27	37.24
R	2.21	2.13	12.88	1.03

---

Table 8 Analysis of variance for extract yield

Factor	Sums of squared deviations	Degrees of freedom	Mean square	F	F0.05	F0.01
A	7.6601	2	3.8301	4.2505	19	99
B	6.9231	2	3.4616	3.8415	19	99
C	259.8989	2	129.9495	144.2121	19	99
D	1.8022	2	0.9011
Total	276	8

---

Table 9 OED and range analysis of paeoniflorin content

No.	Factor A solid–liquid ratio	Factor B extraction time/h	Factor C extraction cycles/time (s)	Factor D blank column	Paeoniflorin content
1	1	1	1	1	48.53
2	1	2	2	2	63.65
3	1	3	3	3	73.66
4	2	1	2	3	72.06
5	2	2	3	1	73.60
6	2	3	1	2	54.20
7	3	1	3	2	73.91
8	3	2	1	3	56.26
9	3	3	2	1	70.60
K1	185.84	194.50	159.00	192.73
K2	199.87	193.51	206.30	191.76
K3	200.77	198.46	221.17	201.98
k1	61.95	64.83	53.00	64.24
k2	66.62	64.50	68.77	63.92
k3	66.92	66.15	73.72	67.33
R	4.97	1.65	20.72	3.41

---

Table 10 Analysis of variance for paeoniflorin content

Factor	Sums of squared deviations	Degrees of freedom	Mean square	F	F0.05	F0.01
A	48.0318	2	24.0159	2.2638	19	99
B	4.5739	2	2.2870	0.2156	19	99
C	702.6130	2	351.3065	33.1156	19	99
D	21.2170	2	10.6085
Total	776	8

---

Evaluation and fitting of linear regression equations for factors and observed values in ML

To further investigate the factors affecting extraction performance, we constructed multiple sets of polynomial features for analysis. The advantage of polynomial features lies in elevating the analytical perspective from “linear” to “nonlinear,” thereby enabling a deeper exploration of the complex relationships between influencing factors and outcomes. The results indicated that the number of extraction cycles exhibited a strong positive correlation with both the extract yield and the paeoniflorin content, with correlation coefficients reaching 0.95 and 0.91 (Fig. 2A), respectively. This suggests that the number of decoctions is the most influential process parameter. In contrast, the solid–liquid ratio and extraction time showed only weak correlations with the target variables (r = 0.058–0.22) (Fig. 2A–D). A very strong synergistic relationship (r = 0.98) (Fig. 2A) was observed between the two target variables, indicating that optimizing the extract yield can simultaneously enhance the paeoniflorin content. Additionally, the correlations among the three process parameters were nearly zero, confirming the good orthogonality of the experimental design.

Fig. 2 Feature association analysis based on multiple sets of polynomial features. (A) Feature–target correlation heatmap, where deeper colors (red) indicate stronger correlations; (B) relationship between extract yield and process parameters, where the x-axis represents the values of process parameters (e.g., solid–liquid ratio, extraction time) and the y-axis represents the extract yield (%), illustrating the scatter distribution of parameters versus extract yield; (C) relationship between total paeoniflorin content and process parameters, x-axis represents the values of process parameters, y-axis represents the total paeoniflorin content; (D) relationship between extract yield and total paeoniflorin content, x-axis represents the extract yield (%), y-axis represents the total paeoniflorin content.

Compared to traditional statistical analysis methods, ML regression techniques demonstrate superior performance in quantifying the relationship between process parameters and target metrics. The efficacy of the nine evaluated models was assessed based on five performance indicators. The results reveal significant differences in the fitting performance of these models for predicting the extraction yield and paeoniflorin content on the training set (Tables 11, 12 and Fig. 3).

Table 11 Model evaluation of extraction yield

Model	Train R^2	Adj_R^2	R^2-Diff	RMSE	MAE	AICc
Linear regression	0.951	0.903	0.049	1.223	1.051	21.63
Ridge (α = 0.01)	0.951	0.903	0.049	1.223	1.051	21.63
Ridge (α = 0.1)	0.951	0.902	0.049	1.225	1.051	21.65
Ridge (α = 1.0)	0.942	0.884	0.058	1.337	1.125	23.23
ElasticNet	0.948	0.896	0.052	1.265	1.051	22.24
Lasso	0.951	0.902	0.049	1.226	1.051	21.67
BayesianRidge	0.951	0.901	0.049	1.231	1.051	21.74
Poly2 + ridge	0.988	0.981	0.007	0.609	0.532	1.89
Random forest (small)	0.839	0.743	0.096	2.221	1.685	25.16
SVR linear	0.904	0.809	0.096	1.713	1.197	27.69
PLS regression	0.951	0.903	0.049	1.223	1.051	21.63

---

Table 12 Model evaluation of paeoniflorin content

Model	Train R^2	Adj_R^2	R^2-Diff	RMSE	MAE	AICc
Linear regression	0.882	0.765	0.118	3.184	2.404	38.85
Ridge (α = 0.01)	0.882	0.765	0.118	3.184	2.404	38.85
Ridge (α = 0.1)	0.882	0.764	0.118	3.186	2.417	38.86
Ridge (α = 1.0)	0.873	0.747	0.127	3.302	2.586	39.5
ElasticNet	0.88	0.759	0.120	3.22	2.499	39.05
Lasso	0.882	0.764	0.118	3.186	2.41	38.86
BayesianRidge	0.878	0.757	0.122	3.237	2.522	39.14
Poly2 + ridge	0.986	0.977	0.009	1.107	1.007	12.63
Random forest (small)	0.8	0.68	0.12	4.151	3.439	36.42
ZSVR linear	0.802	0.604	0.198	4.133	2.987	43.54
PLS regression	0.882	0.765	0.118	3.184	2.404	38.85

---

Fig. 3 Performance evaluation of machine learning models. (A) R² score comparison of models, the x-axis represents different regression models, while the y-axis denotes the R² score (ranging from 0 to 1); (B) RMSE comparison of models, the x-axis lists the different regression models evaluated, and the y-axis shows the RMSE values; (C) Optimal model predictive performance, the x-axis represents the true values, the y-axis represents the predicted values, and the dashed line denotes the ideal fit line (y = x).

In the model incorporating both extraction yield and paeoniflorin content as comprehensive predictive indicators, the Poly2 + ridge demonstrated optimal performance. On the training set, it achieved high R² values of 0.988 and 0.986 (Fig. 3A and C), respectively, for the two indicators, with corresponding Adj_R² values of 0.981 and 0.977. The R²-Diff were minimal, at only 0.006 and 0.009, indicating negligible overfitting. Additionally, the model yielded the lowest error metrics across all compared models: a MAE of 0.532 and 1.007, a RMSE of 0.609 and 1.107 (Fig. 3B), and a AICc of 1.89 and 12.63. These results collectively highlight the model's superior comprehensive performance. For the linear regression, ridge regression, and LASSO regression models, the results were consistent: all yielded stable R² values (0.951 and 0.882 for the two indicators) and similar error metrics, with AICc values ranging from approximately 21.6 to 38.9. This consistency suggests that these models provide reliable but less accurate predictions compared to the Poly2 + ridge combination.

For models excluding the polynomial features + ridge regression combination, a three-tiered hierarchical structure defined their performance across both extraction yield and paeoniflorin content prediction tasks.

The baseline linear group (linear regression, ridge (α = 0.01 and 0.1), PLS regression) exhibited highly consistent results: for extraction yield, R² ≈ 0.951 (0.9512–0.9513), Adj_R² > 0.902, MAE = 1.051, RMSE = 1.223–1.225, and AICc ≈ 21.6; for paeoniflorin content, R² ≈ 0.882 (0.8822–0.8823), Adj_R² ≈ 0.764, MAE = 2.40–2.42, RMSE ≈ 3.18, AICc ≈ 38.9—indicating similar fitting efficacy across tasks.

The regularized extension group (ridge (α = 1.0), ElasticNet, Lasso, BayesianRidge) formed a secondary tier with marginally lower R²: extraction yield (0.942–0.951, ridge α = 1.0: 0.9418, stronger regularization), paeoniflorin content (0.874–0.882, ridge α = 1.0: 0.8735, MAE = 2.59, RMSE = 3.30). ElasticNet consistently showed higher RMSE (extraction yield: 1.265, AICc = 22.24; paeoniflorin: 3.22, AICc = 39.05), while Lasso and BayesianRidge had metrics comparable to the baseline.

Random forest (small) and SVRLinear underperformed significantly. Random forest had poor fit (extraction yield: R² = 0.839, MAE = 1.69, RMSE = 2.22, AICc = 25.2; paeoniflorin content: R² = 0.80, MAE = 3.44, RMSE = 4.15); SVRLinear performed worst (extraction yield: R² = 0.90, RMSE = 1.71, AICc = 27.7; paeoniflorin content: R² = 0.80, RMSE = 4.13, AICc = 43.5), with all metrics substantially higher than linear models—highlighting the superiority of linear approaches for these tasks.

This hierarchy emphasizes the Poly2 + ridge model's advantage, while illustrating trade-offs between model complexity (regularization, nonlinearity) and predictive performance.

Analysis of optimization results based on computational models

To validate the reliability of the model, the optimization results derived from polynomial ridge regression—specifically, solid–liquid ratio of 9.71, extraction time of 1.50 hours, and three extraction cycles—were evaluated against practical process constraints (e.g., solid–liquid ratio, extraction time, and number of extraction cycles). The analysis confirmed that these parameters not only yielded high predicted values but also remained operationally feasible, thereby substantiating their optimality. In terms of model adaptability, polynomial ridge regression demonstrated superior prediction accuracy and stability when applied to small-sample datasets. This model effectively captures the nonlinear relationships between process parameters and target indicators while mitigating overfitting through regularization, ensuring robust performance in practical applications.

In the parameter space optimization analysis, the optimal solutions for process optimization were predominantly concentrated within the region of a water addition ratio of 9 to 11 times and a decoction time of 1.25 to 1.75 hours (Fig. 4A), exhibiting a distinct peak distribution pattern. The improvement magnitude in paeoniflorin content was generally superior to that of the extract yield (Fig. 4B), which aligns with the characteristic observed in the heatmap (Fig. 2A), where paeoniflorin, as an active ingredient, demonstrated greater sensitivity to variations in process parameters. The optimal solutions achieved significant enhancement in both indicators. Furthermore, the optimization results within the objective space (Fig. 4C and D) illustrate the positional relationship between the ML-predicted optimum point and the original experimental points. The predicted optimal process parameters are capable of simultaneously increasing both the extract yield and paeoniflorin content, thereby realizing effective process improvement.

Fig. 4 Parameter space optimization analysis. (A) Parameter space optimization score distribution, the x-axis represent solid–liquid ratio, the y-axis represent extraction time; (B) top 10 solution improvement effects, the x-axis represent solution ranking, the y-axis represent absolution improvement; (C) optimization results in target space, the x-axis represent extract yield, the y-axis represent paeoniflorin content, (D) top 20 optimization solution parameter distribution, the x-axis represent solid–liquid ratio, the y-axis represent extraction time.

In the performance evaluation of process optimization, the comparative analysis of original optimal process versus ML-optimized process parameters (Fig. 5A) revealed that the optimized water volume increased from 8-fold to 9.71-fold, with a decoction time of 1.5 hours and three decoction cycles. The performance improvement analysis (Fig. 5B) quantified the optimization effects, demonstrating a 0.57% increase in extract yield and a 1.09-unit enhancement in paeoniflorin content. The performance trajectories of the top 10 solutions (Fig. 5C) exhibited consistently high-performance levels, indicating the robustness of the optimization algorithm. Furthermore, the relationship between solution quality and model confidence (Fig. 5D) indicated that the optimal solution not only achieved the highest optimization score but also maintained a high model confidence (0.826), ensuring the reliability of the predicted outcomes.

Fig. 5 Process optimization performance evaluation. (A) Optimal vs. original best process parameters, the x-axis represent process parameters, the y-axis represent parameter value; (B) performance improvement analysis, the x-axis represent performance metrics, the y-axis values; (C) top 10 solutions performance trajectory, the x-axis represent solution ranking, the y-axis represent predicted values; (D) solution quality vs. model confidence, the x-axis represent optimization score, the y-axis represent model confidence.

The performance heatmap of the ensemble models (Fig. 6A) revealed that characteristic polynomial + ridge regression, elastic net regression, and ridge regression (α = 1.0) excelled across all evaluation metrics, with their combination forming a stable and reliable ensemble prediction system. The weight distribution of the ensemble models (Fig. 6B) indicated that polynomial ridge regression was assigned the predominant weight (0.353), underscoring its superior performance in predictive accuracy. A comparative analysis between individual models and the ensemble model (Fig. 6C and D) confirmed the effectiveness of the ensemble strategy: across various parameter combinations, the ensemble model yielded more stable predictions and effectively mitigated the deviations that might arise from relying on any single model.

Fig. 6 Ensemble model performance evaluation. (A) Ensemble models performance heatmap, the x-axis represent performance metrics, the y-axis represent models; (B) ensemble model weight distribution, the x-axis represent models, the y-axis represent weight in ensemble; (C) individual vs. ensemble model predictions (extract yield), the x-axis represent sample parameters, the y-axis represent extract yield prediction; (D) individual vs. ensemble model predictions (paeoniflorin), the x-axis represent sample parameters, the y-axis represent paeoniflorin content prediction.

Based on the comprehensive ML analysis, the final recommended process parameters are as follows: solid–liquid ratio of 9.71, decoction time of 1.50 h, and 3 extraction cycles. This parameter combination is predicted to yield an extract rate of 43.21% and a paeoniflorin content of 75 units, representing an improvement of 0.57% in extract yield and an increase of 1.09 units in paeoniflorin content compared to the original optimal experimental results (SI 1).

Characterization of extract and paeoniflorin in PLCTCMP using computational models

As mentioned previously, the extraction yield and paeoniflorin content serve as critical quality standards for the PLCTCMP. By integrating ML to construct a predictive model and analyzing the optimal extraction, further experimental verification revealed that under the selected conditions, the PLCTCMP formula achieved an extraction yield of 43.28% and a total paeoniflorin content of 74.2 mg. These results not only corroborate the findings from the OED but also demonstrate the feasibility of ML in optimizing extraction.

Discussion

Based on the effective anti-liver cancer formula developed through previous data mining and experimental validation, this study focuses on standardizing the extraction process of the formulated preparation. Active components are critical quality control indicators for the extraction process. Paeoniflorin, a representative monoterpene glycoside, is not only a recognized active substance in Paeonia lactiflora but was also confirmed as a primary active component in PLCTCMP in our preliminary research.¹⁹ Paeoniflorin has been extensively studied in liver cancer research. Studies have shown that paeoniflorin inhibits Skp2 activity, thereby suppressing cell viability, inducing apoptosis, and inhibiting invasion and migration, positioning it as a novel inhibitor of liver cancer cells.²⁰ The aberrant expression of programmed death-ligand 1 (PD-L1) in cancer cells facilitates immune escape of liver cancer cells. Paeoniflorin can trigger T cell-mediated anti-tumor immunity by increasing CD8+ T cell counts in tumor tissues, an effect mediated through the SOCS3/STAT3 (ref. 21) and NF-κB/PD-L1 (ref. 22) signaling pathways. Furthermore, the combination of paeoniflorin and sorafenib (Sor) inhibits invasion and activation of the NF-κB/HIF-2α/SerpinB3 pathway in Sor-resistant liver cancer cells, synergistically enhancing the anti-liver cancer effect of Sor.²³

This study focused on PLCTCMP for the treatment of primary liver cancer. A quality control method was established using paeoniflorin as the indicator component, which served as a critical parameter for the systematic optimization of the extraction process. Through HPLC methodology validation, it was confirmed that the detection method exhibits strong specificity, high sensitivity, and is suitable for the quantitative analysis of paeoniflorin in the PLCTCMP.

In this study, the traditional reflux extraction method was employed. Although existing literature indicates that ethanol reflux extraction can significantly improve the extraction efficiency of paeoniflorin,^24,25 aqueous reflux extraction more closely aligns with the traditional application of Chinese herbal formulations and reflects real-world patient usage practices.²⁶ This approach helps preserve thermolabile active components in the formulation, such as volatile oils and polysaccharides, thereby facilitating subsequent process verification and clinical translation.²⁷ Moreover, using water as a green solvent circumvents issues related to ethanol residue, which is consistent with the safety requirements for quality control of TCM formulations as stipulated by the Chinese Pharmacopoeia. It also reduces process complexity and costs.²⁸

In the study of aqueous extraction technology, the solid–liquid ratio, extraction time, and extraction cycles significantly influence the yield of paeoniflorin,²⁹ while the extract yield also serves as a critical indicator of the extraction process.³⁰ Therefore, this research employed both paeoniflorin content and extract yield as quality control metrics to construct an OED. This allowed for a preliminary investigation into the impact of various extraction factors on the outcome indicators. The results revealed that the solid–liquid ratio and extraction time had a relatively weak influence on the extraction of paeoniflorin, whereas the extraction cycles were identified as the key factor affecting both the extract yield and paeoniflorin content. Analysis of variance further validated the significance of the number of decoctions (P < 0.01). Using polynomial features algorithm, we further validated the strong positive correlation between extraction times and both extract yield and paeoniflorin content, and obtained the optimal solution to break the leaching equilibrium state via ML methods. Additionally, the minor error term indicated a reliable experimental design and reproducible results. This is because multiple extraction steps repeatedly “reset” the concentration gradient, continually disrupting the intracellular-extracellular concentration equilibrium, overcoming the resistance in the extraction process, and thereby persistently “driving” the outward migration of active components. However, as the number of extractions increases, the vast majority of the active components will have been essentially leached out completely. Consequently, further increasing the number of extraction steps yields diminishing returns in terms of component recovery while increasing energy consumption.³¹

To better optimize the extraction process, this study proposes an optimization method based on the integration of OED and ML. Specifically tailored for small sample data, nine ML models were selected to analyze the results of the orthogonal experiments. The OED selects the most representative set of few test points from the full factorial combinations, while ML integrates efficient OED, powerful nonlinear fitting capabilities, and intelligent optimization into a unified framework. This approach reduces the number of “trial-and-error” experiments and enables rapid, low-cost screening of optimal parameters.^32,33 Based on the principle of small-sample-friendliness, nine supervised ML models were selected. The learning process of OED data by the nine models essentially consists in capturing the mapping relationship of chemical laws in a high-dimensional space, achieving survival of the fittest, exploring the optimal solution, and the exploration space is defined by the feasible domain derived from chemical principles. These models were evaluated and the optimal model was screened based on R², RMSE, MAE, AIC, and a comprehensive score. In the prediction of extract yield and content of paeoniflorin, the characteristic polynomial + ridge regression demonstrated optimal performance in both cases. It achieved the highest R² of 0.988 and 0.986, respectively, which are the closest to 1 among all evaluated models. Meanwhile, it yielded the smallest values of RMSE (0.609, 1.107), MAE (0.532, 1.007), and AIC (−2.9, 7.8). Eventually, this model attained the highest comprehensive scores (0.809, 0.812). The essence of characteristic polynomial lies in feature transformation. By generating higher-order terms and interaction terms from the original features, the data is mapped into a higher-dimensional space. This process cleverly converts inherently nonlinear relationships in the original feature space into a linear fitting problem in the high-dimensional space, where the relationship can be approximated by a hyperplane.^34,35 However, this feature transformation drastically increases model complexity and the number of variables. Under small-sample conditions, this often leads to overfitting. Ridge regression addresses this issue by incorporating an L2 regularization term into its loss function. This penalty term encourages the shrinkage of model coefficients towards zero, preventing them from becoming excessively large by fitting noise in the training data, thereby enhancing the model's generalization capability. Furthermore, when multicollinearity exists among the transformed features – a common occurrence after polynomial expansion—the solution of Ordinary Least Squares (OLS) becomes highly unstable.^36,37 Ridge regression significantly improves the numerical stability of the solution by introducing the regularization term. This combined strategy, where characteristic polynomial is responsible for expanding the model's capacity and ridge regression imposes necessary constraints, proves particularly suitable for handling small-sample datasets.

Based on the polynomial–ridge regression model, the optimal extraction process was obtained. Further experimental verification ultimately demonstrated that under this ML optimization, both the extraction yield (43.21%) and paeoniflorin content (74.2 mg) achieved the highest improvement. This not only validates the reliability of ML in process optimization but also proves that the chemical regularities learned thereby are accurate. The 0.57% elevation in extract yield translates to a direct reduction in the unit cost of the extract and an expansion of profit margins during large-scale industrial manufacturing. Concurrently, it improves the utilization efficiency of medicinal herb resources, thus demonstrating the extensive application potential of this technology in pharmaceutical formulation practices.

In pharmaceutical preparation processes, while extraction methods serve as the initial step, the efficient extraction of active ingredients is of paramount importance. In this study, a database was constructed using an OED, and artificial intelligence was employed to build a model for calculating the optimal extraction parameters. Preliminary extraction process parameters were successfully obtained and their reliability was experimentally verified. This successful experience is not limited to systems involving two optimization objectives and three factors. Instead, the core advantages of the OED + ML workflow—efficient experimental design, data-driven nonlinear modeling, and multi-objective optimization—render it particularly suitable for multi-herb TCM formulae with complex interactions, especially in terms of its capacity to capture the intricate nonlinear relationships between multiple factors and multiple optimization objectives. Through rational model construction and validation strategies, this workflow can serve as a universal tool for the efficient optimization of TCM extraction processes, effectively bridging the gap between laboratory-scale research and industrial production.

However, the current model exhibits certain limitations due to the constrained dataset volume. Furthermore, the limited number of outcome measures restricted the model's construction robustness. This highlights that for future model development, it is essential not only to expand the sample size but also to incorporate a broader range of outcome measures to seek an optimized solution. This approach will provide a solid experimental foundation for quality control in the production process. It is also anticipated that ML-assisted strategies will find broader application in future production workflows.

Conflicts of interest

The authors confirm that there are no financial, personal, or professional relationships with other people or organizations that could inappropriately influence or bias the work presented in this manuscript.

Data availability

All data generated or analyzed during this study are included in this published article and its supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ra09650b.

Acknowledgements

This work was supported by the National Natural Science Foundation of China [grant 82204698].

References

1. J. Y. Wu, G. Y. Tang and C. S. Chen, et al., Traditional Chinese medicine for the treatment of cancers of hepatobiliary system: from clinical evidence to drug discovery, Mol. Cancer, 2024, 23(1), 218.
2. X. H. Zhou, J. X. Zhou and J. L. Ren, et al., Progress in the Study of Extraction Methods and Pharmacological Effects of Traditional Chinese Medicine-Derived Carbon Dots, Molecules, 2025, 30(19), 4015.
3. G. Y. Li and D. Y. Cheng, Comparison of different extraction methods of active ingredients of Chinese medicine and natural products, J. Sep. Sci., 2024, 47(1), e2300712.
4. W. Wei, H. Pei and L. N. Ma, et al., Comparison of Yizhiqingxin formula extraction methods and their pharmacodynamic differences, Front. Neurosci., 2023, 17, 1097859.
5. A. Sebastià, K. Dawidowicz and N. Pallarés, et al., Chemical characterization and safety assessment of black truffle (tuber melanosporum) leftovers extracts obtained through non-conventional extraction techniques, Food Chem., 2025, 495(Pt 1), 146367.
6. H. Liu, J. Stanslas and J. Y. Ren, et al., Green Co-Extractant-Assisted Supercritical CO2 Extraction of Xanthones from Mangosteen Pericarp Using Tricaprylin and Tricaprin Mixtures, Foods, 2025, 14(17), 2983.
7. T. Khursheed, A. A. Khalil and M. N. Akhtar, et al., Ultrasound-assisted solvent extraction of phenolics, flavonoids, and major triterpenoids from Centella asiatica leaves: A comparative study, Ultrason. Sonochem., 2024, 111, 107091.
8. F. Ding, J. Lan and X. C. Gong, Research progress on modeling methods for the extraction process of traditional Chinese medicine, China J. Chin. Mater. Med., 2025, 50(15), 4209–4217.
9. B. Xu, Y. J. Qiao and S. Y. Du, et al., Intelligent co-design of material, process, and equipment for manufacturing high-quality traditional Chinese medicine preparations, China J. Chin. Mater. Med., 2023, 48(15), 3977–3987.
10. N. S. Arden, A. C. Fisher and K. Tyner, et al., Industry 4.0 for pharmaceutical manufacturing: Preparing for the smart factories of the future, Int. J. Pharm., 2021, 602, 120554.
11. P. Yogendrarajah, L. Natalis and W. Peys, et al., Application of design space and quality by design methodologies combined with ultra high-performance liquid chromatography for the optimization of the sample preparation of complex pharmaceutical dosage forms, J. Pharm. Biomed. Anal., 2023, 227, 115149.
12. H. B. Grangeia, C. Silva and S. P. Simões, et al., Quality by design in pharmaceutical manufacturing: A systematic review of current status, challenges and future perspectives, Eur. J. Pharm. Biopharm., 2020, 147, 19–37.
13. X. Y. Liu, J. Y. Bi and M. H. Li, et al., Optimization of extraction process for classic prescription Yihuang Decoction based on Box-Behnken design-response surface methodology, standard relation, and analytic hierarchy process combined with entropy weight method, Zhongguo Zhongyao Zazhi, 2024, 48(21), 5798–5808.
14. K. Huanbutta, K. Burapapadh and P. Kraisit, et al., Artificial intelligence-driven pharmaceutical industry: A paradigm shift in drug discovery, formulation development, manufacturing, quality control, and post-market surveillance, Eur. J. Pharm. Sci., 2024, 203, 106938.
15. S. A. Kumar, T. D. A. Kumar and N. M. Beeraka, et al., Machine learning and deep learning in data-driven decision making of drug discovery and challenges in high-quality data acquisition in the pharmaceutical industry, Future Med. Chem., 2022, 14(4), 245–270.
16. J. M. Ma, J. L. Yao and X. Y. Ren, et al., Machine learning-assisted data-driven optimization and understanding of the multiple stage process for extraction of polysaccharides and secondary metabolites from natural products, Green Chem., 2023, 25(8), 3057–3068.
17. S. Kunjiappan, L. K. Ramasamy and S. Kannan, et al., Optimization of ultrasound-aided extraction of bioactive ingredients from Vitis vinifera seeds using RSM and ANFIS modeling with machine learning algorithm, Sci. Rep., 2024, 14(1), 1219.
18. J. Zhang, Y. L. Wu and Y. Y. Tian, et al., Chinese herbal medicine for the treatment of intestinal cancer: preclinical studies and potential clinical applications, Mol. Cancer, 2024, 23(1), 217.
19. Q. S. Zhao, G. Y. Dong and X. Y. Zhang, et al., Unraveling the mechanism of core prescription in primary liver cancer: integrative analysis through data mining, network pharmacology, and molecular simulation, In Silico Pharmacology, 2025, 13(2), 63.
20. H. Liu, L. L. Zhang and J. Zhao, et al., Paeoniflorin inhibits cell viability and invasion of liver cancer cells via inhibition of Skp2, Oncol. Lett., 2020, 19(4), 3165–3172.
21. M. Gao, D. J. Zhang and G. H. Jiang, et al., Paeoniflorin inhibits hepatocellular carcinoma growth by reducing PD-L1 expression, Biomed. Pharmacother., 2023, 166, 115317.
22. J. F. Li, C. H. Zhu and Z. Y. Zhang, et al., Paeoniflorin increases the anti-tumor efficacy of sorafenib in tumor-bearing mice with liver cancer via suppressing the NF-κb/PD-l1 axis, Heliyon, 2024, 10(2), e24461.
23. J. F. Li, X. R. Zheng and H. Y. Zhang, et al., Effects of Sensitized Sorafenib with a Paeoniflorin and Geniposide Mixture on Liver Cancer via the NF-κB-HIF-2α-SerpinB3 Pathway, Evid. Based Complement. Alternat. Med., 2022, 2022, 1911311.
24. L. Peng, Z. Ma and W. H. Chu, et al., Identification and hepatoprotective activity of total glycosides of paeony with high content of paeoniflorin extracted from Paeonia lactiflora Pall, Food Chem. Toxicol., 2023, 173, 113624.
25. Y. C. Wu, Y. Y. Jiang and L. Zhang, et al., Chemical Profiling and Antioxidant Evaluation of Paeonia lactiflora Pall. “Zhongjiang” by HPLC-ESI-MS Combined with DPPH Assay, J. Chromatogr. Sci., 2021, 59(9), 795–805.
26. S. T. Cao, J. C. Liang and M. G. Chen, et al., Comparative analysis of extraction technologies for plant extracts and absolutes, Front. Chem., 2025, 13, 1536590.
27. Y. L. Liang, K. G. Wu and D. He, et al., Physicochemical and functional properties of cinnamon essential oil emulsions stabilized by galactomannan-rich aqueous extract from Gleditsia sinensis seeds and soy protein isolate, Int. J. Biol. Macromol., 2025, 295, 139601.
28. R. R. Zhou, J. H. Huang and D. He, et al., Green and Efficient Extraction of Polysaccharide and Ginsenoside from American Ginseng (Panax quinquefolius L.) by Deep Eutectic Solvent Extraction and Aqueous Two-Phase System, Molecules, 2022, 27(10), 3132.
29. T. Paul, A. Mondal and T. K. Bandyopadhyay, et al., Downstream Process Development for Extraction of Prodigiosin: Statistical Optimization, Kinetics, and Biochemical Characterization, Appl. Biochem. Biotechnol., 2022, 194(11), 5403–5418.
30. L. Jin, W. F. Jin and Y. Y. Zhang, et al., Simultaneous optimization of the extraction process of Yangyin Yiqi Huoxue prescription with natural deep eutectic solvents for optimal extraction yield and antioxidant activity: A comparative study of two models, Phytomedicine, 2022, 102, 154156.
31. H. Qian, C. L. Bai and X. Jia, et al., Mechanisms and synergistic effects of the active components of Xanthocerais lignum in inhibiting rheumatoid arthritis through the modulation of the biological behavior of synovial cells, J. Ethnopharmacol., 2025, 352, 120200.
32. P. W. Yun, H. D. Fu and H. T. Zhang, et al., Rapid design of high-end copper alloy processes combining orthogonal experiments, machine learning, and Pareto analysis, J. Mater. Res. Technol., 2025, 36, 1005–1016.
33. T. Wu, D. L. Yan and S. Lin, et al., Design of strictly orthogonal biosensors for maximizing renewable biofuel overproduction, J. Adv. Res., 2025, S2090-1232(25), 00698.
34. F. J. Gonzalez, Determination of the characteristic curves of a nonlinear first order system from Fourier analysis, Sci. Rep., 2023, 13(1), 1955.
35. K. Balasubramanian, Characteristic polynomials, spectral-based Riemann-Zeta functions and entropy indices of n-dimensional hypercubes, J. Math. Chem., 2023, 25, 1–22.
36. H. C. Achterberg, J. J. Rooi and M. W. Vernooij, et al., Spatially Regularized Shape Analysis of the Hippocampus Using P-Spline Based Shape Regression, IEEE J. Biomed. Health Inform., 2020, 24(3), 825–834.
37. Y. Wang, T. Zhou and G. C. Yang, et al., A regularized stochastic configuration network based on weighted mean of vectors for regression, PeerJ Comput. Sci., 2023, 9, e1382.

---

Footnote

† These authors contributed equally to this work.

---