 Open Access Article
Open Access ArticlePrediction of miscibility in chlorinated polyethylene/poly(vinyl chloride) blends via atomistic molecular dynamics simulations
Zhihao Maa,
Xue Li*b,
Huaguo Xua,
Jianxiang Shen *ac and
Jun Liuc
*ac and
Jun Liuc
aDepartment of Polymer Science and Technology, Jiaxing University, Jiaxing 314001, China. E-mail: shenjx@zjxu.edu.cn
bSchool of Advanced Materials Engineering, Jiaxing Nanhu University, Jiaxing 314001, China. E-mail: lixue@jxnhu.edu.cn
cState Key Laboratory of Organic–Inorganic Composites, Beijing University of Chemical Technology, Beijing 100029, China
First published on 2nd January 2026
Abstract
The miscibility of chlorinated polyethylene (CPE)/polyvinyl chloride (PVC) blends is intricately influenced by both chemical structures and environmental conditions. This study employs all-atom molecular dynamics simulations to systematically investigate the effects of CPE chlorine content and molecular architecture, blend composition, and temperature on CPE/PVC miscibility behavior. Analysis of solubility parameters (δ) suggests that the compatibility of CPE/PVC blends improves with increasing chlorine content within the examined range. Random-chlorinated polyethylene (r-CPE) demonstrates superior miscibility with PVC compared to block-chlorinated polyethylene (b-CPE), attributed to enhanced electrostatic contributions arising from intensified polar Cl–Cl interactions. CPE/PVC blends containing approximately 20–80 wt% CPE are found to be thermodynamically immiscible at 300 K. Furthermore, a quantitative relationship between the Flory–Huggins interaction parameter (χ12) and temperature (T) is established, revealing an increase in χ12 with T, indicative of reduced miscibility at higher temperatures. The phase diagram exhibits a low critical solution temperature (LCST) behavior, consistent with the χ12–T relationships. Notably, r-CPE/PVC binary systems exhibit a higher LCST critical temperature (Tcr) than b-CPE/PVC systems. In general, this simulation study provides better understandings of CPE/PVC miscibility and offers valuable guidance for the design and optimization of CPE/PVC composite materials.
1 Introduction
Polyvinyl chloride (PVC) is a widely used synthetic polymer renowned for its versatility, durability, and cost-effectiveness.1–3 However, its performance is somewhat hindered by brittleness at low temperatures, limiting its applications in cold climates.4–7 To address this issue, various modification strategies have been explored,8–10 including the incorporation of rubber modifiers like acrylic rubber (ACR),11 acrylonitrile–butadiene–styrene (ABS),12,13 and nitrile butadiene rubber (NBR),14,15 as well as other modifiers such as polymethyl methacrylate (PMMA),16,17 methyl methacrylate–butadiene–styrene (MBS),18,19 dioctyl phthalate (DOP),20 and chlorinated polyethylene (CPE).21 For example, our recent work combined all-atom molecular dynamics (MD) simulation and experimental tools to investigate the mechanical properties of PVC/CaCO3 nanocomposites, and the results indicated that 12 wt% CaCO3 modified with oleate anion and dodecylbenzenesulfonate can impart high toughness to PVC.Chlorinated polyethylene (CPE), derived from high-density polyethylene (HDPE) through chlorine substitution, offers a promising approach to modifying PVC.22,23 Its structural similarity to PVC, with the introduction of polar groups, enhances compatibility and improves toughness.24 CPE/PVC blends have been shown to form partially thermodynamically compatible systems, leading to improved mechanical properties.25 However, CPE and PVC are probably segmental immiscible, while CPE exhibits good compatibility with polyethylene (PE). To improve the CPE/PVC blend miscibility, nanoparticles are usually added into CPE/PVC blends functionalizing as interfacial compatibilizer. For instance, You et al. investigated the brittle–ductile transition in CPE/PVC blends, finding that CPE and nano-CaCO3 can enhance both mechanical properties and toughness.21 Their results indicated that CPE plays a more significant role than PVC in determining the brittle–ductile transition temperature, while nano-CaCO3 has a minimal impact. Recent work by Zhang et al. also demonstrated that increasing CPE could significantly improve the impact resistance and thermal stability of the PVC composites.26
To optimize the performance of CPE/PVC blends, a deep understanding of their thermodynamic compatibility is essential. However, although many experimental studies have explored CPE/PVC blend compatibility, precise control of experimental parameters can be challenging due to their interconnected nature. Computational simulations offer a powerful tool to predict polymer blend miscibility, particularly for systems that are difficult to study experimentally.27–29 For instance, using molecular dynamics simulation, the miscibility in polylactide/polyvinilphenol blends was analyzed.30 Jawalkar et al. employed atomistic MD simulations to investigate the compatibility of poly(vinyl alcohol) and chitosan blends.31 Their simulation results showed good agreement with experimental data, demonstrating the reliability of this approach. Besides, Patnaik et al. studied the miscibility behavior of PMMA/4-n-pentyl-4′-cyanobiphenyl binary mixtures, a blend of polymeric and low molecular weight molecules, using a combination of modified Flory–Huggins theory and molecular simulation techniques.32 Costa et al. investigated the solubility of hydrophobic or hydrophilic polymers in aliphatic cyclohexane, and compared Flory–Huggins interaction parameters (χ12) using three different molecular dynamics simulation approaches.33 Their results indicated that χ12 obtained from the enthalpy of solvation and Gibbs free energy of solvation were more accurate than that calculated from Hildebrand solubility parameters of the pure components.
While significant attention has been directed towards the molecular simulation of polymer blend miscibility, the CPE/PVC blend system remains relatively unexplored. In this study, we employ all-atom molecular dynamics (MD) simulations to investigate the miscibility behavior of CPE/PVC blends, by varying CPE chlorine content and molecular architecture, blend ratio, and temperature. We systematically examine the cohesive energy density (C.E.D.), solubility parameters (δ), Flory–Huggins interaction parameter (χ12), Gibbs free energy (ΔG), and phase diagrams to evaluate the blend compatibility. Notably, some of our simulation results align well with experimental observations. Our findings could provide some guidance on the design and production of CPE/PVC composites in industrial applications.
2 Simulation models and method
2.1 All-atom models
In this work, atomistic models of CPE/PVC blends were constructed using Avogadro software.34 The CPE chains were generated by replacing some hydrogen atoms with chlorine atoms. Each chain consisted of 20 repeat units, sufficient to capture structural and dynamic characteristics of longer chains.33 The total number of atoms in the system was more than 4000. Each chain consisted of 20 repeat units, which is sufficient to capture structural and dynamic characteristics of longer chains, while intentionally excluding the effects of chain entanglement.35 Although certain quantitative values (e.g., C.E.D. and δ) may display some chain-length dependence, we believe the main conclusions of our study in the qualitive and even certain quantitative aspects should remain robust. The chlorine content (Cl wt%) of CPE is defined by
 | (1) |
| No. of Cl atoms per chain | Degree of polymerization | Cl wt% of CPE |
|---|---|---|
| 6 | 20 | 26.9% |
| 7 | 30.0% | |
| 8 | 32.9% | |
| 9 | 35.6% | |
| 10 | 38.0% | |
| 11 | 40.3% | |
| 12 | 42.4% |
To investigate the effects of CPE chain architecture on CPE/PVC miscibility, two CPE types were established in this study, i.e., random CPE (r-CPE) and block CPE (b-CPE), distinguished by their Cl atom distribution along the molecular chain. Fig. 1 illustrates examples of r-CPE and b-CPE chains.
For each modeled system, the COMPASS (Condensed-Phase Optimized Molecular Potentials for Atomistic Simulation Studies) force field37 was employed in the molecular dynamics (MD) simulations. This force field is well-suited for characterizing polymer blending systems and accurately predicting the miscibility properties of polymeric mixtures. The COMPASS force field ensures a high degree of accuracy by comprehensively accounting for the total potential energy, including bond interactions, cross-coupling terms, and non-bond energies. Within the LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) software,38 the COMPASS force field is implemented via the CLASS2 package, which accounts for bonded interactions (bonds, angles, dihedrals, improper) and non-bonded interactions.39 Specifically, the non-bonded interactions are depicted as the summation of van der Waals forces and electrostatic interactions, as given by
| Enon-bond = Evan der Waals + Eelectrostatic | (2) |
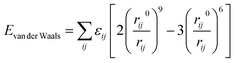 | (3) |
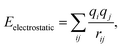 | (4) |
| System no. | No. of PVC chains in composite | PVC wt% | CPE wt% |
|---|---|---|---|
| 1 | 20 | 100% | 0% |
| 2 | 17 | 87.8% | 12.2% |
| 3 | 14 | 74.1% | 25.9% |
| 4 | 10 | 58.9% | 41.1% |
| 5 | 7 | 41.8% | 58.2% |
| 6 | 5 | 30.4% | 69.6% |
| 7 | 4 | 22.3% | 77.7% |
| 8 | 2 | 13.7% | 86.3% |
| 9 | 0 | 0% | 100% |
2.2 Molecular dynamics simulation
All molecular dynamics (MD) simulations were performed using LAMMPS.38 The system was initialized with non-overlapping polymer chain configurations in a large simulation box. Following energy minimization via the steepest descent algorithm, the system was further equilibrated under isothermal–isobaric (NPT) ensemble conditions at a pressure of 0.1 MPa and a temperature of 300 K for a duration of 1 ns. The Nose–Hoover thermostat and barostat42,43 were employed to control temperature and pressure, respectively, while Newtonian equations of motion were integrated using the velocity-Verlet algorithm with a time step of 1 fs. Three-dimensional periodic boundary conditions were applied throughout to reduce the finite-size effects. Fig. 1c and d show some of the simulation systems under equilibrium. After sufficient equilibration, configurations were recorded every 2 ps over an additional 500 ps NPT simulation. To investigate the temperature-dependent miscibility behavior of the CPE/PVC blends (Section 3.3), MD simulations were also conducted across a broader range (250 K, 300 K, 350 K, 400 K, and 450 K), spanning both the glassy and rubbery regimes of PVC (Tg ≈ 370 K). Fig. 2 depicts the evolution of PVC density and system energies as a function of simulation time. It is evident from the figure that the system rapidly reaches equilibrium within the initial 50 ps. In addition, to assess the conformational equilibration at the chain level, the time evolution of the radius of gyration (Rg) was also monitored (Fig. 3). The Rg time series likewise converges quickly to a stable value, indicating that the polymer chains have achieved conformational equilibrium. Together, the convergence of bulk thermodynamic properties and chain conformations corroborates that the systems reach equilibrium on the stated timescale. It should be noted that, unless otherwise specified, all numerical values presented in the tables and principal comparative analysis correspond to the reference temperature of 300 K. | ||
| Fig. 2 Variations in (a) PVC density and (b) system energies as a function of time over the initial 500 ps. | ||
We further validated our simulation results by comparing key parameters, including polymer density (ρ) and solubility parameter (δ), with experimental values, as summarized in Table 3. Experimental reference data for density and solubility parameters are reported at 298 K, whereas all simulation results in this work were obtained at 300 K. As shown, the values of ρ and δ obtained from our MD simulations fall within the ranges reported experimentally. The close agreement between the simulation results and the experimental measurements highlights the reliability and accuracy of our computational approach.
| Polymers | Density (g cm−3) | Solubility parameter (MPa0.5) | ||
|---|---|---|---|---|
| MD simulationsa | Experimentsb | MD simulations | Experiments | |
| a MD simulation data were all obtained at a temperature of 300 K.b Experimental data were obtained at room temperature. | ||||
| b-CPE | 1.301 ± 0.004 | 1.15–1.25 | — | — |
| r-CPE | 1.322 ± 0.004 | 1.15–1.25 | — | — |
| PVC | 1.338 ± 0.005 | 1.34 (ref. 44), 1.35–1.45 | 21.20 ± 0.11 | 23.10 (ref. 45), 21.92 (ref. 36) |
3 Results and discussion
3.1 Effects of CPE chlorine content
 | (5) |
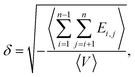 | (6) |
Table 4 summarizes the solubility parameters (δ) of CPE as a function of chlorine content (Cl wt%). To facilitate visual interpretation, Fig. 4 illustrates the corresponding trends in δ for both b-CPE and r-CPE. A consistent increase in δ with rising Cl% is observed for both b-CPE and r-CPE, consistent with findings from prior studies. Notably, r-CPE exhibits a higher δ than b-CPE at equivalent Cl%, suggesting stronger intermolecular interactions in the randomly chlorinated system. At low Cl wt% (e.g., 26.88 wt%), the difference in δ between r-CPE and b-CPE is minimal; however, this disparity grows markedly with increasing Cl wt%. Such a discrepancy is likely attributed to the microphase separation of polar –CH2–CHCl– segments from nonpolar –CH2–CH2– units within the b-CPE polymer, which diminishes the interchain dipole–dipole interactions mediated by Cl atoms. This hypothesis is corroborated by the observed large divergence in electrostatic solubility parameters (Fig. 5), as discussed subsequently.
| Cl wt% | δCPE (MPa0.5) | δPVC (MPa0.5) | |Δδ1|a (MPa0.5) | |Δδ2|b (MPa0.5) | |
|---|---|---|---|---|---|
| b-CPE | r-CPE | ||||
| a |Δδ1| = |δb-CPE − δPVC|.b |Δδ2| = |δr-CPE − δPVC|. | |||||
| 26.9% | 19.39 | 19.41 | 21.20 | 1.81 | 1.79 |
| 30.0% | 19.46 | 19.55 | 1.74 | 1.65 | |
| 32.9% | 19.53 | 19.75 | 1.67 | 1.45 | |
| 35.6% | 19.62 | 19.88 | 1.58 | 1.32 | |
| 38.0% | 19.71 | 19.99 | 1.49 | 1.21 | |
| 40.3% | 19.94 | 20.33 | 1.26 | 0.87 | |
| 42.4% | 19.97 | 20.22 | 1.23 | 0.98 | |
 | ||
| Fig. 4 Changes in (a) solubility parameter (δ) and (b) solubility parameter difference (|Δδ|) as a function of chlorine contents (Cl wt%). | ||
We further compute the absolute solubility parameter differences between CPE and PVC (|Δδ|), enabling direct assessment of their thermodynamic compatibility. Based on Hildebrand's theory, the enthalpy changes of mixing ΔHv can be expressed as
| ΔHm = V0(δ1 − δ2)2ϕ1ϕ2 = V0|Δδ|2ϕ1ϕ2, | (7) |
| δ2 = δd2 + δp2 + δh2, | (8) |
| Cl wt% | δvdw (MPa0.5) | δq (MPa0.5) | ||||
|---|---|---|---|---|---|---|
| PVC | b-CPE | r-CPE | PVC | b-CPE | r-CPE | |
| 26.9% | 18.93 | 18.58 | 18.41 | 8.10 | 3.68 | 4.08 |
| 30.0% | 18.55 | 18.42 | 3.74 | 4.74 | ||
| 32.9% | 18.45 | 18.59 | 4.43 | 4.84 | ||
| 35.6% | 18.56 | 18.63 | 4.33 | 5.16 | ||
| 38.0% | 18.51 | 18.64 | 4.85 | 5.52 | ||
| 40.3% | 18.65 | 18.78 | 5.25 | 6.24 | ||
| 42.4% | 18.55 | 18.68 | 5.65 | 6.12 | ||
Fig. 5 illustrates the dependence of the Hansen solubility parameters on chlorine contents (Cl wt%). Notably, the van der Waals solubility parameters δvdw for both b-CPE and r-CPE exhibit minimal dependent on Cl wt%. Specifically, the δvdw of CPEs remains approximately 18.5 MPa0.5, slightly lower than that of pure PVC, indicating comparable van der Waals contributions to intermolecular interactions. In contrast, the electrostatic solubility parameter δq of CPEs increases markedly and almost linearly with increasing Cl wt%. The δq of CPEs is seen to significantly lower than that of PVC (8.10 MPa0.5), which accounts for the immiscibility behavior between CPE and PVC.
Furthermore, the solubility parameter for r-CPE demonstrates a greater sensitivity to Cl wt% compared to b-CPE, as evidenced by the relationships for δq in r-CPE (δq ∝ 0.161 Cl wt%) and b-CPE (δq ∝ 0.131 Cl wt%). As shown in Fig. 5d, the difference in δq between CPE and PVC decreases substantially with increasing Cl wt%, contributing to the enhanced CPE/PVC miscibility discussed in Section 3.1. It can thus be inferred that the solubility parameters of chlorine-containing vinyl polymers are crucially dependent on their chlorine content and the chlorine distribution, owing to the significant contributions from polar electrostatic interactions.
3.2 Effects of CPE/PVC blend composition
| CPE wt% | δ (MPa0.5) | δvdw (MPa0.5) | δq (MPa0.5) |
|---|---|---|---|
| 0% | 21.20 | 18.93 | 8.10 |
| 12.2% | 20.92 | 18.88 | 7.54 |
| 25.9% | 20.47 | 18.64 | 6.90 |
| 41.1% | 20.31 | 18.65 | 6.42 |
| 58.2% | 20.12 | 18.65 | 5.83 |
| 69.6% | 19.96 | 18.62 | 5.41 |
| 77.7% | 19.72 | 18.52 | 4.88 |
| 86.3% | 19.64 | 18.42 | 4.97 |
| 100% | 19.88 | 18.68 | 6.12 |
Fig. 6 presents the composition dependence of solubility parameters for CPE/PVC blends. It can be found that the Hildebrand solubility parameter δ is decreased with increasing CPE wt% in a modest behavior. This trend primarily reflects the behavior of the electrostatic component (δq), which decreases significantly with increasing CPE content, consistent with our earlier findings highlighting the chlorine-mediated intermolecular interactions in chlorine-containing vinyl polymers. In contrast, the van der Waals component (δvdw) shows negligible compositional dependence.
Notably, the electrostatic solubility parameter δq demonstrates a distinct upturn at CPE concentrations above ∼80 wt%, suggesting enhanced blend compatibility in this regime. We attribute this behavior to intensified polar Cl–Cl interactions between dispersed PVC chains within the CPE matrix. This interpretation is further supported by the free energy analysis and phase behavior presented in Section 3.3, which confirms improved miscibility at high CPE loadings.
 | (9) |
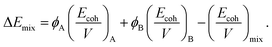 | (10) |
Here, the subscripts A, B, and mix denote CPE, PVC, and their blend, respectively; ϕA and ϕB are the volume fractions of the two polymers. The calculated Flory–Huggins interaction parameters for CPE/PVC blends are given in Table 7.
| CPE wt% | χ12 | χcr |
|---|---|---|
| 12.2% | 0.07 | 0.15 |
| 25.9% | 0.27 | 0.15 |
| 41.1% | 0.22 | 0.15 |
| 58.2% | 0.18 | 0.15 |
| 69.6% | 0.17 | 0.15 |
| 77.7% | 0.26 | 0.15 |
| 86.3% | 0.13 | 0.15 |
In theory, lower (negative) χ12 values indicate favorable miscibility, whereas higher values denote thermodynamic incompatibility and a propensity for phase separation. To predict the miscibility of polymer blends more accurately, the critical Flory–Huggins parameter, χcr, is calculated as follows,
 | (11) |
Fig. 7 illustrates the calculated χ12 parameters of CPE/PVC blends as a function of CPE content. It is evident that the χ12 values of polymer blends with approximately 20–80 wt% CPE lie above the critical χcr line, indicating immiscible behavior. Specifically, when CPE content ranges from approximately 60–80 wt%, the χ12 values are seen to be slightly larger than χcr, potentially suggesting partial miscibility of the CPE/PVC blends. Furthermore, as anticipated, CPE/PVC blends with a predominant proportion of either CPE or PVC (i.e., close to the pure polymer) exhibit miscibility, as evidenced by their relatively small χ12 values, which fall below χcr in Fig. 7.
3.3 Effects of temperature
| T (K) | δPVC (MPa0.5) | δb-CPE (MPa0.5) | δr-CPE (MPa0.5) | |Δδ1|a (MPa0.5) | |Δδ2|b (MPa0.5) | χ12 of b-CPE/PVC | χ12 of r-CPE/PVC |
|---|---|---|---|---|---|---|---|
| a |Δδ1| = |δb-CPE − δPVC|.b |Δδ2| = |δr-CPE − δPVC|. | |||||||
| 250 | 21.18 | 20.31 | 20.48 | 0.87 | 0.70 | 0.21 | 0.13 |
| 300 | 21.26 | 20.13 | 20.31 | 1.13 | 0.95 | 0.34 | 0.24 |
| 350 | 21.24 | 20.18 | 20.27 | 1.06 | 0.97 | 0.31 | 0.25 |
| 400 | 21.18 | 19.92 | 20.17 | 1.26 | 1.01 | 0.43 | 0.28 |
| 450 | 20.96 | 19.81 | 19.80 | 1.15 | 1.14 | 0.36 | 0.35 |
As illustrated in Fig. 8, which plots solubility parameters against blending temperature, both PVC and CPE exhibit a marked decrease in δ with increasing temperature. Specifically, the solubility parameter for both b-CPE and r-CPE shows an almost linear decrease with temperature. This observation aligns well with earlier work on the temperature dependence of solubility parameters for amorphous polymers.49,50
 | ||
| Fig. 8 (a) Solubility parameter (δ) and (b) solubility parameter difference (|Δδ|) as a function of blending temperature. | ||
Within the framework of free volume theory, the temperature dependence of solubility parameters can be described by two distinct regimes.51,52 Below the glass transition temperature (Tg), the solubility parameter δ can be described by:
| δ(T) = αg(T − Tg) + δg, | (12) |
| δ(T) = αr(T − Tg) + δg, | (13) |
| δ(T) = −0.0023 × T + 20.85, | (14) |
| δ(T) = −0.0032 × T + 21.32, | (15) |
for T ≤ Tg,
| δ(T) = −0.00069 × (T − 370.03) + 21.19 | (16) |
for T ≥ Tg,
| δ(T) = −0.0027 × (T − 370.03) + 22.19 | (17) |
These expressions predict thermal expansion coefficients of solubility parameter equal to −0.00069 (MPa0.5 T−1) in the glassy state and −0.0027 (MPa0.5 T−1) in the rubbery state, indicating a significantly enhanced temperature sensitivity above Tg. Although the thermal expansion coefficients (α) reported here are derived from the temperature dependence of solubility parameter δ(T), with no direct experimental validation of α performed, the predicted values and their qualitative behavior should be physically reasonable and indeed consistent with established literature58,59 on PVC.
Furthermore, as shown in Fig. 8b, the difference in solubility parameters (Δδ) between CPE and PVC increase substantially with rising temperature, suggesting a remarkable reduction in the miscibility of the CPE/PVC blend. Notably, under identical thermal conditions, r-CPE demonstrates superior compatibility with PVC compared to b-CPE across the entire temperature ranged studied, as evidenced by consistently lower Δδ values.
 | (18) |
 | ||
| Fig. 9 Temperature dependence of Flory–Huggins interaction parameters (χ12) for CPE/PVC blends with CPEs containing 35.6 wt% chlorine: (a) χ12 as a function of temperature (T), and (b) χ12 versus reciprocal temperature (1/T) for the application of eqn (19). | ||
Fig. 9a presents the Flory–Huggins interaction parameters (χ12) for CPE/PVC blends as a function of temperature. Both b-CPE/PVC and r-CPE/PVC blends exhibit increasing χ12 values with rising temperature, indicting a progressive decline in miscibility. This behavior can be attributed to the enhanced molecular motion at higher temperatures, which intensifies chain mobility and softens the polymer chains, thereby weakening intermolecular electrostatic interactions and diminishing the compatibility between the CPE and PVC components.
Notably, at the lowest examined temperature of 250 K, the value for the r-CPE/PVC blend falls below the critical threshold of the Flory–Huggins parameter line (χcr = 0.15), suggesting the onset of miscibility under such conditions.
The temperature dependence of χ12 can be reliably described by the following equation:60,61
 | (19) |
For b-CPE/PVC blend,
 | (20) |
For r-CPE/PVC blend,
 | (21) |
According to the results, a homogenous phase is expected to emerge upon cooling for both CPE/PVC blends, given that A > 0 and B < 0. However, the phase behavior of r-CPE/PVC blends is found to be more sensitive to blending temperature compared to that of b-CPE/PVC blends.
3.4 Phase diagram analysis
 | (22) |
For our simulated CPE/PVC models with equal chain lengths (nA = nB = 20), the free energy curves exhibit symmetric profiles. As the temperature decreases, the free energy of mixing transitions from positive into negative values, indicating enhanced compatibility. Since the entropic contribution always increases with temperature, the observed improvement in CPE/PVC miscibility at lower temperatures must be attributed to the enthalpic component, reflecting the growing significance of attractive chlorine-mediated intermolecular interactions.
Moreover, the free energy curves evolve from convex to concave shapes at sufficiently low temperatures (e.g., 150 K for b-CPE/PVC blend or 200 K for r-CPE/PVC blend), implying that all blend compositions are thermodynamically stable, as indicated by a negative second derivative of the free energy of mixing. Actually, this scenario corresponds to values of Flory–Huggins interaction parameters than fall below the critical threshold (χ12 < χcr). By the way, the Gibbs free energy may overestimate the miscibility (χ12) for non-polar polymers.33
 | (23) |
 , is determined and depicted as the dashed red curve in Fig. 11. Within this region, slight fluctuations in composition will grow spontaneously, leading to phase separation without an energy barrier.
, is determined and depicted as the dashed red curve in Fig. 11. Within this region, slight fluctuations in composition will grow spontaneously, leading to phase separation without an energy barrier.
However, phase separations via binodal mechanisms (nucleation and growth) may also occur within the locally stable regime where the second derivative of free energy of mixing is positive  if composition fluctuations is sufficiently large to nucleate a new phase (a domain of critical size). The binodal curve, which marks the boundary between coexisting phases, is determined by the condition that the first derivative of free energy of mixing is equal to zero:
if composition fluctuations is sufficiently large to nucleate a new phase (a domain of critical size). The binodal curve, which marks the boundary between coexisting phases, is determined by the condition that the first derivative of free energy of mixing is equal to zero:
 | (24) |
The binodal curve is plotted as the solid black line in the phase diagram (Fig. 12). Consequently, the region bounded by the binodal and spinodal curves corresponds to the metastable regime, where phase separation may proceed via nucleation-driven processes.
 | ||
| Fig. 12 Representative equilibrium snapshots of the r-CPE/PVC blend with 58.2 wt% r-CPE (35.6 wt% Cl) at (a) 300 K and (b) 160 K. The PVC chains are rendered in blue, and the r-CPE chains in red. | ||
As shown in Fig. 11, both CPE/PVC binary systems exhibit a lower critical solution temperature (LCST) behavior, consistent with the earlier observations derived from the solubility parameters and Flory–Huggins interaction parameters. Specifically, CPE/PVC blends of certain compositions may undergo phase separation into two phases at elevated temperatures, while upon cooling, they form a single, thermodynamically stable phase.
Below the LCST temperature (Tcr), the CPE/PVC systems can be prepared as stable homogenous mixtures across all compositions. For our simulated CPE/PVC systems, the b-CPE/PVC blends exhibit a Tcr of approximately 184.43 K, while r-CPE/PVC blends show a higher Tcr of approximately 229.36 K. These results indicate that the r-CPE demonstrates superior miscibility with PVC compared to b-CPE under identical conditions of temperature and blend composition.
To provide a direct validation of the calculated phase diagram, the simulation snapshots corresponding to T = 300 K and T = 160 K for the r-CPE/PVC system (at 35.6 wt% Cl and 58.2 wt% CPE) are further compared in Fig. 12. It can be seen that at the higher temperature of 300 K within the two-phase region of the phase diagram (Fig. 11b), the r-CPE and PVC chains are clearly segregated into aggregated domains, demonstrating the phase separation. In contrast, at the temperature of 160 K below the LCST temperature Tcr, the polymer chains are observed to be more dispersed across the whole simulation box, indicating the well-mixed state. Such phenomenon is consistent with the LCST behavior previously identified for the CPE/PVC blend system, and thus directly corroborates the validity of our predicted phase diagrams shown in Fig. 11.
4 Conclusion
In this study, all-atom molecular dynamics simulations are employed to systematically investigate the effects of CPE chlorine content, molecular architecture, blend composition, and temperature on the miscibility of CPE/PVC binary systems. CPE chains with varying chlorine contents (Cl wt%) and distinct structural configurations—characterized by random versus block distributions of Cl atoms—are considered. The blend miscibility behavior is characterized using Hildebrand and Hansen solubility parameters (δ), Flory–Huggins interaction parameters (χ12) and phase diagrams. The simulation results reveal that the overall δ for both CPEs are increased with Cl wt% within the investigated range. Such a trend is primary driven by electrostatic interactions (δq) arising from polar Cl–Cl interactions, while the van der Waals contributions (δvdw) remains largely independent of Cl wt%. Compared to b-CPE, r-CPE exhibits higher values of δvdw and consequently larger Hildebrand δ, which is mainly attributed to the fact that in b-CPE, polar –CH2–CHCl– segments tend to segregate from nonpolar –CH2–CH2– units, thereby reducing interchain dipole–dipole interactions mediated by Cl atoms. Moreover, the dependence of χ12 on Cl wt% suggests that polymer blends containing approximately 20–80 wt% CPE are thermodynamically immiscible at 300 K, as demonstrated by the χ12 values falling below the critical miscibility threshold (χcr = 0.15 in the present simulations), whereas CPE/PVC blends with a predominant proportion of either CPE or PVC exhibit miscibility. The δ for both CPEs and PVC are found to decrease with increasing temperature.Our simulation results also demonstrate that the χ12 of CPE/PVC blends increase with temperature (T), indicating reduced miscibility at elevated temperatures. A quantitative χ12–T relationship is established, revealing that the phase behavior of r-CPE/PVC blends is more sensitive to temperature changes than that of b-CPE/PVC blends. The free energy of mixing is also computed, showing that both CPE/PVC systems undergo a transition from convex to concave profile upon cooling, further supporting the enhanced CPE/PVC miscibility at lower temperatures. Phase diagrams confirm that CPE/PVC binary systems exhibit a low critical solution temperature (LCST) behavior, delineating the binodal and spinodal decomposition curves along with the associated metastable region. Notably, the r-CPE/PVC system displays a higher critical temperature of Tcr ≃ 229.36 K, compared to b-CPE/PVC blend with Tcr ≃ 184.43 K. Our simulation results show good agreement with experimental data regarding polymer density and solubility parameters, validating the accuracy of our simulation model, forcefield and computational methodology. In conclusion, we believe that our simulation work provides a comprehensive understanding of these factors governing CPE/PVC miscibility and offers valuable guidance for the design and fabrication of CPE/PVC composite materials.
Author contributions
Zhihao Ma: methodology, investigation, simulation, data collection, analysis, and writing – original draft; Xue Li: validation, supervision, and funding acquisition; Huaguo Xu: formal analysis and validation; Jianxiang Shen: conceptualization, supervision, project administration, funding acquisition, and writing – review & editing; Jun Liu: conceptualization, formal analysis, and validation.Conflicts of interest
The authors declare no competing interest.Data availability
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.Acknowledgements
This work is financially supported by the National Natural Science Foundation of Zhejiang Province, China (LY24E030001), the National Natural Science Foundation of China (52203091), the Science and Technology Research Projects of Jiaxing City, Zhejiang Province (2024AY10046), the opening Foundation of State Key Laboratory of Organic–Inorganic Composites, Beijing University of Chemical Technology (oic-202401009), and Jiaxing University Graduate Research, Practice, and Innovation Program (PSRPIP2024003C). Computations were performed at the Wuzhen Supercomputer Center of China.References
- A. Al Alshaikh and J. E. Bara, Chlorinated plastics offer unique opportunities and challenges in upcycling, Polym. Int., 2024, 73(5), 341–348 CrossRef CAS.
- Y. Saeki and T. Emura, Technical progresses for PVC production, Prog. Polym. Sci., 2002, 27(10), 2055–2131 CrossRef CAS.
- A. K. Hussein, E. Yousif, M. K. Rasheed, G. I. Edo, M. Bufaroosha and H. Umar, Synthesis, Modification, and Applications of Poly(vinyl chloride) (PVC), Polym.-Plast. Technol. Mater., 2024, 64(5), 593–632 Search PubMed.
- G. I. Edo, W. Ndudi, A. B. M. Ali, E. Yousif, K. Zainulabdeen, P. N. Onyibe, H. A. Ekokotu, E. F. Isoje, U. A. Igbuku, A. E. A. Essaghah, D. S. Ahmed, H. Umar and D. U. Ozsahin, Poly(vinyl chloride) (PVC): an updated review of its properties, polymerization, modification, recycling, and applications, J. Mater. Sci., 2024, 59(47), 21605–21648 CrossRef CAS.
- J. Leadbitter, PVC and sustainability, Prog. Polym. Sci., 2002, 27(10), 2197–2226 CrossRef CAS.
- K. Lewandowski and K. Skórczewska, A Brief Review of Poly(Vinyl Chloride) (PVC) Recycling, Polymers, 2022, 14(15), 3035 Search PubMed.
- J. Chu, Y. Zhou, Y. Cai, X. Wang, C. Li and Q. Liu, Life-cycle greenhouse gas emissions and the associated carbon-peak strategies for PS, PVC, and ABS plastics in China, Resour., Conserv. Recycl., 2022, 182, 106295 CrossRef CAS.
- A. Alshaikh, S. Ezendu, D. Ryoo, P. S. Shinde, J. L. Anderson, T. Szilvási, P. A. Rupar and J. E. Bara, PVC Modification through Sequential Dehydrochlorination–Hydrogenation Reaction Cycles Facilitated via Fractionation by Green Solvents, ACS Appl. Polym. Mater., 2024, 6(16), 9656–9662 Search PubMed.
- P. W. Skelly, L. Li and R. Braslau, Internal plasticization of PVC, Polym. Rev., 2021, 62(3), 485–528 CrossRef.
- M. Khaleghi, Investigation of thermal and mechanical properties of new nitrogen-rich organic based heat stabilizers for poly (vinyl chloride), J. Thermoplast. Compos. Mater., 2024, 37(4), 1480–1498 CrossRef CAS.
- J. Guo, Y. Li, S. Song, S. Tan, S. Zhao, L. Li and H. Wang, The effects of ACR/MAH ionic cross-linking on the cell morphology, mechanical properties, and dimensional stability of PVC foams, Polym. Degrad. Stab., 2024, 229, 110946 Search PubMed.
- P. R. Kubade and R. Senanayake, Studies on thermo-mechanical properties of HNTs filled ABS/PVC composites, Mater. Today: Proc., 2022, 59, 248–252 CAS.
- P. R. Kubade and R. Senanayake, Thermo-mechanical properties of polyethyleneimine (PEI) modified HNTs filled ABS/PVC composites, Mater. Today: Proc., 2022, 59, 852–857 CAS.
- Y. Komori, A. Taniguchi, H. Shibata, S. Goto and H. Saito, Partial Miscibility and Concentration Distribution of Two-Phase Blends of Crosslinked NBR and PVC, Polymers, 2023, 15(6), 1383 CrossRef CAS.
- C. Thoral, G. Soulagnet, P.-O. Bussiere and S. Therias, Impact of photo- and thermooxidative ageing of NBR/PVC blends on the formation of cracks, Polym. Degrad. Stab., 2024, 220, 110633 Search PubMed.
- S. N. Maiti, U. K. Saroop and A. Misra, Studies on polyblends of poly(vinyl chloride) and acrylonitrile-butadiene-styrene terpolymer, Polym. Eng. Sci., 1992, 32(1), 27–35 CrossRef CAS.
- H.-R. Jung and W.-J. Lee, Electrochemical characteristics of electrospun poly(methyl methacrylate)/polyvinyl chloride as gel polymer electrolytes for lithium ion battery, Electrochim. Acta, 2011, 58, 674–680 CrossRef CAS.
- C. Zhou, S. Wu, H. Liu and G. Wu, Effects of core-shell particle growth manners on morphologies and properties of poly(vinyl chloride)/(methyl methacrylate-butadiene-styrene) blends, J. Vinyl Addit. Technol., 2016, 22(1), 37–42 CrossRef CAS.
- L. Liu, M. Chen, R. J. Dai, S. L. Sun, C. Zhou, H. D. Yang and H. X. Zhang, Toughness and Transparency of Poly(vinyl chloride)/Methyl Methacrylate-Butadiene-Styrene Blends with Varied Shell Phase Composition of Core-Shell Theories, Polym.-Plast. Technol. Eng., 2009, 48(9), 953–957 CrossRef CAS.
- J. Li, S.-H. Jin, G.-C. Lan, Z.-S. Xu, L.-T. Wang, N. Wang and L.-J. Li, Research on the Glass Transition Temperature and Mechanical Properties of Poly(vinyl chloride)/Dioctyl Phthalate (PVC/DOP) Blends by Molecular Dynamics Simulations, Chin. J. Polym. Sci., 2019, 37(8), 834–840 CrossRef CAS.
- F. You, G. Chen, J. Zou, Z. Yang and S. Guo, The experimental results and simulation of temperature dependence of brittle-ductile transition in PVC/CPE blends and PVC/CPE/nano-CaCO3 composites, J. Appl. Polym. Sci., 2012, 123(3), 1833–1842 Search PubMed.
- J. Mnyango, L. Bolo, B. Fouda-Mbanga, Z. Tywabi-Ngeva, Y. Nthwane, K. Pillay, P. Ndibewu and S. Hlangothi, Advances in Chlorinated Polyethylene: Properties, Applications, and Future Directions, J. Appl. Polym. Sci., 2025, e57526 CrossRef CAS.
- B.-M. Quenum, P. Berticat and G. Vallet, Chlorinated Polyethylene. III. Relationships of Microstructure and Thermal Properties, Polym. J., 1975, 7(3), 300–311 CrossRef CAS.
- X. Xie, W. Li and Y. Wei, Effect of Blending Modification on Tensile Performance of CPE/PVC, Adv. Mater. Res., 2011, 1732–1735 Search PubMed.
- D. R. Paul and C. E. Locke, Chlorinated polyethylene modification of blends derived from waste plastics Part I: Mechanical behavior, Polym. Eng. Sci., 1973, 13(3), 202–208 CrossRef CAS.
- Y. Zhang, C. Ding, N. Zhang, H. Li, Y. Zhang, B. Deng and Y. Zhang, Contributions of TCA-KTTO-modified quartz tailings and CPE toughener in PVC composites to enhance the mechanical-thermal performance, Chem. Eng. J., 2024, 495, 153166 Search PubMed.
- A. Ahmadi and J. J. Freire, Molecular dynamics simulation of miscibility in several polymer blends, Polymer, 2009, 50(20), 4973–4978 CrossRef CAS.
- S. S. Jawalkar and T. M. Aminabhavi, Molecular modeling simulations and thermodynamic approaches to investigate compatibility/incompatibility of poly(l-lactide) and poly(vinyl alcohol) blends, Polymer, 2006, 47(23), 8061–8071 Search PubMed.
- S. Patel, A. Lavasanifar and P. Choi, Application of Molecular Dynamics Simulation To Predict the Compatability between Water-Insoluble Drugs and Self-Associating Poly(ethylene oxide)-b-poly(ε-caprolactone) Block Copolymers, Biomacromolecules, 2008, 9(11), 3014–3023 CrossRef CAS PubMed.
- I. Martinez de Arenaza, E. Meaurio, B. Coto and J.-R. Sarasua, Molecular dynamics modelling for the analysis and prediction of miscibility in polylactide/polyvinilphenol blends, Polymer, 2010, 51(19), 4431–4438 Search PubMed.
- S. Jawalkar, R. V. Kothapalli, S. Halligudi, M. Sairam and T. Aminabhavi, Molecular Modeling Simulations to Predict Compatibility of Poly(vinyl alcohol) and Chitosan Blends: A Comparison with Experiments, J. Phys. Chem. B, 2007, 111, 2431–2439 Search PubMed.
- S. S. Patnaik and R. Pachter, A molecular simulations study of the miscibility in binary mixtures of polymers and low molecular weight molecules, Polymer, 2002, 43(2), 415–424 CrossRef CAS.
- G. P. Costa, S. R. Stoyanov, Q. Liu and P. Choi, Solubility of selected polymers in cyclohexane: comparison between Flory–Huggins interaction parameters calculated using three different molecular dynamics simulation approaches, Phys. Chem. Chem. Phys., 2024, 26(47), 29628–29639 RSC.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4(1), 17 CAS.
- F. V. Olowookere, A. Al Alshaikh, J. E. Bara and C. H. Turner, Effects of chain length on the structure and dynamics of polyvinyl chloride during atomistic molecular dynamics simulations, Mol. Simul., 2023, 49(15), 1401–1412 CrossRef CAS.
- J.-C. Huang, Miscibility of PVC with chlorinated PE and chlorinated PVC, Int. J. Polym. Mater., 2003, 52(8), 673–683 CrossRef CAS.
- H. Sun, P. Ren and J. R. Fried, The COMPASS force field: parameterization and validation for phosphazenes, Comput. Theor. Polym. Sci., 1998, 8(1), 229–246 Search PubMed.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- M. Hadipeykani, F. Aghadavoudi and D. Toghraie, A molecular dynamics simulation of the glass transition temperature and volumetric thermal expansion coefficient of thermoset polymer based epoxy nanocomposite reinforced by CNT: a statistical study, Phys. A, 2020, 546, 123995 CrossRef CAS.
- J. Shen, X. Li, P. Li and B. Shentu, Exploring thermodynamic and structural properties of carbon nanotube/thermoplastic polyurethane nanocomposites from atomistic molecular dynamics simulations, RSC Adv., 2023, 13(30), 21080–21087 RSC.
- J. Shen, X. Li, P. Li and B. Shentu, Structural and dynamical properties of thermoplastic polyurethane/fullerene nanocomposites: a molecular dynamics simulations study, Phys. Chem. Chem. Phys., 2023, 25(40), 27352–27363 RSC.
- S. Nosé, A molecular dynamics method for simulations in the canonical ensemble, Mol. Phys., 2002, 100(1), 191–198 CrossRef.
- H. C. Andersen, Molecular dynamics simulations at constant pressure and/or temperature, J. Chem. Phys., 1980, 72(4), 2384–2393 CrossRef CAS.
- E. Fekete and B. Pukánszky, Effect of molecular interactions on the miscibility and structure of polymer blends, Eur. Polym. J., 2005, 41(4), 727–736 CrossRef CAS.
- J.-C. Huang and R. D. Deanin, Multicomponent solubility parameters of poly (vinyl chloride) and poly (tetramethylene glycol), Fluid Phase Equilib., 2005, 227(1), 125–133 CrossRef CAS.
- C. M. Hansen in Hansen Solubility Parameters : A User's Handbook, 2nd edn, 2007 Search PubMed.
- D. P. Faasen, A. Jarray, H. J. Zandvliet, E. S. Kooij and W. Kwiecinski, Hansen solubility parameters obtained via molecular dynamics simulations as a route to predict siloxane surfactant adsorption, J. Colloid Interface Sci., 2020, 575, 326–336 Search PubMed.
- M. Rubinstein. and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- G. P. Costa, P. Choi, S. R. Stoyanov and Q. Liu, The temperature dependence of the Hildebrand solubility parameters of selected hydrocarbon polymers and hydrocarbon solvents: a molecular dynamics investigation, J. Mol. Model., 2024, 30(7), 196 Search PubMed.
- X. Chen, C. Yuan, C. K. Wong and G. Zhang, Molecular modeling of temperature dependence of solubility parameters for amorphous polymers, J. Mol. Model., 2012, 18(6), 2333–2341 Search PubMed.
- K. Chee, Temperature dependence of solubility parameters of polymers, Malays. J. Chem., 2005, 7, 57–61 Search PubMed.
- N. Tanaka, Prediction of solubility parameter from thermal transition behaviour in polymers, Polymer, 1992, 33(3), 623–626 CrossRef CAS.
- T. Sterzyński, J. Tomaszewska, J. Andrzejewski and K. Skorczewska, Evaluation of glass transition temperature of PVC/POSS nanocomposites, Compos. Sci. Technol., 2015, 117, 398–403 CrossRef.
- T. Sterzyński, J. Tomaszewska, K. Piszczek and K. Skórczewska, The influence of carbon nanotubes on the PVC glass transition temperature, Compos. Sci. Technol., 2010, 70(6), 966–969 Search PubMed.
- A. F. Behbahani, S. M. Vaez Allaei, G. H. Motlagh, H. Eslami and V. A. Harmandaris, Structure, dynamics, and apparent glass transition of stereoregular poly (methyl methacrylate)/graphene interfaces through atomistic simulations, Macromolecules, 2018, 51(19), 7518–7532 CrossRef CAS.
- A. Soldera and N. Metatla, Glass transition of polymers: Atomistic simulation versus experiments, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74(6), 061803 CrossRef PubMed.
- N. Metatla and A. Soldera, Computation of densities, bulk moduli and glass transition temperatures of vinylic polymers from atomistic simulation, Mol. Simul., 2006, 32(14), 1187–1193 CrossRef CAS.
- C. Wang, V. Kondrashchenko and A. Matseevich, Prediction of the coefficient of thermal expansion of building materials based on polyvinyl chloride,, J. Phys.: Conf. Ser., 2019, 012094 CAS.
- H. Jayanna and S. Subramanyam, Thermal expansion of irradiated polyvinyl chloride from 10 K to 340 K, Polym. Bull., 1992, 28(4), 481–487 CrossRef CAS.
- C. B. Potter, M. T. Davis, A. B. Albadarin and G. M. Walker, Investigation of the dependence of the Flory–Huggins interaction parameter on temperature and composition in a drug–polymer system, Mol. Pharm., 2018, 15(11), 5327–5335 Search PubMed.
- A. J. Nedoma, M. L. Robertson, N. S. Wanakule and N. P. Balsara, Measurements of the composition and molecular weight dependence of the Flory−Huggins interaction parameter, Macromolecules, 2008, 41(15), 5773–5779 CrossRef CAS.
- J. M. Tesha, Molecular Dynamics Simulation of Polysulfone and Polystyrene-co-maleic Anhydride Blends Compatibility: A mesoscopic, Ewald Approach and Experimental Comparison, Research Square, 2021, preprint, DOI:10.21203/rs.3.rs-1109742/v1.
| This journal is © The Royal Society of Chemistry 2026 |







